1 Introduction

The stability theory has proven to be a versatile and effective tool in comprehending the behaviour of solutions in differential equations in recent years. Over the last few decades, the theory of dynamic equations on time scales has played a pivotal role in bridging the gap between difference and differential equations [2]. Notably, significant results on uniform global asymptotic stability in differential equations [22] and difference equations [6] were extended to the theory of dynamic equations by Wu and Zou in their work [20] (also discussed in [10]). In this direction, Braverman and Karpuz [4] unified the results for differential equations [15] and for difference equations [7]. While some studies in the time scale literature have generalized classical forms like difference equations, q-difference equations, and differential equations, it is essential to note that extending results from these fields to dynamic equations is not always straightforward. In some cases, this process necessitates the development of new tools within the framework of time scale calculus.

Let us now start introducing the objective of this paper. In 1994, Yu and Cheng [21] presented a general form of the following stability test for neutral difference equations with delay.

Theorem A

(Cf. [21, Theorem 2]) Suppose that \(\{p_{n}\}_{n=0}^{\infty }\) is a nonnegative sequence and \(\tau \) is a nonnegative integer such that

$$\begin{aligned} \sum _{j=0}^{\infty }p_{j}=\infty \quad \text {and}\quad \limsup _{n\rightarrow \infty }\sum _{j=n}^{n+2\tau }p_{j}<2. \end{aligned}$$

Then, the trivial solution of

$$\begin{aligned} x(n+1)-x(n)+p(n)x(n-\tau )=0\quad \text {for}\ n\in \mathbb {N}_{0} \end{aligned}$$

is globally attracting.

A continuous counterpart of Theorem A for neutral differential equations with positive and negative coefficients is considered by Shen and Yu. They have obtained the following result as corollaries of their more general main result.

Theorem B

[19, Corollary 1 and Corollary 2] Suppose that \(p\in \textrm{C}([0,\infty ),[0,\infty ))\) and \(\tau \ge 0\) such that

$$\begin{aligned} \int _{0}^{\infty }p(\xi )\textrm{d}\xi =\infty \quad \text {and}\quad \limsup _{n\rightarrow \infty }\int _{t}^{t+2\tau }p(\xi )\textrm{d}\xi <2. \end{aligned}$$

Then, the trivial solution of

$$\begin{aligned} x^{\prime }(t)+p(t)x(t-\tau )=0\quad \text {for}\ t\in [0,\infty ) \end{aligned}$$

is globally attracting.

It is a natural question to ask if Theorems A and B can be generalized to time scales for linear delay dynamic equations. In this work, we aim to give a positive answer to this question. However, the proofs on time scales require very technical computations, which may lead to some expansions in the field of dynamic equations.

In this paper, we consider the linear delay dynamic equation

$$\begin{aligned} x^{\Delta }(t)+p(t)x\bigl (\tau (t)\bigr )=0\quad \text {for}\ t\in [t_{0},\infty )_{\mathbb {T}}, \end{aligned}$$
(1)

where \(\mathbb {T}\) is a time scale unbounded above, \(p\in \textrm{C}_{\textrm{rd}}([t_{0},\infty )_{\mathbb {T}},[0,\infty )_{\mathbb {T}})\) and \(\tau \) satisfies the following two conditions.

  1. (C1)

    \(\tau \in \textrm{C}_{\textrm{rd}}([t_{0},\infty )_{\mathbb {T}},\mathbb {R})\) satisfies \(\tau (t)\le {}t\) for all \(t\in [t_{0},\infty )_{\mathbb {T}}\) and \(\lim _{t\rightarrow \infty }\tau (t)=\infty \).

  2. (C2)

    \(\tau \in \textrm{C}_{\textrm{rd}}^{1}([t_{0},\infty )_{\mathbb {T}},\mathbb {R})\) satisfies \(\tau ^{\Delta }(t)>0\) for all \(t\in [t_{0},\infty )_{\mathbb {T}}\) and \(\tau (\mathbb {T})=\mathbb {T}\).

Due to (C2), \(\tau ^{-1}:\mathbb {T}\rightarrow \mathbb {T}\) exists. Let us define \(t_{-1}:=\inf \{\tau (t),\ t\in [t_{0},\infty )_{\mathbb {T}}\}\), which is a finite value by (C1).

Next, we have two definitions for the completeness of the structure of the paper.

Definition 1

(Solution) A function \(x:[t_{-1},\infty )_{\mathbb {T}}\rightarrow \mathbb {R}\), which is rd-continuous on \([t_{-1},t_{0}]_{\mathbb {T}}\) and \(\Delta \)-differentiable on \([t_{0},\infty )_{\mathbb {T}}\) with an rd-continuous derivative, is called a solution of (1) provided that it satisfies the equality (1) identically on \([t_{0},\infty )_{\mathbb {T}}\).

Definition 2

(Globally Attractivity) The trivial solution of (1) is said to be globally attracting if any solution x of (1) satisfies \(\lim _{t\rightarrow \infty }x(t)=0\).

We mention here the papers [6,7,8, 14] and [12, 13, 15, 16, 19, 22,23,24], which deal with asymptotic behaviour of difference equations and differential equations, respectively. We also refer the readers to the papers [1, 3, 5, 9, 10, 17, 18] for a discussion on asymptotic behaviour of solutions of dynamic equations on time scales.

The paper is organized as follows. In Sect. 2, we state our main theorem, which generalizes Theorems A and B to time scales. Section 3 includes auxiliary lemmas required in the proof of the main theorem. The proof of the main theorem is given in Sect. 4. In Sect. 5, there are two numerical examples illustrating applicability and importance of the main result. Section 6 is dedicated to conclusions. Finally, in Appendices A and B, we give some basic results on time scales required in the proofs of our lemmas.

2 Main Result

The main result of the paper is presented below.

Theorem 1

Assume (C1), (C2),

$$\begin{aligned} \int _{t_0}^{\infty }p(\xi )\Delta \xi =\infty , \end{aligned}$$
(2)

and

$$\begin{aligned} \limsup _{t\rightarrow \infty }\int _{t}^{\tau ^{-2}(\sigma (t))}p(\xi )\Delta \xi <2. \end{aligned}$$
(3)

Then, the trivial solution of (1) is globally attracting.

3 Preparatory Lemmas

The main result is motivated by the following important observations.

Lemma 1

If (C1) and (2) hold, then every convergent solution of (1) tends to zero.

Proof

Let x be a solution of (1), which tends to some constant \(\ell \in \mathbb {R}\). If \(\ell \ne 0\), we may assume without loss of generality that \(\ell >0\). Then, we can find \(t_{1}\in [t_{0},\infty )_{\mathbb {T}}\) such that \(x(t),x(\tau (t))>\frac{\ell }{2}>0\) for all \(t\ge {}t_{1}\). In view of (1), we see that

$$\begin{aligned} x^{\Delta }(t)=-p(t)x(\tau (t)) \le -\frac{\ell }{2}p(t) \end{aligned}$$
(4)

for \(t\in [t_{1},\infty )_{\mathbb {T}}\). Due to (2), there exists a sufficiently large \(t_{2}\in [t_{1},\infty )_{\mathbb {T}}\) such that

$$\begin{aligned} \int _{t_{1}}^{t_{2}}p(\xi )\Delta \xi >\frac{2}{\ell }x(t_{1}). \end{aligned}$$
(5)

By integrating (4), and then using (5), we see that

$$\begin{aligned} x(t_{2})\le {}x(t_{1})-\frac{\ell }{2}\int _{t_{1}}^{t_{2}}p(\xi )\Delta \xi <0. \end{aligned}$$

This contradiction completes the proof. \(\square \)

In the next result, we will define a companion function to get some information on the solutions of (1).

Lemma 2

Suppose that (C1) and (C2) hold. Let x be a solution of (1), and define the companion function

$$\begin{aligned} y(t):=x(t)-\int _{t}^{\tau ^{-1}(t)}p(\xi )x\bigl (\tau (\xi )\bigr )\Delta \xi \quad \text {for}\ t\in [t_{0},\infty )_{\mathbb {T}}. \end{aligned}$$
(6)

If y converges to some value, then x also converges to the same value.

Proof

Suppose x is a solution of (1) and y defined by (6) converges to \(\ell \). We will show that x converges to \(\ell \). It follows that

$$\begin{aligned} y^{\Delta }(t)={}&x^{\Delta }(t)-\bigl [\bigl (\tau ^{-1}\bigr )^{\Delta }(t)p\bigl (\tau ^{-1}(t)\bigr )x(t) -p(t)x(\tau (t))\bigr ]\nonumber \\ ={}&x^{\Delta }(t)+p(t)x(\tau (t))-\frac{p\bigl (\tau ^{-1}(t)\bigr )x(t)}{\tau ^{\Delta }\bigl (\tau ^{-1}(t)\bigr )}\nonumber \\ ={}&-\frac{p\bigl (\tau ^{-1}(t)\bigr )x(t)}{\tau ^{\Delta }\bigl (\tau ^{-1}(t)\bigr )} \end{aligned}$$
(7)

for all \(t\in [t_{0},\infty )_{\mathbb {T}}\) (see Theorem 2 and Theorem 3). Integrating (7) from \(t_{1}\) to \(\infty \), where \(t_{1}\in [t_{0},\infty )_{\mathbb {T}}\) is sufficiently large, we have

$$\begin{aligned} \int _{t_{1}}^{\infty }\frac{p\bigl (\tau ^{-1}(\eta )\bigr )x(\eta )}{\tau ^{\Delta }\bigl (\tau ^{-1}(\eta )\bigr )}\Delta \eta =-\int _{t_{1}}^{\infty }y^{\Delta }(\eta )\Delta \eta =y(t_{1})-\lim _{t\rightarrow \infty }y(t)=y(t_{1})-\ell . \end{aligned}$$

Note that

$$\begin{aligned} \int _{t_{2}}^{\infty }p(\xi )x\bigl (\tau (\xi )\bigr )\Delta \xi =\int _{t_{1}}^{\infty }\frac{p\bigl (\tau ^{-1}(\eta )\bigr )x(\eta )}{\tau ^{\Delta }\bigl (\tau ^{-1}(\eta )\bigr )}\Delta \eta =:L <\infty ,\quad \text {where}\ t_{2}:=\tau ^{-1}(t_{1}) \end{aligned}$$
(8)

(see Theorem 4). We claim that

$$\begin{aligned} \lim _{t\rightarrow \infty }\int _{t}^{\tau ^{-1}(t)}p(\xi )x\bigl (\tau (\xi )\bigr )\Delta \xi =0. \end{aligned}$$
(9)

Indeed, letting

$$\begin{aligned} z(t):=\int _{t_{2}}^{t}p(\xi )x\bigl (\tau (\xi )\bigr )\Delta \xi \quad \text {for}\ t\in [t_{1},\infty )_{\mathbb {T}}, \end{aligned}$$

we see from (8) that

$$\begin{aligned} \lim _{t\rightarrow \infty }z(t)=L \quad \text {and}\quad \lim _{t\rightarrow \infty }z\bigl (\tau ^{-1}(t)\bigr )=L \end{aligned}$$

since \(\lim _{t\rightarrow \infty }\tau ^{-1}(t)=\infty \) because of \(\lim _{t\rightarrow \infty }\tau (t)=\infty \). Therefore, we estimate

$$\begin{aligned} \lim _{t\rightarrow \infty }\int _{t}^{\tau ^{-1}(t)}p(\xi )x\bigl (\tau (\xi )\bigr )\Delta \xi =\lim _{t\rightarrow \infty }\bigl [z\bigl (\tau ^{-1}(t)\bigr )-z(t)\bigr ] =L-L=0, \end{aligned}$$

which proves (9). Rewriting (6) in the form

$$\begin{aligned} x(t)=y(t)+\int _{t}^{\tau ^{-1}(t)}p(\xi )x\bigl (\tau (\xi )\bigr )\Delta \xi \quad \text {for}\ t\in [t_{0},\infty )_{\mathbb {T}}, \end{aligned}$$

and considering (9) yields that \(x(t)\rightarrow \ell \) as \(t\rightarrow \infty \). This completes the proof. \(\square \)

4 Proof of the Main Result

In view of Lemmas 1 and 2, in order to show that the trivial solution of (1) is globally attracting, that is, every solution x tends to zero, we shall need a sufficient condition such that for every solution x of (1), the function y defined by (6) will tend to a constant.

Before proceeding to the next result, we compute

$$\begin{aligned} (y^{2})^{\Delta }(t)&=y^{\Delta }(t)\Bigl (2y(t)+\mu (t)y^{\Delta }(t)\Bigr )\nonumber \\&= -\frac{p\bigl (\tau ^{-1}(t)\bigr )x(t)}{\tau ^{\Delta }\bigl (\tau ^{-1}(t)\bigr )} \biggl [2x(t)-2\int _{t}^{\tau ^{-1}(t)}p(\xi )x\bigl (\tau (\xi )\bigr )\Delta \xi -\mu (t)\frac{p\bigl (\tau ^{-1}(t)\bigr )x(t)}{\tau ^{\Delta }\bigl (\tau ^{-1}(t)\bigr )} \biggr ]\nonumber \\&= \frac{p\bigl (\tau ^{-1}(t)\bigr )}{\tau ^{\Delta }\bigl (\tau ^{-1}(t)\bigr )} \biggl [\mu (t)\frac{p\bigl (\tau ^{-1}(t)\bigr )\bigl (x(t)\bigr )^{2}}{\tau ^{\Delta } \bigl (\tau ^{-1}(t)\bigr )}-2\bigl (x(t)\bigr )^{2} +2\int _{t}^{\tau ^{-1}(t)}p(\xi )x\bigl (\tau (\xi )\bigr )x(t)\Delta \xi \biggr ]\nonumber \\&\le \frac{p\bigl (\tau ^{-1}(t)\bigr )}{\tau ^{\Delta }\bigl (\tau ^{-1}(t)\bigr )} \biggl [\mu (t)\frac{p\bigl (\tau ^{-1}(t)\bigr )\bigl (x(t)\bigr )^{2}}{\tau ^{\Delta }\bigl (\tau ^{-1}(t)\bigr )}-2\bigl (x(t)\bigr )^{2}\nonumber \\&\quad +\int _{t}^{\tau ^{-1}(t)}p(\xi )\biggl (\bigl [x\bigl (\tau (\xi )\bigr )\bigr ]^{2} +\bigl (x(t)\bigr )^{2}\biggr )\Delta \xi \biggr ]\nonumber \\&\le \frac{p\bigl (\tau ^{-1}(t)\bigr )}{\tau ^{\Delta }\bigl (\tau ^{-1}(t)\bigr )} \biggl [\int _{t}^{\sigma (t)}\frac{p\bigl (\tau ^{-1}(\xi )\bigr )\bigl (x(\xi )\bigr )^{2}}{\tau ^{\Delta }\bigl (\tau ^{-1}(\xi )\bigr )}\Delta \xi -2\bigl (x(t)\bigr )^{2}\nonumber \\&\quad +\int _{t}^{\tau ^{-1}(t)}p(\xi )\bigl [x\bigl (\tau (\xi )\bigr )\bigr ]^{2}\Delta \xi +\int _{t}^{\tau ^{-1}(t)}p(\xi )\bigl (x(t)\bigr )^{2}\Delta \xi \biggr ]\nonumber \\&= \frac{p\bigl (\tau ^{-1}(t)\bigr )}{\tau ^{\Delta }\bigl (\tau ^{-1}(t)\bigr )} \biggl [\int _{\tau ^{-1}(t)}^{\tau ^{-1}(\sigma (t))}p(\xi )\bigl (x(\tau (\xi ))\bigr )^{2}\Delta \xi -2\bigl (x(t)\bigr )^{2}\nonumber \\&\quad +\int _{t}^{\tau ^{-1}(t)}p(\xi )\bigl [x\bigl (\tau (\xi )\bigr )\bigr ]^{2}\Delta \xi +\int _{t}^{\tau ^{-1}(t)}p(\xi )\bigl (x(t)\bigr )^{2}\Delta \xi \biggr ]\nonumber \\&= \frac{p\bigl (\tau ^{-1}(t)\bigr )}{\tau ^{\Delta }\bigl (\tau ^{-1}(t)\bigr )}{\int _{t}^{\tau ^{-1}(\sigma (t))}p(\xi )\bigl (x(\tau (\xi ))\bigr )^{2}\Delta \xi } -2\frac{p\bigl (\tau ^{-1}(t)\bigr )}{\tau ^{\Delta }\bigl (\tau ^{-1}(t)\bigr )}\bigl (x(t)\bigr )^{2} \nonumber \\&\quad +\frac{p\bigl (\tau ^{-1}(t)\bigr )}{\tau ^{\Delta }\bigl (\tau ^{-1}(t)\bigr )}\int _{t}^{\tau ^{-1}(t)}p(\xi )\bigl (x\bigl (t)\bigr )\bigr )^{2}\Delta \xi \end{aligned}$$
(10)

for \(t\in [t_{0},\infty )_{\mathbb {T}}\). Note that we have applied the inequality \(2\alpha \beta \le \alpha ^{2}+\beta ^{2}\) in the fourth step above.

Lemma 3

Assume (C1), (C2) and

$$\begin{aligned} \limsup _{t\rightarrow \infty }\int _{t}^{\tau ^{-2}(\sigma (t))}p(\xi )\Delta \xi <2. \end{aligned}$$
(11)

Then, every solution of (1) tends to a constant.

Proof

We shall construct a nonnegative Lyapunov functional V, which is eventually nonincreasing along solutions of (1). Let x be a solution of (1), and let y be defined by (6). Define Lyapunov functional V by

$$\begin{aligned} V\bigl (x(t)\bigr ) ={}&\bigl (y(t)\bigr )^{2}+w(t) \quad \text {for}\ t\in [t_{0},\infty )_{\mathbb {T}}, \end{aligned}$$

where

$$\begin{aligned} w(t):=\int _{t}^{\tau ^{-1}(t)}\int _{\eta }^{\tau ^{-1}(t)}\frac{p\bigl (\tau ^{-1}(\eta )\bigr )}{\tau ^{\Delta }\bigl (\tau ^{-1}(\eta )\bigr )} p(\xi )\bigl [x\bigl (\tau (\xi )\bigr )\bigr ]^{2}\Delta \xi \Delta \eta \quad \text {for}\ t\in [t_{0},\infty )_{\mathbb {T}}. \end{aligned}$$

In view of (10), we estimate that

$$\begin{aligned} (V\circ {}x)^{\Delta }(t)&= \bigl (y^{2}\bigr )^{\Delta }(t)+w^{\Delta }(t) \\&\le \biggl [\frac{p\bigl (\tau ^{-1}(t)\bigr )}{\tau ^{\Delta }\bigl (\tau ^{-1}(t)\bigr )}{\int _{t}^{\tau ^{-1}(\sigma (t))}p(\xi )\bigl (x(\tau (\xi ))\bigr )^{2}\Delta \xi } -2\frac{p\bigl (\tau ^{-1}(t)\bigr )}{\tau ^{\Delta }\bigl (\tau ^{-1}(t)\bigr )}\bigl (x(t)\bigr )^{2} \\&\quad +\frac{p\bigl (\tau ^{-1}(t)\bigr )}{\tau ^{\Delta }\bigl (\tau ^{-1}(t)\bigr )}\int _{t}^{\tau ^{-1}(t)}p(\xi )\bigl (x\bigl (t)\bigr )\bigr )^{2}\Delta \xi \biggr ] \\&\quad -\frac{p\bigl (\tau ^{-1}(t)\bigr )}{\tau ^{\Delta }\bigl (\tau ^{-1}(t)\bigr )} \int _{t}^{\tau ^{-1}(\sigma (t))} p(\xi )\bigl (x(\tau (\xi ))\bigr )^{2}\Delta \xi \\&\quad +\frac{p(\tau ^{-1}(t))\bigl (x(t)\bigr )^{2}}{\tau ^{\Delta }\bigl (\tau ^{-1}(t)\bigr )}{{\int _{\tau ^{-2}(t)}^{\tau ^{-2}(\sigma (t))}p(\xi )\Delta \xi }} \\&\quad +\frac{p\bigl (\tau ^{-1}(t)\bigr )\bigl (x(t)\bigr )^{2}}{\tau ^{\Delta }\bigl (\tau ^{-1}(t)\bigr )}\int _{\tau ^{-1}(t)}^{\tau ^{-2}(t)}p\bigl (\xi \bigr )\Delta \xi \\&= -2\frac{p\bigl (\tau ^{-1}(t)\bigr )}{\tau ^{\Delta }\bigl (\tau ^{-1}(t)\bigr )}\bigl (x(t)\bigr )^{2} +\frac{p\bigl (\tau ^{-1}(t)\bigr )}{\tau ^{\Delta }\bigl (\tau ^{-1}(t)\bigr )}\int _{t}^{\tau ^{-1}(t)}p(\xi )\bigl (x(t)\bigr )^{2}\Delta \xi \\&\quad +\frac{p(\tau ^{-1}(t))\bigl (x(t)\bigr )^{2}}{\tau ^{\Delta }\bigl (\tau ^{-1}(t)\bigr )}{{\int _{\tau ^{-2}(t)}^{\tau ^{-2}(\sigma (t))}p(\xi )\Delta \xi }} \\&\quad +\frac{p\bigl (\tau ^{-1}(t)\bigr )\bigl (x(t)\bigr )^{2}}{\tau ^{\Delta }\bigl (\tau ^{-1}(t)\bigr )}\int _{\tau ^{-1}(t)}^{\tau ^{-2}(t)}p(\xi )\Delta \xi \\&= \frac{p\bigl (\tau ^{-1}(t)\bigr )}{\tau ^{\Delta }\bigl (\tau ^{-1}(t)\bigr )}\bigl (x(t)\bigr )^{2} \biggl [-2+\int _{t}^{\tau ^{-2}(\sigma (t))}p(\xi )\Delta \xi \biggr ] \end{aligned}$$

for \(t\in [t_{0},\infty )_{\mathbb {T}}\). In view of (11), there exists \(t_{1}\in [t_{0},\infty )_{\mathbb {T}}\) and \(\varepsilon \in \mathbb {R}^{+}\) such that

$$\begin{aligned} 2-\int _{t}^{\tau ^{-2}(\sigma (t))}p(\xi )\Delta \xi \le \varepsilon \quad \text {for all}\ t\in [t_{1},\infty )_{\mathbb {T}}. \end{aligned}$$

Thus, we get

$$\begin{aligned} (V\circ {}x)^{\Delta }(t)\le -\varepsilon \frac{p\bigl (\tau ^{-1}(t)\bigr )}{\tau ^{\Delta }\bigl (\tau ^{-1}(t)\bigr )}\bigl (x(t)\bigr )^{2}\le 0 \quad \text {for all}\ t\in [t_{1},\infty )_{\mathbb {T}}. \end{aligned}$$
(12)

Therefore, \((V\circ {}x)\) is nonnegative and nonincreasing on \([t_{1},\infty )_{\mathbb {T}}\). This shows that

$$\begin{aligned} \lim _{t\rightarrow \infty }V\bigl (x(t)\bigr ) =\lim _{t\rightarrow \infty }\Bigl (\bigl (y(t)\bigr )^{2}+w(t)\Bigr ) =\ell \ge 0. \end{aligned}$$

By integrating the inequality (12) from \(t_{1}\) to \(\infty \), we have

$$\begin{aligned} \int _{t_{1}}^{\infty }\frac{p\bigl (\tau ^{-1}(\xi )\bigr )\bigl (x(\xi )\bigr )^{2}}{\tau ^{\Delta }\bigl (\tau ^{-1}(\xi )\bigr )}\Delta \xi \le \frac{V\bigl (x(t_{1})\bigr )-\ell }{\varepsilon }. \end{aligned}$$
(13)

By using (11), we obtain

$$\begin{aligned} w(t)&=\int _{t}^{\tau ^{-1}(t)}\int _{t}^{\sigma (\xi )}\frac{p\bigl (\tau ^{-1}(\eta )\bigr )}{\tau ^{\Delta }\bigl (\tau ^{-1}(\eta )\bigr )} p(\xi )\bigl [x\bigl (\tau (\xi )\bigr )\bigr ]^{2}\Delta \eta \Delta \xi \\&=\int _{t}^{\tau ^{-1}(t)}\int _{\tau ^{-1}(t)}^{\tau ^{-1}(\sigma (\xi ))}p(\eta ) p(\xi )\bigl [x\bigl (\tau (\xi )\bigr )\bigr ]^{2}\Delta \eta \Delta \xi \\&< \int _{t}^{\tau ^{-1}(t)}\int _{t}^{\tau ^{-2}(t)}p(\eta ) p(\xi )\bigl [x\bigl (\tau (\xi )\bigr )\bigr ]^{2}\Delta \eta \Delta \xi \\&< \int _{t}^{\tau ^{-1}(t)}\int _{t}^{\tau ^{-2}(\sigma (t))}p(\eta ) p(\xi )\bigl [x\bigl (\tau (\xi )\bigr )\bigr ]^{2}\Delta \eta \Delta \xi \\&< 2\int _{t}^{\tau ^{-1}(t)}p(\xi )\bigl [x\bigl (\tau (\xi )\bigr )\bigr ]^{2}\Delta \xi , \end{aligned}$$

which together with (13) implies

$$\begin{aligned} \lim _{t\rightarrow \infty }w(t)=0. \end{aligned}$$
(14)

Combining (13) and (14), we find

$$\begin{aligned} \lim _{t\rightarrow \infty }\mid {}y(t)\mid =\lim _{t\rightarrow \infty }\sqrt{V\bigl (x(t)\bigr )-w(t)} =\sqrt{\ell }. \end{aligned}$$

We assert further that y converges. The proof is clear if \(\ell =0\). Let \(\ell >0\). We claim that y cannot be oscillatory. Assume the contrary that y is oscillatory. Then, there exist \(\delta \in (0,\sqrt{\ell })_{\mathbb {R}}\) and \(t_{2}\in [t_{1},\infty )_{\mathbb {T}}\) such that

$$\begin{aligned} 0<\sqrt{\ell }-\delta<\mid {}y(t)\mid <\sqrt{\ell }+\delta \quad \text {for all}\ t\in [t_{2},\infty )_{\mathbb {T}} \end{aligned}$$
(15)

and let

$$\begin{aligned} J_{+}=\{t\in [t_{2},\infty )_{\mathbb {T}}:\ y(t)>0\} \quad \text {and}\quad J_{-}=\{t\in [t_{2},\infty )_{\mathbb {T}}:\ y(t)<0\}. \end{aligned}$$
(16)

Since y is oscillatory, I and J are unbounded and satisfy \(J_{-}\cup {}J_{+}=[t_{2},\infty )_{\mathbb {T}}\). Hence, we may pick an increasing divergent sequence \(\{s_{k}\}_{k\in \mathbb {N}}\subset [t_{2},\infty )_{\mathbb {T}}\) (i.e., \(s_{k+1}>s_{k}\) for \(k\in \mathbb {N}\) and \(s_{k}\rightarrow \infty \) as \(k\rightarrow \infty \)) such that \(\{s_{k}\}\subset {}J_{+}\) and \(\{\sigma (s_{k})\}\subset {}J_{-}\). Then, \(y(s_{k})>0\) and \(y^{\sigma }(s_{k})<0\) for all \(k\in \mathbb {N}\). Furthermore, by (15), we easily see that

$$\begin{aligned} \begin{aligned}&0<\sqrt{\ell }-\delta<\mid {}y^{\sigma }(s_{k})\mid<\sqrt{\ell }+\delta \\&\quad \implies \sqrt{\ell }-\delta<-y^{\sigma }(s_{k})<\sqrt{\ell }+\delta \\&\quad \implies -\bigl (\sqrt{\ell }+\delta \bigr )<y^{\sigma }(s_{k})<-\sqrt{\ell }+\delta \end{aligned} \end{aligned}$$

and

$$\begin{aligned} \begin{aligned}&0<\sqrt{\ell }-\delta<\mid {}y(s_{k})\mid<\sqrt{\ell }+\delta \\&\quad \implies \sqrt{\ell }-\delta<y(s_{k})<\sqrt{\ell }+\delta \\&\quad \implies -\bigl (\sqrt{\ell }+\delta \bigr )<-y(s_{k})<-\sqrt{\ell }+\delta , \end{aligned} \end{aligned}$$

then

$$\begin{aligned} -2\bigl (\sqrt{\ell }+\delta \bigr )<y^{\sigma }(s_{k})-y(s_{k})<2\bigl (-\sqrt{\ell }+\delta \bigr )<0,\quad {}k\in \mathbb {N}. \end{aligned}$$

It follows from (7) that

$$\begin{aligned}&-2\bigl (\sqrt{\ell }+\delta \bigr )<\int _{s_{k}}^{\sigma (s_{k})}y^{\Delta }(\xi )\Delta \xi<2\bigl (-\sqrt{\ell }+\delta \bigr )\nonumber \\&\quad \implies -2\bigl (\sqrt{\ell }+\delta \bigr )<-\int _{s_{k}}^{\sigma (s_{k})}\frac{p\bigl (\tau ^{-1}(\xi )\bigr )x(\xi )}{\tau ^{\Delta }\bigl (\tau ^{-1}(\xi )\bigr )}\Delta \xi<2\bigl (-\sqrt{\ell }+\delta \bigr )\nonumber \\&\quad \implies 2\bigl (\sqrt{\ell }-\delta \bigr )<\int _{s_{k}}^{\sigma (s_{k})}\frac{p\bigl (\tau ^{-1}(\xi )\bigr )x(\xi )}{\tau ^{\Delta }\bigl (\tau ^{-1}(\xi )\bigr )}\Delta \xi<2\bigl (\sqrt{\ell }+\delta \bigr )\nonumber \\&\quad \implies 4\bigl (\sqrt{\ell }-\delta \bigr )^{2}<\biggl (\int _{s_{k}}^{\sigma (s_{k})}\frac{p\bigl (\tau ^{-1}(\xi )\bigr )x(\xi )}{\tau ^{\Delta }\bigl (\tau ^{-1}(\xi )\bigr )}\Delta \xi \biggr )^{2} <4\bigl (\sqrt{\ell }+\delta \bigr )^{2} \end{aligned}$$
(17)

for all \(k\in \mathbb {N}\). By using (11), we obtain the following inequality

$$\begin{aligned} \biggl (\int _{s_{k}}^{\sigma (s_{k})}\frac{p\bigl (\tau ^{-1}(\xi )\bigr )x(\xi )}{\tau ^{\Delta }\bigl (\tau ^{-1}(\xi )\bigr )}\Delta \xi \biggr )^{2} ={}&\biggl (\mu (s_{k})\frac{p\bigl (\tau ^{-1}(s_{k})\bigr )x(s_{k})}{\tau ^{\Delta }\bigl (\tau ^{-1}(s_{k})\bigr )}\biggr )^{2}\nonumber \\ ={}&\int _{s_{k}}^{\sigma (s_{k})}\int _{\xi }^{\sigma (\xi )}\frac{p\bigl (\tau ^{-1}(\eta )\bigr )}{\tau ^{\Delta }\bigl (\tau ^{-1}(\eta )\bigr )} \frac{p\bigl (\tau ^{-1}(\xi )\bigr )\bigl (x(\xi )\bigr )^{2}}{\tau ^{\Delta }\bigl (\tau ^{-1}(\xi )\bigr )}\Delta \eta \Delta \xi \nonumber \\ \le {}&\int _{s_{k}}^{\sigma (s_{k})}\int _{\tau ^{-1}(\xi )}^{\tau ^{-1}(\sigma (\xi ))}p\bigl (\eta \bigr ) \frac{p\bigl (\tau ^{-1}(\xi )\bigr )\bigl (x(\xi )\bigr )^{2}}{\tau ^{\Delta }\bigl (\tau ^{-1}(\xi )\bigr )}\Delta \eta \Delta \xi \nonumber \\ \le {}&\int _{s_{k}}^{\sigma (s_{k})}\int _{\xi }^{\tau ^{-2}(\sigma (\xi ))}p\bigl (\eta \bigr ) \frac{p\bigl (\tau ^{-1}(\xi )\bigr )\bigl (x(\xi )\bigr )^{2}}{\tau ^{\Delta }\bigl (\tau ^{-1}(\xi )\bigr )}\Delta \eta \Delta \xi \nonumber \\ \le {}&2\int _{s_{k}}^{\sigma (s_{k})}\frac{p\bigl (\tau ^{-1}(\xi )\bigr )\bigl (x(\xi )\bigr )^{2}}{\tau ^{\Delta }\bigl (\tau ^{-1}(\xi )\bigr )}\Delta \xi \end{aligned}$$
(18)

for all \(k\in \mathbb {N}\). From (17) and (18), we have

$$\begin{aligned} \int _{s_{k}}^{\sigma (s_{k})}\frac{p\bigl (\tau ^{-1}(\xi )\bigr )\bigl (x(\xi )\bigr )^{2}}{\tau ^{\Delta }\bigl (\tau ^{-1}(\xi )\bigr )}\Delta \xi >2\bigl (\sqrt{\ell }-\delta \bigr )^{2} \quad \text {for all}\ k\in \mathbb {N}. \end{aligned}$$
(19)

From (13) and (19), we get

$$\begin{aligned} \sum _{k=1}^{\infty }2\bigl (\sqrt{\ell }-\delta \bigr )^{2}<{}&\sum _{k=1}^{\infty }\int _{s_{k}}^{\sigma (s_{k})}\frac{p\bigl (\tau ^{-1}(\xi )\bigr )\bigl (x(\xi )\bigr )^{2}}{\tau ^{\Delta }\bigl (\tau ^{-1}(\xi )\bigr )}\Delta \xi \\ \le {}&\int _{s_{1}}^{\infty }\frac{p\bigl (\tau ^{-1}(\xi )\bigr )\bigl (x(\xi )\bigr )^{2}}{\tau ^{\Delta }\bigl (\tau ^{-1}(\xi )\bigr )}\Delta \xi <\infty \end{aligned}$$

but \(\sum _{k=1}^{\infty }2\bigl (\sqrt{\ell }-\delta \bigr )^{2}=\infty \), which is a contradiction. Therefore, y cannot be oscillatory. If y is either eventually positive or eventually negative, then \(\lim _{t\rightarrow \infty }y(t)=\sqrt{\ell }\) or \(\lim _{t\rightarrow \infty }y(t)=-\sqrt{\ell }\), respectively. By Lemma 2, every solution x of (1) converges to some value, and this completes the proof. \(\square \)

Proof of Theorem 1

The proof is an immediate consequence of Lemmas 1 and 3. \(\square \)

5 Some Examples

We start this section with a numerical example on a particular isolated time scale.

Example 1

Let \(\mathbb {T}=\{\ldots ,0,1,3,6,7,9,12,\ldots \}=\cup _{k\in \mathbb {Z}}\{6k,6k+1,6k+3\}\), and consider the equation

$$\begin{aligned} x^{\Delta }(t)+p(t) x(\rho (t))=0\quad \text {for}\ t\in [0,\infty )_{\mathbb {T}}, \end{aligned}$$
(20)

where

$$\begin{aligned} p(t):= {\left\{ \begin{array}{ll} \frac{3}{4},&{}t=6k\\ \frac{1}{2},&{}t=6k+1\\ \frac{1}{36},&{}t=6k+3 \end{array}\right. }\quad \text {for}\ t\in [0,\infty )_{\mathbb {T}}. \end{aligned}$$

Comparing (20) with (1), we see that \(\tau (t)=\rho (t)<t\) for all \(t\in \mathbb {T}\), and \(\tau ^{-1}(t)=\sigma (t)\) for \(t\in \mathbb {T}\). Further, \(\tau ^{\Delta }(t)=\frac{t-\rho (t)}{\mu (t)}>0\) for all \(t\in \mathbb {T}\), i.e., \(\tau \) is differentiable, increasing and that \(\tau (\mathbb {T})=\mathbb {T}\). Next, we compute that

$$\begin{aligned} \limsup _{t\rightarrow \infty }\int _{\tau (t)}^{\sigma (t)}p(\xi )\Delta \xi ={}&\limsup _{t\rightarrow \infty }\int _{\rho (t)}^{\sigma (t)}p(\xi )\Delta \xi \\ ={}&\limsup _{t\rightarrow \infty }\biggl [\int _{\rho (t)}^{t}p(\xi )\Delta \xi +\int _{t}^{\sigma (t)}p(\xi )\Delta \xi \biggr ] \\ ={}&\limsup _{t\rightarrow \infty }[\mu (\rho (t))p(\rho (t))+\mu (t)p(t)] \\ ={}&\limsup _{t\rightarrow \infty } {\left\{ \begin{array}{ll} 3\cdot \frac{1}{36}+1\cdot \frac{3}{4},&{}t=6k\\ 1\cdot \frac{3}{4}+2\cdot \frac{1}{2},&{}t=6k+1\\ 2\cdot \frac{1}{2}+3\cdot \frac{1}{36},&{}t=6k+3 \end{array}\right. } \\ ={}&\limsup _{t\rightarrow \infty } \left. {\left\{ \begin{array}{ll} \frac{5}{6},&{}t=6k\\ \frac{7}{4},&{}t=6k+1\\ \frac{13}{12},&{}t=6k+3 \end{array}\right. } \right\} =\frac{7}{4}\not <1 \end{aligned}$$

and

$$\begin{aligned} \limsup _{t\rightarrow \infty }\int _{\tau (t)}^{\sigma (t)}p(\xi )\Delta \xi ={}&\frac{7}{4}\not <\frac{3}{2}+\frac{1}{3+3}=\frac{5}{3}. \end{aligned}$$

Hence, conditions of [4, §6] and [20, Theorem 1.2] (see also [10]) fail to hold. Fortunately,

$$\begin{aligned} \limsup _{t\rightarrow \infty }\int _{t}^{\tau ^{-2}(\sigma (t))}p(\xi )\Delta \xi ={}&\limsup _{t\rightarrow \infty }\int _{t}^{\sigma ^{3}(t)}p(\xi )\Delta \xi \\ ={}&\limsup _{t\rightarrow \infty }\biggl [\int _{t}^{\sigma (t)}p(\xi )\Delta \xi +\int _{\sigma (t)}^{\sigma ^{2}(t)}p(\xi )\Delta \xi +\int _{\sigma ^{2}(t)}^{\sigma ^{3}(t)}p(\xi )\Delta \xi \biggr ] \\ ={}&\limsup _{t\rightarrow \infty }[\mu (t)p(t)+\mu (\sigma (t))p(\sigma (t))+\mu (\sigma ^{2}(t))p(\sigma ^{2}(t))] \\ ={}&\limsup _{t\rightarrow \infty } \left. {\left\{ \begin{array}{ll} 1\cdot \frac{3}{4}+2\cdot \frac{1}{2}+3\cdot \frac{1}{36},&{}t=6k\\ 2\cdot \frac{1}{2}+3\cdot \frac{1}{36}+1\cdot \frac{3}{4},&{}t=6k+1\\ 3\cdot \frac{1}{36}+1\cdot \frac{3}{4}+2\cdot \frac{1}{2},&{}t=6k+3 \end{array}\right. } \right\} =\frac{11}{6}<2, \end{aligned}$$

which shows by Theorem 1 that the trivial solution of (20) is globally attracting.

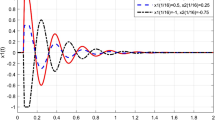
In Fig. 1, we have the plots of the solutions \(x_{1}\) and \(x_{2}\), which have the initial conditions \(x(-3)=0\), \(x(0)=1\), and \(x(-3)=1\), \(x(0)=0\), respectively.

Fig. 1
figure 1

Graphic of the solutions \(x_{1}\) (blue) and \(x_{2}\) (red) on \([-3,45]_{\mathbb {T}}\)

Full size image

We can simply compute \(x_{1}\) as

$$\begin{aligned} x_{1}(t)= {\left\{ \begin{array}{ll} \bigl (-\frac{1}{12}\bigr )^{k},&{}t=6k\ \text {or}\ t=6k+1\\ 0,&{}t=6k+3, \end{array}\right. } \end{aligned}$$

which satisfies \(\lim _{t\rightarrow \infty }x(t)=0\). But, it is not very easy to compute the solution \(x_{2}\) explicitly. Due to the superposition principle, we can say that any solution x of (20) is of the form \(x(t)=x(-3)x_{1}(t)+x(0)x_{2}(t)\) for \(t\in [-3,\infty )_{\mathbb {T}}\). It can be also seen from Fig. 1 that \(\lim _{t\rightarrow \infty }x(t)=0\).

Next, we give an example on a time scale, which is a union of closed intervals of length 1.

Example 2

Let \(\mathbb {T}=\mathbb {P}_{1,1}=\cup _{k\in \mathbb {Z}}[2k,2k+1]_{\mathbb {R}}\), and consider the equation

$$\begin{aligned} x^{\Delta }(t)+p(t)x(t-2)=0\quad \text {for}\ t\in [0,\infty )_{\mathbb {T}}, \end{aligned}$$
(21)

where

$$\begin{aligned} p(t):= {\left\{ \begin{array}{ll} \frac{5}{4},&{}t\in [4k,4k+1)_{\mathbb {R}}\\ \frac{1}{8},&{}t=2k+1\\ \frac{1}{4},&{}t\in [4k+2,4k+3)_{\mathbb {R}} \end{array}\right. }\quad \text {for}\ t\in [0,\infty )_{\mathbb {T}}. \end{aligned}$$

Comparing (21) with (1), we see that \(\tau (t)=t-2<t\) for all \(t\in \mathbb {T}\), and \(\tau ^{-1}(t)=t+2\) for \(t\in \mathbb {T}\). Further, \(\tau ^{\Delta }(t)\equiv 1>0\) for all \(t\in \mathbb {T}\), i.e., \(\tau \) is differentiable, increasing and that \(\tau (\mathbb {T})=\mathbb {T}\).

Fig. 2
figure 2

Graphic of the coefficient p on \([0,9]_{\mathbb {T}}\)

Full size image

It should be mentioned here that \(\min _{t\in \mathbb {T}}\{\mu (t)\}=0\), \(\max _{t\in \mathbb {T}}\{\mu (t)\}=1\) and \(\max _{t\in \mathbb {T}}\{t-\tau (t)\}=2\).

Fig. 3
figure 3

Graphic of the integral of the coefficient p from \(\tau (t)\) to \(\sigma (t)\) for \(t\in [0,9]_{\mathbb {T}}\)

Full size image

Now, we compute

$$\begin{aligned} \limsup _{t\rightarrow \infty }\int _{\tau (t)}^{\sigma (t)}p(\xi )\Delta \xi ={}&\limsup _{t\rightarrow \infty }\biggl [\int _{\tau (t)}^{t}p(\xi )\Delta \xi +\int _{t}^{\sigma (t)}p(\xi )\Delta \xi \biggr ] \\ ={}&\limsup _{t\rightarrow \infty }\biggl [\int _{t-2}^{t}p(\xi )\Delta \xi +\mu (t)p(t)\biggr ] \\ ={}&\limsup _{t\rightarrow \infty } \left. {\left\{ \begin{array}{ll} t-4k+\frac{3}{8},&{}4k\le {}t<4k+1\\ \frac{3}{2},&{}t=4k+1\\ -t+4k+ \frac{27}{8},&{}4k+2\le {}t<4k+3\\ \frac{1}{2},&{}t=4k+3 \end{array}\right. } \right\} =\frac{3}{2} \end{aligned}$$

showing that conditions of [4, §6] and [20, Theorem 1.2] (see also [10]) fail to hold.

Fig. 4
figure 4

Graphic of the integral of the coefficient p from t to \(\tau ^{-2}(\sigma (t))\) for \(t\in [0,9]_{\mathbb {T}}\)

Full size image

On the other hand, we compute that

$$\begin{aligned} \limsup _{t\rightarrow \infty }\int _{t}^{\tau ^{-2}(\sigma (t))}p(\xi )\Delta \xi ={}&\limsup _{t\rightarrow \infty }\int _{t}^{\sigma (t)+4}p(\xi )\Delta \xi \\ ={}&\limsup _{t\rightarrow \infty } \left. {\left\{ \begin{array}{ll} \frac{7}{4},&{}4k\le {}t<4k+1\\ \frac{15}{8},&{}t=4k+1\\ \frac{7}{4},&{}4k+2\le {}t<4k+3\\ \frac{15}{8},&{}t=4k+3 \end{array}\right. } \right\} =\frac{15}{8}<2. \end{aligned}$$

This shows that the conditions of Theorem 1 hold, i.e., the trivial solution of (21) is globally attracting.

Due to Theorem 1, the trivial solution of (21) is globally attracting. A solution of (21) is plotted in Fig. 2 showing that \(\lim _{t\rightarrow \infty }x(t)=0\) (Figs. 3, 4, 5).

Fig. 5
figure 5

Graphic of a solution x on \([-2,31]_{\mathbb {T}}\) under the initial condition \(x(t)=0\) for \(t\in [-2,-1]_{\mathbb {T}}\) and \(x(0)=1\)

Full size image

6 Final Comments

In this section, we make our final comments to conclude the paper. We will start with a remark that holds trivially for the well-known time scales \(\mathbb {T}=\mathbb {R}\) and \(\mathbb {T}=\mathbb {Z}\) with a delay in the linear form.

Remark 1

Suppose that \(\tau \circ \sigma =\sigma \circ \tau \), then

$$\begin{aligned}&\limsup _{t\rightarrow \infty }\int _{\tau (t)}^{\sigma (t)}p(\eta )\Delta \eta<1 \\&\quad \implies \limsup _{t\rightarrow \infty }\int _{t}^{\sigma (\tau ^{-1}(t))}p(\eta )\Delta \eta<1\ \text {and}\ \limsup _{t\rightarrow \infty }\int _{\tau ^{-1}(t)}^{\sigma (\tau ^{-2}(t))}p(\eta )\Delta \eta<1 \\&\quad \implies \limsup _{t\rightarrow \infty }\int _{t}^{\tau ^{-1}(\sigma (t))}p(\eta )\Delta \eta<1\ \text {and}\ \limsup _{t\rightarrow \infty }\int _{\tau ^{-1}(t)}^{\tau ^{-2}(\sigma (t))}p(\eta )\Delta \eta<1 \\&\quad \implies \limsup _{t\rightarrow \infty }\int _{t}^{\tau ^{-1}(t)}p(\eta )\Delta \eta<1\ \text {and}\ \limsup _{t\rightarrow \infty }\int _{\tau ^{-1}(t)}^{\tau ^{-2}(\sigma (t))}p(\eta )\Delta \eta<1 \\&\quad \implies \limsup _{t\rightarrow \infty }\int _{t}^{\tau ^{-2}(\sigma (t))}p(\eta )\Delta \eta <2. \end{aligned}$$

Hence, the condition in [4, §6 (i)] implies Theorem 1 under the condition \(\tau \circ \sigma =\sigma \circ \tau \).

The key point in this paper is to assume conditions such that \(\tau (\mathbb {T})=\mathbb {T}\) holds. This enables us to use the substitution formula in integrals on time scales (see Theorem 4). Note that for the classical types of equations

$$\begin{aligned} x(n+1)-x(n)+p(n)x(n-\tau )=0\quad \text {for}\ n\in \mathbb {N}_{0},\ \mathbb {T}=\mathbb {Z}\end{aligned}$$

and

$$\begin{aligned} x^{\prime }(t)+p(t)x(t-\tau )=0\quad \text {for}\ t\in [0,\infty ),\ \mathbb {T}=\mathbb {R}, \end{aligned}$$

the condition \(\tau (\mathbb {T})=\mathbb {T}\) holds trivially. For more general special types of dynamic equations

$$\begin{aligned}&\Delta _{h}x(t)+p(t)x(t-kh)=0\quad \text {for}\ t\in {}h\mathbb {Z},\ k\in \mathbb {N}_{0},\ \Delta _{h}x(t):=\frac{x(t+h)-x(t)}{h}, \\&x^{\prime }(t)+p(t)x(\alpha {}t)=0\quad \text {for}\ t\in \mathbb {R}_{0}^{+},\ \alpha \in (0,1), \end{aligned}$$

and

$$\begin{aligned} \textrm{D}_{q}x(t)+p(t)x(t/q^{k})=0\quad \text {for}\ t\in {}q^{\mathbb {Z}}\cup \{0\},\ k\in \mathbb {N}_{0},\ \textrm{D}_{q}x(t):=\frac{x(qt)-x(t)}{(q-1)t}, \end{aligned}$$

one can easily see that (C2) holds too. h-difference equations and q-difference equations can be considered under a more general class, that is, dynamic equations on isolated time scales. In this case, with a delay term of the form \(\tau (t)=\rho ^{k}(t):=(\rho \circ \rho ^{k-1})(t)\) and \(\rho ^{0}(t):=t\) for \(t\in \mathbb {T}\) and \(k\in \mathbb {N}_{0}\), (C2) also holds.

We would like to emphasize that Theorem 1 generalizes Theorems A and B to arbitrary time scales. It is also important to mention that Theorem 1 cannot be compared with the results in [4] and [20]. Hence, it is new in the stability theory of dynamic equations.

Finally, we would like to mention that the main result of this paper can be extended to dynamic equations of the neutral form

$$\begin{aligned} \bigl [x(t)-r(t)x\bigl (\gamma (t)\bigr )\bigr ]^{\Delta } +p(t)x\bigl (\alpha (t)\bigr )-q(t)x\bigl (\beta (t)\bigr )=0 \quad \text {for}\ t\in [t_{0},\infty )_{\mathbb {T}}, \end{aligned}$$
(22)

where the coefficients p, q, r and the delays \(\alpha ,\beta ,\gamma \) satisfy suitable conditions (cf. [11]). However, we prefer demonstrating our results on the simple equation (1) because the key point behind the idea can be presented without getting lost in computational details.