1 Introduction and Motivations

Fractional calculus has become a fundamental concept in various branches of mathematics in recent decades. Researchers have increasingly utilized fractional order differential equations to gain valuable insights in diverse fields such as rheology, fluid mechanics, dispersion, porous media, control theory, and electrodynamics (for further details, refer to [1,2,3]). Different definitions of fractional derivatives employ distinct kernels, which can be classified as singular or non-singular. For instance, the Riemann–Liouville and Caputo derivatives are based on singular kernels, while the Caputo–Fabrizio derivative sets itself apart by using a non-singular exponential decay kernel known as CF [4]. On the other hand, the Atangana–Baleanu–Caputo (ABC) derivative stands out by employing a non-singular Mittag–Leffler (ML) kernel denoted as AB [5]. In all these definitions, the kernels remain constant. However, traditional fractional calculus, characterized by long memory effects, encounters challenges in long-term calculations.

The ABC fractional derivative stands out due to its non-singular Mittag–Leffler kernel, extended memory effects, flexibility in modeling various decay behaviors, and its potential for deriving analytical solutions to fractional differential equations (FDEs). These unique characteristics make the ABC fractional derivative a valuable tool for capturing complex memory properties in diverse scientific and engineering applications [6,7,8]. For example simulate the dynamics of infectious diseases like Covid-19 [9, 10], HIV/AIDS model [11], the spread of dengue, Zika virus model [12], prey–predator model [13,14,15], and the response of tumor growth to radiotherapy [16, 17]. Overall, nonsingular fractional derivatives offer enhanced capabilities in modeling and understanding complex phenomena by providing more flexible and accurate mathematical tools that go beyond the limitations of classical derivatives [18]. The qualitative characteristics of solutions play a crucial role in the theory of FDEs, with fractional operators often employed to establish results on existence and uniqueness [19,20,21,22,23,24,25].

Recently, Atangana and Seda [26] introduced the idea of piecewise derivatives, which combines classical and Atangana–Baleanu fractional derivatives, and suggested piecewise modeling as an extension of this concept. Piecewise fractional derivatives provide a modeling framework for capturing non-local behavior in various materials. In the context of biology, piecewise fractional derivatives are particularly effective in modeling systems with time-varying behavior, such as disease development or organism responses to changing environments [27,28,29,30]. Overall, piecewise fractional derivatives serve as versatile tools for modeling non-local and non-linear behavior in diverse mathematical and physical systems, offering accurate and efficient models where traditional calculus approaches may fall short. These characteristics make them important tools for studying and understanding complex phenomena and enable researchers to develop more accurate models and make informed decisions in a wide range of applications. Additionally, the utilization of Piecewise fractional derivatives allows for the representation of crossover phenomena in a wide range of real-world problems (see [31,32,33,34,35]).

In the last few years, Some researchers have focused on studying the properties of solutions to piecewise FDEs. For example, Shah et al. [36] studied and examined the existence and uniqueness of solutions, as well as the Hyers–Ulam type stability results, for a Cauchy-type dynamical system governed by piecewise Caputo fractional derivative. Patanarapeelert et al. [37] conducted a thorough study to investigate and examine the existence and uniqueness of solutions for a coupled system governed by piecewise Caputo–Fabrizio fractional derivative. Ali et al. [38] conducted a study to investigate the existence and stability of solutions for a coupled system of piecewise FDEs with variable kernels and impulsive conditions. Abdo et al. [39], studied the properties of solutions such as existence and uniquness for piecewise Caputo pantograph problems.

Delay fractional differential equations provide a more comprehensive and accurate framework for modeling and analyzing engineering systems with time delays, memory effects, and nonlocal behavior. They enable engineers to capture and understand the dynamics of real-world systems more effectively, leading to improved design, control, and optimization of engineering systems. For examples, Alzabut and Abdeljawad [40] studied the existence of a globally attractive periodic solution of impulsive delay logarithmic population mode. Saker and Alzabut [41] employed the continuation theorem of coincidence degree to establish the existence of a positive periodic solution for the nonlinear impulsive delay hematopoiesis model. Zada et al. [42] studied the existence and uniqueness results of a class of coupled systems of implicit fractional differential equations with initial and impulsive conditions. There are different techniques for the solution of nonlinear variable delay differential equations such as wavelets approach [43] and natural transform [44]. Hasib Khan et al. [45,46,47] studied the existence and uniqueness of solutions for a fractional coupled hybrid systems.

To our knowledge, there is a lack of research or studies addressing the issue of crossover behaviors in coupled systems of fractional differential equations with delays. This gap in the existing literature underscores the necessity for further investigation. For this purpose and inspired by previous research, in this study, we employ the newly developed method of piecewise Atangana–Baleanu fractional derivative to explore crossover behaviors and some properties of solution in the following coupled system with delays

$$\begin{aligned} \left\{ \begin{array}{llll} {}^{PAB}{\mathbb {D}}_{0}^{\rho _{1}}\mu _{1}(\varsigma )=\hslash _{1}(\varsigma ,\mu _{1}(\varsigma ),\mu _{1}(\varsigma -\sigma \left( \varsigma \right) ),\mu _{2}(\varsigma )), \\ {}^{PAB}{\mathbb {D}}_{0}^{\rho _{2}}\mu _{2}(\varsigma )=\hslash _{2}(\varsigma ,\mu _{1}(\varsigma ),\mu _{2}(\varsigma ),\mu _{2}(\varsigma -\sigma \left( \varsigma \right) )), \end{array} \right. \end{aligned}$$
(1.1)

where

  • \(\sigma \left( \varsigma \right) \ge 0\) for all \(\varsigma \in \left[ 0,T\right] :={\mathcal {J}},T>0\).

  • \(^{PAB}{\mathbb {D}}_{0}^{\varpi },\left( \varpi =\rho _{1},\rho _{2}\right) \) are the piecewise derivative of order \(\varpi \in \left( 0,1 \right] \) with classical and Atangana–Baleanu fractional derivative defined as follows [26]

    $$\begin{aligned} {}^{PAB}{\mathbb {D}}_{0}^{\varpi }\mu (\varsigma )=\left\{ \begin{array}{l} {\mathbb {D}}^{1}\mu (\varsigma ) \text{ if } \varsigma \in \left[ 0,\varsigma _{1}\right] , \\ ^{ABC}{\mathbb {D}}_{\varsigma _{1}}^{\varpi }\mu (\varsigma ) \text{ if } \varsigma \in \left[ \varsigma _{1},T\right] , \end{array} \right. \end{aligned}$$
    (1.2)

    where

(i) \({\mathbb {D}}^{1}\mu (\varsigma )=\mu ^{\prime }(\varsigma )\) is the classical derivative on \(\varsigma \in \left[ 0,\varsigma _{1}\right] ,\)

(ii) \(^{ABR}{\mathbb {D}}_{\varsigma }^{\varpi }\mu (\varsigma )\) is the Atangana–Baleanu fractional derivative on \(\varsigma \in \left[ \varsigma _{1},T\right] \).

  • The functions \(\hslash _{i}:\left( 0,T\right] \times {\mathbb {R}} ^{3}\rightarrow {\mathbb {R}},\left( i=1,2\right) \) are given continuous functions satisfies the following conditions: \(\left( H_{1}\right) \) For \(\hslash _{i}:{\mathcal {J}}\times {\mathbb {R}} ^{3}\rightarrow {\mathbb {R}},\left( \mu _{1},\mu _{2}\right) \in {\mathbb {S}},\) there exists constant number \(\varphi _{i}>0,i=1,2\) such that

    $$\begin{aligned}{} & {} \left| \hslash _{i}(\varsigma ,\mu _{1}(\varsigma ),\mu _{i}(\varsigma -\sigma \left( \varsigma \right) ),\mu _{2}(\varsigma ))-\hslash _{i}(\varsigma ,{\widehat{\mu }}_{1}(\varsigma ),{\widehat{\mu }}_{i}(\varsigma -\sigma \left( \varsigma \right) ),{\widehat{\mu }}_{2}(\varsigma ))\right| \\{} & {} \quad \le \varphi _{i}\left[ \left| \mu _{1}(\varsigma )-{\widehat{\mu }} _{1}(\varsigma )\right| +\left| \mu _{i}(\varsigma -\sigma \left( \varsigma \right) )-{\widehat{\mu }}_{i}(\varsigma -\sigma \left( \varsigma \right) )\right| +\left| \mu _{2}(\varsigma )-{\widehat{\mu }} _{2}(\varsigma )\right| \right] . \end{aligned}$$

    \(\left( H_{2}\right) \) \(\hslash _{i}:{\mathcal {J}}\times {\mathbb {R}} ^{3}\rightarrow {\mathbb {R}} \) are continuous and there exist the functions \(\tau _{1},\tau _{2},\tau _{3},\eta _{1},\eta _{2},\eta _{3}\in C\left( {\mathcal {J}}, {\mathbb {R}} \right) \) such that

    $$\begin{aligned}{} & {} \left| \hslash _{1}\left( \varsigma ,\mu _{1}(\varsigma ),\mu _{1}(\varsigma -\sigma \left( \varsigma \right) ),\mu _{2}(\varsigma )\right) \right| \\{} & {} \quad \le \tau _{1}(\varsigma )+\tau _{2}(\varsigma ) \left[ \left| \mu _{1}(\varsigma )\right| +\left| \mu _{1}(\varsigma -\sigma \left( \varsigma \right) )\right| \right] +\tau _{3}(\varsigma )\left| \mu _{2}(\varsigma )\right| , \\{} & {} \left| \hslash _{2}\left( \varsigma ,\mu _{1}(\varsigma ),\mu _{2}(\varsigma ),\mu _{2}(\varsigma -\sigma \left( \varsigma \right) )\right) \right| \\{} & {} \quad \le \eta _{1}(\varsigma )+\eta _{2}(\varsigma )\left| \mu _{1}(\varsigma )\right| +\eta _{3}(\varsigma )\left[ \left| \mu _{2}(\varsigma )\right| +\left| \mu _{2}(\varsigma -\sigma \left( \varsigma \right) )\right| \right] , \end{aligned}$$

    with \(\tau _{i}^{*}=\sup _{\varsigma \in {\mathcal {J}}}\left| \tau _{i}(\varsigma )\right| ,\eta _{i}^{*}=\sup _{\varsigma \in \mathcal {J }}\left| \eta _{i}(\varsigma )\right| ,i=1,2,3.\)

The analytical tools available for studying systems involving piecewise fractional derivatives are relatively limited it continues to be an active area of research, and efforts are being made to address the issues. The main contributions of this paper can be summarized as follows:

  • We focus primarily on employing novel piecewise operators, addressing a research gap in the existing literature. Specifically, we investigate and establish qualitative properties of the coupled system with delays by incorporating both classical and Atangana–Baleanu fractional derivatives.

  • In order to bridge this research gap, we develop and prove several lemmas that serve as fundamental building blocks for our subsequent analyses. These lemmas not only extend our understanding of the system but also provide a foundation for further exploration.

  • By applying the developed lemmas, we expand the sufficient conditions for the existence, uniqueness, and Hyers–Ulam stability results of piecewise derivatives. This extension encompasses both classical and Atangana–Baleanu fractional derivatives, enhancing the applicability and scope of the results.

  • To achieve our results, we utilize well-known fixed-point theorems of both Banach and Leary–Schauder alternative types. These theorems serve as powerful mathematical tools that enable us to establish the desired properties and implications of the piecewise derivatives.

  • Additionally, we employ a numerical method based on Newton polynomials of interpolation. This method facilitates the computation of approximate solutions for the coupled system with delays, allowing us to validate and analyze the theoretical findings through practical applications.

Overall, our contributions aim to fill the research gap, provide fresh insights into the field of piecewise operators, and offer valuable theoretical and numerical results for investigating qualitative properties within the context of both classical and Atangana–Baleanu fractional derivatives.

The remaining sections of the paper are structured as follows: Sect. 2 provides a comprehensive review of fractional calculus, including essential definitions, notations, and lemmas. It also presents a lemma that transforms the suggested system (1.1) into an equivalent integral equation. In Sect. 3, we discuss the existence and uniqueness results for the system (1.1) using fixed-point theorems. Section 4 focuses on the Ulam-Hyers stability result of the system (1.1). In Sect. 5, a numerical method based on Newton polynomials of interpolation is applied to compute approximate solutions for the considered system. A numerical example is presented in Sect. 6 to illustrate the obtained results. Finally, the paper concludes with remarks summarizing the findings and contributions in the last section.

2 Preliminary and Essential Concepts

In this section, we will present and illustrate the characteristics of piecewise derivatives incorporating both classical and Atangana–Baleanu fractional derivatives. These properties play a crucial role in our subsequent analysis and research outcomes. Let \({\mathcal {J}}=\left[ 0,T\right] \subset {\mathbb {R}} ^{+},\) we are defining Banach space \(C\left( {\mathcal {J}}, {\mathbb {R}} \right) \) under the norm

$$\begin{aligned} \left\| \mu \right\| =\sup _{\varsigma \in {\mathcal {J}}}\left| \mu (\varsigma )\right| . \end{aligned}$$

Also, we define the Banach product space \({\mathbb {S}}=C\left( {\mathcal {J}}, {\mathbb {R}} \right) \times C\left( {\mathcal {J}}, {\mathbb {R}} \right) \) with the norm

$$\begin{aligned} \left\| \left( \mu _{1},\mu _{2}\right) \right\| =\left\| \mu _{1}\right\| +\left\| \mu _{2}\right\| , \text{ for } \text{ all } \left( \mu _{1},\mu _{2}\right) \in {\mathbb {S}}. \end{aligned}$$
(2.1)

Also, for \(\left( {\widehat{\mu }}_{1},{\widehat{\mu }}_{2}\right) ,\left( \mu _{1},\mu _{2}\right) \in {\mathbb {S}},\) we have

$$\begin{aligned} \left\| \left( {\widehat{\mu }}_{1},{\widehat{\mu }}_{2}\right) -\left( \mu _{1},\mu _{2}\right) \right\| =\left\| {\widehat{\mu }}_{1}-\mu _{1}\right\| +\left\| \widehat{\mu }_{2}-\mu _{2}\right\| . \end{aligned}$$

Definition 2.1

[26] Let \(\mu \) be a continuous function. The piecewise integral of \(\mu \) is defined as

$$\begin{aligned} {}^{PAB}{\mathbb {I}}_{0}^{\rho }\mu (\varsigma )=\left\{ \begin{array}{l} {\mathbb {I}}^{1}\mu (\varsigma ) \text{ if } \varsigma \in \left[ 0,\varsigma _{1}\right] , \\ ^{AB}{\mathbb {I}}_{\varsigma _{1}}^{\rho }\mu (\varsigma ) \text{ if } \varsigma \in \left[ \varsigma _{1},T\right] , \end{array} \right. \end{aligned}$$

where

(i) \({\mathbb {I}}^{1}\mu (\varsigma )=\int _{0}^{\varsigma }\mu (\varrho )d\varrho ,\) is the classical integral on \(\varsigma \in \left[ 0,\varsigma _{1}\right] .\)

(ii) \(^{AB}{\mathbb {I}}_{\varsigma _{1}}^{\rho }\mu (\varsigma )=\frac{1-\rho }{ \Delta \mathcal {(}\rho \mathcal {)}}\mu (\varsigma )+\frac{\rho }{\Delta \mathcal {(}\rho \mathcal {)}\Gamma \mathcal {(}\rho \mathcal {)}} \int _{\varsigma _{1}}^{\varsigma }(\varsigma -\varrho )^{\rho -1}\mu (\varrho )d\varrho \) is the Atangana–Baleanu integral on \(\varsigma \in \left[ \varsigma _{1},T\right] \).

Before giving our main results, we need to prove some critical Lemmas.

Lemma 2.2

For \(\rho \in \left( 0,1\right] \) and \(\mu \in C\left( {\mathcal {J}}, {\mathbb {R}} \right) \). Then, we have

$$\begin{aligned} {}^{PAB}{\mathbb {I}}_{0}^{\rho }{}^{PAB}{\mathbb {D}}_{0}^{\rho }\mu (\varsigma )=\left\{ \begin{array}{l} \mu (\varsigma _{1})-\mu (0) \text{ if } \varsigma \in \left[ 0,\varsigma _{1}\right] , \\ \mu (T)-\mu (\varsigma _{1}) \text{ if } \varsigma \in \left[ \varsigma _{1},T\right] . \end{array} \right. \end{aligned}$$

Proof

Case (1): For \(\varsigma \in \left[ 0,\varsigma _{1}\right] .\) From Definitions (1.2) and (2.1), we get

$$\begin{aligned} {}^{PAB}{\mathbb {I}}_{0}^{\rho }{}^{PAB}{\mathbb {D}}_{0}^{\rho }\mu (\varsigma )={\mathbb {I}}^{1}{\mathbb {D}}^{1}\mu (\varsigma ). \end{aligned}$$

By the Definitions of classical integral \({\mathbb {I}}^{1}\) and classical integral \({\mathbb {D}}^{1},\) we have

$$\begin{aligned} {\mathbb {I}}^{1}{\mathbb {D}}^{1}\mu (\varsigma )=\int _{0}^{\varsigma }{\mathbb {D}} ^{1}\mu (\varrho )d\varrho =\int _{0}^{\varsigma }\mu ^{\prime }(\varrho )d\varrho =\mu (\varsigma )-\mu (0). \end{aligned}$$

Thus

$$\begin{aligned} {}^{PAB}{\mathbb {I}}_{0}^{\rho }{}^{PAB}{\mathbb {D}}_{0}^{\rho }\mu (\varsigma )=\mu (\varsigma )-\mu (0),{}\varsigma \in \left[ 0,\varsigma _{1}\right] . \end{aligned}$$

Case (2): For \(\varsigma \in \left[ \varsigma _{1},T\right] .\) From Definitions (1.2) and (2.1), we get

$$\begin{aligned} {}^{PAB}{\mathbb {I}}_{0}^{\rho }{}^{PAB}{\mathbb {D}}_{0}^{\rho }\mu (\varsigma )=^{AB}{\mathbb {I}}_{\varsigma _{1}}^{\rho }{}^{ABR}{\mathbb {D}} _{\varsigma _{1}}^{\rho }\mu (\varsigma ). \end{aligned}$$

Following the same steps as outlined in the proof provided by Atangana and Baleanu [5], we obtain

$$\begin{aligned} ^{AB}{\mathbb {I}}_{0}^{\rho }{}^{ABR}{\mathbb {D}}_{0}^{\rho }\mu (\varsigma )=\mu (\varsigma )-\mu (\varsigma _{1}),{}\varsigma \in \left[ \varsigma _{1},T\right] . \end{aligned}$$

Thus, from the above cases, we get

$$\begin{aligned} {}^{PAB}{\mathbb {I}}_{0}^{\rho }{}^{PAB}{\mathbb {D}}_{0}^{\rho }\mu (\varsigma )=\left\{ \begin{array}{l} \mu (\varsigma )-\mu (0), \text{ if } \varsigma \in \left[ 0,\varsigma _{1}\right] , \\ \mu (\varsigma )-\mu (\varsigma _{1}), \text{ if } \varsigma \in \left[ \varsigma _{1},T\right] . \end{array} \right. \end{aligned}$$

\(\square \)

Lemma 2.3

For \(\rho \in \left( 0,1\right] \), \(\mu \in C\left( {\mathcal {J}}, {\mathbb {R}} \right) \). Then, we have

$$\begin{aligned} {}^{PAB}{\mathbb {D}}_{0}^{\rho }{}^{PAB}{\mathbb {I}}_{0}^{\rho }\mu (\varsigma )=\mu (\varsigma ). \end{aligned}$$

Proof

Case (1): For \(\varsigma \in \left[ 0,\varsigma _{1}\right] .\) From Definitions (1.2) and (2.1), we have

$$\begin{aligned} {}^{PAB}{\mathbb {D}}_{0}^{\rho }{}^{PAB}{\mathbb {I}}_{0}^{\rho }\mu (\varsigma )={\mathbb {D}}^{1}{\mathbb {I}}^{1}\mu (\varsigma ). \end{aligned}$$

From Kilbas [3], for \(\rho \in \left( n-1,n\right] ,n\in {\mathbb {N}},\mu \in C\left( {\mathcal {J}}, {\mathbb {R}} \right) ,\) that \({\mathbb {D}}^{\rho }{\mathbb {I}}^{\rho }\mu (\varsigma )=\mu (\varsigma )\) and in the special case for \(\rho =1,\) we have \({\mathbb {D}}^{1} {\mathbb {I}}^{1}\mu (\varsigma )=\mu (\varsigma ).\) Thus, we get

$$\begin{aligned} {}^{PAB}{\mathbb {D}}_{0}^{\rho }{}^{PAB}{\mathbb {I}}_{0}^{\rho }\mu (\varsigma )=\mu (\varsigma ), \text{ if } \varsigma \in \left[ 0,\varsigma _{1}\right] . \end{aligned}$$

Case (2): For \(\varsigma \in \left[ \varsigma _{1},T\right] .\) From Definitions (1.2) and (2.1), we have

$$\begin{aligned} {}^{PAB}{\mathbb {D}}_{0}^{\rho }{}^{PAB}{\mathbb {I}}_{0}^{\rho }\mu (\varsigma )=^{ABR}{\mathbb {D}}_{\varsigma _{1}}^{\rho }{}^{AB}{\mathbb {I}} _{\varsigma _{1}}^{\rho }\mu (\varsigma ). \end{aligned}$$

Following the same steps as outlined in the proof provided by Atangana and Baleanu [5], we obtain

$$\begin{aligned} {}^{PAB}{\mathbb {D}}_{0}^{\rho }{}^{PAB}{\mathbb {I}}_{0}^{\rho }\mu (\varsigma )=\mu (\varsigma ), \text{ if } \varsigma \in \left[ \varsigma _{1},T\right] . \end{aligned}$$

Thus, from the above cases, we get

$$\begin{aligned} {}^{PAB}{\mathbb {D}}_{0}^{\rho }{}^{PAB}{\mathbb {I}}_{0}^{\rho }\mu (\varsigma )=\mu (\varsigma ). \end{aligned}$$

\(\square \)

3 Equivalent Integral Equation

The next lemma involves the transformation of the suggested system (1.1) into an equivalent integral equation.

Lemma 3.1

For \(\sigma \left( \varsigma \right) \ge 0,\varsigma \in \left( 0,T\right] ,T>0,\) the solution of the following system [26]

$$\begin{aligned} \left\{ \begin{array}{l} {}^{PAB}{\mathbb {D}}_{0}^{\rho _{1}}\mu _{1}(\varsigma )=\hslash _{1}(\varsigma ,\mu _{1}(\varsigma ),\mu _{1}(\varsigma -\sigma \left( \varsigma \right) ),\mu _{2}(\varsigma )), \\ {}^{PAB}{\mathbb {D}}_{0}^{\rho _{2}}\mu _{2}(\varsigma )=\hslash _{2}(\varsigma ,\mu _{1}(\varsigma ),\mu _{2}(\varsigma ),\mu _{2}(\varsigma -\sigma \left( \varsigma \right) )), \end{array} \right. \end{aligned}$$
(3.1)

is given by

$$\begin{aligned} \mu _{1}(\varsigma )=\left\{ \begin{array}{l} \mu _{1}(0)+\int _{0}^{\varsigma }\hslash _{1}\left( \varrho ,\mu _{1}(\varrho ),\mu _{1}(\varrho -\sigma \left( \varrho \right) ),\mu _{2}(\varrho )\right) d\varrho ,\varsigma \in \left[ 0,\varsigma _{1}\right] , \\ \mu _{1}(\varsigma _{1})+\frac{1-\rho _{1}}{\Delta \mathcal {(}\rho _{1} \mathcal {)}}\hslash _{1}\left( \varsigma ,\mu _{1}(\varsigma ),\mu _{1}(\varsigma -\sigma \left( \varsigma \right) ),\mu _{2}(\varsigma )\right) \\ +\frac{\rho _{1}}{\Delta \mathcal {(}\rho _{1}\mathcal {)}\Gamma \mathcal {(} \rho _{1}\mathcal {)}}\int _{\varsigma _{1}}^{\varsigma }(\varsigma -\varrho )^{\rho _{1}-1}\hslash _{1}\left( \varrho ,\mu _{1}(\varrho ),\mu _{1}(\varrho -\sigma \left( \varrho \right) ),\mu _{2}(\varrho )\right) d\varrho ,\varsigma \in \left[ \varsigma _{1},T\right] . \end{array} \right. \end{aligned}$$

and

$$\begin{aligned} \mu _{2}(\varsigma )=\left\{ \begin{array}{l} \mu _{2}(0)+\int _{0}^{\varsigma }\hslash _{2}\left( \varrho ,\mu _{1}(\varrho ),\mu _{2}(\varrho ),\mu _{2}(\varrho -\sigma \left( \varrho \right) )\right) d\varrho ,\varsigma \in \left[ 0,\varsigma _{1}\right] , \\ \mu _{2}(\varsigma _{1})+\frac{1-\rho _{2}}{\Delta \mathcal {(}\rho _{2} \mathcal {)}}\hslash _{2}\left( \varsigma ,\mu _{1}(\varsigma ),\mu _{2}(\varsigma ),\mu _{2}(\varsigma -\sigma \left( \varsigma \right) )\right) \\ +\frac{\rho _{2}}{\Delta \mathcal {(}\rho _{2}\mathcal {)}\Gamma \mathcal {(} \rho _{2}\mathcal {)}}\int _{\varsigma _{1}}^{\varsigma }(\varsigma -\varrho )^{\rho _{2}-1}\hslash _{2}\left( \varrho ,\mu _{1}(\varrho ),\mu _{2}(\varrho ),\mu _{2}(\varrho -\sigma \left( \varrho \right) )\right) d\varrho ,\varsigma \in \left[ \varsigma _{1},T\right] . \end{array} \right. \end{aligned}$$

3.1 Assumptions and Notations

To simplify our analysis, we employ the following notations:

$$\begin{aligned} {\mathcal {A}}_{i}=\left[ \frac{1-\rho _{i}}{\Delta \mathcal {(}\rho _{i} \mathcal {)}}+\frac{(T-\varsigma _{1})^{\rho _{i}}}{\Delta \mathcal {(}\rho _{i}\mathcal {)}\Gamma \mathcal {(}\rho _{i}\mathcal {)}}\right] ,i=1,2, \end{aligned}$$
(3.2)

and

$$\begin{aligned} \hslash _{i}^{\left( \mu _{1},\mu _{2}\right) }\left( \varsigma \right) =\hslash _{i}\left( \varsigma ,\mu _{1}(\varsigma ),\mu _{i}(\varsigma -\sigma \left( \varsigma \right) ),\mu _{2}(\varsigma )\right) ,i=1,2. \end{aligned}$$

By (\(H_{1}\)), for \(i=1,2,\) we have

$$\begin{aligned}{} & {} \left| \hslash _{i}^{\left( \mu _{1},\mu _{2}\right) }\left( \varsigma \right) \right| =\left| \hslash _{i}\left( \varsigma ,\mu _{1}(\varsigma ),\mu _{i}(\varsigma -\sigma \left( \varsigma \right) ),\mu _{2}(\varsigma )\right) \right| \nonumber \\{} & {} \quad \le \left| \hslash _{i}\left( \varsigma ,\mu _{1}(\varsigma ),\mu _{i}(\varsigma -\sigma \left( \varsigma \right) ),\mu _{2}(\varsigma )\right) -\hslash _{i}(\varsigma ,0,0,0)\right| +\left| \hslash _{i}(\varsigma ,0,0,0)\right| \nonumber \\{} & {} \quad \le 3\varphi _{i}\left\| \left( \mu _{1},\mu _{2}\right) \right\| + {\mathcal {M}}_{i}, \end{aligned}$$
(3.3)

where \({\mathcal {M}}_{i}\mathcal {=}\sup _{\varsigma \in {\mathcal {J}}}\left| \hslash _{i}(\varsigma ,0,0,0)\right| .\)

Based on Lemma 3.1, to facilitate the discussion of our results using fixed-point theorems, we define an operator \(\Phi :{\mathbb {S}}\rightarrow {\mathbb {S}}\) by

$$\begin{aligned} \Phi \left( \mu _{1},\mu _{1}\right) (\varsigma )=\left( \Phi _{1}\left( \mu _{1},\mu _{1}\right) (\varsigma ),\Phi _{2}\left( \mu _{1},\mu _{1}\right) (\varsigma )\right) , \end{aligned}$$
(3.4)

such that

$$\begin{aligned} \Phi _{1}\left( \mu _{1},\mu _{1}\right) (\varsigma )=\left\{ \begin{array}{l} \mu _{1}(0)+\int _{0}^{\varsigma }\hslash _{1}^{\left( \mu _{1},\mu _{2}\right) }\left( \varrho \right) d\varrho ,\varsigma \in \left[ 0,\varsigma _{1}\right] , \\ \mu _{1}(\varsigma _{1})+\frac{1-\rho _{1}}{\Delta \mathcal {(}\rho _{1} \mathcal {)}}\hslash _{1}^{\left( \mu _{1},\mu _{2}\right) }\left( \varsigma \right) \\ +\frac{\rho _{1}}{\Delta \mathcal {(}\rho _{1}\mathcal {)}\Gamma \mathcal {(} \rho _{1}\mathcal {)}}\int _{\varsigma _{1}}^{\varsigma }(\varsigma -\varrho )^{\rho _{1}-1}\hslash _{1}^{\left( \mu _{1},\mu _{2}\right) }\left( \varrho \right) d\varrho ,\varsigma \in \left[ \varsigma _{1},T\right] . \end{array} \right. \end{aligned}$$

and

$$\begin{aligned} \Phi _{2}\left( \mu _{1},\mu _{1}\right) (\varsigma )=\left\{ \begin{array}{l} \mu _{2}(0)+\int _{0}^{\varsigma }\hslash _{2}^{\left( \mu _{1},\mu _{2}\right) }\left( \varrho \right) d\varrho ,\varsigma \in \left[ 0,\varsigma _{1}\right] , \\ \mu _{2}(\varsigma _{1})+\frac{1-\rho _{2}}{\Delta \mathcal {(}\rho _{2} \mathcal {)}}\hslash _{2}^{\left( \mu _{1},\mu _{2}\right) }\left( \varsigma \right) \\ +\frac{\rho _{2}}{\Delta \mathcal {(}\rho _{2}\mathcal {)}\Gamma \mathcal {(} \rho _{2}\mathcal {)}}\int _{\varsigma _{1}}^{\varsigma }(\varsigma -\varrho )^{\rho _{2}-1}\hslash _{2}^{\left( \mu _{1},\mu _{2}\right) }\left( \varrho \right) d\varrho ,\varsigma \in \left[ \varsigma _{1},T\right] . \end{array} \right. \end{aligned}$$

We note that our system (1.1) has a solution if and only if the operator \(\Phi \) has fixed points.

4 Existence Result

In this section, we will utilize the Leary–Schauder alternative fixed-point theorem [48] to establish the existence result.

Theorem 4.1

Let \({\mathbb {S}}\) be a non-empty, closed convex subset of a Banach space X. If \(\Phi :{\mathbb {S}}\rightarrow {\mathbb {S}}\) is completely continuous operator and \({\mathbb {V}}\left( \Phi \right) =\big \{ \mu \in {\mathbb {S}}:\mu =\epsilon \Phi \left( \mu \right) \text{ for } \text{ some } 0\le \epsilon \le 1\big \}.\) Then, either \({\mathbb {V}}\left( \Phi \right) \) is unbounded or \( \Phi \) has fixed point.

Theorem 4.2

(Existence result) Suppose \(\left( H_{1}\right) \) and \( \left( H_{2}\right) \) are satisfied. Then, the system (1.1) has a solution, provided that

$$\begin{aligned} 0<\max \left\{ \varsigma _{1}\left( 2\tau _{2}^{*}+\eta _{2}^{*}\right) ,\varsigma _{1}\left( \tau _{3}^{*}+2\eta _{3}^{*}\right) ,\left( 2{\mathcal {A}}_{1}\tau _{2}^{*}+{\mathcal {A}}_{2}\eta _{2}^{*}\right) ,\left( {\mathcal {A}}_{1}\tau _{3}^{*}+2{\mathcal {A}}_{2}\eta _{3}^{*}\right) \right\} <\frac{1}{2}, \end{aligned}$$

where \({\mathcal {A}}_{i},i=1,2\) are given by (3.2).

Proof

To apply the Leary–Schauder alternative fixed-point Theorem, we divide the proof into three steps as follows:

\(\underline{{\mathrm{Step\,} (1)\,\Phi :{\mathbb {S}}\rightarrow {\mathbb {S}}}\,\mathrm{is\,a\,continuous. }}\) By considering the Definition of the operator \(\Phi \) and the continuity of the functions \(\hslash _{1}\) and \(\hslash _{2}\), we can conclude that \( \Phi \) is continuous.

\(\underline{{\textrm{Step }\,(2)\, \Phi \,\mathrm{is \,uniformly \,bounded.}}}\) Let \(Q\subset {\mathbb {S}}\) be a bounded set. Then for all \(\left( \mu _{1},\mu _{2}\right) \in Q\), there exists \(\Bbbk _{1},\Bbbk _{2}>0\), such that

$$\begin{aligned} \left\{ \begin{array}{l} \left| \hslash _{1}^{\left( \mu _{1},\mu _{2}\right) }\left( \varsigma \right) \right| \le \Bbbk _{1}, \\ \\ \left| \hslash _{2}^{\left( \mu _{1},\mu _{2}\right) }\left( \varsigma \right) \right| \le \Bbbk _{2}. \end{array} \right. \end{aligned}$$

Then for any \(\left( \mu _{1},\mu _{2}\right) \in Q,\) we have two cases as follows:

Case (1): For \(\varsigma \in \left[ 0,\varsigma _{1}\right] \) and \( \left( \mu _{1},\mu _{2}\right) \in Q,\) we have

$$\begin{aligned} \left| \Phi _{1}\left( \mu _{1},\mu _{2}\right) \right|= & {} \left| \mu _{1}(0)+\int _{0}^{\varsigma }\hslash _{1}^{\left( \mu _{1},\mu _{2}\right) }\left( \varrho \right) d\varrho \right| \\\le & {} \left| \mu _{1}(0)\right| +\int _{0}^{\varsigma }\left| \hslash _{1}^{\left( \mu _{1},\mu _{2}\right) }\left( \varrho \right) \right| d\varrho \\\le & {} \left| \mu _{1}(0)\right| +\Bbbk _{1}\varsigma _{1}. \end{aligned}$$

Thus

$$\begin{aligned} \left\| \Phi _{1}\left( \mu _{1},\mu _{2}\right) \right\| \le \left| \mu _{1}(0)\right| +\Bbbk _{1}\varsigma _{1}<\infty . \end{aligned}$$
(4.1)

In the same manner with second operator \(\Phi _{2}\), we have

$$\begin{aligned} \left\| \Phi _{2}\left( \mu _{1},\mu _{2}\right) \right\| \le \left| \mu _{2}(0)\right| +\Bbbk _{2}\varsigma _{1}<\infty . \end{aligned}$$
(4.2)

From (4.1), (4.2) and Definition of the norm of Banach product space (2.1), we get

$$\begin{aligned} \left\| \Phi \left( \mu _{1},\mu _{2}\right) \right\| \le \left| \mu _{1}(0)\right| +\left| \mu _{2}(0)\right| +\varsigma _{1}\left( \Bbbk _{1}+\Bbbk _{2}\right) <\infty . \end{aligned}$$
(4.3)

Hence, the operator \(\Phi \) is uniformly bounded in the subinterval \(\left[ 0,\varsigma _{1}\right] .\)

Case (2): For \(\varsigma \in \left[ \varsigma _{1},T\right] \) and \( \left( \mu _{1},\mu _{2}\right) \in Q,\) we have

$$\begin{aligned} \left| \Phi _{1}\left( \mu _{1},\mu _{2}\right) \right|= & {} \left| \mu _{1}(\varsigma _{1})+\frac{1-\rho _{1}}{\Delta \mathcal {(} \rho _{1}\mathcal {)}}\hslash _{1}^{\left( \mu _{1},\mu _{2}\right) }\left( \varsigma \right) +\frac{\rho _{1}}{\Delta \mathcal {(}\rho _{1}\mathcal {)} \Gamma \mathcal {(}\rho _{1}\mathcal {)}}\int _{\varsigma _{1}}^{\varsigma }(\varsigma -\varrho )^{\rho _{1}-1}\hslash _{1}^{\left( \mu _{1},\mu _{2}\right) }\left( \varrho \right) d\varrho \right| \\\le & {} \left| \mu _{1}(\varsigma _{1})\right| +\frac{1-\rho _{1}}{ \Delta \mathcal {(}\rho _{1}\mathcal {)}}\left| \hslash _{1}^{\left( \mu _{1},\mu _{2}\right) }\left( \varsigma \right) \right| +\frac{\rho _{1}}{ \Delta \mathcal {(}\rho _{1}\mathcal {)}\Gamma \mathcal {(}\rho _{1}\mathcal {)}} \int _{\varsigma _{1}}^{\varsigma }(\varsigma -\varrho )^{\rho _{1}-1}\left| \hslash _{1}^{\left( \mu _{1},\mu _{2}\right) }\left( \varrho \right) \right| d\varrho \\\le & {} \left| \mu _{1}(\varsigma _{1})\right| +\left( \frac{1-\rho _{1}}{\Delta \mathcal {(}\rho _{1}\mathcal {)}}+\frac{(T-\varsigma _{1})^{\rho _{1}}}{\Delta \mathcal {(}\rho _{1}\mathcal {)}\Gamma \mathcal {(}\rho _{1} \mathcal {)}}\right) \Bbbk _{1}. \end{aligned}$$

Thus

$$\begin{aligned} \left\| \Phi _{1}\left( \mu _{1},\mu _{2}\right) \right\| \le \left| \mu _{1}(\varsigma _{1})\right| +{\mathcal {A}}_{1}\Bbbk _{1}<\infty . \end{aligned}$$
(4.4)

In the same manner with second operator \(\Phi _{2}\), we have

$$\begin{aligned} \left\| \Phi _{2}\left( \mu _{1},\mu _{2}\right) \right\| \le \left| \mu _{2}(\varsigma _{1})\right| +{\mathcal {A}}_{2}\Bbbk _{2}<\infty , \end{aligned}$$
(4.5)

where \({\mathcal {A}}_{i},i=1,2\) are defined by (3.2).

From (4.4), (4.5) and Definition of the norm of Banach product space (2.1), we get

$$\begin{aligned} \left\| \Phi \left( \mu _{1},\mu _{2}\right) \right\| \le \left| \mu _{1}(\varsigma _{1})\right| +\left| \mu _{2}(\varsigma _{1})\right| +{\mathcal {A}}_{1}\Bbbk _{1}+{\mathcal {A}}_{1}\Bbbk _{1}<\infty . \end{aligned}$$
(4.6)

Hence, the operator \(\Phi \) is uniformly bounded in the subinterval \(\left[ \varsigma _{1},T\right] .\)

By (4.3) and (4.6), we conclude that the operator \(\Phi \) is uniformly bounded in the interval \(\left[ 0,T\right] .\)

\(\underline{\textrm{Step }\,(3) \Phi \mathrm{\, is \,equicontinuous}}\). For any \(\left( \mu _{1},\mu _{2}\right) \in Q,\) we have two cases as follows:

Case (1): For \(\varsigma \in \left[ 0,\varsigma _{1}\right] ,0\le \varsigma _{a}<\varsigma _{b}\le \varsigma _{1}\) and \(\left( \mu _{1},\mu _{2}\right) \in Q,\) we have

$$\begin{aligned} \left| \Phi _{1}\left( \mu _{1},\mu _{2}\right) \left( \varsigma _{b}\right) -\Phi _{1}\left( \mu _{1},\mu _{2}\right) \left( \varsigma _{a}\right) \right|= & {} \left| \int _{0}^{\varsigma _{b}}\hslash _{1}^{\left( \mu _{1},\mu _{2}\right) }\left( \varrho \right) d\varrho -\int _{0}^{\varsigma _{a}}\hslash _{1}^{\left( \mu _{1},\mu _{2}\right) }\left( \varrho \right) d\varrho \right| \\\le & {} \int _{\varsigma _{a}}^{\varsigma _{b}}\left| \hslash _{1}^{\left( \mu _{1},\mu _{2}\right) }\left( \varrho \right) \right| d\varrho . \end{aligned}$$

Hence

$$\begin{aligned} \left\| \Phi _{1}\left( \mu _{1},\mu _{2}\right) \left( \varsigma _{b}\right) -\Phi _{1}\left( \mu _{1},\mu _{2}\right) \left( \varsigma _{a}\right) \right\| \le \left( \varsigma _{b}-\varsigma _{a}\right) \Bbbk _{1}. \end{aligned}$$
(4.7)

In the same manner with second operator \(\Phi _{2}\), we have

$$\begin{aligned} \left\| \Phi _{2}\left( \mu _{1},\mu _{2}\right) \left( \varsigma _{b}\right) -\Phi _{2}\left( \mu _{1},\mu _{2}\right) \left( \varsigma _{a}\right) \right\| \le \left( \varsigma _{b}-\varsigma _{a}\right) \Bbbk _{2}. \end{aligned}$$
(4.8)

It is clear that, when \(\varsigma _{b}-\varsigma _{a}\rightarrow 0\), the right-hand sides of Eqs. (4.7) and (4.8) tend to zero.

Case (2): For \(\varsigma \in \left[ \varsigma _{1},T\right] ,\varsigma _{1}\le \varsigma _{a}<\varsigma _{b}\le T\) and \(\left( \mu _{1},\mu _{2}\right) \in Q,\) we have

$$\begin{aligned}{} & {} \left| \Phi _{1}\left( \mu _{1},\mu _{2}\right) \left( \varsigma _{b}\right) -\Phi _{1}\left( \mu _{1},\mu _{2}\right) \left( \varsigma _{a}\right) \right| \\{} & {} \quad \le \frac{1-\rho _{1}}{\Delta \mathcal {(}\rho _{1}\mathcal {)}}\left| \hslash _{1}^{\left( \mu _{1},\mu _{2}\right) }\left( \varsigma _{b}\right) -\hslash _{1}^{\left( \mu _{1},\mu _{2}\right) }\left( \varsigma _{b}\right) \right| \\{} & {} \qquad +\left| \frac{\rho _{1}}{\Delta \mathcal {(}\rho _{1}\mathcal {)}\Gamma \mathcal {(}\rho _{1}\mathcal {)}}\int _{\varsigma _{1}}^{\varsigma _{b}}(\varsigma _{b}-\varrho )^{\rho _{1}-1}\hslash _{1}^{\left( \mu _{1},\mu _{2}\right) }\left( \varrho \right) d\varrho \right. \\{} & {} \qquad \left. -\frac{\rho _{1}}{\Delta \mathcal {(}\rho _{1}\mathcal {)}\Gamma \mathcal {(}\rho _{1}\mathcal {)}}\int _{\varsigma _{1}}^{\varsigma _{a}}(\varsigma _{a}-\varrho )^{\rho _{1}-1}\hslash _{1}^{\left( \mu _{1},\mu _{2}\right) }\left( \varrho \right) d\varrho \right| \\{} & {} \quad \le \frac{1-\rho _{1}}{\Delta \mathcal {(}\rho _{1}\mathcal {)}}\left| \hslash _{1}^{\left( \mu _{1},\mu _{2}\right) }\left( \varsigma _{b}\right) -\hslash _{1}^{\left( \mu _{1},\mu _{2}\right) }\left( \varsigma _{b}\right) \right| \\{} & {} \qquad +\frac{\rho _{1}}{\Delta \mathcal {(}\rho _{1}\mathcal {)}\Gamma \mathcal {(} \rho _{1}\mathcal {)}}\int _{\varsigma _{1}}^{\varsigma _{a}}\left[ (\varsigma _{b}-\varrho )^{\rho _{1}-1}-(\varsigma _{a}-\varrho )^{\rho _{1}-1}\right] \left| \hslash _{1}^{\left( \mu _{1},\mu _{2}\right) }\left( \varrho \right) \right| d\varrho \\{} & {} \qquad +\frac{\rho _{1}}{\Delta \mathcal {(}\rho _{1}\mathcal {)}\Gamma \mathcal {(} \rho _{1}\mathcal {)}}\int _{\varsigma _{a}}^{\varsigma _{b}}(\varsigma _{b}-\varrho )^{\rho _{1}-1}\left| \hslash _{1}^{\left( \mu _{1},\mu _{2}\right) }\left( \varrho \right) \right| d\varrho . \end{aligned}$$

Hence

$$\begin{aligned}{} & {} \left\| \Phi _{1}\left( \mu _{1},\mu _{2}\right) \left( \varsigma _{b}\right) -\Phi _{1}\left( \mu _{1},\mu _{2}\right) \left( \varsigma _{a}\right) \right\| \nonumber \\{} & {} \quad \le \frac{1-\rho _{1}}{\Delta \mathcal {(}\rho _{1}\mathcal {)}}\left| \hslash _{1}^{\left( \mu _{1},\mu _{2}\right) }\left( \varsigma _{b}\right) -\hslash _{1}^{\left( \mu _{1},\mu _{2}\right) }\left( \varsigma _{b}\right) \right| \nonumber \\{} & {} \qquad +\frac{\Bbbk _{1}}{\Delta \mathcal {(}\rho _{1}\mathcal {)}\Gamma \mathcal {(}\rho _{1}\mathcal {)}}\left[ (\varsigma _{b}-\varsigma _{1})^{\rho _{1}}-(\varsigma _{a}-\varsigma _{1})^{\rho _{1}}\right] . \end{aligned}$$
(4.9)

In the same manner with second operator \(\Phi _{2}\), we have

$$\begin{aligned}{} & {} \left\| \Phi _{2}\left( \mu _{1},\mu _{2}\right) \left( \varsigma _{b}\right) -\Phi _{2}\left( \mu _{1},\mu _{2}\right) \left( \varsigma _{a}\right) \right\| \end{aligned}$$
(4.10)
$$\begin{aligned}{} & {} \quad \le \frac{1-\rho _{2}}{\Delta \mathcal {(}\rho _{2}\mathcal {)}}\left| \hslash _{2}^{\left( \mu _{1},\mu _{2}\right) }\left( \varsigma _{b}\right) -\hslash _{2}^{\left( \mu _{1},\mu _{2}\right) }\left( \varsigma _{b}\right) \right| \nonumber \\{} & {} \qquad +\frac{\Bbbk _{2}}{\Delta \mathcal {(}\rho _{2}\mathcal {)}\Gamma \mathcal {(}\rho _{2}\mathcal {)}}\left[ (\varsigma _{b}-\varsigma _{1})^{\rho _{2}}-(\varsigma _{a}-\varsigma _{1})^{\rho _{2}}\right] . \end{aligned}$$
(4.11)

It is clear that, when \(\varsigma _{b}-\varsigma _{a}\rightarrow 0\), the right-hand sides of Eqs. (4.9) and (4.10) tend to zero. Thus, we conclude that the operator \(\Phi \) is equicontinuous. By the above steps, we conclude that \(\Phi :{\mathbb {S}}\rightarrow {\mathbb {S}}\) is completely continuous.

\(\underline{\mathrm{Step \,(4) \,the \,following \,set \,}{\mathbb {V}}\,\mathrm{\,is \,bounded.}}\)

$$\begin{aligned} {\mathbb {V}}=\left\{ \left( \mu _{1},\mu _{2}\right) \in {\mathbb {S}}:\mu _{1}=\epsilon \Phi _{1}\left( \mu _{1},\mu _{2}\right) ,\mu _{2}=\epsilon \Phi _{1}\left( \mu _{1},\mu _{2}\right) ,0\le \epsilon \le 1\right\} . \end{aligned}$$

Case (1): For \(\varsigma \in \left[ 0,\varsigma _{1}\right] \) and \( \left( \mu _{1},\mu _{2}\right) \in Q,\) we have

$$\begin{aligned} \left| \mu _{1}\left( \varsigma \right) \right| =\left| \epsilon \Phi _{1}\left( \mu _{1},\mu _{2}\right) \left( \varsigma \right) \right| \le \left| \Phi _{1}\left( \mu _{1},\mu _{2}\right) \left( \varsigma \right) \right| , \end{aligned}$$

and

$$\begin{aligned} \left| \mu _{2}\left( \varsigma \right) \right| =\left| \epsilon \Phi _{2}\left( \mu _{1},\mu _{2}\right) \left( \varsigma \right) \right| \le \left| \Phi _{2}\left( \mu _{1},\mu _{2}\right) \left( \varsigma \right) \right| . \end{aligned}$$

Case (1): For \(\varsigma \in \left[ 0,\varsigma _{1}\right] \) and \( \left( \mu _{1},\mu _{2}\right) \in Q,\) with using (H\(_{2}\)), we have have

$$\begin{aligned} \left| \mu _{1}\left( \varsigma \right) \right|\le & {} \left| \mu _{1}(0)\right| +\int _{0}^{\varsigma }\left| \hslash _{1}^{\left( \mu _{1},\mu _{2}\right) }\left( \varrho \right) \right| d\varrho \nonumber \\\le & {} \left| \mu _{1}(0)\right| +\left( \tau _{1}^{*}+2\tau _{2}^{*}\left\| \mu _{1}\right\| +\tau _{3}^{*}\left\| \mu _{2}\right\| \right) \varsigma _{1}. \end{aligned}$$
(4.12)

In the same manner with respect to the \(\mu _{2},\) we get

$$\begin{aligned} \left| \mu _{2}\left( \varsigma \right) \right| \le \left| \mu _{2}(0)\right| +\left( \eta _{1}^{*}+\eta _{2}^{*}\left\| \mu _{1}\right\| +2\eta _{3}^{*}\left\| \mu _{2}\right\| \right) \varsigma _{1}. \end{aligned}$$
(4.13)

From (4.12) and (4.13), we get

$$\begin{aligned} \left\| \mu _{1}\right\| \le \left| \mu _{1}(0)\right| +\varsigma _{1}\tau _{1}^{*}+2\varsigma _{1}\tau _{2}^{*}\left\| \mu _{1}\right\| +\varsigma _{1}\tau _{3}^{*}\left\| \mu _{2}\right\| , \end{aligned}$$

and

$$\begin{aligned} \left\| \mu _{2}\right\| \le \left| \mu _{2}(0)\right| +\varsigma _{1}\eta _{1}^{*}+\varsigma _{1}\eta _{2}^{*}\left\| \mu _{1}\right\| +2\varsigma _{1}\eta _{3}^{*}\left\| \mu _{2}\right\| . \end{aligned}$$

Hence

$$\begin{aligned} \left\| \mu _{1}\right\| +\left\| \mu _{2}\right\|\le & {} \left| \mu _{1}(0)\right| +\left| \mu _{2}(0)\right| +\varsigma _{1}\tau _{1}^{*}+\varsigma _{1}\eta _{1}^{*} \\{} & {} +\left( 2\varsigma _{1}\tau _{2}^{*}+\varsigma _{1}\eta _{2}^{*}\right) \left\| \mu _{1}\right\| \\{} & {} +\left( \varsigma _{1}\tau _{3}^{*}+2\varsigma _{1}\eta _{3}^{*}\right) \left\| \mu _{2}\right\| . \end{aligned}$$

Consequently, for all \(\varsigma \in \left[ 0,\varsigma _{1}\right] \), we have

$$\begin{aligned} \left\| \left( \mu _{1},\mu _{2}\right) \right\| \le \frac{\left| \mu _{1}(0)\right| +\left| \mu _{2}(0)\right| +\varsigma _{1}\tau _{1}^{*}+\varsigma _{1}\eta _{1}^{*}}{{\mathbb {W}}_{1}}, \end{aligned}$$
(4.14)

where

$$\begin{aligned} {\mathbb {W}}_{1}=\min \left\{ 1-\left( 2\varsigma _{1}\tau _{2}^{*}+\varsigma _{1}\eta _{2}^{*}\right) ,1-\left( \varsigma _{1}\tau _{3}^{*}+2\varsigma _{1}\eta _{3}^{*}\right) \right\} . \end{aligned}$$

Case (2): For \(\varsigma \in \left[ \varsigma _{1},T\right] \) and \( \left( \mu _{1},\mu _{2}\right) \in Q,\) with using (H\(_{2}\)), we have

$$\begin{aligned} \left| \mu _{1}\left( \varsigma \right) \right|\le & {} \left| \mu _{1}(\varsigma _{1})\right| +\left( \frac{1-\rho _{1}}{\Delta \mathcal {(}\rho _{1}\mathcal {)}}+\frac{(T-\varsigma _{1})^{\rho _{1}}}{ \Delta \mathcal {(}\rho _{1}\mathcal {)}\Gamma \mathcal {(}\rho _{1}\mathcal {)}} \right) \left( \tau _{1}^{*}+2\tau _{2}^{*}\left\| \mu _{1}\right\| +\tau _{3}^{*}\left\| \mu _{2}\right\| \right) \nonumber \\\le & {} \left| \mu _{1}(\varsigma _{1})\right| +{\mathcal {A}}_{1}\left( \tau _{1}^{*}+2\tau _{2}^{*}\left\| \mu _{1}\right\| +\tau _{3}^{*}\left\| \mu _{2}\right\| \right) . \end{aligned}$$
(4.15)

In the same manner with respect to \(\mu _{2},\) we get

$$\begin{aligned} \left| \mu _{2}\left( \varsigma \right) \right| \le \left| \mu _{2}(\varsigma _{1})\right| +{\mathcal {A}}_{2}\left( \eta _{1}^{*}+\eta _{2}^{*}\left\| \mu _{1}\right\| +2\eta _{3}^{*}\left\| \mu _{2}\right\| \right) . \end{aligned}$$
(4.16)

From (4.15) and (4.16), we get

$$\begin{aligned} \left\| \mu _{1}\right\| \le \left| \mu _{1}(\varsigma _{1})\right| +{\mathcal {A}}_{1}\tau _{1}^{*}+2{\mathcal {A}}_{1}\tau _{2}^{*}\left\| \mu _{1}\right\| +{\mathcal {A}}_{1}\tau _{3}^{*}\left\| \mu _{2}\right\| , \end{aligned}$$

and

$$\begin{aligned} \left\| \mu _{2}\right\| \le \left| \mu _{2}(\varsigma _{1})\right| +{\mathcal {A}}_{2}\eta _{1}^{*}+{\mathcal {A}}_{2}\eta _{2}^{*}\left\| \mu _{1}\right\| +2{\mathcal {A}}_{2}\eta _{3}^{*}\left\| \mu _{2}\right\| . \end{aligned}$$

Hence

$$\begin{aligned} \left\| \mu _{1}\right\| +\left\| \mu _{2}\right\|\le & {} \left| \mu _{1}(\varsigma _{1})\right| +\left| \mu _{2}(\varsigma _{1})\right| +{\mathcal {A}}_{1}\tau _{1}^{*}+{\mathcal {A}} _{2}\eta _{1}^{*} \\{} & {} +\left( 2{\mathcal {A}}_{1}\tau _{2}^{*}+{\mathcal {A}}_{2}\eta _{2}^{*}\right) \left\| \mu _{1}\right\| \\{} & {} +\left( {\mathcal {A}}_{1}\tau _{3}^{*}+2{\mathcal {A}}_{2}\eta _{3}^{*}\right) \left\| \mu _{2}\right\| . \end{aligned}$$

Consequently, for all \(\varsigma \in \left[ \varsigma _{1},T\right] \), we have

$$\begin{aligned} \left\| \left( \mu _{1},\mu _{2}\right) \right\| \le \frac{\left| \mu _{1}(\varsigma _{1})\right| +\left| \mu _{2}(\varsigma _{1})\right| +{\mathcal {A}}_{1}\tau _{1}^{*}+{\mathcal {A}}_{2}\eta _{1}^{*}}{{\mathbb {W}}_{2}}, \end{aligned}$$
(4.17)

where

$$\begin{aligned} {\mathbb {W}}_{2}=\min \left\{ 1-\left( 2{\mathcal {A}}_{1}\tau _{2}^{*}+ {\mathcal {A}}_{2}\eta _{2}^{*}\right) ,1-\left( {\mathcal {A}}_{1}\tau _{3}^{*}+2{\mathcal {A}}_{2}\eta _{3}^{*}\right) \right\} . \end{aligned}$$

Hence from (4.14) and (4.17), we conclude that the set \({\mathbb {V}} \) is bounded in the interval \(\left[ 0,T\right] .\) Thus, all conditions in Leary–Schauder alternative fixed point theorem are satisfied and hence the operator \(\Phi \) has at least one fixed point. Therefore, the system (1.1) has at least one solution. \(\square \)

5 Uniqueness Result

In this section, we shall apply the following Banach contraction principle [49] to prove the uniqueness result.

Theorem 5.1

Let \(C\left( {\mathcal {J}}, {\mathbb {R}} \right) \) be a Banach space. The operator \(\Phi :{\mathbb {S}}\rightarrow {\mathbb {S}}\) is a contraction if there exists a constant \(0<L<1\) such that i.e., \(\left\| \Phi (\mu )-\Phi (\mu ^{*})\right\| \le L\left\| \mu -\mu ^{*}\right\| \) for all \(\mu ,\mu ^{*}\in {\mathbb {S}}.\)

Theorem 5.2

(Uniqueness result) Assume that \((H_{1})\) holds and also the following inequalities are hold true

$$\begin{aligned} 0<\max \left\{ 3\varphi _{i}{\mathcal {A}}_{i},6\varphi _{i}\varsigma _{1}\right\} <\frac{1}{2}.i=1.2, \end{aligned}$$
(5.1)

where \({\mathcal {A}}_{i}\) are given by (3.2). Then, the system (1.1) has unique solution.

Proof

Consider the closed ball \({\mathcal {K}}_{\lambda }\) defined as \({\mathcal {K}} _{\lambda }=\left\{ \left( \mu _{1},\mu _{2}\right) \in {\mathbb {S}}:\left\| \left( \mu _{1},\mu _{2}\right) \right\| \le \lambda \right\} \) with

$$\begin{aligned} \lambda \ge \max \left\{ \frac{\left| \mu _{1}(0)\right| +\left| \mu _{2}(0)\right| +\left( {\mathcal {M}}_{1}+{\mathcal {M}} _{2}\right) \varsigma _{1}}{\frac{1}{2}-3\varphi _{i}\varsigma _{1}},\frac{ \ell _{i}+{\mathcal {A}}_{i}{\mathcal {M}}_{i}}{\frac{1}{2}-\varphi _{i}{\mathcal {A}} _{i}}\right\} ,i=1,2, \end{aligned}$$

where \({\mathcal {M}}_{i}\mathcal {=}\sup _{\varsigma \in {\mathcal {J}}}\left| \hslash _{i}(\varsigma ,0,0,0)\right| ,\ell _{i}=\left| \mu _{i}(\varsigma _{1})\right| ,i=1,2\). To apply the Banach contraction principle, we divide the proof into the following steps.

\(\underline{\mathrm{Step \,(1)\, }\,\Phi {\mathcal {K}}_{\lambda }\subset {\mathcal {K}}_{\lambda },\,\textrm{where }\,\Phi \,\mathrm{defined \,in }}\)(3.4). For all \(\left( \mu _{1},\mu _{2}\right) \in {\mathcal {K}}_{\lambda }\), we have two cases as follows:

Case 1 For \(\varsigma \in \left[ 0,\varsigma _{1}\right] ,\) we have

$$\begin{aligned} \left| \Phi _{1}\left( \mu _{1},\mu _{2}\right) (\varsigma )\right| \le \left| \mu _{1}(0)\right| +\int _{0}^{\varsigma }\left| \hslash _{1}^{\left( \mu _{1},\mu _{2}\right) }\left( \varrho \right) \right| d\varrho . \end{aligned}$$

By (3.3), we get

$$\begin{aligned} \left\| \Phi _{1}\left( \mu _{1},\mu _{2}\right) \right\|\le & {} \left| \mu _{1}(0)\right| +\varphi _{1}\left( 2\left\| \mu _{1}\right\| +\left\| \mu _{2}\right\| \right) \varsigma _{1}+ {\mathcal {M}}_{1}\varsigma _{1} \nonumber \\\le & {} \left| \mu _{1}(0)\right| +3\varphi _{1}\lambda \varsigma _{1}+{\mathcal {M}}_{1}\varsigma _{1}\le \frac{\lambda }{2}. \end{aligned}$$
(5.2)

In the same manner, we have

$$\begin{aligned} \left\| \Phi _{2}\left( \mu _{1},\mu _{2}\right) \right\| \le \left| \mu _{2}(0)\right| +3\varphi _{2}\lambda \varsigma _{1}+ {\mathcal {M}}_{2}\varsigma _{1}\le \frac{\lambda }{2}. \end{aligned}$$
(5.3)

Thus, from 5.2 and 5.3, we get

$$\begin{aligned} \left\| \Phi \left( \mu _{1},\mu _{2}\right) \right\|= & {} \left\| \Phi _{1}\left( \mu _{1},\mu _{1}\right) \right\| +\left\| \Phi _{2}\left( \mu _{1},\mu _{1}\right) \right\| \\\le & {} \frac{\lambda }{2}+\frac{\lambda }{2}\le \lambda . \end{aligned}$$

Case 2 For \(\varsigma \in \left[ \varsigma _{1},T\right] \) and \(\left( \mu _{1},\mu _{1}\right) \in {\mathcal {K}}_{\lambda },\) we have

$$\begin{aligned} \left| \Phi _{1}\left( \mu _{1},\mu _{2}\right) (\varsigma )\right|\le & {} \left| \mu _{1}(\varsigma _{1})\right| +\frac{1-\rho _{1}}{ \Delta \mathcal {(}\rho _{1}\mathcal {)}}\left| \hslash _{1}^{\left( \mu _{1},\mu _{2}\right) }\left( \varsigma \right) \right| \\{} & {} +\frac{\rho _{1}}{\Delta \mathcal {(}\rho _{1}\mathcal {)}\Gamma \mathcal {(} \rho _{1}\mathcal {)}}\int _{\varsigma _{1}}^{\varsigma }(\varsigma -\varrho )^{\rho -1}\left| \hslash _{1}^{\left( \mu _{1},\mu _{2}\right) }\left( \varrho \right) \right| d\varrho . \end{aligned}$$

Put \(\ell _{1}=\left| \mu _{1}(\varsigma _{1})\right| .\) Then, by ( 3.3), we get

$$\begin{aligned} \left\| \Phi _{1}\left( \mu _{1},\mu _{2}\right) \right\|\le & {} \ell _{1}+\left( \frac{1-\rho _{1}}{\Delta \mathcal {(}\rho _{1}\mathcal {)}}+\frac{ (T-\varsigma _{1})^{\rho _{1}}}{\Delta \mathcal {(}\rho _{1}\mathcal {)}\Gamma \mathcal {(}\rho _{1}\mathcal {)}}\right) \left[ 3\varphi _{1}\lambda + {\mathcal {M}}_{1}\right] \nonumber \\\le & {} \ell _{1}+3{\mathcal {A}}_{1}\varphi _{1}\lambda +{\mathcal {A}}_{1} {\mathcal {M}}_{1}\le \frac{\lambda }{2}. \end{aligned}$$
(5.4)

In the same manner with respect to the second operator \(\Phi _{2}\), we have

$$\begin{aligned} \left\| \Phi _{2}\left( \mu _{1},\mu _{2}\right) \right\| \le \ell _{2}+3{\mathcal {A}}_{2}\varphi _{2}\lambda +{\mathcal {A}}_{2}{\mathcal {M}}_{2}\le \frac{\lambda }{2}. \end{aligned}$$
(5.5)

From (5.4) and (5.5), we have

$$\begin{aligned} \left\| \Phi \left( \mu _{1},\mu _{2}\right) \right\| =\left\| \Phi _{1}\left( \mu _{1},\mu _{2}\right) \right\| +\left\| \Phi _{2}\left( \mu _{1},\mu _{2}\right) \right\| \le \lambda . \end{aligned}$$

Thus, \(\Phi {\mathcal {K}}_{\lambda }\subset {\mathcal {K}}_{\lambda }.\)

\(\underline{\mathrm{Step \,(2)\, }\Phi \,\mathrm{is \,a \,contraction.}}\) For all \(\left( \mu _{1},\mu _{2}\right) ,\left( {\widehat{\mu }}_{1},{\widehat{\mu }}_{2}\right) \in {\mathcal {K}}_{\lambda },\) we have

Case (1): For \(\varsigma \in \left[ 0,\varsigma _{1}\right] \), we have

$$\begin{aligned} \left| \Phi _{1}\left( \mu _{1},\mu _{2}\right) (\varsigma )-\Phi _{1}\left( {\widehat{\mu }}_{1},{\widehat{\mu }}_{2}\right) (\varsigma )\right| \le \int _{0}^{\varsigma }\left| \hslash _{1}^{\left( \mu _{1},\mu _{2}\right) }\left( \varrho \right) -\hslash _{1}^{\left( \widehat{ \mu }_{1},{\widehat{\mu }}_{2}\right) }\left( \varrho \right) \right| d\varrho . \end{aligned}$$

By (\(H_{2}\)), we get

$$\begin{aligned} \left\| \Phi _{1}\left( \mu _{1},\mu _{2}\right) -\Phi _{1}\left( {\widehat{\mu }}_{1},{\widehat{\mu }}_{2}\right) \right\| \le 3\varphi _{1}\varsigma _{1}\left\| \left( \mu _{1},\mu _{2}\right) -\left( {\widehat{\mu }}_{1},{\widehat{\mu }}_{2}\right) \right\| . \end{aligned}$$
(5.6)

In the same manner with respect to the operator \(\Phi _{2}\), we have

$$\begin{aligned} \left\| \Phi _{2}\left( \mu _{1},\mu _{2}\right) -\Phi _{2}\left( {\widehat{\mu }}_{1},{\widehat{\mu }}_{2}\right) \right\| \le 3\varphi _{2}\varsigma _{1}\left\| \left( \mu _{1},\mu _{2}\right) -\left( {\widehat{\mu }}_{1},{\widehat{\mu }}_{2}\right) \right\| . \end{aligned}$$
(5.7)

Thus, from (5.6) and (5.7), we get

$$\begin{aligned} \left\| \Phi \left( \mu _{1},\mu _{2}\right) -\Phi \left( {\widehat{\mu }} _{1},{\widehat{\mu }}_{2}\right) \right\| \le 3\left( \varphi _{1}+\varphi _{2}\right) \varsigma _{1}\left\| \left( \mu _{1},\mu _{2}\right) -\left( {\widehat{\mu }}_{1},{\widehat{\mu }}_{2}\right) \right\| . \end{aligned}$$
(5.8)

Case (2): For \(\varsigma \in \left[ \varsigma _{1},T\right] \) and \( \left( \mu _{1},\mu _{2}\right) ,\left( {\widehat{\mu }}_{1},{\widehat{\mu }} _{2}\right) \in {\mathcal {K}}_{\lambda }\) with (\(H_{2}\)), we have

$$\begin{aligned} \left| \Phi _{1}\left( \mu _{1},\mu _{2}\right) (\varsigma )-\Phi _{1}\left( {\widehat{\mu }}_{1},{\widehat{\mu }}_{2}\right) (\varsigma )\right|\le & {} \frac{1-\rho _{1}}{\Delta \mathcal {(}\rho _{1}\mathcal {)}}\left| \hslash _{1}^{\left( \mu _{1},\mu _{2}\right) }\left( \varsigma \right) -\hslash _{1}^{\left( {\widehat{\mu }}_{1},{\widehat{\mu }}_{2}\right) }\left( \varsigma \right) \right| \nonumber \\{} & {} +\frac{\rho _{1}}{\Delta \mathcal {(}\rho _{1} \mathcal {)}\Gamma \mathcal {(}\rho _{1}\mathcal {)}}\int _{\varsigma _{1}}^{\varsigma }(\varsigma -\varrho )^{\rho _{1}-1} \nonumber \\ \left| \hslash _{1}^{\left( \mu _{1},\mu _{2}\right) }\left( \varrho \right) -\hslash _{1}^{\left( {\widehat{\mu }}_{1},{\widehat{\mu }}_{2}\right) }\left( \varrho \right) \right| d\varrho\le & {} 3\varphi _{1}{\mathcal {A}}_{1}\left\| \left( \mu _{1},\mu _{2}\right) -\left( {\widehat{\mu }}_{1},{\widehat{\mu }}_{2}\right) \right\| . \end{aligned}$$
(5.9)

In the same manner with respect to the operator \(\Phi _{2}\), we have

$$\begin{aligned} \left\| \Phi _{2}\left( \mu _{1},\mu _{2}\right) -\Phi _{2}\left( {\widehat{\mu }}_{1},{\widehat{\mu }}_{2}\right) \right\| \le 3\varphi _{2} {\mathcal {A}}_{2}\left\| \left( \mu _{1},\mu _{2}\right) -\left( \widehat{ \mu }_{1},{\widehat{\mu }}_{2}\right) \right\| . \end{aligned}$$
(5.10)

Thus, from (5.9) and (5.10), we get

$$\begin{aligned} \left\| \Phi \left( \mu _{1},\mu _{2}\right) -\Phi \left( {\widehat{\mu }} _{1},{\widehat{\mu }}_{2}\right) \right\|\le & {} 3\varphi _{1}{\mathcal {A}} _{1}\left\| \left( \mu _{1},\mu _{2}\right) -\left( {\widehat{\mu }}_{1}, {\widehat{\mu }}_{2}\right) \right\| \nonumber \\{} & {} +\,3\varphi _{2}{\mathcal {A}}_{2}\left\| \left( \mu _{1},\mu _{2}\right) -\left( {\widehat{\mu }}_{1},{\widehat{\mu }}_{2}\right) \right\| \nonumber \\\le & {} 3\left( \varphi _{1}{\mathcal {A}}_{1}+\varphi _{2}{\mathcal {A}} _{2}\right) \left\| \left( \mu _{1},\mu _{2}\right) -\left( {\widehat{\mu }} _{1},{\widehat{\mu }}_{2}\right) \right\| . \qquad \end{aligned}$$
(5.11)

By (5.8) and (5.11) with (5.1), we conclude that the operator \(\Phi \) is contraction. Thus, via the Banach contraction principle, we deduce that the system (1.1) has a unique solution. \(\square \)

6 Hyers–Ulam Stability

In this section, we will define and investigate the Ulam-type stability [50] of a coupled system governed by piecewise Atangana–Baleanu fractional differential equations with delays, as formulated in (1.1). For \( \varsigma \in \left[ 0,T\right] \), we present the following inequalities:

$$\begin{aligned} \left\{ \begin{array}{l} \left| ^{PAB}{\mathbb {D}}_{0}^{\rho _{1}}{\widehat{\mu }}_{1}(\varsigma )-\hslash _{1}^{\left( {\widehat{\mu }}_{1},{\widehat{\mu }}_{2}\right) }(\varsigma )\right| \le \varepsilon _{1}, \\ \\ \left| ^{PAB}{\mathbb {D}}_{0}^{\rho _{2}}{\widehat{\mu }}_{2}(\varsigma )-\hslash _{2}^{\left( {\widehat{\mu }}_{1},{\widehat{\mu }}_{2}\right) }(\varsigma )\right| \le \varepsilon _{2}, \end{array} \right. \end{aligned}$$
(6.1)

and

$$\begin{aligned} \left\{ \begin{array}{l} \left| ^{PAB}{\mathbb {D}}_{0}^{\rho _{1}}{\widehat{\mu }}_{1}(\varsigma )-\hslash _{1}^{\left( {\widehat{\mu }}_{1},{\widehat{\mu }}_{2}\right) }(\varsigma )\right| \le \varepsilon _{1}k\left( \varsigma \right) , \\ \\ \left| ^{PAB}{\mathbb {D}}_{0}^{\rho _{2}}{\widehat{\mu }}_{2}(\varsigma )-\hslash _{1}^{\left( {\widehat{\mu }}_{1},{\widehat{\mu }}_{2}\right) }(\varsigma )\right| \le \varepsilon _{2}k\left( \varsigma \right) , \end{array} \right. \end{aligned}$$
(6.2)

where \(\varepsilon _{1},\varepsilon _{2}\) are positive real numbers and \(k: \left[ 0,T\right] \rightarrow {\mathbb {R}} ^{+}\) is continuous function.

Definition 6.1

[50] The system (1.1) is Hyers–Ulam (HU) stable if there exists a real number \({\mathcal {M}}=\max \left\{ {\mathcal {M}}_{1},{\mathcal {M}} _{2}\right\} >0\) such that for each \(\varepsilon =\max \left\{ \varepsilon _{1},\varepsilon _{2}\right\} >0\) there exists a function \(\left( \widehat{ \mu }_{1},{\widehat{\mu }}_{2}\right) \in {\mathbb {S}}\) satisfies the inequalities (6.1) corresponding to a solution \(\left( \mu _{1},\mu _{2}\right) \in {\mathbb {S}}\) of system (1.1) with

$$\begin{aligned} \left\| \left( {\widehat{\mu }}_{1},{\widehat{\mu }}_{2}\right) -\left( \mu _{1},\mu _{2}\right) \right\| \le {\mathcal {M}}\varepsilon ,\varsigma \in {\mathcal {J}}. \end{aligned}$$

Definition 6.2

[51] The system (1.1) is HUR stable with respect to the function k if there exists a real number \({\mathcal {M}}=\max \left\{ {\mathcal {M}}_{1},{\mathcal {M}}_{2}\right\} >0\) such that for each \(\varepsilon =\max \left\{ \varepsilon _{1},\varepsilon _{2}\right\} >0\) there exists a function \(\left( {\widehat{\mu }}_{1},{\widehat{\mu }}_{2}\right) \in {\mathbb {S}}\) satisfies the inequalities (6.2) corresponding to a solution \(\left( \mu _{1},\mu _{2}\right) \in {\mathbb {S}}\) of system (1.1) with

$$\begin{aligned} \left\| \left( {\widehat{\mu }}_{1},{\widehat{\mu }}_{2}\right) -\left( \mu _{1},\mu _{2}\right) \right\| \le {\mathcal {M}}k\left( \varsigma \right) \varepsilon ,\varsigma \in {\mathcal {J}}. \end{aligned}$$

Remark 6.3

A function \(\left( {\widehat{\mu }}_{1},{\widehat{\mu }}_{2}\right) \in {\mathbb {S}}\) is a solution of the inequalities (6.1) if and only if there exist a small perturbation \(\left( z_{1},z_{2}\right) \in {\mathbb {S}}\) such that

(i) \(\left\{ \begin{array}{l} \left| z_{1}(\varsigma )\right| \le \varepsilon _{1}, \\ \\ \left| z_{2}(\varsigma )\right| \le \varepsilon _{2}. \end{array} \right. \)

(ii) \(\left\{ \begin{array}{l} {}^{PAB}{\mathbb {D}}_{0}^{\rho _{1}}{\widehat{\mu }}_{1}(\varsigma )=\hslash _{1}^{\left( {\widehat{\mu }}_{1},{\widehat{\mu }}_{2}\right) }(\varsigma )+z_{1}(\varsigma ), \\ \\ {}^{PAB}{\mathbb {D}}_{0}^{\rho _{2}}{\widehat{\mu }}_{2}(\varsigma )=\hslash _{1}^{\left( {\widehat{\mu }}_{1},{\widehat{\mu }}_{2}\right) }(\varsigma )+z_{1}(\varsigma ). \end{array} \right. \)

Lemma 6.4

Let \(\left( {\widehat{\mu }}_{1},{\widehat{\mu }}_{2}\right) \in {\mathbb {S}}\) be a function satisfies the inequalities (6.1), then \( \left( {\widehat{\mu }}_{1},{\widehat{\mu }}_{2}\right) \) satisfies the following integral inequalities

$$\begin{aligned} \left| {\widehat{\mu }}_{i}(\varsigma )-\Sigma _{{\widehat{\mu }} _{i}}^{1}\right|\le & {} \varsigma _{1}\varepsilon _{i},\varsigma \in \left[ 0,\varsigma _{1}\right] , \\ \left| {\widehat{\mu }}_{1}(\varsigma )-\Sigma _{{\widehat{\mu }} _{1}}^{2}\right|\le & {} {\mathcal {A}}_{i}\varepsilon _{i},\varsigma \in \left[ \varsigma _{1},T\right] , \end{aligned}$$

where

$$\begin{aligned} \Sigma _{{\widehat{\mu }}_{i}}^{1}={\widehat{\mu }}_{i}(0)+\int _{0}^{\varsigma }\hslash _{i}^{\left( {\widehat{\mu }}_{1},{\widehat{\mu }}_{2}\right) }\left( \varsigma \right) d\varrho , \end{aligned}$$
(6.3)

and

$$\begin{aligned} \Sigma _{{\widehat{\mu }}_{i}}^{2}={\widehat{\mu }}_{i}(\varsigma _{1})+\frac{ 1-\rho _{i}}{\Delta \mathcal {(}\rho _{i}\mathcal {)}}\hslash _{i}^{\left( {\widehat{\mu }}_{1},{\widehat{\mu }}_{2}\right) }\left( \varsigma \right) + \frac{\rho _{i}}{\Delta \mathcal {(}\rho _{i}\mathcal {)}\Gamma \mathcal {(} \rho _{i}\mathcal {)}}\int _{\varsigma _{1}}^{\varsigma }(\varsigma -\varrho )^{\rho _{i}-1}\hslash _{i}^{\left( {\widehat{\mu }}_{1},{\widehat{\mu }} _{2}\right) }\left( \varrho \right) d\varrho , \nonumber \\ \end{aligned}$$
(6.4)

\(i=1,2.\)

Proof

Let \(\left( {\widehat{\mu }}_{1},{\widehat{\mu }}_{2}\right) \in {\mathbb {S}}\) be a function satisfies the inequalities (6.1). Then, by Remark 6.3, we have

$$\begin{aligned} \left\{ \begin{array}{l} {}^{PAB}{\mathbb {D}}_{0}^{\rho _{1}}{\widehat{\mu }}_{1}(\varsigma )=\hslash _{1}^{\left( {\widehat{\mu }}_{1},{\widehat{\mu }}_{2}\right) }(\varsigma )+z_{1}(\varsigma ), \\ \\ {}^{PAB}{\mathbb {D}}_{0}^{\rho _{2}}{\widehat{\mu }}_{2}(\varsigma )=\hslash _{2}^{\left( {\widehat{\mu }}_{1},{\widehat{\mu }}_{2}\right) }(\varsigma )+z_{2}(\varsigma ). \end{array} \right. \end{aligned}$$
(6.5)

According to Lemma 3.1, the solutions of the system (6.5) in the case \(\varsigma \in \left[ 0,\varsigma _{1}\right] ,\) is given as follows

$$\begin{aligned} {\widehat{\mu }}_{1}(\varsigma )={\widehat{\mu }}_{1}(0)+\int _{0}^{\varsigma }\left( \hslash _{1}^{\left( {\widehat{\mu }}_{1},{\widehat{\mu }}_{2}\right) }(\varrho )+z_{1}(\varrho )\right) d\varrho . \end{aligned}$$

Thus, by (6.3), we get

$$\begin{aligned} \left| {\widehat{\mu }}_{1}(\varsigma )-\Sigma _{{\widehat{\mu }} _{1}}^{1}\right| \le \int _{0}^{\varsigma }\left| z_{1}(\varrho )\right| d\varrho \le \varsigma _{1}\varepsilon _{1}. \end{aligned}$$

In the same manner with respect to \({\widehat{\mu }}_{2}\ \)with (6.3), we get

$$\begin{aligned} \left| {\widehat{\mu }}_{2}(\varsigma )-\Sigma _{{\widehat{\mu }} _{2}}^{1}\right| \le \int _{0}^{\varsigma }\left| z_{2}(\varrho )\right| d\varrho \le \varsigma _{1}\varepsilon _{2}. \end{aligned}$$

According to Lemma 3.1, the solutions of the system (6.5) in the case \(\varsigma \in \left[ \varsigma _{1},T\right] ,\) is given as follows

$$\begin{aligned} {\widehat{\mu }}_{1}(\varsigma )=\left\{ \begin{array}{l} {\widehat{\mu }}_{1}(\varsigma _{1})+\frac{1-\rho _{1}}{\Delta \mathcal {(}\rho _{1}\mathcal {)}}\left( \hslash _{1}^{\left( {\widehat{\mu }}_{1},{\widehat{\mu }} _{2}\right) }\left( \varsigma \right) +z_{1}(\varsigma )\right) \\ +\frac{\rho _{1}}{\Delta \mathcal {(}\rho _{1}\mathcal {)}\Gamma \mathcal {(} \rho _{1}\mathcal {)}}\int _{\varsigma _{1}}^{\varsigma }(\varsigma -\varrho )^{\rho _{1}-1}\left( \hslash _{1}^{\left( {\widehat{\mu }}_{1},{\widehat{\mu }} _{2}\right) }\left( \varrho \right) +z_{1}(\varrho )\right) d\varrho . \end{array} \right. \end{aligned}$$

Thus, by (6.4), we get

$$\begin{aligned} \left| {\widehat{\mu }}_{1}(\varsigma )-\Sigma _{{\widehat{\mu }} _{1}}^{2}\right|\le & {} \frac{1-\rho _{1}}{\Delta \mathcal {(}\rho _{1} \mathcal {)}}\left| z_{1}(\varsigma )\right| +\frac{\rho _{1}}{\Delta \mathcal {(}\rho _{1}\mathcal {)}\Gamma \mathcal {(}\rho _{1}\mathcal {)}} \int _{\varsigma _{1}}^{\varsigma }(\varsigma -\varrho )^{\rho _{1}-1}\left| z_{1}(\varsigma )\right| d\varrho \\\le & {} {\mathcal {A}}_{1}\varepsilon _{1}. \end{aligned}$$

In the same manner with respect to \({\widehat{\mu }}_{2},\) we get

$$\begin{aligned} \left| {\widehat{\mu }}_{2}(\varsigma )-\Sigma _{{\widehat{\mu }} _{2}}^{2}\right| \le {\mathcal {A}}_{2}\varepsilon _{2}. \end{aligned}$$

\(\square \)

Theorem 6.5

Assume that the conditions of Theorem 5.2 hold. Then the system (1.1) is HU stable, provided that

$$\begin{aligned} 0<\max \left\{ 3\varsigma _{1}\left( \varphi _{1}+\varphi _{2}\right) ,\left( {\mathcal {A}}_{1}\varphi _{1}+{\mathcal {A}}_{2}\varphi _{2}\right) \right\} <1. \end{aligned}$$
(6.6)

Proof

Let \(\varepsilon =\max \left\{ \varepsilon _{1},\varepsilon _{2}\right\} >0\ \) and \(\left( {\widehat{\mu }}_{1},\widehat{\mu }_{2}\right) \in {\mathbb {S}}\) be a function satisfying the inequalities (6.1) and let \(\left( \mu _{1},\mu _{2}\right) \in {\mathbb {S}}\) be a unique solution of the following system (1.1). Now, according to Lemma 3.1 and (H\(_{1}\)),  we have two cases as follows

Case (1): For \(\varsigma \in \left[ 0,\varsigma _{1}\right] \), with respect to the operator \(\mu _{1},\) we have

$$\begin{aligned} \left| {\widehat{\mu }}_{1}(\varsigma )-\mu _{1}(\varsigma )\right|= & {} \left| {\widehat{\mu }}_{1}(\varsigma )-\mu _{1}(0)+\int _{0}^{\varsigma }\hslash _{1}^{\left( \mu _{1},\mu _{2}\right) }(\varrho )d\varrho \right| \\= & {} \left| {\widehat{\mu }}_{1}(\varsigma )-\mu _{1}(0)+\int _{0}^{\varsigma }\hslash _{1}^{\left( \widehat{\mu }_{1},{\widehat{\mu }}_{2}\right) }\left( \varrho \right) d\varrho \right. \\{} & {} \left. -\int _{0}^{\varsigma }\hslash _{i}^{\left( \widehat{ \mu }_{1},{\widehat{\mu }}_{2}\right) }\left( \varrho \right) d\varrho -\int _{0}^{\varsigma }\hslash _{1}^{\left( \mu _{1},\mu _{2}\right) }(\varrho )d\varrho \right| \\\le & {} \left| {\widehat{\mu }}_{1}(\varsigma )-\mu _{1}(0)-\int _{0}^{\varsigma }\hslash _{1}^{\left( \widehat{\mu }_{1}, {\widehat{\mu }}_{2}\right) }\left( \varrho \right) d\varrho \right| \\{} & {} +\int _{0}^{\varsigma }\left| \hslash _{i}^{\left( {\widehat{\mu }}_{1}, {\widehat{\mu }}_{2}\right) }\left( \varrho \right) -\hslash _{1}^{\left( \mu _{1},\mu _{2}\right) }(\varrho )\right| d\varrho \\\le & {} \left| {\widehat{\mu }}_{1}(\varsigma )-\Sigma _{{\widehat{\mu }} _{1}}^{1}\right| +\int _{0}^{\varsigma }\left| \hslash _{i}^{\left( {\widehat{\mu }}_{1},\widehat{\mu }_{2}\right) }\left( \varrho \right) -\hslash _{1}^{\left( \mu _{1},\mu _{2}\right) }(\varrho )\right| d\varrho . \end{aligned}$$

By (H\(_{1}\)), we have

$$\begin{aligned} \left\| {\widehat{\mu }}_{1}-\mu _{1}\right\| \le \left| {\widehat{\mu }}_{1}(\varsigma )-\Sigma _{\widehat{\mu }_{1}}^{1}\right| +3\varphi _{1}\varsigma _{1}\left[ \left\| {\widehat{\mu }}_{1}-\mu _{1}\right\| +\left\| \widehat{\mu }_{2}-\mu _{2}\right\| \right] . \end{aligned}$$

By Lemma 6.4, we get

$$\begin{aligned} \left\| {\widehat{\mu }}_{1}-\mu _{1}\right\| \le \varsigma _{1}\varepsilon _{1}+3\varphi _{1}\varsigma _{1}\left[ \left\| {\widehat{\mu }}_{1}-\mu _{1}\right\| +\left\| \widehat{\mu }_{2}-\mu _{2}\right\| \right] . \end{aligned}$$
(6.7)

In the same manner with respect to \(\mu _{2},\) we get

$$\begin{aligned} \left\| {\widehat{\mu }}_{2}-\mu _{2}\right\| \le \left| {\widehat{\mu }}_{2}(\varsigma )-\Sigma _{\widehat{\mu }_{2}}^{1}\right| +3\varphi _{2}\varsigma _{1}\left[ \left\| {\widehat{\mu }}_{1}-\mu _{1}\right\| +\left\| \widehat{\mu }_{2}-\mu _{2}\right\| \right] . \end{aligned}$$

By Lemma 6.4, we get

$$\begin{aligned} \left\| {\widehat{\mu }}_{2}-\mu _{2}\right\| \le \varsigma _{1}\varepsilon _{2}+3\varphi _{2}\varsigma _{1}\left[ \left\| \widehat{ \mu }_{1}-\mu _{1}\right\| +\left\| {\widehat{\mu }}_{2}-\mu _{2}\right\| \right] . \end{aligned}$$
(6.8)

Adding Eqs. (6.7), and (6.8), we have

$$\begin{aligned} \left\| {\widehat{\mu }}_{1}-\mu _{1}\right\| +\left\| {\widehat{\mu }} _{2}-\mu _{2}\right\| \le 2\varsigma _{1}\varepsilon +3\varsigma _{1}\left( \varphi _{1}+\varphi _{2}\right) \left[ \left\| {\widehat{\mu }} _{1}-\mu _{1}\right\| +\left\| {\widehat{\mu }}_{2}-\mu _{2}\right\| \right] . \end{aligned}$$

Then, we have

$$\begin{aligned} \left\| \left( {\widehat{\mu }}_{1},{\widehat{\mu }}_{2}\right) -\left( \mu _{1},\mu _{2}\right) \right\| \le \frac{2\varsigma _{1}}{1-3\varsigma _{1}\left( \varphi _{1}+\varphi _{2}\right) }\varepsilon . \end{aligned}$$
(6.9)

Case (2): For \(\varsigma \in \left[ \varsigma _{1},T\right] \), with respect to the operator \(\mu _{1},\) we have

$$\begin{aligned} \left\| {\widehat{\mu }}_{1}-\mu _{1}\right\| \le \left| \widehat{ \mu }_{1}(\varsigma )-\Sigma _{{\widehat{\mu }}_{1}}^{2}\right| +\mathcal {A }_{1}\varphi _{1}\left[ \left\| {\widehat{\mu }}_{1}-\mu _{1}\right\| +\left\| {\widehat{\mu }}_{2}-\mu _{2}\right\| \right] . \end{aligned}$$

By Lemma 6.4, we get

$$\begin{aligned} \left\| {\widehat{\mu }}_{1}-\mu _{1}\right\| \le {\mathcal {A}} _{1}\varepsilon _{1}+{\mathcal {A}}_{1}\varphi _{1}\left[ \left\| \widehat{ \mu }_{1}-\mu _{1}\right\| +\left\| {\widehat{\mu }}_{2}-\mu _{2}\right\| \right] . \end{aligned}$$
(6.10)

In the same manner with respect to \(\mu _{2},\) we get

$$\begin{aligned} \left\| {\widehat{\mu }}_{2}-\mu _{2}\right\| \le \left| \widehat{ \mu }_{2}(\varsigma )-\Sigma _{{\widehat{\mu }}_{2}}^{2}\right| +\mathcal {A }_{2}\varphi _{2}\left[ \left\| {\widehat{\mu }}_{1}-\mu _{1}\right\| +\left\| {\widehat{\mu }}_{2}-\mu _{2}\right\| \right] . \end{aligned}$$

By Lemma 6.4, we get

$$\begin{aligned} \left\| {\widehat{\mu }}_{2}-\mu _{2}\right\| \le {\mathcal {A}} _{2}\varepsilon _{2}+{\mathcal {A}}_{2}\varphi _{2}\left[ \left\| \widehat{ \mu }_{1}-\mu _{1}\right\| +\left\| {\widehat{\mu }}_{2}-\mu _{2}\right\| \right] . \end{aligned}$$
(6.11)

Adding Eqs. (6.10), and (6.11), we have

$$\begin{aligned}{} & {} \left\| {\widehat{\mu }}_{1}-\mu _{1}\right\| +\left\| \widehat{\mu }_{2}-\mu _{2}\right\| \\{} & {} \quad \le \left( {\mathcal {A}}_{1}+{\mathcal {A}}_{2}\right) \varepsilon +\left( {\mathcal {A}}_{1}\varphi _{1}+{\mathcal {A}}_{2}\varphi _{2}\right) \left[ \left\| {\widehat{\mu }}_{1}-\mu _{1}\right\| +\left\| {\widehat{\mu }} _{2}-\mu _{2}\right\| \right] . \end{aligned}$$

It implies that

$$\begin{aligned} \left\| \left( {\widehat{\mu }}_{1},{\widehat{\mu }}_{2}\right) -\left( \mu _{1},\mu _{2}\right) \right\| \le \frac{\left( {\mathcal {A}}_{1}+\mathcal {A }_{2}\right) }{1-\left( {\mathcal {A}}_{1}\varphi _{1}+{\mathcal {A}}_{2}\varphi _{2}\right) }\varepsilon . \end{aligned}$$
(6.12)

Hence from Eqs. (6.9) and (6.12), we have

$$\begin{aligned} \left\| \left( {\widehat{\mu }}_{1},{\widehat{\mu }}_{2}\right) -\left( \mu _{1},\mu _{2}\right) \right\| \le \max \left\{ \frac{2\varsigma _{1}}{ 1-3\varsigma _{1}\left( \varphi _{1}+\varphi _{2}\right) },\frac{\left( {\mathcal {A}}_{1}+{\mathcal {A}}_{2}\right) }{1-\left( {\mathcal {A}}_{1}\varphi _{1}+{\mathcal {A}}_{2}\varphi _{2}\right) }\right\} \varepsilon . \end{aligned}$$

Due to 6.6, we can write

$$\begin{aligned} \left\| \left( {\widehat{\mu }}_{1},{\widehat{\mu }}_{2}\right) -\left( \mu _{1},\mu _{2}\right) \right\| \le {\mathcal {M}}\varepsilon . \end{aligned}$$

where

$$\begin{aligned} {\mathcal {M}}\mathfrak {=}\max \left\{ \frac{2\varsigma _{1}}{1-3\varsigma _{1}\left( \varphi _{1}+\varphi _{2}\right) },\frac{\left( {\mathcal {A}}_{1}+ {\mathcal {A}}_{2}\right) }{1-\left( {\mathcal {A}}_{1}\varphi _{1}+{\mathcal {A}} _{2}\varphi _{2}\right) }\right\} >0. \end{aligned}$$

Hence the system (1.1) is HU stable. \(\square \)

7 Numerical Scheme with Piecewise Derivative

This section presents the numerical resolution of the adopted fractional order model by Adams–Bashforth method. The Adams–Bashforth method is a multi-step method that utilizes previously evaluated approximations to compute the solution of FDEs. In the context of FDEs, the fractional-order operators require specialized techniques for their numerical approximation. One such technique is the Atangana–Baleanu derivative, which is a non-local derivative that captures the memory effects associated with fractional calculus. By combining the Atangana–Baleanu derivative with the Adams–Bashforth method, researchers have been able to effectively solve FDEs with fractional orders. Additionally, the use of piecewise integral local methods has also been employed in solving FDEs. These methods involve dividing the domain into smaller intervals and applying local approximations within each interval. This approach allows for a more efficient and accurate numerical solution of FDEs. For further details on the specific applications and implementations of the Adams–Bashforth method, Atangana–Baleanu derivative, and piecewise integral local methods in solving FDEs see [52,53,54]. By applying the piecewise integral local and Atangana–Baleanu derivative, we have

$$\begin{aligned} \mu _{1}(\varsigma )=\left\{ \begin{array}{l} \mu _{1}(0)+\int _{0}^{\varsigma }\hslash _{1}^{\left( \mu _{1},\mu _{2}\right) }\left( \varrho \right) d\varrho ,\varsigma \in \left[ 0,\varsigma _{1}\right] , \\ \mu (\varsigma _{1})+\frac{1-\rho _{1}}{\Delta \mathcal {(}\rho _{1}\mathcal {) }}\hslash _{1}^{\left( \mu _{1},\mu _{2}\right) }\left( \varsigma \right) \\ +\frac{\rho _{1}}{\Delta \mathcal {(}\rho _{1}\mathcal {)}\Gamma \mathcal {(} \rho _{1}\mathcal {)}}\int _{\varsigma _{1}}^{\varsigma }(\varsigma -\varrho )^{\rho _{1}-1}\hslash _{1}^{\left( \mu _{1},\mu _{2}\right) }\left( \varrho \right) d\varrho ,\varsigma \in \left[ \varsigma _{1},T\right] , \end{array} \right. \end{aligned}$$

and

$$\begin{aligned} \mu _{2}(\varsigma )=\left\{ \begin{array}{l} \mu _{2}(0)+\int _{0}^{\varsigma }\hslash _{2}^{\left( \mu _{1},\mu _{2}\right) }\left( \varrho \right) d\varrho ,\varsigma \in \left[ 0,\varsigma _{1}\right] , \\ \mu (\varsigma _{1})+\frac{1-\rho _{2}}{\Delta \mathcal {(}\rho _{2}\mathcal {) }}\hslash _{2}^{\left( \mu _{1},\mu _{2}\right) }\left( \varsigma \right) \\ +\frac{\rho _{2}}{\Delta \mathcal {(}\rho _{2}\mathcal {)}\Gamma \mathcal {(} \rho _{2}\mathcal {)}}\int _{\varsigma _{1}}^{\varsigma }(\varsigma -\varrho )^{\rho _{2}-1}\hslash _{2}^{\left( \mu _{1},\mu _{2}\right) }\left( \varrho \right) d\varrho ,\varsigma \in \left[ \varsigma _{1},T\right] . \end{array} \right. \end{aligned}$$

Now, put \(\varsigma =\varsigma _{n+1}\), \(n=0,1,2, \ldots \) in above equation, we get

$$\begin{aligned} \mu _{1}(\varsigma _{n+1})=\left\{ \begin{array}{l} \mu _{1}(0)-\int _{0}^{\varsigma }\hslash _{1}^{\left( \mu _{1},\mu _{2}\right) }\left( \varrho \right) d\varrho +\int _{0}^{\varsigma _{n+1}}\hslash _{1}^{\left( \mu _{1},\mu _{2}\right) }\left( \varrho \right) d\varrho ,\varsigma \in \left[ 0,\varsigma _{1}\right] , \\ \mu _{1}(\varsigma _{1})+\frac{1-\rho _{1}}{\Delta \mathcal {(}\rho _{1} \mathcal {)}}\hslash _{1}^{\left( \mu _{1},\mu _{2}\right) }\left( \varsigma _{n+1}\right) \\ +\frac{\rho _{1}}{\Delta \mathcal {(}\rho _{1}\mathcal {)}\Gamma \mathcal {(} \rho _{1}\mathcal {)}}\int _{\varsigma _{1}}^{\varsigma _{n+1}}(\varsigma _{n+1}-\varrho )^{\rho _{1}-1}\hslash _{1}^{\left( \mu _{1},\mu _{2}\right) }\left( \varrho \right) d\varrho ,\varsigma \in \left[ \varsigma _{1},T \right] , \end{array} \right. \end{aligned}$$

and

$$\begin{aligned} \mu _{2}(\varsigma _{n+1})=\left\{ \begin{array}{l} \mu _{2}(0)-\int _{0}^{\varsigma }\hslash _{2}^{\left( \mu _{1},\mu _{2}\right) }\left( \varrho \right) d\varrho +\int _{0}^{\varsigma _{n+1}}\hslash _{2}^{\left( \mu _{1},\mu _{2}\right) }\left( \varrho \right) d\varrho ,\varsigma \in \left[ 0,\varsigma _{1}\right] , \\ \mu _{2}(\varsigma _{1})+\frac{1-\rho _{2}}{\Delta \mathcal {(}\rho _{2} \mathcal {)}}\hslash _{2}^{\left( \mu _{1},\mu _{2}\right) }\left( \varsigma _{n+1}\right) \\ +\frac{\rho _{2}}{\Delta \mathcal {(}\rho _{2}\mathcal {)}\Gamma \mathcal {(} \rho _{2}\mathcal {)}}\int _{\varsigma _{1}}^{\varsigma _{n+1}}(\varsigma _{n+1}-\varrho )^{\rho _{2}-1}\hslash _{2}^{\left( \mu _{1},\mu _{2}\right) }\left( \varrho \right) d\varrho ,\varsigma \in \left[ \varsigma _{1},T \right] . \end{array} \right. \end{aligned}$$

By applying Newton Polynomial interpolation scheme,  we have

$$\begin{aligned} \mu _{1}(\varsigma _{n+1})=\left\{ \begin{array}{l} \mu _{1}(0)+\sum _{k=2}^{i}\left[ \frac{5}{12}\hslash _{1}^{\left( \mu _{1},\mu _{2}\right) }\left( \varsigma _{k-2}\right) -\frac{4}{3}\hslash _{1}^{\left( \mu _{1},\mu _{2}\right) }\left( \varsigma _{k-1}\right) +\frac{ 23}{12}\hslash _{1}^{\left( \mu _{1},\mu _{2}\right) }\left( \varsigma _{k}\right) \Delta \varsigma \right] , \\ \mu _{1}(\varsigma _{1})+\left\{ \begin{array}{llll} \frac{1-\rho _{1}}{\Delta \mathcal {(}\rho _{1}\mathcal {)}}\hslash _{1}^{\left( \mu _{1},\mu _{2}\right) }\left( \varsigma _{n}\right) +\frac{ \rho \left( \Delta \varsigma \right) ^{\rho -1}}{\Delta \mathcal {(}\rho \mathcal {)}\Gamma \mathcal {(}\rho +1\mathcal {)}}\sum _{k=i+3}^{n}\hslash _{1}^{\left( \mu _{1},\mu _{2}\right) }\left( \varsigma _{k-2}\right) \Phi _{1} \\ +\frac{\rho \left( \Delta \varsigma \right) ^{\rho -1}}{\Delta \mathcal {(} \rho \mathcal {)}\Gamma \mathcal {(}\rho +2\mathcal {)}}\sum _{k=i+3}^{n}\left[ \hslash _{1}^{\left( \mu _{1},\mu _{2}\right) }\left( \varsigma _{k-1}\right) -\hslash _{1}^{\left( \mu _{1},\mu _{2}\right) }\left( \varsigma _{k-2}\right) \right] \Sigma _{1} \\ +\frac{\rho }{\Delta \mathcal {(}\rho \mathcal {)}}+\frac{\rho \left( \Delta \varsigma \right) ^{\rho -1}}{2\Gamma \mathcal {(}\rho +3\mathcal {)}} \sum _{k=i+3}^{n}\left[ \hslash _{1}^{\left( \mu _{1},\mu _{2}\right) }\left( \varsigma _{k}\right) \right. \\ \left. -2\hslash _{1}^{\left( \mu _{1},\mu _{2}\right) }\left( \varsigma _{k-1}\right) +\hslash _{1}^{\left( \mu _{1},\mu _{2}\right) }\left( \varsigma _{k-2}\right) \right] \Psi _{1}, \end{array} \right. \end{array} \right. \end{aligned}$$

and

$$\begin{aligned} \mu _{2}(\varsigma _{n+1})=\left\{ \begin{array}{lll} \mu _{2}(0)+\sum _{k=2}^{i}\left[ \frac{5}{12}\hslash _{2}^{\left( \mu _{1},\mu _{2}\right) }\left( \varsigma _{k-2}\right) -\frac{4}{3}\hslash _{2}^{\left( \mu _{1},\mu _{2}\right) }\left( \varsigma _{k-1}\right) +\frac{ 23}{12}\hslash _{2}^{\left( \mu _{1},\mu _{2}\right) }\left( \varsigma _{k}\right) \Delta \varsigma \right] , \\ \mu _{2}(\varsigma _{1})+\left\{ \begin{array}{llll} \frac{1-\rho _{1}}{\Delta \mathcal {(}\rho _{1}\mathcal {)}}\hslash _{2}^{\left( \mu _{1},\mu _{2}\right) }\left( \varsigma _{n}\right) +\frac{ \rho \left( \Delta \varsigma \right) ^{\rho -1}}{\Delta \mathcal {(}\rho \mathcal {)}\Gamma \mathcal {(}\rho +1\mathcal {)}}\sum _{k=i+3}^{n}\hslash _{2}^{\left( \mu _{1},\mu _{2}\right) }\left( \varsigma _{k-2}\right) \Phi _{2} \\ +\frac{\rho \left( \Delta \varsigma \right) ^{\rho -1}}{\Delta \mathcal {(} \rho \mathcal {)}\Gamma \mathcal {(}\rho +2\mathcal {)}}\sum _{k=i+3}^{n}\left[ \hslash _{2}^{\left( \mu _{1},\mu _{2}\right) }\left( \varsigma _{k-1}\right) -\hslash _{2}^{\left( \mu _{1},\mu _{2}\right) }\left( \varsigma _{k-2}\right) \right] \Sigma _{2} \\ +\frac{\rho }{\Delta \mathcal {(}\rho \mathcal {)}}+\frac{\rho \left( \Delta \varsigma \right) ^{\rho -1}}{2\Gamma \mathcal {(}\rho +3\mathcal {)}} \sum _{k=i+3}^{n}\left[ \hslash _{2}^{\left( \mu _{1},\mu _{2}\right) }\left( \varsigma _{k}\right) \right. \\ \left. -2\hslash _{2}^{\left( \mu _{1},\mu _{2}\right) }\left( \varsigma _{k-1}\right) +\hslash _{2}^{\left( \mu _{1},\mu _{2}\right) }\left( \varsigma _{k-2}\right) \right] \Psi _{2} \end{array} \right. \end{array} \right. \end{aligned}$$

where \(\Psi _{i},\Sigma _{i}\) and \(\Phi _{i},i=1,2\) are given as follows

$$\begin{aligned} \Psi _{i}= & {} \left( n-k+1\right) ^{\rho _{i}}\left[ 2\left( n-k\right) ^{2}+\left( 3\rho _{i}+10\right) \left( n-k\right) +2\rho _{i}^{2}+9\rho _{i}+12\right] \\{} & {} -(n-k)^{\rho _{i}}\left[ 2\left( n-k\right) ^{2}+\left( 5\rho _{i}+10\right) \left( n-k\right) +6\rho _{i}^{2}+18\rho _{i}+12\right] , \\ \Sigma _{i}= & {} \left( n-k+1\right) ^{\rho _{i}}\left( n-k+3+2\rho _{i}\right) -\left( n-k\right) ^{\rho _{i}}\left( n-k+3+3\rho _{i}\right) , \end{aligned}$$

and

$$\begin{aligned} \Phi _{i}=\left( n-k+1\right) ^{\rho _{i}}-\left( n-k\right) ^{\rho _{i}}. \end{aligned}$$

8 An Example

This section presents a theoretical example of the piecewise Atangana–Baleanu system (1.1) to emphasize our main findings and conclusions. The example has been meticulously chosen based on the conditions outlined in the employed theorems and the specific conditions stated in our proposed findings. By exploring various parameter values and fractional-order derivatives, this example validates the arguments presented in the preceding section. Additionally, it showcases the wider applicability of the obtained results.

Example 8.1

Let \(\varsigma \in \left[ 0,1\right] ,\) \(\varsigma _{1}=\frac{1}{3},\) we consider the following coupled system under Piecewise Atangana–Baleanu fractional derivative with delays

$$\begin{aligned} \left\{ \begin{array}{l} {}^{PAB}{\mathbb {D}}_{0}^{\rho _{1}}\mu _{1}(\varsigma )=\hslash _{1}(\varsigma ,\mu _{1}(\varsigma ),\mu _{1}(\varsigma -\sigma \left( \varsigma \right) ),\mu _{2}(\varsigma )),\sigma \left( \varsigma \right) \ge 0,\varsigma \in \left( 0,T\right] ,T>0, \\ {}^{PAB}{\mathbb {D}}_{0}^{\rho _{2}}\mu _{2}(\varsigma )=\hslash _{2}(\varsigma ,\mu _{1}(\varsigma ),\mu _{2}(\varsigma ),\mu _{2}(\varsigma -\sigma \left( \varsigma \right) )),\sigma \left( \varsigma \right) \ge 0,\varsigma \in \left( 0,T\right] ,T>0, \\ \mu _{1}(0)=\mu _{1}(0),\mu _{2}(0)=\mu _{2}(0), \end{array} \right. \nonumber \\ \end{aligned}$$
(8.1)

Here \(\rho _{1}=\rho _{2}=\frac{4}{5}\in \left( 0,1\right] ,\mu _{1}(0)=2,\mu _{2}(0)=4,T=1,\sigma \left( \varsigma \right) =\frac{1}{5}>0\) and

$$\begin{aligned}{} & {} \hslash _{1}(\varsigma ,\mu _{1}(\varsigma ),\mu _{1}(\varsigma -\sigma \left( \varsigma \right) ),\mu _{2}(\varsigma ))\\{} & {} \quad =\frac{1}{2\left( 3e^{2}+\varsigma \right) }\left( \cos \mu _{1}(\varsigma )+\sin \mu _{1}(\varsigma -\frac{1}{5})+\frac{\left| \mu _{2}(\varsigma )\right| }{1+\left| \mu _{2}(\varsigma )\right| }\right) , \end{aligned}$$

and

$$\begin{aligned}{} & {} \hslash _{2}(\varsigma ,\mu _{1}(\varsigma ),\mu _{2}(\varsigma ),\mu _{2}(\varsigma -\sigma \left( \varsigma \right) ))\\{} & {} =\frac{e^{\varsigma }}{ \left( e^{2}+\varsigma \right) }\left( \cos \mu _{1}(\varsigma )+\frac{ \left| \mu _{1}(\varsigma )\right| }{1+\left| \mu _{1}(\varsigma )\right| }+\sin \mu _{2}(\varsigma -\frac{1}{5})\right) . \end{aligned}$$

Clearly, the functions \(\hslash _{i},i=1,2\ \)are continuous. For \(\left( \mu _{1},\mu _{2}\right) ,\left( \widehat{\mu }_{1},{\widehat{\mu }}_{2}\right) \in {\mathbb {S}}\) and \(\varsigma \in {\mathcal {J}},\) we have

$$\begin{aligned}{} & {} \left| \hslash _{1}(\varsigma ,\mu _{1}(\varsigma ),\mu _{1}(\varsigma -\sigma \left( \varsigma \right) ),\mu _{2}(\varsigma ))-\hslash _{1}(\varsigma ,{\widehat{\mu }}_{1}(\varsigma ),{\widehat{\mu }}_{1}(\varsigma -\sigma \left( \varsigma \right) ),{\widehat{\mu }}_{2}(\varsigma ))\right| \\{} & {} \quad \le \frac{1}{2\left( 3e^{2}+\varsigma \right) }\left[ 2\left| \mu _{1}(\varsigma )-{\widehat{\mu }}_{1}(\varsigma )\right| +\left| \mu _{2}(\varsigma )-{\widehat{\mu }}_{2}(\varsigma )\right| \right] , \end{aligned}$$

and

$$\begin{aligned}{} & {} \left| \hslash _{2}(\varsigma ,\mu _{1}(\varsigma ),\mu _{2}(\varsigma ),\mu _{2}(\varsigma -\sigma \left( \varsigma \right) ))-\hslash _{2}(\varsigma ,{\widehat{\mu }}_{1}(\varsigma ),{\widehat{\mu }}_{2}(\varsigma ),{\widehat{\mu }}_{2}(\varsigma -\sigma \left( \varsigma \right) ))\right| \\{} & {} \quad \le \frac{1}{\left( e^{2}+\varsigma \right) }\left[ \left| \mu _{1}(\varsigma )-{\widehat{\mu }}_{1}(\varsigma )\right| +2\left| \mu _{2}(\varsigma )-{\widehat{\mu }}_{2}(\varsigma )\right| \right] . \end{aligned}$$

Thus, the condition (H\(_{1}\)) holds with \(\varphi _{1}=\frac{1}{6e^{2}}>0\) and \(\varphi _{2}=\frac{1}{e^{2}}>0.\) Thus, we get \({\mathcal {A}}_{1}=1.22,\) \( {\mathcal {A}}_{2}=1.2\) and \(3\varphi _{1}{\mathcal {A}}_{1}\simeq 0.08,\) \( 3\varphi _{2}{\mathcal {A}}_{2}\simeq 0.4,\) \(3\varphi _{1}\varsigma _{1}\simeq 0.02\) and \(3\varphi _{2}\varsigma _{1}\simeq 0.14.\) Thus the conditions \( \max \left\{ 3\varphi _{i}{\mathcal {A}}_{i},3\varphi _{i}\varsigma _{1}\right\} =\max \left\{ 0.08,0.4,0.02,0.14\right\} =0.4<\frac{1}{2}.\) Thus, all conditions in Theorem 5.2 are satisfied and hence the piecewise system (8.1) has a unique solution. For every \(\varepsilon =\max \left\{ \varepsilon _{1},\varepsilon _{2}\right\} >0\) and each \(\left( \widehat{\mu }_{1},{\widehat{\mu }}_{2}\right) \in {\mathbb {S}}\) satisfies satisfies

$$\begin{aligned} \left\{ \begin{array}{l} \left| ^{PAB}{\mathbb {D}}_{0}^{\rho _{1}}{\widehat{\mu }}_{1}(\varsigma )-\hslash _{1}^{\left( {\widehat{\mu }}_{1},{\widehat{\mu }}_{2}\right) }(\varsigma )\right| \le \varepsilon _{1}, \\ \\ \left| ^{PAB}{\mathbb {D}}_{0}^{\rho _{2}}{\widehat{\mu }}_{2}(\varsigma )-\hslash _{2}^{\left( {\widehat{\mu }}_{1},{\widehat{\mu }}_{2}\right) }(\varsigma )\right| \le \varepsilon _{2}, \end{array} \right. \end{aligned}$$

There exists a solution \(\left( \mu _{1},\mu _{2}\right) \in {\mathbb {S}}\) of the piecewise terminal value system (8.1) with

$$\begin{aligned} \left\| \left( {\widehat{\mu }}_{1},{\widehat{\mu }}_{2}\right) -\left( \mu _{1},\mu _{2}\right) \right\| \le {\mathcal {M}}\varepsilon . \end{aligned}$$

where

$$\begin{aligned} {\mathcal {M}}\mathfrak {=}\max \left\{ \frac{2\varsigma _{1}}{1-3\varsigma _{1}\left( \varphi _{1}+\varphi _{2}\right) },\frac{\left( {\mathcal {A}}_{1}+ {\mathcal {A}}_{2}\right) }{1-\left( {\mathcal {A}}_{1}\varphi _{1}+{\mathcal {A}} _{2}\varphi _{2}\right) }\right\} >0, \end{aligned}$$

such that \(3\varsigma _{1}\left( \varphi _{1}+\varphi _{2}\right) \simeq 0.2\), \({\mathcal {A}}_{1}\varphi _{1}+{\mathcal {A}}_{2}\varphi _{2}\simeq 0.18,\ \)and

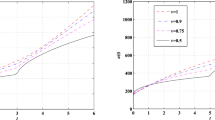
$$\begin{aligned} \max \left\{ 3\varsigma _{1}\left( \varphi _{1}+\varphi _{2}\right) ,\left( {\mathcal {A}}_{1}\varphi _{1}+{\mathcal {A}}_{2}\varphi _{2}\right) \right\} =\max \left\{ 0.2,0.18\right\} =0.2<1. \end{aligned}$$

Therefore, all conditions in Theorem 6.5 are satisfied and hence the piecewise system (8.1) is UH stable. Now, by choosing \({\mathcal {M}} (\varepsilon )={\mathcal {M}}(0)=0\) such that \({\mathcal {M}}(0)=0\), then the piecewise system (8.1) is GUH stability. Here in Figs. 1, 2 and 3 we present the numerical results graphically for the given example.

Fig. 1
figure 1

Graphical solutions for the given fractional order of Example (8.1)

Full size image
Fig. 2
figure 2

Graphical solutions for the given fractional order of Example (8.1)

Full size image
Fig. 3
figure 3

Graphical solutions for the given fractional order of Example (8.1)

Full size image

9 Conclusion

The investigation of piecewise fractional derivatives is a vibrant and rapidly evolving research area, which brings forth numerous unresolved questions and potential applications. As more researchers delve into this field, we can anticipate further progress in both the theoretical foundations and practical implications of piecewise fractional derivatives. In this study, we have expanded and developed sufficient conditions for the existence, uniqueness, and stability of solutions to fractional equations by introducing innovative piecewise Atangana–Baleanu fractional derivatives. By employing Banach’s contraction mapping and the Leary–Schauder alternative fixed-point theorem, we have achieved significant results in terms of solution properties. Moreover, functional analysis techniques have been utilized to establish stability results within the Hyers–Ulam framework. To provide a numerical interpretation, we have employed a numerical scheme based on Newton interpolation polynomials, and we present a numerical example to illustrate the obtained results. Building upon the conclusions drawn in this study, we propose a more comprehensive exploration of piecewise fractional equations, encompassing similar systems and associated challenges. Our future work aims to extend this research by incorporating psi piecewise fractional derivatives within the frameworks of Atangana–Baleanu, Caputo and Fabrizio. By doing so, we seek to further enhance our understanding of the theoretical aspects and practical applications of piecewise fractional derivatives.