Threshold Dynamics and Probability Density Function of a Stochastic Multi-Strain Coinfection Model with Amplification and Vaccination

Abstract

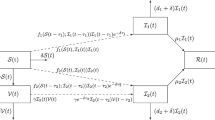
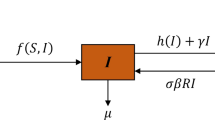
Multi-strain infectious diseases, which are usually prevented from spreading widely by vaccination, have two main transmission mechanisms: competitive exclusion and co-existence. In this paper, a stochastic multi-strain coinfection model with amplification and vaccination is developed. For the deterministic model, the basic reproduction number $R_0$ and fixed points are provided. For the stochastic model, we first prove the existence and uniqueness of the positive solution under any initial value. Then, a portion of those infected with the common strain will always become patients with the amplified strain, which increases the risk of death from the disease. Therefore, we verified that patients with common strains would become extinct if $R_1^s<1$. Furthermore, by constructing the Lyapunov function, we find that model (3) has a unique ergodic stationary distribution if $R_0^S>1$. Particularly, we get a concrete form of the probability density of the distribution $\kappa (\cdot )$ near equilibrium $E^*$, where $E^*$ is the quasi-local equilibrium of the stochastic model. Finally, the results are verified by numerical simulation. The results show that vaccination can control disease outbreaks or even eliminate them.

Appendix

For the same dimensional symmetric matrices $Q_1$ and $Q_2$, we have

$Q_1\succ 0$: $Q_1$ is a positive definite matrix,

$Q_1\succeq 0$: $Q_1$ is a positive semi-definite matrix,

$Q_1\succeq Q_2$: $Q_1-Q_2$ is at least a positive semi-definite matrix.

Moreover, for any invertible matrix Q, it is found that $Q\Sigma Q^{T}\succ 0$ if $\Sigma \succ 0$. Furthermore, define $\Sigma _j$ as the solutions of the following algebraic equations

$$\begin{aligned} \mathcal {N}_j+\mathcal {A}\Sigma _j+\Sigma _j\mathcal {A}^T=0, ~j=1,2,3,4,\end{aligned}$$

where

$$\begin{aligned}{} & {} \mathcal {N}_1=diag\{\sigma _1,0,0,0\},~\mathcal {N}_2=diag\{0,\sigma _2,0,0\},~ \mathcal {N}_3=diag\{0,0,\sigma _3,0\} ~and\\{} & {} \quad \mathcal {N}_4=diag\{0,0,0,\sigma _4\}.\end{aligned}$$

Consider the algebraic equation

$$\begin{aligned} \mathcal {N}_1+\mathcal {A}\Sigma _1+\Sigma _1\mathcal {A}^T=0, \end{aligned}$$

(28)

which the related proof can be divided into two conditions:

$$\begin{aligned}(\aleph _1)~a_{j1}=0~(\forall j=2,3,4),~~(\hbar _1)=a_{21}^2+a_{31}^2+a_{41}^2\ne 0.\end{aligned}$$

Case 1. If $(\aleph _1)$ is satisfied, an intuitive calculation shows that

$$\begin{aligned}\Sigma _1=diag\Big \{\frac{\sigma _1}{2a_{11}},0,0,0\Big \}=\vartheta _{11}.\end{aligned}$$

The characteristic polynomial of $\mathcal {A}$ is that $\varphi _\mathcal {A}(\lambda )=(\lambda -a_{11})(\lambda I_4-\mathcal {H}_1)$, where $\mathcal {H}_1=(a_{ij})_{\{2\le i,j\le 4\}}$ is the matrix. Obviously, $\mathcal {A}$ has one of the eigenvalue $\lambda =a_{11}$. Based on the Theorem 2.1, we know that $a_{11}>0$, which implies that $\vartheta _{11}\succeq 0$ and

$$\begin{aligned} \Sigma _1\succeq \vartheta _{11}. \end{aligned}$$

(29)

Case 2. If $(\hbar _1)$ is satisfied, $a_{21}\ne 0$, or $a_{31}\ne 0$, or $a_{41}\ne 0$ can be obtained. We must illustrate that the elements $a_{j1}~(j = 2, 3, 4,)$ have the equivalent status in $\mathcal {A}$.

Define the invertible matrices $\mathcal {J}_1$ and $\mathcal {J}_2$ as follows

$$\begin{aligned}\mathcal {J}_1=\left( \begin{array}{cccc} 1&{}0&{}0&{}0\\ 0&{}0&{}1&{}0\\ 0&{}1&{}0&{}0\\ 0&{}0&{}0&{}1 \end{array}\right) ,\qquad \mathcal {J}_2=\left( \begin{array}{cccc} 1&{}0&{}0&{}0\\ 0&{}0&{}0&{}1\\ 0&{}0&{}1&{}0\\ 0&{}1&{}0&{}0 \end{array}\right) , \end{aligned}$$

which satisfies $\dot{\mathcal {A}}=\mathcal {J}_1\mathcal {A}\mathcal {J}_1^{-1}$, $\ddot{\mathcal {A}}=\mathcal {J}_2\mathcal {A}\mathcal {J}_2^{-1}$, $\dot{\Sigma _1}=\mathcal {J}_1\Sigma _1\mathcal {J}_1^T$ and $\ddot{\Sigma _1}=\mathcal {J}_2\Sigma _1\mathcal {J}_2^T$.

Then (28) can be equivalently expressed as

$$\begin{aligned} \mathcal {J}_1\mathcal {N}_1\mathcal {J}_1^T+\dot{\mathcal {A}}\dot{\Sigma _1}+\dot{\Sigma _1}\dot{\mathcal {A}}^T=0,~and~ \mathcal {J}_2\mathcal {N}_1\mathcal {J}_2^T+\ddot{\mathcal {A}}\ddot{\Sigma _1}+\ddot{\Sigma _1}\ddot{\mathcal {A}}^T=0.\end{aligned}$$

Now, we can find that $\Sigma _1$, $\dot{\Sigma _1}$ and $\ddot{\Sigma _1}$ not only have the same positive definiteness, but also they are Hurwitz matrix. Additionally, we can obtain that $\dot{a_{21}}=a_{31}$ and $\ddot{a_{21}}=a_{41}$. Therefore, we only consider the condition of $a_{21}\ne 0$.

Let $\mathcal {B}=\mathcal {J}_3\mathcal {A}\mathcal {J}_3^{-1}$, where the elimination matrix $\mathcal {J}_3$ is given by

$$\begin{aligned} \begin{array}{rl} \mathcal {J}_3=\left( \begin{array}{cccc} 1&{}0&{}0&{}0\\ 0&{}1&{}0&{}0\\ 0&{}-\frac{a_{31}}{a_{21}}&{}1&{}0\\ 0&{}-\frac{a_{41}}{a_{21}}&{}0&{}1 \end{array}\right) . \end{array} \end{aligned}$$

By calculation, we denote

$$\begin{aligned} \begin{array}{rl} \mathcal {B}=\left( \begin{array}{cccc} b_{11}&{}b_{12}&{}b_{13}&{}b_{14}\\ b_{21}&{}b_{22}&{}b_{23}&{}b_{24}\\ 0&{}b_{32}&{}b_{33}&{}b_{34}\\ 0&{}b_{42}&{}b_{43}&{}b_{44} \end{array}\right) . \end{array} \end{aligned}$$

There is $b_{21}=a_{21}\ne 0$, equation (28) can be rewritten as:

$$\begin{aligned} \mathcal {J}_3\mathcal {N}_1\mathcal {J}_3^T+\mathcal {B}(\mathcal {J}_3\Sigma _1\mathcal {J}_3^T)+(\mathcal {J}_3\Sigma _1\mathcal {J}_3^T)\mathcal {B}^T=0. \end{aligned}$$

(30)

Next, the parameters $(b_{32}, b_{42})$ are similarly considered for two conditions:

$$\begin{aligned} (\aleph _2)~b_{m2}=0~(\forall m=3,4),~~(\hbar _2)~=b_{32}^2+b_{42}^2\ne 0. \end{aligned}$$

Case 2.1 If $(\aleph _2)$ is satisfied, by direct computation

$$\begin{aligned} \begin{array}{rl} \mathcal {J}_3\Sigma _1\mathcal {J}_3^T=\left( \begin{array}{cccc} \mathcal {H}_2&{}O_{2,2}\\ O_{2,2}&{}O_{2,2} \end{array}\right) =\mathcal {H}_3, \end{array} \end{aligned}$$

where O is zero matrix and $\mathcal {H}_2=(\varsigma _{ij})_{2\times 2}$ is the symmetric matric, where

$$\begin{aligned}\begin{aligned}&\varsigma _{22}=-\frac{\sigma _1b_{21}^2}{2(b_{11}+b_{22})(b_{11}b_{22}-b_{12}b_{21})},\\&\varsigma _{11}=\frac{\sigma _1\Big (b_{22}^2+b_{11}b_{22}-b_{12}b_{21}\Big )\varsigma _{22}}{b_{21}^2},\\&\varsigma _{12}=\varsigma _{21}=-\frac{\sigma _1b_{22}\varsigma _{22}}{b_{21}}. \end{aligned}\end{aligned}$$

It is easy to obtain the characteristic polynomial of $\mathcal {A}$:

$$\begin{aligned}\varphi _\mathcal {A}(\lambda )=\varphi _\mathcal {B}(\lambda )=\Big (\lambda ^2-(b_{11}+b_{22})\lambda +(b_{11}b_{22} -b_{12}b_{21})\Big )\Big (\lambda I_2-\mathcal {H}_4\Big )=0,\end{aligned}$$

where $\mathcal {H}_4=(b_{ij})_{\{3\le i,j\le 4\}}$ is the matrix. Because of the $\mathcal {A}$ is a Hurwtiz matrix, all of the roots of the equation $\lambda ^2-(b_{11}+b_{22})\lambda +(b_{11}b_{22}-b_{12}b_{21})=0$ have negative real part. Moreover, we have $b_{11}+b_{22}<0$ and $b_{11}b_{22}-b_{12}b_{21}>0$. Since $b_{21}\ne 0$, we have

$$\begin{aligned}\varsigma _{11}>0,~\varsigma _{11}\varsigma _{22}-\varsigma _{12}^2=\frac{\sigma _1(b_{11}b_{22}-b_{12}b_{21}) \varsigma _{22}^2}{b_{21}^2}>0, \end{aligned}$$

which shows that $\mathcal {H}_2\succ 0$ and $\mathcal {J}_3\Sigma _1\mathcal {J}_3^T\succeq 0$.

Define two positive semi-definite matrices $\vartheta _{12}$ and $\tilde{\vartheta _{12}}$ by

$$\begin{aligned}\vartheta _{12}=diag\Big \{\frac{\sigma _1(\varsigma _{11}\varsigma _{22}-\varsigma _{12}^2)}{\varsigma _{22}},0,0,0\Big \}, ~\tilde{\vartheta _{12}}=\mathcal {H}_3-\vartheta _{12}.\end{aligned}$$

We have

$$\begin{aligned}\Sigma _1=\mathcal {J}_3^{-1}\mathcal {H}_3(\mathcal {J}_3^{-1})^T=\mathcal {J}_3\vartheta _{12} (\mathcal {J}_3^{-1})^T+\mathcal {J}_3^{-1}\tilde{\vartheta _{12}}(\mathcal {J}_3^{-1})^T =\vartheta _{12}+\mathcal {J}_3^{-1}\tilde{\vartheta _{12}}(\mathcal {J}_3^{-1})^T.\end{aligned}$$

Through $\vartheta _{12}\succeq 0$, it can be obtained that $\mathcal {J}_3^{-1}\tilde{\vartheta _{12}}(\mathcal {J}_3^{-1})^T\succeq 0$ and

$$\begin{aligned} \Sigma _1\succeq \vartheta _{12}. \end{aligned}$$

(31)

Case 2.2 If $(\hbar _2)$ is satisfied, Similar to Case 2, we have $b_{32}\ne 0$ or $b_{42}\ne 0$ and the elements $b_{m2}~(m=3,4)$ have the equivalent status in $\mathcal {B}$. Therefore, we only consider the condition of $b_{32}\ne 0$.

Define the invertible matrices $\mathcal {J}_4$ as follows

$$\begin{aligned} \begin{array}{rl} \mathcal {J}_4=\left( \begin{array}{cccc} 1&{}0&{}0&{}0\\ 0&{}1&{}0&{}0\\ 0&{}0&{}0&{}1\\ 0&{}0&{}1&{}0 \end{array}\right) , \end{array} \end{aligned}$$

which satisfies $\hat{\mathcal {B}}=\mathcal {J}_4\mathcal {B}\mathcal {J}_4^{-1}$ and $\hat{\Sigma _1}=\mathcal {J}_4\Sigma _1\mathcal {J}_4^T$. That is, (30) also can be rewritten as $\mathcal {J}_4\mathcal {N}_1\mathcal {J}_4^T+\hat{\mathcal {B}}\hat{\Sigma _1}+\hat{\Sigma _1}\hat{\mathcal {B}}^T=0$.

Let $\mathcal {C}=\mathcal {J}_5\mathcal {B}\mathcal {J}_5^{-1}$, where $\mathcal {J}_2$ is called the second elimination metric

$$\begin{aligned} \begin{array}{rl} \mathcal {J}_5=\left( \begin{array}{cccc} 1&{}0&{}0&{}0\\ 0&{}1&{}0&{}0\\ 0&{}0&{}1&{}0\\ 0&{}0&{}-\frac{b_{42}}{b_{32}}&{}1 \end{array}\right) , \end{array} \end{aligned}$$

By calculation, it can be denoted

$$\begin{aligned} \begin{array}{rl} \mathcal {C}=\left( \begin{array}{cccc} c_{11}&{}c_{12}&{}c_{13}&{}c_{14}\\ c_{21}&{}c_{22}&{}c_{23}&{}c_{24}\\ 0&{}c_{32}&{}c_{33}&{}c_{34}\\ 0&{}0&{}c_{43}&{}c_{44} \end{array}\right) . \end{array} \end{aligned}$$

We have $c_{21}=b_{21}=a_{21}(\ne 0)$ and $c_{32}=b_{32}(\ne 0)$. Equations (30) or (28) can be rewritten as:

$$\begin{aligned} (\mathcal {J}_5\mathcal {J}_3)\mathcal {N}_1(\mathcal {J}_5\mathcal {J}_3)^T+\mathcal {C}\Big ((\mathcal {J}_5\mathcal {J}_3)\Sigma _1(\mathcal {J}_5\mathcal {J}_3)^T\Big ) +\Big ((\mathcal {J}_5\mathcal {J}_3)\Sigma _1(\mathcal {J}_5\mathcal {J}_3)^T\Big )\mathcal {C}^T=0. \end{aligned}$$

(32)

Next, the parameter $c_{43}$ is similarly considered for two conditions:

$$\begin{aligned}(\aleph _3)~c_{43}=0,~~(\hbar _3)~c_{43}^2\ne 0.\end{aligned}$$

Case 2.2.1 If $(\hbar _3)$ is satisfied, let $\mathcal {D}=\mathcal {J}_6\mathcal {C}\mathcal {J}_6^T$, where the standardized transformation matrix

$$\begin{aligned} \begin{array}{rl} \mathcal {J}_6=\left( \begin{array}{cccc} d_{11}&{}d_{12}&{}d_{13}&{}d_{14}\\ 0&{}d_{22}&{}d_{23}&{}d_{24}\\ 0&{}0&{}d_{33}&{}d_{34}\\ 0&{}0&{}0&{}1 \end{array}\right) . \end{array} \end{aligned}$$

where

$$\begin{aligned}\begin{aligned}&d_{11}=c_{21}c_{32}c_{43},~ d_{12}=c_{32}c_{43}(c_{22}+c_{33}+c_{44}),~d_{22}=c_{32}c_{43},\\&d_{13}=c_{43}\Big (c_{23}c_{32}+c_{33}(c_{33}+c_{44}) +c_{34}c_{43}+c_{44}^2\Big ),\\&d_{14}=c_{43}\Big (c_{24}c_{32}+c_{34}(c_{33}+c_{44})\Big )+c_{44}(c_{34}c_{43}+c_{44}^2),\\&d_{22}=c_{32}c_{43}, ~d_{23}=c_{43}(c_{33}+c_{44}), ~d_{24}=c_{34}c_{43}+c_{44}^2, ~d_{33}=c_{43}, ~d_{34}=c_{44}. \end{aligned}\end{aligned}$$

By calculation, it can be obtained

$$\begin{aligned} \begin{array}{rl} \mathcal {D}=\left( \begin{array}{cccc} -\varphi _1&{}-\varphi _2&{}-\varphi _3&{}-\varphi _4\\ 1&{}0&{}0&{}0\\ 0&{}1&{}0&{}0\\ 0&{}0&{}1&{}0 \end{array}\right) , \end{array} \end{aligned}$$

where $\varphi _1, \varphi _2, \varphi _3, \varphi _4$ are the same as above. Furthermore, equation (32) can be rewritten as:

$$\begin{aligned}{} & {} (\mathcal {J}_6\mathcal {J}_5\mathcal {J}_3)\mathcal {N}_1(\mathcal {J}_6\mathcal {J}_5\mathcal {J}_3)^T+\mathcal {C}\Big ((\mathcal {J}_6\mathcal {J}_5\mathcal {J}_3)\Sigma _1(\mathcal {J}_6\mathcal {J}_5 \mathcal {J}_3)^T\Big )\nonumber \\{} & {} \quad +\Big ((\mathcal {J}_6\mathcal {J}_5\mathcal {J}_3) \Sigma _1(\mathcal {J}_6\mathcal {J}_5\mathcal {J}_3)^T\Big )\mathcal {C}^T=0. \end{aligned}$$

(33)

Moreover, using the Lemma 2.2, we can obtain that the matrix $\Sigma _1$ is positive definite whose explicit form is

$$\begin{aligned} \begin{array}{rl} \Sigma _1=\left( \begin{array}{cccc} \frac{\sigma _1(\varpi _2\varpi _3-\varpi _1\varpi _4)}{2(\varpi _1\varpi _2\varpi _3-\varpi _3^2-\varpi _1^2\varpi _4)} &{}0&{}-\frac{\sigma _1\varpi _3}{2(\varpi _1\varpi _2\varpi _3-\varpi _3^2-\varpi _1^2\varpi _4)}&{}0\\ 0&{}\frac{\sigma _1\varpi _3}{2(\varpi _1\varpi _2\varpi _3-\varpi _3^2-\varpi _1^2\varpi _4)}&{}0&{}-\frac{\sigma _1\varpi _1}{2(\varpi _1\varpi _2\varpi _3-\varpi _3^2-\varpi _1^2\varpi _4)}\\ -\frac{\sigma _1\varpi _3}{2(\varpi _1\varpi _2\varpi _3-\varpi _3^2-\varpi _1^2\varpi _4)}&{}0&{} \frac{\sigma _1\varpi _1}{2(\varpi _1\varpi _2\varpi _3-\varpi _3^2-\varpi _1^2\varpi _4)}&{}0\\ 0&{}-\frac{\sigma _1\varpi _1}{2(\varpi _1\varpi _2\varpi _3-\varpi _3^2-\varpi _1^2\varpi _4)}&{}0&{} \frac{\sigma _1(\varpi _1\varpi _2-\varpi _3)}{2(\varpi _1\varpi _2\varpi _3-\varpi _3^2-\varpi _1^2\varpi _4)} \end{array}\right) . \end{array} \end{aligned}$$

Compared the $\mathcal {N}_1^2+\mathcal {D}\Sigma _1+\Sigma _1\mathcal {D}^T=0$, we have $\Sigma _1=\Xi ^{-2}(\mathcal {J}_6\mathcal {J}_5\mathcal {J}_3)\Sigma _1(\mathcal {J}_6\mathcal {J}_5\mathcal {J}_3)^T$, where $\Xi =d_{11}\sigma _1$. Thus, the matrix $\Sigma _1=\Xi ^{-2}(\mathcal {J}_6\mathcal {J}_5\mathcal {J}_3)^{-1}\Sigma _1((\mathcal {J}_6\mathcal {J}_5\mathcal {J}_3)^{-1})^T$ is at least a semi-positive matrix.

Case 2.2.2 If $(\aleph _3)$ is satisfied, then the characteristic polynomial of $\mathcal {C}$ is

$$\begin{aligned}\phi _\mathcal {C}(\lambda )=\phi _\mathcal {A}(\lambda )=(\lambda -c_{44})(\lambda ^3+ \xi _1\lambda ^2+\xi _2\lambda +\xi _3)=0,\end{aligned}$$

where

$$\begin{aligned}\begin{aligned}&\xi _1=-(c_{11}+c_{22}+c_{33}),~\xi _2=c_{11}c_{22}+c_{11}c_{33}+c_{22}c_{33}-c_{12}c_{21}-c_{23}c_{32},\\&\xi _3=-c_{11}c_{22}c_{33}-c_{13}c_{21}c_{32}+c_{33}c_{21}c_{12}+c_{32}c_{23}c_{11}. \end{aligned}\end{aligned}$$

Using Theorem 1 and $\mathcal {A}$ is a Hurwitz matrix, the solution of equation $\lambda ^3+\xi _1\lambda ^2+\xi _2\lambda +\xi _3=0$ have roots with all negative real components, that is

$$\begin{aligned}\xi _1>0,~\xi _2>0,~\xi _3>0,~\xi _1\xi _2-\xi _3>0.\end{aligned}$$

Let $\mathcal {D}=\mathcal {J}_7\mathcal {C}\mathcal {J}_7^{-1}$ and using the Lemma 2.3, where the standardized transformation matrix $\mathcal {J}_7$

$$\begin{aligned} \begin{array}{rl} \mathcal {J}_7=\left( \begin{array}{cccc} c_{21}c_{32}&{}c_{32}c_{22}&{}c_{32}c_{23}+c_{33}^2+c_{34}&{}c_{24}c_{32}+c_{34}c_{33}\\ 0&{}c_{32}&{}c_{33}&{}c_{34}\\ 0&{}0&{}1&{}0\\ 0&{}0&{}0&{}1 \end{array}\right) . \end{array} \end{aligned}$$

By calculation, we have

$$\begin{aligned} \begin{array}{rl} \mathcal {D}=\left( \begin{array}{cccc} -\epsilon _1&{}-\epsilon _2&{}-\epsilon _3&{}-\epsilon _4\\ 1&{}0&{}0&{}0\\ 0&{}1&{}0&{}0\\ 0&{}0&{}0&{}c_{44} \end{array}\right) . \end{array} \end{aligned}$$

where

$$\begin{aligned}\begin{aligned}&\epsilon _1=-(c_{11}+c_{22}),~\epsilon _2=c_{11}c_{22}-c_{33}^2-c_{34}-c_{23}c_{32}\\&\epsilon _3=c_{11}c_{34}+c_{22}c_{34}+(c_{11}+c_{22})c_{33}^2+c_{11}c_{23}c_{32}+c_{12}c_{21}c_{33} -c_{11}c_{22}c_{33}\\&\qquad -c_{13}c_{21}c_{32}-c_{24}c_{32}c_{43}-c_{33}c_{34}c_{43},\\&\epsilon _4=c_{11}c_{24}c_{32}+c_{12}c_{21}c_{34}+c_{11}c_{33}c_{34}+c_{22}c_{33}c_{34} -c_{11}c_{22}c_{34}-c_{14}c_{21}c_{32}-c_{24}c_{32}c_{44}\\&\qquad -c_{24}c_{32}c_{44}-c_{33}c_{34}c_{44}. \end{aligned}\end{aligned}$$

Then, the equation (32) can be rewritten as

$$\begin{aligned}{} & {} (\mathcal {J}_7\mathcal {J}_5\mathcal {J}_3)\mathcal {N}_1(\mathcal {J}_7\mathcal {J}_5\mathcal {J}_3)^T+\mathcal {C}\Big ((\mathcal {J}_7\mathcal {J}_5\mathcal {J}_3)\Sigma _1 (\mathcal {J}_7\mathcal {J}_5\mathcal {J}_3)^T\Big )\nonumber \\{} & {} \quad +\Big ((\mathcal {J}_7\mathcal {J}_5\mathcal {J}_3) \Sigma _1(\mathcal {J}_7\mathcal {J}_5\mathcal {J}_3)^T\Big )\mathcal {C}^T=0. \end{aligned}$$

(34)

where the $\Sigma _1$ is shown as

$$\begin{aligned} \begin{array}{rl} \Sigma _1=\left( \begin{array}{cccc} \frac{\sigma _1\epsilon _1}{2(\epsilon _1\epsilon _2-\epsilon _3)}&{}0&{}-\frac{\sigma _1}{2(\epsilon _1\epsilon _2-\epsilon _3)}&{}0\\ 0&{}\frac{\sigma _1}{2(\epsilon _1\epsilon _2-\epsilon _3)}&{}0&{}0\\ -\frac{\sigma _1}{2(\epsilon _1\epsilon _2-\epsilon _3)}&{}0&{}\frac{\sigma _1\epsilon _1}{2\epsilon _3(\epsilon _1\epsilon _2-\epsilon _3)} &{}0\\ 0&{}0&{}0&{}0 \end{array}\right) . \end{array} \end{aligned}$$

Compared the $\mathcal {N}_1^2+\mathcal {D}\tilde{\Sigma _1}+\tilde{\Sigma _1}\mathcal {D}^T=0$, we have $\tilde{\Sigma _1}=\Xi ^{-2}(\mathcal {J}_7\mathcal {J}_5\mathcal {J}_3)\Sigma _1 (\mathcal {J}_7\mathcal {J}_5\mathcal {J}_3)^T$, where $\Xi =c_{21}c_{32}\sigma _1$. Thus, the matrix $\Sigma _1=\Xi ^{-2}(\mathcal {J}_7\mathcal {J}_5\mathcal {J}_3)^{-1}\tilde{\Sigma _1}((\mathcal {J}_7 \mathcal {J}_5\mathcal {J}_3)^{-1})^T$ is at least a semi-positive matrix.

For $\mathcal {N}_i~(i=2,3,4)$, its approach is similar to that of $\mathcal {N}_1$. Therefore, we ignore it here. The proof is complete.