Super-Explosion and Inverse Canard Explosion in a Piecewise-Smooth Slow–Fast Leslie–Gower Model

Abstract

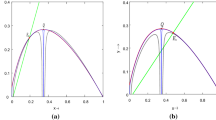
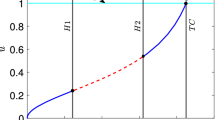
In this paper, we study a slow–fast Leslie-type predator–prey model with piecewise-linear functional response. Our approach is based on the geometric singular perturbation theory and the canard theory. When the fold point of the critical curve is lower than the transcritical bifurcation point, theoretical and numerical analyses show that a supercritical super-explosion occurs near the non-smooth corner followed by an inverse canard explosion close to the smooth fold. The critical values of parameters corresponding to these dynamical behaviors are obtained. Moreover, a stable relaxation oscillation is generated by the supercritical super-explosion, which will vanish as the occurrence of the inverse canard explosion.

Appendix

Consider the slow–fast piecewise-smooth system in a general form, namely,

$$\begin{aligned} \begin{aligned} \frac{dx}{dt}&=f(x,y,\lambda ,\epsilon ),\\ \frac{dy}{dt}&=\epsilon g(x,y,\lambda ,\epsilon )\\ \end{aligned} \end{aligned}$$

(5.1)

with

$$\begin{aligned} f(x,y,\lambda ,\epsilon )=\left\{ \begin{aligned} x\big (-y+f_{1}(x, \lambda )\big ),\quad&(x,y)\in \Sigma _{-},\\ -y+f_{2}(x, \lambda ),\quad&(x,y)\in \Sigma _{+},\\ \end{aligned}\right. \end{aligned}$$

(5.2)

where $0<\epsilon \ll 1$ is the perturbation parameter, $\lambda$ stands for the multi-dimensional bifurcation parameters, and $f_{1}, f_{2}\in C^{k}, k\ge 3$, in which, $f_{1}$ is linear in x while $f_{2}$ is a cubic-like function of x.

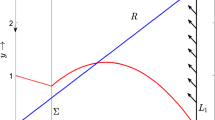
Let $\Sigma =\{(x,y)|\ x=\alpha \}$ be the switching boundary, then $\Sigma _{-}=\{(x,y)|\ x<\alpha \}$ and $\Sigma _{+}=\{(x,y)|\ x>\alpha \}$ are respectively the left and right region in the plane. Thus, we can define the left system and the right system respectively. On the switching boundary $\Sigma$, it is assumed that the vector field satisfies

$$\begin{aligned} f_{1}(\alpha , y_0, \lambda _0, 0)=f_{2}((\alpha , y_0, \lambda _0, 0)) \end{aligned}$$

(5.3)

and

$$\begin{aligned} f_{1}'((\alpha , y_0, \lambda _0, 0))< 0, f_{2}'((\alpha , y_0, \lambda _0, 0))> 0, \end{aligned}$$

(5.4)

where $(\alpha , y_0)\in \Sigma$ is the corner when $\lambda =\lambda _0$, and the prime means the derivative with respect to x. Under the conditions (5.3)–(5.4), the vector field is continuous but not differentiable at the switching boundary $\Sigma$.

Since $f_{2}(x)$ is cubic-like, it admits a maximum supposing at $Q=(x_{\textrm{Q}}, y_{\textrm{Q}})$ with $x_{\textrm{Q}}>\alpha$. Moreover, the critical curve associated with system (5.1) has a transcritical bifurcation point at $P=(0, f_1(0, \lambda ))$.

Let

$$\begin{aligned} y_{\textrm{Q}}<f_1(0, \lambda ),\quad \textrm{for}\,\, \lambda \in \Lambda , \end{aligned}$$

(5.5)

then the smooth fold is lower than the non-smooth corner. Under this assumption, the entry-exit function cannot be used to detect the birth and the number of relaxation oscillations since the transcritical bifurcation point $P=(0, f_1(0, \lambda ))$ cannot organize the slow–fast dynamics in this situation.

By following the methods developed in this article and imposing suitable conditions of the functions $f_i, i=1, 2$ near the non-smooth corner $(\alpha , y_0)\in \Sigma$ and the smooth fold $Q=(x_{\textrm{Q}}, y_{\textrm{Q}})$, the birth as well as the disappearance of relaxation oscillations can be analyzed for the general slow–fast piecewise-smooth system (5.1), where $(\alpha , y_0)\in \Sigma$ and $Q=(x_{\textrm{Q}}, y_{\textrm{Q}})$ are taken as the organizing centers controlling the slow–fast dynamics. The details are left for future work.