Directed communication in games with directed graphs

Abstract

We introduce a novel concept of directed communication and a related connectedness in directed graphs, and apply this to model certain cooperation restrictions in cooperative games. In the literature on communication in directed networks or directed graphs, one can find different notions of connectedness, and different ways how directed communication restricts cooperation possibilities of players in a game. In this paper, we introduce a notion of connectedness in directed graphs that is based on directed paths. We assume that a coalition of players in a game can only cooperate if these players form a directed path in a directed communication graph. We define a restricted game following the same approach as Myerson for undirected communication situations, and consider the allocation rule that applies the Shapley value to this restricted game. We characterize this value by extended versions of the well-known component efficiency, fairness and balanced contributions axioms. Moreover, using the new notion of connectedness, we apply this allocation rule to define network centrality, efficiency and vulnerability measures for directed networks.

1 Introduction

A cooperative game with transferable utility (TU-game, for short) models a situation in which a finite set of agents (players) can generate worths by cooperation. Such a game consists of a set of players and a characteristic function that assigns to every coalition of players a real number, called its worth, which is the transferable utility that the players in the coalition can earn when they agree to cooperate. In a TU-game, there are no restrictions on coalition formation and every subset of the player set can get together and cooperate. However, in many real-life situations, there are restrictions on coalition formation and not every coalition is feasible.

One of the most studied restrictions in coalition formation is communication restrictions where it is assumed that not every pair of players is able to communicate directly with each other. Following Myerson (1977), these communication restrictions are modeled by an undirected (communication) graph and it is assumed that only coalitions that are connected in the graph are feasible and the players in these coalitions can cooperate and generate the worth described by the game. The resulting model is a triple consisting of a player set, characteristic function and communication graph on the player set, and is referred to as a communication situation. Myerson (1977) proposed to apply the Shapley value (Shapley 1953a) to a modified game in which every feasible coalition can earn its worth, and every other coalition’s worth equals the sum of the worths of its connected components in the original game. This solution is nowadays known as the Myerson value. He also showed that this solution is the only one that satisfies component efficiency (in every component, the sum of the payoffs assigned to the players in that component equals its worth in the original game) and fairness (breaking a link between two players has the same effect on the payoffs of these two players). Later, Myerson (1980) provided another axiomatization replacing fairness by balanced contributions (the effect of isolating a player, in the sens that all its links are broken, on the payoff of another player is the same as the effect the other way around).

In the Myerson model, it is assumed that the links are symmetric. But, frequently, communication is directed and thus we need alternative models. This occurs, for example, when only one of the two players on a link is able to initiate the communication. To model these situations, in this paper, we introduce directed communication situations where the players in a game belong to a directed network that is represented by a directed graph. Although this model is not novel, the interpretation in this paper, and therefore the desirable properties of allocation rules, is. Similar as Myerson (1977), we introduce a restricted game that takes account of the communication restrictions. In the literature, there are different notions of connectedness in directed graphs, and different ways how directed communication restricts cooperation possibilities of players in a game where players can only communicate by one direction communication. In this paper, we consider a new type of connectedness in directed communication situations and apply this to coalition formation in cooperative games, where a coalition of players in a game can only cooperate if these players form a directed path in a directed communication graph. We say that a path in a directed graph is a connection path of a coalition if all players in this coalition belong to the path. In our restricted game, the worth of a coalition is equal to the “sum” of the worths of its (path) maximally connected subcoalitions. As allocation rule we propose, similar as Myerson (1977), to apply the Shapley value to this restricted game. We characterize this value by extended versions of the above mentioned component efficiency, fairness and balanced contributions axioms. Fairness and balanced contributions are stated the same as for undirected graphs, just that the edges are oriented arcs. Component efficiency is modified to reflect our new cooperation restrictions.

After introducing the model, solution and axiomatizations, we will apply the proposed method to some issues arising in social networks. Specifically, by taking any symmetric game (i.e., a game where all players are identical in their contributions), applying our solution to every directed network gives a new centrality measure for directed networks. In this way, we obtain a family of (directed) network centrality measures that is parameterized by the symmetric game that is used. Moreover, the axiomatizations of our allocation rule for directed communication situations can be directly applied as an axiomatization for centrality measures for directed networks. Whereas all the centrality measures in this family satisfy fairness and balanced contributions, within the family each measure is characterized by the (symmetric) game that is used in the connection efficiency axiom. Thus, reflecting the appropriate value in a specific application in the (symmetric) game, the axioms provide the corresponding centrality measure. We stress the role of the game in this case. Usually, TU-games are used to assess the different individual contributions of the players. However, since in this application of measuring centrality the game is symmetric, it is not assessing the differences between players, but only the overall value that can be obtained. The players/nodes only differ in their position in the directed network, as is measured by a network centrality measure. Finally, we illustrate how our allocation rule can be applied to measure efficiency and vulnerability in networks. Our work on network centrality contributes to the topic of finding game-theoretical centrality measures for social networks whose seminal work was due to Grofman and Owen (1972). Other contributions in this setting are given in van den Brink and Borm (2002), Gómez et al. (2003), Amer et al. (2007), Aadithya et al. (2010), del Pozo et al. (2011), Michalak et al. (2013), Mazalov and Trukhina (2014), Michalak et al. (2015), Mazalov et al. (2016), Szczepański et al. (2016), Tarkowski et al. (2018), Gallardo et al. (2018) and Navarro (2020). Tarkowski et al. (2017) is an interesting review on game-theoretic network centrality. On the other hand, the proposed measures of efficiency and vulnerability are related to the prominent measure of efficiency introduced in Latora and Marchiori (2001). Bell (2003), Gueye et al. (2012) and Lee et al. (2018) are also different game-theoretical approaches to measure efficiency and vulnerability in networks.

We conclude the paper by comparing our approach to other models in which restrictions in the communications are given by a directed graph. In fact, for asymmetric directed graphs (i.e., there can be at most one arc between each pair of nodes), our model is mathematically equivalent to the games with a permission structure of Gilles et al. (1992) and Gilles and Owen (1994). Based on this approach, the conjunctive permission value is proposed by van den Brink and Gilles (1996). For the special class of acyclic digraphs, the disjunctive permission value, proposed by vandenBrink, R. (1997), satisfies our fairness requirement, but only applied to arcs which head has in-degree at least 2. The games under precedence constraints of Faigle and Kern (1992) are slightly different in the sense that the characteristic function is defined only on the set of ‘feasible’ coalitions derived from the digraph. Both models do not generalize the Myerson restricted game nor the Myerson value for communication situations. Slikker and van den Nouweland (2001) characterized allocation rules for a more general model of a directed communication situation consisting of a set of players, a directed reward function, and a directed communication network, where the directed reward function assigns a value to every possible directed communication network defined on the player set. Our model is also related to Khmelnitskaya et al. (2016), and in comparison with the solution defined in Li and Shan (2020), our value mainly differs in the type of connectivity that is considered.

The remaining of this paper is organized as follows. After the preliminaries, in Sect. 3, we describe the model of directed communication situations and in Sect. 4, we introduce our allocation rule which is axiomatized in Sect. 5. In Sect. 6, we discuss applications to social networks. Section 7 compares our allocation rule with other rules in the literature.

2 Preliminaries

2.1 $\varvec{Cooperative TU-games}$

A cooperative game with transferable utility (or a TU-game for short) is a pair (N, v) in which $N=\{1,\dots ,n\}$ is the set of players and $v :2^N \rightarrow {\mathbb {R}}$, verifying $v(\emptyset )=0$, is the characteristic function. In this model, $v(S) \in {\mathbb {R}}$ is the payoff that the $s =|S|$ members of the coalition $S \in 2^N=\{S \;| \; S\ \subseteq N \}$ can obtain by cooperating. We will denote by $G^{N}$ the vector space of all TU-games with player set N. The null game $(N,\varvec{0})$ is the game with characteristic function given by $\varvec{0}(S) = 0$ for all $S \subseteq N.$ Similarly, $(N,\varvec{1})$ will be the game with characteristic function defined as $\varvec{1}(S)=1$ for all $\emptyset \ne S \subseteq N$. The family of TU-games $\{(N,u_S)\}_{\emptyset \ne S\subseteq N}$ with characteristic functions given by

$$\begin{aligned} u_S(T)=\left\{ \begin{array}{cc} 1, &{} \text{ if } S\subseteq T\\ 0, &{} \text{ otherwise }\end{array}\right. \end{aligned}$$

is a basis in $G^N$ known as the unanimity games basis. As a consequence, given $(N,v)\in G^N$, its characteristic function v admits the following (unique) expression:

$$\begin{aligned} v=\sum _{\emptyset \ne S\subseteq N}\Delta _v(S)u_{S}, \end{aligned}$$

where the coordinates $\{ \Delta _{v}(S) \}_{\emptyset \ne S \subseteq N}$ are known as the Harsanyi dividends (Harsanyi 1959). For each non-empty coalition S:

$$\begin{aligned} \Delta _{v}(S)= \sum _{T \subseteq S}(-1)^{s-t}v(T). \end{aligned}$$

An allocation rule (or a point solution) on $G^{N}$ is a map $\psi : G^{N}\rightarrow {\mathbb {R}}^{n}$. For each $(N,v) \in G^{N}$, $\psi _{i} (N,v)$ represents the outcome or payoff for player $i \in N$ in the game (N, v). Shapley (1953a) proposed a solution for TU-games that still is one of the most prominent solutions. It assigns to every player in a TU-game a linear combination of his marginal contributions to different coalitions as follows:

$$\begin{aligned} Sh_i(N,v)=\sum _{S\subseteq N\setminus \{i\}}\frac{(n-s-1)!s!}{n!}[v(S\cup \{i\})-v(S)],\;\; i\in N, \end{aligned}$$

which coincides with

$$\begin{aligned} Sh_i(N,v)=\sum _{i\in S\subseteq N}\frac{\Delta _v(S)}{s},\;\; i\in N. \end{aligned}$$

2.2 Graphs or networks

A graph or a network is a pair $(N,\gamma )$ with $N=\{1,2,\dots ,n\}$ being the set of nodes and $\gamma \subseteq \gamma _N=\{\{i,j\} | i,j\in N, i\ne j\}$. Each pair $\{i,j\} \in \gamma$ is called an edge or link. We often denote a graph $(N,\gamma )$ just by its set of edges $\gamma$. $\Gamma ^N$ denotes the set of all graphs with nodes set N.

Two nodes i and j are directly connected in $(N,\gamma )$, if $\{i,j\}\in \gamma$. Two nodes i and j are connected in $\gamma$ if there exists a sequence of nodes $i_1, i_2,\dots i_k$ with $i_1=i$, $i_k=j$ and $\{i_l,i_{l+1}\}\in \gamma$, for $l=1,\dots , k-1$. The graph $(N,\gamma )$ is connected if all $i,j \in N$ are connected in $\gamma$. A set $\emptyset \ne S\subseteq N$ is connected in $\gamma$ if $|S|=1$ or every pair of nodes in S is connected in $(S,\gamma _{|_S})$ with $\gamma _{|_S}=\{\{i,j\} \in \gamma | \{i,j\} \subseteq S\}$. A coalition C is a connected component in the graph $(N, \gamma )$ if it is maximally connected, meaning that (i) C is connected in the graph and, (ii) for all $C'\subseteq N$, if $C\subsetneq C'$ then, $C'$ is not connected. We will denote by $N/\gamma$ the partition of N in connected components induced by $(N,\gamma )$. We will denote by $S/\gamma$ the set of the connected components of S in $(S,\gamma _{|_S})$. A graph $(N,\gamma ')$ with $\gamma '\subseteq \gamma$ is a subgraph of $(N,\gamma )$. For $i\in N,$ $(N,\gamma _{i})$ is given by $\gamma _{i} = \{l \in \gamma \;| \; i \in l\}$, and $(N,\gamma _{-i})$ is given by $\gamma _{-i} = \gamma {\setminus } \gamma _{i}$.

2.3 Communication situations and allocation rules

A communication situation is a triple $(N,v,\gamma )$, where (N, v) is a TU-game and $(N,\gamma )$ is a graph which set of nodes corresponds to the set of players in the game. ${\mathcal {C}}{\mathcal {S}}^N$ will denote the set of all communication situations with players-nodes set N. An allocation rule for communication situations is a map $\psi : {\mathcal {C}}{\mathcal {S}}^N\rightarrow {\mathbb {R}}^n$, where $\psi _i(N,v,\gamma )$ represents the outcome or payoff for player i.

For communication situations $(N,v,\gamma )$, Myerson (1977) defined the graph-restricted game $(N,v^\gamma )$ as the TU-game $(N,v^\gamma )$, given by:

$$\begin{aligned} v^\gamma (S)=\sum _{C\in S/\gamma }v(C) \text{, } \text{ for } \text{ all } S \subseteq N, \end{aligned}$$

expressing the idea that only coalitions that are connected in the graph can form and generate their worth.

As allocation rule for communication situations, Myerson proposed to apply the Shapley value to the graph-restricted game, yielding the allocation rule $\mu$ given by $\mu (N,v,\gamma )=Sh(N,v^{\gamma })$ for all $(N,v,\gamma ) \in {\mathcal {C}}{\mathcal {S}}^N$. Nowadays, this rule, $\mu$, is known as the Myerson value. Myerson (1977) showed that the value $\mu$ is the unique allocation rule for communication situations satisfying the following two axioms.

An allocation rule $\psi$ on ${\mathcal {C}}{\mathcal {S}}^N$ satisfies component efficiency (Myerson 1977) if, $\text{ for } \text{ all } (N,v,\gamma )\in {\mathcal {C}}{\mathcal {S}}^N$ and all $C\in N/\gamma ,\;\; \sum _{i\in C}\psi _i(N,v,\gamma )=v(C)$.

An allocation rule $\psi$ on ${\mathcal {C}}{\mathcal {S}}^N$ satisfies fairness (Myerson 1977) if, for all $(N,v,\gamma )\in {\mathcal {C}}{\mathcal {S}}^N$ and every $l=\{i,j\} \in \gamma$, $\psi _i(N,v,\gamma )-\psi _i(N,v,\gamma \setminus \{l\})=\psi _j(N,v,\gamma )-\psi _j(N,v,\gamma \setminus \{l\}).$

Later, Myerson (1980) showed that the value $\mu$ is the unique allocation rule for communication situations satisfying component efficiency and balanced contributions.

An allocation rule $\psi$ on ${\mathcal {C}}{\mathcal {S}}^N$ satisfies balanced contributions (Myerson 1980) if, for all $(N,v,\gamma )\in {\mathcal {C}}{\mathcal {S}}^N$ and all $i,j\in N,$ $\psi _i(N,v,\gamma )-\psi _i(N,v,\gamma _{-j})=\psi _j(N,v,\gamma )-\psi _j(N,v,\gamma _{-i})$.

2.4 Directed graphs or digraphs

A directed graph or a digraph is a pair (N, D) where $N=\{1,2,\dots ,n\}$ is a (finite) set of nodes and $D \subseteq N\times N$ is a binary relation on N. Each directed edge or arc $(i,j) \in D$ is an ordered pair of nodes called endpoints of the arc: i is the tail and j is the head. We say that an arc is from its tail to its head. Also, if $(i,j) \in D$, then i is called a predecessor of j, and j a successor of i. A loop in a digraph is an arc in which its endpoints are equal. Multiple arcs are those with identical tails and identical heads. We will assume the digraph to be (i) irreflexive, i.e., with no loops, and (ii) simple, i.e., with no multiple arcs. When there is no ambiguity with respect to N, we will simply identify the digraph with its set of arcs D. ${\mathcal {D}}^N$ denotes the set of all irreflexive, simple digraphs with nodes set N.

Given $(N,D) \in {\mathcal {D}}^N$ and $i \in N$, the out-degree, $d_i^O(N,D) = \big |\{j \in N \mid (i,j) \in D\}\big |$ (respectively, the in-degree, $d_i^I(N,D) = \big |\{j \in N \mid (j,i) \in D\}\big |$) is the number of arcs with i as the tail (respectively, i as the head). Then, $d_i(N,D)=d_i^O(N,D)+d_i^I(N,D)$ is the degree of node i in (N, D).

For $(N,D)\in {\mathcal {D}}^N$, a graph $(N,D')$ with $D' \subseteq D$, is called a subdigraph of (N, D). For each $i\in N$, the subdigraph $(N,D_{-i})$ of (N, D) is obtained when severing all arcs incident with i, i.e. $D_{-i}=\{(j,k) \in D { | i \not \in \{j,k\} \} }$. Moreover, the restriction of (N, D) to $\emptyset \ne S \subseteq N$ is the directed graph $(S,D_{|_S})$ in which $D_{|_S}=\{(i,j)\in D | i,j\in S\}$. For $L\subseteq D$, we will use the abuse of notation $\{L\}$ to indicate the nodes corresponding to the arcs in L, i.e., $\{L\}=\{i \in N | \text{ there } \text{ is } j \in N \text{ with } (i,j)\in L \text{ or } { (j,i)} \in L \}$. Notice that the restriction $(\{L\},D_{|_{\{L\}}})$ coincides with $(\{L\},L)$. Given a digraph (N, D), a (directed) path from i to j is a sequence of distinct nodes $P=(i_1,...,i_t)$ with $i_1=i$, $i_t=j$ and $(i_k,i_{k+1}) \in D$ for $k=1,\ldots ,t-1$. We assume that (i), $i\in N$, is a path. For convenience, we will sometimes identify P with its set of arcs $\{(i_1,i_2),\ldots ,(i_{t-1},i_t)\}.$ We also will use the abuse of notation $\{P\}$ to denote the set of nodes of a path P, and thus $\{P\}=\{i_1,\ldots ,i_t\}$ for $P=(i_1, \ldots , i_t)$. Given two paths $P=(i_1,...,i_t)$ and $Q=(j_1,...,j_r)$ in (N, D), we say that P is a subpath of Q, denoted by $P {\widetilde{\subseteq }}Q$, if for each $k=1,...,t-1$ there exists $l=1,...,r-1$ such that $j_l=i_k$ and $j_{l+1}=i_{k+1}$. A path P in (N, D) is maximal if it is maximal for the defined partial order ${\widetilde{\subseteq }}$, i.e., if there is no other path $P'\ne P$ such that $P {\widetilde{\subseteq }}P'.$ Given a digraph (N, D), we will denote by ${\mathcal {P}}(N,D)$ the set of all maximal paths of (N, D). Given a digraph (N, D) and $\emptyset \ne S \subseteq N$, we say that a path P in (N, D) is a connection path of S in (N, D) if $S\subseteq \{P\}$. We say that a path P is a minimal connection path of S in (N, D) if P is a connection path of S and there does not exist another connection path $P'\ne P$ of S such that $P' {\widetilde{\subseteq }}P.$ By ${\mathcal {M}} {\mathcal {C}} {\mathcal {P}}(S,N,D)$ we will denote the family (occasionally empty) of all minimal connection paths of S in (N, D). A Hamiltonian path (or traceable path) is a path in which $t=n$, where n is the cardinality of N, i.e., it is a path that visits each node exactly once. Thus, if P is a Hamiltonian path, then $\{P\}=N$. A Hamiltonian path in a digraph is necessarily maximal.

Given a digraph $(N,D)\in {\mathcal {D}}^N$, its underlying (undirected) graph $(N,\gamma _D)\in \Gamma ^N$ is obtained by replacing all directed arcs with corresponding undirected links, i.e. $\gamma _D = \{\{i,j\} | (i,j) \in D\}$. A digraph (N, D) is weakly connected if its underlying graph $(N,\gamma _D)$ is connected. A weak component of (N, D) is a component of $(N,\gamma _D)$. A digraph $(N,D)\in {\mathcal {D}}^N$, is strongly connected or strong if for every $i,j \in N$ there is a directed path P starting at i and ending at j. A set of nodes C is a strongly connected component of a given digraph (N, D) if $(C, D_{|_C})$ is strongly connected, and for $C' \supset C$, $(C',D_{|_{C'}})$ is not strong. Notice that every strongly connected digraph is weakly connected.

We illustrate these notions with an example.

Example 2.1

Consider the digraph $(N,D^1)$ with $N=\{1,2,3,4\}$ and $D^1=\{(1,2),(1,3),(2,3),(2,4),(3,4),(4,1)\}$ (see Fig. 1). This digraph is strongly connected, and ((1, 2), (2, 3), (3, 4)) is a Hamiltonian path.

Consider the digraph $(N,D^2)$ with $N=\{1,2,3,4\}$ and $D^2=\{(1,2),(1,3),(2,3),(2,4),(3,4)\}$ (see Fig. 1). This digraph is weakly connected, but not strongly connected, and ((1, 2), (2, 3), (3, 4)) is a Hamiltonian path. This is also a connection path of $S=\{1,2,4\}$, but it is not a minimal connection path of S. The path ((1, 2), (2, 4)) is a minimal connection path of $S=\{1,2,4\}$.

Finally, consider the digraph $(N,D^3)$ with $N=\{1,2,3,4\}$ and $D^3=\{(1,2),(1,3),(2,3),(2,4)\}$ (see Fig. 1). This digraph is weakly connected, but not strongly connected. It does not have a Hamiltonian path. The path ((1, 2), (2, 4)) is a maximal path in (N, D). It is also a minimal connection path of $S=\{1,2,4\}$.

Fig. 1

Digraphs $(N,D^1)$,$(N,D^2)$ and $(N,D^3)$ Example 2.1

3 Directed communication situations

A situation where cooperation among players in a TU-game is limited because of restricted directed communication possibilities can be modeled by a directed communication situation.

Definition 3.1

A directed communication situation is a triple (N, v, D) in which (N, v) is a TU-game and (N, D) is a directed graph, the nodes in the digraph being the players in the game.

The set of all directed communication situations with players set N will be denoted by ${\mathcal {D}}{\mathcal {C}}{\mathcal {S}}^{N}$.

The model of a directed communication situation is mathematically identical to other models of a game with an order (or digraph) on the player set (see introduction), but because of the interpretation of the directed graph as a directed communication network, we refer to it as a directed communication situation. In the following definition, we introduce a modification of the original game to take into account the restrictions in the communication given by the digraph. In this modified game, we assume that the worth of each coalition is the “sum” of the values of its (path) maximally connected subcoalitions.¹

Definition 3.2

A subcoalition $T \subseteq S$ is a (path) maximally connected subcoalition of S in directed graph (N, D) if there is a maximal path P in $(S,D_{|_S})$ with $T =\{P\}$.

For $\emptyset \ne S \subseteq N$, we denote the family of the maximal paths in $(S,D_{|_S})$ by ${\mathcal {P}}(S,D_{|_S})$.

To clarify the previous definition, let us consider the following example.

Example 3.1

Consider the directed communication situation (N, v, D) with N=$\{1,2,3,4\}$, and $D=\{(1,2),(1,3),(2,4),(3,4)\}.$ See Fig. 2.

Fig. 2

Digraph (N,D). Example 3.1

In this case,

$$\begin{aligned} {\mathcal {P}}(S,D_{|_S})=\left\{ \begin{array}{cc} \{(i)\}, &{} \text{ if } S=\{i\}, i=1,2,3,4, \\ \{(1,2)\},&{} \text{ if } S=\{1,2\}, \\ \{(1,3)\},&{} \text{ if } S=\{1,3\},\\ \{(1),(4)\} &{} \text{ if } S=\{1,4\}, \\ \{(2),(3)\}&{} \text{ if } S=\{2,3\},\\ \{(2,4)\},&{} \text{ if } S=\{2,4\},\\ \{(3,4)\},&{} \text{ if } S=\{3,4\},\\ \{(1,2),(1,3)\},&{} \text{ if } S=\{1,2,3\},\\ \{(1,2,4)\},&{} \text{ if } S=\{1,2,4\},\\ \{(1,3,4)\},&{} \text{ if } S=\{1,3,4\},\\ \{(2,4),(3,4)\},&{} \text{ if } S=\{2,3,4\},\\ \{(1,2,4),(1,3,4)\},&{} \text{ if } S=N.\end{array}\right. \end{aligned}$$

Connectedness being related to directed (connection) paths occurs in, for example, supply chain management, attribution models and vaccination policy. In supply chains, value can be created when a manufacturer (source) is connected to a retailer (sink) by a sequence of intermediaries (wholesalers, shipping companies etc.). In the other direction, to dampen the bullwhip effect² efficiency gains can be reached when the agents on a supply chain share information. In marketing attribution, advertisers use ‘attractiveness’ of various advertisement strategies, including online advertising, to decide in which form of advertisement they will invest. Typically, the attractiveness of one form of advertisement depends on its position in the advertisement channel and the rate to which a customer visiting a path containing multiple ads from the same advertiser (channel) eventually results in a conversion. Attribution models assess the ‘value’ of each ad on the path leading to conversion. Regarding the third example mentioned above, vaccination was one of the main strategies to ‘beat’ the Covid19 pandemic. To increase the vaccination grade, it is essential to get information about the virus and vaccination policy to members of the society. Problematic was that some parts of society was difficult to reach, for example because of language problems or distrust in government organizations. To get information from the government to those parts of society a chain of intermediary social clubs, doctors, etc., helped in passing the information from government to the people.

Notice that the maximal paths might have players/nodes in common, who will contribute only once in the coalition, and therefore, we must use the classical inclusion–exclusion principle to respect that coalitions cannot obtain more under the restrictions than in the original game. This brings us to the following definition of the modified game, taking account of the cooperation restrictions.

Definition 3.3

Given $(N,v,D) \in {\mathcal {D}}{\mathcal {C}}{\mathcal {S}}^{N}$, the digraph restricted game is defined as the TU-game $(N,v^D)$ with characteristic function given by:

$$\begin{aligned}{} {} v^D(S) &=\displaystyle \sum _{i=1}^{r(S)}v(\{P_i^S\})-\displaystyle \sum _{i=1}^{r(S)-1} \displaystyle \sum _{j=i+1}^{r(S)}v(\{P_i^S\}\cap \{P_j^S\}) \\{} & {} \quad +\displaystyle \sum _{i=1}^{r(S)-2}\displaystyle \sum _{j=i+1}^{r(S)-1} \displaystyle \sum _{k=j+1}^{r(S)}v(\{P_i^S\}\cap \{P_j^S\}\cap \{P_k^S\})+\cdots + \\{} & {} \quad +(-1)^{r(S)-1}v(\{P_1^S\}\cap \cdots \cap \{P_{r(S)}^S\}), \end{aligned}$$

where for $\emptyset \ne S \subseteq N$, ${\mathcal {P}}(S,D_{|_S}) =\{P_1^S,\cdots ,P_{r(S)}^S\}$ is the family of the maximal paths in $(S,D_{|_S})$, and $v^{ D} ( \emptyset )=0$.

Example 3.2

Consider the directed communication situation (N, v, D) of Example 3.1. Using the (path) maximally connected sets given in Example 3.1,

$$\begin{aligned} v^D(S)=\left\{ \begin{array}{cc} v(\{i\}), &{} \text{ if } S=\{i\}, i=1,2,3,4, \\ v(\{1\})+v(\{4\}) &{} \text{ if } S=\{1,4\}, \\ v(\{2\})+v(\{3\})&{} \text{ if } S=\{2,3\},\\ v(\{1,2\})+v(\{1,3\}) - v(\{1\}),&{} \text{ if } S=\{1,2,3\},\\ v(\{2,4\})+v(\{3,4\}) - v(\{4\}),&{} \text{ if } S=\{2,3,4\},\\ v(\{1,2,4\})+v(\{1,3,4\}) - v(\{1,4\}),&{} \text{ if } S=N\\ v(S)&{} \text{ otherwise }. \end{array}\right. \end{aligned}$$

Notice that in determining the worth of the grand coalition N, we use the worth of coalition $\{1,4\}$ although $\{1,4\}$ is not connected. Since worth is generated by directed paths, players 1 and 4 cooperate in the coalition/path $\{1,2,4\}$, as well as in $\{1,3,4\}$. To avoid that the worth generated by cooperation of 1 and 4 would be double counted, we subtract the worth of $\{1,4\}$.

Remark 3.1

Given $(N,v,D) \in {\mathcal {D}}{\mathcal {C}}{\mathcal {S}}^{N}$, the characteristic functions $v^D$ and v coincide if for all $S \subseteq N$, the digraph restricted to S, $(S,D_{|_S})$, has a Hamiltonian path. As an example, the digraphs (N, D) with $N=\{1,2,3\}$ and $D=\{(1,2),(1,3),(2,3) \}$ and $(N,D')$ with $N=\{1,2,3,4\}$ and $D'=\{(1,2),(1,3),(2,3),(2,4),(3,4),(4,1)\}$ satisfy such a condition (see Fig. 3). For the digraph of Example 3.1, the digraphs restricted to the coalitions $S \in \{\{1,4\},\{2,3\},\{1,2,3\},\{2,3,4\}, \{1,2,3,4\}\}$ do not have a Hamiltonian path.

Fig. 3

Digraphs (N,D) and (N,D') Remark 3.1

Remark 3.2

Given (N, v, D), the characteristic functions $v^D$ and $v^{\gamma _D}$ coincide if for all $S \subseteq N$, there exists a Hamiltonian path in each element of $S/({\gamma _D})_{|S}$, i.e., in each component of S. As an example, the digraph (N, D) with $N=\{1,2,3\}$ and $D=\{(1,2),(2,3)\}$ satisfies such a condition. Specifically, every line-digraph, i.e., rooted tree with a single sink, satisfies this condition.

In the following proposition, we obtain an expression of the digraph restricted game of unanimity games.

Proposition 3.1

Given $(N,u_S,D)\in {\mathcal {D}}{\mathcal {C}}{\mathcal {S}}^{N}$ with $\emptyset \ne S \subseteq N$, if ${\mathcal {M}}{\mathcal {C}}{\mathcal {P}}(S,N,D)=\{Q_1^S,\cdots , Q_{t(S)}^S\}\ne \emptyset$, then

$$\begin{aligned} u_S^D=1-\displaystyle \prod _{i=1}^{t(S)}(1-u_{\{Q_i^S\}}), \end{aligned}$$

and $u_S^D \equiv \varvec{0}$ otherwise.

Proof

Suppose that $\emptyset \ne S \subseteq N$ and ${\mathcal {M}}{\mathcal {C}}{\mathcal {P}}(S,N,D)=\{Q_1^S,\cdots , Q_{t(S)}^S\}\ne \emptyset$. Let $T \subseteq N$. For $T=\emptyset$, trivially $u_S^D(\emptyset )=0=\left[ 1-\displaystyle \prod _{i=1}^{t(S)}(1-u_{\{Q_i^S\}} (\emptyset ))\right] ,$ since $u_{\{Q\}}(\emptyset )=0$ for all $Q \in {\mathcal {M}}{\mathcal {C}}{\mathcal {P}}(S,N,D)$. For $T\ne \emptyset$, let ${\mathcal {P}}(T,D_{|_T})=\{P_1^T,\cdots ,P_{r(T)}^T\}$ be the family of the maximal paths in $(T,D_{|_T})$. Then, by the definition of the digraph restricted game,

$$\begin{aligned}{} & {} u_S^D(T)=\displaystyle \sum _{i=1}^{r(T)}u_S(\{P_i^T\})-\displaystyle \sum _{i=1}^{r(T)-1} \displaystyle \sum _{j=i+1}^{r(T)}u_S(\{P_i^T\}\cap \{P_j^T\}) \\{} & {} \quad +\displaystyle \sum _{i=1}^{r(T)-2}\displaystyle \sum _{j=i+1}^{r(T)-1}\displaystyle \sum _{k=j+1}^{r(T)} u_S(\{P_i^T\}\cap \{P_j^T\}\cap \{P_k^T\})+(-1)^{r(T)-1}u_S(\{P_1^T\}\cap \cdots \cap \{P_{r(T)}^T\}). \end{aligned}$$

We consider the following two cases with respect to $r'(T)$, the cardinality of the subset of ${\mathcal {P}}(T,D_{|_T})$ with nodes set containing S, i.e., we assume there are $r'(T)$ maximal paths in $(T,D_{|_T})$ which nodes set contains S.

Case (i) Suppose $1\le r'(T).$ Then,

$$\begin{aligned}{} & {} u_S^D(T)=\left( {\begin{array}{c} r'(T)\\ 1\end{array}}\right) -\left( {\begin{array}{c} r'(T)\\ 2\end{array}}\right) +\cdots +(-1)^{ r'(T)-1}\left( {\begin{array}{c} r'(T)\\ r'(T)\end{array}}\right) \\{} & {} \quad =-\left( {\begin{array}{c} r'(T)\\ 0\end{array}}\right) +\left( {\begin{array}{c}r'(T)\\ 1\end{array}}\right) -\left( {\begin{array}{c} r'(T)\\ 2\end{array}}\right) +\cdots +(-1)^{ r'(T)}\left( {\begin{array}{c} r'(T)\\ r'(T)\end{array}}\right) +\left( {\begin{array}{c}r'(T)\\ 0\end{array}}\right) \\{} & {} \quad =(1-1)^{ r'(T)}+\left( {\begin{array}{c} r'(T)\\ 0\end{array}}\right) =1, \end{aligned}$$

where the first equality follows since $u_S(\{P_1^T\}\cap \cdots \cap \{P_{k}^T\})$, $1 \le k \le r(T)$, equals 1 if the set of nodes S belongs to every path in $\{P_1^T\}\cap \cdots \cap \{P_{k}^T\}$, and equals 0 otherwise, and the third equality follows from the binomial formula.

Case (ii) If, on the other hand, $r'(T)=0$, then $u_S^D(T)=0$.

Thus, we can conclude that

$$\begin{aligned} u_S^D(T)= \left\{ \begin{array}{cl} 1 &{} \text{ if } \text{ there } \text{ exists } \text{ at } \text{ least } \text{ one } \text{ path } \text{ in } P \in {\mathcal {P}}(T,D_{|_T}) \text{ with } S \subseteq \{P\} \\ 0 &{} \text{ otherwise }. \end{array}\right. \end{aligned}$$

Similarly, $\left[ 1-\displaystyle \prod _{i=1}^{ t(S)}(1-u_{\{Q_i^S\}} (T) )\right] =1$ if there is $i=1,..., t(S)$ such that $(1-u_{\{Q_i^S\}} (T))=0$, or equivalently $u_{\{Q_i^S\}}(T)=1$, i.e., if there is a path with nodes set containing S and contained in T.

Finally, if for $\emptyset \ne S \subseteq N$, ${\mathcal {M}}{\mathcal {C}}{\mathcal {P}}(S,N,D)=\emptyset ,$ by the definition of $u_S^D$, $u_S^D(T)=0$ for all $T \subseteq N$, as the nodes in the elements of ${\mathcal {P}}(T,D_{|T})$ cannot contain S since S has no minimal connection paths in (N, D). This completes the proof. $\square$

4 A value for directed communication situations

First of all, we introduce the definition of a value or allocation rule on ${\mathcal {D}}{\mathcal {C}}{\mathcal {S}}^N.$ As usual, an allocation rule assigns a payoff vector to every, in this case, directed communication situation.

Definition 4.1

A value or an allocation rule on ${\mathcal {D}}{\mathcal {C}}{\mathcal {S}}^N$ is a function $\psi :{\mathcal {D}}{\mathcal {C}}{\mathcal {S}}^N\rightarrow {\mathbb {R}}^n$. For $(N,v,D) \in {\mathcal {D}}{\mathcal {C}}{\mathcal {S}}^N$, $\psi _i(N,v,D)$ represents the outcome for player i, $i \in N$, in the directed communication situation (N, v, D).

Following Myerson (1977) for undirected communication situations, we define an allocation rule that assigns to every directed communication situation, the Shapley value of the corresponding digraph restricted game.

Definition 4.2

The Directed Communication-value (or DC-value for short) $\mu ^d$ is given by $\mu ^d(N,v,D)=Sh(N,v^D)$, for all $(N,v,D)\in {\mathcal {D}}{\mathcal {C}}{\mathcal {S}}^N$, where $v^D$ is given by Definition 3.3.

Remark 4.1

Taking Remark 3.1 into account, given $(N,v,D) \in {\mathcal {D}}{\mathcal {C}}{\mathcal {S}}^N$, $\mu ^d(N,v,D)=\mu (N,v,\gamma _D)$=Sh(N,v) if for all $S \subseteq N$, the digraph restricted to S, $(S,D_{|_S})$, has a Hamiltonian path. Moreover, representing $\gamma \in \Gamma ^N$ as $D^\gamma = \{(i,j), (j,i) \mid \{i,j\} \in \gamma \}$, it is clear that $D^\gamma$ has a Hamiltonian path if $\gamma$ is connected, and thus $\mu ^d(N,v,D^\gamma )=\mu (N,v,\gamma )$ in that case.

The digraph restricted game for a directed communication situation $(N,v, D ) \in {\mathcal {D}}{\mathcal {C}}{\mathcal {S}}^N$ coincides with the graph-restricted game of the communication situation $(N,v,\gamma _D) \in {\mathcal {C}}{\mathcal {S}}^N$ if in (N, v, D) each “component” has a Hamiltonian path.

Example 4.1

Consider the directed communication situation (N, v, D) in which (N, D) is as in the Example 3.1 and (N, v) is the messages game (see Gómez et al. (2003)), i.e., the worth of a coalition is the number of pairs, with the interpretation that this is the number of messages that can be sent between members of the coalition. Its characteristic function is

$$\begin{aligned} v(S)= \left\{ \begin{array}{cl} \frac{s(s-1)}{2} &{} \text{ if } \text{ s } \ge \text{2 } \\ 0 &{} \text{ otherwise }. \end{array}\right. \end{aligned}$$

(1)

Particularizing the expression of $v^D$ obtained in Example 3.2, we have

$$\begin{aligned} v^D(S)=\left\{ \begin{array}{cc} 0 &{} \text{ if } S=\emptyset , s=1 , S=\{1,4\} \text{ or } S=\{2,3\} \\ 1 &{} \text{ if } S=\{1,2\}, S=\{1,3\}, S=\{2,4\} or S=\{3,4\} \\ 2 &{} \text{ if } S=\{1,2,3\} or S=\{2,3,4\}\\ 3 &{} \text{ if } S=\{1,2,4\} or S=\{1,3,4\} \\ 5 &{} \text{ if } S=N, \end{array}\right. \end{aligned}$$

which in terms of the unanimity basis is

$$\begin{aligned} v^D(S)=u_{\{1,2\}}+u_{\{1,3\}}+u_{\{2,4\}}+u_{\{3,4\}}+u_{\{1,2,4\}}+u_{\{1,3,4\}}-u_N. \end{aligned}$$

Thus, the DC-value in this case is

$$\begin{aligned} \mu ^d(N,v,D)=Sh(N,v^D)=\left( \frac{17}{12},\frac{13}{12},\frac{13}{12},\frac{17}{12}\right) . \end{aligned}$$

5 Characterizations of the DC-value

In this section, we characterize the DC-value with modifications of properties as component efficiency, fairness and balanced contributions for directed networks. First, connection efficiency expresses that worth is generated by (maximal) paths. This occurs, for example, in marketing attribution or supply chains, where worth is generated when, through a sequence of advertisements, respectively a sequence of intermediary retailers and other agents on the supply chain, a conversion takes place when a consumer (sink of the path) buys a product that is produced by a producer (source of the path). Another situation where this occurs is in communications (e.g., sending messages) when the only thing that matters is whether a message from a sender reaches the intended receiver, possibly through a chain of intermediaries. As we will see in Sect. 6 this notion of connection efficiency can be used to introduce game-theoretical measures of efficiency and vulnerability for directed networks.

Definition 5.1

An allocation rule $\psi$ on ${\mathcal {D}}{\mathcal {C}}{\mathcal {S}}^N$ satisfies connection efficiency if, $\text{ for } \text{ all } (N,v,D) \in {\mathcal {D}}{\mathcal {C}}{\mathcal {S}}^N$ and all $C\in N/\gamma _D,\;\; \sum _{i\in C}\psi _i(N,v,D)=v^D(C)$.

Connection efficiency reflects our new cooperation restrictions and requires that the sum of the payoffs of the players in a component is equal to the "sum" of the worths of the (path) maximally connected subcoalitions in this component. This emphasizes our idea of connectedness that is needed to generate worth. Notice that the axiom of connection efficiency explicitly uses the worth $v^D(C)$ of components C. In terms of the original game v and digraph D, this means that the total payoff in every component is equal to the worth generated by all directed paths in D in the original game v.

Fairness and balanced contributions are expressed the same as in Myerson 1977, 1980) (see preliminaries), but for digraphs, requiring that the payoffs of two nodes on a directed arc change by the same amount when the arc is deleted.

Definition 5.2

An allocation rule $\psi$ on ${\mathcal {D}}{\mathcal {C}}{\mathcal {S}}^N$ satisfies fairness if, for all $(N,v,D)\in {\mathcal {D}}{\mathcal {C}}{\mathcal {S}}^N$ and every $e=(i,j) \in D$, $\psi _i(N,v,D)-\psi _i(N,v,D\setminus \{e\})=\psi _j(N,v,D)-\psi _j(N,v,D\setminus \{e\}).$

Notice that fairness is more or less stated the same way as Myerson’s fairness for undirected communication situations (as mentioned in the preliminaries), just replacing undirected graphs and undirected edges by directed networks and arcs.

Finally, balanced contributions requires that the effect of isolation of a player on the payoff of another player, is equal to the effect the other way around, that is the effect on the payoff of this player of the isolation of the other player.

Definition 5.3

An allocation rule $\psi$ on ${\mathcal {D}}{\mathcal {C}}{\mathcal {S}}^N$ satisfies balanced contributions if, for all $(N,v,D)\in {\mathcal {D}}{\mathcal {C}}{\mathcal {S}}^N$ and all $i,j\in N,$ $\psi _i(N,v,D)-\psi _i(N,v,D_{-j})=\psi _j(N,v,D)-\psi _j(N,v,D_{-i})$.

In the following propositions, we prove that the DC-value $\mu ^d$ is the unique connection efficient rule that satisfies either fairness or balanced contributions. Notice that this mimics other results in the literature on undirected graph games, starting with the results of Myerson (1977) and Myerson (1980), that characterize a value by an efficiency and a fairness or balanced contributions property. Since uniqueness follows similar as in Myerson (1977) or Myerson (1980), we first prove that $\mu ^d$ satisfies the three previous properties.

Proposition 5.1

The DC-value, $\mu ^d$, satisfies connection efficiency.

Proof

Let $(N,v,D) \in {\mathcal {D}}{\mathcal {C}}{\mathcal {S}}^N$. Suppose that $C \in N/\gamma _D$ is a weak component in (N, D). Then,

$$\begin{aligned} \displaystyle \sum _{i \in C}\mu _i^d(N,v,D)=\displaystyle \sum _{i \in C}Sh_i(N,v^D)=\displaystyle \sum _{i \in C}Sh_i(C,(v^D)_{|C})=(v^D)_{|C}(C)=v^D(C), \end{aligned}$$

the first equality holding by the definition of $\mu ^d$, the second one as the Shapley value of a player in $(N,v^D)$ only depends on the component to which he belongs,³ the third one by the efficiency of the Shapley value, and the fourth one by the definition of the restriction of a game to a coalition. $\square$

Proposition 5.2

The DC-value, $\mu ^d$, satisfies fairness.

Proof

As $\mu ^d$ is clearly linear in the game, it is sufficient to prove the result for directed communication situations of the form $(N,u_S,D)$ with $\emptyset \ne S \subseteq N$. Suppose that $i,j \in N$ are such that $(i,j) \in D$. If ${\mathcal {M}} {\mathcal {C}} {\mathcal {P}}(S,N,D)=\emptyset$, then $\mu _k^d(N,u_S,D)=\mu _k^d( N,u_S,D\backslash \{(i,j)\})=0$, for $k=i,j$, by connection efficiency, and thus the result is proved in this case.

If, on the other hand, ${\mathcal {M}} {\mathcal {C}} {\mathcal {P}} (S,N,D)=\{Q_1^S,\cdots ,Q_{t(S)}^S\} \ne \emptyset$ then, for $k=i,j$, $\mu _k^d(N,u_S,D)=Sh_k[N,1-\prod _{l=1}^{t(S)}(1-u_{\{Q_l^S\}})]$, by Proposition 3.1.

Since ${\mathcal {M}}{\mathcal {C}} {\mathcal {P}} (S,N,D\backslash \{(i,j)\}) \subseteq {\mathcal {M}}{\mathcal {C}} {\mathcal {P}} (S,N,D)$, suppose, without loss of generality, that ${\mathcal {M}}{\mathcal {C}} {\mathcal {P}} (S,N,D\backslash \{(i,j)\})=\{Q_1^S,\cdots ,Q_{t'(S)}^S\}$ with $t'(S) \le t(S)$. The case $t'(S)=t(S)$ is trivial. Therefore, suppose that $t'(S) < t(S)$, i.e., $Q_{t'(S)}^S,\cdots ,Q_{t(S)}^S$ are the paths in ${\mathcal {M}} {\mathcal {C}} {\mathcal {P}}(S,N,D)$ to which the arc (i, j) belongs.

Then, for k=i, j,

$$\begin{aligned}{} & {} \mu _k^d(N,u_S,D)-\mu _k^d(N,u_S,D\backslash \{(i,j)\}) \\{} & {} \quad =Sh_k[N,1-\prod _{l=1}^{t(S)}(1-u_{\{Q_l^S\}})]- Sh_k[N,1-\prod _{l=1}^{t'(S)}(1-u_{\{Q_l^S\}})] \\{} & {} \quad =Sh_k\left[ N,\left( \prod _{l=1}^{t'(S)}(1-u_{\{Q_l^S\}}) - \prod _{l=1}^{t(S)}(1-u_{\{Q_l^S\}}) \right) \right] \end{aligned}$$

$$\begin{aligned} =Sh_k\left[ N,\left( \prod _{l=1}^{t'(S)}(1-u_{\{Q_l^S\}})\right) \left( 1-\prod _{l=t'(S)+1} ^{t(S)}(1-u_{\{Q_l^S\}})\right) \right] , \end{aligned}$$

(2)

where the second equality follows from linearity of the Shapley value. The characteristic function $1-\displaystyle \prod _{l=t'(S)+1}^{t(S)}(1-u_{\{Q_l^S\}})$ can be written as a linear combination of unanimity games as follows

$$\begin{aligned}{} & {} \displaystyle \sum _{l=t'(S)+1}^{t(S)}u_{\{Q_l^S\}}-\displaystyle \sum _{l=t'(S)+1} ^{t(S)-1}\displaystyle \sum _{m=l+1}^{t(S)}u_{\{Q_l^S\}\cup {\{Q_m^S\}}} \nonumber \\{} & {} \quad +\cdots +(-1)^{t(S)-t'(S)-1}u_{{\{Q_{t'(S)+1}^S\}}\cup \cdots \cup {\{Q_{t(S)}^S\}}}. \end{aligned}$$

(3)

Notice that players i and j belong to every coalition in $\{\{Q_{t'(S)}^S\},\cdots ,\{Q_{t(S)}^S\}\}$, and thus both players belong to every unanimity coalition in this expression. As a consequence, $\displaystyle \prod _{l=1}^{t(S)}(1-u_{\{Q_l^S\}})(1-\prod _{l=t'(S)+1}^{t(S)}(1-u_{\{Q_l^S\}}))$ is also a linear combination of unanimity games $u_T$ with $i,j \in T$. Given the symmetry of the Shapley value, we have that

$$\begin{aligned}{} & {} Sh_i[N,\displaystyle \prod _{l=1}^{t'(S)}(1-u_{\{Q_l^S\}})(1-\prod _{l=t'(S)+1}^{t(S)}(1-u_{\{Q_l^S\}}))] \\{} & {} \quad =Sh_j[N,\displaystyle \prod _{l=1}^{t'(S)}(1-u_{\{Q_l^S\}})(1-\prod _{l=t'(S)+ 1}^{t(S)}(1-u_{\{Q_l^S\}}))], \end{aligned}$$

and thus the result follows with (2). $\square$

Proposition 5.3

The DC-value, $\mu ^d$, satisfies balanced contributions.

Proof

Again, as $\mu ^d$ is linear in the game, it is sufficient to prove that $\mu ^d$ satisfies the property for directed communication situations of the form $(N,u_{ S},D)$ with $\emptyset \ne S\subseteq N$.

Suppose $i,j \in N$. If ${\mathcal {M}} {\mathcal {C}} {\mathcal {P}}(S,N,D)=\emptyset$, then $u_S^D=u_S^{D\backslash D_i}=u_S^{D\backslash D_j}\equiv {\textbf{0}}$, and thus $\mu _i^d(N,u_S,D)=\mu _j^d(N,u_S,D)= \mu _i^d(N,u_S, D_{-j} )= \mu _j^d(N,u_S, D_{-i} ) = 0$ by connection efficiency, and then, the result is proved in this case.

Consider, then, the case in which ${\mathcal {M}} {\mathcal {C}} {\mathcal {P}}(S,N,D)=\{Q_1^S,\cdots ,Q_{t(S)}^S\} \ne \emptyset$ and (without loss of generality) ${\mathcal {M}} {\mathcal {C}} {\mathcal {P}}(S,N,D\backslash D_j)=\{Q_1^S,\cdots ,Q_{t'(S)}^S\}$ with $t'(S) \le t(S)$. Again (similar as in the proof of Proposition 5.2) the case $t'(S)=t(S)$ is trivial. Therefore, suppose that $t'(S) < t(S)$.

Then, in a parallel way to the proof of the previous proposition,

$$\begin{aligned}{} & {} \mu _i^d(N,u_S,D)-\mu _i^ d(N,u_S, D_{-j} ) \\{} & {} \quad =Sh_i\left[ N,\displaystyle \prod _{l=1}^{t'(S)}(1-u_{\{Q_l^S\}})\left( 1-\prod _{l=t'(S)+1} ^{t(S)}(1-u_{\{Q_l^S\}})\right) \right] , \end{aligned}$$

but now the sets in $\{Q_1^S,\cdots ,Q_{t'(S)}^S\}$ are the minimal connection paths in $D\backslash D_j$, and thus is the Shapley value of player i in a linear combination of unanimity games $u_T$ with $j\in T$ (and not necessarily $i \in T$). Similar as in the proof of Proposition 5.2, this expression can be written in a form as (3), but with coalitions $\{Q^S_l\}$ containing j (but not necessarily containing i).

On the other hand, $\mu _j^d(N,u_S,D)-\mu _j^ d(N,u_S, D_{-i} )$ is the Shapley value of player j in a linear combination of unanimity games $u_T$ with $i\in T$ (but not necessarily $j \in T$).

By the null player property of the Shapley value, in both expressions, we can ignore the unanimity games of coalitions not containing player i, respectively, player j, and thus both $\mu _i^d(N,u_S,D)-\mu _i^ d(N,u_S,D_{-j})$ as well as $\mu _j^d(N,u_S,D)-\mu _j^ d(N,u_S,D_{-i})$ can be expressed as sum of unanimity games of coalitions containing both i and j, and thus, by the symmetry of the Shapley value,

$$\begin{aligned} \mu _i^d(N,u_S,D)-\mu _i^ d(N,u_S, D_{-j} )=\mu _j^d(N,u_S,D)-\mu _j^ d(N,u_S, D_{-i} ), \end{aligned}$$

which completes the proof. $\square$

In the next two theorems, we obtain two characterizations of $\mu ^d$.

Theorem 5.1

The DC-value $\mu ^d$ is the unique allocation rule on ${\mathcal {D}}{\mathcal {C}}{\mathcal {S}}^N$ satisfying connection efficiency and fairness.

Proof

It is already proved that $\mu ^d$ satisfies connection efficiency and fairness, see Propositions 5.1 and 5.2. Reciprocally, suppose that $\psi$ is an allocation rule on ${\mathcal {D}}{\mathcal {C}}{\mathcal {S}}^N$ satisfying connection efficiency and fairness. We will prove that $\psi (N,v,D)$ is uniquely determined for all $(N,v,D) \in {\mathcal {D}}{\mathcal {C}}{\mathcal {S}}^N$, by induction on the cardinality of D.

If $|D|=0$, then clearly every singleton $\{i\},\ i \in N$, is a weak component, and thus by connection efficiency, $\psi _i(N,v,D)=v^D(\{i\})=v(\{i\})=\mu _i^d(N,v,D)$.

Proceeding by induction, suppose that the result holds for $(N,v, D' )\in {\mathcal {D}}{\mathcal {C}}{\mathcal {S}}^N$ such that $| D'|\le k$ and consider (N, v, D) with $|D|=k+1$. Let $C\in N/\gamma _D$ be a weak component of (N, D), and let $(C,T_C)$ be a spanning tree in $(C,(\gamma _D){_{|_C}})$.

Then, for every $\{i,j\} \in T_C$, fairness implies that

$$\begin{aligned}{} & {} \psi _i(N,v,D) - \psi _i(N,v,D \setminus \{(t(\{i,j\}),h(\{i,j\})\}) \nonumber \\{} & {} \quad = \psi _j(N,v,D) - \psi _j(N,v,D \setminus \{(t(\{i,j\}),h(\{i,j\})\}), \end{aligned}$$

(4)

where t(e) denotes the tail of arc $e \in D$, while h(e) denotes the head of arc $e \in D$.

Notice that $|T_C|=|C|-1$. Moreover, for every weak component $C \in N/\gamma _D$, connection efficiency implies that

$$\begin{aligned} \sum _{i \in C} \psi _i(N,v,D)=v^D(C). \end{aligned}$$

(5)

Since $\psi _i(N,v,D \setminus \{(t(\{i,j\}),h(\{i,j\})\})$ and $\psi _j(N,v,D \setminus \{(t(\{i,j\}),h(\{i,j\})\})$ are uniquely determined by the induction hypothesis, the $(|C|-1) +1 = |C|$ linear equations (4) and (5) are independent. Thus, the numbers (payoffs) $\psi _i(N,v,D)$, $i \in C$, are uniquely determined.

Since we have shown that $\mu ^d$ satisfies connection efficiency and fairness, it must hold that $\psi (N,v,D)=\mu ^d(N,v,D)$ for all $(N,v,D) \in {\mathcal {D}}{\mathcal {C}}{\mathcal {S}}^N$, which completes the proof. $\square$

Looking at the two axioms in Theorem 5.1, it is interesting to observe that fairness has a symmetric flavor in the sense that it seems not to take account of the orientation of the arcs. Although in the model the arcs are oriented, this axiom expresses that both players on an arc benefit equally from building the arc. So, in the axiomatization, the impact of the arc orientation fully comes from connection efficiency which, although it is an axiom requiring an efficiency for the total payoff in a component, takes account of the orientation of the arcs in determining what a component can earn.

Theorem 5.2

The DC-value is the unique allocation rule on ${\mathcal {D}}{\mathcal {C}}{\mathcal {S}}^N$ satisfying connection efficiency and balanced contributions.

Proof

It is already proved that $\mu ^d$ satisfies connection efficiency and balanced contributions, see Propositions 5.1 and 5.3. Reciprocally, suppose that $\psi$ is an allocation rule in ${\mathcal {D}}{\mathcal {C}}{\mathcal {S}}^N$ satisfying connection efficiency and balanced contributions. Consider $(N,v,D) \in {\mathcal {D}}{\mathcal {C}}{\mathcal {S}}^N$ and $i \in N$. We will prove that $\psi _i(N,v,D)=\mu _i^d(N,v,D)$ by induction on the cardinality of D. If $|D|=0$, then i is an isolated node in the digraph and by connection efficiency, $\psi _i(N,v,D)=v^d(\{i\})=v(\{i\})=\mu _i^d(N,v,D)$.

Proceeding by induction, suppose that $\psi (N,v,D')$ is uniquely determined for directed communication situations $(N,v,D')$ such that $|D'|\le k$ and consider (N, v, D) with $|D|=k+1$. Let $C_i$ be the weak component of (N, D) to which i belongs. If $|C_i|=1$, then connection efficiency implies that $\psi _i(N,v,D)={ v^D(\{i\}) =} \mu _i^d(N,v,D)$. Next, suppose $|C_i|>1$, and consider $j \in C_i$, $j \ne i$. As $\psi$ satisfies the balanced contributions property,

$$\begin{aligned} \psi _i(N,v,D)-\psi _i(N,v,D\backslash D_j) = \psi _j(N,v,D)-\psi _j(N,v,D\backslash D_i), \end{aligned}$$

or equivalently,

$$\begin{aligned} \psi _i(N,v,D)-\psi _j(N,v,D) = \psi _i(N,v,D\backslash D_j)-\psi _j(N,v,D\backslash D_i). \end{aligned}$$

(6)

Since $|D\backslash D_i| \le k$ and $|D\backslash D_j| \le k$, by the induction hypothesis, $\psi _i(N,v,D\backslash D_j)-\psi _j(N,v,D\backslash D_i)$ is uniquely determined., Moreover, for the weak component $C_i$, connection efficiency implies that

$$\begin{aligned} \sum _{j \in C_i} \psi _j(N,v,D)=v^D(C_i). \end{aligned}$$

(7)

Since the $(|C_i|-1) +1 = |C_i|$ linear Eqs. (6) and (7) are independent, the numbers (payoffs) $\psi _j(N,v,D)$ for $j \in C_i$, are uniquely determined.

Since we have shown that $\mu ^d$ satisfies connection efficiency and balanced contributions, it must hold that $\psi (N,v,D)=\mu ^d(N,v,D)$ for all $(N,v,D) \in {\mathcal {D}}{\mathcal {C}}{\mathcal {S}}^N$, which completes the proof. $\square$

Remark 5.1

We remark that, instead of the sum of the payoffs of the players in a component being equal to the “sum” of the worths of the (path) maximally connected subcoalitions in this component (i.e. $v^D(C)$), we could use other definitions of efficiency. For example, we could require the sum of the payoffs in a component to be equal to the maximum worth of any connection path in the coalition, or the maximum sum of the connection paths over every partition of the coalition (and thus every player contributing to at most one path). From the proofs of Theorems 5.1 and 5.2, it is easy to see that combining such an alternative efficiency with either fairness or balanced contributions also gives a unique allocation rule. What version of efficiency is most appropriate depends on the application one has in mind. We considered connection efficiency as defined in Definition 5.1 since it seems appropriate for the applications mentioned in the paragraph after Example 3.1.

This also shows the ‘power’ of Myerson’s fairness and balanced contributions axioms in models where efficiency is less obvious than in the undirected communication situations. Although, contrary to undirected communication situations, efficiency in directed communication situations is not obvious, fairness and balanced contributions stated in their original form (but in a different, more general, model) give $c-1$ linear independent equations for every component with c players in every induction step of the proof for every component which, with an efficiency condition, give unique payoffs. In particular, for directed communication situations, this gives the possibility to express the desired efficiency requirement, to get a unique allocation rule that satisfies fairness or balanced contributions.

6 Applications to directed network centrality

In this section, we discuss several applications of the new allocation rule for directed communication situations to centrality in directed networks.

6.1 Connection and betweenness centrality

The defined DC-value can be used to introduce game-theoretical centrality measures for directed networks. A (directed) network centrality measure p is a mapping that assigns to every directed network (N, D) an n-dimensional vector measuring the centrality of nodes in some way. In the literature, there are many concepts of centrality and corresponding centrality measures. Social networks theorist have developed relevant centrality measures as degree (Shaw, 1954; Nieminen 1974), closeness (Beauchamp, 1965; Sabidussi, 1966), betweenness (Bavelas, 1948; Freeman, 1977) and eigenvector centrality (Bonacich, 1972,1987).

Suppose that (N, v, D) is a directed communication situation in which (N, v) is a symmetric game. Following Gómez et al. (2003), for all $i \in N$, since the Shapley value assigns equal payoff $\frac{v(N)}{n}$ to every player in a symmetric game, the difference

$$\begin{aligned} \mu _i^d(N,v,D)-Sh_i (N,v)=\mu _i^d (N,v,D)-\frac{v(N)}{n} \end{aligned}$$

can be viewed as the advantages (or disadvantages)that the (directed) communications present in the network (and the restrictions) provide to player i. Adding $\frac{v(N)}{n}$ to the measure of each player-node, we can use $\mu _i^d(N,v,D)$ as a centrality measure. This gives rise to the following family of centrality measures for directed networks.

Definition 6.1

Given a symmetric game (N, v), the centrality measure $\kappa ^d_v$ is defined as $\kappa ^d_v(N,D) = \mu ^d(N,v,D)$ for every directed network (N, D).

Remark 6.1

Definition 6.1 defines a family of centrality measures for directed networks that is parameterized by a symmetric game. This implies that each centrality measure in this family is determined by the symmetric game that is used. The appropriate game depends on what kind of centrality one wants to measure. The game reflects (economic or social) interests that motivate the interactions among the players/nodes. But, since it is a symmetric game, differences between the nodes is fully determined by the differences in network positions.

Since in this section, we will only use symmetric games, we denote the class of directed communication situations where the game (N, v) is symmetric by ${\mathcal {D}}{\mathcal {C}}{\mathcal {S}}{\mathcal {S}}^N$. If there is no confusion about the game (N, v), in the following, we will shortly write connection efficiency instead of connection efficiency (with respect to (N, v)).

We can decompose, for each $i\in N$, the characteristic function v in $v_i+v_{-i}$ with

$$\begin{aligned} v_i=\sum _{S:i \in S} \Delta _v(S) u_S \end{aligned}$$

and $v_{-i}=v-v_i$. The game $(N,v_i)$ represents the productivity of i via the characteristic function v, whereas in the game $(N,v_{-i})$, i is a null player. Notice that $(N,v_i)$ and $(N,v_{-i})$ are not symmetric games, but for different $i, j \in N$, the games $(N,v_i)$ and $(N,v_j)$ are isomorphic (similar for $(N,v_{-i})$ and $(N,v_{-j})$). Then, given the obvious linearity (in the game) of the defined centrality measure, we have, for each $(N,v,D) \in {\mathcal {D}}{\mathcal {C}}{\mathcal {S}}{\mathcal {S}}^N$, and each $i \in N$,

$$\begin{aligned} \kappa _{v,i}^d(N,D)=\mu _i^d(N,v_i,D)+\mu _{ i }^d(N,v_{-i},D). \end{aligned}$$

The game (N, v) being symmetric, $\mu _i^d(N,v_i,D)$ represents player $i's$ productivity in the characteristic function that is preserved by the digraph. Since the productivity of all players in the unrestricted game is the same, $\mu _i^d (N,v_i,D)$ can be viewed as the part of $i's$ centrality due to his communication possibilities in the graph. Even though $\mu _i^d(N,v_i,D)$ itself is not a centrality measure, it defines part of the centrality of the nodes in a directed communication network.

On the other hand, as i is a null player in $(N,v_{-i})$, it is obvious that $\mu _i^d(N,v_{-i},D)$ exclusively depends on the ability of i to intermediate between others, improving their communication and, thus, it can be viewed as a contribution to its betweenness centrality. This motivates the following definitions.

Definition 6.2

Given a symmetric game (N, v), we define the connection centrality of i in directed network (N, D) as

$$\begin{aligned} \kappa _{v,i}^{d,C}(N,D)=\mu _i^d(N,v_i,D). \end{aligned}$$

Definition 6.3

Given a symmetric game (N, v), we define the betweenness centrality of i in directed network (N, D) as

$$\begin{aligned} \kappa _{v,i}^{d,B}(N,D)=\mu _i^d(N,v_{-i},D). \end{aligned}$$

A nice feature of Myerson (1977)’s characterization of his value by component efficiency and fairness, is that it also gives uniqueness on smaller classes of games, specifically even on classes that contain only one game. As can be seen from the proofs of Theorems 5.1 and 5.2, the same holds for the characterizations given by these results. Specifically, considering the class that consists of a single symmetric game (N, v), we can obtain the following characterization of the centrality measure $\kappa ^d_v$.

Definition 6.4

A centrality measure p for directed networks satisfies fairness if, for every directed network (N, D) and every $e=(i,j) \in D$, $p_i(N,D)-p_i(N,D\setminus \{e\})=p_j(N,D)-p_j(N,D\setminus \{e\}).$

Definition 6.5

A centrality measure p for directed networks satisfies balanced contributions if, for every directed network (N, D) and all $i,j\in N,$ $p_i(N,D)-p_i(N,D_{-j})=p_j(N,D)-p_j(N,D_{-i})$.

Notice that the above two axioms do not depend on the specific symmetric game that is used. These axioms are satisfied by every centrality measure $\kappa ^d_v$ defined in this section. A specific measure is obtained by applying connection efficiency with respect to a specific symmetric game.

Definition 6.6

Let (N, v) be a symmetric game. A centrality measure p for directed networks satisfies connection efficiency (with respect to v) if, for every directed network (N, D) and all $C \in N / \gamma _D$, $\sum _{i\in C}p_i(N,D)=v^D(C)$.

Theorem 6.1

Let (N, v) be a symmetric game.

• (i) $\kappa ^d_v$ is the unique centrality measure for directed networks satisfying connection efficiency (with respect to (N, v)) and fairness.

• (ii) $\kappa ^d_v$ is the unique centrality measure for directed networks satisfying connection efficiency (with respect to (N, v) and balanced contributions.

Since this theorem is an application of Theorems 5.1 and 5.2 on a smaller class of games, the measure $\kappa ^d_v$ satisfying the axioms is a corollary from Theorems 5.1 and 5.2. Uniqueness is not a corollary, but can be proved in the same way as Theorems 5.1 and 5.2, and the proof is therefore omitted.

Since all centrality measures in our family satisfy fairness and balanced contributions, it can be seen from these characterizations that the choice of the symmetric game v determines the specific centrality measure by connection efficiency. For example, when it is about connecting pairs of nodes, then the messages game seems appropriate.

6.2 Out- and in-centrality in unanimity game

By linearity of the allocation rule $\mu ^d$, for any symmetric game (N, v), the centrality measure $\kappa ^d_v$ can be decomposed into separate ‘centralities’ related to the possibility to generate connection in any subset or coalition of nodes $S \subseteq N$. This also makes it possible to specifically take account of nodes’ possibilities to send or receive messages in their communication by distinguishing their out- and in-degree. We can do this both for connection and for betweenness. We define the following new measures for directed networks using unanimity games. They are extended by linearity. Recall that $d_i^O(N,D)$ and $d_i(N,D)$ are the out-degree and the degree of node $i \in N$ in the digraph (N, D), respectively.

Definition 6.7

Consider a symmetric game (N, v). The out-connection centrality (with respect to (N, v)) of i in (N, D) is defined as,

$$\begin{aligned} \kappa _{v,i}^{d,C_O}(N,D)= \sum _{S \subseteq N} \Delta _{v_i}(S) \kappa _{u_S,i}^{d,C_O}(N,D), \end{aligned}$$

where denoting ${\mathcal {M}}{\mathcal {C}}{\mathcal {P}}(S,N,D)=\{Q_1^S,\cdots ,Q_{t(S)}^S\} \ne \emptyset$ for every $S \subseteq N$, $\kappa _{u_S,i}^{d,C_O}(N,D)$ is given by

$$\begin{aligned}{} & {} \kappa _{u_S,i}^{d,C_O}(N,D)= \sum _{j=1}^{t(S)} Sh_i (N,u_{\{Q_j^S\}}) \frac{d_i^O(N,Q_j^S)}{d_i(N,Q_j^S)} \\{} & {} \quad -\sum _{j=1}^{t(S)-1}\sum _{k=1}^{t(S)} Sh_i (N,u_{\{Q_j^S\}\cup \{Q_k^S\}}) \frac{d_i^O(N,Q_j^S\cup Q_k^S)}{d_i(N,Q_j^S\cup Q_k^S)} \\{} & {} \quad + \cdots + (-1)^{t(S)-1} Sh_i \left[ N,u_{\displaystyle \cup _{j=1}^{t(S)}\{Q_j^S\}}\right] \frac{d_i^O (N,\cup _{j=1}^{t(S)}Q_j^S)}{d_i (N,\cup _{j=1}^{t(S)}Q_j^S)}. \end{aligned}$$

Notice that $\kappa _{u_S}^{d,C_O}$ is not a centrality measure in our family, since $u_S$ is not a symmetric game. But this is used to define the centrality measure $\kappa _{v}^{d,C_O}$ which is in our family. A similar remark applies to the following definitions. Recall that $d_i^I(N,D)$ and $d_i(N,D)$ are the in-degree and the degree of node $i \in N$ in the digraph (N, D), respectively.

Definition 6.8

Consider a symmetric game (N, v). The in-connection centrality (with respect to (N, v)) of i in (N, D) is defined as,

$$\begin{aligned} \kappa _{v,i}^{d,C_I}(N,D)= \sum _{S \subseteq N} \Delta _{v_i}(S) \kappa _{u_S,i}^{d,C_I}(N,D), \end{aligned}$$

where denoting ${\mathcal {M}}{\mathcal {C}}{\mathcal {P}}(S,N,D)=\{Q_1^S,\cdots ,Q_{t(S)}^S\} \ne \emptyset$ for every $S \subseteq N$, $\kappa _{u_S,i}^{d,C_I}(N,D)$ is given by

$$\begin{aligned}{} & {} \kappa _{u_S,i}^{d,C_I}(N,D)= \sum _{j=1}^{t(S)} Sh_i (N,u_{\{Q_j^S\}}) \frac{d_i^I(N,Q_j^S)}{d_i(N,Q_j^S)} \\{} & {} \quad -\sum _{j=1}^{t(S)-1}\sum _{k=1}^{t(S)} Sh_i (N,u_{\{Q_j^S\}\cup \{Q_k^S\}}) \frac{d_i^I(N,Q_j^S\cup Q_k^S)}{d_i(N,Q_j^S\cup Q_k^S)} \\{} & {} \quad + \cdots + (-1)^{t(S)-1} Sh_i \left[ N,u_{\displaystyle \cup _{j=1}^{t(S)}\{Q_j^S\}}\right] \frac{d_i^I (N,\cup _{j=1}^{t(S)}Q_j^S)}{d_i (N,\cup _{j=1}^{t(S)}Q_j^S)}. \end{aligned}$$

Definition 6.9

Consider a symmetric game (N, v). The out-betweenness centrality (with respect to (N, v)) of i in (N, D) is defined as,

$$\begin{aligned} \kappa _{v,i}^{d,B_O}(N,D)= \sum _{S \subseteq N} \Delta _{v_{-i}}(S) \kappa _{u_S,i}^{d,B_O}(N,D), \end{aligned}$$

where denoting ${\mathcal {M}}{\mathcal {C}}{\mathcal {P}}(S,N,D)=\{Q_1^S,\cdots ,Q_{t(S)}^S\} \ne \emptyset$ for every $S \subseteq N$, $\kappa _{u_S,i}^{d,B_O}(N,D)$ is given by

$$\begin{aligned}{} & {} \kappa _{u_S,i}^{d,B_O}(N,D)= \sum _{j=1}^{t(S)} Sh_i (N,u_{\{Q_j^S\}}) \frac{d_i^O(N,Q_j^S)}{d_i(N,Q_j^S)} \\{} & {} \quad -\sum _{j=1}^{t(S)-1}\sum _{k=1}^{t(S)} Sh_i (N,u_{\{Q_j^S\}\cup \{Q_k^S\}}) \frac{d_i^O(N,Q_j^S\cup Q_k^S)}{d_i(N,Q_j^S\cup Q_k^S)} \\{} & {} \quad + \cdots + (-1)^{t(S)-1} Sh_i \left[ N,u_{\displaystyle \cup _{j=1}^{t(S)}\{Q_j^S\}}\right] \frac{d_i^O (N,\cup _{j=1}^{t(S)}Q_j^S)}{d_i (N,\cup _{j=1}^{t(S)}Q_j^S)}. \end{aligned}$$

Definition 6.10

Consider a symmetric game (N, v). The in-betweenness centrality (with respect to (N, v)) of i in (N, D) is defined as,

$$\begin{aligned} \kappa _{v,i}^{d,B_I}(N,D)= \sum _{S \subseteq N} \Delta _{v_{-i}}(S) \kappa _{u_S,i}^{d,B_I}(N,D), \end{aligned}$$

where denoting ${\mathcal {M}}{\mathcal {C}}{\mathcal {P}}(S,N,D)=\{Q_1^S,\dots ,Q_{t(S)}^S\} \ne \emptyset$ for every $S \subseteq N$, $\kappa _{u_S,i}^{d,B_I}(N,D)$ is given by

$$\begin{aligned}{} & {} \kappa _{u_S,i}^{d,B_I}(N,D)= \sum _{j=1}^{t(S)} Sh_i (N,u_{\{Q_j^S\}}) \frac{d_i^I(N,Q_j^S)}{d_i(N,Q_j^S)} \\{} & {} \quad -\sum _{j=1}^{t(S)-1}\sum _{k=1}^{t(S)} Sh_i (N,u_{\{Q_j^S\}\cup \{Q_k^S\}}) \frac{d_i^I(N,Q_j^S\cup Q_k^S)}{d_i(N,Q_j^S\cup Q_k^S)} \\{} & {} \quad +\cdots + (-1)^{t(S)-1} Sh_i \left[ N,u_{\displaystyle \cup _{j=1}^{t(S)}\{Q_j^S\}}\right] \frac{d_i^I (N,\cup _{j=1}^{t(S)}Q_j^S)}{d_i (N,\cup _{j=1}^{t(S)}Q_j^S)}. \end{aligned}$$

Notice the differences between these four definitions. On one hand, the two connection centralities ($\kappa _{v,i}^{d,C_O}$ and $\kappa _{v,i}^{d,C_I}$) use the game $(N,v_i)$, while the two betweenness centralities ($\kappa _{v,i}^{d,B_O}$ and $\kappa _{v,i}^{d,B_I}$) use the game $(N,v_{-i})$. On the other hand, the two ‘out’ centralities ($\kappa _{v,i}^{d,C_O}$ and $\kappa _{v,i}^{d,B_O}$) use the out-degree $d^O_i$, while the two ‘in’ centralities ($\kappa _{v,i}^{d,C_I}$ and $\kappa _{v,i}^{d,B_I}$) use the in-degree $d^I_i$. To clarify these ideas of distinguishing the centrality in a digraph into four components based on out- and in-connection, and out- and in-betweenness centralities, let us consider the following example.

Example 6.1

Consider again the directed communication situation (N, v, D) in Example 4.1 in which $N=\{1,2,3,4\}$, (N, v) is the messages game given by (1) and $D=\{(1,2),(1,3),(2,4),(3,4)\}$.

Then, the characteristic function v in terms of the unanimity basis is

$$\begin{aligned} v=u_{\{1,2\}}+u_{\{1,3\}}+u_{\{1,4\}}+u_{\{2,3\}}+u_{\{2,4\}}+u_{\{3,4\}}. \end{aligned}$$

We have:

$$\begin{aligned}&{\mathcal {M}}{\mathcal {C}}{\mathcal {P}}(\{1,2\},N,D)=\{(1,2)\}\\&{\mathcal {M}}{\mathcal {C}}{\mathcal {P}}(\{1,3\},N,D)=\{(1,3)\}\\&{\mathcal {M}}{\mathcal {C}}{\mathcal {P}}(\{1,4\},N,D)=\{(1,2,4),(1,3,4)\}\\&{\mathcal {M}}{\mathcal {C}}{\mathcal {P}}(\{2,3\},N,D)=\emptyset \\&{\mathcal {M}}{\mathcal {C}}{\mathcal {P}}(\{2,4\},N,D)=\{(2,4)\}\\&{\mathcal {M}}{\mathcal {C}}{\mathcal {P}}(\{3,4\},N,D)=\{(3,4)\} \end{aligned}$$

Then, for player 1, we have

$$\begin{aligned}{} & {} \kappa _{v,1}^{d,C_O} (N,D) = \kappa _{u_{\{1,2\}},1}^{d,C_O} (N,D)+\kappa _{u_{\{1,3\}},1}^{d,C_O} (N,D) \\{} & {} \quad +\kappa _{u_{\{1,4\}},1}^{d,C_O} (N,D)= Sh_1 (N,u_{\{1,2\}}) \frac{d_1^O (N,(1,2))}{d_1(N,(1,2))} +Sh_1 (N,u_{\{1,3\}}) \frac{d_1^O (N,(1,3))}{d_1(N,(1,3))} \\{} & {} \quad + Sh_1 (N,u_{\{1,2,4\}}) \frac{d_1^O (N,(1,2,4))}{d_1(N,(1,2,4))}+ Sh_1 (N,u_{\{1,3,4\}}) \frac{d_1^O (N,(1,3,4))}{d_1(N,(1,3,4))} \\{} & {} \quad -Sh_1(N,u_{\{1,2,3,4\}}) \frac{d_1^O (N,(1,2,3,4))}{d_1(N,(1,2,3,4))} =\frac{1}{2}\cdot \frac{1}{1}+\frac{1}{2}\cdot \frac{1}{1}+\frac{1}{3}\cdot \frac{1}{1}+\frac{1}{3}\cdot \frac{1}{1}-\frac{1}{4}\cdot \frac{1}{1}= \frac{17}{12}, \end{aligned}$$

and thus, as can be expected, all the centrality of player 1 is out-connection centrality. He does not intermediate between the communication of the others and he is tail in all the arcs he is involved in.

The out-connection centrality of player 2 is

$$\begin{aligned}{} & {} \kappa _{v,2}^{d,C_O}(N,D)= \kappa _{u_{\{1,2\}},2}^{d,C_O} (N,D)+\kappa _{u_{\{2,3\}},2}^{d,C_O} (N,D) \\{} & {} \quad +\kappa _{u_{\{2,4\}},2}^{d,C_O} (N,D) =Sh_2 (N,u_{\{1,2\}}) \frac{d_2^O (N,(1,2))}{d_2(N,(1,2))}+ Sh_2 (N,u_{\{2,4\}}) \frac{d_2^O (N,(2,4))}{d_2(N,(2,4))} \\{} & {} \quad =\frac{1}{2}\cdot 0 +\frac{1}{2}\cdot \frac{1}{1}=\frac{1}{2}, \end{aligned}$$

and the in-connection centrality of player 2 is

$$\begin{aligned}{} & {} \kappa _{v,2}^{d,C_I}(N,D)= \kappa _{u_{\{1,2\}},2}^{d,C_I} (N,D)+\kappa _{u_{\{2,3\}},2}^{d,C_I} (N,D) \\{} & {} \quad +\kappa _{u_{\{2,4\}}2}^{d,C_I} (N,D) = Sh_2 (N,u_{\{1,2\}}) \frac{d_2^I (N,(1,2))}{d_2(N,(1,2))} +Sh_2 (N,u_{\{2,4\}}) \frac{d_2^I (N,(2,4))}{d_2(N,(2,4))} \\{} & {} \quad = \frac{1}{2}\cdot \frac{1}{1} +\frac{1}{2}\cdot 0=\frac{1}{2}. \end{aligned}$$

The out-betweenness of player 2 is

$$\begin{aligned}{} & {} \kappa _{v,2}^{d,B_O}(N,D)= \kappa _{u_{\{1,3\}}, 2}^{d,B_O} (N,D)+\kappa _{u_{\{1,4\}}, 2}^{d,B_O} (N,D) \\{} & {} \quad +\kappa _{u_{\{3,4\}},2}^{d,B_O} (N,D)= Sh_2 (N,u_{\{1,3\}}) \frac{d_2^O (N,(1,3))}{d_2(N,(1,3))} + Sh_2 (N,u_{\{1,2,4\}}) \frac{d_2^O (N,(1,2,4))}{d_2(N,(1,2,4))} \\{} & {} \quad +Sh_2 (N,u_{\{1,3,4\}}) \frac{d_2^O (N,(1,3,4))}{d_2(N,(1,3,4))} -Sh_2 (N,u_{\{1,2,3,4\}}) \frac{d_2^O (N,(1,2,4)\cup (1,3,4))}{d_2(N,(1,2,4)\cup (1,3,4))} \\{} & {} \quad +Sh_2 (N,u_{\{3,4\}}) \frac{d_2^O (N,(3,4))}{d_2(N,(3,4))}=0\cdot 0+\frac{1}{3}\cdot \frac{1}{2}+0\cdot 0 -\frac{1}{4}\cdot \frac{1}{2}+0\cdot 0=\frac{1}{24}, \end{aligned}$$

and the in-betweenness centrality of player 2 is

$$\begin{aligned}{} & {} \kappa _{v,2}^{d,B_I}(N,D)= \kappa _{u_{\{1,3\}},2}^{d,B_I} (N,D)+\kappa _{u_{\{1,4\}},2}^{d,B_I} (N,D) \\{} & {} \quad +\kappa _{u_{\{3,4\}},2}^{d,B_I} (N,D) =Sh_2 (N,u_{\{1,3\}}) \frac{d_2^I (N,(1,3))}{d_2(N,(1,3))} + Sh_2 (N,u_{\{1,2,4\}}) \frac{d_2^I (N,(1,2,4))}{d_2(N,(1,2,4))} \\{} & {} \quad +Sh_2 (N,u_{\{1,3,4\}}) \frac{d_2^I (N,(1,3,4))}{d_2(N,(1,3,4))} -Sh_2 (N,u_{\{1,2,3,4\}}) \frac{d_2^I (N,(1,2,4)\cup (1,3,4))}{d_2(N,(1,2,4)\cup (1,3,4))} \\{} & {} \quad +Sh_2 (N,u_{\{3,4\}}) \frac{d_2^I(N,(3,4))}{d_2(N,(3,4))} =0\cdot 0+\frac{1}{3}\cdot \frac{1}{2}+0\cdot 0-\frac{1}{4}\cdot \frac{1}{2}+0\cdot 0=\frac{1}{24}, \end{aligned}$$

and thus, the total centrality of player 2, which is $\frac{13}{12}$, can be obtained by adding $\frac{1}{2},\frac{1}{2},\frac{1}{24}$ and $\frac{1}{24}$ that are, respectively, his out-connection centrality, his in-connection centrality, his out-betweenness centrality and his in-betweenness centrality.

Remark 6.2

Comparing the obtained results for centrality of nodes in Example 6.1 with the ones obtained using the measure, $\kappa$, defined (for undirected graphs) in Gómez et al. (2003) we have $\kappa (N,v,\gamma _D)=(\frac{3}{2},\frac{3}{2},\frac{3}{2},\frac{3}{2})$ in which the part corresponding to communication centrality is $(\frac{17}{12},\frac{17}{12},\frac{17}{12},\frac{17}{12})$, whereas, the betweenness centrality of nodes is $(\frac{1}{12},\frac{1}{12},\frac{1}{12},\frac{1}{12})$. In such a situation the symmetry in the game and in the graph gives the same figures for all players. Then, they have the same ability to communicate and to intermediate in the communication of messages of the others. Let us recall that for the directed communication situation in the Example 6.1 given, the directed edges players 1 and 4 cannot intermediate among the others. For the nodes intermediating the proportion of his centrality due to intermediation is $\frac{1}{13}$ in (N, v, D) and $\frac{1}{17}$ in $(N,v,\gamma _D)$.

6.3 An application to efficiency and vulnerability in directed networks

Finally, in this section, we illustrate how the obtained DC-value $\mu ^d$ can be used to define game-theoretical measures of efficiency and vulnerability for directed networks, in which players have (economic or social) interests given by a TU-game. As mentioned in the previous subsection, given a directed communication situation (N, v, D), and $i\in N$, $v_i$ gives the productivity of player i via the characteristic function; whereas in $v_{-i}$, player i is null. Then, in a connected directed network, $\displaystyle \sum _{i\in N} \mu _i^d(N,v_i,D)$ can be seen as the part of the total worth, v(N), of the grand coalition that players can preserve given the existing communications in the network and thus,

$$\begin{aligned} {\mathcal {E}} (N,v,D)=\frac{\displaystyle \sum _{i\in N}\mu _i^d(N,v_i,D)}{v(N)} =\frac{\displaystyle \sum _{i\in N} \kappa _{v,i}^{d,C}(N,D)}{v(N)} \end{aligned}$$

can be used as a measure of the efficiency of the directed network to preserve the interests of the players.

Similarly,

$$\begin{aligned} {\mathcal {V}}(N,v,D)=\frac{\displaystyle \sum _{i\in N}\mu _i^d(N,v_{-i},D)}{v(N)} = \frac{\displaystyle \sum _{i\in N}\kappa _{v,i}^{d,B}(N,D)}{v(N)} = \frac{v^D(N)}{v(N)}-{\mathcal {E}}(N,v,D) \end{aligned}$$

is a vulnerability network measure that represents the part of the total worth v(N) corresponding to intermediation costs. These costs must be payed by coalitions to unproductive players that permit members in the coalition to be connected. The vulnerability of the network increases with these intermediation costs because the members of the coalitions are more dependent on other members.

We illustrate these measures with the following example.

Example 6.2

Let (N, v, T) be a directed communication situation in which v is the messages game and T is an oriented tree (Harary and Sumner 1980). Then, for each $i\in N$, $v_i=\displaystyle \sum _{j:j\ne i}u_{\{i,j\}}$. As T is an oriented tree for $j\ne i$, ${\mathcal {M}}{\mathcal {C}}{\mathcal {P}}(\{i,j\},N,D)=\{Q^{\{i,j\}}\}$ or is equal to the emptyset. Let us denote the geodesic distance between i and j by d(i, j), i.e., the number of arcs in $Q^{\{i,j\}}$ if such arcs exist, and $d(i,j)= \infty$, otherwise. Then,

$$\begin{aligned} \mu _i^{{d}}(N,v_i,T)=\displaystyle \sum _{j:j\ne i} Sh_i (N,u_{\{Q^{\{i,j\}}\}}) = \displaystyle \sum _{j:j\ne i} \frac{1}{d(i,j)+1}. \end{aligned}$$

As a consequence,

$$\begin{aligned} {\mathcal {E}}(N,v,T)=\frac{2}{n(n-1)}\displaystyle \sum _{i<j}\frac{1}{d(i,j)+1} =\frac{1}{n(n-1)}\displaystyle \sum _{i\ne j}\frac{1}{d(i,j)+1}, \end{aligned}$$

which is very similar to the expression for the average efficiency of Latora and Marchiori (2001). Indeed, the only difference is that in our proposal, the measure is defined in terms of the distance geodesic plus 1 whereas the average efficiency is measure in terms of geodesic.

Example 6.3

For the communication situation (N, v, D) of Example 4.1 (and Example 6.1) we have⁴

$$\begin{aligned}{} & {} {\mathcal {E}}(N,v,D)=\frac{\displaystyle \sum _{i \in N} \mu _i^{d}(N,v_i,D)}{v(N)} = \frac{\displaystyle \sum _{i \in N} \kappa _{v,i}^{d,C}(N,D)}{v(N)} =\frac{\frac{17}{12}+1+1+\frac{17}{12}}{6}=\frac{29}{36} \\{} & {} \quad {\mathcal {V}}(N,v,D)= \frac{\displaystyle \sum _{i \in N} \mu _i^{d}(N,v_{-i},D)}{v(N)} = \frac{\displaystyle \sum _{i \in N} \kappa _{v,i}^{d,B}(N,D)}{v(N)} =\frac{0+\frac{1}{12}+\frac{1}{12}+0}{6}=\frac{1}{36}. \end{aligned}$$

Five of the six total possible messages can be sent using this (directed) network. Only the communication between 1 and 4 is vulnerable because of players 2 and 3 must be rewarded with $\frac{1}{12}$ each. Then, the network efficiency is $\frac{5}{6}-\frac{2\cdot \frac{1}{12}}{6}=\frac{29}{36}=0.806$, measuring the fraction of the total worth (6) that players can retain given the restrictions in the connection, and after paying the intermediation fees. The proportion corresponding to these intermediation fees can be seen as a vulnerability measure.

7 The defined value versus other allocation rules

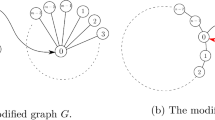
In this section, we illustrate our defined value $\mu ^d$ and compare it with some other values from the literature. To obtain some numerical comparisons, we will use the examples in Khmelnitskaya et al. (2016) that are also used in Li and Shan (2020).

Consider the directed communication situations $(N,v,D_1)$, $(N,v,D_2)$ and $(N,v,D_3)$ with $N=\{1,2,3,4,5\}$, $v(S)=s^2$ for all $S\subseteq N$ and

$$\begin{aligned}{} & {} D_1=\{(1,2),(3,5),(4,5)\} \\{} & {} \quad D_2=\{(1,2),(2,3),(3,4),(4,5),(5,1)\} \\{} & {} \quad D_3=\{(1,2),(2,3),(3,1),(3,4),(4,1),(4,5)\}, \end{aligned}$$

see Fig. 4.

Fig. 4

The examples of Khmelnitskaya et al. (2016)

As $v=\displaystyle \sum _{i=1}^5 u_{\{i\}} + 2\displaystyle \sum _{S \subseteq N, s=2}u_S$, each player can generate a dividend equal to 1 on his own, and each couple generates a dividend of 2 if both players can communicate.

7.1 Illustration of $\mu ^d$

The digraph restricted game defined in this paper, for these directed communication situations, is given by⁵

$$\begin{aligned}{} & {} v^{D_1}=\displaystyle \sum _{i=1}^5 u_{\{i\}} +2u_{\{1,2\}}+2u_{\{3,5\}}+2u_{\{4,5\}}, \\{} & {} \quad v^{D_2}=\displaystyle \sum _{i=1}^5 u_{\{i\}} +2u_{\{1,2\}}+2(u_{\{1,2,3\}}+u_{\{1,3,4,5\}}-u_{\{1,2,3,4,5\}})+2(u_{\{1,2,3,4\}}+u_{\{1,4,5\}} \\{} & {} \quad -u_{\{1,2,3,4,5\}})+2u_{\{1,5\}}+2u_{\{2,3\}}+2(u_{\{2,3,4\}}+u_{\{1,2,4,5\}} -u_{\{1,2,3,4,5\}})+2(u_{\{1,2,5\}} \\{} & {} \quad +u_{\{2,3,4,5\}}-u_{\{1,2,3,4,5\}})+2u_{\{3,4\}}+2(u_{\{3,4,5\}}+u_{\{1,2,3,5\}}-u_{\{1,2,3,4,5\}})+2u_{\{4,5\}}, \end{aligned}$$

and, finally

$$\begin{aligned}{} & {} v^{D_3}=\displaystyle \sum _{i=1}^5 u_{\{i\}} +2u_{\{1,2\}}+2u_{\{1,3\}}+2u_{\{1,4\}}+2u_{\{1,2,3,4,5\}}+2u_{\{2,3\}} \\{} & {} \quad +2(u_{\{2,3,4\}}+u_{\{1,2,4\}}-u_{\{1,2,3,4\}})+2u_{\{2,3,4,5\}} +2u_{\{3,4\}}+2u_{\{3,4,5\}}+2u_{\{4,5\}}. \end{aligned}$$

In game $v^{D_3}$, for example, the coalition $S=\{3,4,5\}$ obtains $v^{D_3}(S)=9$ given that all the subcoalitions $\{3,4\},\{3,5\}$ and $\{4,5\}$ can communicate (players 3 and 5 using 4 as intermediary). However, coalition $S=\{1,4,5\}$ only obtains $v^{D_3}(S)=7$ as the connection between players 1 and 5 is unfeasible, since there is no path within S connecting these three players. Regarding our value, we have,

$$\begin{aligned}{} & {} \mu ^d(N,v,D_1)=Sh(N,v^{D_1})=(2,2,2,2,3) \\{} & {} \quad \mu ^d(N,v,D_2)=Sh(N,v^{D_2})=(5,5,5,5,5) \end{aligned}$$

and

$$\begin{aligned} \mu ^d(N,v,D_3)=Sh(N,v^{D_3})=\left(\frac{137}{30},\frac{142}{30},\frac{172}{30},\frac{192}{30},\frac{107}{30}\right). \end{aligned}$$

Connection efficiency of $\mu ^d$ in these examples says that in $(N,v,D_1)$ player 1 and 2 can communicate and, then, they preserve the 4 units of $v(\{1,2\})$. On the other hand, in the coalition $\{3,4,5\}$ (the other weak component) only the couples $\{3,5\}$ and $\{4,5\}$ can communicate, as there is no directed path connecting 3 and 4. Therefore, this coalition loses 2 units, preserving only 7 units of the initial 9.

In $(N,v,D_2)$ and $(N,v,D_3)$ all couples can communicate and thus, connection efficiency requires the usual efficiency in these two cases.

7.2 Comparison with other values

Next, we compare our value $\mu ^d$ with some other values from the literature for this example.

7.2.1 Myerson value for undirected communication situation

Although the Myerson value is not defined for games with digraphs but for games with graphs, we can compare the obtained figures with the corresponding Myerson values for the (undirected) communication situations $(N,v,\gamma _{D_1})$, $(N,v,\gamma _{D_2})$ and $(N,v,\gamma _{D_3})$. We have

$$\begin{aligned}{} & {} \mu (N,v,\gamma _{D_1})=\left( 2,2,\frac{8}{3},\frac{8}{3},\frac{11}{3}\right) \\{} & {} \quad \mu (N,v,\gamma _{D_2})=(5,5,5,5,5) \end{aligned}$$

and

$$\begin{aligned} \mu (N,v,\gamma _{D_3})=\left( \frac{296}{60},\frac{266}{60},\frac{296}{60},\frac{406}{60},\frac{236}{60}\right) . \end{aligned}$$

As the Myerson value is component efficient, the only case in which players cannot obtain v(N) is $(N,v,\gamma _{D_1})$: $\displaystyle \sum _{i \in N}\mu _i(N,v,\gamma _{D_1})=v(\{1,2\})+v(\{3,4,5\})<v(N)$, as players in the coalition $\{1,2\}$ cannot communicate with players in $\{3,4,5\}$.

As mentioned, in $\mu (N,v,\gamma _{D_2})$ and in $(N,v,\gamma _{D_3})$ all couples can communicate. Nevertheless, $\mu ^d \ne \mu$. In our model this occurs as the communication induced by a digraph needs a higher level of intermediation, which generates a different allocation between players. As an example, in $(N,\gamma _{D_3})$ the connection between players 1 and 5 only needs the intermediation of player 4, whereas in $(N,D_3)$ it also needs the collaboration of 2 and 3. The corresponding dividend (equal to 2) is divided among 1, 4 and 5 in the case of the Myerson value but among players 1, 2, 3, 4 and 5 in our proposal. The difference between both allocation rules is due to the intermediation costs.

7.2.2 Permission values

In Gilles et al. (1992) and Gilles and Owen (1994), the digraph in the model (N, v, D) is interpreted as a permission structure that restricts the cooperation possibilities because some players need permission from other players before they are allowed to cooperate in a coalition. In the conjunctive approach, every player i needs permission from all its predecessors being the players j such that $(j,i) \in D$.⁶ This yields the following conjunctive restricted games $v^D_c$ for $(N,v,D_1),\ (N,v,D_2)$ and $(N,v,D_3)$:

$$\begin{aligned}{} & {} v_c^{D_1}=u_{\{1\}}+u_{\{1,2\}}+u_{\{3\}}+u_{\{4\}}+u_{\{3,4,5\}} \\{} & {} \quad +2u_{\{1,2\}}+2u_{\{1,3\}}+2u_{\{1,4\}}+2u_{\{1,3,4,5\}}+2u_{\{1,2,3\}} \\{} & {} \quad +2u_{\{1,2,4\}}+2u_{\{1,2,3,4,5\}}+2u_{\{3,4\}}+4u_{\{3,4,5\}}, \\{} & {} \quad v_c^{D_2}=\left( 5+2 \left( {\begin{array}{c}5\\ 2\end{array}}\right) \right) u_{\{1,2,3,4,5\}}=25u_{\{1,2,3,4,5\}}, \end{aligned}$$

and

$$\begin{aligned}{} & {} v_c^{D_3}=4u_{\{1,2,3,4\}}+u_{\{1,2,3,4,5\}}+2 \left( {\begin{array}{c}4\\ 2\end{array}}\right) u_{\{1,2,3,4\}}+4 \cdot 2 u_{\{1,2,3,4,5\}} \\{} & {} \quad =16 u_{\{1,2,3,4\}}+9u_{\{1,2,3,4,5\}}. \end{aligned}$$

This results in the following conjunctive permission value payoff vectors:

$$\begin{aligned}{} & {} \varphi ^c(N,v,D^1)=\frac{1}{30}(202,97,187,187,77),\ \varphi ^c(N,v,D^2)=(5,5,5,5,5), \\{} & {} \quad \text{ and } \varphi ^c(N,v,D^3)=\frac{1}{5}(29,29,29,29,9). \end{aligned}$$

Notice that, digraph $(N,D_2)$ having a Hamiltonian cycle, and v being a symmetric game, results in an equal payoff $\frac{v(N)}{n}$ for all players according to the conjunctive permission value, as is also the case in our value $\mu ^d$. The conjunctive permission value yields this equal allocation for any game, while our value might assign different payoffs to the players in case the game is not symmetric.

On the other hand, in the disjunctive approach for acyclic permission structures, every player needs permission from at least one of its predecessors (if it has any). Since $D^1$ is an acyclic digraph, we compute the disjunctive restricted game and disjunctive permission value for this digraph, yielding restricted game

$$\begin{aligned}{} & {} v_d^{D_1}=u_{\{1\}}+u_{\{1,2\}}+u_{\{3\}}+u_{\{4\}}+(u_{\{3,5\}}+u_{\{4,5\}}-u_{\{3,4,5\}}) \\{} & {} \quad +2u_{\{1,2\}}+2u_{\{1,3\}}+2u_{\{1,4\}}+2(u_{\{1,3,5\}}+u_{\{1,4,5\}}-u_{\{1,3,4,5\}}) \\{} & {} \quad +2u_{\{1,2,3\}}+2u_{\{1,2,4\}}+2(u_{\{1,2,3,5\}}+u_{\{1,2,4,5\}}- u_{\{1,2,3,4,5\}}) \\{} & {} \quad +2u_{\{3,4\}}+2u_{\{3,5\}}+2u_{\{4,5\}}, \end{aligned}$$

giving the disjunctive permission value payoff vector:

$$\begin{aligned} \varphi ^d(N,v,D^1)=\frac{1}{30}(218,103,153,153,123). \end{aligned}$$

In the permission approach to games with a digraph, cooperation is restricted by players needing permission from other players before being allowed to cooperate. Since the grand coalition contains all players that can generate worth as well as give permission, the two permission values are efficient, meaning that the total unrestricted worth v(N) of the grand coalition will be allocated. How this is allocated over the players depends on the cooperation restrictions. The disjunctive permission value satisfies a weaker fairness axiom, where we only delete arcs such that the head/successor has at least one more ingoing arc, i.e., the payoff of the two players i, j on an oriented arc (i, j) change by the same amount if the deleted arc (i, j) satisfies $\#\{h \in N \mid (h,i) \in D\} \ge 2$.

The conjunctive permission value satisfies the alternative fairness axiom where the deletion of an arc has the same effect on the payoff of the head/successor of the arc and any other predecessor of this head. Notice that this also fits with the difference in interpretation of conjunctive and disjunctive permission. Every arc (i, j) in the conjunctive approach restricts the cooperation possibilities of the head j. But, in case a player j is the head of at least one arc, adding more arcs with j as head increases the disjunctive cooperation possibilities of j, as is also the case in the directed communication situations considered in this paper. This is also reflected in the weak fairness that these values have in common.

7.2.3 The value of Li and Shan (2020)

Comparing our value with the Myerson value for digraphs introduced in Li and Shan (2020), the more important difference is the type of efficiency used (which depends on the type of connection that is considered) as both rules satisfy fairness and balanced contributions. Their strong component efficiency is a property that assumes a high connection requirement for generating worth which, usually, implies a low level of cooperation. As a consequence, a lot of value of the original coalitions can be lost. Specifically this occurs in directed communication situations $(N,v,D_1)$ and in $(N,v,D_3)$ where Li and Shan (2020)’s Myerson value for digraphs assigns, respectively, (1, 1, 1, 1, 1) and (9/2, 9/2, 9/2, 5/2, 1) (see Li and Shan (2020)). From the total initial worth of 25, the players can only retain a value of 5 in the first case and a value of 17 in the second case. For $(N,v,D_2)$, our value coincides with Li and Shan (2020)’s Myerson value for digraphs. This follows since the presence of a Hamiltonian cycle and the game being symmetric results in payoffs v(N)/n for each player in both values, as is also the case in the conjunctive permission value above.⁷

If the game is not symmetrical, the allocation according to our rule and Li and Shan (2020)’s Myerson value can differ, as is shown in the following example.

Example 7.1

Consider (N, v, D) with $N=\{1,2,3\}$ $v=u_{\{1,2\}}+u_{1,3}-u_{\{1,2,3\}}$ and $D=\{(1,2),(2,3),(3,1)\}$ as in Fig. 5.

Fig. 5

Diograph (N,D) Example 7.1

Then Li and Shan (2020)’s Myerson value for digraphs gives $(\frac{1}{3},\frac{1}{3},\frac{1}{3})$ whereas $\mu ^d(N,v,D)=(\frac{2}{3},\frac{1}{6},\frac{1}{6})$.