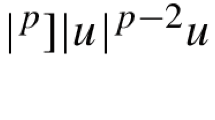Abstract
In the present paper, we study the existence of normalized ground states for the following nonlinear fractional Choquard equations with Hardy–Littlewood–Sobolev upper critical exponent:
having prescribed mass
where \(N>2s\), \(s\in (0,1)\), \(\alpha \in (0,N)\), \( \underline{p}:= \frac{N+\alpha }{N}<p<\overline{p}:=\frac{N+2s+\alpha }{N}<2^*_{\alpha ,s}\), \(2^*_{\alpha ,s}:=\frac{N+\alpha }{N-2s}\) is the upper Hardy–Littlewood–Sobolev critical exponent, \(\mu >0\) and \(\lambda \in \mathbb R\). Furthermore, the qualitative behavior of the ground states as \(\mu \rightarrow 0^+\) is also studied.
Similar content being viewed by others
References
Applebaum, D.: Lévy processes: from probability to finance and quantum groups. Notices Am. Math. Soc. 51(11), 1336–1347 (2004)
Appolloni, L., Secchi, S.: Normalized solutions for the fractional NLS with mass supercritical nonlinearity. J. Differ. Equ. 286, 248–283 (2021)
Bartsch, T., Li, H., Zou, W.: Existence and asymptotic behavior of normalized ground states for Sobolev critical Schrödinger systems. Calc. Var. Partial Differ. Equ. 62, 9 (2023)
Bartsch, T., Liu, Y., Liu, Z.: Normalized solutions for a class of nonlinear Choquard equations. SN Partial Differ. Equ. Appl. 34, 24 (2020)
Bartsch, T., Molle, R., Rizzi, M., Verzini, G.: Normalized solutions of mass supercritical Schrödinger equations with potential. Commun. Partial Differ. Equ. 46, 1729–1756 (2021)
Cingolani, S., Gallo, M., Tanaka, K.: Normalized solutions for fractional nonlinear scalar field equations via Lagrangian formulation. Nonlinearity 34, 4017–4056 (2021)
Cingolani, S., Gallo, M., Tanaka, K.: Symmetric ground states for doubly nonlocal equations with mass constraint. Symmetry 13, 1–17 (2021)
d’Avenia, P., Siciliano, G., Squassina, M.: On fractional Choquard equations. Math. Models Methods Appl. Sci. 25, 1447–1476 (2015)
Feng, B., Zhang, H.: Stability of standing waves for the fractional Schrödinger–Hartree equation. J. Math. Anal. Appl. 460, 352–364 (2018)
Feng, B., Chen, R., Liu, J.: Blow-up criteria and instability of normalized standing waves for the fractional Schrödinger–Choquard equation. Adv. Nonlinear Anal. 10, 311–330 (2021)
Ji, C., Rǎdulescu, V.D.: Multi-bump solutions for the nonlinear magnetic Choquard equation with deepening potential well. J. Differ. Equ. 306, 251–279 (2022)
Gao, F., Yang, M.: On the Brezis–Nirenberg type critical problem for nonlinear Choquard equation. Sci. China Math. 61, 1219–1242 (2018)
Gou, T., Jeanjean, L.: Multiple positive normalized solutions for nonlinear Schrödinger systems. Nonlinearity 31, 2319–2345 (2018)
Guo, Z., Zhao, L.: Ground states for fractional Choquard equations with magnetic fields and critical exponents. Georgian Math. J. 29(5), 699–713 (2022)
Hirata, J., Tanaka, K.: Nonlinear scalar field equations with \(L^2\) constraint: mountain pass and symmetric mountain pass approaches. Adv. Nonlinear Stud. 19, 263–290 (2019)
He, X., Rǎdulescu, V.D.: Small linear perturbations of fractional Choquard equations with critical exponent. J. Differ. Equ. 282, 481–540 (2021)
He, X., Rǎdulescu, V.D., Zou, W.: Normalized ground states for the critical fractional Choquard equation with a local perturbation. J. Geom. Anal. 32, 252 (2022)
Jeanjean, L.: Existence of solutions with prescribed norm for semilinear elliptic equation. Nonlinear Anal. TMA 28, 1633–1659 (1997)
Li, G., Ye, H.: The existence of positive solutions with prescribed \(L^2\)-norm for nonlinear Choquard equations. J. Math. Phys. 55, 121501 (2014)
Li, G., Luo, X.: Existence and multiplicity of normalized solutions for a class of fractional Choquard equations. Sci. China Math. 63, 539–558 (2021)
Liu, M., Zou, W.: Normalized solutions for a system of fractional Schrödinger equations with linear coupling. Minimax Theory Appl. 7, 303–320 (2022)
Lieb, E.: Existence and uniqueness of the minimizing solution of Choquard’s nonlinear equation. Stud. Appl. Math. 57, 93–105 (1976/1977)
Lieb, E., Loss, M.: Analysis, Graduate Studies in Mathematics, vol. 14. American Mathematical Society, Providence (2001)
Lions, P.L.: The concentration-compactness principle in the calculus of variations: the locally compact case, Part II. Ann. Inst. H. Poincaré C Anal. Non Linéaire 2, 223–283 (1984)
Li, G., Ye, H.: The existence of positive solutions with prescribed \(L^2\)-norm for nonlinear Choquard equations. J. Math. Phys. 55, 121501 (2014)
Luo, H., Zhang, Z.: Normalized solutions to the fractional Schrödinger equations with combined nonlinearities. Calc. Var. Partial Differ. Equ. 59, 143 (2020)
Li, Q., Zou, W.: The existence and multiplicity of the normalized solutions for fractional Schrödinger equations involving Sobolev critical exponent in the \(L^2\)-subcritical and \(L^2\)-supercritical cases. Adv. Nonlinear Anal. 11, 1531–1551 (2022)
Li, X., Ma, S.: Choquard equations with critical nonlinearities. Commun. Contemp. Math. 22(04), 1950023 (2020)
Ma, L., Zhao, L.: Classification of positive solitary solutions of the nonlinear Choquard equation. Arch. Ration. Mech. Anal. 195, 455–467 (2010)
Mederski, J., Schino, J.: Least energy solutions to a cooperative system of Schrödinger equations with prescribed \(L^2\)-bounds: at least \(L^2\)-critical growth. Calc. Var. Partial Differ. Equ. 61, 10–31 (2022)
Moroz, V., Schaftingen, J.V.: Groundstates of nonlinear Choquard equations: existence, qualitative properties and decay asymptotics. J. Funct. Anal. 265, 153–184 (2013)
Moroz, V., Schaftingen, J.V.: Existence of ground states for a class of nonlinear Choquard equations. Trans. Am. Math. Soc. 367, 6557–6579 (2015)
Moroz, I.M., Penrose, R., Tod, P.: Spherically-symmetric solutions of the Schrödinger–Newton equations. Class. Quantum Gravity 15, 2733–2742 (1998)
Meng, Y., He, X.: Multiplicity of concentrating solutions for Choquard equation with critical growth. J. Geom. Anal. 33, 78–29 (2023)
Di Nezza, E., Palatucci, G., Valdinoci, E.: Hitchiker’s guide to the fractional Sobolev spaces. Bull. Sci. Math. 136, 521–573 (2012)
Pekar, S.: Untersuchung über die Elektronentheorie der Kristalle. Akademie Verlag, Berlin (1954)
Penrose, R.: Ongravity’s role in quantum state reduction. Gen. Relativ. Gravitat. 28, 581–600 (1996)
Soave, N.: Normalized ground states for the NLS equation with combined nonlinearities. J. Differ. Equ. 269, 6941–6987 (2020)
Soave, N.: Normalized ground states for the NLS equation with combined nonlinearities: the Sobolev critical case. J. Funct. Anal. 279, 108610–43 (2020)
Shang, X., Ma, P.: Normalized solutions to the nonlinear Choquard equations with Hardy–Littlewood–Sobolev upper critical exponent. J. Math. Anal. Appl. 521, 126916–29 (2023)
Wei, J., Wu, Y.: Normalized solutions for Schrödinger equations with critical Sobolev exponent and mixed nonlinearities. J. Funct. Anal. 283, 109574 (2022)
Ye, H.: Mass minimizers and concentration for nonlinear Choquard equations in \(^N\). Topol. Methods Nonlinear Anal. 48(2), 393–417 (2016)
Ye, W., Shen, Z., Yang, M.: Normalized solutions for a critical Hartree equation with perturbation. J. Geom. Anal. 32, 242 (2022)
Yuan, S., Chen, S., Tang, X.: Normalized solutions for Choquard equations with general nonlinearities. Electron. Res. Arch. 28, 291–309 (2020)
Yang, T.: Normalized solutions for the fractional Schrödinger equation with a focusing nonlocal \(L^2\)-critical or \(L^2\)-supercritical perturbation. J. Math. Phys. 61, 051505 (2020)
Yao, S., Chen, H., Rǎdulescu, V.D., Sun, J.: Normalized solutions for lower critical Choquard equations with critical Sobolev perturbation. SIAM J. Math. Anal. 54, 3696–3723 (2022)
Zuo, J., Rădulescu, V.D.: Normalized solutions to fractional mass supercritical NLS systems with Sobolev critical nonlinearities. Anal. Math. Phys. 12, 140 (2022)
Zuo, J., Liu, C., Vetro, C.: Normalized solutions to the fractional Schrödinger equation with potential. Mediterr. J. Math. 20(4), 216 (2023)
Zhen, M., Zhang, B.: Normalized ground states for the critical fractional NLS equation with a perturbation. Rev. Mat. Complut. 35, 89–132 (2022)
Acknowledgements
The first author was supported by the BIT Research and Innovation Promoting Project (Grant No. 2023YCXY046), NNSF (Grant Nos. 11971061 and 12271028), BNSF (Grant No. 1222017) and the Fundamental Research Funds for the Central Universities. The second author was supported by NNSF (Grant Nos. 12171497, 11771468 and 11971027). The authors thank the referees for many helpful comments which clarify the paper.
Author information
Authors and Affiliations
Contributions
Yuxi Meng and Xiaoming He wrote the main manuscript text. All authors reviewed the manuscript.
Corresponding author
Ethics declarations
Conflict of interest
The authors declared that they have no conflict of interest.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Meng, Y., He, X. Normalized Solutions for the Fractional Choquard Equations with Hardy–Littlewood–Sobolev Upper Critical Exponent. Qual. Theory Dyn. Syst. 23, 19 (2024). https://doi.org/10.1007/s12346-023-00875-z
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s12346-023-00875-z