Strange Fractal Attractors and Optimal Chaos of Memristor–Memcapacitor via Non-local Differentials

Abstract

The multi-dimensional electronic devices are so called memory circuit elements (memristor or memcapacitor); such memory circuit elements usually rely on previous applied voltage, current, flux or charge based on memory capability with their resistance, capacitance or inductance. In view of above fact, this manuscript investigates the non-integer modeling of memristor–memcapacitor in discrete-time domain through non-singular kernels of fractal fractional differentials and integrals operators. The governing equations of memristor–memcapacitor have been developed for the sake of the dynamical characteristics of simple chaotic circuit. The fractal fractional differentials and integrals operators have been invoked for non-integer modeling of memristor–memcapacitor that can exhibit a combination of dynamical chaotic phenomena. The numerical schemes, numerical simulations, stability analysis and equilibrium points have been highlighted in detail. The comparative chaotic graphs have been discussed in three ways (i) by keeping fractal component fixed and varying fractional component distinctly, (ii) by keeping fractional component fixed and varying fractal component distinctly and (iii) by varying both fractal component and fractional component distinctly. Our results suggest that fractal-fractional model of memristor–memcapacitor retains the memory characteristics.

1 Introduction

It is well established fact that the built-in memory-properties of mem-elements in the circuit theory play significant role in the condensed matter and engineering instruments based on promising potential applications. Dr. Chua extended his theory to all circuit elements with memory namely memcapacitors, memristors, and meminductors [1,2,3]. Ventra et al. [4] considered pinched hysteretic loops in the two constitutive variables for memristive system to capacitive and inductive elements. They focused that the dynamical properties of electrons and ions depend on the history of the system and time scales. Pershin and Ventra [5] examined the functional effects of memristors, memcapacitors and meminductors (resistors, capacitors, inductors with memory). Wu et al. [6] explored the nonlinear characteristics of the memristor the nonlinear characteristics of the memristor from which a type of heart-shaped attractors was generated. Additionally, they investigated dissipation and the stability of the equilibrium point when the polarity of the memristor is changed. Xu et al. [7] examined meminductor model for exploring its characteristics based on complex nonlinear phenomena. The complex nonlinear phenomena lied on two different kinds of chaotic transients, coexisting attractors and coexisting bifurcation modes. Ye et al. [8] presented two flux-controlled memristors and a charge-controlled memristor within stable and unstable regions in which they emphasized the 2D and 3D complexity characteristics with multiple varying parameters were analyzed. Nariman et al. [9] suggested fractionalized order mem-capacitor and mem-inductor using different combinations. For the finding the hysteresis loop area and the location of the pinched point through fractional technique, they envisaged to validate the theoretical findings. Nowadays, various types of mathematical definitions of fractional calculus are utilized for physical modeling. Due to this reason, fractional modeling of boundary value problems through theory of fractional differentials and integrals have played significant role in science [10,11,12,13] and engineering [14,15,16].

Rajagopal et al. [17] investigated adaptive sliding mode synchronization for fractional order memristor with no equilibrium. Here they optimized fractional order PID controllers as well. Pu and Yuan [18] discussed an interesting conceptual framework of fractional-order memristor through interpolating characteristics. Such interpolating characteristics are non-volatility property of memory and nonlinear predictions via numerical implementation. Liu and Yang [19] employed the powerful fractional techniques for synchronization of uncertain fractional-order strict-feedback chaotic system. Their major emphasis was the simulation of newly proposed control scheme for synchronization of fractional-order Duffing-Holmes system. Motivating by the above discussion of fractional differential operators, we embedded here few recent attempts of fractional singular and non-singular differential operators [20,21,22,23], fractal-fractional local and non-local integrals [24,25,26,27], fractal singular and non-singular differential operators [28,29,30,31,32], fractal-fractional differentials [33,34,35,36,37,38,39] and purely fractional integral based on local and non-local kernel [40,41,42,43,44] and differential operators based on non-local and non-singular kernel [45,46,47,48,49] in scientific studies.

In brevity, this manuscript investigates the non-integer modeling of memristor–memcapacitor in discrete-time domain through non-singular kernels of fractal fractional differentials and integrals operators. The governing equations of memristor–memcapacitor have been developed for the sake of the dynamical characteristics of simple chaotic circuit. The fractal fractional differentials and integrals operators have been invoked for non-integer modeling of memristor–memcapacitor that can exhibit a combination of dynamical chaotic phenomena. The numerical schemes, numerical simulations, stability analysis and equilibrium points have been highlighted in detail. The comparative chaotic graphs have been discussed in three ways (i) by keeping fractal component fixed and varying fractional component distinctly, (ii) by keeping fractional component fixed and varying fractal component distinctly and (iii) by varying both fractal component and fractional component distinctly. Our results suggest that fractal-fractional model of memristor–memcapacitor retains the memory characteristics.

2 Fractal Fractionalized Memristor–Memcapacitor Chaotic Dynamical System

2.1 Mathematical Definition of the Memristor

Chua and Kang summarized the definition of the memristor as expressed in Eqs. (1a, 1b) and the reciprocal expression of the memcapacitance consisting of ideal charge-controlled memcapacitor is illustrated as:

$$ \begin{aligned} x & =G\left(x,y,t\right)y \\ \dot{y} & =H\left(x,y,t\right) \end{aligned},$$

(1a)

$$\begin{aligned} {i}_{M} & ={v}_{M} \left(a{y}^{2}-b\right), \\ \dot{y} & =e{v}_{M}^{2}y-dy-c{v}_{M} \end{aligned},$$

(1b)

For Eqs. (1a) and (1b), $x$ and $y$ denote the memristor’s state variable and $\left(x,y,t\right)$ and $H\left(x,y,t\right)$ are the functions of memristor’s state variable and time. Here, ${i}_{M}$ and ${v}_{M}$ denote the current and voltage across the memristor and a, b, c, d and e are the constants.

2.2 Mathematical Definition of the Memcapacitor

The reciprocal expression of the memcapacitance, based on the definition of ideal charge-controlled memcapacitor, is defined

$$\begin{aligned} u\left(t\right) & =q\left(t\right){C}_{M}^{-1}\left(\sigma \right)\\ {C}_{M}^{-1}\left(\sigma \right)& =\alpha +\beta \sigma \end{aligned},$$

(2a)

While for Eq. (2a), $q(t)$ and $u(t)$ are the charge and the corresponding voltage of the memcapacitor at time $t$ respectively. And $\alpha$ and $\beta$ constant coefficient of the memcapacitor, the charge $q$ passes the memcapacitor by $\sigma$. For designing a chaotic system based on a memristor, a voltage-controlled memristor and integral when the charge $q$ passes the memcapacitor can be presented respectively as

$$\sigma =\underset{{t}_{0}}{\overset{t}{\int }}q\left(\tau \right)d\tau ,$$

(2b)

Here the functional parameters are described for Eq. (2b) as: $a,b,c,d$ and $e$ are the constants and ${i}_{M}$ and ${v}_{M}$ denotes the current and voltage across the memristor. In this context, assuming the voltage of the memristor is a sinusoidal signal and supposing that the memcapacitor’s charge is a sinusoidal signal in simple chaotic circuit as shown in Fig. 1.

Fig. 1

Configuration of chaotic circuit

Figure 1 is the configuration of memristor–memcapacitor-based simple chaotic circuit. The governing equations of the system based on variables $q$ as a flux, $\delta$ as a state variable memcapacitor, $y$ as a state variable of memristor and ${i}_{L}$ as a current can be written as:

$$\begin{aligned} \frac{d{i}_{L}}{dt} & =\frac{q\alpha }{L}+\frac{\sigma q\beta }{L}, \frac{dq}{dt} =-{i}_{L}-q(\alpha +\beta \sigma )(a{y}^{2}-b)\\ \frac{dy}{dt} & =y{q}^{2}e{(\alpha +\beta \sigma )}^{2}-dy-qc\left(\alpha +\beta \sigma \right),\frac{d\sigma }{dt}=q \end{aligned},$$

(3)

Applying non-dimensional parameters ${\eta }_{1}={i}_{L}, {\eta }_{2}=y,{\eta }_{3}=q,{\eta }_{4}=\delta ,{\mathcal{F}}_{0}=r,{\mathcal{F}}_{1}=\alpha ,{\mathcal{F}}_{2}=\beta ,{\mathcal{F}}_{3}=c,{\mathcal{F}}_{4}=d,{\mathcal{F}}_{5}=e,{\mathcal{F}}_{6}=a$ and ${\mathcal{F}}_{7}=b$ on Eq. (3). We arrive at

$$\begin{aligned} \frac{d{\eta }_{1}}{dt} & ={\mathcal{F}}_{0}{\mathcal{F}}_{1}+{\mathcal{F}}_{0}{\mathcal{F}}_{2}{\eta }_{4}{\eta }_{3} \\ \frac{d{\eta }_{2}}{dt} & ={\eta }_{2}{{\eta }_{3}}^{2}{\mathcal{F}}_{5}{({\mathcal{F}}_{1}+{\mathcal{F}}_{2}{\eta }_{4})}^{2}-{\mathcal{F}}_{4}{\eta }_{2}-{\eta }_{3}{\mathcal{F}}_{3}\left({\mathcal{F}}_{1}+{\mathcal{F}}_{2}{\eta }_{4}\right)\\ \frac{d{\eta }_{3}}{dt} & =-{\eta }_{1}-{\eta }_{3}\left({\mathcal{F}}_{6}-{\mathcal{F}}_{2}{{\eta }_{2}}^{2}\right)\left({\mathcal{F}}_{1}+{\mathcal{F}}_{2}{\eta }_{4}\right) \\ \frac{d{\eta }_{4}}{dt} &={\eta }_{3} \end{aligned},$$

(4)

The functional numerical values for different embedded parameters of Eq. (4) are: ${\mathcal{F}}_{0}=0.01,{\mathcal{F}}_{1}=1,{\mathcal{F}}_{2}=1,{\mathcal{F}}_{3}=0.5,{\mathcal{F}}_{4}=3,{\mathcal{F}}_{5}=4,{\mathcal{F}}_{6}=0.001,{\mathcal{F}}_{7}=0.005.$ The step size is taken as $0.001$ and the initial conditions are (0, 3.1, 1.31, 57). Equation (4) is the classical and evolutionary system of differential equation for chaotic circuit based on memristor–memcapacitor that the dynamical characteristics of simple chaotic circuit as depicted in Fig. 1. In order to develop the governing Eq. (4), we invoke the newly defined fractal-fractional integral and differential operator as:

2.2.1 Caputo–Fabrizio Fractal-Fractional Differential and Integral Operators [50]

$${\mathfrak{D}}_{t}^{{\mathcal{K}}_{1}, {\mathcal{K}}_{2}}{\mathcalligra{g}}\left(t\right)=M\left({\mathcal{K}}_{1}\right){\left(1-{\mathcal{K}}_{1}\right)}^{-1}\frac{d}{d{s}^{{\mathcal{K}}_{2}}}\underset{0}{\overset{t}{\int }}exp\left\{\frac{-{\mathcal{K}}_{1}\left(t-s\right)}{1-{\mathcal{K}}_{1}}\right\}{\mathcalligra{g}}\left(s\right) ds.$$

(5)

$${I}_{t}^{{\mathcal{K}}_{1},{\mathcal{K}}_{2}}{\mathcalligra{g}}\left(t\right)={\mathcal{K}}_{1}{\mathcal{K}}_{2}M\left({\mathcal{K}}_{1}\right)\underset{0}{\overset{t}{\int }}{s}^{{\mathcal{K}}_{1}-1}{\mathcalligra{g}}\left(s\right)ds+\frac{{\mathcalligra{g}}\left(t\right){s}^{{\mathcal{K}}_{2}-1}\left(1-{\mathcal{K}}_{1}\right){\mathcal{K}}_{1}}{M\left({\mathcal{K}}_{1}\right)}.$$

(6)

2.2.2 Atangana–Baleanu Fractal-Fractional Differential and Integral Operators [50]

$${\mathfrak{D}}_{t}^{{\mathcal{K}}_{1}, {\mathcal{K}}_{2}}{\mathcalligra{g}}\left(t\right)=AB\left({\mathcal{K}}_{1}\right){\left(1-{\mathcal{K}}_{1}\right)}^{-1}\frac{d}{d{s}^{{\mathcal{K}}_{2}}}\underset{0}{\overset{t}{\int }}{\textbf{E}}_{{\mathcal{K}}_{1}}\left\{\frac{-{\mathcal{K}}_{1}{\left(t-s\right)}^{{\mathcal{K}}_{1}}}{1-{\mathcal{K}}_{1}}\right\}{\mathcalligra{g}}\left(s\right) ds.$$

(7)

$${I}_{t}^{{\mathcal{K}}_{1},{\mathcal{K}}_{2}}{\mathcalligra{g}}\left(t\right)=\frac{{\mathcal{K}}_{1}{\mathcal{K}}_{2}}{AB\left({\mathcal{K}}_{1}\right)}\underset{0}{\overset{t}{\int }}{s}^{{\mathcal{K}}_{2}-1}{\left(t-s\right)}^{{\mathcal{K}}_{1}-1}{\mathcalligra{g}}\left(s\right)ds+\frac{{\mathcalligra{g}}\left(t\right){t}^{{\mathcal{K}}_{2}-1}(1-{\mathcal{K}}_{1}){\mathcal{K}}_{1}}{AB({\mathcal{K}}_{1})}.$$

(8)

Applying Eqs. (5) and (7) on Eq. (4), we arrive at the fractal-fractionalized differential equation for chaotic circuit based on memristor–memcapacitor:

$$\begin {aligned} \frac{{d}^{{\mathcal{K}}_{3},{\mathcal{K}}_{4}}{\eta }_{1}}{d{t}^{{\mathcal{K}}_{3},{\mathcal{K}}_{4}}} & ={\mathcal{F}}_{0}{\mathcal{F}}_{1}+{\mathcal{F}}_{0}{\mathcal{F}}_{2}{\eta }_{4}{\eta }_{3} \\ \frac{{d}^{{\mathcal{K}}_{3},{\mathcal{K}}_{4}}{\eta }_{2}}{d{t}^{{\mathcal{K}}_{3},{\mathcal{K}}_{4}}} & ={\eta }_{2}{{\eta }_{3}}^{2}{\mathcal{F}}_{5}{({\mathcal{F}}_{1}+{\mathcal{F}}_{2}{\eta }_{4})}^{2}-{\mathcal{F}}_{4}{\eta }_{2}-{\eta }_{3}{\mathcal{F}}_{3}\left({\mathcal{F}}_{1}+{\mathcal{F}}_{2}{\eta }_{4}\right)\\ \frac{{d}^{{\mathcal{K}}_{3},{\mathcal{K}}_{4}}{\eta }_{3}}{d{t}^{{\mathcal{K}}_{3},{\mathcal{K}}_{4}}} & =-{\eta }_{1}-{\eta }_{3}\left({\mathcal{F}}_{6}-{\mathcal{F}}_{2}{{\eta }_{2}}^{2}\right)\left({\mathcal{F}}_{1}+{\mathcal{F}}_{2}{\eta }_{4}\right) \\ \frac{{d}^{{\mathcal{K}}_{3},{\mathcal{K}}_{4}}{\eta }_{4}}{d{t}^{{\mathcal{K}}_{3},{\mathcal{K}}_{4}}} & ={\eta }_{3} \end{aligned},$$

(9)

$$\begin {aligned} \frac{{d}^{{\mathcal{K}}_{5},{\mathcal{K}}_{6}}{\eta }_{1}}{d{t}^{{\mathcal{K}}_{5},{\mathcal{K}}_{6}}} & ={\mathcal{F}}_{0}{\mathcal{F}}_{1}+{\mathcal{F}}_{0}{\mathcal{F}}_{2}{\eta }_{4}{\eta }_{3} \\ \frac{{d}^{{\mathcal{K}}_{5},{\mathcal{K}}_{6}}{\eta }_{2}}{d{t}^{{\mathcal{K}}_{5},{\mathcal{K}}_{6}}} & {\eta }_{2}{{\eta }_{3}}^{2}{\mathcal{F}}_{5}{({\mathcal{F}}_{1}+{\mathcal{F}}_{2}{\eta }_{4})}^{2}-{\mathcal{F}}_{4}{\eta }_{2}-{\eta }_{3}{\mathcal{F}}_{3}\left({\mathcal{F}}_{1}+{\mathcal{F}}_{2}{\eta }_{4}\right)\\ \frac{{d}^{{\mathcal{K}}_{5},{\mathcal{K}}_{6}}{\eta }_{3}}{d{t}^{{\mathcal{K}}_{5},{\mathcal{K}}_{6}}} & -{\eta }_{1}-{\eta }_{3}\left({\mathcal{F}}_{6}-{\mathcal{F}}_{2}{{\eta }_{2}}^{2}\right)\left({\mathcal{F}}_{1}+{\mathcal{F}}_{2}{\eta }_{4}\right) \\ \frac{{d}^{{\mathcal{K}}_{5},{\mathcal{K}}_{6}}{\eta }_{4}}{d{t}^{{\mathcal{K}}_{5},{\mathcal{K}}_{6}}} & {\eta }_{3}\end{aligned}.$$

(10)

Equation (9) is the fractal-fractionalized differential equation for chaotic circuit based on memristor–memcapacitor in term of Caputo–Fabrizio differential operator. Equation (10) is the fractal-fractionalized differential equation for chaotic circuit based on memristor–memcapacitor in term of Atangana–Baleanu differential operator.

3 Development of Non-Singular Numerical Scheme

3.1 Caputo–Fabrizio Fractal-Fractional Scheme

For the sake of numerical scheme of Caputo–Fabrizio fractal-fractionalized differential equation, we write Eq. (9), we have

$$\begin{array}{c}{\mathfrak{D}}_{t}^{{\mathcal{K}}_{3}, {\mathcal{K}}_{4}}{\eta }_{1}\left(t\right)={\mathcal{K}}_{3}{t}^{{\mathcal{K}}_{3}-1}{{\mathcalligra{g}}}_{1}\left({\mathfrak{R}}_{0}\right),\\ \begin{array}{c}{\mathfrak{D}}_{t}^{{\mathcal{K}}_{3}, {\mathcal{K}}_{4}}{\eta }_{2}\left(t\right)={\mathcal{K}}_{3}{t}^{{\mathcal{K}}_{3}-1}{{\mathcalligra{g}}}_{2}\left({\mathfrak{R}}_{0}\right),\\ \begin{array}{c}{\mathfrak{D}}_{t}^{{\mathcal{K}}_{3}, {\mathcal{K}}_{4}}{\eta }_{3}\left(t\right)={\mathcal{K}}_{3}{t}^{{\mathcal{K}}_{3}-1}{{\mathcalligra{g}}}_{3}\left({\mathfrak{R}}_{0}\right),\\ {\mathfrak{D}}_{t}^{{\mathcal{K}}_{3}, {\mathcal{K}}_{4}}{\eta }_{4}\left(t\right)={\mathcal{K}}_{3}{t}^{{\mathcal{K}}_{3}-1}{{\mathcalligra{g}}}_{4}\left({\mathfrak{R}}_{0}\right),\end{array}\end{array}\end{array}$$

(11)

Equation (11) is developed by using Appendix (A1). Now using integral operator of fractal-fractional for Caputo–Fabrizio, Eq. (11) is solved as

$$\begin{aligned}& {\eta }_{1}\left(t\right)={\eta }_{1}(0)+\frac{{\mathcal{K}}_{4}{t}^{{\mathcal{K}}_{4}-1}\left(1-{\mathcal{K}}_{3}\right)}{M\left({\mathcal{K}}_{3}\right)}{{\mathcalligra{g}}}_{1}\left({\mathfrak{R}}_{0}\right)+\frac{{\mathcal{K}}_{3}}{M\left({\mathcal{K}}_{3}\right)}{\displaystyle \int\limits_{0}^{t}}{\uplambda }^{{\mathcal{K}}_{4}-1}{{\mathcalligra{g}}}_{1}\left({\mathfrak{R}}_{1}\right)d\uplambda , \\ & {\eta }_{2}\left(t\right)={\eta }_{2}(0)+\frac{{\mathcal{K}}_{4}{t}^{{\mathcal{K}}_{4}-1}\left(1-{\mathcal{K}}_{3}\right)}{M\left({\mathcal{K}}_{3}\right)}{{\mathcalligra{g}}}_{2}\left({\mathfrak{R}}_{0}\right)+\frac{{\mathcal{K}}_{3}}{M\left({\mathcal{K}}_{3}\right)}{\displaystyle \int\limits_{0}^{t}}{\uplambda }^{{\mathcal{K}}_{4}-1}{{\mathcalligra{g}}}_{2}\left({\mathfrak{R}}_{1}\right)d\uplambda , \\ & {\eta }_{3}\left(t\right)={\eta }_{3}(0)+\frac{{\mathcal{K}}_{4}{t}^{{\mathcal{K}}_{4}-1}\left(1-{\mathcal{K}}_{3}\right)}{M\left({\mathcal{K}}_{3}\right)}{{\mathcalligra{g}}}_{3}\left({\mathfrak{R}}_{0}\right)+\frac{{\mathcal{K}}_{3}}{M\left({\mathcal{K}}_{3}\right)}{\displaystyle \int\limits_{0}^{t}}{\uplambda }^{{\mathcal{K}}_{4}-1}{{\mathcalligra{g}}}_{3}\left({\mathfrak{R}}_{1}\right)d\uplambda , \\ & {\eta }_{4}\left(t\right)={\eta }_{4}(0)+\frac{{\mathcal{K}}_{4}{t}^{{\mathcal{K}}_{4}-1}\left(1-{\mathcal{K}}_{3}\right)}{M\left({\mathcal{K}}_{3}\right)}{{\mathcalligra{g}}}_{4}\left({\mathfrak{R}}_{0}\right)+\frac{{\mathcal{K}}_{3}}{M\left({\mathcal{K}}_{3}\right)}{\displaystyle \int\limits_{0}^{t}}{\uplambda }^{{\mathcal{K}}_{4}-1}{{\mathcalligra{g}}}_{4}\left({\mathfrak{R}}_{1}\right)d\uplambda,\end{aligned} $$

(12)

By the setting at ${t}_{{\epsilon }_{1}+1}$ in Eq. (12), we obtained the numerical scheme via Appendix (A1, A2) as

$$\begin{aligned} & {{\eta }_{1}}_{{\epsilon }_{1}+1}\left(t\right)={{\eta }_{1}}_{0}+\frac{{\mathcal{K}}_{4}{t}_{{\epsilon }_{1}}^{{\mathcal{K}}_{4}-1}\left(1-{\mathcal{K}}_{3}\right)}{M\left({\mathcal{K}}_{3}\right)}{{\mathcalligra{g}}}_{1}\left({\mathfrak{R}}_{2}\right)+\frac{{\mathcal{K}}_{3}{\mathcal{K}}_{4}}{M\left({\mathcal{K}}_{3}\right)}\underset{0}{\overset{{t}_{{\epsilon }_{1}+1}}{\int }}{\uplambda }^{{\mathcal{K}}_{4}-1}{{\mathcalligra{g}}}_{1}\left({\mathfrak{R}}_{1}\right)d\uplambda , \\ & {{\eta }_{2}}_{{\epsilon }_{1}+1}\left(t\right)={{\eta }_{2}}_{0}+\frac{{\mathcal{K}}_{4}{t}_{{\epsilon }_{1}}^{{\mathcal{K}}_{4}-1}\left(1-{\mathcal{K}}_{3}\right)}{M\left({\mathcal{K}}_{3}\right)}{{\mathcalligra{g}}}_{2}\left({\mathfrak{R}}_{2}\right)+\frac{{\mathcal{K}}_{3}{\mathcal{K}}_{4}}{M\left({\mathcal{K}}_{3}\right)}\underset{0}{\overset{{t}_{{\epsilon }_{1}+1}}{\int }}{\uplambda }^{{\mathcal{K}}_{4}-1}{{\mathcalligra{g}}}_{2}\left({\mathfrak{R}}_{1}\right)d\uplambda ,\\ & {{\eta }_{3}}_{{\epsilon }_{1}+1}\left(t\right)={{\eta }_{3}}_{0}+\frac{{\mathcal{K}}_{4}{t}_{{\epsilon }_{1}}^{{\mathcal{K}}_{4}-1}\left(1-{\mathcal{K}}_{3}\right)}{M\left({\mathcal{K}}_{3}\right)}{{\mathcalligra{g}}}_{3}\left({\mathfrak{R}}_{2}\right)+\frac{{\mathcal{K}}_{3}{\mathcal{K}}_{4}}{M\left({\mathcal{K}}_{3}\right)}\underset{0}{\overset{{t}_{{\epsilon }_{1}+1}}{\int }}{\uplambda }^{{\mathcal{K}}_{4}-1}{{\mathcalligra{g}}}_{3}\left({\mathfrak{R}}_{1}\right)d\uplambda , \\ & {{\eta }_{4}}_{{\epsilon }_{1}+1}\left(t\right)={{\eta }_{4}}_{0}+\frac{{\mathcal{K}}_{4}{t}_{{\epsilon }_{1}}^{{\mathcal{K}}_{4}-1}\left(1-{\mathcal{K}}_{3}\right)}{M\left({\mathcal{K}}_{3}\right)}{{\mathcalligra{g}}}_{4}\left({\mathfrak{R}}_{2}\right)+\frac{{\mathcal{K}}_{3}{\mathcal{K}}_{4}}{M\left({\mathcal{K}}_{3}\right)}\underset{0}{\overset{{t}_{{\epsilon }_{1}+1}}{\int }}{\uplambda }^{{\mathcal{K}}_{4}-1}{{\mathcalligra{g}}}_{4}\left({\mathfrak{R}}_{1}\right)d\uplambda ,\end{aligned}$$

(13)

Equation (13) is subjected to (A3). Applying the concept of difference between the consecutive terms, we get simplified form of Eq. (13) as:

$$\begin{aligned}& {{\eta }_{1}}_{{\epsilon }_{1}+1}\left(t\right)={{\eta }_{1}}_{{\epsilon }_{1}}+\frac{{\mathcal{K}}_{4}\left(1-{\mathcal{K}}_{3}\right)}{{t}^{1-{\mathcal{K}}_{4}}M\left({\mathcal{K}}_{3}\right)}{{\mathcalligra{g}}}_{1}\left({\mathfrak{R}}_{2}\right)-\frac{{\mathcal{K}}_{4}\left(1-{\mathcal{K}}_{3}\right)}{{t}_{{\epsilon }_{1}-1}^{1-{\mathcal{K}}_{4}}M\left({\mathcal{K}}_{3}\right)}{{\mathcalligra{g}}}_{1}\left({\mathfrak{R}}_{3}\right)+\frac{{\mathcal{K}}_{3}{\mathcal{K}}_{4}}{M\left({\mathcal{K}}_{3}\right)}\underset{{t}_{{\epsilon }_{1}}}{\overset{{t}_{{\epsilon }_{1}+1}}{\int }}{\lambda }^{{\mathcal{K}}_{4}-1}{{\mathcalligra{g}}}_{1}\left({\mathfrak{R}}_{1}\right)d\uplambda ,\\ & {{\eta }_{2}}_{{\epsilon }_{1}+1}\left(t\right)={{\eta }_{2}}_{{\epsilon }_{1}}+\frac{{\mathcal{K}}_{4}\left(1-{\mathcal{K}}_{3}\right)}{{t}^{1-{\mathcal{K}}_{4}}M\left({\mathcal{K}}_{3}\right)}{{\mathcalligra{g}}}_{2}\left({\mathfrak{R}}_{2}\right)-\frac{{\mathcal{K}}_{4}\left(1-{\mathcal{K}}_{3}\right)}{{t}_{{\epsilon }_{1}-1}^{1-{\mathcal{K}}_{4}}M\left({\mathcal{K}}_{3}\right)}{{\mathcalligra{g}}}_{2}\left({\mathfrak{R}}_{3}\right)+\frac{{\mathcal{K}}_{3}{\mathcal{K}}_{4}}{M\left({\mathcal{K}}_{3}\right)}\underset{{t}_{{\epsilon }_{1}}}{\overset{{t}_{{\epsilon }_{1}+1}}{\int }}{\lambda }^{{\mathcal{K}}_{4}-1}{{\mathcalligra{g}}}_{2}\left({\mathfrak{R}}_{1}\right)d\uplambda ,\\ & {{\eta }_{3}}_{{\epsilon }_{1}+1}\left(t\right)={{\eta }_{3}}_{{\epsilon }_{1}}+\frac{{\mathcal{K}}_{4}\left(1-{\mathcal{K}}_{3}\right)}{{t}^{1-{\mathcal{K}}_{4}}M\left({\mathcal{K}}_{3}\right)}{{\mathcalligra{g}}}_{3}\left({\mathfrak{R}}_{2}\right)-\frac{{\mathcal{K}}_{4}\left(1-{\mathcal{K}}_{3}\right)}{{t}_{{\epsilon }_{1}-1}^{1-{\mathcal{K}}_{4}}M\left({\mathcal{K}}_{3}\right)}{{\mathcalligra{g}}}_{3}\left({\mathfrak{R}}_{3}\right)+\frac{{\mathcal{K}}_{3}{\mathcal{K}}_{4}}{M\left({\mathcal{K}}_{3}\right)}\underset{{t}_{{\epsilon }_{1}}}{\overset{{t}_{{\epsilon }_{1}+1}}{\int }}{\lambda }^{{\mathcal{K}}_{4}-1}{{\mathcalligra{g}}}_{3}\left({\mathfrak{R}}_{1}\right)d\uplambda ,\\ & {{\eta }_{4}}_{{\epsilon }_{1}+1}\left(t\right)={{\eta }_{4}}_{{\epsilon }_{1}}+\frac{{\mathcal{K}}_{4}\left(1-{\mathcal{K}}_{3}\right)}{{t}^{1-{\mathcal{K}}_{4}}M\left({\mathcal{K}}_{3}\right)}{{\mathcalligra{g}}}_{4}\left({\mathfrak{R}}_{2}\right)-\frac{{\mathcal{K}}_{4}\left(1-{\mathcal{K}}_{3}\right)}{{t}_{{\epsilon }_{1}-1}^{1-{\mathcal{K}}_{4}}M\left({\mathcal{K}}_{3}\right)}{{\mathcalligra{g}}}_{4}\left({\mathfrak{R}}_{3}\right)+\frac{{\mathcal{K}}_{3}{\mathcal{K}}_{4}}{M\left({\mathcal{K}}_{3}\right)}\underset{{t}_{{\epsilon }_{1}}}{\overset{{t}_{{\epsilon }_{1}+1}}{\int }}{\lambda }^{{\mathcal{K}}_{4}-1}{{\mathcalligra{g}}}_{4}\left({\mathfrak{R}}_{1}\right)d\uplambda ,\end{aligned}$$

(14)

Integrating Eq. (14) and invoking Appendix (A2–A4). Using the Lagrange polynomial piece-wise interpolation on Eq. (14), the resulting terms are:

$$\begin{aligned}& {{\eta }_{1}}_{{\epsilon }_{1}+1}\left(t\right)={{\eta }_{1}}_{{\epsilon }_{1}}+\frac{{\mathcal{K}}_{4}\left(1-{\mathcal{K}}_{3}\right){{\mathcalligra{g}}}_{1}\left({\mathfrak{R}}_{2}\right)}{{t}^{{1-\mathcal{K}}_{4}}M\left({\mathcal{K}}_{3}\right)}-\frac{{\mathcal{K}}_{4}\left(1-{\mathcal{K}}_{3}\right){{\mathcalligra{g}}}_{1}\left({\mathfrak{R}}_{3}\right)}{{t}_{{\epsilon }_{1}-1}^{1-{\mathcal{K}}_{4}}M\left({\mathcal{K}}_{3}\right)}+\frac{{\mathcal{K}}_{3}{\mathcal{K}}_{4}}{M\left({\mathcal{K}}_{3}\right)}\left\{\frac{3h}{2}{t}_{{\epsilon }_{1}}^{{\mathcal{K}}_{4}-1}{{\mathcalligra{g}}}_{1}\left({\mathfrak{R}}_{2}\right)-\frac{h}{2}{t}_{{\epsilon }_{1}-1}^{{\mathcal{K}}_{4}-1}{{\mathcalligra{g}}}_{1}\left({\mathfrak{R}}_{3}\right)\right\},\\ & {{\eta }_{2}}_{{\epsilon }_{1}+1}\left(t\right)={{\eta }_{2}}_{{\epsilon }_{1}}+\frac{{\mathcal{K}}_{4}\left(1-{\mathcal{K}}_{3}\right){{\mathcalligra{g}}}_{2}\left({\mathfrak{R}}_{2}\right)}{{t}^{{1-\mathcal{K}}_{4}}M\left({\mathcal{K}}_{3}\right)}-\frac{{\mathcal{K}}_{4}\left(1-{\mathcal{K}}_{3}\right){{\mathcalligra{g}}}_{2}\left({\mathfrak{R}}_{3}\right)}{{t}_{{\epsilon }_{1}-1}^{1-{\mathcal{K}}_{4}}M\left({\mathcal{K}}_{3}\right)}+\frac{{\mathcal{K}}_{3}{\mathcal{K}}_{4}}{M\left({\mathcal{K}}_{3}\right)}\left\{\frac{3h}{2}{t}_{{\epsilon }_{1}}^{{\mathcal{K}}_{4}-1}{{\mathcalligra{g}}}_{2}\left({\mathfrak{R}}_{2}\right)-\frac{h}{2}{t}_{{\epsilon }_{1}-1}^{{\mathcal{K}}_{4}-1}{{\mathcalligra{g}}}_{2}\left({\mathfrak{R}}_{3}\right)\right\},\\ & {{\eta }_{3}}_{{\epsilon }_{1}+1}\left(t\right)={{\eta }_{3}}_{{\epsilon }_{1}}+\frac{{\mathcal{K}}_{4}\left(1-{\mathcal{K}}_{3}\right){{\mathcalligra{g}}}_{3}\left({\mathfrak{R}}_{2}\right)}{{t}^{{1-\mathcal{K}}_{4}}M\left({\mathcal{K}}_{3}\right)}-\frac{{\mathcal{K}}_{4}\left(1-{\mathcal{K}}_{3}\right){{\mathcalligra{g}}}_{3}\left({\mathfrak{R}}_{3}\right)}{{t}_{{\epsilon }_{1}-1}^{1-{\mathcal{K}}_{4}}M\left({\mathcal{K}}_{3}\right)}+\frac{{\mathcal{K}}_{3}{\mathcal{K}}_{4}}{M\left({\mathcal{K}}_{3}\right)}\left\{\frac{3h}{2}{t}_{{\epsilon }_{1}}^{{\mathcal{K}}_{4}-1}{{\mathcalligra{g}}}_{3}\left({\mathfrak{R}}_{2}\right)-\frac{h}{2}{t}_{{\epsilon }_{1}-1}^{{\mathcal{K}}_{4}-1}{{\mathcalligra{g}}}_{3}\left({\mathfrak{R}}_{3}\right)\right\},\\ & {{\eta }_{4}}_{{\epsilon }_{1}+1}\left(t\right)={{\eta }_{4}}_{{\epsilon }_{1}}+\frac{{\mathcal{K}}_{4}\left(1-{\mathcal{K}}_{3}\right){{\mathcalligra{g}}}_{4}\left({\mathfrak{R}}_{2}\right)}{{t}^{{1-\mathcal{K}}_{4}}M\left({\mathcal{K}}_{3}\right)}-\frac{{\mathcal{K}}_{4}\left(1-{\mathcal{K}}_{3}\right){{\mathcalligra{g}}}_{4}\left({\mathfrak{R}}_{3}\right)}{{t}_{{\epsilon }_{1}-1}^{1-{\mathcal{K}}_{4}}M\left({\mathcal{K}}_{3}\right)}+\frac{{\mathcal{K}}_{3}{\mathcal{K}}_{4}}{M\left({\mathcal{K}}_{3}\right)}\left\{\frac{3h}{2}{t}_{{\epsilon }_{1}}^{{\mathcal{K}}_{4}-1}{{\mathcalligra{g}}}_{4}\left({\mathfrak{R}}_{2}\right)-\frac{h}{2}{t}_{{\epsilon }_{1}-1}^{{\mathcal{K}}_{4}-1}{{\mathcalligra{g}}}_{4}\left({\mathfrak{R}}_{3}\right)\right\},\end{aligned}$$

(15)

Equation (15) is simplified by means of Appendix (A3, A4). Now simplifying Eq. (15), we investigated the numerical scheme for Caputo–Fabrizio fractal-fractional operator by considering Appendix (A3, A4) as

$$\begin{aligned}{{\eta }_{1}}_{{\epsilon }_{1}+1}\left(t\right)& ={{\eta }_{1}}_{{\epsilon }_{1}}+{\mathcal{K}}_{4}{t}_{{\epsilon }_{1}}^{{\mathcal{K}}_{4}-1}\left(\frac{1-{\mathcal{K}}_{3}}{M({\mathcal{K}}_{3})}+\frac{3{\mathcal{K}}_{3}h}{2M({\mathcal{K}}_{3})}\right){{\mathcalligra{g}}}_{1}\left({\mathfrak{R}}_{2}\right)-{\mathcal{K}}_{4}{t}_{{\epsilon }_{1}-1}^{{\mathcal{K}}_{4}-1}\left(\frac{1-{\mathcal{K}}_{3}}{M\left({\mathcal{K}}_{3}\right)}+\frac{{\mathcal{K}}_{3}h}{2M\left({\mathcal{K}}_{3}\right)}\right){{\mathcalligra{g}}}_{1}\left({\mathfrak{R}}_{3}\right),\\ {{\eta }_{2}}_{{\epsilon }_{1}+1}\left(t\right)& ={{\eta }_{2}}_{{\epsilon }_{1}}+{\mathcal{K}}_{4}{t}_{{\epsilon }_{1}}^{{\mathcal{K}}_{4}-1}\left(\frac{1-{\mathcal{K}}_{3}}{M({\mathcal{K}}_{3})}+\frac{3{\mathcal{K}}_{3}h}{2M({\mathcal{K}}_{3})}\right){{\mathcalligra{g}}}_{2}\left({\mathfrak{R}}_{2}\right)-{\mathcal{K}}_{4}{t}_{{\epsilon }_{1}-1}^{{\mathcal{K}}_{4}-1}\left(\frac{1-{\mathcal{K}}_{3}}{M\left({\mathcal{K}}_{3}\right)}+\frac{{\mathcal{K}}_{3}h}{2M\left({\mathcal{K}}_{3}\right)}\right){{\mathcalligra{g}}}_{2}\left({\mathfrak{R}}_{3}\right),\\ {{\eta }_{3}}_{{\epsilon }_{1}+1}\left(t\right)& ={{\eta }_{3}}_{{\epsilon }_{1}}+{\mathcal{K}}_{4}{t}_{{\epsilon }_{1}}^{{\mathcal{K}}_{4}-1}\left(\frac{1-{\mathcal{K}}_{3}}{M({\mathcal{K}}_{3})}+\frac{3{\mathcal{K}}_{3}h}{2M({\mathcal{K}}_{3})}\right){{\mathcalligra{g}}}_{3}\left({\mathfrak{R}}_{2}\right)-{\mathcal{K}}_{4}{t}_{{\epsilon }_{1}-1}^{{\mathcal{K}}_{4}-1}\left(\frac{1-{\mathcal{K}}_{3}}{M\left({\mathcal{K}}_{3}\right)}+\frac{{\mathcal{K}}_{3}h}{2M\left({\mathcal{K}}_{3}\right)}\right){{\mathcalligra{g}}}_{3}\left({\mathfrak{R}}_{3}\right),\\ {{\eta }_{4}}_{{\epsilon }_{1}+1}\left(t\right)& ={{\eta }_{4}}_{{\epsilon }_{1}}+{\mathcal{K}}_{4}{t}_{{\epsilon }_{1}}^{{\mathcal{K}}_{4}-1}\left(\frac{1-{\mathcal{K}}_{3}}{M({\mathcal{K}}_{3})}+\frac{3{\mathcal{K}}_{3}h}{2M({\mathcal{K}}_{3})}\right){{\mathcalligra{g}}}_{4}\left({\mathfrak{R}}_{2}\right)-{\mathcal{K}}_{4}{t}_{{\epsilon }_{1}-1}^{{\mathcal{K}}_{4}-1}\left(\frac{1-{\mathcal{K}}_{3}}{M\left({\mathcal{K}}_{3}\right)}+\frac{{\mathcal{K}}_{3}h}{2M\left({\mathcal{K}}_{3}\right)}\right){{\mathcalligra{g}}}_{4}\left({\mathfrak{R}}_{3}\right).\end{aligned}$$

(16)

3.2 Atangana–Baleanu Fractal-Fractional Scheme

For the sake of numerical scheme of Atangana–Baleanu fractal-fractionalized differential equation, we write Eq. (10), we have

$$\begin{array}{c}{\mathfrak{D}}_{t}^{{\mathcal{K}}_{5}, {\mathcal{K}}_{6}}{\eta }_{1}\left(t\right)={\mathcal{K}}_{5}{t}^{{\mathcal{K}}_{5}-1}{{\mathcalligra{g}}}_{1}\left({\mathfrak{R}}_{0}\right),\\ \begin{array}{c}{\mathfrak{D}}_{t}^{{\mathcal{K}}_{5}, {\mathcal{K}}_{6}}{\eta }_{2}\left(t\right)={\mathcal{K}}_{5}{t}^{{\mathcal{K}}_{5}-1}{{\mathcalligra{g}}}_{2}\left({\mathfrak{R}}_{0}\right),\\ \begin{array}{c}{\mathfrak{D}}_{t}^{{\mathcal{K}}_{5}, {\mathcal{K}}_{6}}{\eta }_{3}\left(t\right)={\mathcal{K}}_{5}{t}^{{\mathcal{K}}_{5}-1}{{\mathcalligra{g}}}_{3}\left({\mathfrak{R}}_{0}\right),\\ {\mathfrak{D}}_{t}^{{\mathcal{K}}_{5}, {\mathcal{K}}_{6}}{\eta }_{4}\left(t\right)={\mathcal{K}}_{5}{t}^{{\mathcal{K}}_{5}-1}{{\mathcalligra{g}}}_{4}\left({\mathfrak{R}}_{0}\right),\end{array}\end{array}\end{array}$$

(17)

Equation (17) is developed by means of Appendix (A1). Using integral operator of fractal-fractional for Atangana-Baleanu, Eq. (17) is solved as

$$\begin{aligned}& {\eta }_{1}\left(t\right)={\eta }_{1}(0)+\frac{{\mathcal{K}}_{6}{t}^{{{\mathcal{K}}_{6}}_{-1}}\left(1-{\mathcal{K}}_{5}\right)}{AB\left({\mathcal{K}}_{5}\right)}{{\mathcalligra{g}}}_{1}\left({\mathfrak{R}}_{0}\right)+\frac{{\mathcal{K}}_{5}{\mathcal{K}}_{6}}{AB\left({\mathcal{K}}_{5}\right)\Gamma \left({\mathcal{K}}_{5}\right)}{\int\limits_{0}^{t}}{\uplambda }^{{\mathcal{K}}_{6}-1}{(t-\uplambda )}^{{\mathcal{K}}_{5}-1}{{\mathcalligra{g}}}_{1}\left({\mathfrak{R}}_{1}\right)d\uplambda ,\\ & {\eta }_{2}\left(t\right)={\eta }_{2}(0)+\frac{{\mathcal{K}}_{6}{t}^{{{\mathcal{K}}_{6}}_{-1}}\left(1-{\mathcal{K}}_{5}\right)}{AB\left({\mathcal{K}}_{5}\right)}{{\mathcalligra{g}}}_{2}\left({\mathfrak{R}}_{0}\right)+\frac{{\mathcal{K}}_{5}{\mathcal{K}}_{6}}{AB\left({\mathcal{K}}_{5}\right)\Gamma \left({\mathcal{K}}_{5}\right)}{\int\limits_{0}^{t}}{\uplambda }^{{\mathcal{K}}_{6}-1}{(t-\uplambda )}^{{\mathcal{K}}_{5}-1}{{\mathcalligra{g}}}_{2}\left({\mathfrak{R}}_{1}\right)d\uplambda ,\\ & {\eta }_{3}\left(t\right)={\eta }_{3}(0)+\frac{{\mathcal{K}}_{6}{t}^{{{\mathcal{K}}_{6}}_{-1}}\left(1-{\mathcal{K}}_{5}\right)}{AB\left({\mathcal{K}}_{5}\right)}{{\mathcalligra{g}}}_{3}\left({\mathfrak{R}}_{0}\right)+\frac{{\mathcal{K}}_{5}{\mathcal{K}}_{6}}{AB\left({\mathcal{K}}_{5}\right)\Gamma \left({\mathcal{K}}_{5}\right)}{\int\limits_{0}^{t}}{\uplambda }^{{\mathcal{K}}_{6}-1}{(t-\uplambda )}^{{\mathcal{K}}_{5}-1}{{\mathcalligra{g}}}_{3}\left({\mathfrak{R}}_{1}\right)d\uplambda ,\\ & {\eta }_{4}\left(t\right)={\eta }_{4}(0)+\frac{{\mathcal{K}}_{6}{t}^{{{\mathcal{K}}_{6}}_{-1}}\left(1-{\mathcal{K}}_{5}\right)}{AB\left({\mathcal{K}}_{5}\right)}{{\mathcalligra{g}}}_{4}\left({\mathfrak{R}}_{0}\right)+\frac{{\mathcal{K}}_{5}{\mathcal{K}}_{6}}{AB\left({\mathcal{K}}_{5}\right)\Gamma \left({\mathcal{K}}_{5}\right)}{\int\limits_{0}^{t}}{\uplambda }^{{\mathcal{K}}_{6}-1}{(t-\uplambda )}^{{\mathcal{K}}_{5}-1}{{\mathcalligra{g}}}_{4}\left({\mathfrak{R}}_{1}\right)d\uplambda ,\end{aligned}$$

(18)

Equation (18) is solved by invoking Appendix (A1, A2). By the setting at ${t}_{n+1}$ in Eq. (18), we obtained the numerical scheme with help of Appendix (A2, A3) as

$$\begin{aligned}{{\eta }_{1}}_{+1}& ={{\eta }_{1}}_{0}+\frac{{\mathcal{K}}_{6}{t}_{{\epsilon }_{1}}^{{\mathcal{K}}_{6}-1}\left(1-{\mathcal{K}}_{5}\right)}{AB\left({\mathcal{K}}_{5}\right)}{{\mathcalligra{g}}}_{1}\left({\mathfrak{R}}_{2}\right)+\frac{{\mathcal{K}}_{5}{\mathcal{K}}_{6}}{AB\left({\mathcal{K}}_{5}\right)\Gamma \left({\mathcal{K}}_{5}\right)}\underset{0}{\overset{{t}_{{\epsilon }_{1}+1}}{\int }}{\uplambda }^{{\mathcal{K}}_{6}-1}{\left({t}_{{\epsilon }_{1}+1}-\uplambda \right)}^{{\mathcal{K}}_{5}-1}{{\mathcalligra{g}}}_{1}\left({\mathfrak{R}}_{1}\right)d\uplambda ,\\ {{\eta }_{2}}_{+1}& ={{\eta }_{2}}_{0}+\frac{{\mathcal{K}}_{6}{t}_{{\epsilon }_{1}}^{{\mathcal{K}}_{6}-1}\left(1-{\mathcal{K}}_{5}\right)}{AB\left({\mathcal{K}}_{5}\right)}{{\mathcalligra{g}}}_{2}\left({\mathfrak{R}}_{2}\right)+\frac{{\mathcal{K}}_{5}{\mathcal{K}}_{6}}{AB\left({\mathcal{K}}_{5}\right)\Gamma \left({\mathcal{K}}_{5}\right)}\underset{0}{\overset{{t}_{{\epsilon }_{1}+1}}{\int }}{\uplambda }^{{\mathcal{K}}_{6}-1}{\left({t}_{{\epsilon }_{1}+1}-\uplambda \right)}^{{\mathcal{K}}_{5}-1}{{\mathcalligra{g}}}_{2}\left({\mathfrak{R}}_{1}\right)d\uplambda ,\\ {{\eta }_{3}}_{+1}& ={{\eta }_{3}}_{0}+\frac{{\mathcal{K}}_{6}{t}_{{\epsilon }_{1}}^{{\mathcal{K}}_{6}-1}\left(1-{\mathcal{K}}_{5}\right)}{AB\left({\mathcal{K}}_{5}\right)}{{\mathcalligra{g}}}_{3}\left({\mathfrak{R}}_{2}\right)+\frac{{\mathcal{K}}_{5}{\mathcal{K}}_{6}}{AB\left({\mathcal{K}}_{5}\right)\Gamma \left({\mathcal{K}}_{5}\right)}\underset{0}{\overset{{t}_{{\epsilon }_{1}+1}}{\int }}{\uplambda }^{{\mathcal{K}}_{6}-1}{\left({t}_{{\epsilon }_{1}+1}-\uplambda \right)}^{{\mathcal{K}}_{5}-1}{{\mathcalligra{g}}}_{3}\left({\mathfrak{R}}_{1}\right)d\uplambda ,\\ {{\eta }_{4}}_{+1}& ={{\eta }_{4}}_{0}+\frac{{\mathcal{K}}_{6}{t}_{{\epsilon }_{1}}^{{\mathcal{K}}_{6}-1}\left(1-{\mathcal{K}}_{5}\right)}{AB\left({\mathcal{K}}_{5}\right)}{{\mathcalligra{g}}}_{4}\left({\mathfrak{R}}_{2}\right)+\frac{{\mathcal{K}}_{5}{\mathcal{K}}_{6}}{AB\left({\mathcal{K}}_{5}\right)\Gamma \left({\mathcal{K}}_{5}\right)}\underset{0}{\overset{{t}_{{\epsilon }_{1}+1}}{\int }}{\uplambda }^{{\mathcal{K}}_{6}-1}{\left({t}_{{\epsilon }_{1}+1}-\uplambda \right)}^{{\mathcal{K}}_{5}-1}{{\mathcalligra{g}}}_{4}\left({\mathfrak{R}}_{1}\right)d\uplambda ,\end{aligned}$$

(19)

Employing Appendix (A2, A5) and approximating Eq. (19) within the interval $\left[{t}_{{\epsilon }_{2}},{t}_{{\epsilon }_{2}+1}\right]$, the compact form of Eq. (19) is

$$\begin{aligned}& {{\eta }_{1}}_{{\epsilon }_{1}+1}={{\eta }_{1}}_{0}+\frac{{\mathcal{K}}_{6}\left(1-{\mathcal{K}}_{5}\right){{\mathcalligra{g}}}_{1}\left({\mathfrak{R}}_{4}\right)}{{t}_{{\epsilon }_{1}}^{1-{\mathcal{K}}_{6}}AB\left({\mathcal{K}}_{5}\right)}+\frac{{\mathcal{K}}_{5}{\mathcal{K}}_{6}}{AB\left({\mathcal{K}}_{5}\right)\Gamma \left({\mathcal{K}}_{5}\right)}\sum_{{\epsilon }_{2}=0}^{{\epsilon }_{1}}\underset{{t}_{{\epsilon }_{2}}}{\overset{{t}_{{\epsilon }_{2}+1}}{\int }}{\uplambda }^{{\mathcal{K}}_{6}-1}{\left({t}_{{\epsilon }_{1}+1}-\uplambda \right)}^{{\mathcal{K}}_{5}-1}{{\mathcalligra{g}}}_{1}\left({\mathfrak{R}}_{1}\right)d\uplambda ,\\ & {{\eta }_{2}}_{{\epsilon }_{1}+1}={{\eta }_{2}}_{0}+\frac{{\mathcal{K}}_{6}\left(1-{\mathcal{K}}_{5}\right){{\mathcalligra{g}}}_{2}\left({\mathfrak{R}}_{4}\right)}{{t}_{{\epsilon }_{1}}^{1-{\mathcal{K}}_{6}}AB\left({\mathcal{K}}_{5}\right)}+\frac{{\mathcal{K}}_{5}{\mathcal{K}}_{6}}{AB\left({\mathcal{K}}_{5}\right)\Gamma \left({\mathcal{K}}_{5}\right)}\sum_{{\epsilon }_{2}=0}^{{\epsilon }_{1}}\underset{{t}_{{\epsilon }_{2}}}{\overset{{t}_{{\epsilon }_{2}+1}}{\int }}{\uplambda }^{{\mathcal{K}}_{6}-1}{\left({t}_{{\epsilon }_{1}+1}-\uplambda \right)}^{{\mathcal{K}}_{5}-1}{{\mathcalligra{g}}}_{2}\left({\mathfrak{R}}_{1}\right)d\uplambda ,\\ & {{\eta }_{3}}_{{\epsilon }_{1}+1}={{\eta }_{3}}_{0}+\frac{{\mathcal{K}}_{6}\left(1-{\mathcal{K}}_{5}\right){{\mathcalligra{g}}}_{3}\left({\mathfrak{R}}_{4}\right)}{{t}_{{\epsilon }_{1}}^{1-{\mathcal{K}}_{6}}AB\left({\mathcal{K}}_{5}\right)}+\frac{{\mathcal{K}}_{5}{\mathcal{K}}_{6}}{AB\left({\mathcal{K}}_{5}\right)\Gamma \left({\mathcal{K}}_{5}\right)}\sum_{{\epsilon }_{2}=0}^{{\epsilon }_{1}}\underset{{t}_{{\epsilon }_{2}}}{\overset{{t}_{{\epsilon }_{2}+1}}{\int }}{\uplambda }^{{\mathcal{K}}_{6}-1}{\left({t}_{{\epsilon }_{1}+1}-\uplambda \right)}^{{\mathcal{K}}_{5}-1}{{\mathcalligra{g}}}_{3}\left({\mathfrak{R}}_{1}\right)d\uplambda ,\\ & {{\eta }_{4}}_{{\epsilon }_{1}+1}={{\eta }_{4}}_{0}+\frac{{\mathcal{K}}_{6}\left(1-{\mathcal{K}}_{5}\right){{\mathcalligra{g}}}_{4}\left({\mathfrak{R}}_{4}\right)}{{t}_{{\epsilon }_{1}}^{1-{\mathcal{K}}_{6}}AB\left({\mathcal{K}}_{5}\right)}+\frac{{\mathcal{K}}_{5}{\mathcal{K}}_{6}}{AB\left({\mathcal{K}}_{5}\right)\Gamma \left({\mathcal{K}}_{5}\right)}\sum_{{\epsilon }_{2}=0}^{{\epsilon }_{1}}\underset{{t}_{{\epsilon }_{2}}}{\overset{{t}_{{\epsilon }_{2}+1}}{\int }}{\uplambda }^{{\mathcal{K}}_{6}-1}{\left({t}_{{\epsilon }_{1}+1}-\uplambda \right)}^{{\mathcal{K}}_{5}-1}{{\mathcalligra{g}}}_{4}\left({\mathfrak{R}}_{1}\right)d\uplambda ,\end{aligned}$$

(20)

After simplifying Eq. (20) via Appendix (A3, A5, A6), we investigated the numerical scheme for Atangana–Baleanu fractal-fractional operator as

$$\begin{aligned}{{\eta }_{1}}_{{\epsilon }_{1}+1} & ={{\eta }_{1}}_{0}+\frac{{\mathcal{K}}_{6}{t}_{{\epsilon }_{1}}^{{\mathcal{K}}_{6}-1}\left(1-{\mathcal{K}}_{5}\right){{\mathcalligra{g}}}_{1}\left({\mathfrak{R}}_{2}\right)}{AB\left({\mathcal{K}}_{5}\right)}+\frac{{\left({\mathcal{K}}_{6}t\right)}^{{\mathcal{K}}_{5}}{\mathcal{K}}_{6}}{AB\left({\mathcal{K}}_{5}\right)\Gamma \left({\mathcal{K}}_{5}+2\right)}\sum_{{\epsilon }_{2}=0}^{{\epsilon }_{1}}\left[{t}_{{\epsilon }_{2}}^{{\mathcal{K}}_{6}-1}\right. \\ & \quad \times {{\mathcalligra{g}}}_{1}\left({\mathfrak{R}}_{4}\right)\left\{{\left({\epsilon }_{1}+1-{\epsilon }_{2}\right)}^{{\mathcal{K}}_{5}}\left({\epsilon }_{1}-{\epsilon }_{2}+2+{\mathcal{K}}_{5}\right)-{\left({\epsilon }_{1}-{\epsilon }_{2}\right)}^{{\mathcal{K}}_{5}}({\epsilon }_{1}-{\epsilon }_{2}+2+2{\mathcal{K}}_{5})\right\}\\ & \quad \left.-{t}_{{\epsilon }_{2}-1}^{{\mathcal{K}}_{6}-1}{{\mathcalligra{g}}}_{1}\left({\mathfrak{R}}_{5}\right){\left({\epsilon }_{1}+1-{\epsilon }_{2}\right)}^{{\mathcal{K}}_{5}+1}-{\left({\epsilon }_{1}-{\epsilon }_{2}\right)}^{{\mathcal{K}}_{5}}({\epsilon }_{1}-{\epsilon }_{2}+1+{\mathcal{K}}_{5})\right], \\ {{\eta }_{2}}_{{\epsilon }_{1}+1} & = {{\eta }_{2}}_{0}+\frac{{\mathcal{K}}_{6}{t}_{{\epsilon }_{1}}^{{\mathcal{K}}_{6}-1}\left(1-{\mathcal{K}}_{5}\right){{\mathcalligra{g}}}_{2}\left({\mathfrak{R}}_{2}\right)}{AB\left({\mathcal{K}}_{5}\right)}+\frac{{\left({\mathcal{K}}_{6}t\right)}^{{\mathcal{K}}_{5}}{\mathcal{K}}_{6}}{AB\left({\mathcal{K}}_{5}\right)\Gamma \left({\mathcal{K}}_{5}+2\right)}\sum_{{\epsilon }_{2}=0}^{{\epsilon }_{1}}\left[{t}_{{\epsilon }_{2}}^{{\mathcal{K}}_{6}-1}\right. \\ & \quad \times{{\mathcalligra{g}}}_{2}\left({\mathfrak{R}}_{4}\right)\left\{{\left({\epsilon }_{1}+1-{\epsilon }_{2}\right)}^{{\mathcal{K}}_{5}}\left({\epsilon }_{1}-{\epsilon }_{2}+2+{\mathcal{K}}_{5}\right)-{\left({\epsilon }_{1}-{\epsilon }_{2}\right)}^{{\mathcal{K}}_{5}}({\epsilon }_{1}-{\epsilon }_{2}+2+2{\mathcal{K}}_{5})\right\}\\ & \quad \left.-{t}_{{\epsilon }_{2}-1}^{{\mathcal{K}}_{6}-1}{{\mathcalligra{g}}}_{2}\left({\mathfrak{R}}_{5}\right){\left({\epsilon }_{1}+1-{\epsilon }_{2}\right)}^{{\mathcal{K}}_{5}+1}-{\left({\epsilon }_{1}-{\epsilon }_{2}\right)}^{{\mathcal{K}}_{5}}({\epsilon }_{1}-{\epsilon }_{2}+1+{\mathcal{K}}_{5})\right], \\ {{\eta }_{3}}_{{\epsilon }_{1}+1} & = {{\eta }_{3}}_{0}+\frac{{\mathcal{K}}_{6}{t}_{{\epsilon }_{1}}^{{\mathcal{K}}_{6}-1}\left(1-{\mathcal{K}}_{5}\right){{\mathcalligra{g}}}_{3}\left({\mathfrak{R}}_{2}\right)}{AB\left({\mathcal{K}}_{5}\right)}+\frac{{\left({\mathcal{K}}_{6}t\right)}^{{\mathcal{K}}_{5}}{\mathcal{K}}_{6}}{AB\left({\mathcal{K}}_{5}\right)\Gamma \left({\mathcal{K}}_{5}+2\right)}\sum_{{\epsilon }_{2}=0}^{{\epsilon }_{1}}\left[{t}_{{\epsilon }_{2}}^{{\mathcal{K}}_{6}-1}\right. \\ & \quad \times {{\mathcalligra{g}}}_{3}\left({\mathfrak{R}}_{4}\right)\left\{{\left({\epsilon }_{1}+1-{\epsilon }_{2}\right)}^{{\mathcal{K}}_{5}}\left({\epsilon }_{1}-{\epsilon }_{2}+2+{\mathcal{K}}_{5}\right)-{\left({\epsilon }_{1}-{\epsilon }_{2}\right)}^{{\mathcal{K}}_{5}}({\epsilon }_{1}-{\epsilon }_{2}+2+2{\mathcal{K}}_{5})\right\}\\ & \quad \left.-{t}_{{\epsilon }_{2}-1}^{{\mathcal{K}}_{6}-1}{{\mathcalligra{g}}}_{3}\left({\mathfrak{R}}_{5}\right){\left({\epsilon }_{1}+1-{\epsilon }_{2}\right)}^{{\mathcal{K}}_{5}+1}-{\left({\epsilon }_{1}-{\epsilon }_{2}\right)}^{{\mathcal{K}}_{5}}({\epsilon }_{1}-{\epsilon }_{2}+1+{\mathcal{K}}_{5})\right],\\ {{\eta }_{4}}_{{\epsilon }_{1}+1} & = {{\eta }_{4}}_{0}+\frac{{\mathcal{K}}_{6}{t}_{{\epsilon }_{1}}^{{\mathcal{K}}_{6}-1}\left(1-{\mathcal{K}}_{5}\right){{\mathcalligra{g}}}_{4}\left({\mathfrak{R}}_{2}\right)}{AB\left({\mathcal{K}}_{5}\right)}+\frac{{\left({\mathcal{K}}_{6}t\right)}^{{\mathcal{K}}_{5}}{\mathcal{K}}_{6}}{AB\left({\mathcal{K}}_{5}\right)\Gamma \left({\mathcal{K}}_{5}+2\right)}\sum_{{\epsilon }_{2}=0}^{{\epsilon }_{1}}\left[{t}_{{\epsilon }_{2}}^{{\mathcal{K}}_{6}-1}\right. \\ & \quad \times {{\mathcalligra{g}}}_{4}\left({\mathfrak{R}}_{4}\right)\left\{{\left({\epsilon }_{1}+1-{\epsilon }_{2}\right)}^{{\mathcal{K}}_{5}}\left({\epsilon }_{1}-{\epsilon }_{2}+2+{\mathcal{K}}_{5}\right)-{\left({\epsilon }_{1}-{\epsilon }_{2}\right)}^{{\mathcal{K}}_{5}}({\epsilon }_{1}-{\epsilon }_{2}+2+2{\mathcal{K}}_{5})\right\}\\ & \quad \left.-{t}_{{\epsilon }_{2}-1}^{{\mathcal{K}}_{6}-1}{{\mathcalligra{g}}}_{4}\left({\mathfrak{R}}_{5}\right){\left({\epsilon }_{1}+1-{\epsilon }_{2}\right)}^{{\mathcal{K}}_{5}+1}-{\left({\epsilon }_{1}-{\epsilon }_{2}\right)}^{{\mathcal{K}}_{5}}({\epsilon }_{1}-{\epsilon }_{2}+1+{\mathcal{K}}_{5})\right].\end{aligned}$$

(21)

4 Stability Analysis and Equilibrium Points

It is established fact that performance and efficiency of fractal-fractionalized differential equation for chaotic circuit based on memristor–memcapacitor depends on the stability criteria. The system of fractal-fractionalized differential equation for chaotic circuit based on memristor–memcapacitor can be checked as dissipative system by the divergence of fractal-fractionalized differential equation for chaotic circuit based on memristor–memcapacitor. The divergence formula is:

$$\frac{\partial }{\partial {\eta }_{1}}\dot{{\eta }_{1}}+\frac{\partial }{\partial {\eta }_{2}}\dot{{\eta }_{2}}+\frac{\partial }{\partial {\eta }_{3}}\dot{{\eta }_{3}}+\frac{\partial }{\partial {\eta }_{4}}\dot{{\eta }_{4}}=\nabla V,$$

(22)

$$\frac{\partial }{\partial {\eta }_{1}}\dot{{\eta }_{1}}+\frac{\partial }{\partial {\eta }_{2}}\dot{{\eta }_{2}}+\frac{\partial }{\partial {\eta }_{3}}\dot{{\eta }_{3}}+\frac{\partial }{\partial {\eta }_{4}}\dot{{\eta }_{4}}=-{\mathcal{F}}_{4}+{\mathcal{F}}_{5}\left({\mathcal{F}}_{1}+{\mathcal{F}}_{2}{\eta }_{4}\right){\eta }_{3}^{2}-\left({\mathcal{F}}_{6}{\eta }_{2}^{2}-{\mathcal{F}}_{7}\right)\left({\mathcal{F}}_{1}+{\mathcal{F}}_{2}{\eta }_{4}\right),$$

(23)

Invoking the rheological parameters ${\mathcal{F}}_{0}=0.01, {\mathcal{F}}_{1}=1, {\mathcal{F}}_{2}=1, {\mathcal{F}}_{6}=0.001, {\mathcal{F}}_{7}=0.005, {\mathcal{F}}_{4}=0.5, {\mathcal{F}}_{4}=2, {\mathcal{F}}_{5}=4$ and initial conditions ${\eta }_{1}\left(0\right)=0,{\eta }_{2}\left(0\right)=3.1,{\eta }_{3}\left(0\right)=1.31,{\eta }_{4}\left(0\right)=57$ in Eq. (23). After substituting such parameters in Eq. (23), we have result less than zero. This result represents that the system may have chaotic attractors because the system is dissipative.

Now the set of equilibrium point for finding the eigenvalues depending upon Routh-Hurwitz stability criterion can be investigated through Jacobi matrix. Before discussing Jacobi matrix, we set fractal-fractionalized differential equations for chaotic circuit based on memristor–memcapacitor is equal to $\frac{{d}^{{\mathcal{K}}_{3},{\mathcal{K}}_{4}}{\eta }_{1}}{d{t}^{{\mathcal{K}}_{3},{\mathcal{K}}_{4}}}=\frac{{d}^{{\mathcal{K}}_{3},{\mathcal{K}}_{4}}{\eta }_{2}}{d{t}^{{\mathcal{K}}_{3},{\mathcal{K}}_{4}}}=\frac{{d}^{{\mathcal{K}}_{3},{\mathcal{K}}_{4}}{\eta }_{3}}{d{t}^{{\mathcal{K}}_{3},{\mathcal{K}}_{4}}}=\frac{{d}^{{\mathcal{K}}_{3},{\mathcal{K}}_{4}}{\eta }_{4}}{d{t}^{{\mathcal{K}}_{3},{\mathcal{K}}_{4}}}=0$. Such condition lead to

$$\begin{aligned} & {\mathcal{F}}_{0}{\mathcal{F}}_{1}+{\mathcal{F}}_{0}{\mathcal{F}}_{2}{\eta }_{4}{\eta }_{3}=0\\ & {\eta }_{2}{{\eta }_{3}}^{2}{\mathcal{F}}_{5}{({\mathcal{F}}_{1}+{\mathcal{F}}_{2}{\eta }_{4})}^{2}-{\mathcal{F}}_{4}{\eta }_{2}-{\eta }_{3}{\mathcal{F}}_{3}\left({\mathcal{F}}_{1}+{\mathcal{F}}_{2}{\eta }_{4}\right)=0\\ & -{\eta }_{1}-{\eta }_{3}\left({\mathcal{F}}_{6}-{\mathcal{F}}_{2}{{\eta }_{2}}^{2}\right)\left({\mathcal{F}}_{1}+{\mathcal{F}}_{2}{\eta }_{4}\right)=0\\ & {\eta }_{3}=0 , \end{aligned}$$

(24)

Now the Jacobian matrix is obtained from Eq. (24),

$${\textbf{J}} = \left[ {\begin{array}{*{20}c} 0 & 0 & {{\mathcal{F}}_{0} ({\mathcal{F}}_{1} + {\mathcal{F}}_{2} \eta _{4} )} & 0 \\ 0 & { - {\mathcal{F}}_{4} } & { - {\mathcal{F}}_{3} ({\mathcal{F}}_{1} + {\mathcal{F}}_{2} \eta _{4} )} & 0 \\ { - 1} & 0 & {{\mathcal{F}}_{7} ({\mathcal{F}}_{1} + {\mathcal{F}}_{2} \eta _{4} )} & 0 \\ 0 & 0 & 1 & 0 \\ \end{array} } \right], $$

(25)

Here the line equilibrium set is $P(0, 0, 0, n)$; that indicates fractal-fractionalized differential equations for chaotic circuit based on memristor–memcapacitor has infinite equilibrium. Now computing the characteristic equation from Eq. (25), we arrive at:

$${\lambda }^{4}+{{\lambda }_{0}\lambda }^{3}+{{\lambda }_{1}\lambda }^{2}+{\lambda }_{2}\lambda =0,$$

(26)

Here, ${\lambda }_{0}={\mathcal{F}}_{4}-{\mathcal{F}}_{7}({\mathcal{F}}_{1}+{\mathcal{F}}_{2}{\eta }_{4}),{\lambda }_{1}=({\mathcal{F}}_{1}+{\mathcal{F}}_{2}{\eta }_{4}){\mathcal{F}}_{0}{\mathcal{F}}_{4}{\mathcal{F}}_{7},{\lambda }_{2}={\mathcal{F}}_{0}{\mathcal{F}}_{4}({\mathcal{F}}_{1}+{\mathcal{F}}_{2}{\eta }_{4}).$ Now evaluating non-linear algebraic Eq. (26) through synthetic division method, it is concluded that fractal-fractionalized differential equations for chaotic circuit based on memristor–memcapacitor has three nonzero eigenvalues and one zero eigenvalue. This represents that system is stable and system will be likely to create chaos.

5 Discussion of Results Through Chaotic Phenomenon

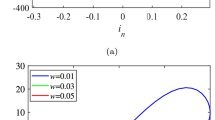
In this section, we describe complex dynamic behaviors for chaotic circuit based on memristor–memcapacitor that contain chaos phenomenon, attractors, and different chaotic states through fractal component fixed and varying fractional component, keeping fractional component fixed and varying fractal component and varying both fractal component and fractional components simultaneously. The numerical schemes of Adams–Bashforth method, numerical simulations via MATLAB, stability analysis and equilibrium points through Eigen values have been highlighted in detail. The Figs. 2, 3, 4, 5, and 6 are depicted for fractional chaos of memristor–memcapacitor at ${\mathcal{K}}_{1}=0.899 \, \mathrm{and} \, {\mathcal{K}}_{2}=1$ for current $({\eta }_{1})$ and state variable memristor $({\eta }_{2})$ via Caputo–Fabrizio (CF) and Atangana–Baleanu (AB) methods, fractal chaos of memristor–memcapacitor at ${\mathcal{K}}_{1}=1 \, \mathrm{and} \, {\mathcal{K}}_{2}=0.787$ for current $({\eta }_{1})$ and state variable memristor $({\eta }_{2})$ via CF and AB methods, fractal-fractional chaos of memristor–memcapacitor at ${\mathcal{K}}_{1}=0.899 \mathrm{and} {\mathcal{K}}_{2}=0.787$ for current $({\eta }_{1})$ and state variable memristor $({\eta }_{2})$ via CF and AB methods, fractal-fractional chaos of memristor–memcapacitor at ${\mathcal{K}}_{1}=0.899 \, \mathrm{and} \, {\mathcal{K}}_{2}=0.787$ for flux $({\eta }_{3})$ and state variable memcapacitor $({\eta }_{4})$ via CF and AB methods and fractal-fractional chaos of memristor–memcapacitor at ${\mathcal{K}}_{1}=0.899 \, \mathrm{and} \, {\mathcal{K}}_{2}=0.787$ for flux $({\eta }_{3})$ and state variable memcapacitor $({\eta }_{4})$ via CF and AB methods. Additionally, initial condition for each parameter is the final value of the trajectory in the previous parameter. In order to examine the deformation of chaotic circuit based on memristor–memcapacitor, the outcomes have been discussed. Figure 2 reflects the comparative analysis of CF and AB fractional differential operators for current $({\eta }_{1})$ and state variable memristor $({\eta }_{2})$ in which the pinched hysteresis curves of the non-integer orders have shown the hysteresis curve of fractional order memristor–memcapacitor under an excitation voltage. Such comparison lead that the local passive (or active) characteristics occur in non-integer modeling of memristor–memcapacitor for current $({\eta }_{1})$ and state variable memristor $({\eta }_{2})$. The CF and AB fractal differential operators have been contrasted in Fig. 3 for current $({\eta }_{1})$ and state variable memristor $({\eta }_{2})$. It is observed that chaotic states as seen in Fig. 3 are reciprocal periodic orbits that appear as the initial value changes declaring that the system has many different reciprocal coexisting attractors with respect to each fractal differential operator. The discrimination of CF and AB fractal-fractional differential operators for current $({\eta }_{1})$ and state variable memristor $({\eta }_{2})$ has been observed in Fig. 4 on the basis of accuracy of numerical method. The trends of CF and AB fractal-fractional differential operators are quite distinct; this is because they strongly depend on values of initial conditions and a memory ability manifested through a closed pinched hysteresis loop in the characteristics. On the contrary, the similar trends CF and AB fractal-fractional differential operators have been depicted for flux $({\eta }_{3})$ and state variable memcapacitor $({\eta }_{4})$ in Fig. 5 and state variable memcapacitor $({\eta }_{4})$ and flux $({\eta }_{3})$ in Fig. 6. Such trends reflect the dissimilarity information due to multidimensional scaling and pattern visualization. Additionally, Fig. 7 presents fractal-fractional chaos of memristor–memcapacitor at ${\mathcal{K}}_{1}=0.899 \mathrm{and} {\mathcal{K}}_{2}=0.787$ for ${\eta }_{1}$ and ${\eta }_{2}$ via CF and AB methods at smaller interval of time. On the other hand, Fig. 8 is depicted for Lyapunov exponent by means of CF and AB fractal-fractional differential operators, in which it is observed that the system exhibits chaotic state because all of the phase diagrams are extremely strong chaotic.

Fig. 2

Fractional chaos of memristor–memcapacitor at ${\mathcal{K}}_{1}=0.899$ and ${\mathcal{K}}_{2}=1$ for ${\eta }_{1}$ and ${\eta }_{2}$ via CF and AB methods

Fig. 3

Fractal chaos of memristor–memcapacitor at ${\mathcal{K}}_{1}=1$ and ${\mathcal{K}}_{2}=0.787$ for ${\eta }_{1}$ and ${\eta }_{2}$ via CF and AB methods

Fig. 4

Fractal-fractional chaos of memristor–memcapacitor at ${\mathcal{K}}_{1}=0.899$ and ${\mathcal{K}}_{2}=0.787$ for ${\eta }_{1}$ and ${\eta }_{2}$ via CF and AB methods

Fig. 5

Fractal-fractional chaos of memristor–memcapacitor at ${\mathcal{K}}_{1}=0.899$ and ${\mathcal{K}}_{2}=0.787$ for ${\eta }_{3}$ and ${\eta }_{4}$ via CF and AB methods

Fig. 6

Fractal-fractional chaos of memristor–memcapacitor at ${\mathcal{K}}_{1}=0.899$ and ${\mathcal{K}}_{2}=0.787$ for ${\eta }_{4}$ and ${\eta }_{3}$ via CF and AB methods

Fig. 7

Fractal-fractional chaos of memristor–memcapacitor at ${\mathcal{K}}_{1}=0.899$ and ${\mathcal{K}}_{2}=0.787$ for ${\eta }_{1}$ and ${\eta }_{2}$ via CF and AB methods at smaller interval of time

Fig. 8

Lyapunov exponent by means of CF and AB fractal-fractional differential operators

6 Conclusion

The new idea is proposed to develop the mathematical models of a memristor and a memcapacitor based on fractal and fractional differential and integral operators. The dynamical characteristics generated by fractal as well fractional operators are highly complex and sensitive as the circuit parameters vary. A chaotic circuit containing a memristor and a memcapacitor is designed with different chaotic strange attractors. The numerical schemes, numerical simulations, stability analysis and equilibrium points have been highlighted in detail. The comparative chaotic graphs have been discussed in three ways (i) by keeping fractal component fixed and varying fractional component distinctly, (ii) by keeping fractional component fixed and varying fractal component distinctly and (iii) by varying both fractal component and fractional component distinctly. After above discussion and concluding remarks, the following results have been accumulated as:

• The current and state variable memristor have pinched hysteresis curves at the non-integer orders that show the hysteresis curve of fractional order memristor–memcapacitor under an excitation voltage.

• The chaotic states are reciprocal and have periodic orbits that appear as the initial value changes declaring that the system has many different reciprocal coexisting attractors with respect to each fractal differential operator.

• The Caputo–Fabrizio fractal-fractional differential operator and Atangana–Baleanu fractal-fractional differential operator have quite distinct chaotic trends depending upon the values of initial conditions.

• The flux $({\eta }_{3})$ and state variable memcapacitor $({\eta }_{4})$ reflect the dissimilarity information due to multidimensional scaling and pattern visualization.

Appendix

$${\mathfrak{R}}_{0}={\eta }_{1},{\eta }_{2},{\eta }_{3},{\eta }_{4},t,$$

(A1)

$${\mathfrak{R}}_{1}={\eta }_{1},{\eta }_{2},{\eta }_{3},{\eta }_{4},\uplambda ,$$

(A2)

$${\mathfrak{R}}_{2}={{\eta }_{1}}^{{\epsilon }_{1}},{{\eta }_{2}}^{{\epsilon }_{1}},{{\eta }_{3}}^{{\epsilon }_{1}},{{\eta }_{4}}^{{\epsilon }_{1}},{t}_{{\epsilon }_{1}},$$

(A3)

$${\mathfrak{R}}_{3}={{\eta }_{1}}^{{\epsilon }_{1-1}},{{\eta }_{2}}^{{\epsilon }_{1-1}},{{\eta }_{3}}^{{\epsilon }_{1-1}},{{\eta }_{4}}^{{\epsilon }_{1-1}},{t}_{{\epsilon }_{1-1}},$$

(A4)

$${\mathfrak{R}}_{4}={{\eta }_{1}}_{{\epsilon }_{2}},{{\eta }_{2}}_{{\epsilon }_{2}},{{\eta }_{3}}_{{\epsilon }_{2}},{{\eta }_{4}}_{{\epsilon }_{2}},{t}_{{\epsilon }_{2}},$$

(A5)

$${\mathfrak{R}}_{5}={{\eta }_{1}}_{{\epsilon }_{2}-1},{{\eta }_{2}}_{{\epsilon }_{2}-1},{{\eta }_{3}}_{{\epsilon }_{2}-1},{{\eta }_{4}}_{{\epsilon }_{2}-1},{t}_{{\epsilon }_{2}-1}$$

(A6)