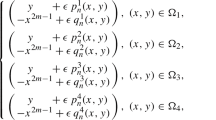1 Introduction

The study of differential equations has been one of the most widely used tools in modeling real phenomena. One of the most relevant problems in the qualitative theory of differential equations is the study of the number, configuration and stability of isolated periodic orbits, the so called limit cycles. These problems attracted the attention of Hilbert and Poincaré, among other mathematicians of the late 19th century. Their famous works opened the minds of a lot of colleagues who have carried out their research in this field for years. The question known as the 16th Hilbert Problem is still open. In last two decades, this question has been extended to piecewise differential equations due to they are very useful for modeling physical systems, technological devices in engineering, mechanics, control theory, nonlinear oscillations, electronics, economics, neuroscience, biology, etc. The first applications were using vector fields defined in two or more zones separated by smooth manifolds. As the nonlinearity was moved to the switching manifold, usually the vector fields were taken linear because of their simplicity and the applicability to real phenomena. Recently, this nonlinearity has been taken breaking the regularity of the switching manifold. In this paper, we deal with the study of lower bounds for the number of limit cycles of planar piecewise linear system defined in two sectorial zones. We write it as

$$\begin{aligned} \begin{aligned} \dot{x}&=(a^\pm +d^\pm )x+b^\pm y+e^\pm , \\ \dot{y}&=c^\pm x+(a^\pm -d^\pm )y+f^\pm , \\ \end{aligned} \end{aligned}$$
(1)

respectively defined in \(\Sigma ^+=\{(x,y)\in {\mathbb {R}}^2, x>0 \text { and } y>0\}\) and \(\Sigma ^-=\{(x,y)\in {\mathbb {R}}^2, x<0 \text { or } y>0\}.\) On the axis, the vector field is defined according to Filippov’s convention. See more details in [8]. This problem was studied some years ago in [5] providing five limit cycles of crossing type using higher order averaging analysis near the linear center. Such isolated periodic orbits, crossing \(\Sigma ,\) were obtained bifurcating from the linear center and computing developments up to sixth order. Recently in [20] the same lower bound was found with second order Melnikov bifurcation technique but perturbing a piecewise linear Hamiltonian system. Our goal is to get the same result with a different approach, easier computations, and only with a first order analysis. The bifurcation procedure used only needs a first order analysis but for a family of centers. First we look for a good family of centers, being infinity of monodromic type, and second, we get five limit cycles bifurcating from infinity showing that this number depends on the parameters of the chosen center. That is, the local cyclicity depends on the parameters of the family. In fact, the cyclicity generically takes a given value, but for some special points it is higher. The first order analysis required to analyze the bifurcation technique that we will use was in fact previously described in [13]. This fact is already known and it has been used recently to increase the local cyclicity in some families of centers. Moreover, we will follow closely the ideas given in [11] for getting the coefficients of the Taylor series of the return map near infinity. This approach has recently followed also in [10]. From previous works, see for example [2, 12, 18], the best lower bound for the number of limit cycles in piecewise linear systems defined in two zones separated by a straight line is three and, in most of the works, it is obtained when the systems chosen in both sides have a dynamic of focus type. Although most experts in the area think that this number will be the upper bound, this problem remains open. The first upper bound is 8 and it has been recently obtained in [6]. Hence, we also restrict our analysis to this special case that we expect will be the best candidate. Without loss of generality, after a rescaling if necessary, we can take

$$\begin{aligned} c^\pm = -((d^\pm )^2+1)/b^\pm . \end{aligned}$$
(2)

The monodromy condition implies that \(b^+b^- > 0.\) We will neither say constantly that this property is satisfied nor that both parameters are nonvanishing. The main advantage of the study of monodromy near infinity is that we avoid the sliding or escaping regions, having only crossing type dynamics in planar Filippov vector fields. For more details on how to define and study the dynamics in these regions using Filippov’s convention, the reader is referred again to [8]. The main goal of our work is to recover the best lower bound but, as we have already mentioned, bifurcating from infinity, for the number of limit cycles of piecewise linear systems with a nonregular switching line provided firstly in [5].

Theorem 1

There exist values of the parameters such that system (1) has five limit cycles bifurcating from infinity.

We remark that the study in the continuous class makes no sense. Because, due to the special form of the boundary between the two zones, the continuity of system (1) along \(\Sigma \) implies analiticity. That is, the system in \(\Sigma ^+\) coincides with the one in \(\Sigma ^-\). Consequently, there are no limit cycles in the continuous class. An intermediate class also interesting to be studied from the physical point of view is the refracted one. The study of their singularities and its local behavior in this intermediate class not only in planar but also higher dimensions can be found in [1, 4, 7, 15]. This class is defined in general for a piecewise vector field \(Z=(Z^+(z),Z^-(z))\) in two zones \(\Sigma ^\pm \) separated by \(h(z)=0\) being \(z\in {\mathbb {R}}^n,\) being h usually a smooth function. The vector field Z is refracted if and only if \(Z^+\cdot \nabla h(z)=Z^-\cdot \nabla h(z)\) for all z such that \(h(z)=0.\) Hence, the differential system (1) is refracted if and only if \(a:=a^+=a^-\), \(d:=d^+=d^-\), \(e:=e^+=e^-,\) and \(f:=f^+=f^-.\) That is, (1) becomes

$$\begin{aligned} \begin{aligned} \dot{x}&=(a+d) x+b^\pm y+e, \\ \dot{y}&=-\frac{x}{b^\pm }+(a-d) y+f. \\ \end{aligned} \end{aligned}$$
(3)

The upper bound for the linear refracted family when the switching line is a straight line reduces to one (see [17, 19]), as it occurs when continuity is imposed (see [9]). Next result shows that, also in the refracted class, the nonregularity of the switching line increases the number of limit cycles.

Proposition 2

There exist values of the parameters such that system (3) has at least two limit cycles bifurcating from infinity.

In the present work we are doing only a partial classification of the center problem of (1), but it is enough to find a simpler proof of the best lower bound for the number of limit cycles provided in [5]. We will explain in the following the main difficulties for solving the center problem near infinity. But, mainly, they are due to the size of the expressions that appear during the computations. The main novelties of the present work are the existence of an alternative proof of the best known lower bound for the number of limit cycles of crossing type, together with the canonical form of system (1) such that the solutions of the initial value problem writes in a good way for getting the Taylor developments. The procedure starts knowing the limiting flying times near infinity. Moreover, we will see in Sect. 2 how they depend on \(d^\pm \). But, in order to simplify computations and avoid huge expressions, we will restrict our attention to the special family \(d^\pm =0.\)

This paper is structured as follows. Section 2 is devoted to recall the necessary classical results on the study of the local stability and degenerated Hopf bifurcation of a nondegenerate monodromic equilibrium point. In Sect. 3 we provide the mentioned partial classification of the center problem in the center-center case. Section 4 is devoted to prove our main result where we have restricted, to simplify computations to the class \(d^\pm =0.\) We finish studying the refracted class in Sect. 5.

2 The Initial Value Problem and the Difference Map Computation

In this section, we recall some classical concepts and bifurcation techniques that are necessary for the proofs of our results. Taking an adequate initial value problem, we can analyze the number of limit cycles of small amplitude instead of the ones that bifurcate near infinity. As the linear part of Eq. (1) is not written in the Jordan normal form we can not use the method described in [3]. Consequently, we will use an alternative and more general mechanism, the one described in [11]. After moving the infinity to the origin, we can use the usual degenerated Hopf bifurcation analysis for piecewise monodromic equilibrium points, see more details in [14]. In the piecewise vector fields defined in two zones, the analysis for finding crossing limit cycles near a monodromic point can be done computing the complete return map by composition of the two half return maps. As usual and by simplicity, instead of using this approach, it is better to get the difference map defined by the distance of the endpoints in \(\Sigma \) of the respective solutions in forward and backward times that start at the same initial condition also in \(\Sigma \). To achieve the proposal goal of this paper, we will need a precise and accurate analysis of the perturbation of families of centers as the one presented in [13]. In that paper, it is shown how the local cyclicity varies with the parameters of the chosen family. In fact, the key point is to find a family of centers having special values for the parameters that provide the highest lower bound for the number of limit cycles of small amplitude.

To simplify writing, we will take the solution of the initial value problem defined by system (1) with \(x(0,x_0)=1/x_0\) and \(y(0,x_0)=0\) in a unified way, without indicating in the superscript which one is written. We notice that, from the definition of \(\Sigma \), \(x_0>0.\) The next solution follows directly integrating the linear equations and imposing the initial conditions:

$$\begin{aligned} x(\theta ,x_0)= & {} \left( \frac{a b f+a d e+e}{a^2+1}+\frac{d}{x_0}\right) {{\,\textrm{e}\,}}^{a \theta }\sin \theta \nonumber \\{} & {} + \left( \frac{a e-b f-d e}{a^2+1} +\frac{1}{x_0}\right) {{\,\textrm{e}\,}}^{a \theta }\cos \theta -\frac{a e-b f-d e}{a^2+1}, \nonumber \\ y(\theta ,x_0)= & {} -\left( \frac{a b d f+a d^2 e+a e-b f}{(a^2+1) b}+\frac{d^2+1}{b x_0}\right) {{\,\textrm{e}\,}}^{a \theta }\sin \theta \nonumber \\{} & {} +\frac{a b f+b d f+d^2 e+e}{(a^2+1) b}({{\,\textrm{e}\,}}^{a \theta }\cos \theta -1). \end{aligned}$$
(4)

Although the previous expressions are not well defined in \(x_0=0,\) we can analyze the behavior of infinity (\(x_0=0\)) considering that it tends to zero. The half return maps are defined from the flying (forward and backward) times \(T^\pm (x_0)\) associated to the first crossing point of (4) with the positive y-axis. That is, solving \(x(T^\pm (x_0),x_0)=0\) and computing \(y(T^\pm (x_0),x_0).\) Consequently, the difference map is defined by

$$\begin{aligned} \Delta (x_0)=y^+(T^+(x_0),x_0)-y^-(T^-(x_0),x_0). \end{aligned}$$
(5)

Here, \(y^\pm \) and \(T^\pm (x_0)\) mean the second components and the flying times of the solution of (4) defined, respectively, in \(\Sigma ^\pm .\) Moreover, \(\Delta (0)=0\) and from our choice of parameters \(b^\pm ,\) we have that \(T^+(x_0)>0\) and \(T^-(x_0)<0.\)

From the Taylor series of (5),

$$\begin{aligned} \Delta (x_0)=\sum _{k=1}^\infty (\Delta _k^+-\Delta _k^-) x_0^k=\sum _{k=1}^\infty \Delta _k x_0^k, \end{aligned}$$
(6)

we can get the stability of the infinity from the sign of the first nonvanishing term. Usually the first nonvanishing coefficient of order \(k+1\) is known as the generalized k-Lyapunov quantity. We notice that all \(\Delta _k\) depends on the parameters of system (1) and, as we will see in the following, we need to take into account all the coefficients for a complete unfolding and for solving the center problem. In smooth context, the subscript k indicates the weak focus order, because it unfolds k limit cycles. In this context, we extend this notion saying that infinity has a weak focus of order k. This definition does not coincide with the one for general discontinuous piecewise smooth vector fields where the sliding phenomenon appears. Because, as \(\Delta _0\) can be different from zero due to existence of a sliding or a escaping segment, we can have one more limit cycle by a pseudo-Hopf bifurcation, see [8, 16]. We notice that this phenomenon does not occur in our situation.

As we are interested in finding the Taylor series (6) of (5), we will first solve equations \(x^+(T^+(x_0),x_0)=0\) and \(x^-(T^-(x_0),x_0)=0\) also in series in \(x_0=0\). Straightforward computations allow us to find recursively the coefficients of the flying times

$$\begin{aligned} T^\pm (x_0)=\sum \limits _{k=0}^\infty T_k^\pm x_0^k. \end{aligned}$$

The main difficulty to deal with the general case is that when \(x_0\) goes to zero the corresponding flying times satisfy \(d^\pm \sin (T^\pm _0)+\cos (T^\pm _0)=0.\) One way to simplify the computations is to study \(d^\pm \approx 0.\) Hence, the Taylor series of \(T^\pm _0\) in \(d^\pm \) start as \(T^+_0=\pi /2+d^++\cdots \) and \(T^-_0=-3\pi /2+d^-+\cdots ,\) respectively. As the size of the expressions that appear during all the computations procedure are so huge, Taylor series in \(a^\pm =0\) have been necessary to be used and the obtained results, up to first order analysis, do not provide better results than the restriction to the case \(d^\pm =0.\) Consequently, from now on we will assume such particular case. Obtaining easier conditions for the limiting flying times, that are \(T^+_0=\pi /2\) and \(T^-_0=-3\pi /2.\) These values do not depend on the remaining parameters as it was shown also in [11]. Straightforward recursive computations get the first values for \(T_k^\pm \) and \(\Delta _k^\pm \):

$$\begin{aligned} \begin{aligned} T^\pm _1=&\,\frac{a^\pm b^\pm f^\pm +e^\pm -(a^\pm e^\pm -b^\pm f^\pm ) {{\,\textrm{e}\,}}^{-\alpha ^\pm a^\pm }}{(a^\pm )^2+1},\\ T^\pm _2=&\,\big ( -a^\pm b^\pm f^\pm -e^\pm +((a^\pm )^2 b^\pm f^\pm +2 a^\pm e^\pm -b^\pm f^\pm ) {{\,\textrm{e}\,}}^{-\alpha ^\pm a^\pm }\\&-a^\pm (a^\pm e^\pm - b^\pm f^\pm ) {{\,\textrm{e}\,}}^{-2\alpha ^\pm a^\pm } \big ) \frac{a^\pm e^\pm -b^\pm f^\pm }{((a^\pm )^2+1)^2},\\ \Delta _1^\pm =&\,-b^\pm {{\,\textrm{e}\,}}^{-\alpha ^\pm a^\pm },\\ \Delta _2^\pm =&\, \big ((a^\pm )^2 b^\pm f^\pm +2 a^\pm e^\pm -b^\pm f^\pm \\&\,- ((a^\pm )^2 e^\pm -2 a^\pm b^\pm f^\pm -e^\pm ){{\,\textrm{e}\,}}^{-\alpha ^\pm a^\pm } \big ) \frac{ b^\pm {{\,\textrm{e}\,}}^{-\alpha ^\pm a^\pm }}{(a^\pm )^2+1},\\ \end{aligned} \end{aligned}$$

where \(\alpha ^+=\pi /2\) and \(\alpha ^-=-3\pi /2.\) We do not write here the other terms because of their size.

3 Center Classification in the Center–Center Case

In this section, we get conditions for having a center at infinity for system (1), when we are in the center-center case. We recall that, as we have mentioned in the introduction, it is not restrictive in this study to assume (2) and \(b^+b^->0.\)

Proposition 3

Assuming that \(a^\pm =d^\pm =0\), system (1) satisfying (2) and \(b^+ b^->0\) has a center at infinity if and only if

$$\begin{aligned} {\mathcal {F}}= \{b^- = b^+, e^- = b^+ f^-, e^+ = b^+ f^+\} \end{aligned}$$
(7)

or \({\mathcal {C}}=\{b^- = b^+,e^- = e^+,f^- = f^+\}.\)

Proof

Under the hypotheses of the statement and using the method detailed in Sect. 2 the Lyapunov quantities can be written as

$$\begin{aligned} \begin{aligned} \Delta _1&=-b^++b^-,\\ \Delta _2&=b^-((f^--f^+)b^--e^-+e^+),\\ \Delta _3&=(b^+)^2(f^--f^+)(b^+ f^--e^-),\\ \end{aligned} \end{aligned}$$

and \(\Delta _k=0\) for \(k=4,\ldots ,7.\) The necessary conditions for having a center at infinity follow vanishing all the Lyapunov quantities. We get easily only the two families of the statement. The second one is clearly a center because it is the global linear one. For the first one we can assume, changing time if necessary, that \(b^\pm <0.\) The piecewise first integral of (1) under the conditions defined by \({\mathcal {F}}\) satisfying \(H^\pm (x_0^{-1},0)=0,\) with \(x_0>0\) and small enough, is

$$\begin{aligned} H^\pm (x,y)= -\frac{1}{2b^{+}}x^2-\frac{b^{+}}{2}y^2+f^{\pm }x-b^{+}f^{\pm }y-\frac{f^{\pm }}{x_0} +\frac{1}{2b^{+}x_0^2}. \end{aligned}$$

The next step is to look for the crossing points \((0,y_0^\pm )\) of the level curves \(\{H^\pm (x,y)=0\}\) with \(y_0^\pm >0\). Straightforward computations show that for each level curve there are two intersection points provided by two values of \(y_0^\pm \) that are

$$\begin{aligned} \left\{ \frac{-1}{b^{+}x_0},\frac{ 1}{b^{+}x_0}-2f^{\pm }\right\} . \end{aligned}$$

The second intersection points are discarded because \(y_0^\pm =(b^{+}x_0)^{-1}-2f^{\pm }<0\) when \(x_0>0\) and small enough. Consequently, both curves \(\{H^\pm (x,y)=0\}\) intersect at the same point \(y_0^\pm =-(b^{+}x_0)^{-1}>0,\) when \(x_0>0\) and small enough. Proving that we have a center at infinity. \(\square \)

4 Cyclicity Near Infinity

This section is devoted to prove Theorem 1 using the perturbation technique presented in [13] and doing an accurate analysis of the cyclicity of infinity for some of the centers obtained in the previous section. We observe that generically the cyclicity of the family of centers defined by \({\mathcal {F}}\) in (7) is less than the cyclicity over two special straight lines on the parameter space as it can be seen in the next result. The fact that family \({\mathcal {C}}\) in (7) is the linear center increases the difficulty of the cyclicity analysis and it was done previously in [5] where developments up to order 6 were necessary. Here we will see that only first order analysis for families is enough to get the same result. Therefore, the advantage of study the bifurcation of families of centers is clearly guaranteed. We remark that a first order analysis for families is in fact a second order analysis for a fixed vector field, see again [13].

Proposition 4

Given \(\alpha \beta \gamma (\beta -\gamma )\psi (\beta ,\gamma )\ne 0,\) being \(\psi (\beta ,\gamma )=3(\pi -2) \gamma -4\beta ,\) the cyclicity of the center \({\mathcal {F}}\) in (7) defined by \(a^\pm = d^\pm = 0, b^\pm = \alpha , e^+ = \alpha \beta , e^- = \alpha \gamma , f^- = \gamma , f^+ = \beta \) and pertubed inside (1), satisfying (2), is at least 4 when \(\varphi _5(\beta ,\gamma )=3( \pi -2)\gamma ^2-8 \gamma \beta -3(3 \pi +2) \beta ^2\ne 0\) and is at least 5 when \(\varphi _5(\beta ,\gamma )=0\) and \(\varphi _6(\beta ,\gamma )= (27 \pi -54)\gamma ^4-(15 \pi +26)\gamma ^3 \beta -60 \pi \gamma ^2 \beta ^2-(45 \pi -26 )\gamma \beta ^3+(81 \pi +54)\beta ^4\ne 0.\)

Proof

After considering the perturbation \(a^- = \varepsilon _8, a^+ = \varepsilon _7, b^- = \alpha +\varepsilon _1, b^+ =\alpha +\varepsilon _2, d^- = \varepsilon _{10}, d^+ = \varepsilon _9, e^- = \alpha \gamma +\varepsilon _3, e ^+ = \alpha \beta +\varepsilon _4, f^- = \gamma +\varepsilon _5, f^+ = \beta +\varepsilon _6\) we compute the first order Taylor series with respect to \(\varepsilon =(\varepsilon _1,\ldots ,\varepsilon _{10})\) of the first Lyapunov quantities. Then with the linear change of variables

$$\begin{aligned} \varepsilon _1=&\,(2u_1+2\varepsilon _2-\alpha \pi \varepsilon _7-3 \varepsilon _8) \pi \alpha /2,\\ \varepsilon _2 =&\,(-2 \alpha \gamma u_1+2 u_2+2 \alpha \varepsilon _3-2 \alpha \varepsilon _4-2 \alpha ^2 \varepsilon _5+2 \alpha ^2 \varepsilon _6\\&+\alpha ^2(\pi \gamma +\pi \beta - \beta )\varepsilon _7 +(6 \pi +8 )\alpha ^2 \gamma \varepsilon _8 )/(2 \alpha (\gamma -\beta )),\\ \varepsilon _3 =&(\alpha ^2 \gamma \beta u_1 -\alpha (\gamma +\beta ) u_2 +u_3 +\alpha ^2 \gamma \varepsilon _4 +\alpha ^3 \beta \varepsilon _5 -\alpha ^3 \gamma \varepsilon _6\\&-\alpha ^3\beta ((\pi -2) \beta +(\pi -4) \gamma )\varepsilon _7 -\alpha ^3\gamma ((3 \pi +4) \beta +(3 \pi +2) \gamma )\varepsilon _8 )/(\alpha ^2 \beta ),\\ \varepsilon _7 =&-(3 \alpha ^2 \gamma \beta u_2-3 \alpha (\beta +\gamma ) u_3+3 u_4 \\&\quad +\alpha ^4\gamma ^2((9 \pi +6) \beta +4 \gamma )\varepsilon _8 )/(\alpha ^4 \beta ^2 \psi (\beta ,\gamma )), \end{aligned}$$

and writing \(\varepsilon _8=u_5,\varepsilon _4=u_6,\varepsilon _5=u_7,\varepsilon _6=u_8,\varepsilon _9=u_9,\varepsilon _{10}=u_{10}\), the first six coefficients write as \(\Delta _k=u_k+O_2(u)\), \(k=1,2,3,4,\) with \(u=(u_1,\ldots ,u_{10}),\) and

$$\begin{aligned} \begin{aligned} \Delta _5=&\,\dfrac{4 \alpha ^3 \gamma \beta ^2 (\gamma -\beta )}{\psi (\beta ,\gamma )}u_2 -\dfrac{\alpha ^2 \beta ((3 \pi -2)\gamma ^2-4 \gamma \beta -4 \beta ^2)}{\psi (\beta ,\gamma )} u_3\\&+\dfrac{\alpha ((3 \pi -6)\gamma (\gamma +\beta )-8 \beta ^2)}{\psi (\beta ,\gamma )} u_4 -\dfrac{4 \alpha ^5 \gamma ^2 (\gamma -\beta ) \varphi _5(\beta ,\gamma )}{3\psi (\beta ,\gamma )}u_5+O_2(u),\\ \Delta _6=&\,\dfrac{4 \alpha ^4 \gamma \beta ^2 (5 \gamma ^2+5 \gamma \beta -9 \beta ^2)}{5\psi (\beta ,\gamma )} u_2-\dfrac{\alpha ^3 \beta (\gamma +\beta ) ((15 \pi -10)\gamma ^2-36 \beta ^2)}{5\psi (\beta ,\gamma )} u_3\\&+\dfrac{\alpha ^2 ((15 \pi -30)(\gamma ^2+\gamma \beta +\beta ^2)\gamma -56 \beta ^3)}{5\psi (\beta ,\gamma )} u_4\\&-\dfrac{4 \alpha ^6 \gamma ^2 \varphi _6(\beta ,\gamma )}{15\psi (\beta ,\gamma )}u_5+O_2(u). \end{aligned} \end{aligned}$$

Clearly, under the hypotheses of the statement on \(\alpha ,\beta ,\gamma ,\) when \(\varphi _5(\beta ,\gamma )\ne 0\) the rank of the linear part of the Taylor series of \(\Delta _1,\ldots ,\Delta _5\) with respect to u at \(u=0\) is 5. Hence, 4 limit cycles of small amplitude bifurcate from \(x_0=0,\) under a degenerated Hopf bifurcation. This proves the first part of the statement.

For the second part, we need to restrict our attention to the special perturbation \(u_6=u_7=u_8=u_9=u_{10}=0.\) In this case, when \(\varphi _5(\beta ,\gamma )=0,\) that is

$$\begin{aligned} \gamma = \dfrac{4\pm \sqrt{27\pi ^2-36\pi -20}}{3(\pi -2)} \beta , \end{aligned}$$
(8)

we have

$$\begin{aligned} \begin{aligned} \varphi _6(\beta ,\gamma )=&-\frac{2}{27 ( \pi -2)^3}\bigl (-1944 \pi ^4+9720 \pi ^3-18000 \pi ^2+7968 \pi +7360 \\&\pm (405 \pi ^3-2070 \pi ^2+2172 \pi +184) \sqrt{27 \pi ^2-36 \pi -20}\bigr ) \beta ^4, \end{aligned} \end{aligned}$$

which is non zero since \(\beta \ne 0.\) Consequently, using the technique described in [13], we can prove that a family of weak foci of higher degeneracy than the later case exists, providing an unfolding of 5 limit cycles of small amplitude bifurcating from \(x_0=0\). We remark that, in (8), as \(\beta \ne 0\) also \(\gamma \ne 0\) and, moreover, the straight lines (8) are both real. \(\square \)

5 Refracted Class Systems

Proposition 2 is a direct consequence of next result, where the highest order in the chosen class of a weak focus is found in the refracted class. As we have done in the previous sections, we restrict system (3) to \(d=0\). Therefore, it becomes

$$\begin{aligned} \begin{aligned} \dot{x}&=a x+b^\pm y+e, \\ \dot{y}&=-\frac{x}{b^\pm }+a y+f. \\ \end{aligned} \end{aligned}$$
(9)

Proposition 5

The infinity of system (9) is a weak focus of order 2 when we take families \({\mathcal {F}}^\pm _R=\{a = \pm 1,b^- = b^+ {{\,\textrm{e}\,}}^{\mp 2\pi },e^2+f^2\ne 0\}\) and \({\mathcal {F}}^0_R=\{f = -{{\,\textrm{e}\,}}^{3a\pi /2}e/b^+, b^-= b^+{{\,\textrm{e}\,}}^{-2a\pi }, ae\ne 0\}.\) Moreover, the centers corresponding to parameter values out of \({\mathcal {F}}^\pm _R \cap {\mathcal {F}}^0_R\) unfold 2 limit cycles.

Proof

With this restriction on the parameters, the first Lyapunov quantities, obtained following the procedure detailed in Sect. 2, are

$$\begin{aligned} \begin{aligned} \Delta _1&=-b^+{{\,\textrm{e}\,}}^{-a\pi /2}+b^-{{\,\textrm{e}\,}}^{3a\pi /2},\\ \Delta _2&=\frac{a^2-1}{a^2+1}(e{{\,\textrm{e}\,}}^{-a\pi }+ b^+f{{\,\textrm{e}\,}}^{-5a\pi /2})b^+({{\,\textrm{e}\,}}^ {2a\pi }-1). \end{aligned} \end{aligned}$$

It is easy to check that \(a\ne 0\) is a necessary condition to have a weak focus at infinity, otherwise we have a center. Consequently, we have only three factors that can vanish \(\Delta _2\) and they provide the three families of the statement. The proof of the first part, finishes checking that, in each case, \(\Delta _3\ne 0.\) Such values, for each family, are:

$$\begin{aligned} \begin{aligned} \Delta _{3,+}&=- \frac{b^+}{4} {{\,\textrm{e}\,}}^{-9 \pi /2} \big ( e^2({{\,\textrm{e}\,}}^{3 \pi } - {{\,\textrm{e}\,}}^{7 \pi } )+2b^+ ef( {{\,\textrm{e}\,}}^{2 \pi } - {{\,\textrm{e}\,}}^{3 \pi }- {{\,\textrm{e}\,}}^{4 \pi }+ {{\,\textrm{e}\,}}^{5 \pi } )\\&\quad +(b^+)^2 f^2(1- {{\,\textrm{e}\,}}^{4 \pi })\big ),\\ \Delta _{3,-}&= \frac{b^+}{4}{{\,\textrm{e}\,}}^{-5 \pi /2} \big ( e^2(1- {{\,\textrm{e}\,}}^{4 \pi }) +2b^+ e f( {{\,\textrm{e}\,}}^{2 \pi } - {{\,\textrm{e}\,}}^{3 \pi } - {{\,\textrm{e}\,}}^{4 \pi } + {{\,\textrm{e}\,}}^{5 \pi })\\&\quad + (b^+)^2 f^2( {{\,\textrm{e}\,}}^{3 \pi }- {{\,\textrm{e}\,}}^{7 \pi }) \big ), \\ \Delta _{3,0}&=(a(1-{{\,\textrm{e}\,}}^{4 a \pi })- {{\,\textrm{e}\,}}^{7 a \pi /2}+ {{\,\textrm{e}\,}}^{5 a \pi /2}+ {{\,\textrm{e}\,}}^{3 a \pi /2}- {{\,\textrm{e}\,}}^{a \pi /2}) \frac{a e^3}{(a^2+1)f}. \end{aligned} \end{aligned}$$

The coefficients \(\Delta _{3,\pm }\) are nonvanishing because \(b^+\ne 0\) (the monodromy condition ensures that) and the last factor is a homogeneous polynomial of degree 2 in e, f with negative discriminant. For \(\Delta _{3,0}\) we need only to check that the first factor is positive when \(a\ne 0.\) In fact, it has a minimum at \(a=0\). This is equivalent to prove that, as \(1-{{\,\textrm{e}\,}}^{4a\pi }\ne 0\) when \(a\ne 0,\) the function

$$\begin{aligned} \frac{{{\,\textrm{e}\,}}^{7a\pi /2}-{{\,\textrm{e}\,}}^{5a\pi /2}-{{\,\textrm{e}\,}}^{3a\pi /2}+{{\,\textrm{e}\,}}^{a\pi /2}}{1-{{\,\textrm{e}\,}}^{4a\pi }}-a \end{aligned}$$

is monotonous decreasing and vanishes at the origin. The first part of the statement follows computing the Taylor series at \(a=0,\) that is \(-a\pi /2+11\pi ^3a^3/48+O(a^5),\) and checking that the numerator of the first derivative writes as the polynomial \(\pi A^7-2A^8-3\pi A^5-3\pi A^3-4 A^4+\pi A-2,\) being \(A={{\,\textrm{e}\,}}^{a\pi /2},\) which has only negative solutions.

Finally, we compute the determinants of the Jacobian matrices of \((\Delta _1,\Delta _2)\) with respect to \((b^-,a)\) on the families \({\mathcal {F}}^\pm _R\) and \({\mathcal {F}}^0_R,\) which are \(b^+{{\,\textrm{e}\,}}^{- \pi }( f b^++e{{\,\textrm{e}\,}}^{\pm 3\pi /2})({{\,\textrm{e}\,}}^{2\pi }-1)\) and \(3\pi (a^2-1)({{\,\textrm{e}\,}}^{2a\pi }-1) {{\,\textrm{e}\,}}^{a\pi /2}e b^+ /(2a^2+2),\) respectively. The proof of the second part of the statement follows because the above determinants only vanish at their intersections. \(\square \)

Near \(d^\pm = 0,\) straightforward computations show that the above result can not be improved.