Skip to main content
SpringerLink
Log in

Historic Behavior in Rock–Paper–Scissor Dynamics

  • Published:
Qualitative Theory of Dynamical Systems Aims and scope Submit manuscript

Abstract

In the evolutionary dynamics of the Rock–Paper–Scissor game, it is common to see the emergence of heteroclinic cycles. The dynamics in the vicinity of a stable heteroclinic cycle is marked by intermittency, where an orbit remains close to the heteroclinic cycle, repeatedly approaching and lingering at the saddles for increasing periods of time, and quickly transitioning from one saddle to the next. This causes the time spent near each saddle to increase at an exponential rate. This highly erratic behavior causes the time averages of the orbit to diverge, a phenomenon known as historic behavior. The problem of describing persistent families of systems exhibiting historic behavior, known as Takens’ Last Problem, has been widely studied in the literature. In this paper, we propose a persistent and broad class of replicator equations generated by increasing functions which exhibit historic behavior wherein the slow oscillation of time averages of the orbit ultimately causes the divergence of higher-order repeated time averages.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2

Similar content being viewed by others

Data Availibility

Data sharing is not applicable to this article as no new data were created or analyzed in this study.

Notes

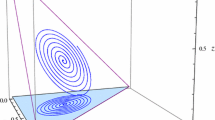
  1. The phenomenological scenario responsible for the formation of a persistent strange attractor in 3D polymatrix replicators was discussed in the literature [35]. This strange attractor is an attractive whirlpool that is generated by a repelling fixed point with complex eigenvalues.

  2. It is possible to choose mutually disjoint convex compact sets \({\mathbb {U}}_1, {\mathbb {U}}_2, {\mathbb {U}}_3\) while maintaining the validity of the results and their proofs. This is due to the fact that the only fixed points of the replicator equation are the vertices of the simplex and the interior point \(\textbf{p}\). As a result, the function \(\Vert \textbf{x}-{\mathcal {R}}(\textbf{x})\Vert \) is positive over the compact subset \(\Delta \) of the simplex which is composed of the complement of sufficiently small neighborhoods around the fixed points. By defining \(\delta :=\min \nolimits _{\textbf{x}\in \Delta }\Vert \textbf{x}-{\mathcal {R}}(\textbf{x})\Vert >0\), it is possible to choose convex compact sets \({\mathbb {U}}_1\subset (G_1\cup G_2){\setminus } {\mathbb {U}}_0, \ {\mathbb {U}}_2\subset (G_3\cup G_4){\setminus } {\mathbb {U}}_0, \ {\mathbb {U}}_3\subset (G_5\cup G_6){\setminus } {\mathbb {U}}_0\) such that the gap between any two of them is less than \(\delta \) in diameter along the boundary of the simplex. It can be demonstrated that as the orbit of the replicator equation approaches the boundary of the simplex, the transition from one convex compact set \({\mathbb {U}}_{i}\) to \({\mathbb {U}}_{i+1}\) results in at most one term of the orbit remaining within the gap between the sets. This deviation does not negatively impact the validity of the proof.

References

  1. Andersson, M., Guiheneuf, P.-A.: Historic behaviour vs. physical measures for irrational flows with multiple stopping points. Adv. Math. 409, 108626 (2022)

    MathSciNet  MATH  Google Scholar 

  2. Araujo, V., Pinheiro, V.: Abundance of wild historic behavior. Bull. Braz Math. Soc., New Series 52(1), 41–76 (2021)

    MathSciNet  MATH  Google Scholar 

  3. Baranski, K., Misiurewicz, M.: Omega-limit sets for the Stein-Ulam spiral map. Top. Proc. 36, 145–172 (2010)

    MathSciNet  MATH  Google Scholar 

  4. Barrientos, P., Kiriki, S., Nakano, Y., Raibekas, A., Soma, T.: Historic behavior in nonhyperbolic homoclinic classes. Proc. Amer. Math. Soc. 148, 1195–1206 (2020)

    MathSciNet  MATH  Google Scholar 

  5. Berger, P.: Emergence and non-typicality of the finiteness of the attractors in many topologies. Proceed. Steklov Instit. Math. 297, 1–27 (2017)

    MATH  Google Scholar 

  6. Berger, P.: Complexities of differentiable dynamical systems. J. Math. Phys. 61, 032702 (2020)

    MathSciNet  MATH  Google Scholar 

  7. Berger, P., Biebler, S.: Emergence of wandering stable components. J. Amer. Math. Soc. 36, 397–482 (2023)

    MathSciNet  MATH  Google Scholar 

  8. Berger, P., Bochi, J.: On emergence and complexity of ergodic decompositions. Adv. Math. 390, 107904 (2021)

    MathSciNet  MATH  Google Scholar 

  9. Bonatti, C., Diaz, L., Viana, M.: Dynamics beyond uniform hyperbolicity. Springer, Berlin (2000)

    MATH  Google Scholar 

  10. Carvalho, M., Varandas, P.: Genericity of historic behavior for maps and flows. Nonlinearity 34(10), 7030–7044 (2021)

    MathSciNet  Google Scholar 

  11. Colli, E., Vargas, E.: Non-trivial wandering domains and homoclinic bifurcations. Ergod. Theor. Dynam. Syst. 21, 1657–1681 (2001)

    MathSciNet  MATH  Google Scholar 

  12. Cressman, R.: Evolutionary dynamics and extensive form games. MIT Press, Cambridge (2003)

    MATH  Google Scholar 

  13. de Santana, H.L.: Historic behavior for flows with the gluing orbit property. J. Korean Math. Soc. 59(2), 337–352 (2022)

    MathSciNet  MATH  Google Scholar 

  14. Ganikhodzhaev, N., Zanin, D.: On a necessary condition for the ergodicity of quadratic operators, defined on the two-dimensional simplex. Russ. Math. Surv. 59(3), 571–572 (2004)

    MathSciNet  MATH  Google Scholar 

  15. Gaunersdorfer, A.: Time averages for heteroclinic attractors. SIAM J. Math. Anal. 52, 1476–1489 (1992)

    MathSciNet  MATH  Google Scholar 

  16. Hofbauer, J.: Heteroclinic cycles in ecological differential equations. Tatra Mount. Math. Publ. 4, 105–116 (1994)

    MathSciNet  MATH  Google Scholar 

  17. Hofbauer, J., Sigmund, K.: The theory of evolution and dynamical systems. Cambridge University Press, Cambridge (1988)

    MATH  Google Scholar 

  18. Hofbauer, J., Sigmund, K.: Evolutionary games and population dynamics. Cambridge University Press, Cambridge (1998)

    MATH  Google Scholar 

  19. Hofbauer, J., Sigmund, K.: Evolutionary game dynamics. Bull. Amer. Math. Soc. 40(4), 479–519 (2003)

    MathSciNet  MATH  Google Scholar 

  20. Jamilov, U., Mukhamedov, F.: A class of Lotka-Volterra operators with historical behavior. Results Math. 77(4), 169 (2022)

    MathSciNet  MATH  Google Scholar 

  21. Jamilov, U., Mukhamedov, F.: Historical behavior for a class of Lotka–Volterra systems. Math. Meth. Appl. Sci. 45(17), 11380–11389 (2022)

    MathSciNet  MATH  Google Scholar 

  22. Jamilov, U., Scheutzow, M., Vorkastner, I.: A prey-predator model with three interacting species. Dyn. Syst. (2023). https://doi.org/10.1080/14689367.2023.2206546

    Article  Google Scholar 

  23. Jordan, T., Naudot, V., Young, T.: Higher order Birkhoff averages. Dyn. Syst. 24(3), 299–313 (2009)

    MathSciNet  MATH  Google Scholar 

  24. Hou, Z., Baigent, S.: Heteroclinic cycles in competitive Kolmogorov systems. Disc. Cont. Dyn. Sys. 33(9), 4071–4093 (2013)

    MathSciNet  MATH  Google Scholar 

  25. Kiriki, S., Li, M., Soma, T.: Geometric lorenz flows with historic behavior. Disc. Cont. Dyn. Sys. 36(12), 7021–7028 (2016)

    MathSciNet  MATH  Google Scholar 

  26. Kiriki, S., Nakano, Y., Soma, T.: Historic behaviour for nonautonomous contraction mappings. Disc. Cont. Dyn. Sys. 32(3), 1111–1124 (2019)

    MathSciNet  MATH  Google Scholar 

  27. Kiriki, S., Nakano, Y., Soma, T.: Emergence via non-existence of averages. Adv. Math. 400, 108254 (2022)

    MathSciNet  MATH  Google Scholar 

  28. Kiriki, S., Soma, T.: Takens’ last problem and existence of non-trivial wandering domains. Adv. Math. 306, 524–588 (2017)

    MathSciNet  MATH  Google Scholar 

  29. Kon, R.: Convex dominates concave: an exclusion principle in discrete-time Kolmogorov systems. Proc. Amer. Math. Soc. 134, 3025 (2006)

    MathSciNet  MATH  Google Scholar 

  30. Krupa, M., Melbourne, I.: Asymptotic stability of heteroclinic cycles in systems with symmetry. Ergod. Th. Dynam. Sys. 15, 121–147 (1995)

    MathSciNet  MATH  Google Scholar 

  31. Kesten, H.: Quadratic transformations: a model for population growth I. Adv. Appl. Probab. 2, 1–82 (1970)

    MathSciNet  MATH  Google Scholar 

  32. Labouriau, I., Rodrigues, A.: On Takens last problem: tangencies and time averages near heteroclinic networks. Nonlinearity 30(5), 1876–1910 (2017)

    MathSciNet  MATH  Google Scholar 

  33. Menzel, M. T., Stein, P. R., Ulam, S. M.: Quadratic transformations. Part 1, Los Alamos Scientific laboratory report LA-2305 (1959)

  34. Marshall, A., Olkin, I., Arnold, B.: Inequalities: theory of majorization and its applications. Springer, Berlin (2011)

    MATH  Google Scholar 

  35. Peixe, T., Rodrigues, A.: Persistent strange attractors in 3D polymatrix replicators. Physica D: Nonlin. Phenom. 438, 133346 (2022)

    MathSciNet  MATH  Google Scholar 

  36. Ruelle, D.: Historic behavior in smooth dynamical Systems in Global Analysis of Dynamical Systems ed H. W. Broer et al (2001)

  37. Saburov, M.: A class of nonergodic Lotka-Volterra operators. Math. Notes 97(5–6), 759–763 (2015)

    MathSciNet  MATH  Google Scholar 

  38. Saburov, M.: On divergence of any order Cesaro mean of Lotka-Volterra operators. Ann. Fun. Anal. 6(4), 247–254 (2015)

    MathSciNet  MATH  Google Scholar 

  39. Saburov, M.: Dichotomy of iterated means for nonlinear operators. Funct. Anal. its Appl. 52(1), 74–76 (2018)

    MathSciNet  MATH  Google Scholar 

  40. Saburov, M.: Nonergodic quadratic stochastic operators. Math. Notes 106(1), 142–145 (2019)

    MathSciNet  MATH  Google Scholar 

  41. Saburov, M.: Iterated means dichotomy for discrete dynamical systems. Qual. Theory Dyn. Syst. 19, 25 (2020)

    MathSciNet  MATH  Google Scholar 

  42. Saburov, M.: The discrete-time Kolmogorov systems with historic behavior. Math. Meth. Appl. Sci. 44(1), 813–819 (2021)

    MathSciNet  MATH  Google Scholar 

  43. Saburov, M.: Uniformly historic behaviour in compact dynamical systems. J. Differ. Equ. Appl. 27(7), 1006–1023 (2021)

    MathSciNet  MATH  Google Scholar 

  44. Saburov, M.: Historic behavior in discrete-time replicator dynamics. Math. Notes 112(1–2), 332–336 (2022)

    MathSciNet  MATH  Google Scholar 

  45. Saburov, M.: Some examples for stable and historic behavior in replicator equations. Examp. Counterexampl. 2, 100091 (2022)

    MathSciNet  Google Scholar 

  46. Saburov, M.: Stable and historic behavior in replicator equations generated by similar-order preserving mappings. Milan J. Math. 91(1), 31–46 (2023)

    MathSciNet  MATH  Google Scholar 

  47. Saburov, M.: Historic behavior in Rock–Paper–Scissor dynamics II, (Submitted)

  48. Sandholm, W.H.: Population games and evolutionary dynamics. MIT Press, Cambridge (2010)

    MATH  Google Scholar 

  49. Schuster, P., Sigmund, K.: Replicator dynamics. J. Theor. Biol. 100(3), 533–538 (1983)

    MathSciNet  Google Scholar 

  50. Sigmund, K.: Time averages for unpredictable orbits of deterministic systems. Ann. Oper. Res. 37, 217–228 (1992)

    MathSciNet  MATH  Google Scholar 

  51. Takens, F.: Orbits with historic behavior, or non-existence of averages - Open Problem. Nonlinearity 21, 33–36 (2008)

    MathSciNet  Google Scholar 

  52. Taylor, P.D., Jonker, L.: Evolutionarily stable strategies and game dynamics. Math. Biosci. 40, 145–156 (1978)

    MathSciNet  MATH  Google Scholar 

  53. Ulam, S.: A collection of mathematical problems. Interscience, New-York & London (1960)

    MATH  Google Scholar 

  54. Vallander, S.S.: The limiting behavior of the sequences of iterates of certain quadratic transformations. Soviet Math. Dokl. 13, 123–126 (1972)

    MATH  Google Scholar 

  55. Yang, D.: On the historical behavior of singular hyperbolic attractors. Proc. Amer. Math. Soc. 148, 1641–1644 (2020)

    MathSciNet  MATH  Google Scholar 

  56. Zakharevich, M.: On the behaviour of trajectories and the ergodic hypothesis for quadratic mappings of a simplex. Russ. Math. Surv. 33(6), 265–266 (1978)

    MATH  Google Scholar 

Download references

Acknowledgements

The author is greatly indebted to two anonymous referees for carefully reading the manuscript and for providing such constructive comments and suggestions which substantially contributed to improving the quality and presentation of the paper.

Author information

Authors and Affiliations

  1. College of Engineering and Technology, American University of the Middle East, Egaila, 54200, Kuwait

    Mansoor Saburov

Authors
  1. Mansoor Saburov
    View author publications

    You can also search for this author in PubMed Google Scholar

Contributions

The Author prepared, wrote, reviewed, and revised the manuscript.

Corresponding author

Correspondence to Mansoor Saburov.

Ethics declarations

Conflict of interest

The authors declare that they have no conflict of interests.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Saburov, M. Historic Behavior in Rock–Paper–Scissor Dynamics. Qual. Theory Dyn. Syst. 22, 121 (2023). https://doi.org/10.1007/s12346-023-00820-0

Download citation

  • Received:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s12346-023-00820-0

Keywords

Mathematics Subject Classification

Search

Navigation