Influence of Human Behavior on COVID-19 Dynamics Based on a Reaction–Diffusion Model

Abstract

To investigate the influence of human behavior on the spread of COVID-19, we propose a reaction–diffusion model that incorporates contact rate functions related to human behavior. The basic reproduction number $\mathcal {R}_{0}$ is derived and a threshold-type result on its global dynamics in terms of $\mathcal {R}_{0}$ is established. More precisely, we show that the disease-free equilibrium is globally asymptotically stable if $\mathcal {R}_{0}\le 1$; while there exists a positive stationary solution and the disease is uniformly persistent if $\mathcal {R}_{0}>1$. By the numerical simulations of the analytic results, we find that human behavior changes may lower infection levels and reduce the number of exposed and infected humans.

1 Introduction

From the Black Plague in Europe in the Middle Ages to COVID-19 outbreak in 2019, all kinds of infectious diseases have been one of the important factors threatening human health and life, and the problem of infectious diseases has been widely concerned by every country in the world. In addition to the treatment of infectious diseases, the prevention of diseases is also of great significance in the process of dealing with infectious diseases. Mathematical modeling for infectious diseases can provide useful insights into disease dynamics that could guide national health authorities for designing effective prevention and control measures against epidemics [1]. Therefore, according to the epidemiological characteristics of the transmission of COVID-19, establishing a mathematical model in line with the law of transmission of COVID-19 and further determining its transmission law have an important guiding role in the formulation of prevention and control measures.

Over the past few decades, the mathematical theory of epidemiological models has gradually been perfected. In 1927, Kermack and McKendrick [2] established the SIR (susceptible-infected-recovered) compartmental model when they investigated the epidemic law of the Black Plague. Since then, various extensions of this mathematical model have been proposed that include more detailed information, such as spatial heterogeneity, seasonality, age-structures, etc., and significant progress has been made in almost all of these aspects. Most of these mathematical epidemic models assume the spread of disease by random contact between individuals, which is usually formulated by the law of group action [3, 4], so behavioral effects are excluded. However, in addition to the disease itself, the mechanisms of disease transmission possibly involve social, economic and psychological factors. In particular, human behavior can have a significant impact on disease transmission [5]. For example, individuals with the awareness of the risk of infection tend to change their behavior, such as paying more attention to personal hygiene, reducing unnecessary going-out, actively wearing masks and receiving vaccinations. Meanwhile, the rapid development of information technology makes it possible for humans to get the latest outbreak situation from various media channels in a timely manner.

Thus, human behavior can make a significant contribution to the spread of a disease. Following the pioneering work of Capasso and Serio [6] in extending the Kermack-McKendric model, mathematical epidemiological modeling of human behavior has increased (see [7]). For example, Liu et al. [8] analyzed the influence of psychological factors on the transmission of multiple infectious diseases. Cui et al. [9] proposed a simple SIS model that included media effects. In addition, Collinson and Heffernan [10] also found that the diseases with large-scale epidemics were strongly influenced by the function of media. Funk et al. [11] divided the epidemiological model into two categories: belief-based and prevalence-based, according to human behavior changes. These examples suggest that human behavior plays an important role in complex epidemic patterns of infectious diseases [12].

The goal of this paper is to improve our understanding of the effect of human behavior on COVID-19. Particularly, we incorporate human behavior into the mathematical modeling of COVID-19. This disease is an acute respiratory infectious disease caused by novel coronavirus infection and it is characterized by fever, dry cough, breathing problems, and even death in severe cases [13]. COVID-19 was found in Wuhan, China in late 2019 for the first time and then traces of this virus were found in various regions and countries. In a short time, COVID-19 caused large-scale infection and death all over the world. Today, COVID-19 is still raging around the world, with a large amount of reported morbidity and mortality in various countries, exerting a huge impact on the economic and social life of countries around the world. Therefore, numerous scholars have published studies on the mathematical modeling and analysis of COVID-19. For example, Wu et al. [14] proposed a SEIR model and predicted the global spread based on the data of the Wuhan epidemic in China. Yang [15] improved the algorithm based on the SEIR model and predicted the epidemic trend of the disease with the method of artificial intelligence, indicating that the implementation of control measures would greatly reduce the chance of transmission. The assumption of the above studies is that the investigated humans are fixed. Nowadays, with the development of transportation, a disease can spread to a remote place in a short time. The COVID-19 outbreak is an example of exactly how far and how fast a disease can now spread. Therefore, it is necessary to consider the spatiotemporal transmission of COVID-19. For example, Omana [16] established the SEIR model based on the reaction–diffusion equation. Mammeri [17] simulated the spread of COVID-19 in France by considering a reaction–diffusion model of the average daily movements of susceptible, exposed and asymptomatic humans. Recently, there are also many works related to reaction–diffusion equations for COVID-19. For example, Zheng et al. [18] proposed a diffusion SEIAR model with Beddington-DeAngelis type incidence to characterize the spread of COVID-19 with spatial transmission. Kammegne et al. [19] used the bias of reaction–diffusion equations to study the susceptible, exposed, infected, recovered, and vaccinated population model of the COVID-19 pandemic. Li et al. [20] developed a reactive-diffusion epidemic model on human mobility networks to characterize the spatio-temporal propagation of COVID-19.

However, the above studies did not specifically consider the influence of human behavior changes on the COVID-19. Motivated by Wang’s study [21] of the impact of human behavior changes on cholera, we consider contact rate functions related to human behavior changes of exposed and infected humans respectively. Then, we analyze the disease dynamics to prove that the lower contact rate due to human behavior changes leads to the reduction of epidemic scale. In this paper, we propose a SEIR model with a monotonic contact function $\beta (t,x)$ to reflect the impact of human behavior factors in the COVID-19, and then expect that this model can provide a new cognition of the COVID-19.

The remainder of this paper is organized as follows. We introduce a PDE model that incorporates human behavior, and then study the well-posedness of the problem in Sect. 2. Section 3 is divided into two parts, the first part derives the basic reproduction number ${\mathcal {R}}_{0}$ and gives its expression, as well as a threshold-type result on the global dynamics in terms of ${\mathcal {R}}_{0}$ is established in the other part. Section 4 conducts numerical simulation by taking appropriate parameters to explore the effect of human behavior on disease dynamics. Finally, this paper ends with a brief discussion.

2 The Model

We know that COVID-19 has an incubation period, a SEIR model can be established to describe the transmission process of the epidemic. Besides, the humans infected with COVID-19 are generally divided into asymptomatic humans and symptomatic humans. By [22,23,24], the novel coronavirus is believed to be infectious during incubation period. In the article [17, 25], the COVID-19 models are proposed with the exposed population, and the exposed humans are assumed to be infectious. Then, we can assume that the exposed humans are someone in the incubation period. Therefore, the exposed humans are infectious and asymptomatic humans are classified into exposed population. Moreover, we can assume that the exposed individuals and the infected individuals play the similar role in the spread of COVID-19. Then, we extend the PDE model in [16] by explicitly including contact rate functions related to exposed and infected humans and taking into account human behavior changes. Here, when people realize the disease outbreak, many people may reduce unnecessary going-out, actively wear masks or other ways to lower the contact rate. These human behavior changes can reduce the number of infected individuals partly (see [5, 21]).

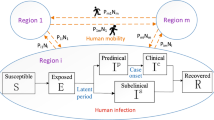
Based on the discussion above, we consider the following diagram Fig. 1 to illustrate the relationship between various groups of the population:

Fig. 1

Flow chart of disease infection

The model can be written as

$$\begin{aligned} \left\{ \begin{array}{l} \dfrac{\partial S}{\partial t}=D_{S}\Delta S+\Lambda -\beta _{1}(E,x)SE-\beta _{2}(I,x)SI-\mu S, \\ \dfrac{\partial E}{\partial t}=D_{E}\Delta E+\beta _{1}(E,x)SE+\beta _{2}(I,x)SI-(\mu +\delta )E, \\ \dfrac{\partial I}{\partial t}=D_{I}\Delta I+\delta E-(\mu +d+\gamma )I, \\ \dfrac{\partial R}{\partial t}=D_{R}\Delta R+\gamma I-\mu R, \\ \end{array}\right. \end{aligned}$$

(2.1)

for $x\in \Omega \subset {\mathbb {R}}$ and $t>0$, with the initial condition:

$$\begin{aligned} S_{0}= & {} S(x,0)\ge 0,~E_{0}=E(x,0)\ge 0,~I_{0}=I(x,0)\ge 0,\nonumber \\ R_{0}= & {} R(x,0)\ge 0,~x\in {\overline{\Omega }}, \end{aligned}$$

(2.2)

and subject to the homogeneous Neumann boundary condition:

$$\begin{aligned} \begin{array}{l} \dfrac{\partial S}{\partial \pmb {n}}=\dfrac{\partial E}{\partial \pmb {n}}=\dfrac{\partial I}{\partial \pmb {n}} =\dfrac{\partial R}{\partial \pmb {n}}=0,~(x,t)\in \partial \Omega \times (0,\infty ). \end{array} \end{aligned}$$

(2.3)

For convenience, we assume $\pmb {U}=(U_{1},U_{2},U_{3},U_{4})=(S,E,I,R)$ and the initial value $\pmb {U_{0}}=(S_{0},E_{0},I_{0},R_{0})$.

Here $\Omega \subset {\mathbb {R}}$ represents the bounded domain with smooth boundary $\partial \Omega$, and $\pmb {n}$ is the outward unit normal vector on $\partial \Omega$ and $\dfrac{\partial }{\partial \pmb {n}}$ means the normal derivative along $\pmb {n}$ on $\partial \Omega$. The population density of susceptible, exposed, infected and recovered humans at location x and time t are measured by $S=S\left( x,t \right)$, $E=E\left( x,t\right)$, $I=I\left( x,t\right)$ and $R=R\left( x,t\right)$, respectively. The parameter ${D}_{i}(i=S,E,I,R)$ denote the diffusion coefficient of S, E, I and R, respectively. The parameter $\Lambda$ is the influx rate of susceptible humans, $\mu$ is the natural death rate of the human, $\delta$ is the rate of asymptomatic humans moving to infected humans, d is the death rate of infected humans due to COVID-19 and finally $\gamma$ is the recovery rate of infectious humans. Particularly, when the COVID-19 outbreak occurs in a specific region, the condition is imposed that nobody can enter or leave the area. So, we employ the no-flux boundary conditions (homogeneous Neumann boundary conditions). One of the most important features of our model is the inclusion of the human behavior. More specifically, we assume that

$$\begin{aligned} \left\{ \begin{array}{l} \beta _{1}(E,x)=(a_{1}-b_{1}m_{1}(E)){\widetilde{\beta }}_{1}(x),\\ \beta _{2}(I,x)=(a_{2}-b_{2}m_{2}(I)){\widetilde{\beta }}_{2}(x), \end{array}\right. \end{aligned}$$

(2.4)

are the contact rate functions of E and I, where $a_{1}$ and $a_{2}$ are the direct contact rates of E and I, $b_{1}$ and $b_{2}$ are the associated largest reduced rates due to human behavior changes of E and I, $m_{1}(E)$ and $m_{2}(I)$ are saturation functions satisfy

$$\begin{aligned} a_{i}\ge & {} b_{i}>0,{~0\le m_{i}\le \dfrac{a_{i}}{b_{i}},}~m_{i}\in C^{1}([0,\infty ))\text { with } m_{i}(0)=0, \nonumber \\ m_{1}^{\prime }(E)\ge & {} 0 \text { and } m_{2}^{\prime }(I)\ge 0. \end{aligned}$$

(2.5)

Here $\widetilde{\beta }_{1}(x)$ and $\widetilde{\beta }_{2}(x)$ are the direct transmission contribution rates of E and I, which are probabilities that measure the contribution of spatial heterogeneity into direct human-to-human transmission.

We make the following assumptions:

• (H1) All the parameters in (2.1) and (2.4) are assumed to be positive;

• (H2) $\pmb {U_{0}}\in \ C({\overline{\Omega }},{\mathbb {R}}^{4}_{+})$;

• (H3) $(E_{0},I_{0})\not \equiv (0,0)$ on ${{\overline{\Omega }}}$;

• (H4) ${\widetilde{\beta }}_{1}(x)$ and ${\widetilde{\beta }}_{2}(x)$ are nontrivial, nonnegative and Hölder continuous functions on ${{\overline{\Omega }}}$.

It follows from the Hölder continuity of ${\widetilde{\beta }}_{i}(x)$ that $\sup _{x\in {\overline{\Omega }}}~|{\widetilde{\beta }}_{i}(x)|<+\infty$ for $i=1,2$ on ${{\overline{\Omega }}}$.

In the remainder of this section, we focus on the well-posedness of system (2.1)–(2.3).

First, let $X:=C({\overline{\Omega }},{\mathbb {R}}^{4})$ be the Banach space with the supremum norm $\left\| \text {}\cdot \text {} \right\| _{X}$, and ${X}^{+}:=C({\overline{\Omega }},{\mathbb {R}}_{+}^{4})$ be the positive cone of the Banach space X. We prove the local existence and positivity of solutions in ${X}^{+}$ according to the theory developed in [26, 27]. Let $Y=C({\overline{\Omega }},{\mathbb {R}})$ and $\pmb {P}(t)=(P_{1}(t),P_{2}(t),P_{3}(t),P_{4}(t))$: $X\rightarrow X$ be the evolution operator associated with

$$\begin{aligned} \left\{ \begin{array}{l} \dfrac{\partial S}{\partial t}=-\mu S+D_{S}\Delta S, \\ \dfrac{\partial E}{\partial t}=-(\mu +\delta )E+D_{E}\Delta E, \\ \dfrac{\partial I}{\partial t}=-(\mu +d+\gamma )I+D_{I}\Delta I, \\ \dfrac{\partial R}{\partial t}=-\mu R+D_{R}\Delta R, \\ \end{array}\right. \end{aligned}$$

(2.6)

for $x\in \Omega$ and $t>0$, which is subject to boundary conditions

$$\begin{aligned} \begin{array}{l} \dfrac{\partial S}{\partial \pmb {n}}=\dfrac{\partial E}{\partial \pmb {n}}=\dfrac{\partial I}{\partial \pmb {n}}=\dfrac{\partial R}{\partial \pmb {n}}=0,~(x,t)\in \partial \Omega \times (0,\infty ). \end{array} \end{aligned}$$

(2.7)

By [27, Corollary 7.2.3], each ${P}_{i}(t)$ $(1\le i\le 4)$ is a compact and strongly positive operator on Y for all $t\ge 0$. We define $\pmb {{\mathcal {F}}}=({\mathcal {F}}_{1},{\mathcal {F}}_{2},{\mathcal {F}}_{3},{\mathcal {F}}_{4})$: ${X}^{+}\rightarrow X$ by

$$\begin{aligned} \left\{ \begin{array}{l} {\mathcal {F}}_{1}(\pmb {\phi })(x):=\Lambda -\beta _{1}(\phi _{2},x)\phi _{1}\phi _{2}-\beta _{2}(\phi _{3},x)\phi _{1}\phi _{3}, \\ {\mathcal {F}}_{2}(\pmb {\phi })(x):=\beta _{1}(\phi _{2},x)\phi _{1}\phi _{2}+\beta _{2}(\phi _{3},x)\phi _{1}\phi _{3},\\ {\mathcal {F}}_{3}(\pmb {\phi })(x):=\delta \phi _{2}, \\ {\mathcal {F}}_{4}(\pmb {\phi })(x):=\gamma \phi _{3}, \\ \end{array}\right. \end{aligned}$$

(2.8)

for any $\pmb {\phi }=(\phi _{1},\phi _{2},\phi _{3},\phi _{4})\in X^{+}$ and $t\ge 0$. Then the solution of system (2.1) can be written as

$$\begin{aligned} \begin{array}{l} U_{i}(x,t)=P_{i}(t)\phi _{i}+\displaystyle \int _{0}^{t}P_{i}(t-s){\mathcal {F}}_{i}(\pmb {U}(x,s))ds, ~1\le i\le 4. \end{array} \end{aligned}$$

(2.9)

By [26, Corollary 4 and Theorem 1], it follows that for each $\pmb {\phi }\in {{X}^{+}}$, system (2.1) has a unique solution $\pmb {U}(x,t;\pmb {\phi })$ on its maximal existence interval $[0,t_{\phi }]$ with $\pmb {U_{0}}=\pmb {\phi }$, where $t_{\phi }\le \infty$, and remains non-negative if it is non-negative initially.

Then, we further prove the global existence and boundedness of solutions to get the following theorem:

Theorem 2.1

For any $\pmb {\phi } \in {{X}^{+}}$, system (2.1) has a unique solution $\pmb {U}(x,t;\pmb {\phi })$ on $[0,+\infty )$ with $\pmb {U_{0}}=\pmb {\phi }$. Moreover, system (2.1) generates a semiflow $Q\left( t\right)$ on $X^{+}$ defined by $Q\left( t\right) \pmb {\phi }=\pmb {U}\left( x,t;\pmb {\phi }\right)$ for all $t\ge 0$, and Q(t) has a strong global attractor in $X^{+}$.

To prove the Theorem 2.1, we need the following result (see [28, Theorem 1 and Corollary 1]):

Lemma 2.2

Consider the parabolic system

$$\begin{aligned} \left\{ \begin{array}{ll} \dfrac{\partial u_{i}}{\partial t}-d_{i}\Delta u_{i}=f_{i}(x,t,\pmb {u}),&{}\quad x\in \Omega ,t>0,i=1,2,\cdots ,m, \\ \dfrac{\partial u_{i}}{\partial \pmb {n}}=0,&{}\quad x\in \partial \Omega ,t>0, \\ u_{i}(x,0)=u_{i}^{0}(x),&{}\quad x\in \Omega , \\ \end{array}\right. \end{aligned}$$

(2.10)

where $\pmb {u}=(u_{1},u_{2},\cdots ,u_{m})$, $u_{i}^{0}(x)\in C({\overline{\Omega }})$, $d_{i}>0$ and $\Omega$ is an open set in ${\mathbb {R}}^{N}$ (N represents spatial dimension, $N\ge 1$) with smooth boundary $\partial \Omega$. Assume that for each $i=1,2,\cdots ,m$, the functions $f_{i}$ satisfy the condition:

$$\begin{aligned} \begin{array}{l} |{f}_{i}(x,t,\pmb {u})|\le {C}_{1}\sum \limits _{i=1}^{m}{\left| u_{i} \right| }^{p}+{C}_{2}, \end{array} \end{aligned}$$

(2.11)

for some nonnegative constants $C_{1}$ and $C_{2}$, and positive constant p. Let $\alpha$ be a positive constant such that $\alpha >\dfrac{N}{2}\max \{0,p-1\}$ and $t_{\phi }$ be the maximal existence time of the solution $\pmb {u}$ corresponding to the initial value $\pmb {u}^{0}$. Suppose that there exists a positive function $C_{\alpha }(\pmb {u}^{0})$ such that ${\left\| \pmb {u}(\cdot ,t) \right\| }_{L^{\alpha }(\Omega )}\le C_{\alpha }(\pmb {u}^{0})$ for all $t\in (0,t_{\phi })$, then the solution $\pmb {u}$ exists for all time and there is a positive function $C_{\infty }$ such that ${\left\| \pmb {u}(\cdot ,t) \right\| }_{L^{\infty }(\Omega )}\le C_{\infty }(\pmb {u}^{0})$ for all $t\in (0,\infty )$. Moreover, if there exists T and $K_{T}$ independent of initial value $\pmb {u}^{0}$ such that ${\left\| \pmb {u}(\cdot ,t)\right\| }_{L^{\alpha }(\Omega )}\le {{K}_{T}}$ for all $t\ge T$, then there exists a positive number $K_{\infty }$ independent of initial value $\pmb {u}^{0}$ such that ${\left\| \pmb {u}(\cdot ,t) \right\| }_{L^{\infty }(\Omega )}\le K_{\infty }$ for all $t\ge T$.

The following proves Theorem 2.1:

Proof of Theorem 2.1

Let $N(x,t;\pmb {\phi })=S(x,t;\pmb {\phi })+E(x,t;\pmb {\phi })+I(x,t;\pmb {\phi })+R(x,t;\pmb {\phi })$ for any $\pmb {\phi }=(\phi _{1},\phi _{2},\phi _{3},\phi _{4})\in {X}^{+}$, then

$$\begin{aligned} \dfrac{d}{dt}\int _{\Omega }N(x,t;\pmb {\phi })dx= & {} \int _{\Omega }{(\Lambda -\mu N(x,t;\pmb {\phi }))dx-d\int _{\Omega }{I(x,t;\pmb {\phi })dx}}\\{} & {} \quad +\int _{\Omega }{({D}_{S}\Delta S+{D}_{E}\Delta E+{D}_{I}\Delta I+{D}_{R}\Delta R)}dx\\\le & {} \Lambda | \Omega |-\mu \int _{\Omega }{N(x,t;\pmb {\phi })dx}, ~\forall t\in (0,t_{\phi }). \end{aligned}$$

By Gronwall’s inequality, we obtain $\displaystyle \int _{\Omega }{N(x,t;\pmb {\phi })dx\le \displaystyle \int _{\Omega }{N_{0}(x)dx+ \dfrac{\Lambda \left| \Omega \right| }{\mu }}}(1-{e}^{-\mu t})$, where ${N}_{0}(x)=N(x,0;\pmb {\phi })=\sum \nolimits _{i=1}^{4}{\phi _{i}(x)}$ and $\left| \Omega \right|$ is length of domain $\Omega$. It follows that there exists a constant $c:=\displaystyle \int _{\Omega }N_{0}(x)dx$ such that

$$\begin{aligned} \int _{\Omega }{U_{i}(x,t;\pmb {\phi })}dx\le & {} \int _{\Omega }{N(x,t;\pmb {\phi })}dx\nonumber \\\le & {} c+\dfrac{\Lambda \left| \Omega \right| }{\mu } (1-{e}^{-\mu t}), \forall t\in (0,t_{\phi }),1\le i\le 4.\nonumber \\ \end{aligned}$$

(2.12)

Moreover, we can obtain

$$\begin{aligned} \underset{t\rightarrow \infty }{\limsup }\int _{\Omega }N(x,t;\pmb {\phi })dx\le c+\dfrac{\Lambda \left| \Omega \right| }{\mu } \end{aligned}$$

(2.13)

uniformly for $x\in \Omega$.

By Lemma 2.2, we take $m=4$, $p=2$, $N=1$. By Young’s inequality, we can prove the global existence and boundedness of the solutions. Here we take the first equation as an example to verify (2.11), and the other cases can be verified in a similar way.

$$\begin{aligned} |f_{1}(x,t,\pmb {U})|\le & {} \Lambda +a_{1}{\widetilde{\beta }}_{1}SE+a_{2}{\widetilde{\beta }}_{2}SI+\mu S\\\le & {} \Lambda +a_{1}{\widetilde{\beta }}_{1}\dfrac{S^{2}+E^{2}}{2}+a_{2}{\widetilde{\beta }}_{2}\dfrac{S^{2}+I^{2}}{2}+\mu \dfrac{S^{2}+1}{2}\\\le & {} \left( \dfrac{a_{1}{\widetilde{\beta }}_{1}}{2}+\dfrac{a_{2}{\widetilde{\beta }}_{2}}{2}+\dfrac{\mu }{2}\right) {S^{2}} +\dfrac{a_{1}{\widetilde{\beta }}_{1}}{2}{E^{2}}+\dfrac{a_{2}{\widetilde{\beta }}_{2}}{2}{I^{2}}+\Lambda +\dfrac{\mu }{2}\\\le & {} C_{1}(S^{2}+E^{2}+I^{2}+R^{2})+C_{2}, \end{aligned}$$

where $f_{1}(x,t,\pmb {U})=\Lambda -\beta _{1}(E,x)SE-\beta _{2}(I,x)SI-\mu S$, $C_{1}=\max \left\{ \dfrac{a_{1}{\widetilde{\beta }}_{1}}{2}+\dfrac{a_{2}{\widetilde{\beta }}_{2}}{2}+\dfrac{\mu }{2}, \dfrac{a_{1}{\widetilde{\beta }}_{1}}{2},\dfrac{a_{2}{\widetilde{\beta }}_{2}}{2}\right\}$ and $C_{2}=\Lambda +\dfrac{\mu }{2}$. In view of (2.12) and Lemma 2.2 with $\alpha =1$, we can show that $U_{i}(1\le i\le 4)$ is $L^{\infty }$-bounded, denoted by $M_{\infty }(\pmb {\phi })$, in other words, $U_{i}$ is uniformly bounded, that is, $\Vert U_{i}(\cdot ,t;\pmb {\phi })\Vert \le M_{\infty }(\pmb {\phi })$ for all $t\in (0,t_{\phi })$, and hence, $t_{\phi }=\infty$. Moreover, by (2.13), we immediately obtain that $U_{i}$ is ultimately bounded.

Define a family of maps $\left\{ Q\left( t\right) \right\} _{t\ge 0}$: $X^{+}\rightarrow X^{+}$ by $Q\left( t\right) \pmb {\phi }=\pmb {U}\left( \cdot ,t;\pmb {\phi } \right)$ for any $\pmb {\phi }\in X^{+}$. It follows that $Q\left( t\right)$ is a semiflow (see [29, Remark 1.1.3]). From the above discussions, we know that $Q\left( t\right)$ is point dissipative. Note that for all $t>0$, $Q\left( t \right)$ is compact. Therefore, we know $Q\left( t \right)$ has a strong global attractor in $X^{+}$ (see [29, Theorem 1.1.3]). $\square$

3 Threshold Dynamics

In this section, our goal is to derive the basic reproduction number ${\mathcal {R}}_{0}$, then we establish the threshold dynamics of the system (2.1) according to ${\mathcal {R}}_{0}$.

3.1 The Basic Reproduction Number

Obviously, there is a disease-free equilibrium point $E_{f}=(S^{*},0,0,0)$ in the system (2.1), where $S^{*}=\dfrac{\Lambda }{\mu }$. By [30, Lemma 1], $S^{*}$ is the unique positive steady-state solution of the following system:

$$\begin{aligned} \left\{ \begin{array}{ll} \dfrac{\partial {\widetilde{S}}}{\partial t}=D_{S}\Delta {\widetilde{S}}+\Lambda -\mu {\widetilde{S}},&{}\quad x\in \Omega ,t>0, \\ \dfrac{\partial {\widetilde{S}}}{\partial \pmb {n}}=0,&{}\quad x\in \partial \Omega ,t>0, \\ {\widetilde{S}}(x,0)=S_{0}(x),&{}\quad x\in \Omega .\\ \end{array}\right. \end{aligned}$$

(3.1)

By the comparison principle [27, Theorem 5.1.1], it implies that S(x, t) in system (2.1) satisfies

$$\begin{aligned} \underset{t\rightarrow \infty }{\limsup }~S(x,t)\le \underset{t\rightarrow \infty }{\limsup }~{\widetilde{S}}(x,t)=S^{*} \end{aligned}$$

(3.2)

uniformly for $x\in {\overline{\Omega }}$.

Linearizing system (2.1)–(2.3) at $({{S}^{*}},0,0,0)$:

$$\begin{aligned} \left\{ \begin{array}{l} \dfrac{\partial S}{\partial t}=D_{S}\Delta S-a_{1}\widetilde{\beta }_{1}(x)S^{*}E- a_{2}\widetilde{\beta }_{2}(x)S^{*}I-\mu S^{*}, \\ \dfrac{\partial E}{\partial t}=D_{E}\Delta E+a_{1}\widetilde{\beta }_{1}(x)S^{*}E+a_{2}\widetilde{\beta }_{2}(x)S^{*}I-(\mu +\delta )E, \\ \dfrac{\partial I}{\partial t}=D_{I}\Delta I+\delta E-(\mu +d+\gamma )I, \\ \dfrac{\partial R}{\partial t}=D_{R}\Delta R+\gamma I-\mu R, \\ \end{array}\right. \end{aligned}$$

(3.3)

for $x\in \Omega$ and $t>0$.

Since the equations of E and I do not contain S and R, we only consider the following subsystem:

$$\begin{aligned} \left\{ \begin{array}{ll} \dfrac{\partial E}{\partial t}=D_{E}\Delta E+a_{1}\widetilde{\beta }_{1}(x)S^{*}E+a_{2}\widetilde{\beta }_{2}(x)S^{*}I-(\mu +\delta )E,&{}\quad x\in \Omega ,t>0, \\ \dfrac{\partial I}{\partial t}=D_{I}\Delta I+\delta E-(\mu +d+\gamma )I,&{}\quad {x}\in \Omega ,t>0, \\ \dfrac{\partial E}{\partial \pmb {n}}=\dfrac{\partial I}{\partial \pmb {n}}=0,&{}\quad {x}\in \partial \Omega ,t>0. \\ \end{array}\right. \nonumber \\ \end{aligned}$$

(3.4)

Define

$$\begin{aligned} {\textbf{A}}= & {} \begin{pmatrix} D_{E}\Delta +a_{1}{\widetilde{\beta }}_{1}(x)S^{*}-(\mu +\delta ) &{}\,\,\,\,\, a_{2}{\widetilde{\beta }}_{2}(x)S^{*} \\ \delta &{} D_{I}\Delta -(\mu +d+\gamma ) \end{pmatrix}\\= & {} \left( \begin{matrix} D_{E}\Delta -(\mu +\delta ) &{}\,\,\,\,\, 0 \\ \delta &{}\,\,\,\,\, D_{I}\Delta -(\mu +d+\gamma ) \\ \end{matrix} \right) +\left( \begin{matrix} a_{1}{\widetilde{\beta }} _{1}(x)S^{*} &{}\,\,\,\,\, a_{2}{\widetilde{\beta }}_{2}(x)S^{*} \\ 0 &{}\,\,\,\,\, 0 \\ \end{matrix} \right) \\= & {} V+F. \end{aligned}$$

Let $T(t):C(\Omega ,{\mathbb {R}}^{2})\rightarrow C(\Omega ,{\mathbb {R}}^{2})$ be the semigroup associated to the problem (3.4). It is easy to see that T(t) has the generator ${\textbf{A}}$. Let $T^{*}(t):C({\overline{\Omega }},{\mathbb {R}}_{+}^{2})\rightarrow C({\overline{\Omega }},{\mathbb {R}}_{+}^{2})$ be the semigroup generated by V.

By the theory in [31, 32], we define next generation operator L:

$$\begin{aligned} L(\pmb {\phi })(x)= & {} \int _{0}^{\infty }F(x)T^{*}(t)\pmb {\phi }(x)dt=F(x)\int _{0}^{\infty }T^{*}(t)\pmb \phi (x)dt, \nonumber \\ \pmb {\phi }= & {} (\phi _{2},\phi _{3})\in C({{\overline{\Omega }}},{\mathbb {R}}^{2}), ~x\in {\overline{\Omega }}. \end{aligned}$$

(3.5)

L represents the total new infection distribution generated by the initial infection distribution $\pmb \phi$ during the infection period. Next, we define the basic reproduction number:

(3.6)

where $\sigma (L)$ is the spectral set of operator L. Let $s({\textbf{A}})=\sup \{{\text {Re}}\lambda :\lambda \in \sigma ({\textbf{A}})\}$ is the spectral bound of ${\textbf{A}}$.

We have the following lemmas:

Lemma 3.1

([32, Theorem 3.1 (i)]) ${\mathcal {R}}_{0}-1$ has the same sign as $s({\textbf{A}})$.

We consider the eigenvalue problems of the second and third equations in linearized system (3.3):

$$\begin{aligned} \left\{ \begin{array}{ll} D_{E}\Delta \varphi _{2}+a_{1}\widetilde{\beta }_{1}(x)S^{*}\varphi _{2}+a_{2}\widetilde{\beta }_{2}(x)S^{*}\varphi _{3}-(\mu +\delta )\varphi _{2} =\lambda \varphi _{2},&{}\quad {x}\in \Omega ,\\ D_{I}\Delta \varphi _{3}+\delta \varphi _{2}-(\mu +\gamma +d)\varphi _{3}=\lambda \varphi _{3},&{}\quad {x}\in \Omega ,\\ \dfrac{\partial \varphi _{2}}{\partial \pmb n}=\dfrac{\partial \varphi _{3}}{\partial \pmb n}=0,&{}\quad {x}\in \partial \Omega . \end{array}\right. \nonumber \\ \end{aligned}$$

(3.7)

By the Appendix A of [33], it is not difficult to see that ${\textbf{A}}$ is irreducible. Therefore, the system (3.4) generates a strongly positive and compact semigroup on $C({\overline{\Omega }},{\mathbb {R}}_{+}^{2})$. According to the conclusions in Chapter 4 and Chapter 7 of [27], we immediately have the following result:

Lemma 3.2

$s({\textbf{A}})$ is the principal eigenvalue of the eigenvalue problem (3.7) associated with a strongly positive eigenfunction.

3.2 Global Dynamics in Terms of ${\mathcal {R}}_{0}$

In this subsection, we prove a threshold-type result on the global dynamics of system (2.1) in terms of ${{{\mathcal {R}}}_{0}}$.

Theorem 3.3

If ${{\mathcal {R}}_{0}}<1$, then the disease-free equilibrium point $E_{f}$ is globally asymptotically stable.

Proof

The local asymptotical stability of $E_{f}$ follows from [32, Theorem 3.1 (ii)]. We only need to prove the global attractivity of $E_{f}$.

Fix $\varepsilon _{0}>0$. By (3.2), there exists a $t_{0}>0$ such that

$$\begin{aligned} 0\le S(x,t)\le S^{*}+\varepsilon _{0}, ~(x,t)\in {\overline{\Omega }}\times [t_{0},\infty ). \end{aligned}$$

For all $(x,t)\in {\overline{\Omega }}\times [t_{0},\infty )$, taking the comparison principle [27, Theorem 5.1.1] for the system (2.1), together with $\beta _{1}(E,x)\le a_{1}\widetilde{\beta }_{1}(x)$ and $\beta _{2}(I,x)\le a_{2}\widetilde{\beta }_{2}(x)$ (see (2.4)–(2.5)), we have

$$\begin{aligned} (E(x,t),I(x,t))\le ({\hat{E}}(x,t),{\hat{I}}(x,t)), \end{aligned}$$

where $({\hat{E}}(x,t),{\hat{I}}(x,t))$ satisfies

$$\begin{aligned} \left\{ \begin{array}{l} \dfrac{\partial {\hat{E}}}{\partial t}={D}_{E}\Delta {\hat{E}}+a_{1}\widetilde{\beta }_{1}(x)({S}^{*}+\varepsilon _{0}){\hat{E}}+a_{2}\widetilde{\beta }_{2}(x)({S}^{*}+ \varepsilon _{0}){\hat{I}}-(\mu +\delta ){\hat{E}}, \\ \dfrac{\partial {\hat{I}}}{\partial t}={D}_{I}\Delta {\hat{I}}+\delta {\hat{E}}-(\mu +d+\gamma ){\hat{I}}, \\ \dfrac{\partial {\hat{E}}}{\partial \pmb n}=\dfrac{\partial {\hat{I}}}{\partial \pmb n}=0, \\ \end{array}\right. \end{aligned}$$

(3.8)

for $x\in {\overline{\Omega }}$ and $t\ge t_{0}$.

Since $s({\textbf{A}})<0$ (see Lemma 3.1), we can choose a $\varepsilon _{0}$ small such that $s({\textbf{A}}_{\varepsilon _{0}})<0$, where

$$\begin{aligned} {\textbf{A}}_{\varepsilon _{0}}= \begin{pmatrix} D_{E}\Delta +{a}_{1}{\widetilde{\beta }}_{1}(x)({S}^{*}+\varepsilon _{0})-(\mu +\delta ) &{}\quad {a}_{2}{\widetilde{\beta }}_{2}(x) ({S}^{*}+ \varepsilon _{0}) \\ \delta &{}\quad D_{I}\Delta -(\mu +d+\gamma ) \end{pmatrix}. \end{aligned}$$

Then we can find a corresponding eigenvector $(\psi _{2}^{\varepsilon _{0}}(x),\psi _{3}^{\varepsilon _{0}}(x))$.

For each $\pmb \phi \in X^{+}$, there exists a $\varrho >0$ such that

$$\begin{aligned} ({\hat{E}}(x,t_{0};\pmb \phi ),{\hat{I}}(x,t_{0};\pmb \phi ))\le \varrho (\psi _{2}^{\varepsilon _{0}}(x),\psi _{3}^{\varepsilon _{0}}(x)). \end{aligned}$$

By the comparison principle, we have

$$\begin{aligned} (E(x,t;\pmb \phi ),I(x,t;\pmb \phi ))\le \varrho e^{s({\textbf{A}}_{\varepsilon _{0}})(t-t_{0})}(\psi _{2}^{\varepsilon _{0}}(x),\psi _{3}^{\varepsilon _{0}}(x)) \end{aligned}$$

for all $t>t_{0}$.

Therefore, we have $(E(x,t),I(x,t))\rightarrow (0,0)$ as $t \rightarrow \infty$ uniformly for $x\in {{\overline{\Omega }}}$. In addition, since $S^{*}$ is the steady-state solution of the system (3.1), we obtain $S(x,t)\rightarrow S^{*}(x)$ uniformly for $x\in {{\overline{\Omega }}}$, and by the asymptotic equation from the fourth equation of the system (2.1), we have $\lim _{t\rightarrow \infty }{R(x,t)=0}$. Hence, $\lim _{t\rightarrow \infty }{\pmb {U}(x,t;\pmb \phi )=(S^{*},0,0,0)}$ uniformly for $x\in {{\overline{\Omega }}}$. $\square$

Next, we discuss the case ${\mathcal {R}}_{0}>1$. First, we need the following result:

Lemma 3.4

Let $\pmb {U}(\cdot ,t;\pmb \phi )$ be the solution of system (2.1)–(2.3) with $\pmb {U_{0}}=\pmb \phi \in X^{+}$. If there exists some $t^{*}\ge 0$ such that $(E(x,t^{*};\pmb \phi ),I(x,t^{*};\pmb \phi )) \not \equiv (0,0)$, then $U_{i}(x,t;\pmb \phi )>0~(1\le i\le 4)$ for all $t>t^{*}$ and $x\in {{\overline{\Omega }}}$. Moreover, if there exists a $\zeta ^{*}>0$ such that $\liminf _{t\rightarrow \infty }{~E(\cdot ,t;\pmb \phi )\ge \zeta ^{*}}$ and $\liminf _{t\rightarrow \infty }{~I(\cdot ,t;\pmb \phi )\ge \zeta ^{*}}$, then there exists a $\zeta \in (0,\zeta ^{*})$ such that $\liminf _{t\rightarrow \infty }{~U_{i}(\cdot ,t;\pmb \phi )\ge \zeta }~(1\le i\le 4)$.

Proof

For a given $\pmb \phi \in X^{+}$, since $E(x,t;\pmb \phi )$ and $I(x,t;\pmb \phi )$ in system (2.1) is uniformly bounded, we know that for $E(x,t;\pmb \phi )$ and $I(x,t;\pmb \phi )$, there exists a constant $m=m(\pmb \phi )>0$ and $n=n(\pmb \phi )>0$ such that $E(x,t;\pmb \phi )<m$ and $I(x,t;\pmb \phi )<n$ for all $t>0$ and $x\in {{\overline{\Omega }}}$. Let ${\overline{S}}(x,t;{{\overline{\phi }}})$ be the solution of

$$\begin{aligned} \left\{ \begin{array}{ll} \dfrac{\partial {\overline{S}}}{\partial t}=D_{S}\Delta {\overline{S}}+\Lambda -(a_{1}{\widetilde{\beta }}_{1}(x)m+a_{2}{\widetilde{\beta }}_{2}(x)n+\mu ){\overline{S}},&{}\quad {x}\in \Omega ,t>0,\\ \ {\overline{S}}(x,0)={{\overline{\phi }}}(x)\le \phi _{1},&{}\quad {x}\in \Omega ,\\ \dfrac{\partial {\overline{S}}}{\partial \pmb n}=0,&{}\quad {x}\in \partial \Omega ,t>0. \\ \end{array}\right. \end{aligned}$$

(3.9)

It is easy to see $S(x,t;\pmb \phi ) \ge {\overline{S}}(x,t;{{\overline{\phi }}})$, $x\in {{\overline{\Omega }}}$. Let ${\overline{S}}^{*}(x;{{\overline{\phi }}})$ be the globally attractive positive equilibrium of system (3.9), then by the comparison principle in [27, Theorem 5.1.1], we have

$$\begin{aligned} \underset{t\rightarrow \infty }{\liminf }{~S(x,t;\pmb \phi )\ge \zeta _{1}}, \end{aligned}$$

where $\zeta _{1}:=\min \nolimits _{x\in {{\overline{\Omega }}}}{~{\overline{S}}^{*}(x;{{\overline{\phi }}})}= \min \nolimits _{x\in {{\overline{\Omega }}}}\left\{ \dfrac{\Lambda }{a_{1}{\widetilde{\beta }}_{1}(x)m+a_{2}{\widetilde{\beta }}_{2}(x)n+\mu }\right\} >0$.

We consider the following system:

$$\begin{aligned} \left\{ \begin{array}{ll} \dfrac{\partial \breve{E}}{\partial t}=D_{E}\Delta \breve{E}-(\mu +\delta )\breve{E},&{}\quad x\in \Omega ,t>0, \\ \dfrac{\partial \breve{I}}{\partial t}={D}_{I}\Delta \breve{I}-(\mu +d+\gamma )\breve{I},&{}\quad x\in \Omega ,t>0. \\ \dfrac{\partial \breve{E}}{\partial \pmb n}=\dfrac{\partial \breve{I}}{\partial \pmb n}=0,&{}\quad x\in \partial \Omega ,t>0. \\ \end{array}\right. \end{aligned}$$

(3.10)

From the comparison principle in [27, Theorem 5.1.1], we have

$$\begin{aligned} (E(x,t),I(x,t))\ge (\breve{E}(x,t),\breve{I}(x,t)),~x\in \Omega ,t>0. \end{aligned}$$

By the strong maximum principle (see [27, Theorem 7.2.1]) and Hopf Lemma (see [34, Lemma 2.1.1]), together with $(E(x,t^{*};\pmb \phi ),I(x,t^{*};\pmb \phi ))\not \equiv (0,0)$, we have $E(x,t;\pmb \phi )>0$ and $I(x,t;\pmb \phi )>0$ for all $t>t^{*}$.

Notice that when $t>t^{*}$,

$$\begin{aligned} \dfrac{\partial R}{\partial t}=D_{R}\Delta R+\gamma I-\mu R>D_{R}\Delta R-\mu R, \end{aligned}$$

(3.11)

it immediately follows that $R(x,t;\pmb \phi )>0$ for all $t>t^{*}$ and $x\in {{\overline{\Omega }}}$. Since there exists a $\zeta ^{*}>0$ such that $\liminf \nolimits _{t\rightarrow \infty }{~E(x,t;\pmb \phi )\ge \zeta ^{*}}$ and $\liminf _{t\rightarrow \infty } {I(x,t;\pmb \phi )\ge \zeta ^{*}}$, we can find a sufficiently large $t_{1}>0$ such that $I(x,t;\pmb \phi )>\dfrac{1}{2}\zeta ^{*}$ for all $t>t_{1}$. Together with (3.11) we have

$$\begin{aligned} \dfrac{\partial R}{\partial t} \ge D_{R}\Delta R+\dfrac{1}{2}\zeta ^{*}\gamma -\mu R. \end{aligned}$$

Therefore, there exists a $\zeta _{2}>0$ such that $\liminf \nolimits _{t\rightarrow \infty }{~R(x,t;\pmb \phi )\ge \zeta _{2}}$. Taking $\zeta =\min \{\zeta ^{*},\zeta _{1},\zeta _{2}\}$, we complete the proof. $\square$

Theorem 3.5

If ${\mathcal {R}}_{0}>1$, then system (2.1)–(2.3) have at least one positive solution, and there exists an $\eta >0$ such that for any $\pmb \phi \in X^{+}$ with $\phi _{2}(x)\not \equiv 0$ or $\phi _{3}(x)\not \equiv 0$, we have

$$\begin{aligned} \underset{t\rightarrow \infty }{\liminf }{~U_{i}(x,t;\pmb \phi )\ge \eta }, ~1\le i\le 4 \end{aligned}$$

uniformly for all $x\in {\overline{\Omega }}$.

Proof

In the case where ${\mathcal {R}}_{0}>1$, we have $s({\textbf{A}})>0$ (see Lemma 3.1). Let

$$\begin{aligned} {\mathbb {W}}_{0}:=\{\pmb \phi \in X^{+}: \phi _{2}(x)\not \equiv 0 \text { and } \phi _{3}(x)\not \equiv 0\} \end{aligned}$$

and

$$\begin{aligned} \partial {\mathbb {W}}_{0}:=X^{+}\backslash {\mathbb {W}}_{0}=\{\pmb \phi \in X^{+}: \phi _{2}(x)\equiv 0 \text { or } \phi _{3}(x)\equiv 0\}. \end{aligned}$$

Note that for any $\pmb \phi \in {\mathbb {W}}_{0}$, Lemma 3.4 implies that $E(x,t;\pmb \phi )>0$ and $I(x,t;\pmb \phi )>0$ for all $t>0$ and $x\in {\overline{\Omega }}$. It follows that $Q(t){\mathbb {W}}_{0}\subset {\mathbb {W}}_{0}$.

Next, we define

$$\begin{aligned} {\mathbb {M}}_{\partial }:=\{\pmb \phi \in \partial {\mathbb {W}}_{0}: Q(t)\pmb \phi \in \partial {\mathbb {W}}_{0}, ~\forall t\ge 0\}. \end{aligned}$$

Let $\omega (\pmb \phi )$ be the omega limit set of the orbit $o^{+}=\{Q(t)\pmb \phi :\forall t\ge 0 \}$ and let $M=(S^{*},0,0,0)$, then $Q(t)(M)=M$.

Next, we prove the theorem by two claims.

Claim 1. M is globally stable in ${\mathbb {M}}_{\partial }$ in the sense that M is globally attractive and locally Lyapunov stable in ${\mathbb {M}}_{\partial }$.

Let ${\mathbb {M}}_{0}=\{\pmb \phi \in X^{+}: \phi _{2}(x)\equiv 0$ and $\phi _{3}(x)\equiv 0\}$. For any $\pmb \phi \in {\mathbb {M}}_{0}$, we have $E(\cdot ,t;\pmb \phi )=[Q(t)\pmb \phi (\cdot )]_{2}=0$ and $I(\cdot ,t;\pmb \phi )=[Q(t)\pmb \phi (\cdot )]_{3}=0$ for all $t\ge 0$. It implies $\pmb \phi \in {\mathbb {M}}_{\partial }$, and hence, ${\mathbb {M}}_{0}\subset {\mathbb {M}}_{\partial }$. On the other hand, for any $\pmb \phi \in {\mathbb {M}}_{\partial }$, we obtain from Lemma 3.4 that $(\phi _{2}(\cdot ),\phi _{3}(\cdot ))\equiv (0,0)$, and hence $\pmb \phi \in {\mathbb {M}}_{0}$, which means that ${\mathbb {M}}_{\partial }\subset {\mathbb {M}}_{0}$. It then follows that ${\mathbb {M}}_{\partial }={\mathbb {M}}_{0}$. In order to prove the global stability of M in ${\mathbb {M}}_{\partial }$, we first show that for any $\pmb \phi \in {\mathbb {M}}_{\partial }$, the omega limit set $\omega (\pmb \phi )=M$. Since ${\mathbb {M}}_{\partial }={\mathbb {M}}_{0}$, we have $E(\cdot ,t;\pmb \phi )=0$ and $I(\cdot ,t;\pmb \phi )=0$ for any $\pmb \phi \in {\mathbb {M}}_{0}$ and $t\ge 0$. Thus, $S(x,t;\pmb \phi )$ and $R(x,t;\pmb \phi )$ satisfy

$$\begin{aligned} \left\{ \begin{array}{ll} \dfrac{\partial S}{\partial t}={{D}_{S}}\Delta S+\Lambda -\mu S,&{}\quad x\in \Omega ,t>0, \\ \dfrac{\partial R}{\partial t}={{D}_{R}}\Delta R-\mu R,&{}\quad x\in \Omega ,t>0,\\ \dfrac{\partial S}{\partial \pmb n}=\dfrac{\partial R}{\partial \pmb n}=0,&{}\quad x\in \partial \Omega ,t>0.\\ \end{array}\right. \end{aligned}$$

(3.12)

Obviously, $\lim \nolimits _{t\rightarrow \infty }{R(x,t;\pmb \phi )}=0$ uniformly for $x\in {\overline{\Omega }}$. For autonomous system (3.12), by limiting system arguments, we can easily obtain $\lim \nolimits _{t\rightarrow \infty }{S(x,t;\pmb \phi )}=S^{*}$ uniformly for $x\in {\overline{\Omega }}$, and hence, $\omega (\pmb \phi )=M$. This shows that M is globally stable in ${\mathbb {M}}_{\partial }$. By [29, Lemma 2.2.1], M is locally Lyapunov stable in ${\mathbb {M}}_{\partial }$. This proves Claim 1.

We consider the following system with a parameter $\eta ^{*}>0$:

$$\begin{aligned} \left\{ \begin{array}{l} \dfrac{\partial w_{1}^{\eta ^{*}}}{\partial t}=D_{E}\Delta w_{1}^{\eta ^{*}}+\beta _{1}(\eta ^{*},x) (S^{*}-\eta ^{*})w_{1}^{\eta ^{*}}+\beta _{2}(\eta ^{*},x)(S^{*}-\eta ^{*})w_{2}^{\eta ^{*}} -(\mu +\delta )w_{1}^{\eta ^{*}}, \\ \dfrac{\partial w_{2}^{\eta ^{*}}}{\partial t}=D_{I}\Delta w_{2}^{\eta ^{*}}+\delta w_{1}^{\eta ^{*}}-(\mu +d+\gamma )w_{2}^{\eta ^{*}}, \\ \dfrac{\partial w_{1}^{\eta ^{*}}}{\partial \pmb n}=\dfrac{\partial w_{2}^{\eta ^{*}}}{\partial \pmb n}=0, \\ \end{array}\right. \end{aligned}$$

(3.13)

for $x\in \Omega$ and $t>0$, where $\beta _{1}(\eta ^{*},x)=(a_{1}-b_{1}m_{1}(\eta ^{*})){\widetilde{\beta }}_{1}(x)$ and $\beta _{2}(\eta ^{*},x)=(a_{2}-b_{2}m_{2}(\eta ^{*})){\widetilde{\beta }}_{2}(x)$. For any $\pmb \psi \in C(\Omega ,{\mathbb {R}}^{2})$, let $\pmb {w^{\eta ^{*}}}(x,t,\pmb \psi )=(w_{1}^{\eta ^{*}}(x,t,\pmb \psi ),w_{2}^{\eta ^{*}}(x,t,\pmb \psi ))$ be the unique solution of system (3.13) with initial value $\pmb \psi$. Let $T_{\eta ^{*}}(t):C(\Omega ,{\mathbb {R}}^{2})\rightarrow C(\Omega ,{\mathbb {R}}^{2})$ be the semigroup associated to the problem (3.13), and define ${\textbf{A}}_{\eta ^{*}}$ is the generator of $T_{\eta ^{*}}(t)$. Let $s({\textbf{A}}_{\eta ^{*}})$ is the spectral bound of ${\textbf{A}}_{\eta ^{*}}$. It is easy to find that $\underset{\eta ^{*}\rightarrow 0}{\lim }s({\textbf{A}}_{\eta ^{*}})=s({\textbf{A}})$, then we can fix a sufficiently small number $\eta ^{*}>0$ such that $\eta ^{*}<S^{*}$ and $s({\textbf{A}}_{\eta ^{*}})>0$. By the continuous dependence of solutions on the initial value, there exists $\eta ^{\prime }>0$ such that for any $\pmb \phi$ with $\Vert \pmb \phi -M\Vert _{X}\le \eta ^{\prime }$, we have $\Vert Q(t)\pmb \phi -M\Vert _{X}<\eta ^{*}$ for all $t\ge 0$.

Claim 2. M is a uniform weak repeller for ${\mathbb {W}}_{0}$ in the sense that

$$\begin{aligned} \underset{t\rightarrow \infty }{\limsup }\Vert Q(t)\pmb \phi -M\Vert _{X}\ge \eta ^{*}, ~\forall \pmb \phi \in {\mathbb {W}}_{0}, \end{aligned}$$

where $\eta ^{*}$ is a sufficiently small positive number and $\eta ^{*}<S^{*}$.

Suppose, by contradiction, there exists $\pmb {\phi ^{*}}\in {\mathbb {W}}_{0}$ such that $\underset{t\rightarrow \infty }{\limsup }\Vert Q(t)\pmb {\phi ^{*}}-M\Vert _{X}<\eta ^{*}$. Then there exists a sufficiently large $t^{\prime }>0$ such that

$$\begin{aligned} S(x,t;\pmb {\phi ^{*}})>S^{*}-\eta ^{*},~E(x,t;\pmb {\phi ^{*}})<\eta ^{*},~I(x,t;\pmb {\phi ^{*}})<\eta ^{*},~R(x,t;\pmb {\phi ^{*}})<\eta ^{*} \end{aligned}$$

for all $(x,t)\in {\overline{\Omega }}\times [t^{\prime },\infty ]$. Thus, when $t\ge t^{\prime }$, by (2.4)–(2.5), we know that $(E(x,t;\pmb {\phi ^{*}}),I(x,t;\pmb {\phi ^{*}}))$ of system (2.1) satisfies

$$\begin{aligned} \left\{ \begin{array}{l} \dfrac{\partial E}{\partial t}\ge D_{E}\Delta E+\beta _{1}(\eta ^{*},x)(S^{*}-\eta ^{*})E+\beta _{2}(\eta ^{*},x)(S^{*}-\eta ^{*})I -(\mu +\delta )E, \\ \dfrac{\partial I}{\partial t}=D_{I}\Delta I+\delta E-(\mu +d+\gamma )I, \\ \dfrac{\partial E}{\partial \pmb n}=\dfrac{\partial I}{\partial \pmb n}=0, \\ \end{array}\right. \end{aligned}$$

(3.14)

for $x\in {\overline{\Omega }}$ and $t\ge t^{\prime }$.

By Lemma 3.4, we have $E(x,t;\pmb {\phi ^{*}})>0$, $I(x,t;\pmb {\phi ^{*}})>0$ when $\pmb {\phi ^{*}}\in {\mathbb {W}}_{0}$. Then there exists a sufficiently small $\rho >0$ such that

$$\begin{aligned} (E(x,t^{\prime };\pmb {\phi ^{*}}),I(x,t^{\prime };\pmb {\phi ^{*}})) \ge \rho \pmb {w^{\eta ^{*}}}(x,t^{\prime }), \end{aligned}$$

where $\pmb {w^{\eta ^{*}}}(x,t)=e^{s(\mathbf {A_{\eta ^{*}}})t}\pmb {w_{\eta ^{*}}^{*}}(x,t)$, and $\pmb {w_{\eta ^{*}}^{*}}(x,t)$ is a positive function such that $\pmb {w^{\eta ^{*}}}(x,t)$ is a solution of system (3.13). By the comparison principle, we have

$$\begin{aligned} (E(x,t;\pmb {\phi ^{*}}),I(x,t;\pmb {\phi ^{*}}))\ge \rho e^{s(\mathbf {A_{\eta ^{*}}})(t-t^{\prime })}\pmb {w_{\eta ^{*}}^{*}}(x,t) \end{aligned}$$

for all $t>t^{\prime }$.

In the case where ${\mathcal {R}}_{0}>1$, i.e., $s({\textbf{A}})>0$, since $\lim \nolimits _{\eta ^{*}\rightarrow 0} s({\textbf{A}}_{\eta ^{*}}) =s({\textbf{A}})$ and $\eta ^{*}$ is sufficiently small, we have $s({\textbf{A}}_{\eta ^{*}})>0$. Therefore, it is easy to see that

$$\begin{aligned} \underset{t\rightarrow \infty }{\lim }{E(x,t;\pmb {\phi ^{*}})}=\infty , ~\underset{t\rightarrow \infty }{\lim }{I(x,t;\pmb {\phi ^{*}})}=\infty . \end{aligned}$$

This leads to a contradiction.

Claim 2 indicates that M is an isolated invariant set for Q(t) in $X^{+}$, and $W^{S}(M)\cap {\mathbb {W}}_{0}=\emptyset$, where $W^{S}(M)$ is the stable manifold of M for Q(t). It then follows from [29, Theorem 1.3.1 and Remark 1.3.1] that Q(t) is uniformly persistent with respect to $({\mathbb {W}}_{0},\partial {\mathbb {W}}_{0})$. Moreover, [35, Theorem 4.5] implies that there exists a global attractor $A_{0}$ in $Q(t):{\mathbb {W}}_{0}\rightarrow {\mathbb {W}}_{0}$ and Q(t) has a fixed point $\pmb {\phi _{0}}$ in ${\mathbb {W}}_{0}$. Clearly, $\pmb {U}(\cdot ,t;\pmb {\phi _{0}})=(S(\cdot ,t;\pmb {\phi _{0}}),E(\cdot ,t;\pmb {\phi _{0}}), I(\cdot ,t;\pmb {\phi _{0}}),R(\cdot ,t;\pmb {\phi _{0}}))$ is a solution of system (2.1)–(2.3), and it is strictly positive by Lemma 3.4. Since $A_{0}=Q(t)A_{0}$, we have $\phi _{2}(\cdot )>0$ and $\phi _{3}(\cdot )>0$ for any $\pmb \phi \in A_{0}$. Let $B_{0}:=\cup _{t\in [0,\infty )} Q(t)A_{0}$. Then $B_{0}\subset {\mathbb {W}}_{0}$ and $\lim \nolimits _{t\rightarrow \infty } d(Q(t)\pmb \phi ,B_{0})=0$ for any $\pmb \phi \in {\mathbb {W}}_{0}$, where d is the norm-induced distance in X. According to [36], we define a continuous function $p:X^{+}\rightarrow [0,\infty )$ by

$$\begin{aligned} p(\pmb \phi )=\min \left\{ \underset{x\in {\overline{\Omega }}}{\min }\phi _{2}(x), \underset{x\in {\overline{\Omega }}}{\min }\phi _{3}(x)\right\} , ~\pmb \phi =(\phi _{1}, \phi _{2}, \phi _{3}, \phi _{4})\in X^{+}. \end{aligned}$$

Since $B_{0}$ is a compact subset of ${\mathbb {W}}_{0}$, it follows that $\inf \nolimits _{\pmb \phi \in B_{0}}{~p(\pmb \phi )} =\min \nolimits _{\pmb \phi \in B_{0}}{~p(\pmb \phi )}>0$. Therefore, there exists an $\eta _{0}^{*}>0$ such that

$$\begin{aligned} \underset{t\rightarrow \infty }{\liminf }{~p(Q(t)\pmb \phi )}=\underset{t\rightarrow \infty }{\liminf }\left\{ \underset{x\in {\overline{\Omega }}}{\min }E(x,t;\pmb \phi ), ~\underset{x\in {\overline{\Omega }}}{\min }I(x,t;\pmb \phi )\right\} \ge \eta _{0}^{*} \end{aligned}$$

for any $\pmb \phi \in {\mathbb {W}}_{0}$. It follows from Lemma 3.4 that there exists an $\eta \in (0,\eta _{0}^{*})$ such that

$$\begin{aligned} \underset{t\rightarrow \infty }{\liminf }{~U_{i}(x,t;\pmb \phi )}\ge \eta , ~\forall \pmb \phi \in {\mathbb {W}}_{0}, ~1\le i\le 4. \end{aligned}$$

Based on the above discussion, we complete the proof. $\square$

In order to discuss the case where ${\mathcal {R}}_{0}=1$, we need the following results.

Lemma 3.6

If ${\mathcal {R}}_{0}=1$, $E_{f}$ is locally stable.

Proof

Let $\epsilon >0$ be given. Suppose $\delta ^{*}>0$ and let $\pmb \phi \in X^{+}$ with $\Vert \pmb \phi -E_{f}\Vert _{X}\le \delta ^{*}$.

Define

$$\begin{aligned} z(x,t)=\dfrac{S(x,t)}{S^{*}}-1 \text { and } h(t)=\underset{x\in {\overline{\Omega }}}{\max }\{z(x,t),0\}. \end{aligned}$$

Noticing $D_{S}\Delta S^{*}+\Lambda -\mu S^{*}=0$ and by the first equation of system (2.1), we have

$$\begin{aligned} \dfrac{\partial z}{\partial t}-D_{S}\Delta z+\mu z=-\dfrac{\beta _{1}(E,x)SE+\beta _{2}(I,x)SI}{S^{*}}. \end{aligned}$$

Let ${{\widetilde{T}}}_{1}(t)$ be the positive semigroup generated by the operator $D_{S}\Delta -\mu$.

Then there exists $r>0$ such that $\Vert {{\widetilde{T}}}_{1}(t)\Vert \le K e^{-rt}$ for some $K>0$. Hence, we have

$$\begin{aligned} z(x,t)= {{\widetilde{T}}}_{1}(t) z(x,0)-\displaystyle \int _{0}^{t}{{{\widetilde{T}}}_{1}(t-s)\dfrac{\beta _{1}(E,x)SE+\beta _{2}(I,x)SI}{S^{*}}}ds, \end{aligned}$$

where $z(x,0)=\dfrac{S_{0}}{S^{*}}-1$. It then follows from the positivity of ${{\widetilde{T}}}_{1}(t)$ that

$$\begin{aligned} h(t)= & {} \underset{x\in {\overline{\Omega }}}{\max }\left\{ {\widetilde{T}}_{1}(t) z(x,0)-\displaystyle \int _{0}^{t}{{\widetilde{T}}_{1}(t-s)\dfrac{\beta _{1}(E,x)SE+\beta _{2}(I,x)SI}{S^{*}}}ds,0\right\} \\\le & {} \underset{x\in {\overline{\Omega }}}{\max }\{{\widetilde{T}}_{1}(t) z(x,0),0\}\\\le & {} \underset{x\in {\overline{\Omega }}}{\sup }\left\| \dfrac{S_{0}}{S^{*}}-1\right\| K e^{-rt}\\\le & {} \dfrac{\delta ^{*}K e^{-rt}}{S^{*}}.\\ \end{aligned}$$

Noticing that (E, I) satisfies

$$\begin{aligned} \left\{ \begin{array}{l} \dfrac{\partial E}{\partial t}={D}_{E}\Delta E+{\beta }_{1}(E,x){S}^{*}E +{\beta }_{2}(I,x){S}^{*}I\\ \qquad \qquad -(\mu +\delta )E +({\beta }_{1}(E,x)S^{*}E+{\beta }_{2}(I,x)S^{*}I)\left( \dfrac{S}{S^{*}}-1\right) , \\ \dfrac{\partial I}{\partial t}={{D}_{I}}\Delta I+\delta E-(\mu +d+\gamma )I, \\ \end{array}\right. \nonumber \\ \end{aligned}$$

(3.15)

for $x\in \Omega$ and $t>0$, we have

$$\begin{aligned} \begin{pmatrix} E(x,t) \\ I(x,t) \end{pmatrix}{} & {} =T(t) \begin{pmatrix} E(x,0) \\ I(x,0) \end{pmatrix}\nonumber \\{} & {} \qquad +\int _{0}^{t}{T(t-s)} \begin{pmatrix} ({{\beta }_{1}}(E,x)S^{*}E+{{\beta }_{2}}(I,x)S^{*}I)\left( \dfrac{S}{S^{*}}-1\right) \\ 0 \end{pmatrix}ds,\nonumber \\ \end{aligned}$$

(3.16)

where T(t) is the semigroup associated to the problem (3.4).

Since ${\mathcal {R}}_{0}=1$, i.e., $s({\textbf{A}})=0$, we have $\Vert T(t)\Vert \le K$ for $t\ge 0$ and some constant $K>0$, where K can be chosen as large as needed. By $h(t)\le \dfrac{\delta ^{*}K e^{-rt}}{S^{*}}$ and (2.4)–(2.5), we obtain

$$\begin{aligned}{} & {} \underset{x\in {\overline{\Omega }}}{\max }\{\Vert E(x,t)\Vert ,\Vert I(x,t)\Vert \}\\{} & {} \quad \le K\underset{x\in {\overline{\Omega }}}{\max }\{\Vert E_{0}\Vert ,\Vert I_{0}\Vert \} +K a_{1}\Vert {\widetilde{\beta }}_{1}\Vert \Vert S^{*}\Vert \int _{0}^{t}{{h(s)}\Vert E(s)\Vert }ds\\{} & {} \qquad +K a_{2}\Vert {\widetilde{\beta }}_{2}\Vert \Vert S^{*}\Vert \int _{0}^{t}{{h(s)}\Vert I(s)\Vert }ds\\{} & {} \quad \le K\delta ^{*}+K_{1}\delta ^{*}\int _{0}^{t}{e^{-rs}\Vert E(s)\Vert }ds+K_{2}\delta ^{*}\int _{0}^{t}{e^{-rs}\Vert I(s)\Vert }ds,\\ \end{aligned}$$

where $K_{1}=a_{1} K^{2}\Vert {\widetilde{\beta }}_{1}\Vert$, $K_{2}=a_{2} K^{2}\Vert {\widetilde{\beta }}_{2}\Vert$. Therefore, we have

$$\begin{aligned} \Vert E(x,t)\Vert +\Vert I(x,t)\Vert \le 2 K\delta ^{*}+2\delta ^{*}K^{*}\displaystyle \int _{0}^{t}{e^{-rs}(\Vert E(s)\Vert +\Vert I(s)\Vert )}ds, \end{aligned}$$

where $K^{*}=\max \{K_{1},K_{2}\}$.

By Gronwall’s inequality, we obtain

$$\begin{aligned} \Vert E(x,t)\Vert +\Vert I(x,t)\Vert \le 2 K\delta ^{*}e^{\frac{2\delta ^{*}K^{*}}{r}}. \end{aligned}$$

Moveover, we have

$$\begin{aligned} \dfrac{\partial S}{\partial t}\ge D_{S}\Delta S+\Lambda -\mu S-2 K\delta ^{*}e^{\frac{2\delta ^{*}K^{*}}{r}}{\beta ^{+}}S, \end{aligned}$$

where ${\beta ^{+}}=\max \{a_{1}{\widetilde{\beta }}_{1}(x), a_{2}{\widetilde{\beta }}_{2}(x)\}$.

Let ${\widehat{S}}$ be the solution of the problem

$$\begin{aligned} \left\{ \begin{array}{ll} \dfrac{\partial {\widehat{S}}}{\partial t}= D_{S}\Delta {\widehat{S}}+\Lambda -\mu {\widehat{S}}- 2K\delta ^{*}e^{\frac{2\delta ^{*}K^{*}}{r}}{\beta ^{+}}{\widehat{S}},&{}\quad (x,t)\in \Omega \times (0,\infty ),\\ \dfrac{\partial {\widehat{S}}}{\partial \pmb n}=0, &{}\quad (x,t)\in \partial \Omega \times (0,\infty ),\\ {\widehat{S}}(x,0)=S_{0}(x),&{}\quad x\in \Omega . \end{array}\right. \nonumber \\ \end{aligned}$$

(3.17)

By the comparison principle, we have $S(x,t)\ge {\widehat{S}}(x,t)$ for all $x \in {{\overline{\Omega }}}$ and $t \ge 0$. Let ${\widehat{U}}$ be the positive steady state of system (3.17) and $w = {\widehat{S}}-{\widehat{U}}$. Then w satisfies

$$\begin{aligned} \left\{ \begin{array}{ll} \dfrac{\partial w}{\partial t}= D_{S}\Delta w -\mu w-2 K\delta ^{*}e^{\frac{2\delta ^{*}K^{*}}{r}}{\beta ^{+}}w,&{}\quad (x,t)\in \Omega \times (0,\infty ),\\ \dfrac{\partial w}{\partial \pmb n}=0,&{}\quad (x,t)\in \partial \Omega \times (0,\infty ),\\ w(x,0)=S_{0}-{\widehat{U}},&{}\quad x\in \Omega . \end{array}\right. \nonumber \\ \end{aligned}$$

(3.18)

We can choose a K large such that $\Vert {{\widetilde{T}}}_{1}(t)\Vert \le K e^{-\mu t}$. By (3.18), we have

$$\begin{aligned} w(x,t)={{\widetilde{T}}}_{1}(t)(S_{0}-{\widehat{U}})-\displaystyle \int _{0}^{t} {{\widetilde{T}}}_{1}(t-s)2 K\delta ^{*}e^{\frac{2\delta ^{*}K^{*}}{r}}{\beta ^{+}}w(x,s)ds. \end{aligned}$$

Moreover, we have

$$\begin{aligned} \Vert w(x,t)\Vert \le K e^{-\mu t}\Vert S_{0}-{\widehat{U}}\Vert +\displaystyle \int _{0}^{t}K e^{-\mu (t-s)}2 K\delta ^{*}e^{\frac{2\delta ^{*}K^{*}}{r}}\Vert {\beta ^{+}}\Vert \Vert w(x,s)\Vert ds. \end{aligned}$$

Let $k=2K^{2}\delta ^{*}e^{\frac{2\delta ^{*}K^{*}}{r}}\Vert {\beta ^{+}}\Vert$. Then, applying the Gronwall’s inequality to the above leads to

$$\begin{aligned} \Vert {\widehat{S}}(x,t)-{\widehat{U}}\Vert = \Vert w(x,t)\Vert \le K\Vert S_{0}-{\widehat{U}}\Vert e^{kt-\mu t}. \end{aligned}$$

Choosing a $\delta ^{*}>0$ sufficiently small such that $k<\dfrac{\mu }{2}$, then

$$\begin{aligned} \Vert {\widehat{S}}(x,t)-{\widehat{U}}\Vert \le K\Vert S_{0}-{\widehat{U}}\Vert e^{-\frac{\mu t}{2}}. \end{aligned}$$

(3.19)

Now by (3.19), we have

$$\begin{aligned} S(x,t)-S^{*}\ge & {} {\widehat{S}}(x,t) -S^{*}={\widehat{S}}(x,t)-{\widehat{U}}+{\widehat{U}}-S^{*}\\\ge & {} -K \Vert S_{0}-{\widehat{U}}\Vert e^{-\frac{\mu t}{2}}+{\widehat{U}}-S^{*}\\\ge & {} -K(\Vert S_{0}-S^{*}\Vert +\Vert S^{*}-{\widehat{U}}\Vert )-\Vert {\widehat{U}}-S^{*}\Vert \\\ge & {} -K\delta ^{*}-(K+1)\Vert {\widehat{U}}-S^{*}\Vert . \end{aligned}$$

On the other hand, noticing that $h(t)\le \dfrac{\delta ^{*}K e^{-rt}}{S^{*}}\le \dfrac{\delta ^{*}K}{S^{*}}$, we have

$$\begin{aligned} S(x,t)-S^{*}=S^{*}\left( \dfrac{S(x,t)}{S^{*}}-1\right) \le \Vert S^{*}\Vert h(t)\le \delta ^{*}K. \end{aligned}$$

(3.20)

Therefore, we obtain

$$\begin{aligned} \Vert S(x,t)-S^{*}\Vert \le K\delta ^{*}+(K+1)\Vert {\widehat{U}}-S^{*}\Vert . \end{aligned}$$

(3.21)

Finally, noticing that $\lim \nolimits _{\delta ^{*}\rightarrow 0} {\widehat{U}}=S^{*}$, we can choose a $\delta ^{*}>0$ small such that

$$\begin{aligned} \Vert S(x,t)-S^{*}\Vert , ~\Vert E(x,t)\Vert , ~\Vert I(x,t)\Vert \le \epsilon \end{aligned}$$

for all $t>0$, and by the asymptotic equation from the fourth equation of system (2.1), we have $\Vert R(x,t)\Vert \le \epsilon$. $\square$

Lemma 3.7

If ${\mathcal {R}}_{0}=1$, $E_{f}$ is globally attractive.

Proof

By Theorem 2.1, Q(t) has a global attractor $\sigma$. Define

$$\begin{aligned} \partial {\mathbb {X}}=\{({\check{S}},{\check{E}},{\check{I}},{\check{R}})\in X^{+}: {\check{E}}={\check{I}}=0\}. \end{aligned}$$

Next, we prove the lemma by two claims.

Claim 1. For any initial value $\pmb {U_{0}}=\pmb \phi =(\phi _{1},\phi _{2},\phi _{3},\phi _{4})\in \sigma$, the omega limit set $\omega (\pmb \phi )\subset \partial {\mathbb {X}}$.

If $E_{0}=I_{0}=0$, the claim is obviously valid. So we can assume that either $E_{0}\ne 0$ or $I_{0}\ne 0$. By Lemma 3.4, we have $U_{i}(x,t)>0~(1\le i\le 4)$ for all $x\in {\overline{\Omega }}$ and $t>0$. Moreover, S(x, t) satisfies

$$\begin{aligned} \left\{ \begin{array}{ll} \dfrac{\partial S}{\partial t}< D_{S}\Delta S+\Lambda -\mu S,&{}\quad x\in \Omega ,t>0,\\ \dfrac{\partial S}{\partial \pmb n}=0,&{}\quad x\in \partial \Omega ,t>0,\\ \end{array}\right. \end{aligned}$$

(3.22)

Noticing (3.2), we must have $S(x,0)\le S^{*}$. Then, by the comparison principle, we must have $S(x,t)\le S^{*}$ for all $x\in {\overline{\Omega }}$ and $t>0$.

By Lemma 3.2, eigenvalue problem (3.7) has a positive eigenvector $(\varphi _{2},\varphi _{3})$. We define

$$\begin{aligned} \xi (t;\pmb {\phi }):=\inf \left\{ \widetilde{\xi }\in {\mathbb {R}}:E(x,t)\le \widetilde{\xi }\varphi _{2} \text { and } I(x,t)\le \widetilde{\xi }\varphi _{3}\right\} . \end{aligned}$$

It is easy to see $\xi (t;\pmb {\phi })>0$ for all $t>0$. We claim that $\xi (t;\pmb {\phi })$ is strictly decreasing with respect to t. To prove this, fix ${\widetilde{t}}_{0}>0$ and let ${\widetilde{E}}(x,t)=\xi ({\widetilde{t}}_{0};\pmb {\phi })\varphi _{2}$ and ${\widetilde{I}}(x,t) =\xi ({\widetilde{t}}_{0};\pmb {\phi })\varphi _{3}$ for $t \ge {\widetilde{t}}_{0}$. By $S(x,t)\le S^{*}$ and (3.7), we have

$$\begin{aligned} \left\{ \begin{array}{ll} \dfrac{\partial {\widetilde{E}}}{\partial t}>D_{E}\Delta {\widetilde{E}}+\beta _{1}({\widetilde{E}},x)S{\widetilde{E}}+\beta _{2}({\widetilde{I}},x)S{\widetilde{I}}-(\mu +\delta ){\widetilde{E}}, &{}\quad x\in \Omega ,t>{\widetilde{t}}_{0},\\ \dfrac{\partial {\widetilde{I}}}{\partial t}=D_{I}\Delta {\widetilde{I}}+\delta {\widetilde{E}}-(\mu +d+\gamma ){\widetilde{I}},&{}\quad x\in \Omega ,t>{\widetilde{t}}_{0},\\ \dfrac{\partial {\widetilde{E}}}{\partial \pmb n}=\dfrac{\partial {\widetilde{I}}}{\partial \pmb n}=0,&{}\quad x\in \partial \Omega ,t>{\widetilde{t}}_{0},\\ {\widetilde{E}}(x,{\widetilde{t}}_{0})\ge E(x,{\widetilde{t}}_{0}),{\widetilde{I}}(x,{\widetilde{t}}_{0})\ge I(x,{\widetilde{t}}_{0}),&{}\quad x\in \Omega . \end{array}\right. \nonumber \\ \end{aligned}$$

(3.23)

By the comparison principle, we obtain $( {\widetilde{E}}(x,t),{\widetilde{I}}(x,t))\ge (E(x,t),I(x,t))$ for all $x \in {\overline{\Omega }}$ and $t \ge {\widetilde{t}}_{0}$. Then by system (3.23) and the strong maximum principle, we obtain

$$\begin{aligned} \xi ({\widetilde{t}}_{0};\pmb {\phi })\varphi _{2}={\widetilde{E}}(x,t)>E(x,t) \text { and } \xi ({\widetilde{t}}_{0};\pmb {\phi })\varphi _{3}={\widetilde{I}}(x,t)>I(x,t) \end{aligned}$$

for all $x\in {\overline{\Omega }}$ and $t>{\widetilde{t}}_{0}$. Since ${\widetilde{t}}_{0}>0$ is arbitrary, $\xi (t;\pmb {\phi })$ is strictly decreasing. Moreover, we have $\lim _{t\rightarrow \infty }~\xi (t;\pmb {\phi })=\xi ^{*}=0$ (see [37, Proof of Theorem 1.1(a)]).

Let $\pmb u=(u_{1},u_{2},u_{3},u_{4})\in \omega (\pmb \phi )$, then there exists a sequence $\{t_{k}\}$ with $t_{k}\rightarrow \infty$ such that $\lim _{t_{k}\rightarrow \infty }Q(t_{k})\pmb \phi =\pmb u$. Since $\lim _{t_{k}\rightarrow \infty }Q(t+t_{k})\pmb \phi =Q(t)\lim _{t_{k}\rightarrow \infty }Q(t_{k})\pmb \phi =Q(t)\pmb u$, we must have $\xi (t;\pmb u)=\xi ^{*}$ for all $t\ge 0$. If $u_{2} \ne 0$ or $u_{3} \ne 0$, we can repeat the previous arguments to show that $\xi (t;\pmb u)$ is strictly decreasing, which contradicts that $\xi (t;\pmb u)=\xi ^{*}$. Hence, $(E(x,t),I(x,t))\rightarrow (0,0)$ as $t\rightarrow \infty$. This proves Claim 1.

Claim 2. $\sigma =\{E_{f}\}$

Since $\{E_{f}\}$ is globally attractive for system (2.1)–(2.3) in $\partial {\mathbb {X}}$, and $\{E_{f}\}$ generates the only compact invariant subset of system (2.1)–(2.3) in $\partial {\mathbb {X}}$. Therefore, for any $\pmb \phi \in \sigma$, we conclude that $\omega (\pmb \phi )=\{E_{f}\}$. On the other hand, we have $\sigma =\{E_{f}\}$ in that the global attractor $\sigma$ is compactly invariant in $X^{+}$. By Claim 1 and Claim 2, we complete the proof. $\square$

By Lemmas 3.6 and 3.7, we immediately obtain the following theorem:

Theorem 3.8

If ${\mathcal {R}}_{0}=1$, $E_{f}$ is globally asymptotically stable.

4 Numerical Simulations

In this section, we present numerical simulations to illustrate the effects of the human behavior changes on the spread of COVID-19. For convenience, we take the domain ${{\overline{\Omega }}}$ to be $[0,3\pi ]$, and set $D_{S}=1$, $D_{E}=1$, $D_{I}=0.2$ and $D_{R}=0.5$ to indicate humans’ mobility under the influence of COVID-19. We assume the direct transmission contribution rates of E and I to be ${\widetilde{\beta }}_{1}(x)=0.5+0.25\cos (2\pi x)$ and ${\widetilde{\beta }}_{2}(x)=0.4+0.15\cos (2\pi x)$ to reflect the direct transmission contribution rates of exposed and infected individuals with spatial heterogeneity. In addition, we consider the saturation functions $m_{1}(E)=\dfrac{E}{E+M_{1}}$ and $m_{2}(I)=\dfrac{I}{I+M_{2}}$ as in [5] to describe the human behaviors. To verify the previous threshold dynamics in terms of ${\mathcal {R}}_{0}$, the parameter values are chosen as $\Lambda =100$, $\mu =0.01$, $\delta =0.14$, $d=0.02$, $\gamma =0.2$, $b_{i}=0.8a_{i} (i=1,2)$, $M_{1}=500$, $M_{2}=300$ and initial data $S_{0}=10,000$, $E_{0}=100$, $I_{0}=40$, $R_{0}=0$.

When we choose $a_{1}=4.6\times 10^{-5}$ and $a_{2}=1.9\times 10^{-5}$, we obtain ${\mathcal {R}}_{0}=2.87>1$. We find that the COVID-19 is uniformly persistent, which is shown in Fig. 2.

Fig. 2

The evolution of COVID-19 in humans when ${\mathcal {R}}_{0}=2.87>1$

If we reduce the direct contact rate $a_{1}$, $a_{2}$ to $7.3\times 10^{-6}$, $3.1\times 10^{-6}$, we obtain ${\mathcal {R}}_{0}=0.46<1$. Figure 3 shows that the disease-free equilibrium point $E_{f}$ is globally asymptotically stable, which indicates the spread of COVID-19 cannot be sustained.

Fig. 3

The evolution of COVID-19 in humans when ${\mathcal {R}}_{0}=0.46<1$

Finally, we observe the impact of human behavior changes on the spread of COVID-19. Figure 4 shows how human interventions affect the spread of COVID-19, where the red, green and blue curves represent the densities of exposed and infected individuals with no human behavior changes ($b_{i}= 0$, $i=1,2$), small behavior changes ($b_{i}= 0.8a_{i}$, $M_{1}=500$, $M_{2}=300$, $i=1,2$) and large behavior changes ($b_{i}= 0.8a_{i}$, $M_{1}=200$, $M_{2}=100$, $i=1,2$), respectively. We find that the curve trends of exposed and infected individuals are similar in the Fig. 4, which shows that human behavior changes have the same effect on exposed individuals and infected individuals. Moreover, we observe that the severest outbreaks occur in the early phase among the three situations mentioned above. These observations indicate that the human interventions may be a very effective control strategy not only in the early stage of the transmission, but also in the whole transmission process. The appropriate human behavior changes significantly reduce the density of exposed and infected individuals. However, Fig. 4 also tells us that we fail to eliminate COVID-19 by taking human interventions alone. Furthermore, we notice that the number of exposed is always more than that of infected by comparing the number of exposed individuals and infected individuals, so we need to pay more attention to the situations of exposed individuals.

Fig. 4

Impacts of human behavior on COVID-19 transmission at location x=$\pi$ (other parameters values are the same as those in Fig. 2)

5 Discussion

In this paper, we have proposed and analyzed a SEIR reaction–diffusion model that incorporates human behavior. We assume that people are well informed of the current situation of the COVID-19 outbreak through various social media, so they will take action to reduce contact with others by wearing masks and avoiding crowded places. The assumed contact rate functions represent the changes caused by human behavior, which can be used to observe the impact of human behavior on the whole transmission process of COVID-19.

Firstly, we apply the theory in [31] to derive the basic reproduction number ${\mathcal {R}}_{0}$. Next, with the help of the theories mentioned in [21] and [38], we prove the threshold-type result on the global dynamics in terms of ${\mathcal {R}}_{0}$: if ${\mathcal {R}}_{0}\le 1$, the disease-free equilibrium point $E_{f}$ is globally asymptotically stable, which indicates that COVID-19 cannot be sustained; if ${\mathcal {R}}_{0}>1$, COVID-19 will be persistent.

By numerical simulation, we show the effect of human behavior changes on the spread of COVID-19. Comparing the density of exposed and infected individuals under different behavioral changes in the Fig. 4, we notice that COVID-19 cannot be eliminated by taking human interventions alone. A mathematical explanation is that the terms $b_{1}$ and $b_{2}$ do not appear in the expression of ${\mathcal {R}}_{0}$, and hence, human behavior changes fail to be a key factor to determine whether COVID-19 persists or not. However, we find that human behavior changes play a positive role in lowering the level of infection during the whole transmission process of COVID-19 (from the early outbreak to the later stabilization). Furthermore, since the impact of human behavior changes on exposed and infected individuals is almost the same, we need to pay more attention to the exposed individuals.

The human behavior in response to the epidemics is assumed to be “rational” in this paper. For example, the government can block epidemic areas. People in epidemic regions should take protective measures, such as practicing personal hygiene and wearing masks, and reduce contact with infected individuals. However, we may obtain some false information on the details of the epidemics, which may lead to inappropriate responses. In this case, the contact rate functions $\beta _{1}(t,x)$ and $\beta _{2}(t,x)$ in our model will not be a simple monotone function. During the outbreak of diseases, human behavior is more likely to be affected by the total number of infections and deaths than by the real-time number of infected individuals [39]. These factors are worthy of our consideration and analysis, but they are not reflected in this paper. Meanwhile, there are other limitations in our paper. For instance, the diffusion coefficients as well as several parameters in the model, can be regarded as spatial functions rather than constants, to obtain the information of spatial heterogeneity. We leave these problems for future studies.