Strong Resonance Bifurcations and State Feedback Control in a Discrete Prey-Predator Model with Harvesting Effect

Abstract

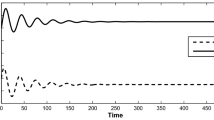
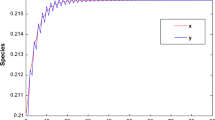
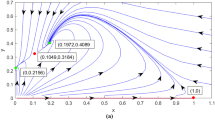
This paper investigates a discrete-time predator–prey model with predator harvesting. The stability analysis for different fixed points of the discretized model is shown briefly. In this study, different types of bifurcation and their normal forms are determined. As the prey harvesting and conversion rate of prey into predator are ecologically significant, the impact of theirs have been studied by choosing the bifurcation parameter. The system exhibits a sequence of bifurcations of codim-1 viz. Neimark–Sacker bifurcation and flip bifurcation (period-doubling) and codim-2 resonance bifurcation (1:2, 1:3 and 1:4) at a positive fixed point. For each bifurcation, by using the critical normal form coefficient method, various critical states are calculated under non-degeneracy conditions. Further, a detailed numerical simulation is presented for supporting the analytical findings. The bifurcation curves, phase plots and Maximum Lyapunov exponent (MLE) are drawn. The system exhibits a wide range of bifurcation, including periodic orbits, quasi-periodicity, resonance bifurcation and chaos. Moreover, it is shown that predator harvesting has a stabilizing effect on the dynamics of the model. The chaos that occurred in the system is reduced beyond the critical value of harvesting. The predator population goes extinct after crossing the threshold value of harvesting. This work reflects that the feasible upper bound of the harvesting rate for the species coexistence can be guaranteed. Further, a state feedback controller is employed to suppress the dense chaos in the discrete system. The control technique applied for codim-1 Neimark–Sacker bifurcation and codim-2 1:4 resonance bifurcation is instrumental to reduce the complexity in the system.

Appendix A

$$\begin{aligned} c_{R3}&=\dfrac{c_{R31}}{c_{R32}},\\ c_{R31}&=\gamma ^2 (-18 i h^6+6 i \gamma h^6+6 \gamma \sqrt{3} h^6-6 \sqrt{3} h^6-93 i h^5+12 i \gamma h^5-108 i \delta h^5\\&\quad +\,36 i \gamma \delta h^5-36 \sqrt{3} \delta h^5+18 \gamma \sqrt{3} h^5+36 \gamma \delta \sqrt{3} h^5-39 \sqrt{3} h^5+6 i \gamma ^2 h^4\\&\quad -\,2 \sqrt{3} \gamma ^2 h^4-270 i \delta ^2 h^4+90 i \gamma \delta ^2 h^4-90 \sqrt{3} \delta ^2 h^4-201 i h^4-12 i \gamma h^4\\&\quad -\,465 i \delta h^4+60 i \gamma \delta h^4-195 \sqrt{3} \delta h^4+90 \gamma \delta ^2 \sqrt{3} h^4+32 \gamma \sqrt{3} h^4\\&\quad +\,90 \gamma \delta \sqrt{3} h^4-57 \sqrt{3} h^4-i \gamma ^3 h^3-360 i \delta ^3 h^3+120 i \gamma \delta ^3 h^3-120 \sqrt{3} \delta ^3 h^3\\&\quad +\,34 i \gamma ^2 h^3-2 \sqrt{3} \gamma ^2 h^3-930 i \delta ^2 h^3+120 i \gamma \delta ^2 h^3-390 \sqrt{3} \delta ^2 h^3-207 i h^3\\&\quad +\,9 i \gamma h^3+24 i \gamma ^2 \delta h^3-8 \sqrt{3} \gamma ^2 \delta h^3-804 i \delta h^3-48 i \gamma \delta h^3-228 \sqrt{3} \delta h^3\\&\quad +\,\gamma ^3 \sqrt{3} h^3+120 \gamma \delta ^3 \sqrt{3} h^3+180 \gamma \delta ^2 \sqrt{3} h^3+35 \gamma \sqrt{3} h^3+128 \gamma \delta \sqrt{3} h^3\\&\quad +\,51 \sqrt{3} h^3-270 i \delta ^4 h^2+90 i \gamma \delta ^4 h^2-90 \sqrt{3} \delta ^4 h^2-930 i \delta ^3 h^2+120 i \gamma \delta ^3 h^2\\&\quad -\,390 \sqrt{3} \delta ^3 h^2+28 i \gamma ^2 h^2+36 i \gamma ^2 \delta ^2 h^2-12 \sqrt{3} \gamma ^2 \delta ^2 h^2-1206 i \delta ^2 h^2\\&\quad -\,72 i \gamma \delta ^2 h^2-342- \sqrt{3} \delta ^2 h^2-75 i h^2+72 i \gamma h^2-3 i \gamma ^3 \delta h^2+102 i \gamma ^2 \delta h^2\\&\quad -\,6 \sqrt{3} \gamma ^2 \delta h^2-621 i \delta h^2+27 i \gamma \delta h^2+90 \gamma \delta ^4 \sqrt{3} h^2+180 \gamma \delta ^3 \sqrt{3} h^2\\&\quad +\,192 \gamma \delta ^2 \sqrt{3} h^2+16 \gamma \sqrt{3} h^2+3 \gamma ^3 \delta \sqrt{3} h^2+105 \gamma \delta \sqrt{3} h^2+153 \delta \sqrt{3} h^2\\&\quad +\,195 \sqrt{3} h^2-108 i \delta ^5 h+36 i \gamma \delta ^5 h-36 \sqrt{3} \delta ^5 h-465 i \delta ^4 h+60 i \gamma \delta ^4 h\\&\quad -\,195 \sqrt{3} \delta ^4 h+24 i \gamma ^2 \delta ^3 h-8 \sqrt{3} \gamma ^2 \delta ^3 h-804 i \delta ^3 h-48 i \gamma \delta ^3 h-228 \sqrt{3} \delta ^3 h\\&\quad -\,3 i \gamma ^3 \delta ^2 h+102 i \gamma ^2 \delta ^2 h-6 \sqrt{3} \gamma ^2 \delta ^2 h-621 i \delta ^2 h+27 i \gamma \delta ^2 h+24 i h\\&\quad +\,45 i \gamma h+56 i \gamma ^2 \delta h-150 i \delta h+144 i \gamma \delta h+36 \gamma \delta ^5 \sqrt{3} h+90 \gamma \delta ^4 \sqrt{3} h\\&\quad +\,128 \gamma \delta ^3 \sqrt{3} h+3 \gamma ^3 \delta ^2 \sqrt{3} h+105 \gamma \delta ^2 \sqrt{3} h+153 \delta ^2 \sqrt{3} h+\gamma \sqrt{3} h\\&\quad +\,32 \gamma \delta \sqrt{3} h+390 \delta \sqrt{3} h+168 \sqrt{3} h-18 i \delta ^6+6 i \gamma \delta ^6-6 \sqrt{3} \delta ^6-93 i \delta ^5\\&\quad +\,12 i \gamma \delta ^5-39 \sqrt{3} \delta ^5+6 i \gamma ^2 \delta ^4-2 \sqrt{3} \gamma ^2 \delta ^4-201 i \delta ^4-12 i \gamma \delta ^4-57 \sqrt{3} \delta ^4\\&\quad -\,i \gamma ^3 \delta ^3+34 i \gamma ^2 \delta ^3-2 \sqrt{3} \gamma ^2 \delta ^3-207 i \delta ^3+9 i \gamma \delta ^3+28 i \gamma ^2 \delta ^2-75 i \delta ^2\\&\quad +\,72 i \gamma \delta ^2+18 i+24 i \delta +45 i \gamma \delta +6 \gamma \delta ^6 \sqrt{3}+18 \gamma \delta ^5 \sqrt{3}+32 \gamma \delta ^4 \sqrt{3}\\&\quad +\,\gamma ^3 \delta ^3 \sqrt{3}+35 \gamma \delta ^3 \sqrt{3}+51 \delta ^3 \sqrt{3}+16 \gamma \delta ^2 \sqrt{3}+195 \delta ^2 \sqrt{3}+\gamma \delta \sqrt{3}\\&\quad +\,168 \delta \sqrt{3}+48 \sqrt{3}).\\ c_{R32}&=12 \left( \sqrt{3}-3 i\right) (\delta +h+1)^3. \end{aligned}$$