Abstract
A nilpotent endomorphism of a quiver representation induces a linear transformation on the vector space at each vertex. Generically among all nilpotent endomorphisms, there is a well-defined Jordan form for these linear transformations, which is an interesting new invariant of a quiver representation. If Q is a Dynkin quiver and m is a minuscule vertex, we show that representations consisting of direct sums of indecomposable representations all including m in their support, the category of which we denote by \(\mathcal C_{Q,m}\), are determined up to isomorphism by this invariant. We use this invariant to define a bijection from isomorphism classes of representations in \(\mathcal C_{Q,m}\) to reverse plane partitions whose shape is the minuscule poset corresponding to Q and m. By relating the piecewise-linear promotion action on reverse plane partitions to Auslander–Reiten translation in the derived category, we give a uniform proof that the order of promotion equals the Coxeter number. In type \(A_n\), we show that special cases of our bijection include the Robinson–Schensted–Knuth and Hillman–Grassl correspondences.











Similar content being viewed by others
Notes
We recommend the pronunciation “en-ne” for
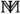 .
.
References
Assem, I., Skowronski, A., and Simson, D.: Elements of the Representation Theory of Associative Algebras: Volume 1: Techniques of Representation Theory, volume 65. Cambridge University Press (2006)
Berenstein, A., Kirillov, A.N.: Groups generated by involutions, Gelfand-Tsetlin patterns, and combinatorics of young tableaux. Algebra i Analiz 7(1), 92–152 (1995)
Berenstein, A., Zelevinsky, A.: Tensor product multiplicities, canonical bases, and totally positive varieties. Inventiones Mathematicae 143, 77–128 (2001)
Bernstein, I.N., Gel’fand, I.M., Ponomarev, V.A.: Coxeter functors and Gabriel’s theorem. Russ. Math. Surv. 28(2), 17–32 (1973)
Bourbaki, N.: Lie groups and lie algebras. Springer, Cham (2008)
Britz, T., Fomin, S.: Finite posets and Ferrers shapes. Adv. Math. 158, 86–127 (2001)
Dauvergne, D.: Hidden invariance of last passage percolation and directed polymers. Ann. Probab. 50(1), 18–60 (2022)
Derksen, H. and Weyman, J.: An Introduction to Quiver Representations. American Mathematical Society (2017)
Einstein, D., Propp, J.: Combinatorial, piecewise-linear, and birational homomesy for products of two chains. Algebr. Combinator. 4(2), 201–224 (2021)
Gabriel, P.: Auslander–Reiten sequences and representation-finite algebras. In: Representation theory I, pp. 1–71. Springer (1980)
Gansner, E.R.: Acyclic digraphs, Young tableaux and nilpotent matrices. SIAM J. Algebr. Discr. Methods 2(4), 429–440 (1981)
Gansner, E.R.: The Hillman–Grassl correspondence and the enumeration of reverse plane partitions. J. Comb. Theory Ser. A 30(1), 71–89 (1981)
Garver, A., Patrias, R.: Greene-Kleitman invariants for Sulzgruber insertion. Electr. J. Combinator. 26(3), 25 (2019)
Green, R.M.: Combinatorics of Minuscule Representations, vol. 199. Cambridge University Press, Cambridge (2013)
Greene, C., Kleitman, D.J.: The structure of Sperner \(k\)-families. J. Combinator. Theory Ser. A 20(1), 41–68 (1976)
Grinberg, D., Roby, T.: Iterative properties of birational rowmotion II: rectangles and triangles. Electr. J. Combinator. 22(3), 3–40 (2015)
Happel, D.: Tilting sets on cylinders. Proc. Londn. Math. Soc. 3(1), 21–55 (1985)
Hillman, A.P., Grassl, R.M.: Reverse plane partitions and tableau hook numbers. J. Combinator. Theory Ser. A 21(2), 216–221 (1976)
Hopkins, S.: RSK via local transformations. available at http://samuelfhopkins.com/docs/rsk.pdf (2014)
Kac, V.: Infinite root systems, representations of graphs and invariant theory. Inventiones Mathematicae 56, 57–92 (1980)
Keller, B.: On triangulated orbit categories. Documenta Mathematica 10, 551–581 (2005)
Knuth, D.: Permutations, matrices, and generalized Young tableaux. Pac. J. Math. 34(3), 709–727 (1970)
Kraft, H. and Riedtmann, C.: Geometry of representations of quivers. In: Representations of algebras (Durham, 1985), volume 116 of London Math. Soc. Lecture Note Ser., pp. 109–145. Cambridge University Press (1986)
Pak, I.: Hook length formula and geometric combinatorics. Séminaire Lotharingien de Combinatoire 46, 6 (2001)
Peng, L., Xiao, J.: Root categories and simple Lie algebras. J. Algebr. 198(1), 19–56 (1997)
Proctor, R.A.: Bruhat lattices, plane partition generating functions, and minuscule representations. Eur. J. Combinator. 5(4), 331–350 (1984)
Ringel, C.M., Schmidmeier, M.: Invariant subspaces of nilpotent linear operators, I. J. Für Die Reine Angew. Math. (Crelles Journal) 2008(614), 1–52 (2008)
de Robinson, G.B.: On the representations of the symmetric group. Am. J. Math. 745–760 (1938)
Roby, T.: Dynamical algebraic combinatorics and the homomesy phenomenon. In: Beveridge, A., et al. (eds.) Recent Trends in Combinatorics, vol. 159, pp. 619–652. Springer, Cham (2016)
Schensted, C.: Longest increasing and decreasing subsequences. Can. J. Math. 13, 179–191 (1961)
Stanley, R.P.: Enumerative Combinatorics, vol. 2. Cambridge University Press, Cambridge (1999)
Striker, J., Williams, N.: Promotion and rowmotion. Eur. J. Combinator. 33(8), 1919–1942 (2012)
Sulzgruber, R.: Building reverse plane partitions with rim-hook-shaped bricks. Séminaire Lotharingien do Combinatoire 78(65), 12 (2017)
Sulzgruber, R.: Inserting rim-hooks into reverse plane partitions. J. Combinator. 11(2), 275–303 (2020)
Wildberger, N.J.: Minuscule posets from neighbourly graph sequences. Eur. J. Combinator. 24(6), 741–757 (2003)
Acknowledgements
AG was suppported by NSERC grant RGPIN/05999-2014 and the Canada Research Chairs program. AG thanks Gabe Frieden for useful discussions and helpful comments on an earlier version of the paper. BP was supported by NSERC, CRM-ISM, and the Canada Research Chairs program. HT was supported by an NSERC Discovery Grant and the Canada Research Chairs program. He thanks Arkady Berenstein and Steffen Oppermann for helpful discussions, and Guillaume Chapuy for an inspiring explanation of Robinson–Schensted–Knuth. He also thanks the Université Paris VII for the excellent working conditions under which part of the research was carried out. The authors thank Bernhard Keller for a comment on an earlier version of the paper and Robin Sulzgruber for sharing an early version of his paper [33], which was inspirational to the authors.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Garver, A., Patrias, R. & Thomas, H. Minuscule reverse plane partitions via quiver representations. Sel. Math. New Ser. 29, 37 (2023). https://doi.org/10.1007/s00029-023-00831-4
Accepted:
Published:
DOI: https://doi.org/10.1007/s00029-023-00831-4


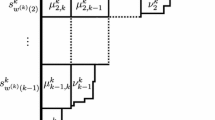


 .
.