1 Introduction

Tuberculosis, which results from Mycobacterium tuberculosis (MTB), is the leading lethal disease from a single infectious pathogen worldwide [1]. In light of the global TB report 2021 from the WHO, about a quarter of the population around the world has been infected with MTB, meanwhile, the prevention and treatment of TB has been facing new risks and challenges since the COVID-19 became pandemic [2]. TB treatment has saved more than 60 million deaths since 2000 [1], which mainly includes the Bacille Calmette–Gurin (BCG) vaccination for children [3] and treatment of LTBI [4]. However, TB still remains a great risk and challenge to the global public health, mainly due to the recurrent TB, which usually includes two types, one is the relapse of the original strain, and the other is the reinfection with a new strain [5].

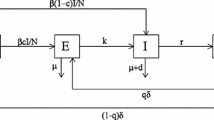
Once infected with MTB, individuals will enter a variable latent period, which lasts from months to decades [6]. If individuals become infectious in a relatively short length of time after infection, they are considered to turn into infectious individuals directly without going through a latent period, which is called the fast progression of TB. If not, it is considered that the individuals become the latent individuals after infection, which is called a slow progression of TB [7]. During the slow progression, a small fraction of latent individuals will develop to infectious individuals, which is called as endogenous reactivation [8]. Many scholars [7, 9,10,11] have studied infectious diseases related to the fast and slow progression, among them, Blower et al. [9] initially developed the following model of TB transmission,

$$\begin{aligned} \left\{ \begin{aligned}&{\dot{S}}(t)=\lambda _{s}-\beta SI-\mu _{N} S,\\&{\dot{E}}(t)=(1-p)\beta SI-\sigma E-\mu _{N}E,\\&{\dot{I}}(t)=p\beta SI+\sigma E-d_{TB}I-\mu _{N}I, \end{aligned} \right. \nonumber \\ \end{aligned}$$
(1)

where S(t), E(t), I(t) denote susceptible, latent and infectious individuals separately; \(\beta \) is the transmission rate between susceptible and infectious individuals; \(\lambda _{s}\) represents the recruitment rate of susceptible individuals; \(\sigma \) is progression rate from latent compartment to infectious compartment; \(\mu _{N}\) is the natural mortality rate; \(d_{TB}\) is the death rate due to TB; p denotes the proportion of susceptible individuals developing to infectious individuals(fast progression). They found that TB would persist for a long time to stay at a stable state.

Subsequently, Castillo-Chavez and Feng [12] investigated the following TB model with treatment and reinfection,

$$\begin{aligned} \left\{ \begin{aligned} {\dot{S}}(t)=&\lambda _{s}-\frac{\beta SI}{N}-\mu _{N} S,\\ {\dot{E}}(t)=&\frac{\beta SI}{N}+\frac{\beta ' TI}{N}-(\mu _{N}+\sigma +\gamma _{l})E,\\ {\dot{I}}(t)=&\sigma E-(\mu _{N}+d_{TB}+\gamma _{I})I,\\ {\dot{T}}(t)=&\gamma _{l}E+\gamma _{I}I-\frac{\beta ' TI}{N}-\mu _{N} T \end{aligned} \right. \nonumber \\ \end{aligned}$$
(2)

where T(t) denotes treated individuals; N(t) implies the total population; \(\beta '\) is the transmission rate between treated and infectious individuals; \(\gamma _{l}, \gamma _{I}\) represent the treatment rates for LTBI and infectious individuals separately. They found that treatment reduced prevalence and increased proportion of uninfected population.

It is shown in model (2) that all individuals come into latent period after being infected, and all new infectious individuals come from the rate of disease progression \(\sigma \). But in fact, the probability of latent individuals to become infectious during the first few years after infection is relatively high, whereas over time, it decreases. Meanwhile the individuals who do not become infectious during these few years may remain latently infected for many years or even whole life [13]. Employing the parameter p to distinguish individuals between fast and slow progression, though there are advantages such as concise and direct, there are also disadvantages, such as it is very difficult to measure the real value of p and ignoring the latency of individuals who account for the proportion p, etc. Therefore, Colign et al. [13] incorporated the compartment \(L_{1}(t)\) and time delay \(\tau _{L_{1}}\) of fast-progressing latency into their modelling process. During this period, the infected individuals die at rate \(\mu _{N}\) and progress to infectious individuals at rate \(p_{l}\). The individual number of compartment \(L_{1}(t)\) at time t is shown by

$$\begin{aligned} L_{1}(t)=\int _{t-\tau _{L_{1}}}^{t}\beta S(s)I(s)e^{-(\mu _{N}+p_{l})(t-s)}ds, \end{aligned}$$

then by differentiating \(L_{1}(t)\), the term \(\beta S(t-\tau _{L_{1}})I(t-\tau _{L_{1}})e^{-(\mu _{N}+p_{l})\tau _{L_{1}}}\) represents the number of individuals of \(L_{1}(t)\) who enters the latency L(t) of slow progression. Meanwhile they assumed that individuals of \(L_{1}(t)\) who progress to infectious individuals all experience a latency no more than \(\tau _{L_{1}}\) after infection, then the infectious compartment I(t) gains a term \(\beta S(t-\tau _{L_{1}})I(t-\tau _{L_{1}})e^{-\mu _{N}\tau _{L_{1}}}(1-e^{-p_{l}\tau _{L_{1}}})\), where \(1-e^{-p_{l}\tau _{L_{1}}}\) represents the proportion of the number of those individuals. Thereby, they developed the TB model with discrete delay and slow-progressing latency as follows,

$$\begin{aligned} \left\{ \begin{aligned} {\dot{S}}(t)=&\lambda _{s}-\beta S(t)I(t)-\mu _{N} S(t),\\ {\dot{L}}(t)=&\beta S(t-\tau _{L_{1}})I(t-\tau _{L_{1}})e^{-(\mu _{N}+p_{l})\tau _{L_{1}}}+\beta I(t-\tau _{L_{1}}) (L(t-\tau _{L_{1}})\\&+T(t-\tau _{L_{1}}))e^{-(\mu _{N}+p_{r})\tau _{L_{1}}}-\beta L(t)I(t)-k_{l}L(t)-\mu _{N} L(t)+r_{s}I(t),\\ {\dot{I}}(t)=&\beta S(t-\tau _{L_{1}})I(t-\tau _{L_{1}})e^{-\mu _{N}\tau _{L_{1}}}(1-e^{-p_{l}\tau _{L_{1}}})+\beta I(t-\tau _{L_{1}}) (L(t-\tau _{L_{1}})\\&+T(t-\tau _{L_{1}}))e^{-\mu _{N}\tau _{L_{1}}}(1-e^{-p_{r}\tau _{L_{1}}})+k_{l}L(t)+\theta _{T} T(t)\\&-(r_{s}+d_{TB}+\gamma _{I})I(t),\\ {\dot{T}}(t)=&\gamma _{I}I(t)-\beta I(t)T(t)-(\theta _{T}+\mu _{N}) T(t), \end{aligned} \right. \nonumber \\ \end{aligned}$$
(3)

where the latent and treated individuals contact with the infectious individuals again and become infectious with a rate \(p_{r}\); \(r_{s}\) denotes the self-recovery rate of infectious individuals; \(k_{l}\) denotes the endogenous reactivation rate of latent individuals; \(\theta _{T}\) represents the relapse rate of treated individuals. They found that contact heterogeneity could lead to local outbreaks in the presence of declining epidemics. Okuonghae [14] carried out some qualitative analysis on the model (3), found that a backward bifurcation existed with exogenous reinfection, criteria on the local stability and a necessary condition for the global stability of disease-free equilibrium (DFE) was obtained as well.

Recently, in addition to the work mentioned above, there has been plenty of other important work of TB models [15,16,17,18,19] focusing on various aspects e.g., vaccination, multi-strain infection, and co-infection with other diseases, etc., which mainly discussed the stability of equilibria (or periodic solution), the persistence (or extinction) of disease, bifurcation and chaos etc.

As well known, incidence function performs a vital role in epidemic models to characterize the interaction between susceptible and infectious individuals, and usually includes bilinear and non-linear incidences etc. [20], in which nonlinear incidences such as saturated, ratio-dependent and Beddington–DeAngelis incidences have been proven that are more appropriate and exact to describe the complicated interactive course of disease transmission [21,22,23,24,25]. However, most TB epidemic models usually used bilinear [6, 13, 14, 26] and standard incidences [12, 27, 28], while very few considered non-linear incidence. Xu et al. [23, 29] introduced ratio-dependent and saturated incidences into epidemic models respectively to describe the transmission of TB, influenza, measles etc., and the globally asymptotic stability of equilibria was attained. Baba et al. [30] presented a TB epidemic model with saturated incidence, showed that effective control strategies would give rise to a reduction of infectious population. Additionally, the Beddington–DeAngelis incidence function \(\frac{\beta SI}{1+\eta _{s} S+\eta _{I} I}\) containing the inhibitory effect of susceptible and infectious individuals, has been gradually employed in epidemic models [21, 24], which could include the bilinear incidence function \(\beta SI\) (\(\eta _{s}=0, \eta _{I}=0\)) and saturated incidence function \(\frac{\beta SI}{1+\eta _{I} I}\) (\(\eta _{s}=0\)) as special cases.

Furthermore, time delays are normally used to describe a required time period for an individual from infection to be infectious [31]. Meanwhile, distributed delay which describes infectivity as a function of duration since infection [32] is assumed to be better than discrete delay to model variable latency [17] and the long-term disease infection [22, 33]. Beretta and Takeuchi [34, 35] pioneered epidemic models with distributed delay, Feng et al. [17] developed an SEI model with distributed delay describing TB transmission dynamics, and argued that distributed latency would not turn the qualitative dynamics of TB. Based on the method in [13], considering Beddington–DeAngelis incidence and distributed delay, the latent compartment \(L_{1}(t)\) of fast progression could shown as follows,

$$\begin{aligned} L_{1}(t)=\int _{t-\kappa }^{t}\int _{0}^{\tau _{L_{1}}}\frac{\beta S(s)I(s)}{1+\eta _{s} S(s)+\eta _{I} I(s)}e^{-(\mu _{N}+p_{l})(t-s)}f(\kappa )d\kappa ds. \end{aligned}$$

Thus,

$$\begin{aligned}&\dot{L_{1}}(t)=-(\mu _{N}+p_{l})L_{1}(t)+\frac{\beta S(t)I(t)}{1+\eta _{s} S(t)+\eta _{I} I(t)}\\&\quad -\int _{0}^{\tau _{L_{1}}}\frac{\beta S(t-\kappa )I(t-\kappa )}{1+\eta _{s} S(t-\kappa )+\eta _{I} I(t-\kappa )}e^{-(\mu _{N}+p_{l})\kappa }f(\kappa )d\kappa , \end{aligned}$$

the term

$$\begin{aligned} \int _{0}^{\tau _{L_{1}}}\frac{\beta S(t-\kappa )I(t-\kappa )}{1+\eta _{s} S(t-\kappa )+\eta _{I} I(t-\kappa )}e^{-(\mu _{N}+p_{l})\kappa }f(\kappa )d\kappa \end{aligned}$$

leaves \(L_{1}(t)\) and enters the latent compartment L(t) of slow progression. Then we also assume that the progression from fast-progressing latency to infectious compartment all take place within a time \(\tau _{L_{1}}\) after infection, then the infectious compartment I(t) gains a delayed term

$$\begin{aligned} \int _{0}^{\tau _{L_{1}}}{\frac{\beta S(t-\kappa )I(t-\kappa )}{1+\eta _{s} S(t-\kappa )+\eta _{I} I(t-\kappa )}e^{-\mu _{N} \kappa }(1-e^{-p_{l}\kappa })f(\kappa )d\kappa }, \end{aligned}$$

where, \(\int _{0}^{\tau _{L_{1}}}f(\kappa )d\kappa =1\), \(f(\kappa )\) is the distribution function satisfying \(f(\kappa )\ge 0\) for all \(\kappa \in [0,+\infty )\).

Moreover, Several studies [36, 37] have shown that relapse of TB accounts for a higher proportion of TB infection than reinfection. Therefore we incorporate the relapse of TB along with the treatment of LTBI and endogenous reactivation in the modelling process, propose the TB epidemic model (4) with distributed delay and Beddington–DeAngelis incidence,

$$\begin{aligned} \left\{ \begin{aligned} {\dot{S}}(t)=&\lambda _{s}-\frac{\beta S(t)I(t)}{1+\eta _{s} S(t)+\eta _{I} I(t)}-\mu _{N} S(t),\\ {\dot{L}}(t)=&\int _{0}^{\tau _{L_{1}}}{\frac{\beta S(t-\kappa )I(t-\kappa )}{1+\eta _{s} S(t-\kappa )+\eta _{I} I(t-\kappa )}e^{-(\mu _{N}+p_{l})\kappa }f(\kappa )d\kappa }\\&-(\mu _{N}+k_{l}+\gamma _{l})L(t),\\ {\dot{I}}(t)=&\int _{0}^{\tau _{L_{1}}}{\frac{\beta S(t-\kappa )I(t-\kappa )}{1+\eta _{s} S(t-\kappa )+\eta _{I} I(t-\kappa )}e^{-\mu _{N} \kappa }(1-e^{-p_{l}\kappa })f(\kappa )d\kappa }+k_{l}L(t)\\&-(\mu _{N}+d_{TB}+\gamma _{I})I(t)+\theta _{T} T(t),\\ {\dot{T}}(t)=&\gamma _{l}L(t)+\gamma _{I}I(t)-\mu _{N} T(t)-\theta _{T} T(t), \end{aligned} \right. \nonumber \\ \end{aligned}$$
(4)

where, \(\eta _{s}>0\), \(\eta _{I}>0\) is the protection level against the disease of susceptible and infectious individuals respectively. All parameters are positive constants.

The following is how the remaining of this article is structured. In Sect. 2, the positivity and boundedness of solutions for model (4) are discussed. In Sect. 3, the basic reproduction number \({\mathcal {R}}_0\) is defined, and the existence and locally asymptotic stability of equilibria are obtained. In Sect. 4, the globally asymptotic stability of equilibria is proved. In Sect. 5, theoretical results are validated through performing numerical simulations, sensitivity analysis on some parameters is also conducted. Finally, we give a brief summary.

2 Basic properties

     The nonnegativity and boundedness of solutions for model (4) are shown in this section. The initial conditions of model (4) are

$$\begin{aligned} S(\nu )=\Phi _{1}(\nu ),~L(\nu )=\Phi _{2}(\nu ),~I(\nu )=\Phi _{3}(\nu ),~ T(\nu )=\Phi _{4}(\nu ),~\nu \in [-\tau _{L_{1}},0], \end{aligned}$$
(5)

where \(\Phi =(\Phi _{1},\Phi _{2},\Phi _{3},\Phi _{4})^T\in {\mathcal {B}}([-\tau _{L_{1}},0],~R_{+}^{4}),~ \Phi _{i}(\nu )\ge 0 ~(-\tau _{L_{1}}\le \nu \le 0,i=1,2,3,4),\) and \({\mathcal {B}}\) is the Banach space of continuous functions \(\Phi : [-\tau _{L_{1}}, 0]\rightarrow R_{+}^{4}\) with \(\parallel \Phi \parallel =\max _{-\tau _{L_{1}}\le \nu \le 0}\mid \Phi (\nu )\mid \).

Theorem 1

The arbitrary solution \((S(t),L(t),I(t),T(t))^T\) of model (4) with initial conditions (5) is non-negative and ultimately bounded on  \([0,+\infty )\).

Proof

Since the theorem of functional differential equations [38], a unique solution (S(t), L(t),  \(I(t),T(t))^T\) of model (4) with initial conditions (5) exsists on maximum existing interval \([0,T_{\max })\), where \(T_{\max }\le \infty \). Assume that there exists \(t_{s}\in [0,T_{\max })\) satisfying \(S(t_{s})=0\), and that for any \(t\in [0,t_s)\), \(S(t)>0\) holds, thereby \({\dot{S}}(t_{s})\le 0\). However, it is easy to see that \({\dot{S}}(t_{s})=\lambda _{s}>0\), which leads to a contradiction, so \(S(t)>0\) holds for any \(t\in [0,T_{\max })\). Assume existence of \(t_{2}\in [0,T_{\max })\) satisfying \(I(t_{2})=0\), and that for any \(t\in [0,t_2)\), \(I(t)>0\) holds, thus \({\dot{I}}(t_{2})\le 0\). However, it holds that

$$\begin{aligned} {\dot{I}}(t_{2})=&\int _{0}^{\tau _{L_{1}}}{\frac{\beta S(t_{2}-\kappa )I(t_{2}-\kappa )}{1+\eta _{s} S(t_{2}-\kappa )+\eta _{I} I(t_{2}-\kappa )}e^{-\mu _{N} \kappa }(1-e^{-p_{l}\kappa })f(\kappa )d\kappa } \nonumber \\&+k_{l}L(t_{2})+\theta _{T} T(t_{2}), \nonumber \\ I(t)=&\int _{0}^{t}\left[ \int _{0}^{\tau _{L_{1}}}\frac{\beta S(\xi -\kappa )I(\xi -\kappa )}{1+\eta _{s} S(\xi -\kappa )+\eta _{I} I(\xi -\kappa )}e^{-\mu _{N} \kappa }(1-e^{-p_{l}\kappa })f(\kappa )d\kappa \right. \nonumber \\&\left. +k_{l}L(\xi )+\theta _{T} T(\xi )\right] e^{-(\mu _{N}+d_{TB}+\gamma _{I})(t-\xi )}d\xi +I(0)e^{-(\mu _{N}+d_{TB}+\gamma _{I})t},\end{aligned}$$
(6)
$$\begin{aligned} L(t)=&\int _{0}^{t}\int _{0}^{\tau _{L_{1}}}\frac{\beta S(\xi -\kappa )I(\xi -\kappa )}{1+\eta _{s} S(\xi -\kappa )+\eta _{I} I(\xi -\kappa )}e^{-(\mu _{N}+p_{l})\kappa }f(\kappa )d\kappa \nonumber \\&\times e^{-(\mu _{N}+k_{l}+\gamma _{l})(t-\xi )}d\xi +L(0)e^{-(\mu _{N}+k_{l}+\gamma _{l})t},\end{aligned}$$
(7)
$$\begin{aligned} T(t)=&\int _{0}^{t}[\gamma _{l}L(\xi )+\gamma _{I}I(\xi )]e^{-(\mu _{N}+\theta _{T})(t-\xi )}d\xi +T(0)e^{-(\mu _{N}+\theta _{T})t}. \end{aligned}$$
(8)

It is obvious that \(I(t_{2}-\kappa ),~S(t_{2}-\kappa ),~L(t_{2}),~T(t_{2})>0\), where \(t_{2}\in [0,T_{\max }),and ~\kappa \in (0,\tau _{L_{1}})\). Hence, we have \({\dot{I}}(t_{2})>0\), which induce a contradiction. Therefore, \(I(t)>0\) holds for any \(t\in [0,T_{\max })\). Further from Eqs. (7) and (8), \(L(t),~T(t)>0\) hold for any \(t\in [0,T_{\max })\). Hence, \((S(t),L(t),I(t),T(t))^T\) is non-negative on \([0,T_{\max })\).

Next, we demonstrate the boundedness of model (4). Obtainable from the first equation of model (4),

$$\begin{aligned} {\dot{S}}(t)=\lambda _{s}-\frac{\beta S(t)I(t)}{1+\eta _{s} S(t)+\eta _{I} I(t)}-\mu _{N} S(t)\le \lambda _{s}-\mu _{N} S(t). \end{aligned}$$

In accordance with the comparison theorem, we get \(\lim \limits _{t\rightarrow \infty }\sup S(t)\le \frac{\lambda _{s}}{\mu _{N}}\), then S(t) is ultimate bounded. Define

$$\begin{aligned} A(t)=\int _{0}^{\tau _{L_{1}}}S(t-\kappa )f(\kappa )e^{-\mu _{N} \kappa }d\kappa +L(t)+I(t)+T(t), \end{aligned}$$

we have

$$\begin{aligned} {\dot{A}}(t)&=\lambda _{s}\int _{0}^{\tau _{L_{1}}}f(\kappa )e^{-\mu _{N} \kappa }d\kappa -\mu _{N} \int _{0}^{\tau _{L_{1}}}f(\kappa )e^{-\mu _{N} \kappa }S(t-\kappa )d\kappa -\mu _{N} L(t)\\&\quad -(\mu _{N}+d_{TB})I(t)-\mu _{N} T(t)\\&<\lambda _{s}\int _{0}^{\tau _{L_{1}}}f(\kappa )e^{-\mu _{N} \kappa }d\kappa -\mu _{N} A(t). \end{aligned}$$

By the same discussion as above, it implies that A(t) is bounded on \(t\in [0,T_{\max })\) and thus L(t),  I(t),  T(t) are ultimate bounded on \(t\in [0,T_{\max })\). Therefore, from the extension theorem of solutions we see \(T_{\max }=+\infty \). So the arbitrary solution \((S(t),L(t),I(t),T(t))^T\) of model (4) with initial conditions (5) is non-negative and ultimately bounded on \([0,+\infty )\). \(\square \)

3 Existence and local stability of equilibria

It is clear that there is a DFE \(E^{0}(\frac{\lambda _{s}}{\mu _{N}},0,0,0)\) of model (4). Denoting

$$\begin{aligned} \rho (\tau _{L_{1}})&=(k_{l}(\mu _{N}+\theta _{T})+\theta _{T} \gamma _{l})\int _{0}^{\tau _{L_{1}}}e^{-(\mu _{N}+p _{l})\kappa } f(\kappa )d\kappa \\&\quad +(\mu _{N}+\theta _{T})(\mu _{N}+k_{l}+\gamma _{l})\int _{0}^{\tau _{L_{1}}}{e^{-\mu _{N} \kappa }(1-e^{-p_{l}\kappa })f(\kappa )d\kappa }, \end{aligned}$$

then we can get the endemic equilibrium (EE) \({\tilde{E}}({\tilde{S}},{\tilde{L}},{\tilde{I}},{\tilde{T}})\) of model (4), where

$$\begin{aligned} {\tilde{I}}=&\frac{\rho (\tau _{L_{1}})(\lambda _{s}-\mu _{N} {\tilde{S}})}{(\mu _{N}+k_{l}+\gamma _{l})[(\mu _{N}+\theta _{T})(\mu _{N}+d_{TB}+\gamma _{I})-\theta _{T} \gamma _{I}]},\\ {\tilde{T}}=&\frac{\lambda _{s}-\mu _{N} {\tilde{S}}}{(\mu _{N}+\theta _{T})(\mu _{N}+k_{l}+\gamma _{l})}\left[ \gamma _{l}\int _{0}^{\tau _{L_{1}}}e^{-(\mu _{N}+p_{l})\kappa } f(\kappa )d\kappa \right. \\&\left. +\frac{\gamma _{I}\rho (\tau _{L_{1}})}{((\mu _{N}+\theta _{T})(\mu _{N}+d_{TB}+\gamma _{I})-\theta _{T} \gamma _{I})}\right] ,\\ {\tilde{L}}=&\frac{\int _{0}^{\tau _{L_{1}}}e^{-(\mu _{N}+p_{l})\kappa } f(\kappa )d\kappa (\lambda _{s}-\mu _{N} {\tilde{S}})}{\mu _{N}+k_{l}+\gamma _{l}},\\ {\tilde{S}}=&\frac{(\mu _{N}+k_{l}+\gamma _{l})[(\mu _{N}+\theta _{T})(\mu _{N}+d_{TB}+\gamma _{I})-\theta _{T} \gamma _{I}]+\eta _{I}\lambda _{s}\rho (\tau _{L_{1}})}{(\beta +\mu _{N}\eta _{I})\rho (\tau _{L_{1}})-\eta _{s}(\mu _{N}+k_{l}+\gamma _{l})[(\mu _{N}+\theta _{T})(\mu _{N}+d_{TB}+\gamma _{I})-\theta _{T} \gamma _{I}]}. \end{aligned}$$

Define basic reproduction number of model (4) as

$$\begin{aligned} {\mathcal {R}}_0=\frac{\beta \lambda _{s} \rho (\tau _{L_{1}})}{(\mu _{N}+\eta _{s}\lambda _{s})(\mu _{N}+k_{l}+\gamma _{l})[(\mu _{N}+\theta _{T})(\mu _{N}+d_{TB}+\gamma _{I})-\theta _{T} \gamma _{I}]}. \end{aligned}$$

Then when  \({\mathcal {R}}_0>1\),we have

$$\begin{aligned} {\tilde{S}}&=\frac{\beta \lambda _{s}(\mu _{N}+k_{l}+\gamma _{l})[(\mu _{N}+\theta _{T})(\mu _{N}+d_{TB}+\gamma _{I})-\theta _{T} \gamma _{I}]+\beta \eta _{I}\lambda _{s}^{2}\rho (\tau _{L_{1}})}{(\mu _{N}+\eta _{s}\lambda _{s})(\mu _{N}+k_{l}+\gamma _{l})[(\mu _{N}+\theta _{T})(\mu _{N}+d_{TB}+\gamma _{I})-\theta _{T} \gamma _{I}]}\\&\qquad \times \frac{1}{(\beta +\mu _{N}\eta _{I})[{\mathcal {R}}_0-\frac{\eta _{s}\beta \lambda _{s}}{(\beta +\mu _{N}\eta _{I})(\mu _{N}+\eta _{s}\lambda _{s})}]}\\&\quad >0, \end{aligned}$$

and

$$\begin{aligned}&\lambda _{s}-\mu _{N} {\tilde{S}}\\&\quad =\frac{(\mu _{N}+\eta _{s}\lambda _{s})(\mu _{N}+k_{l}+\gamma _{l})[(\mu _{N}+\theta _{T})(\mu _{N}+d_{TB}+\gamma _{I})-\theta _{T} \gamma _{I}]({\mathcal {R}}_0-1)}{(\beta +\mu _{N}\eta _{I})\rho (\tau _{L_{1}})-\eta _{s}(\mu _{N}+k_{l}+\gamma _{l})[(\mu _{N}+\theta _{T})(\mu _{N}+d_{TB}+\gamma _{I})-\theta _{T} \gamma _{I}]}\\&\quad =\frac{\beta \lambda _{s}({\mathcal {R}}_0-1)}{(\beta +\mu _{N}\eta _{I})[{\mathcal {R}}_0-\frac{\eta _{s}\beta \lambda _{s}}{(\beta +\mu _{N}\eta _{I})(\mu _{N}+\eta _{s}\lambda _{s})}]}>0. \end{aligned}$$

Theorem 2

The DFE \(E^{0}(\frac{\lambda _{s}}{\mu _{N}},0,0,0)\) of model (4) is locally asymptotically stable if  \({\mathcal {R}}_0<1\).

Proof

The characteristic equation of model (4) at \(E^{0}(\frac{\lambda _{s}}{\mu _{N}},0,0,0)\) is

$$\begin{aligned} \begin{aligned}&(\lambda _{1}+\mu _{N})[(\lambda _{1}+\mu _{N}+k_{l}+\gamma _{l})((\lambda _{1}+\mu _{N}+\theta _{T})(\lambda _{1}+\mu _{N}+d_{TB}+\gamma _{I})-\theta _{T} \gamma _{I})\\&\quad -(\lambda _{1}+\mu _{N}+\theta _{T})(\lambda _{1}+\mu _{N}+k_{l}+\gamma _{l})\frac{\beta \lambda _{s}}{\mu _{N}+\eta _{s}\lambda _{s}}\int _{0}^{\tau _{L_{1}}}e^{-\mu _{N} \kappa }(1-e^{-p_{l}\kappa })f(\kappa )d\kappa \\&\quad \times e^{-\lambda _{1}\tau _{L_{1}}} -(\lambda _{1}+\mu _{N}+\theta _{T}) k_{l}\frac{\beta \lambda _{s}}{\mu _{N}+\eta _{s}\lambda _{s}}\int _{0}^{\tau _{L_{1}}}e^{-(\mu _{N}+p_{l})\kappa }f(\kappa )d\kappa e^{-\lambda _{1}\tau _{L_{1}}}\\&\quad -\theta _{T} \gamma _{l}\frac{\beta \lambda _{s}}{\mu _{N}+\eta _{s}\lambda _{s}}\int _{0}^{\tau _{L_{1}}}e^{-(\mu _{N}+p_{l})\kappa }f(\kappa )d\kappa e^{-\lambda _{1}\tau _{L_{1}}}]=0. \end{aligned} \end{aligned}$$
(9)

Obviously, the characteristic equation (9) has a negative characteristic root \(\lambda _{0}=-\mu _{N}\), and the other characteristic roots depend on

$$\begin{aligned} \begin{aligned} p(\lambda _{1})&=(\lambda _{1}+\mu _{N}+k_{l}+\gamma _{l})((\lambda _{1}+\mu _{N}+\theta _{T})(\lambda _{1}+\mu _{N}+d_{TB}+\gamma _{I})-\theta _{T} \gamma _{I})\\&\quad -(\lambda _{1}+\mu _{N}+\theta _{T})(\lambda _{1}+\mu _{N}+k_{l}+\gamma _{l})\frac{\beta \lambda _{s}}{\mu _{N}+\eta _{s}\lambda _{s}}\int _{0}^{\tau _{L_{1}}}e^{-\mu _{N} \kappa }(1-e^{-p_{l}\kappa })\\&\quad \times f(\kappa )d\kappa e^{-\lambda _{1}\tau _{L_{1}}}-(\lambda _{1}+\mu _{N}+\theta _{T}) k_{l}\frac{\beta \lambda _{s}}{\mu _{N}+\eta _{s}\lambda _{s}}\int _{0}^{\tau _{L_{1}}}e^{-(\mu _{N}+p_{l})\kappa }f(\kappa )d\kappa \\&\quad \times e^{-\lambda _{1}\tau _{L_{1}}}-\theta _{T} \gamma _{l}\frac{\beta \lambda _{s}}{\mu _{N}+\eta _{s}\lambda _{s}}\int _{0}^{\tau _{L_{1}}}e^{-(\mu _{N}+p_{l})\kappa }f(\kappa )d\kappa e^{-\lambda _{1}\tau _{L_{1}}}. \end{aligned} \end{aligned}$$
(10)

When \({\mathcal {R}}_0<1\), from \(p(\lambda _{1})=0\), we have

$$\begin{aligned} 1&=\frac{\frac{\beta \lambda _{s}}{\mu _{N}+\eta _{s}\lambda _{s}}(\lambda _{1}+\mu _{N}+\theta _{T})\int _{0}^{\tau _{L_{1}}}e^{-\mu _{N} \kappa }(1-e^{-p_{l}\kappa })f(\kappa )d\kappa e^{-\lambda _{1}\tau _{L_{1}}}}{(\lambda _{1}+\mu _{N}+\theta _{T})(\lambda _{1}+\mu _{N}+d_{TB}+\gamma _{I})-\theta _{T} \gamma _{I}}\\&\quad +\frac{\frac{\beta \lambda _{s}}{\mu _{N}+\eta _{s}\lambda _{s}}(\lambda _{1}+\mu _{N}+\theta _{T}) k_{l}\int _{0}^{\tau _{L_{1}}}e^{-(\mu _{N}+p_{l})\kappa }f(\kappa )d\kappa e^{-\lambda _{1}\tau _{L_{1}}}}{(\lambda _{1}+\mu _{N}+k_{l}+\gamma _{l})((\lambda _{1}+\mu _{N}+\theta _{T})(\lambda _{1}+\mu _{N}+d_{TB}+\gamma _{I})-\theta _{T} \gamma _{I})}\\&\quad +\frac{\frac{\beta \lambda _{s}}{\mu _{N}+\eta _{s}\lambda _{s}}\theta _{T} \gamma _{l}\int _{0}^{\tau _{L_{1}}}e^{-(\mu _{N}+p_{l})\kappa }f(\kappa )d\kappa e^{-\lambda _{1}\tau _{L_{1}}}}{(\lambda _{1}+\mu _{N}+k_{l}+\gamma _{l})((\lambda _{1}+\mu _{N}+\theta _{T})(\lambda _{1}+\mu _{N}+d_{TB}+\gamma _{I})-\theta _{T} \gamma _{I})}. \end{aligned}$$

Let \(\lambda _{1}=a+ib,~a,~b\in R\), if \(a\ge 0\), then it follows that

$$\begin{aligned} 1&= |\frac{\frac{\beta \lambda _{s}}{\mu _{N}+\eta _{s}\lambda _{s}}(\lambda _{1}+\mu _{N}+\theta _{T})\int _{0}^{\tau _{L_{1}}}e^{-\mu _{N} \kappa }(1-e^{-p_{l}\kappa })f(\kappa )d\kappa e^{-\lambda _{1}\tau _{L_{1}}}}{(\lambda _{1}+\mu _{N}+\theta _{T})(\lambda _{1}+\mu _{N}+d_{TB}+\gamma _{I})-\theta _{T} \gamma _{I}}\\&\quad +\frac{\frac{\beta \lambda _{s}}{\mu _{N}+\eta _{s}\lambda _{s}}(\lambda _{1}+\mu _{N}+\theta _{T}) k_{l}\int _{0}^{\tau _{L_{1}}}e^{-(\mu _{N}+p_{l})\kappa }f(\kappa )d\kappa e^{-\lambda _{1}\tau _{L_{1}}}}{(\lambda _{1}+\mu _{N}+k_{l}+\gamma _{l})((\lambda _{1}+\mu _{N}+\theta _{T})(\lambda _{1}+\mu _{N}+d_{TB}+\gamma _{I})-\theta _{T} \gamma _{I})}\\&\quad +\frac{\frac{\beta \lambda _{s}}{\mu _{N}+\eta _{s}\lambda _{s}}\theta _{T} \gamma _{l}\int _{0}^{\tau _{L_{1}}}e^{-(\mu _{N}+p_{l})\kappa }f(\kappa )d\kappa e^{-\lambda _{1}\tau _{L_{1}}}}{(\lambda _{1}+\mu _{N}+k_{l}+\gamma _{l})((\lambda _{1}+\mu _{N}+\theta _{T})(\lambda _{1}+\mu _{N}+d_{TB}+\gamma _{I})-\theta _{T} \gamma _{I})}|\\&\le \frac{\beta \lambda _{s}}{\mu _{N}+\eta _{s}\lambda _{s}}\int _{0}^{\tau _{L_{1}}}e^{-\mu _{N} \kappa }(1-e^{-p_{l}\kappa })f(\kappa )d\kappa \\&\quad \times |\frac{(\lambda _{1}+\mu _{N}+\theta _{T})e^{-\lambda _{1}\tau _{L_{1}}}}{(\lambda _{1}+\mu _{N}+\theta _{T})(\lambda _{1}+\mu _{N}+d_{TB}+\gamma _{I})-\theta _{T} \gamma _{I}}|\\&\quad +\frac{k_{l}\beta \lambda _{s}}{\mu _{N}+\eta _{s}\lambda _{s}}\int _{0}^{\tau _{L_{1}}}e^{-(\mu _{N}+p_{l})\kappa }f(\kappa )d\kappa \\&\quad \times |\frac{(\lambda _{1}+\mu _{N}+\theta _{T})e^{-\lambda _{1}\tau _{L_{1}}}}{(\lambda _{1}+\mu _{N}+k_{l}+\gamma _{l})((\lambda _{1}+\mu _{N}+\theta _{T})(\lambda _{1}+\mu _{N}+d_{TB}+\gamma _{I})-\theta _{T} \gamma _{I})}|\\&\quad +\frac{\beta \lambda _{s}}{\mu _{N}+\eta _{s}\lambda _{s}}\theta _{T} \gamma _{l}\int _{0}^{\tau _{L_{1}}}e^{-(\mu _{N}+p_{l})\kappa }f(\kappa )d\kappa \\&\quad \times |\frac{e^{-\lambda _{1}\tau _{L_{1}}}}{(\lambda _{1}+\mu _{N}+k_{l}+\gamma _{l})((\lambda _{1}+\mu _{N}+\theta _{T})(\lambda _{1}+\mu _{N}+d_{TB}+\gamma _{I})-\theta _{T} \gamma _{I})}|\\&\le \frac{\beta \lambda _{s}}{\mu _{N}+\eta _{s}\lambda _{s}}\int _{0}^{\tau _{L_{1}}}e^{-\mu _{N} \kappa }(1-e^{-p_{l}\kappa })f(\kappa )d\kappa \frac{(\mu _{N}+\theta _{T})}{(\mu _{N}+\theta _{T})(\mu _{N}+d_{TB}+\gamma _{I})-\theta _{T} \gamma _{I}}\\&\quad +\frac{\beta \lambda _{s}}{\mu _{N}+\eta _{s}\lambda _{s}}\frac{(k_{l}(\mu _{N}+\theta _{T})+\theta _{T} \gamma _{l})\int _{0}^{\tau _{L_{1}}}e^{-(\mu _{N}+p_{l})\kappa }f(\kappa )d\kappa }{(\mu _{N}+k_{l}+\gamma _{l})((\mu _{N}+\theta _{T})(\mu _{N}+d_{TB}+\gamma _{I})-\theta _{T} \gamma _{I})}\\&={\mathcal {R}}_0<1, \end{aligned}$$

which leads to a contradiction. Hence, if \({\mathcal {R}}_0<1\), then we have \(a<0\). Therefore, \(E^{0}\) is locally asymptotically stable. \(\square \)

Theorem 3

The EE \({\tilde{E}}({\tilde{S}},{\tilde{L}},{\tilde{I}},{\tilde{T}})\) of model (4) is locally asymptotically stable if  \({\mathcal {R}}_0>1\).

Proof

The characteristic equation for model (4) at EE is obtained as

$$\begin{aligned} \begin{aligned}&(\lambda _{1}+\mu _{N}+\frac{\beta {\tilde{I}}(1+\eta _{I} {\tilde{I}})}{(1+\eta _{s} {\tilde{S}}+\eta _{I} {\tilde{I}})^{2}})(\lambda _{1}+\mu _{N}+k_{l}+\gamma _{l})[(\lambda _{1}+\mu _{N}+d_{TB}+\gamma _{I})\\&\quad \times (\lambda _{1}+\mu _{N}+\theta _{T})-\theta _{T} \gamma _{I}]-(\lambda _{1}+\mu _{N})(\lambda _{1}+\mu _{N}+k_{l}+\gamma _{l})(\lambda _{1}+\mu _{N}+\theta _{T})\\&\quad \times \frac{\beta {\tilde{S}}(1+\eta _{s} {\tilde{S}})}{(1+\eta _{s} {\tilde{S}}+\eta _{I} {\tilde{I}})^{2}}\int _{0}^{\tau _{L_{1}}}e^{-\mu _{N} \kappa }(1-e^{-p_{l}\kappa })f(\kappa )d\kappa e^{-\lambda _{1}\tau _{L_{1}}}-k_{l}(\lambda _{1}+\mu _{N})\\&\quad \times (\lambda _{1}+\mu _{N}+\theta _{T})\frac{\beta {\tilde{S}}(1+\eta _{s} {\tilde{S}})}{(1+\eta _{s} {\tilde{S}}+\eta _{I} {\tilde{I}})^{2}}\int _{0}^{\tau _{L_{1}}}e^{-(\mu _{N}+p_{l})\kappa }f(\kappa )d\kappa e^{-\lambda _{1}\tau _{L_{1}}}\\&\quad -\theta _{T} \gamma _{l}(\lambda _{1}+\mu _{N})\frac{\beta {\tilde{S}}(1+\eta _{s} {\tilde{S}})}{(1+\eta _{s} {\tilde{S}}+\eta _{I} {\tilde{I}})^{2}}\int _{0}^{\tau _{L_{1}}}e^{-(\mu _{N}+p_{l})\kappa }f(\kappa )d\kappa e^{-\lambda _{1}\tau _{L_{1}}}=0. \end{aligned}\nonumber \\ \end{aligned}$$
(11)

Then,

$$\begin{aligned} \begin{aligned}&\frac{\lambda _{1}+\mu _{N}+\frac{\beta {\tilde{I}}(1+\eta _{I} {\tilde{I}})}{(1+\eta _{s} {\tilde{S}}+\eta _{I} {\tilde{I}})^{2}}}{\lambda _{1}+\mu _{N}}\\&\quad =\frac{(\lambda _{1}+\mu _{N}+\theta _{T})\int _{0}^{\tau _{L_{1}}}e^{-\mu _{N} \kappa }(1-e^{-p_{l}\kappa })f(\kappa )d\kappa e^{-\lambda _{1}\tau _{L_{1}}}\frac{\beta {\tilde{S}}(1+\eta _{s} {\tilde{S}})}{(1+\eta _{s} {\tilde{S}}+\eta _{I} {\tilde{I}})^{2}}}{((\lambda _{1}+\mu _{N}+d_{TB}+\gamma _{I})(\lambda _{1}+\mu _{N}+\theta _{T})-\theta _{T} \gamma _{I})}\\&\qquad +\frac{(\lambda _{1}+\mu _{N}+\theta _{T})k_{l}\int _{0}^{\tau _{L_{1}}}e^{-(\mu _{N}+p_{l})\kappa }f(\kappa )d\kappa e^{-\lambda _{1}\tau _{L_{1}}}\frac{\beta {\tilde{S}}(1+\eta _{s} {\tilde{S}})}{(1+\eta _{s} {\tilde{S}}+\eta _{I} {\tilde{I}})^{2}}}{(\lambda _{1}+\mu _{N}+k_{l}+\gamma _{l})((\lambda _{1}+\mu _{N}+d_{TB}+\gamma _{I})(\lambda _{1}+\mu _{N}+\theta _{T})-\theta _{T} \gamma _{I})}\\&\qquad +\frac{\theta _{T} \gamma _{l}\int _{0}^{\tau _{L_{1}}}e^{-(\mu _{N}+p_{l})\kappa }f(\kappa )d\kappa e^{-\lambda _{1}\tau _{L_{1}}}\frac{\beta {\tilde{S}}(1+\eta _{s} {\tilde{S}})}{(1+\eta _{s} {\tilde{S}}+\eta _{I} {\tilde{I}})^{2}}}{(\lambda _{1}+\mu _{N}+k_{l}+\gamma _{l})((\lambda _{1}+\mu _{N}+d_{TB}+\gamma _{I})(\lambda _{1}+\mu _{N}+\theta _{T})-\theta _{T} \gamma _{I})}. \end{aligned} \end{aligned}$$

Note that

$$\begin{aligned} O&=\frac{\lambda _{1}+\mu _{N}+\frac{\beta {\tilde{I}}(1+\eta _{I} {\tilde{I}})}{(1+\eta _{s} {\tilde{S}}+\eta _{I} {\tilde{I}})^{2}}}{\lambda _{1}+\mu _{N}}\\ W&=\frac{(\lambda _{1}+\mu _{N}+\theta _{T})\int _{0}^{\tau _{L_{1}}}e^{-\mu _{N} \kappa }(1-e^{-p_{l}\kappa })f(\kappa )d\kappa e^{-\lambda _{1}\tau _{L_{1}}}\frac{\beta {\tilde{S}}(1+\eta _{s} {\tilde{S}})}{(1+\eta _{s} {\tilde{S}}+\eta _{I} {\tilde{I}})^{2}}}{((\lambda _{1}+\mu _{N}+d_{TB}+\gamma _{I})(\lambda _{1}+\mu _{N}+\theta _{T})-\theta _{T} \gamma _{I})}\\&\quad +\frac{(\lambda _{1}+\mu _{N}+\theta _{T})k_{l}\int _{0}^{\tau _{L_{1}}}e^{-(\mu _{N}+p_{l})\kappa }f(\kappa )d\kappa e^{-\lambda _{1}\tau _{L_{1}}}\frac{\beta {\tilde{S}}(1+\eta _{s} {\tilde{S}})}{(1+\eta _{s} {\tilde{S}}+\eta _{I} {\tilde{I}})^{2}}}{(\lambda _{1}+\mu _{N}+k_{l}+\gamma _{l})((\lambda _{1}+\mu _{N}+d_{TB}+\gamma _{I})(\lambda _{1}+\mu _{N}+\theta _{T})-\theta _{T} \gamma _{I})}\\&\quad +\frac{\theta _{T} \gamma _{l}\int _{0}^{\tau _{L_{1}}}e^{-(\mu _{N}+p_{l})\kappa }f(\kappa )d\kappa e^{-\lambda _{1}\tau _{L_{1}}}\frac{\beta {\tilde{S}}(1+\eta _{s} {\tilde{S}})}{(1+\eta _{s} {\tilde{S}}+\eta _{I} {\tilde{I}})^{2}}}{(\lambda _{1}+\mu _{N}+k_{l}+\gamma _{l})((\lambda _{1}+\mu _{N}+d+\gamma _{I})(\lambda _{1}+\mu _{N}+\theta _{T})-\theta _{T} \gamma _{I})}. \end{aligned}$$

Let \(\lambda _{1}=a+ib,~a,~b\in R\), if \(a\ge 0\), then we have \(\mid O\mid >1\). However,

$$\begin{aligned} \mid W\mid&\leqslant \frac{\beta {\tilde{S}}(1+\eta _{s} {\tilde{S}})}{(1+\eta _{s} {\tilde{S}}+\eta _{I} {\tilde{I}})^{2}}\int _{0}^{\tau _{L_{1}}}e^{-\mu _{N} \kappa }(1-e^{-p_{l}\kappa })f(\kappa )d\kappa \\&\quad \times |\frac{(\lambda _{1}+\mu _{N}+\theta _{T})e^{-\lambda _{1}\tau _{L_{1}}}}{(\lambda _{1}+\mu _{N}+d_{TB}+\gamma _{I})(\lambda _{1}+\mu _{N}+\theta _{T})-\theta _{T} \gamma _{I}}|\\&\quad +k_{l}\frac{\beta {\tilde{S}}(1+\eta _{s} {\tilde{S}})}{(1+\eta _{s} {\tilde{S}}+\eta _{I} {\tilde{I}})^{2}}\int _{0}^{\tau _{L_{1}}}e^{-(\mu _{N}+p_{l})\kappa }f(\kappa )d\kappa \\&\quad \times |\frac{(\lambda _{1}+\mu _{N}+\theta _{T})e^{-\lambda _{1}\tau _{L_{1}}}}{(\lambda _{1}+\mu _{N}+k_{l}+\gamma _{l})((\lambda _{1}+\mu _{N}+d_{TB}+\gamma _{I})(\lambda _{1}+\mu _{N}+\theta _{T})-\theta _{T} \gamma _{I})}|\\&\quad +\theta _{T} \gamma _{l}\frac{\beta {\tilde{S}}(1+\eta _{s} {\tilde{S}})}{(1+\eta _{s} {\tilde{S}}+\eta _{I} {\tilde{I}})^{2}}\int _{0}^{\tau _{L_{1}}}e^{-(\mu _{N}+p_{l})\kappa }f(\kappa )d\kappa \\&\quad \times |\frac{e^{-\lambda _{1}\tau _{L_{1}}}}{(\lambda _{1}+\mu _{N}+k_{l}+\gamma _{l})((\lambda _{1}+\mu _{N}+d_{TB}+\gamma _{I})(\lambda _{1}+\mu _{N}+\theta _{T})-\theta _{T} \gamma _{I})}|\\&\leqslant \frac{\beta {\tilde{S}}(1+\eta _{s} {\tilde{S}})}{(1+\eta _{s} {\tilde{S}}+\eta _{I} {\tilde{I}})^{2}}\int _{0}^{\tau _{L_{1}}}e^{-\mu _{N} \kappa }(1-e^{-p_{l}\kappa })f(\kappa )d\kappa \\&\quad \times \frac{\mu _{N}+\theta _{T}}{(\mu _{N}+d_{TB}+\gamma _{I})(\mu _{N}+\theta _{T})-\theta _{T} \gamma _{I}}+k_{l}\frac{\beta {\tilde{S}}(1+\eta _{s} {\tilde{S}})}{(1+\eta _{s} {\tilde{S}}+\eta _{I} {\tilde{I}})^{2}}\int _{0}^{\tau _{L_{1}}}e^{-(\mu _{N}+p_{l})\kappa }\\&\quad \times f(\kappa )d\kappa \frac{\mu _{N}+\theta _{T}}{(\mu _{N}+k_{l}+\gamma _{l})((\mu _{N}+d_{TB}+\gamma _{I})(\mu _{N}+\theta _{T})-\theta _{T} \gamma _{I})}\\&\quad +\theta _{T} \gamma _{l}\frac{\beta {\tilde{S}}(1+\eta _{s} {\tilde{S}})}{(1+\eta _{s} {\tilde{S}}+\eta _{I} {\tilde{I}})^{2}}\frac{\int _{0}^{\tau _{L_{1}}}e^{-(\mu _{N}+p_{l})\kappa }f(\kappa )d\kappa }{(\mu _{N}+k_{l}+\gamma _{l})((\mu _{N}+d_{TB}+\gamma _{I})(\mu _{N}+\theta _{T})-\theta _{T} \gamma _{I})}\\&= \left[ \frac{(\mu _{N}+\theta _{T})\int _{0}^{\tau _{L_{1}}}e^{-\mu _{N} \kappa }(1-e^{-p_{l}\kappa })f(\kappa )d\kappa }{((\mu _{N}+d_{TB}+\gamma _{I})(\mu _{N}+\theta _{T})-\theta _{T} \gamma _{I})}\right. \\&\quad \left. +\frac{(k_{l}(\mu _{N}+\theta _{T})+\theta _{T} \gamma _{l})\int _{0}^{\tau _{L_{1}}}e^{-(\mu _{N}+p_{l})\kappa }f(\kappa )d\kappa }{(\mu _{N}+k_{l}+\gamma _{l})((\mu _{N}+d_{TB}+\gamma _{I})(\mu _{N}+\theta _{T})-\theta _{T} \gamma _{I})}\right] \frac{\beta {\tilde{S}}(1+\eta _{s} {\tilde{S}})}{(1+\eta _{s} {\tilde{S}}+\eta _{I} {\tilde{I}})^{2}}\\&= \frac{\beta {\tilde{S}}{\tilde{I}}(1+\eta _{s} {\tilde{S}})}{(\lambda _{s}-\mu _{N} {\tilde{S}})(1+\eta _{s} {\tilde{S}}+\eta _{I} {\tilde{I}})^{2}}\\&= \frac{1+\eta _{s} {\tilde{S}}}{1+\eta _{s} {\tilde{S}}+\eta _{I} {\tilde{I}}}<1, \end{aligned}$$

which leads to a contradiction, so we have \(a<0\). Therefore, if \({\mathcal {R}}_0>1\), \({\tilde{E}}\) exists and is locally asymptotically stable. \(\square \)

4 Global stability of equilibria

Theorem 4

The DFE \(E^{0}(\frac{\lambda _{s}}{\mu _{N}},0,0,0)\) of model (4) is globally asymptotically stable if \({\mathcal {R}}_0<1\).

Proof

Define \(S^{0}=\frac{\lambda _{s}}{\mu _{N}}\) and Lyapunov function \(H_{1}(t)\), where

$$\begin{aligned} \begin{aligned} H_{1}(t)&=\frac{S^{0}}{1+\eta _{s}S^{0}}\rho (\tau _{L_{1}})(\frac{S(t)}{S^{0}}-1-\ln \frac{S(t)}{S^{0}})+[k_{l}(\mu _{N}+\theta _{T})+\theta _{T} \gamma _{l}]L(t)\\&\quad +(\mu _{N}+\theta _{T})(\mu _{N}+k_{l}+\gamma _{l})I(t)+\theta _{T}(\mu _{N}+k_{l}+\gamma _{l})T(t)+U_{1}(t), \end{aligned} \end{aligned}$$

where

$$\begin{aligned} U_{1}(t)&=[k_{l}(\mu _{N}+\theta _{T})+\theta _{T} \gamma _{l}]\int _{0}^{\tau _{L_{1}}}\int _{t-\kappa }^{t}\frac{\beta S(t-\xi )I(t-\xi )}{1+\eta _{s} S(t-\xi )+\eta _{I} I(t-\xi )}\\&\quad \times e^{-(\mu _{N}+p_{l})\kappa }f(\kappa )d\xi d\kappa +(\mu _{N}+\theta _{T})(\mu _{N}+k_{l}+\gamma _{l})\\&\quad \times \int _{0}^{\tau _{L_{1}}}\int _{t-\kappa }^{t}\frac{\beta S(t-\xi )I(t-\xi )}{1+\eta _{s} S(t-\xi )+\eta _{I} I(t-\xi )}e^{-\mu _{N} \kappa }(1-e^{-p_{l}\kappa })f(\kappa )d\xi d\kappa . \end{aligned}$$

Differentiating \(U_{1}(t)\) along with any positive solution of model (4), we have

$$\begin{aligned} \begin{aligned} {\dot{U}}_{1}(t)&=\rho (\tau _{L_{1}})\frac{\beta S(t)I(t)}{1+\eta _{s} S(t)+\eta _{I} I(t)}-[k_{l}(\mu _{N}+\theta _{T})+\theta _{T} \gamma _{l}]\\&\quad \times \int _{0}^{\tau _{L_{1}}}\frac{\beta S(t-\kappa )I(t-\kappa )}{1+\eta _{s} S(t-\kappa )+\eta _{I} I(t-\kappa )}e^{-(\mu _{N}+p_{l})\kappa } f(\kappa )d\kappa -(\mu _{N}+\theta _{T})(\mu _{N}\\&\quad +k_{l}+\gamma _{l})\int _{0}^{\tau _{L_{1}}}\frac{\beta S(t-\kappa )I(t-\kappa )}{1+\eta _{s} S(t-\kappa )+\eta _{I} I(t-\kappa )}e^{-\mu _{N} \kappa }(1-e^{-p_{l}\kappa })f(\kappa )d\kappa . \end{aligned} \end{aligned}$$

Then, it follows that

Then it holds that \({\dot{H}}_{1}(t)\le 0\) when \({\mathcal {R}}_0<1\), and \({\dot{H}}_{1}(t)=0\) when and only when \(S(t)=S^{0},~L(t)=0,~I(t)=0,~T(t)=0\). Let \(\Gamma \) be the largest invariant set \(\{(\phi _{1},\phi _{2},\phi _{3},\phi _{4})^T\in R_{4}^{+},{\dot{H}}_{1}(t)=0\}\), then we have \(\Gamma =\{E^{0}\}\). Therefore, when  \({\mathcal {R}}_0<1\), \(E^{0}(\frac{\lambda _{s}}{\mu _{N}},0,0,0)\) is globally asymptotically stable from the LaSalle’s invariance principle [39]. \(\square \)

Theorem 5

The EE \({\tilde{E}}({\tilde{S}},{\tilde{L}},{\tilde{I}},{\tilde{T}})\) of model (4) is globally asymptotically stable if  \({\mathcal {R}}_0>1\).

Proof

For convenience, denoting

$$\begin{aligned}&X(S(\alpha ),I(\alpha ))=\frac{\beta S(\alpha )I(\alpha )}{1+\eta _{s} S(\alpha )+\eta _{I} I(\alpha )},~X({\tilde{S}},{\tilde{I}})=\frac{\beta {\tilde{S}}{\tilde{I}}}{1+\eta _{s} {\tilde{S}}+\eta _{I} {\tilde{I}}},\\&Y(m(t))=m(t)-1-\ln m(t) \end{aligned}$$

Define Lyapunov function \(H_{2}(t)\) as below,

$$\begin{aligned} H_{2}(t)=H_{0}(t)+U_{2}(t), \end{aligned}$$

where

$$\begin{aligned} H_{0}(t)&=\rho (\tau _{L_{1}})\left[ S(t)-{\tilde{S}}-\int _{{\tilde{S}}}^{S(t)}\frac{1+\eta _{s}\xi +\eta _{I} {\tilde{I}}}{1+\eta _{s} {\tilde{S}}+\eta _{I} {\tilde{I}}}\frac{{\tilde{S}}}{\xi }d\xi \right] +[k_{l}(\mu _{N}+\theta _{T})+\theta _{T} \gamma _{l}]\\&\quad \times {\tilde{L}}\left[ Y\left( \frac{L(t)}{{\tilde{L}}}\right) \right] +(\mu _{N}+\theta _{T})(\mu _{N}+k_{l}+\gamma _{l}){\tilde{I}}\left[ Y\left( \frac{I(t)}{{\tilde{I}}}\right) \right] \\&\quad +\theta _{T}(\mu _{N}+k_{l}+\gamma _{l}){\tilde{T}}\left[ Y\left( \frac{T(t)}{{\tilde{T}}}\right) \right] ,\\ U_{2}(t)=&[k_{l}(\mu _{N}+\theta _{T})+\theta _{T} \gamma _{l}]X({\tilde{S}},{\tilde{I}})\int _{0}^{\tau _{L_{1}}}\int _{t-\kappa }^{t}\left[ Y\left( \frac{X(S(\xi ),I(\xi ))}{X({\tilde{S}},{\tilde{I}})}\right) \right] \\&\quad \times f(\kappa ) e^{-(\mu _{N}+p_{l})\kappa }d\xi d\kappa +(\mu _{N}+\theta _{T})(\mu _{N}+k_{l}+\gamma _{l})X({\tilde{S}},{\tilde{I}})\\&\quad \times \int _{0}^{\tau _{L_{1}}}\int _{t-\kappa }^{t}\left[ Y\left( \frac{X(S(\xi ),I(\xi ))}{X({\tilde{S}},{\tilde{I}})}\right) \right] f(\kappa )e^{-\mu _{N} \kappa }(1-e^{-p_{l}\kappa })d\xi d\kappa . \end{aligned}$$

Differentiating \(U_{2}(t)\) along with any positive solution of model (4), we have

$$\begin{aligned} \dot{U_{2}}(t)&=\rho (\tau _{L_{1}})X(S(t),I(t)) -[k_{l}(\mu _{N}+\theta _{T})+\theta _{T} \gamma _{l}]\int _{0}^{\tau _{L_{1}}}X(S(t-\kappa ),I(t-\kappa ))f(\kappa )\\&\quad \times e^{-(\mu _{N}+p_{l})\kappa }d\kappa -(\mu _{N}+\theta _{T})(\mu _{N}+k_{l}+\gamma _{l})\int _{0}^{\tau _{L_{1}}}X(S(t-\kappa ),I(t-\kappa ))f(\kappa )\\&\quad \times e^{-\mu _{N} \kappa }(1-e^{-p_{l}\kappa })d\kappa +[k_{l}(\mu _{N}+\theta _{T})+\theta _{T} \gamma _{l}]X({\tilde{S}},{\tilde{I}})\int _{0}^{\tau _{L_{1}}}f(\kappa )\\&\quad \times e^{-(\mu _{N}+p_{l})\kappa }\ln \left( \frac{X(S(t-\kappa ),I(t-\kappa ))}{X(S(t),I(t))}\right) d\kappa +(\mu _{N}+\theta _{T})(\mu _{N}+k_{l}+\gamma _{l})\\&\quad \times X({\tilde{S}},{\tilde{I}})\int _{0}^{\tau _{L_{1}}}\ln \left( \frac{X(S(t-\kappa ),I(t-\kappa ))}{X(S(t),I(t))}\right) f(\kappa )e^{-\mu _{N} \kappa }(1-e^{-p_{l}\kappa })d\kappa . \end{aligned}$$

Hence,

$$\begin{aligned} \dot{H_{2}}(t)&=\rho (\tau _{L_{1}})\left[ 1-\frac{(1+\eta _{s} S(t)+\eta _{I} {\tilde{I}}){\tilde{S}}}{(1+\eta _{s} {\tilde{S}}+\eta _{I} {\tilde{I}})S(t)}\right] [\lambda _{s}-X(S(t),I(t))-\mu _{N} S(t)]+[k_{l}(\mu _{N}\\&\quad +\theta _{T})+\theta _{T} \gamma _{l}](1-\frac{{\tilde{L}}}{L(t)})\left[ \int _{0}^{\tau _{L_{1}}}X(S(t-\kappa ),I(t-\kappa ))e^{-(\mu _{N}+p_{l})\kappa }f(\kappa )d\kappa \right. \\&\quad \left. -(\mu _{N}+k_{l}+\gamma _{l})L(t)\right] +(\mu _{N}+\theta _{T})(\mu _{N}+k_{l}+\gamma _{l})(1-\frac{{\tilde{I}}}{I(t)})\\&\quad \times \left[ \int _{0}^{\tau _{L_{1}}}\right. X(S(t-\kappa ),I(t-\kappa ))e^{-\mu _{N} \kappa }(1-e^{-p_{l}\kappa })f(\kappa )d\kappa +k_{l}L(t)\\&\quad -(\mu _{N}+d_{TB}+\gamma _{I})I(t)+\theta _{T} T(t)\bigg ]+\theta _{T}(\mu _{N}+k_{l}+\gamma _{l})(1-\frac{{\tilde{T}}}{T(t)})[\gamma _{l}L(t)\\&\quad +\gamma _{I}T(t)-(\mu _{N}+\theta _{T})T(t)]+\dot{U_{2}}(t)\\&=-\rho (\tau _{L_{1}})\frac{\mu _{N}(1+\eta _{I} {\tilde{I}})(S(t)-{\tilde{S}})^{2}}{(1+\eta _{s} {\tilde{S}}+\eta _{I} {\tilde{I}})S(t)}-\rho (\tau _{L_{1}})\frac{{\tilde{S}}(1+\eta _{s} S(t)+\eta _{I} {\tilde{I}})}{(1+\eta _{s} {\tilde{S}}+\eta _{I} {\tilde{I}})S(t)}X({\tilde{S}},{\tilde{I}})\\&\quad +\rho (\tau _{L_{1}})X({\tilde{S}},{\tilde{I}})+\rho (\tau _{L_{1}})\frac{{\tilde{S}}(1+\eta _{s} S(t)+\eta _{I} {\tilde{I}})}{(1+\eta _{s} {\tilde{S}}+\eta _{I} {\tilde{I}})S(t)}X(S(t),I(t))-[k_{l}(\mu _{N}+\theta _{T})\\&\quad +\theta _{T} \gamma _{l}]\frac{{\tilde{L}}}{L(t)}\int _{0}^{\tau _{L_{1}}}X(S(t-\kappa ),I(t-\kappa ))e^{-(\mu _{N}+p_{l})\kappa }f(\kappa )d\kappa +(\mu _{N}+k_{l}+\gamma _{l})\\&\quad \times [k_{l}(\mu _{N}+\theta _{T})+\theta _{T} \gamma _{l}]{\tilde{L}}-(\mu _{N}+\theta _{T})(\mu _{N}+k_{l}+\gamma _{l})\frac{{\tilde{I}}}{I(t)}\\&\quad \times \int _{0}^{\tau _{L_{1}}}X(S(t-\kappa ),I(t-\kappa )e^{-\mu _{N} \kappa }(1-e^{-p_{l}\kappa })f(\kappa )d\kappa -k_{l}(\mu _{N}+\theta _{T})\\&\quad \times (\mu _{N}+k_{l}+\gamma _{l}){\tilde{I}}\frac{L(t)}{I(t)} -(\mu _{N}+\theta _{T})(\mu _{N}+k_{l}+\gamma _{l})(\mu _{N}+d_{TB}+\gamma _{I})I(t)\\&\quad +(\mu _{N}+\theta _{T})(\mu _{N}+k_{l}+\gamma _{l})(\mu _{N}+d_{TB}+\gamma _{I}){\tilde{I}}-\theta _{T}(\mu _{N}+\theta _{T})(\mu _{N}+k_{l}\\&\quad +\gamma _{l}){\tilde{I}}\frac{T(t)}{I(t)}+\theta _{T} \gamma _{I}(\mu _{N}+k_{l}+\gamma _{l})I(t)-\theta _{T} \gamma _{l}(\mu _{N}+k_{l}+\gamma _{l}){\tilde{T}}\frac{L(t)}{T(t)}-\theta _{T}(\mu _{N}\\&\quad +k_{l}+\gamma _{l})\gamma _{I}{\tilde{T}}\frac{I(t)}{T(t)}+\theta _{T}(\mu _{N}+\theta _{T})(\mu _{N}+k_{l}+\gamma _{l}){\tilde{T}}+[k_{l}(\mu _{N}+\theta _{T})+\theta _{T} \gamma _{l}]\\&\quad \times X({\tilde{S}},{\tilde{I}}) \int _{0}^{\tau _{L_{1}}}\ln \left( \frac{X(S(t-\kappa ),I(t-\kappa ))}{X(S(t),I(t))}\right) f(\kappa )e^{-(\mu _{N}+p_{l})\kappa }d\kappa \\&\quad +(\mu _{N}+\theta _{T})(\mu _{N}+k_{l}+\gamma _{l})X({\tilde{S}},{\tilde{I}})\int _{0}^{\tau _{L_{1}}}\ln \left( \frac{X(S(t-\kappa ),I(t-\kappa ))}{X(S(t),I(t))}\right) \\&\quad \times f(\kappa ) e^{-\mu _{N} \kappa }(1-e^{-p_{l}\kappa })d\kappa \\&=-\rho (\tau _{L_{1}})\frac{\mu _{N}(1+\eta _{I} {\tilde{I}})(S(t)-{\tilde{S}})^{2}}{(1+\eta _{s} {\tilde{S}}+\eta _{I} {\tilde{I}})S(t)}-\rho (\tau _{L_{1}})X({\tilde{S}},{\tilde{I}})\\&\quad \times \left[ Y\left( \frac{{\tilde{S}}(1+\eta _{s} S(t)+\eta _{I} {\tilde{I}})}{(1+\eta _{s} {\tilde{S}}+\eta _{I} {\tilde{I}})S(t)}\right) \right] -[k_{l}(\mu _{N}+\theta _{T})+\theta _{T} \gamma _{l}]X({\tilde{S}},{\tilde{I}})\\&\quad \times \int _{0}^{\tau _{L_{1}}}\left[ Y\left( \frac{X(S(t-\kappa ),I(t-\kappa )){\tilde{L}}}{X({\tilde{S}},{\tilde{I}})L(t)}\right) \right] f(\kappa )e^{-(\mu _{N}+p_{l})\kappa }d\kappa \\&\quad -(\mu _{N}+\theta _{T})(\mu _{N}+k_{l}+\gamma _{l})X({\tilde{S}},{\tilde{I}})\int _{0}^{\tau _{L_{1}}}\left[ Y\left( \frac{X(S(t-\kappa ),I(t-\kappa )){\tilde{I}}}{X({\tilde{S}},{\tilde{I}})I(t)}\right) \right] \\&\quad \times f(\kappa )e^{-\mu _{N} \kappa } (1-e^{-p_{l}\kappa })d\kappa -k_{l}(\mu _{N}+\theta _{T})X({\tilde{S}},{\tilde{I}})\int _{0}^{\tau _{L_{1}}}\left[ Y\left( \frac{{\tilde{I}}L(t)}{I(t){\tilde{L}}}\right) \right] \\&\quad \times f(\kappa )e^{-(\mu _{N}+p_{l})\kappa }d\kappa -\theta _{T} \gamma _{l}X({\tilde{S}},{\tilde{I}})\int _{0}^{\tau _{L_{1}}}\left[ Y\left( \frac{T(t){\tilde{I}}}{I(t){\tilde{T}}}\right) +Y\left( \frac{L(t){\tilde{T}}}{T(t){\tilde{L}}}\right) \right] \\&\quad \times f(\kappa )e^{-(\mu _{N}+p_{l})\kappa }d\kappa -\theta _{T} \gamma _{I}(\mu _{N}+k_{l}+\gamma _{l}){\tilde{I}}\left[ Y\left( \frac{T(t){\tilde{I}}}{I(t){\tilde{T}}}\right) +Y\left( \frac{I(t){\tilde{T}}}{T(t){\tilde{I}}}\right) \right] \\&\quad -\rho (\tau _{L_{1}})X({\tilde{S}},{\tilde{I}})\left[ Y\left( \frac{1+\eta _{s} S(t)+\eta _{I} I(t)}{1+\eta _{s} S(t)+\eta _{I} {\tilde{I}}}\right) \right] +\rho (\tau _{L_{1}})X({\tilde{S}},{\tilde{I}})\\&\quad \times \left[ \frac{1+\eta _{s} S(t)+\eta _{I} I(t)}{1+\eta _{s} S(t)+\eta _{I} {\tilde{I}}}-1+\frac{(1+\eta _{s} S(t)+\eta _{I} {\tilde{I}})I(t)}{{\tilde{I}}(1+\eta _{s} S(t)+\eta _{I} I(t))}-\frac{I(t)}{{\tilde{I}}}\right] , \end{aligned}$$

where

$$\begin{aligned}&\frac{1+\eta _{s} S(t)+\eta _{I} I(t)}{1+\eta _{s} S(t)+\eta _{I} {\tilde{I}}}-1+\frac{(1+\eta _{s} S(t)+\eta _{I} {\tilde{I}})I(t)}{{\tilde{I}}(1+\eta _{s} S(t)+\eta _{I} I(t))}-\frac{I(t)}{{\tilde{I}}}\\&\quad =\frac{-\eta _{I}(1+\eta _{s} S(t))(I(t)-{\tilde{I}})^{2}}{{\tilde{I}}(1+\eta _{s} S(t)+\eta _{I} {\tilde{I}})(1+\eta _{s} S(t)+\eta _{I} I(t))}\le 0. \end{aligned}$$

Since the function \(Y(m(t))=m(t)-1-\ln m(t)\ge 0\), and \(Y(m(t))=0\) when and only when \(m(t)=1\), thereby \(\dot{H_{2}}(t)\le 0\), and \(\dot{H_{2}}(t)=0\) implies that \(S(t)={\tilde{S}},~L(t)={\tilde{L}},~I(t)={\tilde{I}},~T(t)={\tilde{T}}\). Therefore, in accordance with the LaSalle’s invariance principle [39], when \({\mathcal {R}}_0>1\), equilibrium \({\tilde{E}}\) of the model (4) exits and is globally asymptotically stable. \(\square \)

5 Numerical simulations

In this section, several numerical simulations are performed to demonstrate the validity of theoretical results of model (4). We compare the effect of discrete and distributed delays as well as different incidence functions on dynamic behavior of TB. Next, sensitivity analysis is conducted on the treatment rates of LTBI and infectious individuals, relapse rate, endogenous reactivation rate, protection level against disease of susceptible and infectious individuals separately. Finally, comparison between simulation results with model (4) and actual data of annual new TB cases in China is shown.

As a special case of model (4), the corresponding discrete delay TB model could be formulated as model (12),

$$\begin{aligned} \left\{ \begin{aligned} {\dot{S}}(t)&=\lambda _{s}-\frac{\beta S(t)I(t)}{1+\eta _{s} S(t)+\eta _{I} I(t)}-\mu _{N} S(t),\\ {\dot{L}}(t)&={\frac{\beta S(t-\tau _{L_{1}})I(t-\tau _{L_{1}})}{1+\eta _{s} S(t-\tau _{L_{1}})+\eta _{I} I(t-\tau _{L_{1}})}e^{-(\mu _{N}+p_{l})\tau _{L_{1}}}}-(\mu _{N}+k_{l}+\gamma _{l})L(t),\\ {\dot{I}}(t)&={\frac{\beta S(t-\tau _{L_{1}})I(t-\tau _{L_{1}})}{1+\eta _{s} S(t-\tau _{L_{1}})+\eta _{I} I(t-\tau _{L_{1}})}e^{-\mu _{N}\tau _{L_{1}}}(1-e^{-p_{l}\tau _{L_{1}}})}+k_{l}L(t)\\&\quad -(\mu _{N}+d_{TB}+\gamma _{I})I(t)+\theta _{T} T(t),\\ {\dot{T}}(t)&=\gamma _{l}L(t)+\gamma _{I}I(t)-\mu _{N} T(t)-\theta _{T} T(t). \end{aligned} \right. \nonumber \\ \end{aligned}$$
(12)

By calculation as same as model (4), the basic reproduction number of model (12) is formulated as

$$\begin{aligned} \hat{{\mathcal {R}}}_{0}&=\frac{\beta \lambda _{s} e^{-\mu _{N}\tau _{L_{1}}}(k_{l}(\mu _{N}+\theta _{T})+\theta _{T} \gamma _{l})e^{-p_{l}\tau _{L_{1}}}}{(\mu _{N}+\eta _{s}\lambda _{s})(\mu _{N}+k_{l}+\gamma _{l})[(\mu _{N}+\theta _{T})(\mu _{N}+d_{TB}+\gamma _{I})-\theta _{T} \gamma _{I}]}\\&\quad +\frac{\beta \lambda _{s} e^{-\mu _{N}\tau _{L_{1}}}(\mu _{N}+\theta _{T})(\mu _{N}+k_{l}+\gamma _{l})(1-e^{-p_{l}\tau _{L_{1}}})}{(\mu _{N}+\eta _{s}\lambda _{s})(\mu _{N}+k_{l}+\gamma _{l})[(\mu _{N}+\theta _{T})(\mu _{N}+d_{TB}+\gamma _{I})-\theta _{T} \gamma _{I}]}, \end{aligned}$$

and the DFE and EE of model (12) are \({\hat{E}}^{0}=(\frac{\lambda _{s}}{\mu _{N}},0,0,0)\) and \({\hat{E}}=({\hat{S}},{\hat{L}},{\hat{I}},{\hat{T}})\), where

$$\begin{aligned} {\hat{S}}&=\frac{\lambda _{s}-\textrm{e}^{(\mu _{N}+p_{l})\tau _{L_{1}}}(\mu _{N}+k_{l}+\gamma _{l}){\hat{L}}}{\mu _{N}},\\ {\hat{L}}&=\frac{\textrm{e}^{-(\mu _{N}+p_{l})\tau _{L_{1}}}\beta \lambda _{s}(\hat{{\mathcal {R}}}_{0}-1)}{(\beta +\mu _{N}\eta _{I})(\mu _{N}+k_{l}+\gamma _{l})[\hat{{\mathcal {R}}}_{0}-\frac{\eta _{s}\beta \lambda _{s}}{(\mu _{N}+\eta _{s}\lambda _{s})(\beta +\mu _{N}\eta _{I})}]},\\ {\hat{I}}&=\frac{((\mu _{N}+\theta _{T})(\mu _{N}+k_{l}+\gamma _{l})\textrm{e}^{p_{l}\tau _{L_{1}}}-\mu _{N}(\mu _{N}+\theta _{T}+\gamma _{l})){\hat{L}}}{(\mu _{N}+\theta _{T})(\mu _{N}+d_{TB}+\gamma _{I})-\theta _{T} \gamma _{I}},\\ {\hat{T}}&=\frac{[(\mu _{N}+\theta _{T})(\mu _{N}+d_{TB}+\gamma _{I})-\theta _{T} \gamma _{I}]\gamma _{l}}{(\mu _{N}+\theta _{T})[(\mu _{N}+\theta _{T})(\mu _{N}+d_{TB}+\gamma _{I})-\theta _{T} \gamma _{I}]}{\hat{L}}\\&\quad +\frac{\gamma _{I}((\mu _{N}+\theta _{T})(\mu _{N}+k_{l}+\gamma _{l})\textrm{e}^{p_{l}\tau _{L_{1}}}-\mu _{N}(\mu _{N}+\theta _{T}+\gamma _{l}))}{(\mu _{N}+\theta _{T})[(\mu _{N}+\theta _{T})(\mu _{N}+d_{TB}+\gamma _{I})-\theta _{T} \gamma _{I}]}{\hat{L}}. \end{aligned}$$

For convenience, we take

$$\begin{aligned} f(\kappa )=\frac{1}{\tau _{L_{1}}},~~0<\tau _{L_{1}}<\kappa , \end{aligned}$$

then we have

$$\begin{aligned} \int _{0}^{\tau _{L_{1}}}f(\kappa )d\kappa =\int _{0}^{\tau _{L_{1}}}\frac{1}{\tau _{L_{1}}}d\kappa =1. \end{aligned}$$

Hence the basic reproduction number of model (4) is rewritten as

$$\begin{aligned} \begin{aligned} {\mathcal {R}}_{0}&=\frac{\beta \lambda _{s}(\mu _{N}+\theta _{T})(1-e^{-\mu _{N}\tau _{L_{1}}})}{\mu _{N}\tau _{L_{1}}(\mu _{N}+\eta _{s}\lambda _{s})[(\mu _{N}+\theta _{T})(\mu _{N}+d_{TB}+\gamma _{I})-\theta _{T} \gamma _{I}]}+\frac{1}{(\mu _{N}+p_{l})}\\&\quad \times \frac{\beta \lambda _{s}\mu _{N}(\mu _{N}+\theta _{T}+\gamma _{l})(e^{-(\mu _{N}+p_{l})\tau _{L_{1}}}-1)}{\tau _{L_{1}}(\mu _{N}+\eta _{s}\lambda _{s})(\mu _{N}+k_{l}+\gamma _{l})[(\mu _{N}+\theta _{T})(\mu _{N}+d_{TB}+\gamma _{I})-\theta _{T} \gamma _{I}]}. \end{aligned}\nonumber \\ \end{aligned}$$
(13)

The values of parameters are taken as shown in Table 1, and the other parameters \(\lambda _{s}, \beta , \eta _{s}, \eta _{I}, \tau _{L_{1}}\) are chosen as given in the cases.

  1. 1.

    When \(\beta =0.023, \lambda _{s}=10, \eta _{s}=0.08, \eta _{I}=0.04, \tau _{L_{1}}=74\), we have \({\mathcal {R}}_0=0.9444<1\), as shown in Fig. 1a, b, the DFE \(E^{0}=(780,0,0,0)\) of model is globally asymptotically stable. Therefore, the result of Theorem 4 is true.

  2. 2.

    When \(\beta =0.023, \lambda _{s}=10, \eta _{s}=0.08, \eta _{I}=0.04, \tau _{L_{1}}=5\), we have \({\mathcal {R}}_0=1.2132>1\), the endemic equilibrium \({\tilde{E}}=(130.4,35.7,63.5,195.8)\) of model (4) is globally asymptotically stable as shown in Fig. 1e, f. Therefore, the result of Theorem 5 is true.

Table 1 Values of parameters
Full size table
Fig. 1
figure 1

Time series phases of solutions \((S(t),L(t),I(t),T(t))^T\) and 3-dimension phases of solutions S(t), L(t), I(t) of model (4). a, b: \(\tau _{L_{1}}=74\) with initial functions \((S(\nu ,L(\nu ),I(\nu ),T(\nu ))=(10+2\sin (\nu )+40k,5+2sin(\nu )+10k,5+2sin(\nu )+10k,5+2sin(\nu )+35k)\), \(k=1,2,\ldots ,20\), for all \(\nu \in [-74,0]\); c, d: \(\tau _{L_{1}}=35\) with initial functions \((S(\nu ),L(\nu ),I(\nu ),T(\nu ))=(80+2\sin (\nu )+12k,5+2sin(\nu )+5k,5+2sin(\nu )+4k,100+2sin(\nu )+12k)\), \(k=1,2,\ldots ,20\), for all \(\nu \in [-35,0]\); e, f: \(\tau _{L_{1}}=5\) with initial functions \((S(\nu ),L(\nu ),I(\nu ),T(\nu ))=(100+2\sin (\nu )+10k,10+2sin(\nu )+6k,10+2sin(\nu )+5k,80+2sin(\nu )+12k)\), \(k=1,2,\ldots ,20\), for all \(\nu \in [-5,0]\)

Full size image
Fig. 2
figure 2

Time series phases of solutions \((S(t),L(t),I(t),T(t))^T\) and 3-dimension phases of solutions S(t), L(t), I(t) of model (12). a, b: \(\tau _{L_{1}}=74\) with initial functions \((S(\nu ),L(\nu ),I(\nu ),T(\nu ))=(200+2\sin (\nu )+25k,10+2sin(\nu )+12k,10+2sin(\nu )+10k,20+2sin(\nu )+32k)\), \(k=1,2,\ldots ,20\), for all \(\nu \in [-74,0]\); c, d: \(\tau _{L_{1}}=35\) with initial functions \((S(\nu ),L(\nu ),I(\nu ),T(\nu ))=(200+2\sin (\nu )+25k,10+2sin(\nu )+12k,10+2sin(\nu )+10k,20+2sin(\nu )+32k)\), \(k=1,2,\ldots ,20\), for all \(\nu \in [-35,0]\); e, f: \(\tau _{L_{1}}=5\) with initial functions \((S(\nu ),L(\nu ),I(\nu ),T(\nu ))=(80+2\sin (\nu )+5k,5+2sin(\nu )+8k,5+2sin(\nu )+5k,120+2sin(\nu )+6k)\), \(k=1,2,\ldots ,20\), for all \(\nu \in [-5,0]\)

Full size image

Next, we compare the difference of the reproduction number between models (4) and (12) as \(\tau _{L_{1}}\) changes. It can be seen that the following conclusion holds, and the values of other parameters are chosen as Case 1 and 2.

$$\begin{aligned} \left\{ \begin{aligned}&{\mathcal {R}}_{0}\ge 1, \hat{{\mathcal {R}}}_{0}\ge 1, ~0<\tau _{L_{1}}<32.44.\\&{\mathcal {R}}_{0}\ge 1, \hat{{\mathcal {R}}}_{0}\le 1, ~32.44<\tau _{L_{1}}<62.69.\\&{\mathcal {R}}_{0}\le 1, \hat{{\mathcal {R}}}_{0}\le 1, ~\tau _{L_{1}}>62.69. \end{aligned} \right. \end{aligned}$$
(14)

If \(\tau _{L_{1}}=74\), we can see \({\mathcal {R}}_0=0.9512<1\), as shown in Fig. 1a, b, the DFE \(E^{0}=(780,0,0,0)\) of model (4) is globally asymptotically stable; and \(\hat{{\mathcal {R}}}_0=0.6367<1\), the DFE \({\hat{E}}^{0}=(780,0,0,0)\) of model (12) is globally asymptotically stable (Fig. 2a, b). If \(\tau _{L_{1}}=35\), we can see \({\mathcal {R}}_0=1.1193>1\), the endemic equilibrium \({\tilde{E}}=(198.5,29.5,32.7,130.3)\) of model (4) is globally asymptotically stable (Fig. 1c, d); and \(\hat{{\mathcal {R}}}_0=0.9762<1\), the DFE \({\hat{E}}^{0}=(780,0,0,0)\) of model (12) is globally asymptotically stable (Fig. 2c, d). If \(\tau _{L_{1}}=5\), we can see \({\mathcal {R}}_0=1.2132>1\), the endemic equilibrium \({\tilde{E}}=(130.4,35.7,63.5,195.8)\) of model (4) is globally asymptotically stable (Fig. 1e, f); and \(\hat{{\mathcal {R}}}_0=1.2055>1\), the endemic equilibrium \({\hat{E}}=(134.1,56.6,35.3,183.7)\) of model (12) is globally asymptotically stable (Fig. 2e, f).

The details of above numerical simulations for both models (4) and (12) are as in Table 2,

Table 2 Numerical simulations for models (4) and (12)
Full size table
Fig. 3
figure 3

a: Effect of the protection level \(\eta _{s}\) on \({\mathcal {R}}_{0}\) with \(\beta =0.03\), all other parameters as in Case 2. b: Contour plot of \({\mathcal {R}}_{0}\) as a function of \(\eta _{s}, \beta \), all other parameters as in Case 2. c: Effect of the protection level \(\eta _{I}\) on the number of infectious individuals, all other parameters as in Case 2. d: Sensitivity indicators of \({\mathcal {R}}_{0}\) for different parameters with \(k_{l}=0.01, \theta _{T}=0.005\), all other parameters as in Case 2. e: The number of new TB cases in China from 2015 to 2021

Full size image

We find that there exists evident difference of dynamics between models (4) and (12). When the latency delay \(\tau _{L_{1}}\) increases, the dynamical behavior of model (12) with discrete delay is as same as that of model (4) with distributed delay under the same conditions when \(0<\tau _{L_{1}}<32.44\) or \(\tau _{L_{1}}>62.69\). There may also exist the opposite dynamical behavior between model (4) and model (12), i.e., if \(32.44<\tau _{L_{1}}<62.69\), the disease in model (12) is extinct, while it continues to spread in model (4). Obviously, the disease is more persistent in the model (4) with distributed delay than the model (12) with discrete delay.

It can be seen from Fig. 3a, \({\mathcal {R}}_0\) increases as the protection level \(\eta _{s}\) against the disease of susceptible individuals decreases. When \(\eta _{s}>0\), the incidence function is Beddington–DeAngelis type, while it is saturated incidence function for the infectious when \(\eta _{s}=0\). In particular, as \(\eta _{s}\) decreases from 0.1 to 0, susceptible individuals no longer take any protection, the incidence function changes from Beddington–DeAngelis type to saturated incidence function and the value of \({\mathcal {R}}_0\) increases from 1.27 to around 100, which is quite high.

In Fig. 3b, it shows that a lower value of \(\beta \) is required to maintain the same value of \({\mathcal {R}}_0\) when \(\eta _{s}\) decreases, which means when the susceptible individuals take no protection, their contact rate with infectious individuals needs to be controlled for the purpose of reducing the transmission rate so that \({\mathcal {R}}_0\) can be kept at the same threshold level.

It can be seen from representation (13) of \({\mathcal {R}}_0\), the protection level \(\eta _{I}\) against the disease of infectious individuals is not related to \({\mathcal {R}}_0\). However, it is shown that raising the protection level of infectious individuals will bring about a reduction of infectious population in Fig. 3c.

Sensitivity indicators of \({\mathcal {R}}_{0}\) for parameter q is

$$\begin{aligned} r_{q}^{{\mathcal {R}}_0}=\frac{\partial {\mathcal {R}}_0}{\partial q}\times \frac{q}{{\mathcal {R}}_0}. \end{aligned}$$

In Fig. 3d, sensitivity indicators of \({\mathcal {R}}_{0}\) for the cure rates \(\gamma _{l}\), \(\gamma _{I}\) for LTBI and infectious individuals, the relapse rate \(\theta _{T}\), the disease progression rate \(p_{l}\) and the endogenous reactivation rate \(k_{l}\) of latent individuals is demonstrated. It should be mentioned that

$$\begin{aligned} \frac{\partial {\mathcal {R}}_{0}}{\partial \gamma _{l}}&=\frac{\beta \lambda _{s}\mu _{N}(e^{-(\mu _{N}+p_{l})\tau _{L_{1}}}-1)(k_{l}-\theta _{T})}{\tau _{L_{1}}(\mu _{N}+\eta _{s}\lambda _{s})(\mu _{N}+k_{l}+\gamma _{l})^{2}[(\mu _{N}+\theta _{T})(\mu _{N}+d_{TB}+\gamma _{I})-\theta _{T} \gamma _{I}]}\\&\quad \times \frac{1}{(\mu _{N}+p_{l})}. \end{aligned}$$

Therefore, when \(k_{l}>\theta _{T}\), \(\frac{\partial {\mathcal {R}}_{0}}{\partial \gamma _{l}}<0\). However, when \(k_{l}<\theta _{T}\), \(\frac{\partial {\mathcal {R}}_{0}}{\partial \gamma _{l}}>0\), it means that \({\mathcal {R}}_{0}\) increases with the increasing treatment rate \(\gamma _{l}\) of LTBI, which is not quite in line with the commonly accepted view [4], mainly due to the model assumption and the higher relapse rate.

Table 3 New cases from 2015 to 2021 in China
Full size table

Next, a simulation of annual new TB cases in China from 2015 to 2021 is performed with model (4). We choose the recruitment rate \(\lambda _{s}=1.661\times 10^{7}\), \(N(0)=1.36782\times 10^{9}\), \(S(0)=7.4546\times 10^{8}\), \(I(0)=6.2927\times 10^{6}\), \(T(0)=2.7067\times 10^{7}\) which is calculated in the literature [40], thus \(L(0)=N(0)-S(0)-I(0)-T(0)=5.89\times 10^{8}\). The value of natural mortality rate is chosen as \(\mu _{N}=1/76.34\) in accordance with the China Statistical Yearbook [41], time delay \(\tau _{L_{1}}\) of fast-progressing latency is 5 years [13] and the value of the remaining parameters are taken as in Table 1. The actual data is obtained from the Chinese Center for Disease Control and Prevention [42] as in Table 3 and the number of new TB cases is represented by function \(g(t)=\int _{0}^{\tau _{L_{1}}}{\frac{\beta S(t-\kappa )I(t-\kappa )}{1+\eta _{s} S(t-\kappa )+\eta _{I} I(t-\kappa )}e^{-\mu _{N}\kappa }f(\kappa )d\kappa }\). Then when \(\beta =0.0058, \eta _{s}=0.318, \eta _{I}=0.65\), the comparison between the simulation results and the actual data of the number of annual new TB cases in China is shown in Fig. 3e. It can be seen that the simulation results are well consistent with the actual data, which means that model (4) is also consistent with the real circumstance of TB transmission.

6 Conclusion

In this article, an endogenous-reactivated TB model with Beddington–DeAngelis incidence, distributed delay and relapse is proposed. We prove the local (and global) stability of equilibria on the basis of the basic reproduction number \({\mathcal {R}}_0\). We find that the DFE is globally asymptotically stable when \({\mathcal {R}}_0<1\), meanwhile the EE is globally asymptotically stable when \({\mathcal {R}}_0>1\). Comparing models (4) and (12), we find that the dynamic behavior between distributed and discrete delays may be same or opposite, and TB is more persistent in the model with distributed delay than a model with discrete delay. Besides, we find that increase the protection level \(\eta _{s}\), \(\eta _{I}\) of susceptible and infectious individuals is very crucial for the control of TB. Finally, we discuss the effect of treatment rate \(\gamma _{l}\) for LTBI, treatment rate \(\gamma _{I}\) for infectious individuals, the relapse rate \(\theta _{T}\), the the disease progression rate \(p_{l}\), and the endogenous reactivation rate \(k_{l}\) respectively. The results suggest that increasing the treatment rates is beneficial to disease control, while the higher relapse rate and disease progression rate could accelerate the spread of TB. The comparison between simulation results and actual data of annual new TB cases in China from 2015 to 2021 demonstrate the feasibility of the model we construct.

In fact, TB transmission is very complicated in reality, especially, we have not yet considered exogenous reinfection in model (4), which is an essential factor of TB transmission and could cause backward bifurcations [6, 13,14,15]. Therefore, model (4) with exogenous reinfection would be a more meaningful research subject in the future.