Analysis of Stochastic SIRC Model with Cross Immunity Based on Ornstein–Uhlenbeck Process

Abstract

In this paper, we analyze a stochastic SIRC model with Ornstein–Uhlenbeck process. Firstly, we give the existence and uniqueness of global solution of stochastic SIRC model and prove it. In addition, the existence of ergodic stationary distributions for stochastic SIRC system is proved by constructing a suitable series of Lyapunov functions. A quasi-endemic equilibrium related to endemic equilibrium of deterministic systems is defined by considering randomness. And we obtain the probability density function of the linearized system near the equilibrium point. After the proof of probability density function, the sufficient condition of disease extinction is given and proved. We prove the theoretical results in the paper by numerical simulation at the end of the paper.

1 Introduction

Until now, COVID-19 has been considered the most devastating infectious disease to affect humans worldwide. Infected persons transmit the disease to others mainly through person-to-person transmission [1], including airborne transmission and contact transmission. Therefore, it is essential to study the spread and control of COVID-19 and determine the conditions for the extinction of the epidemic [2].

Since 1972, Kermack and Mckendrick began to link the spread of infectious diseases to mathematics [3]. At present, the construction of mathematical models of infectious diseases and epidemics has become an important tool for analyzing and investigating the characteristics of diseases. Accurate and precise mathematical model plays an important part in decision making [4]. For the spread of COVID-19, we consider the most standard epidemic-susceptible-recovered(SIR) epidemic model [5].

If you’re vaccinated against a particular virus and you develop immunity to another virus, we call this cross-immunity. In the spread of COVID-19, some vaccines also provide cross-immunity to the novel coronavirus. Casagnandi [6] and Rihan et al. [7] introduced the SIRC model to analyze different infectious behavior by inserting a new state C between Susceptible (S) and Recovered (R). Compartment C is used to describe COVID-19 infected persons in a state of cross-immunity. In terms of cross-immunity, Kwang et al. [8] developed a two-strain SIR model for inferring the cross-immune responses of different strains. Shrock et al. [9] suggest that perhaps previous CoV infection infers an “immune response memory”. Therefore, we study a stochastic SIRC epidemiological model that includes cross-immune states. Based on the existing literature, we know that few scholars have considered the impact of cross-immune status on COVID-19 transmission [10].

The rest of this article is structured as follows. In the part 2, we show the stochastic SIRC model including the mean reversion process Ornstein–Uhlenbeck process. The existence and uniqueness of stochastic systems (4) are proved in the part 3. In the part 4, the existence of ergodic stationary distribution of stochastic system (4) is proved by constructing a suitable Lyapunov function. In the part 5, we use the corresponding Foker-Planck equation to derive the explicit expression of the probability density function for the stationary distribution $\pi$(.) of the stochastic SIRC system (4). Sufficient conditions for the extinction of infectious diseases are given and proved in Sect. 6. Finally, we prove the theoretical results through numerical simulation and summarize the work of the whole paper at the end of the paper, and further give the research direction of related problems.

2 Model Formulation and Local Stability of the Equilibrium States

2.1 Mathematical Model

In this paper, we use the SIRC model that includes cross-immune status because it can effectively describe the transmission mechanism of COVID-19 [11]. SIRC model adopts the following form: [7, 10] 

$$\begin{aligned} \left\{ \begin{array}{l} {\dot{S}}(t)=\eta (1-S(t))-\xi S(t)I(t)+\beta C(t),~\\ {\dot{I}}(t)=\xi S(t)I(t)+\sigma \xi C(t)I(t)-(\eta +\alpha )I(t),~\\ {\dot{R}}(t)=(1-\sigma )\xi C(t)I(t)+\alpha I(t)-(\eta +\gamma )R(t),~\\ {\dot{C}}(t)=\gamma R(t)-\xi C(t)I(t)-(\eta +\beta )C(t), \end{array} \right. \end{aligned}$$

(1)

where S(t), I(t), R(t), C(t) represent the density of susceptible individuals, infected individuals, recovered individuals and cross-immune individuals from the disease at time t, respectively. $\eta$ denotes the natural mortality rate, which is equal to the rate of newborns. $\beta$ represents the rate of cross-immune individuals C(t) becomes susceptible individuals S(t). $\xi$ denotes the infection rate of susceptible individuals S(t) infected with infectious disease to become infected individuals I(t). $\sigma$ is the average reinfection probability of a cross-immune individuals, where we assume that $\sigma <1$. $\alpha$ denotes the recovery rate of infected individuals I(t) to recovered individuals R(t). $\gamma$ is the rate at which the recovered individuals R(t) becomes the cross-immune individuals C(t) and moves from total to partial immunity. All of the parameters $\beta$, $\xi$, $\sigma$, $\alpha$, $\gamma$ are assumed to be positive.

For the system (1) mentioned above, we can get

$$\begin{aligned} d(S(t)+I(t)+R(t)+C(t))=[\eta -\eta (S(t)+I(t)+R(t)+C(t))]dt. \end{aligned}$$

Then we obtain

$$\begin{aligned} S(t)+I(t)+R(t)+C(t)\equiv 1 \quad if\quad S(0)+I(0)+R(0)+C(0)=1. \end{aligned}$$

Let ${\mathbb {R}}^n$ be an n-dimensional Euclidean space and ${\mathbb {R}}_+^n=\{(x_1,\ldots ,x_n)\in {\mathbb {R}}^n|x_i>0,1\le i\le n\}.$ Thus the region

$$\begin{aligned} \Gamma _0=\{(S,I,R,C)\in {\mathbb {R}}_+^4: S+I+R+C=1\} \end{aligned}$$

is a positively invariant set of system (1), then, model (1) is simplified to analyze a three-dimensional system as follows:

$$\begin{aligned} \left\{ \begin{array}{l} {\dot{I}}(t)=\xi (1-I(t)-R(t)-C(t))I(t)+\sigma \xi C(t)I(t)-(\eta +\alpha )I(t),~\\ {\dot{R}}(t)=(1-\sigma )\xi C(t)I(t)+\alpha I(t)-(\eta +\gamma )R(t),~\\ {\dot{C}}(t)=\gamma R(t)-\xi C(t)I(t)-(\eta +\beta )C(t). \end{array} \right. \end{aligned}$$

(2)

The above system has two equilibria, where the basic regeneration number is defined as $R_0=\frac{\xi }{\eta +\alpha }$, the disease-free equilibrium is defined as $E_0=(I_0,R_0,C_0)$=(0,0,0). In addition, if $R_0>1$, we can easily get a unique endemic equilibrium point $E_*=(I_*,R_*,C_*)$, $I_*,R_*,C_*$ are defined as follows: 

$$\begin{aligned}{} & {} R_*=\frac{\alpha I_*(\xi I_*+\eta +\beta )}{[(\eta +\gamma )-(1-\sigma )\gamma ]\xi I_*+(\eta +\beta )(\eta +\gamma )},\\{} & {} C_*=\frac{\gamma \alpha I_*}{[(\eta +\gamma )-(1-\sigma )\gamma ]\xi I_*+(\eta +\beta )(\eta +\gamma )}, \end{aligned}$$

and the value of $I_*$ is the root of the following equation $h_1I_*^2+h_2I_*+h_3=0$, where

$$\begin{aligned} \begin{aligned}&h_1=\eta \xi (\eta +\alpha +\sigma \gamma ),\\&h_2=\eta \xi [\alpha (2\eta +\gamma +\beta )+(\eta +\beta ) (\eta +\gamma )+(\eta +\sigma \gamma )(\eta -\xi )],\\&h_3=\eta (\eta +\beta )(\eta +\gamma )(\eta +\alpha )(1-R_0). \end{aligned} \end{aligned}$$

2.2 Stochastic Model

However, in real life, according to the existing literature, the spread of infectious diseases and the formulation of control policies are affected by random factors [12]. For example, Nadjat et al. [13] showed that population density is an important factor affecting the spread of COVID-19. In [14], Wilfried Allaerts proposed that national public media and government advisory bodies play an important role in policy formulation. Therefore, we have to consider the influence of random factors on the mathematical model. The stochastic model has gradually become the core of various scholars’ research on the behavior of infectious diseases. To simulate the stochastic effects, we usually introduce stochastic models with linear perturbations [15,16,17,18,19,20].

For the linear perturbation, we assume that both $\xi (t)$ and $\beta (t)$ are influenced by the linear white noises: so we get

$$\begin{aligned} \xi (t)={\bar{\xi }}+\frac{\sigma _1dB_1(t)}{dt},\quad \beta (t)={\bar{\beta }}+\frac{\sigma _2dB_2(t)}{dt}. \end{aligned}$$

(3)

By calculating two equations ${\mathbb {E}}[\xi (t)]={\bar{\xi }}$ and ${\mathbb {E}}[\beta (t)]={\bar{\beta }}$, give the average values of $\xi (t)$ and $\beta (t)$ respectively. $B_i(t) (i = 1,2)$ are two independent standard Brownian motions, and $\sigma _i$ (i = 1,2) are the strength of each Brownian motion.

However, linear perturbation and (3) are something irrational. Our biological explanation for this is as follows: for any time interval [0, t], integrating (3) from 0 to t, then we have

$$\begin{aligned}{} & {} \frac{1}{t}\int _{0}^{t}\xi (s)ds={\bar{\xi }}+\sigma _1\frac{B_1(t)}{t} \sim {\mathbb {N}}\bigg ({\bar{\xi }},\frac{\sigma _1^2}{t}\bigg ),\\{} & {} \frac{1}{t}\int _{0}^{t}\beta (s)ds={\bar{\beta }}+\sigma _2\frac{B_2(t)}{t} \sim {\mathbb {N}}\bigg ({\bar{\beta }},\frac{\sigma _2^2}{t}\bigg ). \end{aligned}$$

This states that as $t\rightarrow 0$, the variance of $\xi (t)$ and $\beta (t)$ will go to infinity, which produces the unreasonable result that $\xi (t)$ and $\beta (t)$ fluctuations will become larger in a small time interval.

In this paper, a new method for simulating random disturbances is presented. Ornstein–Uhlenbeck process [21,22,23,24,25] plays an important role in the exchange rate of money, sale price of commodities and interest rate in economics. Dixit and Pindyck [26] analyzed Ornstein–Uhlenbeck process (Dixit & Pindyck model) for the first time in finance, which was inspired by it. We use the Ornstein–Uhlenbeck process in this paper to simulate the interference of random factors in the mathematical model in the biological population. In [27], Zhou et al., in their paper, studied a stochastic non-autonomous population model of two mean-reverting Ornstein–Uhlenbeck processes. Song et al. [28] studied a stochastic SVEIS infectious disease model with Ornstein–Uhlenbeck processes and presented the conditions for the stationary distribution and extinction of the stochastic model, which also inspired me. Here we assume that the contact or transmission rate $\xi$ and the rate at which the cross-immune population becomes susceptible again $\beta$ in the system (2) satisfy Ornstein–Uhlenbeck process. Then we have the results of $\xi (t)$ and $\beta (t)$ under the influence of the mean-reverting Ornstein–Uhlenbeck process.

$$\begin{aligned} d\xi (t)=\theta _1({{\bar{\xi }}}-\xi (t))dt+\sigma _1dB_1(t),\quad d\beta (t)=\theta _2({{\bar{\beta }}}-\beta (t))dt+\sigma _2dB_2(t). \end{aligned}$$

According to the conclusion in reference [29], we obtain that $\xi (t)$ and $\beta (t)$ have unique explicit solutions of the form defined as follows

$$\begin{aligned} \xi (t){} & {} ={\bar{\xi }}+(\xi (0)-{\bar{\xi }})e^{-\theta _1t}+\sigma _1 \int _{0}^{t}e^{-\theta _1(t-s)}dB_1(s),\\ \beta (t){} & {} ={\bar{\beta }}+(\beta (0)-{\bar{\beta }})e^{-\theta _2t} +\sigma _2\int _{0}^{t}e^{-\theta _2(t-s)}dB_2(s). \end{aligned}$$

According to the above formula and references [29], it shows that $\xi (t)$ follows the Gaussian distribution ${\mathbb {N}}({\mathbb {E}}(\xi (t)),Var(\xi (t)))$ on [0, t],where ${\mathbb {E}}(\xi (t))={\bar{\xi }}+(\xi (0)-{\bar{\xi }})e^{-\theta _1t}$ and $Var(\xi (t))=\frac{\sigma _1^2}{2\theta _1}(1-e^{-2\theta _1t})$. Because of $\lim \nolimits _{t\rightarrow \infty }{\mathbb {E}}(\xi (t))={\bar{\xi }}$ and $\lim \lim \nolimits _{t\rightarrow \infty }Var(\xi (t))=\frac{\sigma _1^2}{2\theta _1}$. Obviously, $\xi (t)$ follows the Gaussian distribution ${\mathbb {N}}({\bar{\xi }},\frac{\sigma _1^2}{2\theta _1})$ as t tends to infinity.

Similarly, the correlation analysis of $\beta (t)$ is similar to that of $\xi (t)$, thus we can conclude that $\beta (t)$ also follows the Gaussian distribution ${\mathbb {N}}({\bar{\beta }},\frac{\sigma _2^2}{2\theta _2})$ as t tends to infinity.

In summary, in this article, it is reasonable to characterize random factors in infectious disease models by introducing Ornstein–Uhlenbeck processes. Therefore, define an invariant set

$$\begin{aligned} \Gamma =\bigg \{(I,R,C,\xi ,\beta )\in {\mathbb {R}}_+^3\times {\mathbb {R}}^2: I+R+C<1\bigg \}, \end{aligned}$$

then we get the following stochastic IRC system incorporating Ornstein–Uhlenbeck process:

$$\begin{aligned} \left\{ \begin{array}{l} {\dot{I}}(t)=\xi ^+ (1-I(t)-R(t)-C(t))I(t)+\sigma \xi ^+ C(t)I(t)-(\eta +\alpha )I(t),~\\ {\dot{R}}(t)=(1-\sigma )\xi ^+ C(t)I(t)+\alpha I(t)-(\eta +\gamma )R(t),~\\ {\dot{C}}(t)=\gamma R(t)-\xi ^+ C(t)I(t)-(\eta +\beta ^+)C(t),~\\ d\xi (t)=\theta _1({{\bar{\xi }}}-\xi (t))dt+\sigma _1dB_1(t),~\\ d\beta (t)=\theta _2({{\bar{\beta }}}-\beta (t))dt+\sigma _2dB_2(t), \end{array} \right. \end{aligned}$$

(4)

where $\xi ^+(t)=\max \{\xi (t),0\}$, in the same way, $\beta ^+(t)=\max \{\beta (t),0\}$. In addition, we write $a\wedge b$ as $\min \{a,b\}$, similarly, we write $a\vee b$ as $\max \{a,b\}$.

3 Existence and Uniqueness of the Global Positive Solution

Theorem 3.1

For any initial value $(I(0),R(0),C(0),\xi (0),\beta (0))\in \Gamma$, there exists a unique solution (I(t), R(t), 

$C(t),\xi (t),\beta (t))$ to the system (4) on t$\ge$ 0 and the solution will remain in $\Gamma$ with probability one, namely, the solution $(I(t), R(t),C(t),\xi (t),\beta (t))\in \Gamma$ for all t$\ge$ 0 almost surely (a.s.).

Proof

For any initial value $(I(0),R(0),C(0),\xi (0),\beta (0))\in \Gamma$, the coefficients of system (4) are locally Lipschitz continuous [30], so there is a unique local solution $(I(t), R(t),C(t),\xi (t),\beta (t))\in \Gamma$ on t$\in$ [0,$\tau _e$], where $\tau _e$ is an explosion time [31]. To testify that $(I(t), R(t),C(t),\xi (t),\beta (t))$ is global, we need to prove that $\tau _e=\infty$ a.s. Set $s_0> 0$ big enough to make that each element of $(I(0),R(0),C(0),\xi (0),\beta (0))$ are all on the interval [ $\frac{1}{s_0}$,$s_0$]. For each integer $s\ge s_0$, let $Z(t)=(I(t),R(t),C(t))$, and let’s define the stopping time $\tau _s$ as follows [32]

$$\begin{aligned} \tau _s=\inf \bigg \{t\in \left( 0,\tau _e\right) |min\{Z(t),e^{\xi (t)},e^{\beta (t)}\}\le \frac{1}{s}\quad or\quad max\{Z(t),e^{\xi (t)},e^{\beta (t)}\}\ge s\bigg \}, \end{aligned}$$

where throughout our paper, we set inf{$\emptyset \}=\infty$. Obviously, $\tau _s$ is increasing as s$\rightarrow \infty$. Set $\tau _{\infty }=\lim \nolimits _{s \rightarrow \infty }\tau _s$, then we derive that $\tau _{\infty }\le \tau _e$ a.s. If we show that $\tau _{\infty }=\infty$ a.s., then $\tau _e=\infty$ a.s., then $(I(t), R(t),C(t),\xi (t),$

$\beta (t))\in \Gamma$ a.s. for all t $\ge$0.

If $\tau _{\infty }<\infty$, suppose there is that a pair of constants ${\tilde{t}}>0$ and $\varepsilon \in (0,1)$ such that $\mathbb P\{\tau _{\infty }\le {\tilde{t}}\}>\varepsilon$, so there is an integer $s_1\ge s_0$, which makes

$$\begin{aligned} {\mathbb {P}}\{\tau _{s}\le {\tilde{t}}\}\ge \varepsilon , \end{aligned}$$

(5)

for all s$\ge s_1$. We define a non-negative $C^2$-function V: ${\mathbb {R}}_+^3\times {\mathbb {R}}^2\rightarrow {\mathbb {R}}_+$,

$$\begin{aligned} V(I(t),R(t),C(t),\xi (t),\beta (t)){} & {} =(I-1-\ln I)+(R-1-\ln R)+(C-1-\ln C)\\{} & {} \quad +[(1-I-R-C)-1-\ln (1-I-R-C)] \\{} & {} \quad +\frac{\xi ^2}{2}+\frac{\beta ^2}{2}. \end{aligned}$$

Using It${\hat{o}}$’s formula [30], we get

$$\begin{aligned} dV={\mathcal {L}}Vdt+\sigma _1\xi dB_1(t)+\sigma _2\beta dB_2(t). \end{aligned}$$

In Appendix B of the article by Zhou et al. [15], the definition of differential operators ${\mathcal {L}}$ is given, then

$$\begin{aligned} {\mathcal {L}}V{} & {} =\left( -\frac{1}{I}\right) [\xi ^+ (1-I-R-C)I+\sigma \xi ^ + CI-(\eta +\alpha )I]\\{} & {} \quad +\left( -\frac{1}{R}\right) [(1-\sigma )\xi ^+ CI+\alpha I -(\eta +\gamma )R]+\left( -\frac{1}{C}\right) [\gamma R-\xi ^+ CI-(\eta +\beta ^+)C]\\{} & {} \quad +\left( \frac{1}{1-I-R-C}\right) [\xi ^+(1-I-R-C)-\eta (I+R+C)-\beta ^+C]\\{} & {} \quad +\theta _1\xi ({\bar{\xi }}-\xi )+\frac{\sigma _1^2}{2}+\theta _2\beta ({\bar{\beta }}-\beta )+\frac{\sigma _2^2}{2}\\{} & {} \le 3\eta +2\xi ^++\alpha +\gamma +\beta ^++\frac{\sigma _1^2}{2}+\frac{\sigma _2^2}{2}+\theta _1\xi ({\bar{\xi }}-\xi ) +\theta _2\beta ({\bar{\beta }}-\beta )\\{} & {} \le 3\eta +2|\xi |+|\beta |+\alpha +\gamma +\frac{\sigma _1^2+\sigma _2^2}{2} -\theta _1\xi ^2(t)+\theta _1{\bar{\xi }}|\xi |-\theta _2\beta ^2+\theta _2{\bar{\beta }}|\beta |\\{} & {} \le 3\eta +\alpha +\gamma +\frac{\sigma _1^2+\sigma _2^2}{2} +\frac{(\theta _1{\bar{\xi }}+2)^2}{4\theta _1} +\frac{(\theta _2{\bar{\beta }}+1)^2}{4\theta _2}:=K, \end{aligned}$$

where K is a constant satisfying the condition independent of S, I, R, C and t. The rest of the proof is similar to Mao et al. [33]’s article and hence is omitted. So we have completed the proof of Theorem 3.1. $\square$

4 Existence of a Stationary Distribution

In this part, we are concerned about the existence of a stationary distribution in the system (4), which matters whether infectious diseases will continue to spread. To prove the existence of a stationary distribution for system (4), we first introduce Lemma 4.1 before the proof.

Let X(t) be a homogeneous Markov process in $\Omega _l$ ($\Omega _l$ denotes the l-dimensional Euclidean space) satisfying the following stochastic differential equation.

$$\begin{aligned} dX(t)=b(t,X(t))dt+\sum _{j=1}^{k}\sigma _j(t,X(t))dB_j(t). \end{aligned}$$

(6)

Lemma 4.1

(Khasminskii [34]). Let the vectors b(s, x), $\sigma _1(s,x),\ldots , \sigma _k(s,x)(s\in [t_0,T],x\in {\mathbb {R}}^k)$ be continuous functions of (s,x), such that for some constant B the following conditions hold in the entire domain of definition:

$$\begin{aligned} \begin{aligned} |b(s,x)-b(s,y)|+\sum _{j=1}^{k}|\sigma _j(s,x)-\sigma _j(s,y)|\le B|x-y|,\\ |b(s,x)|+\sum _{j=1}^{k}|\sigma _j(s,x)|\le B(1+|x|). \end{aligned} \end{aligned}$$

Moreover, there exists a non-negative function $V^*(x)$ such that

$$\begin{aligned} {\mathcal {L}}V^*(x)\le -1,\quad \forall x\in {\mathbb {R}}^k\backslash {\mathbb {H}}, \end{aligned}$$

where ${\mathbb {H}}$ is a compact subset defined on ${\mathbb {R}}^k$.

Then the Markov process (6) has at least one stationary solution X(t), which has a stationary distribution $\varpi$(.) on ${\mathbb {R}}^k$.

Define a critical value,

$$\begin{aligned} R_0^h=\frac{{\bar{\xi }}}{\eta +\alpha +\frac{\sigma _1}{\sqrt{2\theta _1}}}. \end{aligned}$$

Theorem 4.2

Assume that $R_0^h>1$. For any initial value $(I(0),R(0),C(0),\xi (0),\beta (0))\in \Gamma$, the system (4) has a stationary distribution $\pi$.

Proof

First we give a definition of a $C^2$-function $V_1$ as follows

$$\begin{aligned} V_1=-\ln I+a_1(R+C)+a_2\bigg (\frac{(\xi -{\bar{\xi }})^2}{2}\bigg ), \end{aligned}$$

where $a_1$ and $a_2$ are positive constants, and they will be fixed later. Using It${\hat{o}}$’s formula [30], we have

$$\begin{aligned} \begin{aligned} {\mathcal {L}}V_1&=-\xi ^+(1-I-R-C)-\sigma \xi ^+C+(\eta +\alpha )+a_1(\alpha I-\eta R-\eta C-\sigma \xi ^+ CI)\\ {}&\quad +a_2\left( \theta _1\left( \xi -{\bar{\xi }}\right) ^2+\frac{\sigma _1^2}{2}\right) \\&\le -{\bar{\xi }}(1-I-R-C)+|{\bar{\xi }}-\xi ^+|(1-I-R-C)+\eta +\alpha \\ {}&\quad +a_1(\alpha I-\eta R-\eta C) +a_2\left( -\theta _1(\xi -{\bar{\xi }})^2+\frac{\sigma _1^2}{2}\right) , \end{aligned} \end{aligned}$$

where $\quad a_1=\frac{{\bar{\xi }}}{\eta },a_2=\frac{1}{\sigma _1\sqrt{2\theta _1}}$, then

$$\begin{aligned} \begin{aligned} {\mathcal {L}}V_1&\le -{\bar{\xi }}+\eta +\alpha +{\bar{\xi }}I+a_1\alpha I+|\xi -{\bar{\xi }}|-a_2\theta _1(\xi -{\bar{\xi }})^2+\frac{a_2\sigma _1^2}{2}\\&\le -{\bar{\xi }}+\eta +\alpha +{\bar{\xi }}I+a_1\alpha I+\frac{1}{4a_2\theta _1}+\frac{a_2\sigma _2^2}{2}\\&\le -(R_0^h-1)\bigg (\eta +\alpha +\frac{\sigma _1}{\sqrt{2\theta _1}}\bigg )+({\bar{\xi }}+a_1\alpha )I. \end{aligned} \end{aligned}$$

Denote

$$\begin{aligned} V_2{} & {} =-\ln R, \quad V_3=-\ln C, \quad V_4=-\ln (1-I-R-C), \quad V_5=\frac{\xi ^2}{2}+\frac{\beta ^2}{2}.\\ {\mathcal {L}}V_2{} & {} =-\frac{\alpha I}{R}+(\eta +\gamma ) -\frac{(1-\sigma )\xi ^+CI}{R}\le -\frac{\alpha I}{R}+\eta +\gamma ,\\ {\mathcal {L}}V_3{} & {} =-\frac{\gamma R}{C}+\xi ^+I+\eta +\beta ^+,\\ {\mathcal {L}}V_4{} & {} =\xi ^+I-\frac{\beta ^+C}{1-(I+R+C)} -\frac{\eta (I+R+C)}{1-(I+R+C)}\le \xi ^+I-\frac{\eta I}{1-(I+R+C)},\\ {\mathcal {L}}V_5{} & {} =\theta _1\xi ({\bar{\xi }}-\xi ) +\theta _2\beta ({\bar{\beta }}-\beta )+\frac{\sigma _1^2+\sigma _2^2}{2}. \end{aligned}$$

Define a $C^2$-function W: ${\mathbb {R}}_+^3\times {\mathbb {R}}^2\rightarrow {\mathbb {R}},$

$$\begin{aligned} W(I,R,C,\xi ,\beta ){} & {} =MV_1-\ln R-\ln C-\ln (1-I-R-C)+\frac{\xi ^2}{2}+\frac{\beta ^2}{2}\\{} & {} \quad :=MV_1+V_2+V_3+V_4+V_5, \end{aligned}$$

where $\hbox {M}>0$ is a sufficiently large number such that the inequality (7) holds.

We give a definition of a non-negative $C^2$-function ${\overline{W}}$ as follows

$$\begin{aligned} {\overline{W}}(I,R,C,\xi ,\beta )=W(I,R,C,\xi ,\beta )-W({\overline{X}}_0), \end{aligned}$$

where W(X) is a continuous function, ${\overline{X}}_0$ is a minimum point (${\overline{I}}_0$,${\overline{R}}_0$,${\overline{C}}_0$,${\overline{\xi }}_0$,${\overline{\beta }}_0$) in the interior domain of $\Gamma$. Using It${\hat{o}}$’s formula, we obtain

$$\begin{aligned} {\mathcal {L}}{\overline{W}}{} & {} \le -M(R_0^h-1)\bigg (\eta +\alpha +\frac{\sigma _1}{\sqrt{2\theta _1}}\bigg )+M({\bar{\xi }}+a_1\alpha )I+2\xi ^+I+2\eta +\gamma \\{} & {} \quad -\frac{\alpha I}{R}-\frac{\gamma R}{C}+\beta ^+-\frac{\eta I}{1-(I+R+C)} -\theta _1\xi (\xi -{\bar{\xi }})-\theta _2\beta (\beta -{\bar{\beta }})\\{} & {} \quad +\frac{\sigma _1^2}{2}+\frac{\sigma _2^2}{2}\\{} & {} \le -M(R_0^h-1)\bigg (\eta +\alpha +\frac{\sigma _1}{\sqrt{2\theta _1}}\bigg ) +M({\bar{\xi }}+a_1\alpha )I+2\eta +\gamma +2|\xi |+|\beta |\\{} & {} \quad -\frac{\alpha I}{R}-\frac{\gamma R}{C}\\{} & {} \quad +\beta ^+-\frac{\eta I}{1-(I+R+C)}-\theta _1\xi ^2+\theta _1|\xi |{\bar{\xi }}-\theta _2\beta ^2 +\theta _2|\beta |{\bar{\beta }} +\frac{\sigma _1^2+\sigma _2^2}{2}\\{} & {} \le -M(R_0^h-1)\bigg (\eta +\alpha +\frac{\sigma _1}{\sqrt{2\theta _1}}\bigg )+M({\bar{\xi }}+a_1\alpha )I+2\eta +\gamma -\frac{\alpha I}{R}-\frac{\gamma R}{C}\\{} & {} \quad -\frac{\eta I}{1-(I+R+C)} +\frac{\sigma _1^2+\sigma _2^2}{2}+\frac{(\theta _1{\bar{\xi }}+2)^2}{2\theta _1} \\{} & {} \quad +\frac{(\theta _2{\bar{\beta }}+1)^2}{2\theta _2}-\frac{\theta _1\xi ^2}{2}-\frac{\theta _2\beta ^2}{2}. \end{aligned}$$

We choose a positive constant M that satisfies the following conditions

$$\begin{aligned} -M\mu _1+\mu _2\le -2, \end{aligned}$$

(7)

where

$$\begin{aligned} \mu _1{} & {} =(R_0^h-1)\bigg (\eta +\alpha +\frac{\sigma _1}{\sqrt{2\theta _1}}\bigg ), \\ \mu _2{} & {} =2\eta +\gamma +\frac{\sigma _1^2+\sigma _2^2}{2} +\frac{(\theta _1{\bar{\xi }}+2)^2}{2\theta _1}+\frac{(\theta _2{\bar{\beta }}+1)^2}{2\theta _2}. \end{aligned}$$

Define $\mu _3=M({\bar{\xi }}+a_1\alpha )$. Next, in order for the conditions of Lemma 4.1 to hold, we construct a compact subset $D_{\varepsilon }$. The form of bounded closed set we establish is as follows

$$\begin{aligned} D_{\varepsilon }=\bigg (I,R,C,\xi ,\beta \in \Gamma |I\ge \varepsilon ,R\ge \varepsilon ^2,C\ge \varepsilon ^3,I+R+C\le 1-\varepsilon ^2,|\xi |\le \frac{1}{\varepsilon }, |\beta |\le \frac{1}{\varepsilon }\bigg ), \end{aligned}$$

where $\varepsilon$ is a small enough constant to satisfy the following conditions

$$\begin{aligned} -2+\mu _3\varepsilon \le -1, \end{aligned}$$

(8)

$$\begin{aligned} -2+\mu _3-\frac{\alpha }{\varepsilon }\le -1, \end{aligned}$$

(9)

$$\begin{aligned} -2+\mu _3-\frac{\gamma }{\varepsilon }\le -1, \end{aligned}$$

(10)

$$\begin{aligned} -2+\mu _3-\frac{\eta }{\varepsilon }\le -1, \end{aligned}$$

(11)

$$\begin{aligned} -2+\mu _3-\frac{\theta _1}{2\varepsilon ^2}\le -1, \end{aligned}$$

(12)

$$\begin{aligned} -2+\mu _3-\frac{\theta _2}{2\varepsilon ^2}\le -1. \end{aligned}$$

(13)

For the sake of clarity, we split $(\Gamma )\backslash D_\varepsilon$ into the following six domains,

$$\begin{aligned} \begin{aligned}&D_1^c=\{(I,R,C,\xi ,\beta )\in \Gamma |I<\varepsilon \},\\&D_2^c=\{(I,R,C,\xi ,\beta )\in \Gamma |I\ge \varepsilon , R<\varepsilon ^2\},\\&D_3^c=\{(I,R,C,\xi ,\beta )\in \Gamma |R\ge \varepsilon ^2, C<\varepsilon ^3\},\\&D_4^c=\{(I,R,C,\xi ,\beta )\in \Gamma |I\ge \varepsilon , I+R+C>1-\varepsilon ^2\},\\&D_5^c=\left\{ (I,R,C,\xi ,\beta )\in \Gamma ||\xi |>\frac{1}{\varepsilon }\right\} ,\\&D_6^c=\left\{ (I,R,C,\xi ,\beta )\in \Gamma ||\beta |>\frac{1}{\varepsilon }\right\} . \end{aligned} \end{aligned}$$

Obviously, $D_\varepsilon ^c=\bigcup \nolimits _{i=1}^6D_i^c$,  Case 1: if $(I,R,C,\xi ,\beta )\in D_1^c$, according to (8), we get

$$\begin{aligned} {\mathcal {L}}{\overline{W}}\le -2+\mu _3\varepsilon \le -1. \end{aligned}$$

  Case 2: if $(I,R,C,\xi ,\beta )\in D_2^c$, according to (9), we get

$$\begin{aligned} {\mathcal {L}}{\overline{W}}\le -2+\mu _3-\frac{\alpha }{\varepsilon }\le -1. \end{aligned}$$

  Case 3: if $(I,R,C,\xi ,\beta )\in D_3^c$, according to (10), we get

$$\begin{aligned} {\mathcal {L}}{\overline{W}}\le -2+\mu _3-\frac{\gamma }{\varepsilon }\le -1. \end{aligned}$$

  Case 4: if $(I,R,C,\xi ,\beta )\in D_4^c$, according to (11), we get

$$\begin{aligned} {\mathcal {L}}{\overline{W}}\le -2+\mu _3-\frac{\eta }{\varepsilon }\le -1. \end{aligned}$$

  Case 5: if $(I,R,C,\xi ,\beta )\in D_5^c$, according to (12), we get

$$\begin{aligned} {\mathcal {L}}{\overline{W}}\le -2+\mu _3-\frac{\theta _1}{2\varepsilon ^2}\le -1. \end{aligned}$$

  Case 6: if $(I,R,C,\xi ,\beta )\in D_6^c$, according to (13), we get

$$\begin{aligned} {\mathcal {L}}{\overline{W}}\le -2+\mu _3-\frac{\theta _2}{2\varepsilon ^2}\le -1. \end{aligned}$$

  By the above proof, obviously, there admits a sufficiently small $\varepsilon$, such that

$$\begin{aligned} {\mathcal {L}}{\overline{W}}(I,R,C,\xi ,\beta )\le -1 \;for\;all\;(I,R,C,\xi ,\beta )\in D_\varepsilon ^c. \end{aligned}$$

So that proves the conditions in the Lemma 4.1. Thus, system (4) has a stationary distribution $\pi (\cdot )$. We have completed the proof of Theorem 4.2. $\square$

5 Density Function of Stochastic Epidemic Model

In Sect. 4, we prove that the system (4) has at least one stationary distribution. Next, we analyze the local probability density function of the system (4).

Firstly, we give the following definition of the quasi-positive equilibrium $E^*$ of system (4), where

$$\begin{aligned} E^*=(I^*,R^*,C^*,{\bar{\xi }},{\bar{\beta }})\in \Gamma , \end{aligned}$$

the quasi-endemic equilibrium $E^*$ is the same as the endemic equilibrium $E_*$ in the ordinary differential equation if there is no fluctuations.

Next, we perform an equilibrium offset transformation, let $y_1=I-I^*$, $y_2=R-R^*$, $y_3=C-C^*$, $y_4=\xi -{\bar{\xi }}$, $y_5=\beta -{\bar{\beta }}$, we get the linearized system (14) of system (4) [35, 36],

$$\begin{aligned} \left\{ \begin{array}{l} dy_1=-a_{11}y_1-a_{11}y_2-a_{13}y_3+a_{14}y_4,\\ dy_2=a_{21}y_1-a_{22}y_2+a_{13}y_3+a_{24}y_4,\\ dy_3=-a_{31}y_1+a_{32}y_2-a_{33}y_3-a_{34}y_4-a_{35}y_5,\\ dy_4=-a_{44}y_4+\sigma _1dB_1(t),\\ dy_5=-a_{55}y_5+\sigma _2dB_2(t), \end{array} \right. \end{aligned}$$

(14)

where

$$\begin{aligned}{} & {} a_{11}={\bar{\xi }}I^*,\quad a_{13}=(1-\sigma ){\bar{\xi }}I^*, \quad a_{14}=(1-I^*-R^*-C^*)I^*+\sigma C^*I^*,\\{} & {} a_{21}=\alpha +(1-\sigma ){\bar{\xi }}C^*, a_{22}=\eta +\gamma ,\quad a_{24}=(1-\sigma )I^*C^*,\quad a_{31}={\bar{\xi }}C^*,\\{} & {} a_{32}=\gamma , a_{33}={\bar{\xi }}I^*+(\eta +{\bar{\beta }}),a_{34}=C^*I^*,\quad a_{35}=C^*,\quad a_{44}=\theta _1,\quad a_{55}=\theta _2. \end{aligned}$$

According to the definition of the quasi-endemic equilibrium point $E^*$, we can conclude that the values of all the above parameters are positive.

Theorem 5.1

For any initial value $I(0),R(0),C(0),\xi (0),\beta (0))\in \Gamma$, when

$$\begin{aligned}{} & {} (1-\sigma )\bigg [\xi ^2C^*I^*+\gamma \xi I^*+\xi C^*(\eta +\gamma )-[(1-\sigma )\xi C^*+\alpha ]\gamma \bigg ]\nonumber \\{} & {} \quad <[\eta +\gamma +\alpha +(1-\sigma )\xi C^*](\xi I^*+\eta +\beta ), \end{aligned}$$

(15)

$$\begin{aligned}{} & {} (1-\sigma )\xi I^{*} \nonumber \\{} & {} \quad <\frac{(\xi I^*+\eta +\gamma )\bigg ((\xi I^*+\eta +\beta )(2\xi I^*+2\eta +\gamma +\beta )+\xi I^*\big (\eta +\gamma +\alpha +(1-\sigma )\xi C^*\big )\bigg )}{(\eta +\gamma )\gamma +\xi C^*(\xi I^*+\eta +\beta ) +(\xi I^*+\eta +\beta )\gamma +\big ((1-\sigma )\xi C^*+\alpha \big )\gamma },\nonumber \\ \end{aligned}$$

(16)

$$\begin{aligned}{} & {} (1-\sigma )\xi C^* > \frac{(\eta +\gamma )(1-\sigma )I^*C^*}{(1-I^*-R^*-C^*)I^*+\sigma C^*I^*}-\alpha , \end{aligned}$$

(17)

system (4) has a probability density $\Psi (y_1,y_2,y_3,y_4,y_5)$ around the quasi-endemic equilibrium $E^*$. $\Sigma$ is a positive definite matrix, and the special form of $\Sigma$ is given as follows.

Case 1, if $w_4\ne 0$,we get

$$\begin{aligned} \Sigma= & {} \rho _1^2(M_1J_4J_3J_2J_1)^{-1}\Sigma _1[(M_1J_4J_3J_2J_1)^{-1}]^T\\{} & {} +\rho _2^2(M_3\tilde{J_3}\tilde{J_2}\tilde{J_1})^{-1}\Sigma _2[(M_3\tilde{J_3} \tilde{J_2}\tilde{J_1})^{-1}]^T. \end{aligned}$$

Case 2, if $w_4=0$,we get

$$\begin{aligned} \Sigma= & {} \rho _{1w}^2(M_2J_4J_3J_2J_1)^{-1}{\tilde{\Sigma }}_1 [(M_2J_4J_3J_2J_1)^{-1}]^T\\{} & {} +\rho _2^2(M_3\tilde{J_3}\tilde{J_2}\tilde{J_1}) ^{-1}\Sigma _2[(M_3\tilde{J_3}\tilde{J_2}\tilde{J_1})^{-1}]^T, \end{aligned}$$

where

$$\begin{aligned} w_1= & {} a_{21}+\frac{a_{11}a_{24}}{a_{14}}+(-a_{22}+\frac{a_{11}a_{24}}{a_{14}}) \frac{a_{24}}{a_{14}},\quad w_2=-a_{31}+\frac{a_{32}a_{24}}{a_{14}}-\frac{a_{34}a_{11}}{a_{24}}+\frac{a_{33}a_{34}}{a_{14}},\\ w_3= & {} a_{21}-\frac{a_{22}a_{24}}{a_{14}},\quad w_4=a_{32}-\frac{a_{11}a_{34}}{a_{14}}-\frac{w_2}{w_3}\left( -a_{22} +\frac{a_{11}a_{24}}{a_{14}}\right) \\{} & {} -\frac{w_2}{w_3}\bigg (a_{33}+\frac{a_{13}a_{34}}{a_{14}} +\frac{w_2}{w_3}(a_{13}+\frac{a_{13}a_{24}}{a_{14}})\bigg ) \end{aligned}$$

$$\begin{aligned}{} & {} \rho _1=w_3w_4a_{14}\sigma _1,\quad \rho _{1w}=w_3a_{14}\sigma _1,\quad \rho _2=-a_{35}a_{13}g_3\sigma _2, \end{aligned}$$

$$\begin{aligned}{} & {} J_1= \begin{pmatrix} 0&{}\quad 0&{}\quad 0&{}\quad 1&{}\quad 0\\ 1&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0\\ 0&{}\quad 1&{}\quad 0&{}\quad 0&{}\quad 0\\ 0&{}\quad 0&{}\quad 1&{}\quad 0&{}\quad 0\\ 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 1 \end{pmatrix},\quad J_2= \begin{pmatrix} 1&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0\\ 0&{}\quad 1&{}\quad 0&{}\quad 0&{}\quad 0\\ 0&{}\quad -\frac{a_{24}}{a_{14}}&{}\quad 1&{}\quad 0&{}\quad 0\\ 0&{}\quad 0&{}\quad 0&{}\quad 1&{}\quad 0\\ 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 1 \end{pmatrix}, \\{} & {} J_3= \begin{pmatrix} 1&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0\\ 0&{}\quad 1&{}\quad 0&{}\quad 0&{}\quad 0\\ 0&{}\quad 0&{}\quad 1&{}\quad 0&{}\quad 0\\ 0&{}\quad \frac{a_{34}}{a_{14}}&{}\quad 0&{}\quad 1&{}\quad 0\\ 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 1 \end{pmatrix},\quad J_4= \begin{pmatrix} 1&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0\\ 0&{}\quad 1&{}\quad 0&{}\quad 0&{}\quad 0\\ 0&{}\quad 0&{}\quad 1&{}\quad 0&{}\quad 0\\ 0&{}\quad 0&{}\quad -\frac{-w_2}{w_3}&{}\quad 1&{}\quad 0\\ 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 1 \end{pmatrix}, \\ {}{} & {} \tilde{J_1}= \begin{pmatrix} 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 1\\ 1&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0\\ 0&{}\quad 1&{}\quad 0&{}\quad 0&{}\quad 0\\ 0&{}\quad 0&{}\quad 1&{}\quad 0&{}\quad 0\\ 0&{}\quad 0&{}\quad 0&{}\quad 1&{}\quad 0 \end{pmatrix},\quad \tilde{J_2}= \begin{pmatrix} 1&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0\\ 0&{}\quad 0&{}\quad 0&{}\quad 1&{}\quad 0\\ 0&{}\quad 0&{}\quad 1&{}\quad 0&{}\quad 0\\ 0&{}\quad 1&{}\quad 0&{}\quad 0&{}\quad 0\\ 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 1 \end{pmatrix}, \\{} & {} \tilde{J_3}= \begin{pmatrix} 1&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0\\ 0&{}\quad 1&{}\quad 0&{}\quad 0&{}\quad 0\\ 0&{}\quad 0&{}\quad 1&{}\quad 0&{}\quad 0\\ 0&{}\quad 0&{}\quad 1&{}\quad 1&{}\quad 0\\ 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 1 \end{pmatrix} \\ {}{} & {} M_1= \begin{pmatrix} w_3w_4a_{14}&{}w_3w_4(f_1+f_3+f_5)&{}e_1&{}e_2&{}e_3\\ 0&{}w_3w_4&{}w_4(f_3+f_5)&{}w_4f_4+f_5^2&{}-f_5a_{35}+a_{35}a_{55}\\ 0&{}0&{}w_4&{}f_5&{}-a_{35}\\ 0&{}0&{}0&{}1&{}0\\ 0&{}0&{}0&{}0&{}1 \end{pmatrix}, \end{aligned}$$

and

$$\begin{aligned}{} & {} e_1=w_3w_4f_2+w_4f_3(f_3+f_5)+w_4(w_4f_4+f_5^2),\\{} & {} e_2=-w_3w_4a_{13}+w_4f_4(f_3+f_5)+f_5(w_4f_4+f_5^2),\\{} & {} e_3=-a_{35}(w_4f_4+f_5^2)+a_{35}a_{55}f_5-a_{35}a_{55}^2,\\{} & {} f_1=-a_{11}-\frac{a_{11}a_{24}}{a_{14}}+\frac{a_{13}a_{34}}{a_{14}},\quad f_2=-a_{11}-\frac{a_{13}w_2}{w_3},\\{} & {} f_3=-a_{22}+\frac{a_{11}a_{24}}{a_{14}}+\frac{w_2}{w_3}\left( a_{13}+\frac{a_{13}a_{24}}{a_{14}}\right) ,\quad f_4=a_{13}+\frac{a_{13}a_{24}}{a_{14}},\\{} & {} f_5=-a_{33}-\frac{a_{13}a_{34}}{a_{14}}-\frac{w_2}{w_3}\left( a_{13}+\frac{a_{13}a_{24}}{a_{14}}\right) , \\{} & {} M_2= \begin{pmatrix} a_{14}w_3&{}\quad w_3(f_1+f_3)&{}\quad w_3f_2+f_3^2&{}\quad -a_{13}w_3+f_4(f_3+f_5)&{}\quad -a_{35}f_4\\ 0&{}\quad w_3&{}\quad f_3&{}\quad f_4&{}\quad 0\\ 0&{}\quad 0&{}\quad 1&{}\quad 0&{}\quad 0\\ 0&{}\quad 0&{}\quad 0&{}\quad 1&{}\quad 0\\ 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 1 \end{pmatrix}, \\{} & {} M_3= \begin{pmatrix} -a_{35}a_{13}g_3&{}g_3a_{13}(-a_{33}+g_2+g_4)&{}h_1&{}h_2&{}h_3\\ 0&{}g_3a_{13}&{}g_3(g_2+g_4)&{}g_3a_{21}+g_4^2&{}g_3a_{24}+g_4g_5-a_{44}g_5\\ 0&{}0&{}g_3&{}g_4&{}g_5\\ 0&{}0&{}0&{}1&{}0\\ 0&{}0&{}0&{}0&{}1 \end{pmatrix}, \end{aligned}$$

where

$$\begin{aligned}{} & {} g_1=a_{32}+a_{31},\quad g_2=-a_{22}-a_{21},\quad g_3=-a_{22}-a_{21},\\{} & {} g_4=-a_{11}+a_{21},\quad g_5=-a_{34}+a_{24}.\\{} & {} h_1=g_1a_{13}g_3+g_2g_3(g_2+g_4)+g_3(g_3a_{21}+g_4^2),\\{} & {} h_2=-g_3a_{13}a_{31}+g_3a_{21}(g_2+g_4)+g_4(g_3a_{21}+g_4^2),\\{} & {} h_3=-g_3a_{13}a_{34}+g_3a_{24}(g_2+g_4)+g_5(g_3a_{21}+g_4^2)-a_{44}(g_3a_{24}+g_4g_5-g_5a_{44}),\\{} & {} \Sigma _1= \begin{pmatrix} \frac{a_1a_4-a_2a_3}{\Lambda _1}&{}\quad 0&{}\quad \frac{a_3}{\Lambda _1}&{}\quad 0&{}\quad 0\\ 0&{}\quad -\frac{a_3}{\Lambda _1}&{}\quad 0&{}\quad \frac{a_1}{\Lambda _1}&{}\quad 0\\ \frac{a_3}{\Lambda _1}&{}\quad 0&{}\quad -\frac{a_1}{\Lambda _1}&{}\quad 0&{}\quad 0\\ 0&{}\quad \frac{a_1}{\Lambda _1}&{}\quad 0&{}\quad \frac{a_3-a_1a_2}{\Lambda _1}&{}\quad 0\\ 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0 \end{pmatrix}, \end{aligned}$$

and

$$\begin{aligned} \Lambda _1= & {} 2(a_4a_1^2 - a_2a_1a_3 + a_3^2), \\ {\tilde{\Sigma }}_1= & {} \begin{pmatrix} -\frac{b_2}{2(b_3-b_1b_2)}&{}\quad 0&{}\quad \frac{1}{2(b_3-b_1b_2)}&{}\quad 0&{}\quad 0\\ 0&{}\quad -\frac{1}{2(b_3-b_1b_2)}&{}\quad 0&{}\quad 0&{}\quad 0\\ \frac{1}{2(b_3-b_1b_2)}&{}\quad 0&{}\quad -\frac{b_1}{2(b_3-b_1b_2)}&{}\quad 0&{}\quad 0\\ 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0\\ 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0 \end{pmatrix}, \\ \Sigma _2= & {} \begin{pmatrix} \frac{c_1c_4-c_2c_3}{\Lambda _2}&{}\quad 0&{}\quad \frac{c_3}{\Lambda _2}&{}\quad 0&{}\quad 0\\ 0&{}\quad -\frac{c_3}{\Lambda _2}&{}\quad 0&{}\quad \frac{c_1}{\Lambda _2}&{}\quad 0\\ \frac{c_3}{\Lambda _2}&{}\quad 0&{}\quad -\frac{c_1}{\Lambda _2}&{}\quad 0&{}\quad 0\\ 0&{}\quad \frac{c_1}{\Lambda _2}&{}\quad 0&{}\quad \frac{c_3-c_1c_2}{c_4\Lambda _2}&{}\quad 0\\ 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0 \end{pmatrix}, \end{aligned}$$

among them

$$\begin{aligned} \Lambda _2=2(c_4c_1^2 - c_2c_1c_3 + c_3^2), \end{aligned}$$

$a_1,a_2,a_3,a_4,c_1,c_2,c_3,c_4,b_1,b_2$ and $b_3$ will be described below.

Proof

For convenience, we define the matrix as follows

$$\begin{aligned} A= \begin{pmatrix} -a_{11}&{}\quad -a_{11}&{}\quad -a_{13}&{}\quad a_{14}&{}\quad 0\\ a_{21}&{}\quad -a_{22}&{}\quad a_{13}&{}\quad a_{24}&{}\quad 0\\ -a_{31}&{}\quad a_{32}&{}\quad -a_{33}&{}\quad -a_{34}&{}\quad -a_{35}\\ 0&{}\quad 0&{}\quad 0&{}\quad -a_{44}&{}\quad 0\\ 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad -a_{55} \end{pmatrix}. \end{aligned}$$

$G=diag(0,0,0,\sigma _1,\sigma _2), B(t)=(0,0,0,B_1(t),B_2(t))$, then the linearized system (14) can be simplified to

$$\begin{aligned} dY=AYdt+GdB(t). \end{aligned}$$

By the relevant theory of Gardiner and the continuous Markov processes theory [37], the probability density function can be given by the following Fokker–Planck equation [38],

$$\begin{aligned} \begin{aligned}&-\frac{\sigma _1^2}{2}\frac{\partial ^2\Psi }{\partial y_4^2}-\frac{\sigma _2^2}{2}\frac{\partial ^2\Psi }{\partial y_5^2}+\frac{\partial }{\partial y_1}[(-a_{11}y_1-a_{11}y_2-a_{13}y_3+a_{14}y_4)\Psi ]\\&\quad +\frac{\partial }{\partial y_2}[(a_{21}y_1-a_{22}y_2+a_{13}y_3+a_{24}y_4)\Psi ]\\&\quad +\frac{\partial }{\partial y_3}[(-a_{31}y_1+a_{32}y_2-a_{33}y_3-a_{34}y_4-a_{35}y_5)\Psi ]\\&\quad +\frac{\partial }{\partial y_4}(-a_{44}y_4\Psi ) +\frac{\partial }{\partial y_5}(-a_{55}y_5\Psi )=0 \end{aligned}, \end{aligned}$$

and it can be approximated by a Gaussian distribution

$$\begin{aligned} \Psi (y_1,y_2,y_3,y_4,y_5)=\phi _0e^{-\frac{1}{2} (y_1,y_2,y_3,y_4,y_5)Q(y_1,y_2,y_3,y_4,y_5)^T}, \end{aligned}$$

where $\phi _0$ is a positive constant, which is obtained by the normalized condition $\int _{R^5}\Psi (Y)dy_1dy_2dy_3dy_4dy_5=1$, and Q is a real symmetric matrix satisfying the following equation

$$\begin{aligned} QG^2Q+A^TQ+QA=0. \end{aligned}$$

If Q is still an inverse matrix, let $Q^{-1}=\Sigma$, the above equation can be rewritten as

$$\begin{aligned} G^2+A\Sigma +\Sigma A^T=0. \end{aligned}$$

According to the finite independent superposition principle in [39], the above equation is equivalent to the sum of the following two equations

$$\begin{aligned} G_i^2+A\Sigma _i+\Sigma _iA^T=0 \quad \quad (i=a,b), \end{aligned}$$

where $G_a=(0,0,0,\sigma _1,0)$, $G_b=(0,0,0,0,\sigma _2)$, $\Sigma =\Sigma _a+\Sigma _b$ and $G^2=G_a^2+G_b^2$. Before proving the positive definiteness of $\Sigma$, we firstly verify that all the eigenvalues of A have negative real parts. The corresponding characteristic polynomial of A is defined by

$$\begin{aligned} \varphi _A(\lambda )=(\lambda +a_{44})(\lambda +a_{55}) (\lambda ^3+q_1\lambda ^2+q_2\lambda +q_3), \end{aligned}$$

where $q_1,q_2$ and $q_3$ has been defined as follows:

$$\begin{aligned} \begin{aligned}&q_1=a_{11}+a_{22}+a_{33},\\&q_2=a_{11}a_{21}+a_{11}a_{22}+a_{11}a_{33} +a_{22}a_{33}-a_{13}(a_{31}+a_{32}),\\&q_3=a_{11}a_{22}a_{33}+a_{11}a_{21}a_{33} +a_{13}(a_{21}a_{32}-a_{22}a_{31}-a_{11}a_{32}-a_{11}a_{31}),\\ \end{aligned} \end{aligned}$$

By simple calculation, we can have $q_1>0$ and $q_2>a_{11}a_{22}+a_{22}a_{33}>0$. According to (15), then we can simplify $q_3$ to get $q_3>0$, and similarly, from (16) we can simplify to get $q_1q_2>q_3$. Then we have that matrix A has all negative real-part eigenvalues.

Next, we prove the positive characterization of $\Sigma$ in two steps. $\textbf{Step1}$ Consider the algebraic equation

$$\begin{aligned} G_a^2+A\Sigma _a+\Sigma _aA^T=0. \end{aligned}$$

(18)

By letting $A_1=J_1AJ_1^{-1}$, we have

$$\begin{aligned} A_1= \begin{pmatrix} -a_{44}&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0\\ a_{14}&{}\quad -a_{11}&{}\quad -a_{11}&{}\quad -a_{13}&{}\quad 0\\ a_{24}&{}\quad a_{21}&{}\quad -a_{22}&{}\quad a_{13}&{}\quad 0\\ -a_{34}&{}\quad -a_{31}&{}\quad a_{32}&{}\quad -a_{33}&{}\quad -a_{35}\\ 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad -a_{55} \end{pmatrix}. \end{aligned}$$

Next, let $A_2=J_4J_3J_2A_1(J_4J_3J_2)^{-1}$, we get

$$\begin{aligned} A_2= \begin{pmatrix} -a_{44}&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0\\ a_{14}&{}\quad f_1&{}\quad f_2&{}\quad -a_{13}&{}\quad 0\\ 0&{}\quad w_3&{}\quad f_3&{}\quad f_4&{}\quad 0\\ 0&{}\quad 0&{}\quad w_4&{}\quad f_5&{}\quad -\quad a_{35}\\ 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad -a_{55} \end{pmatrix}, \end{aligned}$$

where according to (17), we have $w_3=a_{21}-\frac{a_{22}a_{24}}{a_{14}}>0$.

Dependent on the value of $w_4$, so we’re going to have two cases.

$\mathbf {Case(I)}$ If $w_4\ne 0$, based on the method given in the references [36], let $A_3=M_1A_2M_1^{-1}$, where the standardized transformation matrix

$$\begin{aligned} M_1= \begin{pmatrix} w_3w_4a_{14}&{}w_3w_4(f_1+f_3+f_5)&{}e_1&{}e_2&{}e_3\\ 0&{}w_3w_4&{}w_4(f_3+f_5)&{}w_4f_4+f_5^2&{}-f_5a_{35}+a_{35}a_{55}\\ 0&{}0&{}w_4&{}f_5&{}-a_{35}\\ 0&{}0&{}0&{}1&{}0\\ 0&{}0&{}0&{}0&{}1 \end{pmatrix}, \end{aligned}$$

then we have

$$\begin{aligned} A_3= \begin{pmatrix} -a_1&{}\quad -a_2&{}\quad -a_3&{}\quad -a_4&{}\quad -a_5\\ 1&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0\\ 0&{}\quad 1&{}\quad 0&{}\quad 0&{}\quad 0\\ 0&{}\quad 0&{}\quad 1&{}\quad 0&{}\quad 0\\ 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad -a_{55} \end{pmatrix}, \end{aligned}$$

where

$$\begin{aligned} \begin{aligned}&a_1=q_1+a_{44}>0,\quad&a_2=q_2+q_1a_{44}>0,\\&a_3=q_3+q_2a_{44}>0,\quad&a_4=q_3a_{44}>0,\\ \end{aligned} \end{aligned}$$

So with conditions (15) and (16), we verify that

$$\begin{aligned} a_1(a_2a_3-a_1a_4)-a_3^2>0. \end{aligned}$$

Since the value of $a_5$ has no influence on the results of this paper, we omit the value of $a_5$ here. Equation (18) can be equivalently transformed into

$$\begin{aligned} \begin{aligned} (M_1J_4J_3J_2J_1)G_a^2(M_1J_4J_3J_2J_1)^T+A_3[(M_1J_4J_3J_2J_1)\Sigma _a(M_1J_4J_3J_2J_1)^T]\\ +[(M_1J_4J_3J_2J_1)\Sigma _a(M_1J_4J_3J_2J_1)^T]A_3^T=0. \end{aligned} \end{aligned}$$

Let $\Sigma _1=\rho _1^{-2}(M_1J_4J_3J_2J_1)\Sigma _a(M_1J_4J_3J_2J_1)^T$, where $\rho _1=w_3w_4a_{14}\sigma _1$, it can be simplified as

$$\begin{aligned} G_0^2+A_3\Sigma _1+\Sigma _1A_3^T=0. \end{aligned}$$

By solving the equation above, we get

$$\begin{aligned} \Sigma _1= \begin{pmatrix} \frac{a_1a_4-a_2a_3}{\Lambda _1}&{}\quad 0&{}\quad \frac{a_3}{\Lambda _1}&{}\quad 0&{}\quad 0\\ 0&{}\quad -\frac{a_3}{\Lambda _1}&{}\quad 0&{}\quad \frac{a_1}{\Lambda _1}&{}\quad 0\\ \frac{a_3}{\Lambda _1}&{}\quad 0&{}\quad -\frac{a_1}{\Lambda _1}&{}\quad 0&{}\quad 0\\ 0&{}\quad \frac{a_1}{\Lambda _1}&{}\quad 0&{}\quad \frac{a_3-a_1a_2}{a_4\Lambda _1}&{}\quad 0\\ 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0 \end{pmatrix}= \begin{pmatrix} \Sigma _x&{}\quad 0\\ 0&{}\quad 0 \end{pmatrix}, \end{aligned}$$

where

$$\begin{aligned} \Lambda _1=2(a_4a_1^2 - a_2a_1a_3 + a_3^2). \end{aligned}$$

From the reference [40], we can conclude that $\Sigma _1$ is a semi-positive definite matrix. In the same way, we also get that $\Sigma _x$ is a positive definite matrix. Therefore,

$$\begin{aligned} \Sigma _{ax}=\rho _1^2(M_1J_4J_3J_2J_1)^{-1}\Sigma _x[(M_1J_4J_3J_2J_1)^{-1}]^T. \end{aligned}$$

It is also a positive definite matrix. Similarly,

$$\begin{aligned} \Sigma _a=\rho _1^2(M_1J_4J_3J_2J_1)^{-1}\Sigma _1[(M_1J_4J_3J_2J_1)^{-1}]^T. \end{aligned}$$

It is also a semi-positive definite matrix.

Let $n_1$ be the minimum eigenvalue of the matrix $\Sigma _x$, then

$$\begin{aligned} \Sigma _{ax}\ge n_1 \begin{pmatrix} 1&{}\quad 0&{}\quad 0&{}\quad 0\\ 0&{}\quad 1&{}\quad 0&{}\quad 0\\ 0&{}\quad 0&{}\quad 1&{}\quad 0\\ 0&{}\quad 0&{}\quad 0&{}\quad 1\\ \end{pmatrix}, \end{aligned}$$

and so,

$$\begin{aligned} \Sigma _a\ge n_1 \begin{pmatrix} 1&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0\\ 0&{}\quad 1&{}\quad 0&{}\quad 0&{}\quad 0\\ 0&{}\quad 0&{}\quad 1&{}\quad 0&{}\quad 0\\ 0&{}\quad 0&{}\quad 0&{}\quad 1&{}\quad 0\\ 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0 \end{pmatrix}. \end{aligned}$$

$\mathbf {Case(II)}$ If $w_4=0$, let $A_{3w}=M_2A_2M_2^{-1}$, where the standardized transformation matrix is

$$\begin{aligned} M_2= \begin{pmatrix} a_{14}w_3&{}w_3(f_1+f_3)&{}w_3f_2+f_3^2&{}-a_{13}w_3+f_4(f_3+f_5)&{}-a_{35}f_4\\ 0&{}w_3&{}f_3&{}f_4&{}0\\ 0&{}0&{}1&{}0&{}0\\ 0&{}0&{}0&{}1&{}0\\ 0&{}0&{}0&{}0&{}1 \end{pmatrix}. \end{aligned}$$

Using the same method, we can get

$$\begin{aligned} A_{3w}= \begin{pmatrix} -b_1&{}\quad -b_2&{}\quad -b_3&{}\quad -b_4&{}\quad -b_5\\ 1&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0\\ 0&{}\quad 1&{}\quad 0&{}\quad 0&{}\quad 0\\ 0&{}\quad 0&{}\quad 0&{}\quad f_5&{}\quad -a_{35}\\ 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad -a_{55} \end{pmatrix}, \end{aligned}$$

where

$$\begin{aligned}{} & {} b_1=q_1+a_{44}+f_5>0,\quad b_2=q_2+q_1a_{44}+f_5b_1>0,\\{} & {} b_3=q_3+q_2a_{44}+f_5b_2>0.\\ \end{aligned}$$

By direct calculation, we have

$$\begin{aligned} b_1b_2-b_3>0. \end{aligned}$$

Since the value of $b_4$ and $b_5$ has no influence on the results of this paper, we omit the value of $b_4$ and $b_5$ here. Meanwhile, equation (18) can be equivalently transformed into

$$\begin{aligned} \begin{aligned} (M_2J_4J_3J_2J_1)G_a^2(M_2J_4J_3J_2J_1)^T+A_{3w}[(M_2J_4J_3J_2J_1) \Sigma _a(M_2J_4J_3J_2J_1)^T]\\ +[(M_2J_4J_3J_2J_1) \Sigma _a(M_2J_4J_3J_2J_1)^T]A_{3w}^T=0. \end{aligned} \end{aligned}$$

Let ${\tilde{\Sigma }}_1=\rho _{1w}^{-2}(M_2J_4J_3J_2J_1)\Sigma _a(M_2J_4J_3J_2J_1)^T$, where $\rho _{1w}=w_3a_{14}\sigma _1$, we similarly obtain

$$\begin{aligned} G_0^2+A_{3w}{\tilde{\Sigma }}_1+{\tilde{\Sigma }}_1A_{3w}^T=0. \end{aligned}$$

By solving the equation above, we have

$$\begin{aligned} {\tilde{\Sigma }}_1= \begin{pmatrix} -\frac{b_2}{2(b_3-b_1b_2)}&{}\quad 0&{}\quad \frac{1}{2(b_3-b_1b_2)}&{}\quad 0&{}\quad 0\\ 0&{}\quad -\frac{1}{2(b_3-b_1b_2)}&{}\quad 0&{}\quad 0&{}\quad 0\\ \frac{1}{2(b_3-b_1b_2)}&{}\quad 0&{}\quad -\frac{b_1}{2(b_3-b_1b_2)}&{}\quad 0&{}\quad 0\\ 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0\\ 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0 \end{pmatrix}. \end{aligned}$$

From the reference [40], we can conclude that ${\tilde{\Sigma }}_1$ is a semi-positive definite matrix. Hence,

$$\begin{aligned} \Sigma _a=\rho _{1w}^2(M_2J_4J_3J_2J_1)^{-1} {\tilde{\Sigma }}_1[(M_2J_4J_3J_2J_1)^{-1}]^T. \end{aligned}$$

It is also a semi-positive definite matrix. Therefore, we get that $\Sigma _a$ is semi-positive definite and there is a positive constant $n_2$ such that

$$\begin{aligned} \Sigma _a\ge n_2 \begin{pmatrix} 1&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0\\ 0&{}\quad 1&{}\quad 0&{}\quad 0&{}\quad 0\\ 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0\\ 0&{}\quad 0&{}\quad 0&{}\quad 1&{}\quad 0\\ 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0 \end{pmatrix}. \end{aligned}$$

$\textbf{Step2 }$ For the following algebraic equation

$$\begin{aligned} G_b^2+A\Sigma _b+\Sigma _bA^T=0. \end{aligned}$$

(19)

We first let $B_1=\tilde{J_1}A\tilde{J_1}^{-1}$, and then define $B_2=(\tilde{J_3}\tilde{J_3})B_1(\tilde{J_3}\tilde{J_2})^{-1}$, where

$$\begin{aligned}{} & {} \tilde{J_1}= \begin{pmatrix} 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 1\\ 1&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0\\ 0&{}\quad 1&{}\quad 0&{}\quad 0&{}\quad 0\\ 0&{}\quad 0&{}\quad 1&{}\quad 0&{}\quad 0\\ 0&{}\quad 0&{}\quad 0&{}\quad 1&{}\quad 0 \end{pmatrix},\quad B_1= \begin{pmatrix} -a_{55}&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0\\ 0&{}\quad -a_{11}&{}\quad -a_{11}&{}\quad -a_{13}&{}\quad a_{14}\\ 0&{}\quad a_{21}&{}\quad -a_{22}&{}\quad a_{13}&{}\quad a_{24}\\ -a_{35}&{}\quad -a_{31}&{}\quad a_{32}&{}\quad -a_{33}&{}\quad -a_{34}\\ 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad -a_{44} \end{pmatrix}, \\{} & {} \tilde{J_2}= \begin{pmatrix} 1&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0\\ 0&{}\quad 0&{}\quad 0&{}\quad 1&{}\quad 0\\ 0&{}\quad 0&{}\quad 1&{}\quad 0&{}\quad 0\\ 0&{}\quad 1&{}\quad 0&{}\quad 0&{}\quad 0\\ 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 1 \end{pmatrix},\quad \tilde{J_3}= \begin{pmatrix} 1&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0\\ 0&{}\quad 1&{}\quad 0&{}\quad 0&{}\quad 0\\ 0&{}\quad 0&{}\quad 1&{}\quad 0&{}\quad 0\\ 0&{}\quad 0&{}\quad 1&{}\quad 1&{}\quad 0\\ 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 1 \end{pmatrix},\\{} & {} B_2= \begin{pmatrix} -a_{55}&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0\\ -a_{35}&{}\quad -a_{33}&{}\quad g_1&{}\quad -a_{31}&{}\quad -a_{34}\\ 0&{}\quad a_{13}&{}\quad g_2&{}\quad a_{21}&{}\quad a_{24}\\ 0&{}\quad 0&{}\quad g_3&{}\quad g_4&{}\quad g_5\\ 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad -a_{44} \end{pmatrix}. \end{aligned}$$

Let $B_3=M_3B_3M_3^{-1}$, we construct the following standardized transformation matrix

$$\begin{aligned} M_3= \begin{pmatrix} -a_{35}a_{13}g_3&{}g_3a_{13}(-a_{33}+g_2+g_4)&{}h_1&{}h_2&{}h_3\\ 0&{}g_3a_{13}&{}g_3(g_2+g_4)&{}g_3a_{21}+g_4^2&{}g_3a_{24}+g_4g_5-a_{44}g_5\\ 0&{}0&{}g_3&{}g_4&{}g_5\\ 0&{}0&{}0&{}1&{}0\\ 0&{}0&{}0&{}0&{}1 \end{pmatrix}. \end{aligned}$$

According to the same method above, we can get directly

$$\begin{aligned} B_3= \begin{pmatrix} -c_1&{}\quad -c_2&{}\quad -c_3&{}\quad -c_4&{}\quad -c_5\\ 1&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0\\ 0&{}\quad 1&{}\quad 0&{}\quad 0&{}\quad 0\\ 0&{}\quad 0&{}\quad 1&{}\quad 0&{}\quad 0\\ 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad -a_{44} \end{pmatrix}, \end{aligned}$$

where

$$\begin{aligned} \begin{aligned}&c_1=q_1+a_{55}>0,\quad c_2=q_2+q_1a_{55}>0,\\&c_3=q_3+q_2a_{55}>0,\quad c_4=q_3a_{55}>0.\\ \end{aligned} \end{aligned}$$

Similarly, we have

$$\begin{aligned} c_1(c_2c_3-c_1c_4)-c_3^2>0. \end{aligned}$$

Since the value of $c_5$ has no influence on the results of this paper, we omit the value of $c_5$ here. Similarly to the method in $\textbf{Step1}$, equation (19) can be equalized to

$$\begin{aligned} \begin{aligned} (M_3\tilde{J_3}\tilde{J_2}\tilde{J_1})G_b^2(M_3\tilde{J_3}\tilde{J_2} \tilde{J_1})^T+B_3[(M_3\tilde{J_3}\tilde{J_2}\tilde{J_1}) \Sigma _b(M_3\tilde{J_3}\tilde{J_2}\tilde{J_1})^T]\\ +[(M_3\tilde{J_3}\tilde{J_2}\tilde{J_1})\Sigma _b(M_3\tilde{J_3} \tilde{J_2}\tilde{J_1})^T]B_3^T=0. \end{aligned} \end{aligned}$$

Let $\Sigma _2=\rho _2^{-2}(M_3\tilde{J_3}\tilde{J_2}\tilde{J_1}) \Sigma _b(M_3\tilde{J_3}\tilde{J_2}\tilde{J_1})^T$, where $\rho _2=-a_{35}a_{13}g_3\sigma _2$, we similarly obtain

$$\begin{aligned} G_0^2+B_3\Sigma _2+\Sigma _2B_3^T=0. \end{aligned}$$

After direct calculation of the above equation, we have

$$\begin{aligned} \Sigma _2= \begin{pmatrix} \frac{c_1c_4-c_2a_3}{\Lambda _2}&{}\quad 0&{}\quad \frac{c_3}{\Lambda _2}&{}\quad 0&{}\quad 0\\ 0&{}\quad -\frac{c_3}{\Lambda _2}&{}\quad 0&{}\quad \frac{c_1}{\Lambda _2}&{}\quad 0\\ \frac{c_3}{\Lambda _2}&{}\quad 0&{}\quad -\frac{c_1}{\Lambda _2}&{}\quad 0&{}\quad 0\\ 0&{}\quad \frac{c_1}{\Lambda _2}&{}\quad 0&{}\quad \frac{c_3-c_1c_2}{c_4\Lambda _2}&{}\quad 0\\ 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0 \end{pmatrix}, \end{aligned}$$

According to reference [40] and its proof, we get $\Sigma _2$ is a semi-positive definite matrix. It can be concluded from the above proof, $\Sigma _b=\rho _2^{2}[(M_3\ title{J_3}\tilde{J_2}\tilde{J_1})^{-1} \Sigma _2(M_3\ title{J_3}\tilde{J_2}\tilde{J_1})^{-1}]^T$ is also a semi-positive definite matrix and there is a positive constant $n_3$ such that

$$\begin{aligned} \Sigma _b\ge n_3 \begin{pmatrix} 1&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0\\ 0&{}\quad 1&{}\quad 0&{}\quad 0&{}\quad 0\\ 0&{}\quad 0&{}\quad 1&{}\quad 0&{}\quad 0\\ 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0\\ 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 1 \end{pmatrix}. \end{aligned}$$

Now let’s discuss the above situation in two cases. $\mathbf {Case(I)}$ If $w_4\ne 0$, then the covariance matrix

$$\begin{aligned} \begin{aligned} \Sigma =\Sigma _a+\Sigma _b&\ge n_1 \begin{pmatrix} 1&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0\\ 0&{}\quad 1&{}\quad 0&{}\quad 0&{}\quad 0\\ 0&{}\quad 0&{}\quad 1&{}\quad 0&{}\quad 0\\ 0&{}\quad 0&{}\quad 0&{}\quad 1&{}\quad 0\\ 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0 \end{pmatrix}+n_3 \begin{pmatrix} 1&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0\\ 0&{}\quad 1&{}\quad 0&{}\quad 0&{}\quad 0\\ 0&{}\quad 0&{}\quad 1&{}\quad 0&{}\quad 0\\ 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0\\ 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 1 \end{pmatrix}\\&\ge (n_1\wedge n_3) \begin{pmatrix} 1&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0\\ 0&{}\quad 1&{}\quad 0&{}\quad 0&{}\quad 0\\ 0&{}\quad 0&{}\quad 1&{}\quad 0&{}\quad 0\\ 0&{}\quad 0&{}\quad 0&{}\quad 1&{}\quad 0\\ 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 1 \end{pmatrix}. \end{aligned} \end{aligned}$$

And then we can prove that $\Sigma$ is positive definite.

$\mathbf {Case(II)}$ If $w_4=0$, similarly, then the covariance matrix

$$\begin{aligned} \Sigma =\Sigma _a+\Sigma _b&\ge n_2 \begin{pmatrix} 1&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0\\ 0&{}\quad 1&{}\quad 0&{}\quad 0&{}\quad 0\\ 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0\\ 0&{}\quad 0&{}\quad 0&{}\quad 1&{}\quad 0\\ 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0 \end{pmatrix}+n_3 \begin{pmatrix} 1&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0\\ 0&{}\quad 1&{}\quad 0&{}\quad 0&{}\quad 0\\ 0&{}\quad 0&{}\quad 1&{}\quad 0&{}\quad 0\\ 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0\\ 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 1 \end{pmatrix}\\&\ge (n_2\wedge n_3) \begin{pmatrix} 1&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0\\ 0&{}\quad 1&{}\quad 0&{}\quad 0&{}\quad 0\\ 0&{}\quad 0&{}\quad 1&{}\quad 0&{}\quad 0\\ 0&{}\quad 0&{}\quad 0&{}\quad 1&{}\quad 0\\ 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 1 \end{pmatrix}. \end{aligned}$$

Similarly, we can show that $\Sigma$ is positive definite.

In summary, we have now shown that $\Sigma$ is a positive definite matrix, and that the form of $\Sigma =\Sigma _a+\Sigma _b$ is determined by the steps above. By the positive definiteness of $\Sigma$, we can compute that $\phi _0=(2\pi )^{-\frac{5}{2}}|\Sigma |^{-\frac{1}{2}}$. System (4) has a probability density $\Psi (y_1,y_2,y_3,y_4,y_5)$ around the quasi-endemic equilibrium $E^*$.

We have completed the proof of Theorem 5.1. $\square$

6 Extinction of the Disease

Next, we’ll talk about the extinction of diseases.

Theorem 6.1

For any initial value $(I(0),R(0),C(0),\xi (0),\beta (0))\in \Gamma$, if $R_0^d<1$, then the solution $(I(t),R(t),C(t),\xi (t),\beta (t))$ of system (4) follows

$$\begin{aligned} \lim \limits _{t\rightarrow \infty }sup\frac{\ln I(t)}{t}\le (\eta +\alpha )(R_0^d-1)<0,a.s. \end{aligned}$$

where

$$\begin{aligned} R_0^d=\frac{{\bar{\xi }}\Phi \bigg (\frac{{\bar{\xi }}\sqrt{2\theta _1}}{\sigma _1}\bigg ) +\frac{\sigma _1}{2\sqrt{\theta _1\pi }}e^{-\frac{{\bar{\xi }}^2 \theta _1}{\sigma _1^2}}}{\eta +\alpha }. \end{aligned}$$

Proof

Employing It${\hat{o}}'s$ formula to $\ln I(t)$, we get

$$\begin{aligned} \begin{aligned} d\ln I(t)&=[\xi ^+(1-I-R-C)+\sigma \xi ^+C-(\eta +\alpha )]dt\\&=[\xi ^+(1-I-R)+(\sigma -1)\xi ^+C-(\eta +\alpha )]dt\\&\le [\xi ^+-(\eta +\alpha )]dt. \end{aligned} \end{aligned}$$

(20)

Let’s integrate both sides of this inequality (20) from 0 to t, and divide by t, we get

$$\begin{aligned} \begin{aligned} \frac{\ln I(t)-\ln I(0)}{t}&\le \frac{1}{t}\int _{0}^{t}[\xi ^+(u)-(\eta +\alpha )]du\\&=\frac{1}{t}\int _{0}^{t}\xi ^+(u)du-(\eta +\alpha ). \end{aligned} \end{aligned}$$

(21)

Taking the superior limit of $t\rightarrow \infty$ on both sides of the inequality (21), because of $\xi ^+\sim N({\bar{\xi }},\frac{\sigma _1^2}{2\theta _1})$. By the strong law of large numbers [41], we get

$$\begin{aligned} \lim \limits _{t\rightarrow \infty }\frac{1}{t}\int _{0}^{t}\xi ^+(u)du{} & {} =\int _{0}^{\infty }x \frac{\sqrt{\theta _1}}{\sqrt{\pi }\sigma _1}e^{-\frac{\theta _1x^2}{\sigma _1^2}}dx\\{} & {} = \frac{\sigma _1}{2\sqrt{\theta _1\pi }}e^{-\frac{{\bar{\xi }}^2\theta _1}{\sigma _1^2}} +{\bar{\xi }}\bigg [\Phi (\infty )-\Phi \bigg (-\frac{{\bar{\xi }}\sqrt{2\theta _1}}{\sigma _1}\bigg )\bigg ]\\{} & {} ={\bar{\xi }}\Phi \bigg (\frac{{\bar{\xi }}\sqrt{2\theta _1}}{\sigma _1}\bigg ) +\frac{\sigma _1}{2\sqrt{\theta _1\pi }}e^{-\frac{{\bar{\xi }}^2\theta _1}{\sigma _1^2}}, \end{aligned}$$

where $\Phi (x)=\int _{-\infty }^{x}\frac{1}{\sqrt{2\pi }}e^{-\frac{u^2}{2}}du$, according to $\lim \nolimits _{t\rightarrow \infty }\frac{\ln I(0)}{t}=0$, then we get

$$\begin{aligned} \lim \limits _{t\rightarrow \infty }sup\frac{\ln I(t)}{t}\le (\eta +\alpha )(R_0^d-1), \end{aligned}$$

where

$$\begin{aligned} R_0^d=\frac{{\bar{\xi }}\Phi \bigg (\frac{{\bar{\xi }}\sqrt{2\theta _1}}{\sigma _1}\bigg )+\frac{\sigma _1}{2\sqrt{\theta _1\pi }} e^{-\frac{{\bar{\xi }}^2\theta _1}{\sigma _1^2}}}{\eta +\alpha }. \end{aligned}$$

If $R_0^d<1$, then $\limsup \nolimits _{t\rightarrow \infty }\frac{\ln I(t)}{t}<0$, which means that the epidemic of system (4) will go to extinction with probability 1.

Thus the Theorem 6.1 is proved. $\square$

7 Numerical Simulations

In order to verify the theoretical results in the paper, we conduct numerical simulation on it in this section. Making use of the common higher-order method developed by Milstein’s Higher Order Method mentioned in [42], we have the discretization equation of system (4),

$$\begin{aligned} \left\{ \begin{array}{l} I^{i+1}=I^i+[\xi ^i (1-I^i-R^i-C^i)I^i+\sigma \xi ^i C^iI^i-(\eta +\alpha )I^i]\Delta t,~\\ R^{i+1}=R^i+[(1-\sigma )\xi ^i C^iI^i+\alpha I^i-(\eta +\gamma )R^i]\Delta t,~\\ C^{i+1}=C^i+[\gamma R^i-\xi ^i C^iI^i-(\eta +\beta ^+)C^i]\Delta t,~\\ \xi ^{i+1}=\xi ^i+\theta _1({\bar{\xi }}-\xi ^i)\Delta t +\sigma _1\zeta _i\sqrt{\Delta }+\frac{\sigma _1^2}{2}(\zeta _i^2-1)\Delta t,~\\ \beta ^{i+1}=\beta ^i+\theta _2({\bar{\beta }}-\beta ^i)\Delta t+\sigma _2\iota _i\sqrt{\Delta t}+\frac{\sigma _2^2}{2}(\iota _i^2-1)\Delta t, \end{array} \right. \end{aligned}$$

(22)

where $\Delta t>0$ denotes the time increment, $\zeta _i$ and $\iota _i$ are the Gaussian random variables which follows the distribution N(0, 1).

Fig. 1

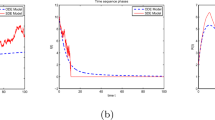
When $R_0^h=1.9299>1$, simulations of the solution in the stationary distribution of stochastic system (4). On the left, the blue and red lines represent simulations of the stochastic system (4) and the deterministic system (2), respectively, where the stochastic system is perturbed by the Ornstein–Uhlenbeck process. The picture on the right means the density of the stochastic system (4) (color figure online)

Fig. 2

When $R_0^d=0.5830<1$, simulations of the system (4) will be extinct. On the left,The blue and red lines represent simulations of the stochastic system (4) and the deterministic system (2), respectively, where the stochastic system is perturbed by the Ornstein–Uhlenbeck process. The picture on the right means the density of the stochastic system (4) (color figure online)

Fig. 3

Simulations of the solution I(t), R(t),  and C(t) in system (4) under the different value of ${\bar{\xi }}$

Fig. 4

Simulations of the solution I(t), R(t),  and C(t) in system (4) under the different value of $\alpha$

Fig. 5

Simulations of the solution I(t), R(t),  and C(t) in system (4) under the different value of $\eta$

$\mathbf {Case (1)}$ Consider the parameters $\theta _1=0.1$, $\theta _2=0.09$, $\sigma _1=0.1$, $\sigma _2=0.1$, $\eta =0.09$, $\beta =0.05$, $\sigma =0.9$, $\gamma =0.09$, $\alpha =0.36$, $\xi =1.3$. According to the Theorem 4.2, system (4) has a stationary distribution which can be proved by numerical simulation as shown in Fig. 1.

$\mathbf {Case (2)}$   Consider the parameters $\theta _1=0.1$, $\theta _2=0.09$, $\sigma _1=0.1$, $\sigma _2=0.1$, $\eta =0.09$, $\beta =0.05$, $\sigma =0.9$, $\gamma =0.09$, $\alpha =0.45$, $\xi =0.58$. By the Theorem 5.1, it verifies the conclusion that the disease will be extinct.

To sum up, we verified the conclusion through numerical simulation in Figs. 1, 2 and 3. In Fig. 1, the blue and red lines represent the simulations for the stochastic system (4) and the deterministic system (2), respectively. The picture on the right shows the density of the stochastic system (4). In Fig. 2, when $R_0^d<1$, system (4) will be extinct with the data of $\mathbf {Case (2)}$. From the right of the Fig. 3, it displays the curve tend to zero point. It also means that the system (4) will be extinct.

In the process of numerical simulation, the change of the important parameters ${\bar{\xi }}$, $\alpha$, $\eta$ have a great influence on the change of the curve of the system (4). We apply the method of control variables, by changing the different values of an important parameter, with the change of the curve to show the effect of simulation, examples can be found in Figs. 4 and 5.

$\mathbf {Case (3)}$ Consider the parameters $\theta _1=0.1$, $\theta _2=0.09$, $\sigma _1=0.1$, $\sigma _2=0.1$, $\eta =0.09$, $\beta =0.05$, $\sigma =0.9$, $\gamma =0.09$, $\alpha =0.36$. And

$$\begin{aligned} \begin{aligned}&R_0^h=2.9691, \quad when\quad {\bar{\xi }}=2.0.\\&R_0^h=2.5237, \quad when\quad {\bar{\xi }}=1.7.\\&R_0^h=1.9299, \quad when\quad {\bar{\xi }}=1.3.\\&R_0^d=0.7442, \quad when\quad {\bar{\xi }}=0.3.\\ \end{aligned} \end{aligned}$$

Which implies that for ${\bar{\xi }}$ = 2.0, ${\bar{\xi }}$ =1.7, ${\bar{\xi }}$ =1.3, the diseases will persist, and then when ${\bar{\xi }}=0.3$, the diseases will be extinct. In Fig. 4, we can clearly observe the image changes caused by parameters change.

$\mathbf {Case (4)}$ Consider the parameters $\theta _1=0.1$, $\theta _2=0.09$, $\sigma _1=0.1$, $\sigma _2=0.1$, $\eta =0.09$, $\beta =0.05$, $\sigma =0.9$, $\gamma =0.09$, ${\bar{\xi }}=1.3$. And

$$\begin{aligned} \begin{aligned}&R_0^d=0.8457, \quad when\quad \alpha =1.44.\\&R_0^h=1.2577,\quad when\quad \alpha =0.72.\\&R_0^h=1.9299,\quad when\quad \alpha =0.36.\\&R_0^h=2.6337,\quad when\quad \alpha =0.18.\\ \end{aligned} \end{aligned}$$

Similarly, which implies that for $\alpha$ = 0.72, $\alpha$ = 0.36, $\alpha$ = 0.18, the diseases will persist, and then when $\alpha$ = 1.44, the diseases will be extinct. The variation of these parameters can be clearly observed in Fig. 5.

$\mathbf {Case (5)}$ Consider the parameters $\theta _1=0.1$, $\theta _2=0.09$, $\sigma _1=0.1$, $\sigma _2=0.1$, $\alpha =0.36$, $\beta =0.05$, $\sigma =0.9$, $\gamma =0.09$, ${\bar{\xi }}=1.3$. And

$$\begin{aligned} \begin{aligned}&R_0^d=0.9028, \quad when\quad \eta =1.08.\\&R_0^h=1.5229, \quad when\quad \eta =0.27.\\&R_0^h=1.9299, \quad when\quad \eta =0.09.\\&R_0^h=2.0681, \quad when\quad \eta =0.045.\\ \end{aligned} \end{aligned}$$

Similarly, which implies that for $\eta =0.27$, $\eta =0.09$, $\eta =0.045$, the diseases will persist, and then when $\eta =1.08$, the diseases will be extinct. The effect of different changes in the value of $\eta$ is clearly reflected in Fig. 5.

8 Conclusions

In this article, we analyze a stochastic SIRC model with Ornstein–Uhlenbeck process. We first give the theoretical result that the stochastic SIRC system (4) has a unique global positive solution and prove it. Then, the theoretical results on the existence of ergodic stationary distributions for random SIRC systems (4) are given. We prove the theoretical results by constructing a series of suitable Lyapunov functions. It reveals the influence of Ornstein–Uhlenbeck process on the existence of stationary distribution. In addition, the theoretical results of probability density function are obtained and proved. In addition, we derive the sufficient conditions for the extinction of the disease, providing a theoretical basis for the prevention and control of infectious diseases. Finally, we use numerical simulation to simulate the theoretical results in order to verify the theoretical results in the paper.

However, there are still many questions about this article to be resolved. In this paper, we only get the local probability density expression of stochastic systems, and the global probability density expression is still a problem to be considered. In addition, whether other types of random disturbances are more suitable for solving the problem also needs further verification.