Point line geometry in the tropical plane

Abstract

We study the classical result by Bruijn and Erdős regarding the bound on the number of lines determined by a n-point configuration in the plane, and in the light of the recently proven Tropical Sylvester-Gallai theorem, come up with a tropical version of the above-mentioned result. In this work, we introduce stable tropical lines, which help in answering questions pertaining to incidence geometry in the tropical plane. Projective duality in the tropical plane helps in translating the question for stable lines to stable intersections that have been previously studied in depth. Invoking duality between Newton subdivisions and line arrangements, we are able to classify stable intersections with shapes of cells in subdivisions, and this ultimately helps us in coming up with a bound. In this process, we also encounter various unique properties of linear Newton subdivisions which are dual to tropical line arrangements.

1 Introduction

Point-line geometry has been studied for a long time, and it mainly deals with the question of incidence, i.e. when a point meets a line. There are many classical results established about the incidence of points and lines in projective and affine planes like the Sylvester-Gallai theorem, de-Bruijn Erdős theorem, Szemeredi-Trotter theorem, Beck’s theorem etc. In recent times, there has been a lot of development in generalising these classical results, like [7] surveys the work done on generalizations of de-Bruijn Erdős theorem. In a recent study in [8], tropical lines present in a fixed tropical plane are also studied.

Since tropical geometry provides a piecewise linear model of point line geometry, many incidence geometric results have also been proved in it. In [3] a tropical version of Sylvester-Gallai theorem and Motzkin-Rabin theorem is established along with the universality theorem. In [15] the term geometric construction is coined , in order to identify all the types of classical incidence geometric results which can have a tropical analogue. Even in [13] and [14] a tropical version of Pappus theorem is discussed along with classical point-line configurations. Another aspect is the relation to tropical oriented matroids, and as mentioned in [3], it is elaborated in [1], in the context of hyperplane arrangements and how they correspond to tropical oriented matroids and how these matroids encode incidence information about point-line structures in the tropical plane. A important tool used in the proofs is a version of projective duality in the tropical plane which we elaborate later.

In this article, we start with some basic notions of point line geometry and specifically the point-line geometry in the tropical plane. Subsequently, using the results obtained in [3] and by introducing the notion of stable tropical lines we state a tropical counterpart to de-Bruijn-Erdős theorem. We also establish the equivalence between a much general notion of stability for curves, in [15], and the stable lines that we define in our work. We find that tropicalization of generic lifts of points determines the stable tropical line passing through them. We establish the duality between stable lines and stable intersections and provide a full classification of the faces that they correspond to in the dual Newton subdivision. With this setup, we prove the tropical analogue of de-Bruijn-Erdős theorem,

Theorem 1

(Tropical de-Bruijn-Erdős Theorem) Let ${\mathcal {S}}$ denote a set of points in the tropical plane. Let v $(v \ge 4)$ denote the number of points in ${\mathcal {S}}$, and let b denote the number of stable tropical lines determined by these points. Then,

• 1. $b \ge v - 3$

• 2. If $b = v - 3$, then ${\mathcal {S}}$ forms a tropical near-pencil.

2 Classical incidence geometry

In classical incidence geometry a linear space is defined in the following manner [6],

Definition 1

A finite linear space is a pair $(X,{\mathcal {B}})$, where X is a finite set and ${\mathcal {B}}$ is a set of proper subsets of X, such that

• 1. Every unordered pair of elements of X occur in a unique B $\in {\mathcal {B}}.$

• 2. Every B $\in {\mathcal {B}}$ has cardinality at least two.

Essentially, a linear space is a point-line incidence structure, in which any two points lie on a unique line.

Example 1

Consider $L = (X, {\mathcal {B}})$, where X is the set of points in the Euclidean plane and ${\mathcal {B}}$ is the set of lines determined by X .

Erdős and de-Bruijn, came up with a theorem about point-line arrangements in a linear space [5], which is established in [2] and stated in Theorem 2.

Theorem 2

(de-Bruijn-Erdős Theorem) Let $S = (X,{\mathcal {B}})$ be a linear space. Let v denote the number of points in $S (= |X|$), and b denote the number of lines determined by these points $(= |{\mathcal {B}}|$), $b > 1$. Then

• 1. $b \ge v$,

• 2. If $b = v$, any two lines have a point in common. In case (2), either one line has $v - 1$ points and all others have two points, or every line has $k + 1$ points and every point is on $k + 1$ lines, $k \ge 2$.

For a more general treatment and recent developments, one can read [7], where enumerative results like the above have been discussed in a more general setting of geometric lattices.

Theorem 2 clearly is a very general statement, and in the case for points and lines in the Euclidean plane, the bound on the number of lines is attained when points are in a near -pencil configuration and the proof follows by induction and invoking Theorem 3.

Theorem 3

(Sylvester-Gallai Theorem) Given a finite collection of points in the Euclidean plane, such that not all of them lie on one line, then there exists a line which passes through exactly two of the points.

3 A brief introduction to tropical geometry

Tropical geometry can be defined as the study of geometry over the tropical semiring ${\mathbb {T}} = ({\mathbb {R}} \cup \{-\infty \}$, max, +). A tropical polynomial $p(x_{1}, \cdots , x_{n})$ is defined as a linear combination of tropical monomials with operations as the tropical addition and tropical multiplication.

$$\begin{aligned} p(x_{1}, \cdots , x_{n}) = a \odot {x_{1}}^{i_{1}}{x_{2}}^{i_{2}} \cdots {x_{n}}^{i_{n}} \oplus b \odot {x_{1}}^{j_{1}}{x_{2}}^{j_{2}} \cdots {x_{n}}^{j_{n}} \oplus \cdots \end{aligned}$$

Here the coefficients $a,b, \cdots$ are real numbers and the exponents $i_{1}, j_{1} \cdots$ are integers. With the above definitions, we see that a tropical polynomial is a function $p : {\mathbb {R}}^{n} \longrightarrow {\mathbb {R}}$ given by maximum of a finite set of affine linear functions.

Definition 2

The hypersurface V(p) of p is is the set of all points w $\in {\mathbb {R}}^{n}$ at which the maximum is attained at least twice. Equivalently, a point w $\in {\mathbb {R}}^{n}$ lies in V(p) if and only if p is not linear at w.

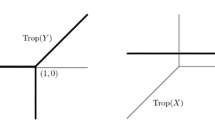
The tropical polynomial defining a tropical line is given as

$p(x,y) = a \odot x \oplus b \odot y \oplus c,$ where $a,b,c \in {\mathbb {R}}$,

and the corresponding hypersurface is the corner locus defined by the above polynomial,which is a collection of three half rays emanating from the point $(c - a, c - b)$ in the primitive directions of $(-1,0),(0,-1)$ and (1, 1) (see Fig. 1, refer [11]).

Fig. 1

A tropical line

Now we look at the intersections of lines in the tropical plane. As is evident from the setup, tropical lines can intersect over a half ray. However, two tropical lines have a unique stable intersection, where a stable intersection is the limit of points of intersection of nearby lines which have a unique point of intersection, within a suitable $\epsilon$, with the limit being taken as $\epsilon$ tends to 0 [11]. We refer the reader to [11] for further details about stable intersections in full generality.

A tropical line arrangement is a finite collection of distinct tropical lines in ${\mathbb {R}}^{2}$. We note that tropical line arrangements fail to define a finite linear space because they fail the uniqueness condition in Definition 1. We also define the two types of stable intersections which we encounter in the case of line arrangements,

Definition 3

A stable intersection point in a tropical line arrangement is called stable intersection of first kind if no vertex of any line from the line arrangement is present at the point of intersection.

Definition 4

A stable intersection point in a tropical line arrangement is called stable intersection of second kind if the vertex of a line from the line arrangement is present at the point of intersection.

For the sake of simplicity, subsequently whenever we refer to stable intersection of tropical lines within a tropical line arrangement, we mean the stable intersection point.

An important observation is the projective duality which exists in the tropical plane [3], which means that given a set of points ${\mathcal {P}}$, there exists a incidence preserving map $\phi$ which maps ${\mathcal {P}}$ to its dual set of tropical lines ${\mathcal {L}}$, where for each point $P \in {\mathcal {P}}$, $\phi (P) = l$ with $-P$ as the vertex of the line $l \in {\mathcal {L}}$.

The support of a tropical polynomial is the collection of the exponents of the monomials which have a finite coefficient. The convex hull of the exponents in the support of a tropical polynomial defines a Newton polytope. A subdivision of a set of points in ${\mathbb {R}}^{2}$, is a polytopal complex which covers the convex hull of the set of points and uses a subset of the point set as vertices. If such a subdivision of points is induced by a weight vector c, then it is called a regular subdivision. There exists a duality between a tropical curve T, defined by a tropical polynomial p, and the subdivision of the Newton polygon corresponding to p, induced by the coefficients of the tropical polynomial p. For further details about the description of this duality, the reader can refer to [11, Chap. 3] and [4, Proposition 2.5].

For a comprehensive study in a general setting, we analyze the underlying field K. A valuation on K is a map $val : K \rightarrow {\mathbb {R}} \cup \{\infty \}$ such that it follows the following three axioms [11]

• 1. $val(a) = \infty$ if and only if $a=0$;

• 2. $val(ab) = val(a) + val(b)$;

• 3. $val(a + b) \ge min\{val(a),val(b)\}$ for all $a, b \in$ K.

An important example of a field with a non-trivial valuation is the field of Puiseux series over a arbitrary field k, represented as $K = k\{\{t\}\}$. The elements in this field are formal power series

$$\begin{aligned} k(t) = k_{1}t^{a_{1}} + k_{2}t^{a_{2}} + k_{3}t^{a_{3}} \cdots ,\end{aligned}$$

where each $k_{i} \> \in \> k, \> \forall \> i$ and $a_{1}< a_{2}< a_{3} < ....$ are rational numbers with a common denominator. This field has a natural valuation $val : k\{\{t\}\} \rightarrow {\mathbb {R}}$ given by taking a nonzero element $k(t) \in k\{\{t\}\}^{*}$, (where $k\{\{t\}\}^{*}$ represents the non zero element in the field $k\{\{t\}\}$) and mapping it to the lowest exponent $a_{1}$ in the series expansion of k(t) [11].

It is an important observation that the valuation on the field of Puiseux series mimics the operations of a tropical semiring in essence and for further discussions one can think of the underlying field for the computations to be a Puiseux series with non-trivial valuation. So points which are considered in the plane, would have lifts residing in corresponding field of Puiseux series and the map which maps these lifts back to the points is the tropicalization map. For a polynomial $f = \sum _{u \in {\mathbb {N}}^{n+1}} c_{u}x^{u}$, where the coefficients are from the field with a non-trivial valuation, the tropicalization of f can be defined as [11]

$$\begin{aligned} \text {trop}(f)(w) = \text {max}\{ -val(c_{u}) + w \cdot u : u \in {\mathbb {N}}^{n+1} \> \text {and} \> c_{u} \ne 0 \} \end{aligned}$$

We refer the reader to [11] for further details about this map.

Definition 5

A tropical line arrangement ${\mathcal {L}}$ is said to be a tropical near-pencil arrangement if in the dual Newton subdivision, for all triangular faces present in the subdivision; at least one of the edges of the triangular face lies on the boundary of the Newton polygon (see Fig. 2).

Fig. 2

An example of a tropical near pencil arrangement

Definition 6

A set of points ${\mathcal {N}}$ in the tropical plane, is said to form a tropical near-pencil if the dual tropical line arrangement is a tropical near pencil arrangement (see Fig. 3).

Fig. 3

An example of a tropical near pencil

For a tropical line arrangement with lines $l_{1},\cdots ,l_{n}$ with corresponding tropical polynomials being $f_{1},\cdots ,f_{n}$ the tropical line arrangement, as a union of tropical hypersurfaces, is defined by the polynomial,

$$\begin{aligned} f = f_{1} \cdot f_{2} \cdots \cdot f_{n} \end{aligned}$$

The dual Newton subdivision corresponding to the tropical line arrangement is the Newton subdivision dual to the tropical hypersurface defined by the tropical polynomial f (cf. [9]). We realize that stable intersections of first kind correspond to parallelograms and hexagons in the dual Newton subdivision and stable intersections of second kind correspond to irregular cells with four, five or six edges in the dual Newton subdivision.

For an elaborate description of dual Newton subdivisions, corresponding to tropical line arrangements, the reader is advised to refer to [3, Sect. 2.3].

4 Tropical incidence geometry

The behaviour of point-line structures in the tropical plane is distinct from the Euclidean case, specifically with the appearance of coaxial points.

Definition 7

Two points are said to be coaxial if they lie on the same axis of a tropical line containing them [3].

Fig. 4

The infinite number of lines passing through the coaxial points $p_{0}$ and $p_{1}$

A recent result in [3] proves the tropical version of the Sylvester Gallai Theorem,

Theorem 4

(Tropical Sylvester-Gallai) Any set of four or more points in the tropical plane determines at least one ordinary tropical line.

An important observation is that if we consider a point set with no two points being coaxial, then there is a unique tropical line passing through any two points, and therefore the point-line incidence structure in this case forms a linear space. We recall that a point set P is said to determine a line l, if l passes through at least two points of P. Hence, we can invoke the classical de-Bruijn-Erdős theorem to conclude that such a set of n points determines at least n tropical lines.

With the existence of a Tropical Sylvester-Gallai theorem, it is quite natural to explore the possibility of a tropical version of the de-Bruijn-Erdős theorem, i.e., a lower bound on the number of tropical lines determined by a n point set in the tropical plane. However, the number of lines determined by coaxial points are infinite in this setting. For the question of counting lines to be well posed, we would like to be in a scenario where a finite set of points determines a finite set of lines. Hence, rather than counting the number of lines as shown in Fig. 4, we count a special class of lines, namely stable tropical lines.

Definition 8

Consider $(L, p_{1}, \cdots , p_{n}), (n \ge 2)$ where L is a tropical line with the points $(p_{1}, \cdots , p_{n})$ on the line L, then $(L, p_{1}, \cdots , p_{n})$, is called stable (see Fig. 5) if

• 1. Either L is the unique line passing through the $p_{i}$’s, or

• 2. One of the points $p_{1}, \cdots , p_{n}$ is the vertex of L.

Fig. 5

A stable tropical line $(L,p_{0},p_{1})$

Now we show that this restriction on the counting of lines, turns out to be quite general as these stable lines turn out to be the tropicalization of the line passing through generic lifts of the points.

Proposition 1

Given two coaxial points $p_{1} = (-u,-v)$, $p_{2}=(-u',-v') \in {{\mathbb {K}}}^{2}$, pick lifts $P_{1} = (a_{1}t^{u}+ \cdots$ , $b_{1}t^{v} + \cdots )$ and $P_{2} = (a_{2}t^{u'} + \cdots$ , $b_{2}t^{v} + \cdots )$ over ${\mathbb {K}}\{\{t\}\}$. If $a_{1} \ne a_{2}$, $b_{1} \ne b_{2}$, and $a_{1}b_{2} - a_{2}b_{1} \ne 0$ then $trop({P_{1}P_{2}})$ is the stable tropical line through $p_{1}$ and $p_{2}$.

Proof

Since we assume that the two points, $p_{1}$ and $p_{2}$ are coaxial, we take $v = v'$ which would imply that the two points are coaxial in the $(-1,0)$ primitive direction.

An equation of a line in the plane is $ax + by = c$. So if the lifts $P_{1}$ and $P_{2}$ lie on this line, then they satisfy this equation

$$\begin{aligned} a(a_{1}t^{u}+ \cdots ) + b(b_{1}t^{v} + \cdots ) = c \end{aligned}$$

(1)

$$\begin{aligned} a(a_{2}t^{u'}+ \cdots ) + b(b_{2}t^{v} + \cdots ) = c \end{aligned}$$

(2)

Without loss of generality we assume $u >u'$ and $a = 1$. So subtracting the two equations gives us

$$\begin{aligned}&-a_{2}t^{u'} + O(t^{u'}) + b((b_{1} - b_{2})t^{v} + O(t^{v})) = 0\\&\quad \implies b = \frac{a_{2}t^{u'} + O(t^{u'})}{(b_{1} - b_{2})t^{v} + O(t^{v})} \\&\quad \implies c = a_{2}t^{u'} + \cdots + \frac{(a_{2}t^{u} + O(t^{u'})) \cdots (b_{2}t^{v} + \cdots )}{(b_{1} - b_{2})(t^{v}) + \cdots )} \end{aligned}$$

Therefore $val(c) = -u'$ and $val(b) = -u'-v$, and we get the Newton polytope and the tropicalization as shown in Fig. 6,

Fig. 6

Newton polytope and tropicalization for $trop(P_{1}P_{2})$

which is a stable tropical line passing through $\hbox {p}_{1}=(-u',-v)$ and $\hbox {p}_{2}=(-u,-v)$.

The result for two points being coaxial in the other two primitive directions also follows with a similar computation. $\square$

Alternatively, in [15] in Sect. 2.2 a notion of a stable curve though a set of n points is introduced. The definition of a stable curve in [15] is as follows

Definition 9

The stable curve of support I passing through $\{q_{1}, \cdots ,q_{\delta -1}\}$ is the curve defined by the polynomial f = “$\sum _{i \in I}$ $a_{i}x^{i_{1}} y^{i_{2}}$”, where the coordinates $a_{i}$ of f are the stable solutions to the linear system imposed by passing through the points $q_{j}$ .

where for a curve H given by a polynomial f, the support is the set of tuples of $i \in {\mathbb {Z}}^{n}$ such that $a_{i}$ appears in f, $\delta (I)$ denotes the number of elements in I and the stable solution for a set of tropical linear forms is the common solution for all the linear forms, which is also stable under small perturbations of the coefficients of the linear forms [13, 14].

Remark 1

The linear form that represents a tropical line in the tropical plane is given by

$$\begin{aligned} a\odot x \oplus b \odot y \oplus c \end{aligned}$$

(3)

So the support in this case is a set of 3-tuples of ${\mathbb {Z}}^{3}$ and $\delta (I) = 3$. We take two arbitrary points in the (-1,0) direction of a tropical line $P_{1} = (-u,v)$ and $P_{2} = (-u',v)$, where u and $u'$ both are positive and $u'$ $\le u$. Now let us compute the stable line passing through $P_{1}$ and $P_{2}$ in the setup of [15].

The tropical linear system obtained by plugging in the points in 3 is as follows

$$\begin{aligned} \left\{ \begin{array}{c} a\odot (-u) \oplus b \odot v \oplus c = 0\\ a\odot (-u') \oplus b \odot v \oplus c = 0\\ \end{array} \right. \end{aligned}$$

Now the stable solution of the above tropical linear system provides the coefficients for the linear form which defines the stable line passing through the two given points. The corresponding coefficient matrix is given as

$$\begin{aligned} C = \begin{bmatrix} -u &{} v &{} 0\\ -u'&{} v &{} 0 \end{bmatrix}. \end{aligned}$$

With the help of explicit computations for calculating stable solutions of tropical linear systems elaborated in [14] and [13], in the case above, we find that the stable solution is given by ($|O^{1}|_{t} : |O^{2}|_{t} : |O^{3}|_{t}$) = $(v : -u' : -u' + v)$ and hence the linear form representing the stable line through $\hbox {P}_{{1}}$ and $\hbox {P}_{{2}}$ is given as

$$\begin{aligned} v\odot x \oplus -u' \odot y \oplus -u'+ v \end{aligned}$$

(4)

This is a tropical line with vertex $(\alpha ,\beta )$ satisfying

$\alpha + v = -u' + v \implies \alpha = -u'$ and $\beta - u' = -u' + v \implies \beta = v$.

Fig. 7

Stable line passing through two given points

The computation for a two point configuration in the other two primitive directions also follows in the same manner (see Fig. 7).

So as is evident from the above discussion, taking two points on any one of the rays of a tropical line, we see that the definition of a stable line in [15] coincides with 8.

An important observation here is that the Sylvester-Gallai Theorem fails if we restrict ourselves to stable tropical lines. Fig. 8 shows explicit examples of sets of points in the tropical plane with $n = 4$ and 5 points such that these point sets do not determine an ordinary stable tropical line.

Fig. 8

Point sets which do not determine an ordinary stable tropical line

Proposition 2

Given a n-point set P in the tropical plane, the number of stable lines determined by P is equal to the number of stable intersections obtained in the corresponding dual line arrangement.

Fig. 9

Duality between stable lines and stable intersections

Proof

Consider an arbitrary stable tropical line $(L,p_{1}, p_{2} \cdots p_{n})$, then by definition either the points $p_{1}, p_{2} \cdots p_{n}$ uniquely determine L or one of the points amongst the $p_{i}'s$ is the vertex of the line L. We first consider the case when the points $p_{1}, p_{2} \cdots p_{n}$ determine the line uniquely, and in this case there must be at least two non coaxial points present on the line L, and we realize that under the duality given by the incidence preserving map $\phi$ that we defined earlier, the reflection of the vertex of the line L with respect to the origin corresponds to a unique stable intersection obtained in the dual line arrangement, illustrated in the Fig. 9. This implies a one to one correspondence between stable lines determined by such points and the stable intersections obtained in the dual line arrangement.

Also, if one of the points amongst the $p_{i}'s$ is the vertex of the stable tropical line L, then we again observe that the reflection of the the vertex of the line L with respect to the origin, corresponds to a unique stable intersection in the dual line arrangement, illustrated in the Fig. 9. Hence, we see a one to one correspondence between stable tropical lines and the number of stable intersections in the dual line arrangement. $\square$

Remark 2

We realize that this duality between stable intersections and stable lines is a bit stronger; if the stable line is the unique line passing through the points on it, then the vertex of the line corresponds to a stable intersection of first kind and if the stable line has one of the points as a vertex, then the vertex corresponds to a stable intersection of second kind.

Proposition 2 illustrates the fact that stable tropical lines are in fact dual to stable intersections of tropical lines. Proposition 2 leads on to the following corollary.

Corollary 1

For a given tropical line arrangement ${\mathcal {L}}$ in the tropical plane, the number of stable intersection points equals the number of non-triangular faces in the dual Newton subdivision corresponding to the tropical line arrangement.

Proof

Since all stable intersections are obtained as intersections of two or more rays, each point of intersection has at least four or more rays emanating from it in the primitive directions. This corresponds through duality to faces with at least four edges or more and the only other faces which contribute in the dual Newton subdivision are triangular faces which are not stable intersections. Hence, the number of stable intersections in the line arrangement is equal to the number of non-triangular faces in the dual Newton subdivision. $\square$

With this duality established, let us look at the total number of faces, which we denote as t, present in a dual Newton subdivision of a tropical line arrangement of n tropical lines, where n remains fixed for our discussion. Firstly, there is a trivial lower bound of n on t, since the n vertices of the tropical lines contribute at least n faces in the corresponding Newton subdivision. Also t is bounded above by the number $\left( {\begin{array}{c}n\\ 2\end{array}}\right) + n$, which is the number of faces when any two lines in the line arrangement intersect transversally at a unique point [3]. Therefore, t satisfies the following inequality

$$\begin{aligned} n \le t \le \left( {\begin{array}{c}n\\ 2\end{array}}\right) + n \end{aligned}$$

We recall that stable intersection of first kind correspond to parallelograms and hexagons in the dual Newton subdivision and stable intersections of second kind correspond to irregular cells with four, five or six edges in the dual Newton subdivision. A parameterized description of all the faces appearing in a dual Newton subdivision is described in the Fig. 10 also present in [3],

Fig. 10

A cell in the Newton Subdivision, which is dual to a tropical line arrangement

where $w_{1},w_{2}$ and $w_{3}$ are the number of lines, which are coaxial in the three primitive directions, and c represents the number of lines centered at the point dual to the face in the tropical line arrangement. A Newton subdivision with faces of the shape described in Fig. 10, is called a linear Newton subdivision and if the only faces occurring in a linear Newton subdivision are triangles, parallelograms and hexagons which are dual to stable intersections of first kind, then such a subdivision is called a semiuniform subdivision [3].

We refer to faces in the shapes of parallelograms and hexagons dual to stable intersections of first kind as semiuniform faces and faces dual to stable intersections of second kind as non-uniform faces.

Figure 11 shows all the possible shapes of cells present in the dual Newton subdivision of a tropical line arrangement; in the figure for all semiuniform faces, for each edge length parameter we consider $w_{i} = 1$ and for all non-uniform faces we take $w_{i} = c = 1$. For higher values of $w_{i}'s$ and c the shapes remain the same however the edge lengths corresponding to each parameter get elongated according to the values described in Fig. 10.

Fig. 11

All possible shapes of faces present in the Newton subdivision of a tropical line arrangement; with the labelings having type of stable intersections on the left along with the type of face that corresponds to it on the right

We move on to discuss one of the extremal cases for the values of t, which is the case when $t = n$.

Lemma 1

Let ${\mathcal {L}}$ be a tropical line arrangement of n lines, having exactly n faces in the corresponding dual Newton subdivision, then ${\mathcal {L}}$ has no stable intersections of first kind in the tropical line arrangement.

Proof

We start with a tropical line arrangement ${\mathcal {L}}$ of n tropical lines, such that it has exactly n faces. We continue by contradiction, assuming that there does exist a stable intersection of first kind in the line arrangement ${\mathcal {L}}$. However, since there are at least n faces contributed by the n vertices of the n tropical lines, and the face corresponding to a stable intersection of first kind is not one of them, therefore this would imply that the total number of faces in the dual Newton subdivision corresponding to ${\mathcal {L}}$ has at least $n + 1$ faces, which is a contradiction to the fact that ${\mathcal {L}}$ has n faces in the dual Newton subdivision. Hence, the proof. $\square$

Fig. 12

An example of a line arrangement with exactly n faces and three triangular faces

Example 2

We look at an example of a n line arrangement with exactly n faces. The example depicted in Fig. 12 shows a tropical line arrangement of n tropical lines $\{l_{1},l_{2},l_{3},l_{4}, \cdots ,l_{n}\}$, such that the total number of faces in the corresponding Newton subdivision is n, and it has exactly three triangular faces located at the corners of the Newton polygon.

We use $({v}{^{max}})_{t}$ to represent the maximum number of triangular faces present in a Newton subdivision corresponding to a tropical line arrangement with total number of faces in the Newton subdivision being equal to t.

Lemma 2

Let ${\mathcal {L}}$ be a tropical line arrangement of n tropical lines such that the dual Newton subdivision ${\mathcal {N}}$ has exactly n faces, then the maximum number of triangular faces in ${\mathcal {N}}$ is 3, i.e., $({v}{^{max}})_{n} = 3$ .

Proof

As can be seen from Fig. 12, there are explicit tropical line arrangements of n tropical lines with n faces in the dual Newton subdivision with exactly 3 triangular faces. We proceed by contradiction, and assume that $({v}{^{max}})_{n} > 3$. With $({v}{^{max}})_{n} > 3$, we can conclude that there does exist at least one triangular face T in the interior of the Newton polygon, i.e., when no edges of T lie on the boundary of the Newton polygon or exactly one edge of T lies on the boundary of the Newton polygon. We first consider the case when T is in the relative interior of the Newton polygon, i.e., when no edges of T lie on the boundary of the Newton polygon .

Let us consider the three faces $C_{1},C_{2}$ and $C_{3}$ that share an edge with the triangular face T and we consider an example of the local line arrangement around T as depicted in the Fig. 13.

Fig. 13

Positions of cells in the Newton subdivision and the local line arrangement dual to it

In the figure we see that the points D, E and F represent the vertices of the tropical lines $l_{1},l_{2}$ and $l_{3}$ which are present at the stable intersections of second kind at these points, dual to the cells $C_{1},C_{2}$ and $C_{3}$ in ${\mathcal {N}}$. Also $l_{0}$ represents the line dual to the triangular face T. Also, by Lemma 1 we know that no stable intersections of first kind are present in the line arrangement.

In the local picture, we obtain three stable intersections of first kind at the points A, B and C. Since these points are stable intersections and by Lemma 1 we know we can not have any stable intersections of first kind therefore there must exist a line with its vertex at these points. Let us consider one of these intersections, A. The points D, A and F are represented as $(x_{1},y_{1}),(x_{2},y_{2})$ and $(x_{3},y_{3})$, then it is easy to see that

$$\begin{aligned} x_{1}< x_{2} < x_{3} \end{aligned}$$

This helps to conclude that if there is a tropical line present with vertex at A, then it would either intersect the lines $l_{0}$ and $l_{3}$ at two points, or meet the vertex of the line $l_{0}$. There cannot be a line with vertex at A meeting the vertex of the line $l_{0}$ as that would contradict the fact that the face corresponding to $l_{0}$ is a triangular face T in ${\mathcal {N}}$. So we continue with the other case when the line has the vertex at A and intersects the lines $l_{0}$ and $l_{3}$ at two points. But there cannot be a tropical line present at A with two points of intersection with the lines $l_{0}$ and $l_{3}$, as that would contradict the fact that the cells $C_{1},C_{2}$ and $C_{3}$ corresponding to the stable intersections at D, E and F, share an edge with the triangular face T. Hence, there cannot be a tropical line with a vertex at A, and therefore A has to be a stable intersection of first kind, which contradicts Lemma 1. The same argument follows for the other two points of intersections, B and C. However, this is a contradiction to the Lemma 1. Another observation is that for all possibilities of non-uniform faces (arising from stable intersections of second kind) surrounding T, we obtain points of intersections in similar positions as A, B and C which establishes the existence of at least three stable intersections of first kind, and hence gives a contradiction. Therefore, this shows that it is not possible to place a triangular face in the relative interior of the Newton polygon.

The other possible case is when the triangular face intersects the boundary of the Newton polygon in exactly one edge. Without loss of generality, we take the triangular face to be intersecting with one of the edges of the Newton polygon as depicted in the Fig. 14 and we look at the local line arrangement around the triangular face T.

Fig. 14

Positions of cell in the Newton subdivision and the local line arrangement dual to it

We argue in the same way as we did in the previous case, and realize that by Lemma 1, $C_{1}$ and $C_{2}$ in Fig. 14 are non-uniform faces. Also, we see that in Fig. 14 the points B and C represent the vertices of the tropical lines $l_{1}$ and $l_{2}$ which are present at the stable intersection of second kind at these points, dual to the cells $C_{1}$ and $C_{2}$ in ${\mathcal {N}}$. Here $l_{0}$ represents the line dual to the triangular face T.

In the local picture, we obtain a stable intersection of first kind at the point A. If the points B, A and C are represented as $(x_{1},y_{1}),(x_{2},y_{2})$ and $(x_{3},y_{3})$, then it is easy to see that

$$\begin{aligned} x_{1}< x_{2} < x_{3} \end{aligned}$$

This helps to conclude that if there is a tropical line present with vertex at A, then it would either intersect the line $l_{0}$, or meet the vertex of the line $l_{0}$. There cannot be a line with vertex at A meeting the vertex of the line $l_{0}$ as that would contradict the fact that the face corresponding to $l_{0}$ is a triangular face T in ${\mathcal {N}}$. So we continue with the other case when the line has the vertex at A and intersects the lines $l_{0}$. But there cannot be a tropical line present at this intersection as that would contradict the fact that the cells $C_{1}$ and $C_{2}$ corresponding to the stable intersections of second kind at B and C share an edge with the triangular face T. Hence, there cannot be a tropical line with a vertex at A, and therefore A has to be a stable intersection of first kind, which contradicts Lemma 1. It is easy to verify that this contradiction occurs for all possibilities of non-uniform faces (arising from stable intersections of second kind), which can be adjacent to T.

Therefore, the only places left to place a triangular face in the Newton polygon, are the three corners, and hence the maximum number of triangular faces that can be obtained is three, i.e., $({v}{^{max}})_{n} = 3$. $\square$

Using Lemma 2 we obtain Corollary 2,

Corollary 2

Let ${\mathcal {L}}$ be a tropical line arrangement of n lines, such that $t = n$ and let v denote the number of triangular faces present in the dual Newton subdivision ${\mathcal {N}}$. Then

$$\begin{aligned} n - v \ge n - 3 \end{aligned}$$

Remark 3

An important inference is that for tropical line arrangements of n lines, with n faces in the dual Newton subdivision, they occur in four distinct classes. Each class is represented by the number of triangular faces at the corners, which varies between 0, 1, 2 and 3.

With Lemma 2, we now know the bound on the number of stable intersections of an n line arrangement with exactly n faces in the corresponding dual Newton subdivision. We now move on to the more general situation.

We now define what it means for a semiuniform face to be determined by a triangular face T.

Definition 10

A semiuniform face S in a dual Newton subdivision is said to be determined by a triangular face T if,

• 1. S is adjacent to T, i.e., T and S share an edge, or

• 2. S is located as the faces $S_{1},S_{2}$ or $S_{3}$ depicted in the Fig. 15

Here the shapes and location of these three semiuniform faces has to be exactly the same as shown in the figure in order for the faces to be determined by the triangular face T. We also note that edge lengths of these faces need not be unit length, and they could be elongated depending on the lattice length parameters $w_{i}$ and c of the adjacent faces to T. We also note that a triangular face determines at most six semiuniform faces; at most three adjacent to it and at most three non adjacent to it.

Fig. 15

The non-adjacent semiuniform faces determined by a triangular face T

We note that as a consequence of the definition, the determined faces $S_{1},S_{2}$ or $S_{3}$ cannot be hexagonal faces.

With the above definitions, we look at the number of semiuniform faces determined by a triangular face depending on the location of the triangular face in the dual Newton subdivision.

Proposition 3

Let ${\mathcal {L}}$ be a tropical line arrangement of n lines and let ${\mathcal {N}}$ be its dual Newton subdivision. If T is a triangular face in ${\mathcal {N}}$ (excluding the corners), then

• 1. T determines at least three seminuniform faces if T is in the relative interior of the Newton polygon.

• 2. T determines at least one seminuniform face if T is at the boundary of the Newton polygon.

Proof

We continue with the discussion in the Lemma 2. As we see in Fig. 13, it is shown that a triangular face T, which is not adjacent to a semiuniform face, determines at least three semiuniform faces if T is in the interior and at least one semiuniform face if T is located at the boundary. However, semiuniform faces might also occur as faces adjacent to the triangular face. Therefore, when we consider the triangular face T in the interior, then T can be adjacent to either one, two or at most three semiuniform faces. We know that if T is adjacent to semiuniform faces at all edges, then there are at least three semiuniform faces determined by T in the subdivision, trivially. Now we consider the case, when the triangular face is adjacent to two semiuniform faces. In this case, the location of the triangular face, implies existence of at least one non-adjacent semiuniform faces. Similarly, in the case when the triangular face is adjacent to one semiuniform face, at least two non-adjacent semiuniform faces are obtained. Both these cases are illustrated through an example in the Fig. 16. Hence if a triangular face is in the interior of the Newton polygon, then it implies the existence of at least three semiuniform faces.

Fig. 16

Examples depicting local line arranagements dual to a triangular face with 1 or 2 semiuniform faces adjacent to it

Similarly, if we consider the case when the triangular face T is located at the boundary, then if there are semiuniform faces adjacent to T at one or two edges, then there exists at least one semiuniform face in the subdivision, trivially. If T is not adjacent to any semiuniform faces, then we see in Fig. 14, that T determines at least one semiuniform face. Hence, we can conclude that if a triangular face is at the boundary then it determines at least one semiuniform face. $\square$

We now move on to count the total number of semiuniform face determined by the triangular faces. Since two or more triangular faces can determine common semiuniform faces, therefore the total count cannot be a direct sum of determined faces of all triangular faces.

With an abuse of notation we denote T to be a triangular face and n(T) represent the number of semiuniform faces determined by the triangular face T. Hence, $n(T_{1} \cup ... \cup T_{m})$ denotes the total number of semiuniform faces determined by the triangular faces $T_{1},...,T_{m}$.

Theorem 5

Let ${\mathcal {L}}$ be a tropical line arrangement of n lines and ${\mathcal {N}}$ be its dual Newton subdivision, with $T_{1} \cdots T_{m}$ being the triangular faces in ${\mathcal {N}}$ (excluding the corners) and k be the number of stable intersections of first kind. Then,

$$\begin{aligned} k \ge n(T_{1} \cup T_{2} \cdots \cup T_{m}) \ge m \end{aligned}$$

Proof

We proceed with induction on m, with the base case being $m=1$. We see that in this case, by Proposition 3, we know that the unique triangle present in the interior of ${\mathcal {N}}$ determines at least one semiuniform face, therefore

$$\begin{aligned} k \ge n(T) \ge 1 \end{aligned}$$

Fig. 17

An example to illustrate the rearrangement when T is adjacent to semiuniform faces

Fig. 18

An example to illustrate the rearrangement when T is adjacent to five or six edged non-uniform faces

Firstly, we consider a subdivision ${\mathcal {N}}$ with m triangular faces in the interior. We now show that for any such subdivision ${\mathcal {N}}$, we can always construct a subdivision ${\mathcal {N}}'$, such that ${\mathcal {N}}'$ has exactly $m-1$ triangular faces, via a rearrangement of ${\mathcal {L}}$ to ${\mathcal {L}}'$ . We consider a triangular face T in ${\mathcal {N}}$, dual to $l'$ in ${\mathcal {L}}$, which we rearrange to obtain a stable intersection in order to construct the subdivision ${\mathcal {N}}'$. We go through the following cases based on the types of faces adjacent to T in ${\mathcal {N}}$,

• 1. If T has at least one semiuniform face adjacent to it, dual to a stable intersection of first kind P.

We move the vertex of the line $l'$ (which is dual to T) along with coaxial lines to $l'$, towards P, such that the vertex of $l'$ is superimposed on the point P, illustrated in the Fig. 17. If during the rearrangement, any rays of the lines coaxial to $l'$ meet the vertex of another line, which might result in a reduction in the total number of triangular faces, we can consider a local perturbation of the vertex of such a line, along the half ray, and in this way we can prevent such a situation. In this way we obtain a subdivision ${\mathcal {N}}'$ with exactly $m-1$ triangular faces, via a local rearrangement. We also notice that the determined semiuniform face dual to the point P in ${\mathcal {N}}$, ceases to exist in $\mathcal {N'}$, since the vertex of $l'$ gets superimposed on P.

• 2. If T is adjacent only to non-uniform faces, with at least one of the adjacent non-uniform faces being five or six edged.

If T is adjacent to non-uniform faces in ${\mathcal {N}}$, then by the definition of determined faces from the Fig. 15, we realize that T determines uniquely at least one non-adjacent semiuniform face dual to a stable intersection of first kind P, in ${\mathcal {N}}$. We move the vertex of the line $l'$ dual to T (along with any coaxial lines to $l'$ if there exist any), illustrated in Fig. 18, such that it meets the half ray of another line in ${\mathcal {L}}$ and there is an effective decrease in the number of triangular faces by 1 (in our example we assume $P_{2}$ to be the face which has to be a five or six edged face). We show the location of lines coaxial to $l'$ (if present) by a dotted arrow along the ray of coaxiality in the rearrangement. If during the rearrangement, any rays of the lines coaxial to $l'$ meet the vertex of another line, which might result in the reduction in the total number of triangular faces, we can consider a local perturbation of the vertex of such a line, along the half ray, and in this way we can prevent such a situation. Hence, in this way we construct a subdivision ${\mathcal {N}}'$ with exactly $m-1$ triangular faces, via a local rearrangement. We also observe that the determined semiuniform face dual to P in ${\mathcal {N}}$ no more remains a determined semiuniform face in $\mathcal {N'}$, because firstly by the definition of determined faces, the face dual to P cannot be a hexagon. Additionally, out of the four edges of the face dual to P, only at two edges can it be adjacent to triangular faces, and we realize that in ${\mathcal {N}}'$ at both these edges, the face is adjacent to non-triangular faces. Hence, the face dual to P cannot be a determined face by virtue of being adjacent to a triangular face in ${\mathcal {N}}'$. Also, it can neither be a non-adjacent determined face, since the face dual to P was the unique non-adjacent determined face with respect to T, and the triangular face T no longer exists in ${\mathcal {N}}'$.

• 3. If T is adjacent to only four-edged non-uniform faces.

Fig. 19

All cases where T is adjacent to two or three four edged non uniform faces along with the corresponding rearrangement ${\mathcal {L}}'$

Firstly, by the definition of determined faces from the Fig. 15, we realize that T determines uniquely at least one non-adjacent semiuniform face dual to a stable intersection of first kind P in ${\mathcal {N}}$. We notice that in such this case, we cannot obtain ${\mathcal {N}}'$ by the movement of just $l'$ and its coaxial lines since it results in an increase in the number of triangular faces. However, we observe that with a local rearrangement of $l'$ along with its neighbouring lines which are coaxial to $l'$, we can obtain ${\mathcal {N}}'$. When T is adjacent to three or two such four edged faces, the local rearrangement is illustrated in Fig. 19. In the first case we see that no lines can be present inside the hexagon $Pl_{1}Ql_{3}Rl_{2}$, where we abuse the notation to denote $l_{i}$ as the vertex of the line $l_{i}, i \in \{ 1,2,3 \}$, because that would contradict the adjacency of the faces dual to vertices of $l_{1},l_{2}$,$l_{3}$ and T. Also other lines coaxial to any of the $l_{i}$’s (if present) are depicted by dotted arrows in the figure. Essentially, one can think of this rearrangement as moving the line $l_{3}$ and $l_{2}$ along with the coaxial lines (if present) on the half rays not shared with $l'$, such that the vertices of $l_{2}$ and $l_{3}$ lie on the segments $Ql_{1}$ and $Pl_{1}$ respectively and one of the rays from each $l_{3}$ and $l_{2}$ meets the vertex of $l'$. In this way we obtain a subdivision ${\mathcal {N}}'$ with one less triangular face. Once again if during the rearrangement, any rays of the lines coaxial to $l'$ meet the vertex of another line, which might result in the reduction in the total number of triangular faces, we can consider a local perturbation of the vertex of such a line, along the half ray, and in this way we can prevent such a situation. A similar argument works for the remaining case in Fig. 19. Also, we realize that the face dual to P ceases to exist as we go from ${\mathcal {N}}$ to $\mathcal {N'}$, and this is illustrated in the Fig. 19.

Hence, we see that in all cases for any subdivision ${\mathcal {N}}$ we can perform a rearrangement of ${\mathcal {L}}$ to ${\mathcal {L}}'$, to obtain a subdivision ${\mathcal {N}}'$ with exactly $m-1$ triangular faces. Also, we notice that as we change from ${\mathcal {N}}$ to $\mathcal {N'}$, there always exists a determined semiuniform face, dual to a stable intersection of first kind (P), which either ceases to exist in $\mathcal {N'}$ (Case (1) and (3)) or does not remain a determined semiuniform face in $\mathcal {N'}$ (Case (2)). Hence, there exists a determined semiuniform face in ${\mathcal {N}}$, which can never contribute to the total count of determined semiuniform faces in $\mathcal {N'}$. We now invoke the induction hypothesis for $\mathcal {N'}$ with $m-1$ triangular faces and we obtain,

$$\begin{aligned} k \ge n(T_{1} \cup T_{2} \cdots \cup T_{m-1}) \ge m - 1 \end{aligned}$$

Since, the face dual to P cannot contribute to the $m-1$ faces determined by triangular faces present in ${\mathcal {N}}'$. Hence for ${\mathcal {N}}$, we have

$$\begin{aligned} n(T_{1} \cup T_{2} \cdots \cup T_{m}) \ge n(T_{1} \cup T_{2} \cdots \cup T_{m-1}) + 1 \ge m-1 + 1 \ge m \end{aligned}$$

Therefore, we realize that for all cases, given a subdivision ${\mathcal {N}}$ with m triangular faces,

$$\begin{aligned} k \ge n(T_{1} \cup T_{2} \cdots \cup T_{m}) \ge m \end{aligned}$$

Hence, the proof. $\square$

Lemma 3

If ${\mathcal {L}}$ is a tropical line arrangement of n tropical lines, then it determines at least $n - 3$ stable intersections.

Proof

We try to look at all possible places where triangular faces occur in a Newton subdivision. If v is the number of triangular faces present in a subdivision, then we can write v as

$$\begin{aligned} v = p + q \end{aligned}$$

where p be the number of triangular faces present in the interior of the Newton polygon, i.e., triangular faces which are adjacent to at least two or more faces in the subdivision and q be the number of triangular faces present at the corners of the Newton polygon, i.e., triangular faces which are adjacent to exactly one other face in the subdivision. It is easy to see that $q \in \{0,1,2,3\}$. Then the lower bound on the number of semiuniform faces, which are determined by these triangular faces, is p (by Theorem 5). Therefore if k is the total number of faces corresponding to stable intersections of first kind, then

$$\begin{aligned} k \ge p \end{aligned}$$

Also, the number of stable intersections of second kind h = $n - v$ (since triangular faces and faces corresponding to stable intersections of second kind are contributed by vertices of lines, hence their sum is equal to n).

Therefore, the total number of stable intersections b is given as

$$\begin{aligned} b = n - v + k \ge n - p - q + p = n - q \ge n - 3 \end{aligned}$$

Hence, $b \ge n-3$. $\square$

The following lemma provides a partial classification of the case in which the bound in Lemma 3 is achieved. Although, subdivided in cases and a bit technical, this completes the result and helps in phrasing our final tropical result as a proper counterpart to the de Bruijn-Erdős Theorem.

Lemma 4

Let ${\mathcal {L}}$ be a tropical line arrangement of n tropical lines and let ${\mathcal {N}}$ be its dual Newton subdivision. If ${\mathcal {L}}$ determines $n-3$ stable intersections, then there are three triangular faces present at the corners of the Newton polygon and ${\mathcal {N}}$ can not have any triangular faces in the relative interior of the Newton polygon.

Before we start the proof, we provide an outline. The proof proceeds on contradiction and runs on case distinctions on how the faces determined by a triangular face present in the relative interior of the Newton polygon can be shared with other triangular faces. In all these cases, we conclude that the presence of such a triangular face in the relative interior would contradict the count of number of stable intersection i.e., $n-3$.

Proof

If ${\mathcal {L}}$ determines $n-3$ stable intersections, it is the case when the bound from Lemma 3 is sharp, which happens when the following equalities hold true

$$\begin{aligned} q = 3 \end{aligned}$$

(5)

and

$$\begin{aligned} k = n(T_{1} \cup T_{2} \cdots \cup T_{m}) = m \end{aligned}$$

(6)

The first equality implies that there must be three triangular faces present at the corners of the Newton polygon.

We now assume to the contrary, that there does exist triangular faces in the relative interior. We now consider one such triangular face T in the relative interior of the Newton polygon. We consider all possible cases for T, where it can share faces with other triangular faces in ${\mathcal {N}}$,

• 1. If T does not share any semiuniform faces with any other triangular face in ${\mathcal {N}}$.

By Proposition 3 we know that any triangular face in the relative interior determines at least three semiuniform face. Then

$$\begin{aligned} \begin{aligned} k = n((T_{1} \cup T_{2} \cdots \cup T_{m-1}) \cup T) = n(T_{1} \cup T_{2} \cdots \cup T_{m-1}) + n(T) \\ \ge m-1 + 3 = m + 2 \end{aligned} \end{aligned}$$

which gives a contradiction to the Eq. 6.

• 2. If T shares a semiuniform face with exactly one other triangular face $T_{\alpha }$ in ${\mathcal {N}}$.

Fig. 20

All possibilities for T, when it shares a semiuniform face with another triangular face

All possible cases for T, upto symmetry, are listed in Fig. 20. We realize that in all such cases, when we consider all possible adjacent faces to T, for all of them $n(T) = 4$, and none of the $m-2$ triangular faces apart from T and $T_{\alpha }$, can determine the four faces determined by T, because that would contradict the fact that T can share faces with exactly one other triangular face. Also, by Theorem 5, for the $m-2$ triangular faces apart from T and $T_{\alpha }$,

$$\begin{aligned} n(T_{1} \cup T_{2} \cdots \cup T_{m-2}) \ge m-2 \end{aligned}$$

therefore,

$$\begin{aligned} k = n(T_{1} \cup T_{2} \cdots \cup T_{m}) \ge n(T_{1} \cup T_{2} \cdots \cup T_{m-2}) + n(T) \ge m-2 + 4 = m+2 \end{aligned}$$

which again gives a contradiction to the Eq. 6.

We also remark that for this case and all subsequent cases, semiuniform faces which are parallelograms, and are determined by two different triangular faces, can not have edge lengths greater than one, since they share one edge, per pair of parallel edges, with a triangular face, whose edges always have unit lattice length. Hence, for all cases, the parallelogram faces are of unit lattice length. However, for hexagonal faces, edges not adjacent with triangular faces, can be of lattice length greater than one, although this does not change the count of determined faces for T, i.e., n(T), rather it only enlarges the lengths of the edges adjacent to the hexagonal face. Hence, in our considerations, we would consider all hexagonal faces having unit lattice length.

• 3. If T shares a semiuniform face with exactly two other triangular faces $T_{\alpha }$ and $T_{\beta }$ in ${\mathcal {N}}$.

Fig. 21

Possibilities for T, when it shares semiuniform faces with exactly two other triangular faces

Fig. 22

The case when T shares semiuniform with two other triangular faces, with one of the determined faces being a hexagon

All possible cases for T, upto symmetry, are listed in Figs. 21 and 22. We realize that in all cases in Fig. 21, when we consider all possible adjacent faces for T, $n(T) = 5$, and for the first case in Fig. 22, $n(T) = 4$, while for all others in Fig. 22, $n(T) = 5$. Also none of the $m-3$ triangular faces apart from T, $T_{\alpha }$ and $T_{\beta }$, can determine the faces determined by T, because that would contradict the fact that T can share faces with only two other triangular faces. By Theorem 5, for the $m-3$ triangular faces apart from T, $T_{\alpha }$ and $T_{\beta }$, we have

$$\begin{aligned} n(T_{1} \cup T_{2} \cdots \cup T_{m-3}) \ge m-3 \end{aligned}$$

therefore,

$$\begin{aligned} k = n(T_{1} \cup T_{2} \cdots \cup T_{m}) \ge n(T_{1} \cup T_{2} \cdots \cup T_{m-3}) + n(T) \ge m-3 + 4 = m+1 \end{aligned}$$

which again gives a contradiction to the Eq. 6.

• 4. If T shares a semiuniform face with exactly three other triangular faces $T_{\alpha }$, $T_{\beta }$ and $T_{\gamma }$ in ${\mathcal {N}}$.

Fig. 23

Possibilities for T, when it shares semiuniform faces with three other triangular faces

Fig. 24

Possibilities for T, when it shares semiuniform faces with three another triangular faces, involving a hexagonal face which T shares with one other triangular face

Fig. 25

Possibilities for T, when it shares semiuniform faces with three other triangular faces, involving a hexagonal face which T shares with two other triangular face

All possible cases for T, upto symmetry, are listed in Figs. 23, 24 and 25. We realize that in all cases in Figs. 23 and 24, $n(T) = 6$, and for all the cases in Fig. 25, $n(T) = 5$. Also none of the $m-4$ triangular faces apart from T, $T_{\alpha }$, $T_{\beta }$ and $T_{\gamma }$, can determine the faces determined by T, because that would contradict the fact that T can share faces with only three other triangular faces. By Theorem 5, for the $m-4$ triangular faces apart from T, $T_{\alpha }$, $T_{\beta }$ and $T_{\gamma }$,

$$\begin{aligned} n(T_{1} \cup T_{2} \cdots \cup T_{m-4}) \ge m-4 \end{aligned}$$

therefore,

$$\begin{aligned} k = n(T_{1} \cup T_{2} \cdots \cup T_{m}) \ge n(T_{1} \cup T_{2} \cdots \cup T_{m-4}) + n(T) \ge m-4 + 5 = m+1 \end{aligned}$$

which again gives a contradiction to the Eq. 6.

• 5. If T shares a semiuniform face with exactly four other triangular faces $T_{\alpha }$, $T_{\beta }$, $T_{\gamma }$ and $T_{\phi }$ in ${\mathcal {N}}$.

Fig. 26

The case for T, when it shares two hexagonal faces with four other triangular faces

Fig. 27

Possibilities for T, when it shares semiuniform faces with four other triangular faces

All possible cases for T, upto symmetry, are listed in Figs. 26 and 27. We realize that for the case in Fig. 26, $n(T) = 5$. However, due to the arrangements of the faces, some of the faces are fixed and are bound to appear in the subdivision, which we show as $S_{1}, S_{2}, S_{3}$ and $S_{4}$ in the Fig. 26. Amongst these faces, $S_{4}$ is a face which can not be determined by $T, T_{\alpha }, T_{\beta }, T_{\phi }$ and $T_{\gamma }$. Additionally, we observe that it can also not be determined by any of the remaining $m-5$ triangular faces in ${\mathcal {N}}$ since it has no free edges which could be adjacent to a triangular face. This implies that the dual point to $S_{4}$ contributes to the count of stable intersections of first kind k, although it is not determined by any triangular face in ${\mathcal {N}}$. This gives a contradiction to the following equality

$$\begin{aligned} k = n(T_{1} \cup T_{2} \cdots \cup T_{m}) \end{aligned}$$

For the other cases in Fig. 27, $n(T) = 6$. None of the $m-5$ triangular faces apart from T, $T_{\alpha }$, $T_{\beta }, T_{\gamma }$ and $T_{\phi }$, can determine the faces determined by T, because that would contradict the fact that T can share faces with only four other triangular faces. By Theorem 5, for the $m-5$ triangular faces apart from T, $T_{\alpha }$, $T_{\beta }$ and $T_{\gamma }$,

$$\begin{aligned} n(T_{1} \cup T_{2} \cdots \cup T_{m-5}) \ge m-5 \end{aligned}$$

therefore,

$$\begin{aligned} k = n(T_{1} \cup T_{2} \cdots \cup T_{m}) \ge n(T_{1} \cup T_{2} \cdots \cup T_{m-5}) + n(T) \ge m-5 + 6 = m+1 \end{aligned}$$

which again gives a contradiction to the Eq. 6.

The remaining three cases illustrated in Fig. 28 can also be eliminated by a similar argument, since in all these cases we obtain a semiuniform face $S'$, which cannot be determined by a triangular face, which gives a contradiction to the Eq. 6.

Fig. 28

The cases where T shares faces with five or six other triangular faces

Hence, we completed all cases and we infer that the presence of a triangular face in the relative interior contradicts the sharpness of the bound. Hence, the proof. $\square$

Remark 4

We note that the converse of Lemma 4 does not hold true, meaning that if ${\mathcal {L}}$ is a tropical near-pencil arrangement, then it does not imply that the number of stable intersections equals $n-3$, an example of which is illustrated in Fig. 2. However, such a converse does hold true trivially in the classical case of Theorem 2.

Now we have established the required setup to state the tropical versions of the de-Bruijn Erdős Theorem,

Theorem 6

(Dual Tropical de Bruijn-Erdős Theorem) Let ${\mathcal {L}}$ be a tropical line arrangement of n $(n \ge 4)$ tropical lines in the plane. Let b denote the number of stable intersections determined by ${\mathcal {L}}$. Then,

• 1. $b \ge n - 3$

• 2. If $b = n - 3$, then ${\mathcal {L}}$ is a tropical near-pencil arrangement.

Proof

Follows by proof of Lemmas 3 and 4. $\square$

With the duality elaborated in Proposition 2, we can now state the main theorem,

Theorem 7

(Tropical de Bruijn-Erdős Theorem) Let ${\mathcal {S}}$ denote a set of points in the tropical plane. Let v $(v \ge 4)$ denote the number of points in ${\mathcal {S}}$, and let b denote the number of stable tropical lines determined by these points. Then,

• 1. $b \ge v - 3$

• 2. If $b = v - 3$, then ${\mathcal {S}}$ forms a tropical near-pencil.

Proof

Follows by proofs of Theorem 6 and projective duality established in Proposition 2. $\square$

5 Further Perspectives

In [1] a type of a point is defined as follows,

Definition 11

A (n, d) type is a n tuple $A = (A_{1}, \cdots , A_{n})$ of nonempty subsets of $[d]:= \{ 1,2, \cdots ,d \}$. The $A_{i}$’s are called coordinates of A, $1, \cdots , n$ are called the positions and $1, \cdots , d$ are called the directions.

which assigns a tuple to each point in the plane based on its location with respect to a collection of hyperplanes, which in our case are lines and so $d = 3$ in this case. It might be interesting to look into the derivation of our results in terms of these types. Fig. 29, depicts the types corresponding to all the various faces that are present in a linear Newton subdivision. The $'*'$ in the tuples represents a singleton, while the coordinates which have multiple elements may not occur consecutively, but they can be made consecutive, by rearranging the way we count the lines in the arrangement. We can obtain the type for a face P with edge lengths greater than one, by assigning copies of the directions 12, 13 or 23 depending on the direction of coaxiality of other lines with the vertex of the line dual to P. Such an analysis could help in trying to look for generalizations of our results in higher dimensions.

Also there has been a lot of interest in the study of tropical lines present in tropical cubic surfaces owing to the existence of classical results such as the famous 27 lines on a cubic surface, which has provided detailed analysis about lines embedded in surfaces and is explored widely in [12] and [10], and one can try to generalize our results to higher dimensions using techniques from their work.

Fig. 29

All possible shapes of faces present in the Newton subdivision of a tropical line arrangement; with the corresponding type in the tropical oriented matroid on the right