Modular Frobenius pseudo-varieties

Abstract

If $m \in {\mathbb {N}} \setminus \{0,1\}$ and A is a finite subset of $\bigcup _{k \in {\mathbb {N}} \setminus \{0,1\}} \{1,\ldots ,m-1\}^k$, then we denote by

$$\begin{aligned} {\mathscr {C}}(m,A) =&\{ S\in {\mathscr {S}}_m \mid s_1+\cdots +s_k-m \in S \text { if } (s_1,\ldots ,s_k)\in S^k \text { and } \\ {}&\qquad (s_1 \bmod m, \ldots , s_k \bmod m)\in A \}. \end{aligned}$$

In this work we prove that ${\mathscr {C}}(m,A)$ is a Frobenius pseudo-variety. We also show algorithms that allows us to establish whether a numerical semigroup belongs to ${\mathscr {C}}(m,A)$ and to compute all the elements of ${\mathscr {C}}(m,A)$ with a fixed genus. Moreover, we introduce and study three families of numerical semigroups, called of second-level, thin and strong, and corresponding to ${\mathscr {C}}(m,A)$ when $A=\{1,\ldots ,m-1\}^3$, $A=\{(1,1),\ldots ,(m-1,m-1)\}$, and $A=\{1,\ldots ,m-1\}^2 \setminus \{(1,1),\ldots ,(m-1,m-1)\}$, respectively.

1 Introduction

Let ${\mathbb {N}}$ be the set of non-negative integers. A numerical semigroup is a subset S of ${\mathbb {N}}$ that is closed under addition, $0 \in S$ and ${\mathbb {N}} \setminus S$ is finite. The Frobenius number of S, denoted by $\mathrm {F}(S)$, is the greatest integer that does not belong to S. The cardinality of ${\mathbb {N}}\setminus S$, denoted by $\mathrm {g}(S)$, is the genus of S.

A Frobenius pseudo-variety is a non-empty family ${\mathcal {P}}$ of numerical semigroups that fulfils the following conditions.

• 1. ${\mathcal {P}}$ has a maximum element (with respect to the inclusion order).

• 2. If $S,T \in {\mathcal {P}}$, then $S\cap T\in {\mathcal {P}}$.

• 3. If $S\in {\mathcal {P}}$ and $S\ne \max ({\mathcal {P}})$, then $S\cup \{\mathrm{F}(S)\} \in {\mathcal {P}}$.

The multiplicity of a numerical semigroup S, denoted by $\mathrm {m}(S)$, is the least positive integer that belongs to S. If m is a positive integer, then we denote by ${\mathscr {S}}_m=\left\{ S \mid S \text{ is } \text{ a } \text{ numerical } \text{ semigroup } \text{ with } \mathrm {m}(S)=m \right\}$.

Let $m\in {\mathbb {N}} \setminus \{0,1\}$ and let A be a finite subset of $\bigcup _{k \in {\mathbb {N}} \setminus \{0,1\}} \{1,\ldots ,m-1 \}^k$ (where $X^k=X\times {\mathop {\cdots }\limits ^{^{(k)}}} \times X = \left\{ (x_1,\ldots ,x_k) \mid x_1,\ldots ,x_k \in X \right\}$). We denote by

$$\begin{aligned} {\mathscr {C}}(m,A) =&\{ S\in {\mathscr {S}}_m \mid s_1+\cdots +s_k-m \in S \text { if } (s_1,\ldots ,s_k)\in S^k \text { and } \\ {}&\qquad (s_1 \bmod m, \ldots , s_k \bmod m)\in A \} . \end{aligned}$$

Our main purpose in this work is to study the set ${\mathscr {C}}(m,A)$.

In Sect. 2 we show that ${\mathscr {C}}(m,A)$ is a Frobenius pseudo-variety with maximum element given by $\Delta (m)=\left\{ 0,m,\rightarrow \right\}$ (where the symbol $\rightarrow$ means that every integer greater than m belongs to $\Delta (m)$). Thus, we call the pseudo-varieties that arise in this way modular Frobenius pseudo-varieties. Also, we give an algorithm that allows us to establish whether a numerical semigroup belongs to ${\mathscr {C}}(m,A)$. In addition, with the help of the results in [9], we can arrange ${\mathscr {C}}(m,A)$ in a rooted tree and we find an algorithm to compute all the elements of ${\mathscr {C}}(m,A)$ with a fixed genus.

If X is a non-empty subset of ${\mathbb {N}}$, then we denote by $\langle X \rangle$ the submonoid of $({\mathbb {N}},+)$ generated by X, that is,

$$\langle X \rangle =\big \{\lambda _1x_1+\cdots +\lambda _nx_n \mid n\in {\mathbb {N}}\setminus \{0\}, \ x_1,\ldots ,x_n\in X, \ \lambda _1,\ldots ,\lambda _n\in {\mathbb {N}}\big \}.$$

It is well known (see Lemma 2.1 of [11]) that $\langle X \rangle$ is a numerical semigroup if and only if $\gcd (X)=1$. If M is a submonoid of $({\mathbb {N}},+)$ and $M=\langle X \rangle$, then we say that X is a system of generators of M. Moreover, if $M\not =\langle Y \rangle$ for any subset $Y\subsetneq X$, then we say that X is a minimal system of generators of M. In Corollary 2.8 of [11] it is shown that each submonoid of $({\mathbb {N}},+)$ has a unique minimal system of generators and that such a system is finite. We denote by $\mathrm {msg}(M)$ the minimal system of generators of M. The cardinality of $\mathrm {msg}(M)$, denoted by $\mathrm {e}(M)$, is the embedding dimension of M.

By applying Proposition 2.10 of [11], if S is a numerical semigroup, then we know that $\mathrm {e}(S)\le \mathrm {m}(S)$. A numerical semigroup S has maximal embedding dimension if $\mathrm {e}(S)=\mathrm {m}(S)$. This family of numerical semigroups has been extensively studied (for instance, see [2] and [11]). Let us denote by ${\mathcal {M}}_m$ the set formed by the numerical semigroups that have maximal embedding dimension and with multiplicity m. It is easy to see that ${\mathcal {M}}_m={\mathscr {C}}(m,\{1,\ldots ,m-1\}^2)$.

In Sects. 3, 4, and 5 we study the family ${\mathscr {C}}(m,A)$ for

• $A=\{1,\ldots ,m-1\}^3$,

• $A=\{(1,1),\ldots ,(m-1,m-1)\}$,

• $A=\{1,\ldots ,m-1\}^2 \setminus \{(1,1),\ldots ,(m-1,m-1)\}$,

respectively. Observe that, in a certain sense, these families are generalisation of ${\mathcal {M}}_m$.

To finish this introduction, we are going to comment several ideas (see [3, 4, 14]) that motivate the study of modular Frobenius pseudo-varieties.

First of all, observe that modular Frobenius pseudo-varieties are related to the non-homogeneous patterns with positive coefficients that involve in their constant parameter the multiplicity of the numerical semigroup (see [4]).

The notion of non-homogeneous pattern was introduced in [4] as a generalisation of the notion of homogeneous pattern [3]. Thus, a linear pattern $p(x_1,\ldots ,x_n)$ is an expression of the form $a_1x_1+\cdots +a_nx_n+a_0$, with $a_0\in {\mathbb {Z}}$ (as usual, ${\mathbb {Z}}$ is the set of integers numbers) and $a_1,\ldots ,a_n\in {\mathbb {Z}}\setminus \{0\}$. In particular, the (linear) pattern p is homogeneous if $a_0=0$, and non-homogeneous if $a_0\not =0$.

On the other hand, it is said that a numerical semigroup S admits the homogeneous pattern p if $p(s_1,\ldots ,s_n)\in S$ for every non-increasing sequence $(s_1,\ldots ,s_n)\in S^n$. The corresponding definition for non-homogeneous patterns is a bit different: a numerical semigroup S admits the non-homogeneous pattern p if $p(s_1,\ldots ,s_n)\in S$ for every non-increasing sequence $(s_1,\ldots ,s_n)\in (S\setminus \{0\})^n$.

Having in mind that $M(S)=S\setminus \{0\}$ is an ideal of the numerical semigroup S (in fact, M(S) is the maximal ideal of S), in [14] the concepts of the above paragraph were extended in the following way: an ideal I of a numerical semigroups S admits the pattern p if $p(s_1,\ldots ,s_n)\in S$ for every non-increasing sequence $(s_1,\ldots ,s_n)\in I^n$.

At this point we have the main difference between the above-mentioned papers and our proposal in this work: we do not keep the non-increasing condition (on the sequences in which we evaluate the pattern) in mind. In addition, we take sequences in sets A without structure (that is, A does not have to be an ideal of a numerical semigroup).

Now, let us denote by ${\mathscr {S}}_m(p)$ the family of numerical semigroups with multiplicity m that admit the pattern p. If we take the patterns $p_1=2x_1+x_2-m$ and $p_2=x_1+2x_2-m$, then ${\mathscr {S}}_m(p_1,p_2) = {\mathscr {S}}_m(p_1) \cap {\mathscr {S}}_m(p_2)$ (that is, the family of numerical semigroups which admit $p_1$ and $p_2$ simultaneously) is equal to ${\mathscr {C}}(m,A)$ for

$$\begin{aligned} A = \left\{ (a_1,a_2,a_3) \in \{1,\ldots ,m-1\}^3 \mid a_1\equiv a_2 \pmod m \right\} , \end{aligned}$$

being this one an easy example of the connection between modular Frobenius pseudo-varieties and families of numerical semigroups defined by non-homogeneous patterns (as considered in [4]).

A first question studied in [4, 14] is the next one: if $p=a_1x_1+\cdots +a_nx_n+a_0$ is a non-homogeneous pattern, for which values of $a_0$ we have that the family ${\mathscr {S}}(p)$, of numerical semigroups that admit the pattern p, is non-empty? If the answer is affirmative, then it is said that p is an admissible pattern. In our case, we have imposed that $a_0=-m$, where m will be the multiplicity of all the numerical semigroups, in order to get a relevant advantage: we want to build in a (more or less) easy and explicit way the Apéry set of the numerical semigroups belonging to ${\mathscr {C}}(m,A)$. As a consequence of this fact, we will be able to obtain extra information about such families of numerical semigroups.

Of course, in addition to $-m$, it is possible to consider other values that maintain the pseudo-variety structure. Thus, for $p=x_1+\cdots +x_n+a_0$, we have that, independently of the chosen set A, every numerical semigroup S, such that $a_0\in S$, admits the pattern p.

Now, let us observe that, if $A_1\subseteq A_2$, then ${\mathscr {C}}(m,A_2)\subseteq {\mathscr {C}}(m,A_1)$. This fact allow us to have sufficient conditions on the patterns $p=a_1x_1+\cdots +a_nx_n-km$, with $k\in {\mathbb {N}}\setminus \{0,1\}$, from the results in [4, 14]. For example, from [4, Theorem 4.1] or [14, Proposition 20], we can assert that ${\mathscr {C}}(m,A)\not =\emptyset$ if $n-k\ge 1$.

A second question that appears in [3, 14] is about the equivalence of patterns. Briefly, the pattern $p_1$ induces the pattern $p_2$ if ${\mathscr {S}}(p_2)\subseteq {\mathscr {S}}(p_1)$ and, moreover, $p_1$ and $p_2$ are equivalent patterns if they induce each other. Maybe the first result of this type is the equivalence between the homogeneous patterns $2x_1-x_2$ and $x_1+x_2-x_3$, which correspond to the family of Arf numerical semigroups (see [5]). Since the set A has an important role (not to say the main role) in the families ${\mathscr {C}}(m,A)$, the large number of possibilities in the choice of A leads us to believe that this is an issue that deserves a new work.

By the way, in Sect. 4 we study the family of thin numerical semigroups, denoted by ${\mathscr {T}}_m$, and in Sect. 5 we consider the family of strong numerical semigroups, denoted by ${\mathscr {R}}_m$. These families are associated with the patterns $2x-m$ and $x+y-m$, respectively. However, the set A is different in each case and, as a consequence, we have that there is not a inclusion relation between both of them (see Examples 4.6 and 5.6). This fact may give an idea about the difficulty of obtaining similar results to those seen in [3, 14].

In any case, we can show simple results about the equivalence (or, at least, the inclusions) of the families ${\mathscr {C}}(m,A)$.

Remark 1.1

All the patterns $p=x_1+\cdots +x_n-m$ are equivalent (independently of the chosen set A) if $n\ge m$, in which case we have that ${\mathscr {C}}(m,A)={\mathscr {S}}_m$. Indeed, applying the pigeonhole principle, if $s_1,\ldots ,s_n$ are elements of $S\in {\mathscr {S}}_m$ such that $s_i\not \equiv 0 \pmod m$, $1\le i\le n$, then there exist $i,j\in \{1,\ldots ,n\}$, with $i<j$, such that $s_i+\cdots +s_j=km$ for some $k\in {\mathbb {N}}\setminus \{0\}$. Consequently, $S\in {\mathscr {C}}(m,A)$.

Remark 1.2

Let us set $A=\{(1,1),(3,4)\}$, $B=\{(1,1,2),(1,3,1),(1,3,4)\}$, and $m\ge 5$. Then ${\mathscr {C}}(m,A) \subseteq {\mathscr {C}}(m,B)$. In order to verify this inclusion, we take $a_1,a_2,a_3\in S \in {\mathscr {C}}(m,A)$.

• If $a_1\equiv 1 \pmod m$, $a_2\equiv 1 \pmod m$, $a_3\equiv 2 \pmod m$, then $a_1+a_2+a_3-m=(a_1+a_2-m)+a_3\in S$ .

• If $a_1\equiv 1 \pmod m$, $a_2\equiv 3 \pmod m$, $a_3\equiv 1 \pmod m$, then $a_1+a_2+a_3-m=(a_1+a_3-m)+a_2\in S$.

• If $a_1\equiv 1 \pmod m$, $a_2\equiv 3 \pmod m$, $a_3\equiv 4 \pmod m$, then $a_1+a_2+a_3-m=(a_2+a_3-m)+a_1\in S$.

More generally, let us suppose that, for each $b\in B$, there exists $a\in A$ such that b is obtained by adding coordinates to a. Then ${\mathscr {C}}(m,A) \subseteq {\mathscr {C}}(m,B)$.

As a final recommendation, it is worth mentioning that in [4, Section 2] and in [14, Introduction] there are several motivating examples, and references, as to why it is interesting to study (non-homogeneous) patterns of numerical semigroups.

2 The pseudo-variety ${\mathscr {C}}{\varvec{(}m,A)}$

In this section, m is an integer greater than or equal to 2 and A is a finite subset of $\bigcup _{k \in {\mathbb {N}} \setminus \{0,1\}} \{1,\ldots ,m-1 \}^k$. Moreover, recall that

$$\begin{aligned} {\mathscr {C}}(m,A) =&\{ S\in {\mathscr {S}}_m \mid s_1+\cdots +s_k-m \in S \text { if } (s_1,\ldots ,s_k)\in S^k \text { and } \\ {}&\qquad (s_1 \bmod m, \ldots , s_k \bmod m)\in A \} , \end{aligned}$$

where $x \bmod m$ denotes the remainder after division of x by m.

If S is a numerical semigroup and $x\in S\setminus \{0\}$, then the Apéry set of x in S (see [1]) is $\mathrm {Ap}(S,x)=\{w(0)=0,w(1),\ldots ,w(x-1)\}$, where w(i) is the least element of S that is congruent with i modulus x. Observe that an integer s belongs to S if and only if there exists $t\in {\mathbb {N}}$ such that $s=w(s\bmod x)+tx$.

Proposition 2.1

Let $S\in {\mathscr {S}}_m$ and $\mathrm {Ap}(S,m)=\{w(0)=0,w(1),\ldots ,w(m-1)\}$. Then the following conditions are equivalent.

• 1. $S\in {\mathscr {C}}(m,A)$.

• 2. $w(i_1)+\cdots +w(i_k)-m\in S$ for all $(i_1,\ldots ,i_k)\in A$.

Proof

(1. $\Rightarrow$ 2.) Since $w(i_1),\ldots ,w(i_k)\in S$ and $(w(i_1) \bmod m,\ldots ,w(i_k) \bmod m) = (i_1,\ldots ,i_k)\in A$, then $w(i_1)+\cdots +w(i_k)-m\in S$.

(2. $\Rightarrow$ 1.) Let $s_1,\ldots ,s_k \in S$ such that

$$(s_1 \bmod m,\ldots ,s_k \bmod m) = (i_1,\ldots ,i_k)\in A.$$

Then there exist $t_1,\ldots ,t_k \in {\mathbb {N}}$ such that $s_j=w(i_j)+t_jm$, $1\le j\le k$, and thus, $s_1+\cdots +s_k = (w(i_1)+\cdots +w(i_k)-m)+(t_1+\cdots +t_k)m\in S$. $\square$

By using the function AperyListOfNumericalSemigroupWRTElement(S,m) of [6], we can compute $\mathrm {Ap}(S,m)$ from a system of generators of S. Thereby, we have the following algorithm to decide if a numerical semigroup S belongs or not to ${\mathscr {C}}(m,A)$.

Algorithm 2.2

INPUT: A finite subset G of positive integers.

OUTPUT: $\langle G \rangle \in \mathscr {C}(m,A)$ or $\langle G \rangle \notin \mathscr {C}(m,A)$.

• (1) If $\min$(G)$\not =m$, return $\langle G \rangle \notin \mathscr {C}(m,A)$.

• (2) If $\gcd (G)\not =1$, return $\langle G \rangle \notin \mathscr {C}(m,A)$.

• (3) Compute $\mathrm {Ap}(\langle G \rangle , m) = \{w(0),w(1),\ldots ,w(m-1)\}$.

• (4) If $w(i_1)+\cdots +w(i_k)-m\in S$ for all $(i_1,\ldots ,i_k)\in A$, return $\langle G \rangle \in \mathscr {C}(m,A)$.

• (5) Return $\langle G \rangle \notin \mathscr {C}(m,A)$.

Let us illustrate the working of the previous algorithm through an example.

Example 2.3

Let us make use of Algorithm 2.2 with $G=\{5,7,9\}$, $m=5$, and $A=\{(1,3),(2,2)\}$.

• $\min (G)=5$.

• $\gcd (G)=1$.

• $\mathrm {Ap}(\langle G \rangle ,5) = \{w(0)=0, w(1)=16, w(2)=7, w(3)=18, w(4)=19\}$.

• $w(1)+w(3)-5=29\in \langle G \rangle$ and $w(2)+w(2)-5=9\in \langle G \rangle$.

  Therefore, $\langle G \rangle = \langle 5,7,9 \rangle \in {\mathscr {C}}(5,\{(1,3),(2,2)\})$.

Recall that, if m is an integer greater than or equal to 2, then we denote by $\Delta (m)=\{0,m,\rightarrow \}$. It is clear that $\Delta (m)\in {\mathscr {S}}_m$ and that, if $s_1,\ldots ,s_k\in \Delta (m)\setminus \{0\}$ and $k\ge 2$, then $s_1+\cdots +s_k-m\in \Delta (m)$. Therefore, we have the next result.

Lemma 2.4

Let $m\in {\mathbb {N}}\setminus \{0,1\}$ and $A\subseteq \bigcup _{k\in \{2,\rightarrow \}} \{1,\ldots ,m-1\}^k$ (A finite). Then $\Delta (m)\in {\mathscr {C}}(m,A)$.

Let $m\in {\mathbb {N}}\setminus \{0,1\}$. Then it is easy to show that $S\cap T\in {\mathscr {S}}_m$ for all $S,T\in {\mathscr {S}}_m$. Moreover, $\Delta (m)$ is the maximum of ${\mathscr {S}}_m$ and, if $S\in {\mathscr {S}}_m$ and $S\not =\Delta (m)$, then $S\cup \{\mathrm {F}(S)\} \in {\mathscr {S}}_m$. From all this, we conclude the following result.

Lemma 2.5

Let $m\in {\mathbb {N}}\setminus \{0,1\}$. Then ${\mathscr {S}}_m$ is a Frobenius pseudo-variety with $\Delta (m)$ as maximum element.

Proposition 2.6

${\mathscr {C}}(m,A)$ is a Frobenius pseudo-variety.

Proof

From Lemmas 2.4 and 2.5, we have that $\Delta (m)$ is the maximum of ${\mathscr {C}}(m,A)$. It is also easy to see that, if $S,T \in {\mathscr {C}}(m,A)$, then $S\cap T\in {\mathscr {C}}(m,A)$. In order to finish the proof, let us see that, if $S\in {\mathscr {C}}(m,A)$ and $S\not =\Delta (m)$, then $S\cup \{\mathrm {F}(S)\} \in {\mathscr {C}}(m,A)$. For that, we have to show that, if $s_1,\ldots ,s_k\in S\cup \{\mathrm {F}(S)\}$ and $(s_1 \bmod m, \ldots , s_k \bmod m) \in A$, then $s_1+\cdots +s_k-m\in S\cup \{\mathrm {F}(S)\}$. In effect, if $\mathrm {F}(S)\notin \{s_1,\ldots ,s_k\}$, then the result is true because $S\in {\mathscr {C}}(m,A)$. On the other hand, if $\mathrm {F}(S)\in \{s_1,\ldots ,s_k\}$, then $s_1+\cdots +s_k-m\ge \mathrm {F}(S)$ and, consequently, $s_1+\cdots +s_k-m \in S\cup \{\mathrm {F}(S)\}$. $\square$

Our next purpose in this section is to show an algorithm that allows us to build all the elements of ${\mathscr {C}}(m,A)$ that have a fixed genus. To do that, we use the concept of rooted tree.

A graph G is a pair (V, E) where V is a non-empty set (whose elements are called vertices of G) and E is a subset of $\{(v,w) \in V \times V \mid v \ne w\}$ (whose elements are called edges of G). A path (of length n) connecting the vertices x and y of G is a sequence of different edges $(v_0,v_1),(v_1,v_2),\ldots ,(v_{n-1},v_n)$ such that $v_0=x$ and $v_n=y$.

We say that a graph G is a (rooted) tree if there exists a vertex r (known as the root of G) such that, for any other vertex x of G, there exists a unique path connecting x and r. If there exists a path connecting x and y, then we say that x is a descendant of y. In particular, if (x, y) is an edge of the tree, then we say that x is a child of y. (See [12].)

We define the graph $\mathrm {G}\big ({\mathscr {C}}(m,A)\big )$ in the following way: ${\mathscr {C}}(m,A)$ is the set of vertices and $(S,S')\in {\mathscr {C}}(m,A) \times {\mathscr {C}}(m,A)$ is an edge if $S\cup \{\mathrm {F}(S)\}=S'$. The following result is a consequence of Lemma 4.2 and Theorem 4.3 of [9].

Theorem 2.7

$\mathrm {G}\big ({\mathscr {C}}(m,A)\big )$ is a tree with root $\Delta (m)$. Moreover, the children set of $S\in {\mathscr {C}}(m,A)$ is $\big \{S \setminus \{x\} \mid x \in \mathrm {msg}(S), \ S\setminus \{x\} \in {\mathscr {C}}(m,A), \ x>\mathrm {F}(S) \big \}.$

Let S be a numerical semigroup and let $x\in S$. Then it is clear that $S\setminus \{x\}$ is a numerical semigroup if and only if $x\in \mathrm {msg}(S)$. Moreover, let us observe that, if $x\in \mathrm {msg}(S)$ and $m\in S\setminus \{0,x\}$, then

$$\begin{aligned}\mathrm {Ap}(S\setminus \{x\},m) = \big (\mathrm {Ap}(S,m)\setminus \{x\}\big )\cup \{x+m\}.\end{aligned}$$

In the following result we characterise the children of $S\in {\mathscr {C}}(m,A)$.

Proposition 2.8

Let $S\in {\mathscr {C}}(m,A)$, $\mathrm {Ap}(S,m)=\{w(0),w(1),\ldots ,w(m-1)\}$ and $x\in \mathrm {msg}(S)\setminus \{m\}$. Then $S\setminus \{x\}\in {\mathscr {C}}(m,A)$ if and only if $w(i_1)+\cdots +w(i_k)\ne m+x$ for all $(i_1,\ldots ,i_k)\in A$.

Proof

Let us suppose that $\mathrm {Ap}(S\setminus \{x\},m) = \big (\mathrm {Ap}(S,m)\setminus \{x\}\big )\cup \{x+m\}=\{w'(0),w'(1),\ldots ,$$w'(m-1)\}$.

(Necessity.) If $w(i_1)+\cdots +w(i_k) = m+x$, then $m+x \notin \{w(i_1),\ldots ,w(i_k)\}$ and, therefore, $w(i_1)=w'(i_1),\ldots ,w(i_k)=w'(i_k)$. Moreover, $w(i_1)+\cdots +w(i_k)-m=x\notin S\setminus \{x\}$ and, consequently, $S\setminus \{x\} \notin {\mathscr {C}}(m,A)$.

(Sufficiency.) In order to prove that $S\setminus \{x\}\in {\mathscr {C}}(m,A)$, by Proposition 2.1, it is enough to see that, if $(i_1,\ldots ,i_k)\in A$, then $w'(i_1)+\cdots +w'(i_k)-m\in S\setminus \{x\}$.

Since $S\in {\mathscr {C}}(m,A)$, we easily deduce that $w'(i_1)+\cdots +w'(i_k)-m\in S$. Now, if $w'(i_1)+\cdots +w'(i_k)-m\notin S\setminus \{x\}$, then $w'(i_1)+\cdots +w'(i_k)=m+x$. Thus, $w(i_1)=w'(i_1),\ldots ,w(i_k)=w'(i_k)$ and $w(i_1)+\cdots +w(i_k)=m+x$, where the last equality is in contradiction with $S\in {\mathscr {C}}(m,A)$. $\square$

Let us observe that a tree can be built in a recurrent way starting from its root and connecting each vertex with its children. Let us also observe that the elements of ${\mathscr {C}}(m,A)$ with genus equal to $g+1$ are precisely the children of the elements of ${\mathscr {C}}(m,A)$ with genus equal to g.

We are ready to show the above announced algorithm.

Algorithm 2.9

INPUT: A positive integer g.

OUTPUT: $\{S \in \mathscr {C}(m,A) \mid \mathrm {g}(S)=g \}$.

• (1) If $g<m-1$, return $\emptyset$.

• (2) $X=\{\Delta (m)\}$ and $i=m-1$.

• (3) If $i=g$, return X.

• (4) For each $S\in X$, compute the set

  $$\begin{aligned} \mathscr {B}_S=\big \{x\in \mathrm {msg}(S) \mid x>\mathrm {F}(S), \ x\not =m, \ S\setminus \{x\}\in \mathscr {C}(m,A) \big \}. \end{aligned}$$

• (5) If $\ \bigcup _{S\in X} \mathscr {B}_S=\emptyset$, return $\emptyset$.

• (6) $X=\bigcup _{S\in X} \big \{S\setminus \{x\} \mid x \in \mathscr {B}_S \big \}$, $i=i+1$, and go to (3).

For computing item (4) in the above algorithm, we use Proposition 2.8 and the following Lemma 2.10, which is a reformulation of Corollary 18 of [8], and is useful to obtain the minimal system of generators of $S\setminus \{x\}$ starting from the minimal system of generators of S.

Lemma 2.10

Let S be a numerical semigroup with $\mathrm {msg}(S)=\{n_1<n_2<\cdots <n_e\}$. If $i \in \{2,\ldots ,e\}$ and $n_i>\mathrm {F}(S)$, then

$$\begin{aligned} \mathrm {msg}(S \setminus \{n_i\})= \left\{ \begin{array}{l} \{n_1,\ldots ,n_{e}\} \setminus \{n_i\}, \quad \text{ if } \text{ there } \text{ exists } j \in \{2,\ldots ,i-1\} \\ \text{ such } \text{ that } n_i+n_1-n_j \in S; \\ \big (\{n_1,\ldots ,n_{e}\} \setminus \{n_i\}\big ) \cup \{n_i+n_1\}, \quad \text{ in } \text{ other } \text{ case. } \end{array} \right. \end{aligned}$$

We illustrate the functioning of Algorithm 2.9 with an example.

Example 2.11

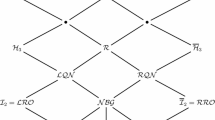
Let us compute all the elements of ${\mathscr {C}}(5,\{(1,1),(1,2)\})$ with genus equal to 6.

• $X=\{\langle 5,6,7,8,9 \rangle \}$ and $i=4$.

• $B_{\langle 5,6,7,8,9 \rangle } = \{6,9\}$.

• $X=\{\langle 5,7,8,9,11 \rangle , \langle 5,6,7,8 \rangle \}$ and $i=5$.

• $B_{\langle 5,7,8,9,11 \rangle } = \{7,8,9,11\}$ and $B_{\langle 5,6,7,8 \rangle } = \emptyset$.

• $X=\{\langle 5,8,9,11,12 \rangle , \langle 5,7,9,11,13\rangle , \langle 5,7,8,11\rangle , \langle 5,7,8,9\rangle \}$ and $i=6$.

• Return $\{\langle 5,8,9,11,12 \rangle , \langle 5,7,9,11,13\rangle , \langle 5,7,8,11\rangle , \langle 5,7,8,9\rangle \}$.

Taking advantage of the above example, we finish this section building the first three levels of the tree $\mathrm {G}\big ({\mathscr {C}}(5,\{(1,1),(1,2)\})\big )$.

Observe that the number which appear next to each edge $(S',S)$ is the minimal generator x of S such that $S'=S \setminus \{x\}$.

3 Second-level numerical semigroups

We say that a numerical semigroup S is of second-level if $x+y+z-\mathrm {m}(S)\in S$ for all $(x,y,z)\in (S\setminus \{0\})^3$. We denote by ${\mathscr {L}}_{2,m}$ the set of all the second-level numerical semigroups with multiplicity equal to m.

Proposition 3.1

Let S be a numerical semigroup with minimal system of generators given by $\{m=n_1<n_2<\cdots <n_e\}$. Then the following two conditions are equivalents.

• 1. $S\in {\mathscr {L}}_{2,m}$.

• 2. If $(i,j,k)\in \{2,\ldots ,e\}^3$, then $n_i+n_j+n_k-m\in S$.

Proof

(1. $\Rightarrow$ 2.) It is evident from the definition of second-level numerical semigroup.

(2. $\Rightarrow$ 1.) Let $(x,y,z) \in (S\setminus \{0\})^3$. If $0\in \{x\bmod m, y\bmod m, z\bmod m \}$, then it is clear that $x+y+z-m\in S$. Now, if $0\notin \{x\bmod m, y\bmod m, z\bmod m \}$, then we easily deduce that there exist $(i,j,k)\in \{2,\ldots ,e\}^3$ and $(s_1,s_2,s_3)\in S^3$ such that $(x,y,z)=(n_i,n_j,n_k)+(s_1,s_2,s_3)$. Therefore, $x+y+z-m=(n_i+n_j+n_k-m)+s_1+s_2+s_3\in S$. Consequently, $S\in {\mathscr {L}}_{2,m}$. $\square$

The above proposition allows us to easily decide whether a numerical semigroup is of second-level or not.

Example 3.2

Let us see that $S=\langle 5,7,16 \rangle \in {\mathscr {L}}_{2,m}$. In effect, it is clear that $\{7+7+7-5,7+7+16-5,7+16+16,16+16+16-5\} = \{16,25,34,43\} \subseteq S$. Therefore, by Proposition 3.1, we have that $S\in {\mathscr {L}}_{2,m}$.

Now our intention is to show that ${\mathscr {L}}_{2,m}$ is a modular Frobenius pseudo-variety.

Proposition 3.3

Let $m\in {\mathbb {N}}\setminus \{0,1\}$. Then ${\mathscr {L}}_{2,m}={\mathscr {C}}(m,\{1,\ldots ,m-1\}^3)$.

Proof

Let $S\in {\mathscr {L}}_{2,m}$ and $\mathrm {Ap}(S,m)=\{w(0),w(1),\ldots ,w(m-1)\}$. If $(i,j,k)\in \{1,\ldots ,m-1\}^3$, then $(w(i),w(j),w(k))\in (S\setminus \{0\})^3$ and, therefore, $w(i)+w(j)+w(k)-m\in S$. By applying Proposition 2.1, we have that $S\in {\mathscr {C}}(m,\{1,\ldots ,m-1\}^3)$.

In order to see the other inclusion, let $S\in {\mathscr {C}}(m,\{1,\ldots ,m-1\}^3)$ and $(x,y,z)\in (S\setminus \{0\})^3$. Firstly, if $0\in \{x\bmod m,y\bmod m,z\bmod m\}$, then it is clear that $x+y+z-m\in S$. Secondly, if $0\notin \{x\bmod m, y\bmod m, z\bmod m \}$, then there exist $(i,j,k)\in \{1,\ldots ,m-1\}^3$ and $(p,q,r)\in {\mathbb {N}}^3$ such that $x=w(i)+pm$, $y=w(j)+qm$, and $z=w(k)+rm$. Thus, $x+y+z-m=(w(i)+w(j)+w(k)-m)+(p+q+r)m\in S$ and, therefore, $S\in {\mathscr {L}}_{2,m}$. $\square$

As an immediate consequence of Propositions 2.6 and 3.3, we have the following result.

Corollary 3.4

Let $m\in {\mathbb {N}}\setminus \{0,1\}$. Then ${\mathscr {L}}_{2,m}$ is a modular pseudo-Frobenius variety and, in addition, $\Delta (m)$ is the maximum of ${\mathscr {L}}_{2,m}$.

Our next step is to build the tree associated with the pseudo-variety ${\mathscr {L}}_{2,m}$. To do this, we should characterise the possible children of each element in ${\mathscr {L}}_{2,m}$.

Let S be a numerical semigroup with $\mathrm {msg}(S)=\{n_1,\ldots ,n_e\}$. If $s\in S$, then we denote by

$$\begin{aligned} L_S(s)=\max \{a_1+\cdots +a_e \mid (a_1,\ldots ,a_e)\in {\mathbb {N}}^e \text{ and } a_1n_1+\cdots +a_en_e=s\}. \end{aligned}$$

Proposition 3.5

Let $m\in {\mathbb {N}}\setminus \{0,1\}$, $S\in {\mathscr {L}}_{2,m}$, and $x\in \mathrm {msg}(S)\setminus \{m\}$. Then $S\setminus \{x\}\in {\mathscr {L}}_{2,m}$ if and only if $L_{S\setminus \{x\}}(x+m)\le 2$.

Proof

(Necessity.) Let us suppose that $L_{S\setminus \{x\}}(x+m)\ge 3$. Then there exists $(a,b,c)\in (S\setminus \{0,x\})^3$ such that $x+m=a+b+c$. Thus, $a+b+c-m=x\notin S\setminus \{x\}$ and, therefore, $S\setminus \{x\}\notin {\mathscr {L}}_{2,m}$.

(Sufficiency.) If $(a,b,c)\in (S\setminus \{0,x\})^3$, then $a+b+c-m\in S$, since $S\in {\mathscr {L}}_{2,m}$. Now, if $a+b+c-m=x$, then $L_{S\setminus \{x\}}(x+m)\ge 3$. Therefore, $a+b+c-m\not = x$ and, consequently, $a+b+c-m\in S\setminus \{x\}$. Thus, we conclude that $S\setminus \{x\}\in {\mathscr {L}}_{2,m}$. $\square$

By applying Theorem 2.7, Propositions 3.3 and 3.5, and Lemma 2.10, we can easily build the tree $\mathrm {G}({\mathscr {L}}_{2,m})$.

Example 3.6

The first four levels of $\mathrm {G}({\mathscr {L}}_{2,4})$ appear in the following figure.

The Frobenius problem (see [7]) consists in finding formulas that allow us to compute the Frobenius number and the genus of a numerical semigroup in terms of the minimal system of generators of such a numerical semigroup. This problem was solved in [15] for numerical semigroups with embedding dimension two. At present, the Frobenius problem is open for embedding dimension greater than or equal to 3. However, if we know the Apéry set $\mathrm {Ap}(S,x)$ for some $x\in S\setminus \{0\}$, then we have solved the Frobenius problem for S because we have the following result from [13].

Lemma 3.7

Let S be a numerical semigroup and let $x\in S\setminus \{0\}$. Then

• 1. $\mathrm {F}(S)=(\max (\mathrm {Ap}(S,x)))-x$,

• 2. $\mathrm {g}(S)=\frac{1}{x}(\sum _{w\in \mathrm {Ap}(S,x)} w)-\frac{x-1}{2}$.

The knowledge of $\mathrm {Ap}(S,x)=\{w(0),w(1),\ldots ,w(x-1)\}$ also allows us to determine the membership of an integer to the numerical semigroup S. In fact, if $n\in {\mathbb {N}}$, then $n\in S$ if and only if $n\ge w(n\bmod x)$.

Now our purpose is to show that, if $S\in {\mathscr {L}}_{2,m}$, then is rather easy to compute $\mathrm {Ap}(S,m)$. We need the following easy result.

Lemma 3.8

Let $m\in {\mathbb {N}}\setminus \{0,1\}$, $S\in {\mathscr {L}}_{2,m}$, $\mathrm {msg}(S)=\{n_1\!=\!m,n_2,\ldots ,n_e\}$. Then $\{0,n_2,\ldots ,n_e\} \! \subseteq \! \mathrm {Ap}(S,m) \! \subseteq \! \{0,n_2,\ldots ,n_e\} \cup \{n_i+n_j \mid (i,j)\in \{2,\ldots ,e\}^2\}.$

As an immediate consequence of the above lemma we can formulate the following result.

Proposition 3.9

Let $m\in {\mathbb {N}}\setminus \{0,1\}$, $S\in {\mathscr {L}}_{2,m}$, $\mathrm {msg}(S)=\{n_1\!=\!m,n_2,\ldots ,n_e\}$. Then $\mathrm {Ap}(S,m)=\{w(0),w(1),\ldots ,w(m-1)\}$ where w(i) is the least element of $\{0,n_2,\ldots ,n_e\} \cup \{n_i+n_j \mid (i,j)\in \{2,\ldots ,e\}^2\}$ that is congruent to i modulo m.

Corollary 3.10

Let $m\in {\mathbb {N}}\setminus \{0,1\}$ and $S\in {\mathscr {L}}_{2,m}$. Then $m = \mathrm {m}(S) \le \frac{\mathrm {e}(S)\left( \mathrm {e}(S)+1\right) }{2}$.

Following the notation introduced in [10], we say that $x\in {\mathbb {Z}}\setminus S$ is a pseudo-Frobenius number of S if $x+s\in S$ for all $s\in S\setminus \{0\}$. We denote by $\mathrm {PF}(S)$ the set of all the pseudo-Frobenius numbers of S. The cardinality of $\mathrm {PF}(S)$ is an important invariant of S (see [2]) that is the so-called type of S and it is denoted by $\mathrm {t}(S)$.

Let S be a numerical semigroup. Then we define the following binary relation over ${\mathbb {Z}}$: $a\le _S b$ if $b-a\in S$. In [11] it is shown that $\le _S$ is a partial order (that is, reflexive, transitive, and antisymmetric). Moreover, Proposition 2.20 of [11] is the next result.

Proposition 3.11

Let S be a numerical semigroup and $x\in S\setminus \{0\}$. Then

$$\begin{aligned}\mathrm {PF}(S)=\{w-x \mid w\in \mathrm {Maximals}_{\le _S} (\mathrm {Ap}(S,x)) \}\end{aligned}$$

Let us observe that, if $w,w'\in \mathrm {Ap}(S,x)$, then $w'-w\in S$ if and only if $w'-w\in \mathrm {Ap}(S,x)$. Therefore, $\mathrm {Maximals}_{\le _S} (\mathrm {Ap}(S,x))$ is the set

$$\begin{aligned}\{w\in \mathrm {Ap}(S,x) \mid w'-w\notin \mathrm {Ap}(S,x)\setminus \{0\} \text{ for } \text{ all } w'\in \mathrm {Ap}(S,x) \}.\end{aligned}$$

We finish this section with an example that illustrates the above results.

Example 3.12

Having in mind that $S=\langle 5,6,13 \rangle$ is a second-level numerical semigroup, it is easy to compute $\mathrm {Ap}(S,5)$. In fact, by applying Lemma 3.8, we have that $\mathrm {Ap}(S,5) \subseteq \{0,6,13\} \cup \{12,19,26\}$ and, by Proposition 3.9, we conclude that $\mathrm {Ap}(S,5) = \{0,6,12,13,19\}$. On the other hand, by Lemma 3.7, we know that $\mathrm {F}(S)=19-5=14$ and $\mathrm {g}(S)=\frac{1}{5}(6+12+13+19)-\frac{5-1}{2}=8$. Finally, since $\mathrm {Maximals}_{\le _S} (\mathrm {Ap}(S,5)) = \{12,19\}$, Proposition 3.11 allows us to claim that $\mathrm {PF}(S)=\{7,12\}$ and $\mathrm {t}(S)=2$.

Remark 3.13

The definition of second-level numerical semigroup can be easily generalised to greater levels. Thus, we say that a numerical semigroup is of nth-level if $x_1+\cdots +x_{n+1}-\mathrm {m}(S)\in S$ for all $(x_1,\ldots ,x_{n+1})\in (S\setminus \{0\})^{n+1}$ and denote by ${\mathscr {L}}_{n,m}$ the set of all the nth-level numerical semigroups with multiplicity equal to m.

It is clear that for nth-level we obtain similar results to those of second-level. In particular, ${\mathscr {L}}_{n,m}={\mathscr {C}}(m,\{1,\ldots ,m-1\}^{n+1})$ and Proposition 3.5 remains true taking $L_{S\setminus \{x\}}(x+m)\le n$.

On the other hand, having in mind that ${\mathscr {L}}_{1,m}$ is the family of numerical semigroups with maximal embedding dimension and that (by Remark 1.1) ${\mathscr {L}}_{m-1,m}={\mathscr {S}}_m$, we can observe that

$$\begin{aligned} {\mathscr {L}}_{1,m} \subseteq {\mathscr {L}}_{2,m} \subseteq \cdots \subseteq {\mathscr {L}}_{m-1,m} = {\mathscr {S}}_m, \end{aligned}$$

where all the inclusions are strict, as we can deduce from the following example.

Example 3.14

Let us set $m=5$ and

$$\begin{aligned} S_1=\langle 5,6 \rangle =\{0,5,6,10,11,12,15,16,17,18,20, \rightarrow \}. \end{aligned}$$

Then,

• $S_1\in {\mathscr {L}}_{4,5} \setminus {\mathscr {L}}_{3,5} = {\mathscr {S}}_5 \setminus {\mathscr {L}}_{3,5}$, because $4\times 6-5\not \in S_1$ and $s_1+\cdots +s_5-5 \ge 5\times 6-5\ge F(S_1)+1$;

• $S_2=S_1\cup \{19\}=\langle 5,6,19 \rangle \in {\mathscr {L}}_{3,5} \setminus {\mathscr {L}}_{2,5}$, because $3\times 6-5\not \in S_2$ and $s_1+\cdots +s_4-5 \ge 4\times 6-5\ge F(S_2)+1$;

• $S_3=S_2\cup \{13,14\}=\langle 5,6,13,14 \rangle \in {\mathscr {L}}_{2,5} \setminus {\mathscr {L}}_{1,5}$, because $2\times 6-5\not \in S_2$ and $s_1+s_2+s_3-5 \ge 3\times 6-5\ge F(S_3)+1$.

Generalising this example to other values of m is trivial.

Remark 3.15

Let us observe that the chain obtained in Remark 3.13 is reminiscent, in some sense, of the chain associated with subtraction patterns (see [3, Section 6]).

4 Thin numerical semigroups

We say that a numerical semigroup S is thin if $2x-\mathrm {m}(S)\in S$ for all $x\in S\setminus \{0\}$. We denote by ${\mathscr {T}}_{m}$ the set of all the thin numerical semigroups with multiplicity equal to m.

Proposition 4.1

Let S be a numerical semigroup with minimal system of generators given by $\{m=n_1<n_2<\cdots <n_e\}$. Then the following two conditions are equivalents.

• 1. $S\in {\mathscr {T}}_{m}$.

• 2. $2n_i-m\in S$ for all $i\in \{2,\ldots ,e\}$.

Proof

(1. $\Rightarrow$ 2.) It follows from the definition of thin numerical semigroup.

(2. $\Rightarrow$ 1.) Let $x \in S\setminus \{0\}$. If $x\equiv 0\pmod m$, then it is clear that $2x-m\in S$. Now, if $x\not \equiv 0\pmod m$, then we have that there exist $i\in \{2,\ldots ,e\}$ and $s\in S$ such that $x=n_i+s$. Therefore, $2x-m=(2n_i-m)+2s\in S$ and, consequently, $S\in {\mathscr {T}}_{m}$. $\square$

The above proposition allows us to easily decide whether a numerical semigroup is thin or not.

Example 4.2

Let us see that $S=\langle 4,6,7 \rangle \in {\mathscr {T}}_{4}$. In effect, it is clear that $\{2\cdot 6-4,2\cdot 7-4\} = \{8,10\} \subseteq S$. Therefore, by Proposition 4.1, we have that $S\in {\mathscr {T}}_{m}$.

Now we want to show that ${\mathscr {T}}_{m}$ is a modular Frobenius pseudo-variety.

Proposition 4.3

${\mathscr {T}}_{m}={\mathscr {C}}(m,\{(1,1),(2,2)\ldots ,(m-1,m-1)\})$ for all $m\in {\mathbb {N}}\setminus \{0,1\}$.

Proof

If $S\in {\mathscr {T}}_{m}$ and $\mathrm {Ap}(S,m)=\{w(0),w(1),\ldots ,w(m-1)\}$, then it is clear that $\{w(1)+w(1)-m,\ldots ,w(m-1)+w(m-1)-m\}\subseteq S$. Therefore, by applying Proposition 2.1, we have that $S\in {\mathscr {C}}(m,\{(1,1),(2,2)\ldots ,(m-1,m-1)\})$.

To see the other inclusion, let $S\in {\mathscr {C}}(m,\{(1,1),(2,2)\ldots , (m-1,m-1)\})$ and $x\in S\setminus \{0\}$. On the one hand, if $x\equiv 0 \pmod m$, then it is clear that $2x-m\in S$. On the other hand, if $x\not \equiv 0 \pmod m$, then there exist $i\in \{1,\ldots ,m-1\}$ and $t\in {\mathbb {N}}$ such that $x=w(i)+tm$. Therefore, $2x-m=(w(i)+w(i)-m)+ 2tm \in S$ and in consequence $S\in {\mathscr {T}}_{m}$. $\square$

From Propositions 2.6 and 4.3, we get the following result.

Corollary 4.4

Let $m\in {\mathbb {N}}\setminus \{0,1\}$. Then ${\mathscr {T}}_{m}$ is a modular pseudo-Frobenius variety and, in addition, $\Delta (m)$ is the maximum of $S\in {\mathscr {T}}_{m}$.

In order to build the tree associated with the pseudo-variety $S\in {\mathscr {T}}_{m}$, we are going to characterise the possible children of each $S\in {\mathscr {T}}_{m}$.

Proposition 4.5

Let $m\in {\mathbb {N}}\setminus \{0,1\}$, $S\in {\mathscr {T}}_{m}$, and $x\in \mathrm {msg}(S)\setminus \{m\}$. Then $S\setminus \{x\}\in {\mathscr {T}}_{m}$ if and only if $\frac{x+m}{2}\notin S$.

Proof

(Necessity.) If $\frac{x+m}{2}\in S$, then $\frac{x+m}{2}\in S\setminus \{0,x\}$ and $2\frac{x+m}{2}-m=x\notin S \setminus \{x\}$. Therefore, $S\setminus \{x\}\notin {\mathscr {T}}_{m}$.

(Sufficiency.) If $a\in S\setminus \{0,x\}$, then $2a-m\in S$ because $S\in {\mathscr {T}}_{m}$. Now, if $2a-m=x$, then $\frac{x+m}{2}=a\in S$. Therefore, $2a-m\not = x$ and, consequently, $2a-m\in S\setminus \{x\}$. Thereby, $S\setminus \{x\}\in {\mathscr {T}}_{m}$. $\square$

By applying Theorem 2.7, Propositions 4.3 and 4.5, and Lemma 2.10, we can build the tree $\mathrm {G}({\mathscr {T}}_{m})$. Let us see an example.

Example 4.6

In the next figure we have the first four levels of $\mathrm {G}({\mathscr {T}}_{4})$.

We finish this section describing the Apéry set for $S\in {\mathscr {T}}_{m}$.

Proposition 4.7

Let $m\in {\mathbb {N}}\setminus \{0\}$, $S\in {\mathscr {T}}_{m}$, $\mathrm {msg}(S)=\{m=n_1,n_2,\ldots ,n_e\}$. Then $\mathrm {Ap}(S,m)=\{w(0),w(1),\ldots ,w(m-1)\}$, where w(i) is the least element of the set $\{a_2n_2+\ldots +a_en_e\mid (a_2,\ldots ,a_e)\in \{0,1\}^{e-1}\}$ that is congruent to i modulo m.

Corollary 4.8

Let $m\in {\mathbb {N}}\setminus \{0\}$ and $S\in {\mathscr {T}}_{m}$. Then $m = \mathrm {m}(S) \le 2^{\mathrm {e}(S)-1}$.

Remark 4.9

Let us observe that we can generalise the concept of thin numerical semigroups in the following way: setting $n\in {\mathbb {N}}\setminus \{0,1\}$, we say that a numerical semigroup S is n-thin if $nx-\mathrm {m}(S)\in S$ for all $x\in S\setminus \{0\}$, and denote by ${\mathscr {T}}_{n,m}$ the set of all k-thin numerical semigroups with multiplicity equal to m. It is clear that ${\mathscr {T}}_{m}={\mathscr {T}}_{2,m}$.

Again, ${\mathscr {T}}_{n,m}$ is a modular pseudo-variety, Proposition 4.5 is valid for the condition $\frac{x+m}{n}\not \in S$, and we can build the chain

$$\begin{aligned} {\mathscr {T}}_{2,m} \subsetneq {\mathscr {T}}_{3,m} \subsetneq \cdots \subsetneq {\mathscr {T}}_{m,m} = {\mathscr {S}}_m. \end{aligned}$$

Note that Example 3.14 also gives us the construction that ensures the strict inclusions in this case.

5 Strong numerical semigroups

We say that a numerical semigroup S is strong if $x+y-\mathrm {m}(S)\in S$ for all $(x,y)\in (S\setminus \{0\})^2$ such that $x\not \equiv y \pmod {\mathrm {m}(S)}$. We denote by ${\mathscr {R}}_{m}$ the set of all the strong numerical semigroups with multiplicity equal to m.

Proposition 5.1

Let S be a numerical semigroup with minimal system of generators given by $\{m=n_1<n_2<\cdots <n_e\}$. Then the following two conditions are equivalents.

• 1. $S\in {\mathscr {R}}_{m}$.

• 2. $\{n_i+n_j-m,3n_i-m\}\subseteq S$ for all $i\in \{2,\ldots ,e\}$ and for all $(i,j)\in \{2,\ldots ,e\}^2$ such that $i\not = j$.

Proof

(1. $\Rightarrow$ 2.) It is enough to observe that $n_i\not \equiv n_j \pmod m$ and that $2n_i\not \equiv n_i \pmod m$.

(2. $\Rightarrow$ 1.) Let $x,y \in S\setminus \{0\}$ such that $x\not \equiv y \pmod {\mathrm {m}}$. If $x\equiv 0\pmod m$ or $y\equiv 0\pmod m$, then it is clear that $x+y-m\in S$. Now, if $x\not \equiv 0\pmod m$ and $y\not \equiv 0\pmod m$, then there exists $(i,j)\in \{1,\ldots ,m-1\}^2$, with $i\not =j$, and there exists $(p,q)\in {\mathbb {N}}^2$ such that $x=w(i)+pm$ and $y=w(j)+qm$. Moreover, if there exists $(a,b)\in \{2,\ldots ,e\}^2$ such that $a\not =b$ and $w(i)-n_a,w(j)-n_b\in S$, then it is easy to see that $x+y-m\in S$. In other case, there exists $(r,t)\in ({\mathbb {N}}\setminus \{0\})^2$ such that $w(i)=r\cdot n_a$ and $w(j)=t\cdot n_a$ for some $a\in \{2,\ldots ,e\}$. Then, since $i\not =j$, we deduce that $r+t\ge 3$ and, consequently, $x+y-m\in S$. In conclusion, $S\in {\mathscr {R}}_{m}$. $\square$

The above proposition allows us to easily decide whether a numerical semigroup is strong or not.

Example 5.2

If $S=\langle 4,5,7 \rangle$, then $\{5+7-4,3\cdot 5-4,3\cdot 7-4\} = \{8,11,17\} \subseteq S$. Therefore, by Proposition 5.1, we have that $S\in {\mathscr {R}}_{m}$.

Now we want to show that ${\mathscr {R}}_{m}$ is a modular Frobenius pseudo-variety. Let us denote by $A=\{1,\ldots ,m-1\}^2\setminus \{(1,1),(2,2),\ldots ,(m-1,m-1)\}$.

Proposition 5.3

${\mathscr {R}}_{m}={\mathscr {C}}(m,A)$ for all $m\in {\mathbb {N}}\setminus \{0,1\}$.

Proof

Let $S\in {\mathscr {R}}_{m}$, $\mathrm {Ap}(S,m)=\{w(0),w(1),\ldots ,w(m-1)\}$, and $(i,j)\in A$. Then $\{(w(i),w(j)\}\in (S\setminus \{0\})^2$ and $w(i)\not \equiv w(j) \pmod m$. Therefore, $w(i)-w(j)-m\in S$ and, by applying Proposition 2.1, we have that $S\in {\mathscr {C}}(m,A)$.

To see the other inclusion, let $S\in {\mathscr {C}}(m,A)$ and $(x,y)\in (S\setminus \{0\})^2$. On the one hand, if $0 \in \{x \bmod m, y\bmod m\}$, then it is clear that $x+y-m\in S$. On the other hand, if $0 \notin \{x \bmod m, y\bmod m\}$, then there exist $(i,j)\in A$ and $(p,q)\in {\mathbb {N}}^2$ such that $x=w(i)+pm$ and $y=w(j)+qm$. Therefore, $x+y-m=(w(i)+w(i)-m)+ (p+q)m \in S$ and, consequently, $S\in {\mathscr {R}}_{m}$. $\square$

From Propositions 2.6 and 5.3, we get the following result.

Corollary 5.4

Let $m\in {\mathbb {N}}\setminus \{0,1\}$. Then ${\mathscr {R}}_{m}$ is a modular pseudo-Frobenius variety and, in addition, $\Delta (m)$ is the maximum of $S\in {\mathscr {R}}_{m}$.

We are now interested in the description of the tree associated with the pseudo-variety $S\in {\mathscr {R}}_{m}$. In order to do that, we are going to characterise the children of an arbitrary $S\in {\mathscr {R}}_{m}$.

Proposition 5.5

Let $m\in {\mathbb {N}}\setminus \{0,1\}$, $S\in {\mathscr {R}}_{m}$, and $x\in \mathrm {msg}(S)\setminus \{m\}$. Then $S\setminus \{x\}\in {\mathscr {R}}_{m}$ if and only if $x+m\notin \{a+b \mid a,b\in \mathrm {msg}(S)\setminus \{m,x\}, \; a\not = b\} \cup \{3a \mid a \in \mathrm {msg}(S)\setminus \{m,x\}\}$.

Proof

(Necessity.) If $a,b\in \mathrm {msg}(S)\setminus \{m,x\}$ and $a\not = b$, then $(a,b) \in (S\setminus \{0,x\})^2$ and $a\not \equiv b \pmod m$. Since $S\setminus \{x\}\in {\mathscr {R}}_{m}$, we have that $a+b-m\in S\setminus \{x\}$ and, therefore, $a+b-x\not =x$. Thus, $x+m\notin \{a+b \mid a,b\in \mathrm {msg}(S)\setminus \{m,x\}, \; a\not = b\}$.

On the other hand, if $a\in \mathrm {msg}(S)\setminus \{m,x\}$, then $(a,2a)\in (S\setminus \{0,x\})^2$ and $a\not \equiv 2a \pmod m$. Once again, since $S\setminus \{x\}\in {\mathscr {R}}_{m}$, we have that $3a-m\in S\setminus \{x\}$ and, therefore, $a+b-x\not =x$. Thus, $x+m\notin \{3a \mid a\in \mathrm {msg}(S)\setminus \{m,x\}\}$.

(Sufficiency.) Let $a,b\in S\setminus \{0,x\}$ such that $a\not =b$. Since $S\in {\mathscr {R}}_{m}$, we have that $a+b-m\in S$ and $3a-m\in S$. Now, by Lemma 2.10, we know that $\mathrm {msg}(S)\setminus \{x\} \subseteq \mathrm {msg}(S\setminus \{x\}) \subseteq (\mathrm {msg}(S)\setminus \{x\}) \cup \{x+m\}$. Thus, from this fact and the hypothesis, it easily follows that $a+b-m\not =x$ and $3a-m\not =x$, that is, $a+b-m,3a-m\in S\setminus \{x\}$. By applying Proposition 5.1, we conclude that $S\setminus \{x\}\in {\mathscr {R}}_{m}$. $\square$

From Theorem 2.7, Propositions 5.3 and 5.5, and Lemma 2.10, we can build the tree $\mathrm {G}({\mathscr {R}}_{m})$. Let us see an example.

Example 5.6

In the next figure we have the first four levels of $\mathrm {G}({\mathscr {R}}_{4})$.

We finish this section describing the Apéry set for $S\in {\mathscr {R}}_{m}$.

Proposition 5.7

Let $m\in {\mathbb {N}}\setminus \{0,1\}$, $S\in {\mathscr {R}}_{m}$, $\mathrm {msg}(S)=\{m=n_1,n_2,\ldots ,n_e\}$. Then $\mathrm {Ap}(S)=\{w(0),w(1),\ldots ,w(n)\}$, where w(i) is the least element of the set $\{0,n_2,\ldots ,n_e\} \cup \{2n_2,\ldots ,2n_e\}$ that is congruent to i modulo m.

Corollary 5.8

Let $m\in {\mathbb {N}}\setminus \{0,1\}$ and $S\in {\mathscr {R}}_{m}$. Then $m = \mathrm {m}(S) \le 2\mathrm {e}(S)-1$.

It is interesting to observe that, under the hypotheses of Proposition 5.7, $n_i\in \mathrm {Maximals}_{\le _S}(\mathrm {Ap}(S,m))$ if and only if $2n_i\notin \mathrm {Ap}(S,m)$. In addition, $2n_i\in \mathrm {Ap}(S,m)$ if and only if $2n_i\in \mathrm {Maximals}_{\le _S}(\mathrm {Ap}(S,m))$. Therefore, from Propositions 3.11 and 5.7, we get the next result.

Corollary 5.9

Let $m \in {\mathbb {N}}\setminus \{0,1\}$ and $S\in {\mathscr {R}}_{m}$. Then $\mathrm {t}(S)=\mathrm {e}(S)-1$.

It is well known that, if S is a numerical semigroup, then $\mathrm {e}(S) \le \mathrm {m}(S)$ and $\mathrm {t}(S) \le \mathrm {m}(S)-1$ (see Proposition 2.10 and Corollary 2.23 in [11]). Combining these facts with Corollaries 5.8 and 5.9, we have the next result.

Corollary 5.10

Let $m \in {\mathbb {N}}\setminus \{0,1\}$ and $S\in {\mathscr {R}}_{m}$. Then $\frac{\mathrm {m}(S)-1}{2} \le \mathrm {t}(S) \le \mathrm {m}(S)-1$ (or, equivalently, $\frac{\mathrm {m}(S)+1}{2} \le \mathrm {e}(S) \le \mathrm {m}(S)$).

Remark 5.11

Contrary to what happens in Sects. 3 and 4, the concept of strong numerical semigroup does not have a natural generalisation. In fact, we have, at least, two possibilities.

• 1. $x_1+\cdots x_n-\mathrm {m}(S)\in S$ for all $(x_1,\ldots ,x_n) \in (S\setminus \{0\})^n$ such that $x_i\not \equiv x_j \pmod {\mathrm {m}(S)}$, for all $i\not =j$. In this case, $(x_1,\ldots ,x_n) \in A_n$, where

  $$\begin{aligned} A_n=\left\{ (\alpha _1,\ldots ,\alpha _n) \in \{1,\ldots ,m-1\}^n \mid \alpha _i\not =\alpha _j \text{ for } \text{ all } i\not =j \right\} . \end{aligned}$$

• 2. $x_1+\cdots x_n-\mathrm {m}(S)\in S$ for all $(x_1,\ldots ,x_n) \in B_n$, where

  $$\begin{aligned} B_n=\{1,\ldots ,m-1\}^n \setminus \{(1,\ldots ,1),(2,\ldots ,2),\ldots ,(m-1,\ldots ,m-1)\}.\end{aligned}$$

It is clear that, if $n\ge 3$, then $A_n\subsetneq B_n$ and, in consequence, ${\mathscr {C}}(m,B_n) \subseteq {\mathscr {C}}(m,A_n)$. In addition, it is guessed that, if $n<m$, then the second inclusion will be strict.