Abstract
This paper is dedicated to the question of surjectivity of the Cauchy-Riemann operator \(\overline{\partial }\) on spaces \({\mathcal {E}}{\mathcal {V}}(\varOmega ,E)\) of \({\mathcal {C}}^{\infty }\)-smooth vector-valued functions whose growth on strips along the real axis with holes K is induced by a family of continuous weights \({\mathcal {V}}\). Vector-valued means that these functions have values in a locally convex Hausdorff space E over \({\mathbb {C}}\). We derive a counterpart of the Grothendieck-Köthe-Silva duality \({\mathcal {O}}({\mathbb {C}}\setminus K)/{\mathcal {O}}({\mathbb {C}})\cong {\mathscr {A}}(K)\) with non-empty compact \(K\subset {\mathbb {R}}\) for weighted holomorphic functions. We use this duality and splitting theory to prove the surjectivity of \(\overline{\partial }:{\mathcal {E}} {\mathcal {V}}(\varOmega ,E)\rightarrow {\mathcal {E}}{\mathcal {V}} (\varOmega ,E)\) for certain E. This solves the smooth (holomorphic, distributional) parameter dependence problem for the Cauchy-Riemann operator on \({\mathcal {E}}{\mathcal {V}}(\varOmega ,{\mathbb {C}})\).
Similar content being viewed by others
1 Introduction
The smooth (holomorphic, distributional) parameter dependence problem for the Cauchy-Riemann operator \(\overline{\partial }:=(1/2)(\partial _{1}+i\partial _{2})\) on the space \({\mathcal {C}}^{\infty }(\varOmega )\) of smooth complex-valued functions on an open set \(\varOmega \subset {\mathbb {R}}^{2}\) is whether for every family \((f_{\lambda })_{\lambda \in U}\) in \({\mathcal {C}}^{\infty }(\varOmega )\) depending smoothly (holomorphically, distributionally) on a parameter \(\lambda\) in an open set \(U\subset {\mathbb {R}}^{d}\) there is a family \((u_{\lambda })_{\lambda \in U}\) in \({\mathcal {C}}^{\infty }(\varOmega )\) with the same kind of parameter dependence such that
Here, smooth (holomorphic, distributional) parameter dependence of \((f_{\lambda })_{\lambda \in U}\) means that the map \(\lambda \mapsto f_{\lambda }(x)\) is an element of \({\mathcal {C}}^{\infty }(U)\) (of the space of holomorphic functions \({\mathcal {O}}(U)\) on \(U\subset {\mathbb {C}}\) open, the space of distributions \({\mathcal {D}}(V)'\) for open \(V\subset {\mathbb {R}}^{d}\) where \(U={\mathcal {D}}(V)\)) for each \(x\in \varOmega\).
The parameter dependence problem for a variety of partial differential operators on several spaces of (generalised) differentiable functions has been extensively studied, see e.g. [4, 6, 7, 16, 31, 32] and the references and background in [3, 22]. The answer to this problem for the Cauchy-Riemann operator is affirmative since the Cauchy-Riemann operator
on the space \({\mathcal {C}}^{\infty }(\varOmega ,E)\) of E-valued smooth functions is surjective if \(E={\mathcal {C}}^{\infty }(U)\) (\({\mathcal {O}}(U)\), \({\mathcal {D}}(V)'\)) by [8, Corollary 3.9, p. 1112] which is a consequence of the splitting theory of Bonet and Domański for PLS-spaces [3, 4], the topological isomorphy of \({\mathcal {C}}^{\infty }(\varOmega ,E)\) to Schwartz’ \(\varepsilon\)-product \({\mathcal {C}}^{\infty }(\varOmega )\varepsilon E\) and the fact that \(\overline{\partial }:{\mathcal {C}}^{\infty }(\varOmega ) \rightarrow {\mathcal {C}}^{\infty }(\varOmega )\) is surjective on the nuclear Fréchet space \({\mathcal {C}}^{\infty }(\varOmega )\) (with its usual topology). More generally, the Cauchy-Riemann operator (1) is surjective if E is a Fréchet space by Grothendieck’s classical theory of tensor products [12] or if \(E:=F_{b}'\) where F is a Fréchet space satisfying the condition (DN) by [31, Theorem 2.6, p. 174] or if E is an ultrabornological PLS-space having the property (PA) by [8, Corollary 3.9, p. 1112] since the space \({\mathcal {O}}(\varOmega )\) of \({\mathbb {C}}\)-valued holomorphic functions on \(\varOmega\), i.e. the kernel of \(\overline{\partial }\), has the property \((\varOmega )\) by [31, Proposition 2.5 (b), p. 173]. The first and the last result cover the case that \(E={\mathcal {C}}^{\infty }(U)\) or \({\mathcal {O}}(U)\) whereas the last covers the case \(E={\mathcal {D}}(V)'\) as well. More examples of the second or third kind of such spaces E are arbitrary Fréchet–Schwartz spaces, the space \({\mathcal {S}}({\mathbb {R}}^{d})'\) of tempered distributions, the space \({\mathcal {D}}(V)'\) of distributions, the space \({\mathcal {D}}_{(w)}(V)'\) of ultradistributions of Beurling type and some more (see [4, 8, Corollary 4.8, p. 1116] and [22, Example 3, p. 7]).
In the present paper we consider the Cauchy-Riemann operator on weighted spaces \({\mathcal {E}}{\mathcal {V}}(\varOmega ,E)\) of smooth E-valued functions where E is a locally convex Hausdorff space over \({\mathbb {C}}\) with a system of seminorms \((p_{\alpha })_{\alpha \in {\mathfrak {A}}}\) generating its topology. These spaces consist of functions \(f\in {\mathcal {C}}^{\infty }(\varOmega ,E)\) fulfilling additional growth conditions induced by a family \({\mathcal {V}}:=(\nu _{n})_{n\in {\mathbb {N}}}\) of continuous functions \(\nu _{n}:\varOmega \rightarrow (0,\infty )\) on a sequence of open sets \((\varOmega _{n})_{n\in {\mathbb {N}}}\) with \(\varOmega =\bigcup _{n\in {\mathbb {N}}}\varOmega _{n}\) given by the constraint
for every \(n\in {\mathbb {N}}\), \(m\in {\mathbb {N}}_{0}\) and \(\alpha \in {\mathfrak {A}}\), where \((\partial ^{\gamma })^{E}f\) denotes the partial derivative of f w.r.t. the multi-index \(\gamma\). Our main goal is to derive sufficient conditions on \({\mathcal {V}}\) and \((\varOmega _{n})_{n\in {\mathbb {N}}}\) such that
is surjective. We recall the main result of [22], which sets the course of the present paper.
Theorem 1
[22, Theorem 5, p. 7-8] Let \({\mathcal {E}}{\mathcal {V}}(\varOmega )\) be a Schwartz space and \({\mathcal {E}}{\mathcal {V}}_{\overline{\partial }}(\varOmega )\) a nuclear subspace satisfying property \((\varOmega )\). Assume that the \({\mathbb {C}}\)-valued operator \(\overline{\partial }:{\mathcal {E}}{\mathcal {V}}(\varOmega ) \rightarrow {\mathcal {E}}{\mathcal {V}}(\varOmega )\) is surjective. Moreover, if
-
(a)
\(E:=F_{b}'\) where F is a Fréchet space over \({\mathbb {C}}\) satisfying (DN), or
-
(b)
E is an ultrabornological PLS-space over \({\mathbb {C}}\) satisfying (PA),
then
is surjective.
Here \({\mathcal {E}}{\mathcal {V}}(\varOmega ) :={\mathcal {E}}{\mathcal {V}}(\varOmega ,{\mathbb {C}})\) and \({\mathcal {E}}{\mathcal {V}}_{\overline{\partial }}(\varOmega )\) is the kernel of \(\overline{\partial }\) in \({\mathcal {E}}{\mathcal {V}} (\varOmega )\), i.e. its topological subspace
consisting of holomorphic functions.
We restrict to the case where the sequence \((\varOmega _{n})_{n\in {\mathbb {N}}}\) is given by strips \(\varOmega _{n}:=S_{n}(K)\) along the real axis with holes around a compact set \(K\subset [-\infty ,\infty ]=:\overline{{\mathbb {R}}}\), i.e. for \(t\in {\mathbb {R}}\), \(t\ge 1\), we define
where the closure is taken in \({\mathbb {C}}\) and the open sets \(U_{t}(K)\) are given
\(U_{t}(K)\) for \(\pm \infty \in K\) (c.f. [19, Figure 3.1, p. 11])
\(S_{t}(K)\) for \(\pm \infty \in K\) (c.f. [19, Figure 3.2, p. 12])
where \(\mathrm{d}(\{z\},K\cap {\mathbb {C}})\) denotes the Euclidean distance of the sets \(\{z\}\) and \(K\cap {\mathbb {C}}\) (see Figs. 1, 2). We note that \(\bigcup _{n\in {\mathbb {N}}}S_{n}(K)={\mathbb {C}}\setminus K\) and the definition of \(S_{1}(K)\) is motivated by \(\left( {\mathbb {C}}\setminus \overline{U_{1}(\overline{{\mathbb {R}}})}\right) \cap \{z\in {\mathbb {C}}\; | \; |{{\,\mathrm{Im}\,}}(z)| < 1 \}=\varnothing\). As a further simplification we only consider weights of the form \(\nu _{n}(z):=\exp (a_{n}|{{\,\mathrm{Re}\,}}(z)|^{\beta })\), \(z\in {\mathbb {C}}\), for all \(n\in {\mathbb {N}}\) for some \(0<\beta \le 1\) and some strictly increasing real sequence \((a_{n})_{n\in {\mathbb {N}}}\), and in combination with \(\varOmega _{n}:=S_{n}(K)\), \(n\in {\mathbb {N}}\), we fix the notation
with \(\overline{{\mathbb {C}}}:=\overline{{\mathbb {R}}}+i{\mathbb {R}}\). In the case \(\beta =1\) these spaces are of interest because they are the basic spaces for the theory of vector-valued Fourier hyperfunctions, see e.g. [13,14,15, 17, 19, 24]. Looking at Theorem 1, the main obstacle is to prove that \({\mathcal {E}}^{\beta }_{(a_n),\overline{\partial }}(\overline{{\mathbb {C}}}\setminus K)\) satsifies property \((\varOmega )\). In [22, Corollary 14, p. 18] this is accomplished for \(K=\varnothing\) and sequences \((a_{n})_{n\in {\mathbb {N}}}\) such that \(a_{n}\nearrow 0\) or \(a_{n}\nearrow \infty\). We will use this result and extend it to the case that \(K\subset \overline{{\mathbb {R}}}\) is a non-empty compact set.
Let us summarise the content of our paper. In Sect. 2 we recall necessary definitions and preliminaries which are needed in the subsequent sections. Sect. 3 is dedicated to a counterpart for weighted holomorphic functions of the Silva-Köthe-Grothendieck duality
where \(K\subset {\mathbb {R}}\) is a non-empty compact set and \({\mathscr {A}}(K)\) the space of germs of real analytic functions on K (see Theorem 11, Corollary 13, Corollary 15). In Sect. 4 we use this duality to show that \({\mathcal {E}}^{\beta }_{(a_n),\overline{\partial }}(\overline{{\mathbb {C}}}\setminus K)\) satisfies property \((\varOmega )\) under some restrictions on K, or on \((a_n)_{n\in {\mathbb {N}}}\) and \(\beta\) (see Corollary 19). The preceding conditions on K, or on \((a_n)_{n\in {\mathbb {N}}}\) and \(\beta\) are used in Theorem 20 to show that \(\overline{\partial }^{E}:{\mathcal {E}}^{\beta }_{(a_n)}(\overline{{\mathbb {C}}}\setminus K,E) \rightarrow {\mathcal {E}}^{\beta }_{(a_n)}(\overline{{\mathbb {C}}}\setminus K,E)\) is surjective if \(E:=F_{b}'\) where F is a Fréchet space over \({\mathbb {C}}\) satisfying (DN), or if E is an ultrabornological PLS-space over \({\mathbb {C}}\) satisfying (PA).
2 Notation and preliminaries
The notation and preliminaries are essentially the same as in [22, 23, Sect. 2]. We define the distance of two subsets \(M_{0}, M_{1} \subset {\mathbb {R}}^{2}\) w.r.t. the Euclidean norm \(|\cdot |\) on \({\mathbb {R}}^{2}\) via
Moreover, we denote by \({\mathbb {B}}_{r}(x):=\{w\in {\mathbb {R}}^{2}\;|\;|w-x|<r\}\) the Euclidean ball around \(x\in {\mathbb {R}}^{2}\) with radius \(r>0\) and identify \({\mathbb {R}}^{2}\) and \({\mathbb {C}}\) as (normed) vector spaces. We denote the closure of a subset \(M\subset {\mathbb {R}}^{2}\) by \(\overline{M}\), the boundary of M by \(\partial M\) and for a function \(f:M\rightarrow {\mathbb {C}}\) and \(K\subset M\) we denote by \(f_{\mid K}\) the restriction of f to K. We write \({\mathcal {C}}(\varOmega )\) for the space of continuous \({\mathbb {C}}\)-valued functions on a set \(\varOmega \subset {\mathbb {R}}^{2}\) and \(L^{1}(\varOmega )\) for the space of (equivalence classes of) \({\mathbb {C}}\)-valued Lebesgue integrable functions on a measurable set \(\varOmega \subset {\mathbb {R}}^{2}\).
By E we always denote a non-trivial locally convex Hausdorff space over the field \({\mathbb {C}}\) equipped with a directed fundamental system of seminorms \((p_{\alpha })_{\alpha \in {\mathfrak {A}}}\). If \(E={\mathbb {C}}\), then we set \((p_{\alpha })_{\alpha \in {\mathfrak {A}}}:=\{|\cdot |\}\). Further, we denote by L(F, E) the space of continuous linear maps from a locally convex Hausdorff space F to E and sometimes use the notation \(\langle T, f\rangle :=T(f)\), \(f\in F\), for \(T\in L(F,E)\). If \(E={\mathbb {C}}\), we write \(F':=L(F,{\mathbb {C}})\) for the dual space of F. If F and E are (linearly topologically) isomorphic, we write \(F\cong E\). We denote by \(L_{b}(F,E)\) the space L(F, E) equipped with the locally convex topology of uniform convergence on the bounded subsets of F.
We recall that a function \(f:\varOmega \rightarrow E\) on an open set \(\varOmega \subset {\mathbb {C}}\) to E is called holomorphic if the limit
exists in E for every \(z_{0}\in \varOmega\). The linear space of all functions \(f:\varOmega \rightarrow E\) which are holomorphic is denoted by \({\mathcal {O}}(\varOmega ,E)\). For a compact set \(K\subset \overline{{\mathbb {R}}}\), \(0<\beta \le 1\) and a strictly increasing real sequence \((a_{n})_{n\in {\mathbb {N}}}\) we set
where
The subscript \(\alpha\) in the notation of the seminorms is omitted in the \({\mathbb {C}}\)-valued case and we write \({\mathcal {O}}^{\beta }_{(a_n)}(\overline{{\mathbb {C}}}\setminus K) :={\mathcal {O}}^{\beta }_{(a_n)}(\overline{{\mathbb {C}}}\setminus K,{\mathbb {C}})\).
Remark 2
We have \({\mathcal {O}}^{\beta }_{(a_n)}(\overline{{\mathbb {C}}}\setminus K) ={\mathcal {E}}^{\beta }_{(a_n),\overline{\partial }}(\overline{{\mathbb {C}}}\setminus K)\) as Fréchet spaces by [22, Proposition 7 (b), p. 11] and [22, Example 6, p. 11].
Throughout the rest of the paper we make the following standing assumptions.
Assumption 3
-
(i)
E is sequentially complete,
-
(ii)
\(K\subset \overline{{\mathbb {R}}}\) is a non-empty compact set,
-
(iii)
\(0<\beta \le 1\),
-
(iv)
\((a_n)_{n\in {\mathbb {N}}}\) is a strictly increasing sequence with \(a_{n}<0\) for all \(n\in {\mathbb {N}}\) or \(a_{n}\ge 0\) for all \(n\in {\mathbb {N}}\), and \(\lim _{n\to \infty }a_{n}=0\) or \(\lim _{n\to \infty }a_{n}=\infty\).
3 Duality
We recall the well-known topological Silva-Köthe-Grothendieck isomorphy
where E is a quasi-complete locally convex Hausdorff space, \(\varnothing \ne K\subset {\mathbb {R}}\) is compact, \({\mathcal {O}}({\mathbb {C}}\setminus K,E)\) is equipped with the topology of uniform convergence on compact subsets of \({\mathbb {C}}\setminus K\), the quotient space with the induced quotient topology and \({\mathscr {A}}(K)\) is the space of germs of real analytic functions on K with its inductive limit topology (see e.g. [29, p. 6], [11, Proposition 1, p. 46], [18, §27.4, p. 375-378], [27, Theorem 2.1.3, p. 25]). The aim of this section is to prove a counterpart of this isomorphy for weighted vector-valued holomorphic functions and non-empty compact \(K\subset \overline{{\mathbb {R}}}\).
The spaces \({\mathcal {O}}^{\beta }_{(a_n)}(\overline{{\mathbb {C}}}\setminus K,E)\) play the counterpart of \({\mathcal {O}}({\mathbb {C}}\setminus K,E)\) for our version of the isomorphy (2). Next, we introduce the counterparts of \({\mathscr {A}}(K)\). Let \(\varOmega \subset {\mathbb {C}}\) be open and \(f\in {\mathcal {O}}(\varOmega )\). For \(z\in \varOmega\) and \(n\in {\mathbb {N}}_{0}\) we denote the point evaluation of the nth complex derivative at z by \(\delta ^{(n)}_{z}f:=f^{(n)}(z)\).
Proposition 4
For \(n\in {\mathbb {N}}\) let
where
and the spectral maps for \(n,k\in {\mathbb {N}}\), \(n\le k\), are given by the restrictions
Then the following assertions hold.
-
(a)
The inductive limit
$${\mathcal{O}}_{{(a_{n} )}}^{{ - \beta }} (K): = \lim\limits_{\substack{\longrightarrow\\n\in\mathbb{N}}}{\mathcal{O}}_{{a_{n} }}^{{ - \beta }} \left( {\overline{{U_{n} (K)}} } \right)$$exists and is a DFS-space.
-
(b)
The span of the set of point evaluations of complex derivatives \(\{\delta _{x_{0}}^{(n)} \; | \; x_{0} \in K\cap {\mathbb {R}},\, n\in {\mathbb {N}}_{0}\}\) is dense in \({\mathcal {O}}^{-\beta }_{(a_n)}(K)_{b}'\) if \(K\subset {\mathbb {R}}\) or \(K\cap \{\pm \infty \}\) contains no isolated points in K.
Proof
(a) It is easy to see that \({\mathcal {O}}^{-\beta }_{a_n} \left( {\overline{{U_{n} (K)}} } \right)\) is a Banach space for every \(n\in {\mathbb {N}}\). Further, the maps \(\pi _{n,m}:{\mathcal {O}}^{-\gamma }_{a_n} \left( {\overline{{U_{n} (K)}} } \right) \rightarrow {\mathcal {O}}^{-\beta }_{a_m}\left(\overline{U_{m}(K)}\right)\), \(n\le m\), are injective by virtue of the identity theorem and the definition of sets \(U_{n}(K)\). Thus the considered spectrum is an embedding spectrum. For all \(M \subset U_{n}(K)\) compact and \(f\in B_{n}:=\{g\in {\mathcal {O}}^{-\beta }_{a_n} \left( {\overline{{U_{n} (K)}} } \right) \;|\;\Vert g\Vert _{n}\le 1\}\) we have
Thus \(B_{n}\) is bounded in \({\mathcal {O}}(U_{n}(K))\) w.r.t. the system of seminorms generated by \(\Vert \cdot \Vert _{M}\) for compact \(M \subset U_{n}(K)\). As this space is a Fréchet-Montel space, \(B_{n}\) is relatively compact and hence relatively sequentially compact in \({\mathcal {O}}(U_{n}(K))\).
What remains to be shown is that for all \(n\in {\mathbb {N}}\) there exists \(m>n\) such that \(\pi _{n,m}\) is a compact map. Because the considered spaces are Banach spaces, it suffices to prove the existence of \(m>n\) such that \((\pi _{n,m}(f_{k}))_{k\in {\mathbb {N}}}\) has a convergent subsequence in \({\mathcal {O}}^{-\beta }_{a_m}\left(\overline{U_{m}(K)}\right)\) for every sequence \((f_{k})_{k\in {\mathbb {N}}}\) in \(B_{n}\). We choose \(m:=2n\). For \(\varepsilon >0\) we set
and get
Thus condition (RU) in [2, p. 67] is fufilled and it follows analogously to the proof of [2, Theorem (b), p. 67-68] that every sequence \((f_{k})_{k \in {\mathbb {N}}}\) in \(B_{n}\) has a subsequence \((f_{k_{l}})_{l\in {\mathbb {N}}}\) such that \((\pi _{n,2n}(f_{k_{l}}))_{l\in {\mathbb {N}}}\) converges in \({\mathcal {O}}^{-\beta }_{a_{2n}}\left(\overline{U_{2n}(K)}\right)\), proving the compactness of \(\pi _{n,2n}\). Hence the inductive limit \({\mathcal {O}}^{-\beta }_{(a_n)}(K)\) exists and is a DFS-space by [25, Proposition 25.20, p. 304].
(b) We set \(F:=\mathrm{span}\{\delta _{x_{0}}^{(n)}\;| \;x_{0}\in K\cap {\mathbb {R}},\,n\in {\mathbb {N}}_{0}\}\). Let \(x_{0}\in K\cap {\mathbb {R}}\) and \(n\in {\mathbb {N}}_{0}\). It follows from Cauchy’s inequality that \(\delta _{x_{0}}^{(n)}\) is continuous on \({\mathcal {O}}^{-\beta }_{a_k}(\overline{U_{k}(K)})\) for any \(k\in {\mathbb {N}}\), implying \(F\subset {\mathcal {O}}^{-\beta }_{(a_n)}(K)'\). As \({\mathcal {O}}^{-\beta }_{(a_n)}(K)\) is a DFS-space by part (a), it is reflexive by [25, Proposition 25.19, p. 303], which means that the canonical embedding \(J:{\mathcal {O}}^{-\beta }_{(a_n)}(K) \rightarrow ({\mathcal {O}}^{-\beta }_{(a_n)}(K)_{b}')_{b}'\) is a topological isomorphism. We consider the polar set of F, i.e.
Let \(y\in F^{\circ }\). Then there is \(f\in {\mathcal {O}}^{-\beta }_{(a_n)}(K)\) such that \(y=J(f)\). For \(T:=\delta _{x_{0}}^{(n)}\in F\)
is valid for any \(n\in {\mathbb {N}}_{0}\). Thus f is identical to zero on a neighbourhood of \(x_{0}\) (by Taylor series expansion) since f is holomorphic near \(x_{0}\in U_{n}(K)\). Due to the assumptions every component of \(U_{n}(K)\) contains a point \(x_{0}\in K\cap {\mathbb {R}}\) so f is identical to zero on \(\overline{U_{n}(K)}\) by the identity theorem and continuity, yielding to \(y=0\). Therefore \(F^{\circ }=\{0\}\) and thus F is dense in \({\mathcal {O}}^{-\beta }_{(a_n)}(K)_{b}'\) by the bipolar theorem. \(\square\)
In the case \(\beta :=1\) and \(a_{n}:=-1/n\) for all \(n\in {\mathbb {N}}\) the spaces \({\mathcal {O}}^{-1}_{(a_n)}(K)\) play an essential role in the theory of Fourier hyperfunctions and it is already mentioned in [17, p. 469] resp. proved in [15, 1.11 Satz, p. 11] and [19, 3.5 Theorem, p. 17] that they are DFS-spaces.
Remark 5
If \(K\subset {\mathbb {R}}\), then \({\mathcal {O}}^{-\beta }_{(a_n)}(K)\cong {\mathscr {A}}(K)\).
Now, we take a closer look at the sets \(U_{t}(K)\) (c.f. [19, 3.3 Remark, p. 13]).
Remark 6
Let \(t\in {\mathbb {R}}\), \(t\ge 1\).
-
(a)
The set \(U_{t}(K)\) has finitely many components.
-
(b)
Let Z be a component of \(U_{t}(K)\). We define \(a:=\min (Z\cap K)\) and \(b:=\max (Z\cap K)\) if existing (in \({\mathbb {R}}\)).
-
(i)
If Z is bounded, there exists \(0<R\le 1/t\) such that for all \(0<r\le R\): \(\{z\in {\mathbb {C}}\;|\;\mathrm{d}(\{z\},[a,b])< r\}\subset Z\)
-
(ii)
If \(Z\cap {\mathbb {R}}\) is bounded from below and unbounded from above and a exists, there exists \(0<R\le 1/t\) such that for all \(0<r\le R\): \(\{z\in {\mathbb {C}}\;|\;\mathrm{d}(\{z\},[a,\infty ))< r\}\subset Z\)
-
(iii)
If \(Z\cap {\mathbb {R}}\) is bounded from above and unbounded from below and b exists, there exists \(0<R\le 1/t\) such that for all \(0<r\le R\): \(\{z\in {\mathbb {C}}\;|\;\mathrm{d}(\{z\},(-\infty ,b])< r\}\subset Z\)
-
(iv)
If \(Z\cap {\mathbb {R}}\) is unbounded from below and above, there exists \(0<R\le 1/t\) such that for all \(0<r\le R\): \(\{z\in {\mathbb {C}}\;|\;\mathrm{d}(\{z\},{\mathbb {R}})< r\}\subset Z\)
-
(v)
If \(Z\cap {\mathbb {R}}\) is bounded from below and unbounded from above and a does not exist, then \(Z=(t,\infty )+i (-1/t,1/t)\). If \(Z\cap {\mathbb {R}}\) is bounded from above and unbounded from below and b does not exist, then \(Z=(-\infty ,-t)+i (-1/t,1/t)\).
-
(i)
Proof
(a) We only consider the case \(\infty \in K\), \(-\infty \notin K\). Let \((Z_{j})_{j\in J}\) denote the (pairwise disjoint) components of \(U_{t}(K)\). Then \(U_{t}(K) = \bigcup _{j\in J}Z_{j}\) and by definition of a component there is \(k\in J\) such that \(Z_{k}\) is the only component including \((t,\infty )+i(-1/t,1/t)\). Furthermore there exists \(m\in {\mathbb {R}}\) with \(\bigcup _{j\in J\setminus \{k\}}(Z_{j}\cap {\mathbb {R}}) \subset [m,t]\) by assumption. For \(j\ne k\) the length \(\lambda (Z_{j}\cap {\mathbb {R}})\) of the interval \(Z_{j}\cap {\mathbb {R}}\), where \(\lambda\) denotes the Lebesgue measure, is estimated from below by \(\lambda (Z_{j}\cap {\mathbb {R}})\ge 2/t\) by definition of \(U_{t}(K)\). Since all \(Z_{j}\) are pairwise disjoint, this implies that J has to be finite. The others cases follow analogously.
(b)(i) Since \(Z\cap K\) is closed in \({\mathbb {R}}\) and therefore compact, a and b exist. Hence \([a,b]\subset Z\) by the definition of \(U_{t}(K)\) and as Z is connected. [a, b] being a compact subset of the open set Z implies that there is \(0<R< 1/t\) such that \(([a,b]+i(-R,R))\subset Z\) by the tube lemma, which completes the proof.
(ii) If \(Z\cap K\cap (-\infty ,t]\ne \varnothing\), then a exists and analogously to (i) there exists \(0<R<1/t\) such that for all \(0<r\le R\)
By definition of \(U_{t}(K)\) this brings forth \(\{z\in {\mathbb {C}}\;|\;\mathrm{d}(\{z\},[a,\infty ))<r\}\subset Z\). If \(Z\cap K\cap (-\infty ,t]=\varnothing\) and a exists, the desired \(0<R<1/t\) exists by the definition of \(U_{t}(K)\) since \(t\not \in Z\cap K\) and \(Z\cap K\) is closed in \({\mathbb {R}}\), which implies \(\mathrm{d}(\{t\},Z\cap K)>0\).
(iii) Analogously to (ii).
(iv) By the assumptions \(Z\cap K\cap [-t,t]\ne \varnothing\). Analogously to (i) there exists \(0<R<1/t\) such that for all \(0<r\le R\)
Like in (ii) and (iii) this brings forth \(\{z\in {\mathbb {C}}\;|\;\mathrm{d}(\{z\},{\mathbb {R}})<r\}\subset Z\).
(v) This follows directly from the definition of \(U_{t}(K)\) and as Z is a component of \(U_{t}(K)\). \(\square\)
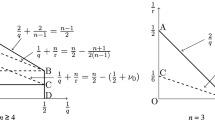
Definition 7
Let \(n\in {\mathbb {N}}\) and \((Z_{j})_{j\in J}\) denote the components of \(U_{n}(K)\). A component \(Z_{j}\) of \(U_{n}(K)\) fulfils one of the cases of Remark 6 (b) and so for \(a=a_{j}\), \(b=b_{j}\) (in the cases (i)-(iii)), for \(0<r_{j}<R_{j}=R\) (in the cases (i)-(iv)) resp. \(0<r_{j}<1/n=:R_{j}\) (in the case (v)) we define
where \(Z_{j}\) fulfils (v) in the last two cases. By Remark 6 (a) there is w.l.o.g. \(k\in {\mathbb {N}}\) with \(U_{n}(K)=\bigcup _{j=1}^{k}Z_{j}\). We set \(r:=(r_{j})_{1\le j\le k}\) and the path
where \(\gamma _{j}\) is the path along the boundary of \(V_{r_{j}}(Z_{j})\) in \({\mathbb {C}}\) in the positive sense (counterclockwise) (see Fig. 3).
Path \(\gamma _{K,n,r}\) for \(\pm \infty \in K\) (c.f. [19, Figure 4.1, p. 40])
Proposition 8
Let \(n\in {\mathbb {N}}\) and \(\gamma _{K,n,r}\) be the path from Definition 7. Then the following assertions hold.
-
(a)
\(F\cdot \varphi\) is Pettis-integrable along \(\gamma _{K,n,r}\) for all \(F\in {\mathcal {O}}^{\beta }_{(a_n)}(\overline{{\mathbb {C}}}\setminus K,E)\) and \(\varphi \in {\mathcal {O}}_{a_n}^{-\beta } \left( {\overline{{U_{n} (K)}} } \right).\)
-
(b)
There are \(m\in {\mathbb {N}}\) and \(C>0\) such that for all \(\alpha \in {\mathfrak {A}}\), \(F\in {\mathcal {O}}^{\beta }_{(a_n)}(\overline{{\mathbb {C}}}\setminus K,E)\) and \(\varphi \in {\mathcal {O}}_{a_n}^{-\beta } \left( {\overline{{U_{n} (K)}} } \right)\)
$$\begin{aligned} p_{\alpha }\left( \int _{\gamma _{K,n,r}}F(\zeta )\varphi (\zeta ) \mathrm{d}\zeta \right) \le C |F|_{m,\alpha }\Vert \varphi \Vert _{n}. \end{aligned}$$ -
(c)
For all \(F\in {\mathcal {O}}^{\beta }_{(a_n)}(\overline{{\mathbb {C}}}\setminus K,E)\), \(\varphi \in {\mathcal {O}}_{a_n}^{-\beta } \left( {\overline{{U_{n} (K)}} } \right)\) and \(\widetilde{r}:=(\widetilde{r}_{j})_{1\le j\le k}\) with \(0<\widetilde{r}_{j}<R_{j}\,\) for all \(1\le j\le k\)
$$\begin{aligned} \int _{\gamma _{K,n,r}}F(\zeta )\varphi (\zeta )\mathrm{d}\zeta =\int _{\gamma _{K,n,\widetilde{r}}}F(\zeta )\varphi (\zeta )\mathrm{d}\zeta . \end{aligned}$$ -
(d)
For all \(F\in {\mathcal {O}}^{\beta }_{(a_n)}(\overline{{\mathbb {C}}},E)\) and \(\varphi \in {\mathcal {O}}_{a_n}^{-\beta } \left( {\overline{{U_{n} (K)}} } \right)\)
$$\begin{aligned} \int _{\gamma _{K,n,r}}F(\zeta )\varphi (\zeta )\mathrm{d}\zeta =0. \end{aligned}$$
Proof
\((a)+(b)\) We have to show that there is \(e_{K,n,r}\in E\) such that
which gives \(\int _{\gamma _{K,n,r}}F(\zeta )\varphi (\zeta )\mathrm{d}\zeta =e_{K,n,r}\).
First, let \(V_{r_{j}}(Z_{j})\) be bounded for some \(1\le j\le k\). There is a parametrisation \(\gamma _{j}:[0,1]\rightarrow {\mathbb {C}}\) which has a continuously differentiable extension \(\widetilde{\gamma }_{j}\) on \((-1,2)\). As the map \((e'\circ (F\cdot \varphi )\circ \gamma _{j})\cdot \gamma _{j}'\) is continuous on [0, 1] for every \(e'\in E'\), it is an element of \(L^{1}([0,1])\) for every \(e'\in E'\). Thus the map
is well-defined and linear. We estimate
Let us denote by \(\overline{\mathrm{acx}} ((F\cdot \varphi )(\gamma _{j}([0,1])))\) the closure of the absolutely convex hull of the set \((F\cdot \varphi )(\gamma _{j}([0,1]))\). Since \(e'\circ (F\cdot \varphi) \circ \widetilde{\gamma }_{j}\in {\mathcal {C}}^{1}((-1,2))\) for every \(e'\in E'\), the absolutely convex set \(\overline{\mathrm{acx}}((F\cdot \varphi ) (\gamma _{j}([0,1])))\) is compact in the sequentially complete space E by [5, Proposition 2, p. 354], yielding \({\mathfrak {I}}_{j}\in (E_{\kappa }')'\cong E\) by the theorem of Mackey-Arens, i.e. there is \(e_{j}\in E\) such that
Therefore \(F\cdot \varphi\) is Pettis-integrable along \(\gamma _{j}\). Furthermore, we choose \(m_{j}\in {\mathbb {N}}\) such that \((1/m_{j})<r_{j}\) and for \(\alpha \in {\mathfrak {A}}\) we set \(B_{\alpha }:=\{x\in E\;|\;p_{\alpha }(x)<1\}\). We note that
where we used [25, Proposition 22.14, p. 256] in the first and the last equation to get from \(p_{\alpha }\) to \(\sup _{e'\in B_{\alpha }^{\circ }}\) and back. If \(K\subset {\mathbb {R}}\), then all \(V_{r_{j}}(Z_{j})\), \(1\le j\le k\), are bounded and with the choice \(e_{K,n,r}:=\sum _{j=1}^{k}e_{j}, \, m:=\max _{1\le j\le k} m_{j} \,\text{and} \, C:=k\max _{1\le j\le k}\ell (\gamma _{j}) \sup _{w\in \gamma _{j}([0,1])}e^{(a_{n}-a_{m_j})|{{\,\mathrm{Re}\,}}(w)|^{\beta }}\) we deduce our statement.
Second, let us consider the case \(\infty \in K\), \(-\infty \not \in K\). Let \(Z_{k}\) be the unique unbounded component of \(U_{n}(K)\). For \(q\in {\mathbb {N}}\), \(q>1/r_{k}>n\), we denote by \(\gamma _{k,q}\) the part of \(\gamma _{k}\) in \(\{z\in {\mathbb {C}}\;|\;{{\,\mathrm{Re}\,}}(z)\le q\}\). Like in the first part the Pettis-integral
exists (in E) and for \(\alpha \in {\mathfrak {A}}\) and \(m_{k}\in {\mathbb {N}}\), \((1/m_{k})<r_{k}\), we have
Next, we prove that \((e_{k,q})_{q>1/r_{k}}\) is a Cauchy sequence in E. We choose \(M:=\max (m_{k},2n)\). For \(q,p\in {\mathbb {N}}\), \(q>p>1/r_{k}>n\), we obtain
and observe that \((\int _{0}^{q}e^{(a_{n}-a_{2n})t^{\beta }}\mathrm{d}t)_{q}\) is a Cauchy sequence in \({\mathbb {C}}\) because
where \(\varGamma\) is the gamma function. Therefore \((e_{k,q})_{q>1/r_{k}}\) is a Cauchy sequence in E, has a limit \(e_{k}\) in the sequentially complete space E and
We fix \(p\in {\mathbb {N}}\), \(p>1/r_{k}>n\), and conclude that
Consequently, our statement holds also in the case \(\infty \in K\), \(-\infty \not \in K\) and in the remaining cases it follows analogously.
(c) We note that
for all \(e'\in E'\). Thus statement (c) follows from Cauchy’s integral theorem and the Hahn-Banach theorem if \(K\subset {\mathbb {R}}\). Now, let us consider the case \(\infty \in K\), \(-\infty \not \in K\). We denote by \(\gamma _{k}\) resp. \(\widetilde{\gamma }_{k}\) the part of \(\gamma _{K,n,r}\) resp. \(\gamma _{K,n,\widetilde{r}}\) in the unbounded component of \(U_{n}(K)\). It suffices to show that
Let \(\varepsilon >0\) and w.l.o.g. \(r_{k}<\widetilde{r}_{k}\). We choose the compact set \(Q\subset \overline{U_{2n}(K)}\) as in the proof of Proposition 4 (b). Further, we take \(q\in {\mathbb {R}}\) such that \(q>1/r_{k}\) and \(q\in \overline{U_{2n}(K)}\setminus Q\) and define the path \(\gamma _{0,q}^{+}:[r_{k},\widetilde{r}_{k}]\rightarrow {\mathbb {C}}\), \(\gamma _{0,q}^{+}(t):=q+it\). We deduce that for \(m_{k}\in {\mathbb {N}}\), \((1/m_{k})<\min (r_{k},1/(2n))\), and every \(e'\in E'\)
In the same way we obtain with \(\gamma _{0,q}^{-} :[-\widetilde{r}_{k},-r_{k}]\rightarrow {\mathbb {C}}\), \(\gamma _{0,q}^{-}(t):=q+it\), that
Hence we get (4) by Cauchy’s integral theorem and the Hahn-Banach theorem as well. The remaining cases follow similarly.
(d) The proof is similar to (c). Let \(F\in {\mathcal {O}}^{\beta }_{(a_n)}(\overline{{\mathbb {C}}},E)\). Again, it suffices to prove that
This follows from Cauchy’s integral theorem and the Hahn-Banach theorem if \(K\subset {\mathbb {R}}\). Again, we only consider the case \(\infty \in K\), \(-\infty \not \in K\) and only need to show that
where \(\gamma _{k}\) is the part of \(\gamma _{K,n,r}\) in the unbounded component of \(U_{n}(K)\). Let \(\varepsilon >0\) and choose q as in (c). Then we have with \(\gamma _{0,q}:[-r_{k},r_{k}]\rightarrow {\mathbb {C}}\), \(\gamma _{0,q}(t):=q+it\), that
for every \(e'\in E'\). Cauchy’s integral theorem and the Hahn-Banach theorem imply our statement. \(\square\)
An essential role in the proof of \({\mathcal {O}}({\mathbb {C}}\setminus K,E)/{\mathcal {O}}({\mathbb {C}},E)\cong L_{b}({\mathscr {A}}(K),E)\) for non-empty compact \(K\subset {\mathbb {R}}\) and quasi-complete E (see (2)) plays the fundamental solution \(z\mapsto 1/(\pi z)\) of the Cauchy-Riemann operator. By the identity theorem we can consider \({\mathcal {O}}^{\beta }_{(a_n)}(\overline{{\mathbb {C}}},E)\) as a subspace of \({\mathcal {O}}^{\beta }_{(a_n)}(\overline{{\mathbb {C}}}\setminus K,E)\) and we equip the quotient space \({\mathcal {O}}^{\beta }_{(a_n)}(\overline{{\mathbb {C}}}\setminus K,E)/{\mathcal {O}}^{\beta }_{(a_n)}(\overline{{\mathbb {C}}},E)\) with the induced locally convex quotient topology (which may not be Hausdorff, see Remark 14). We want to prove the isomorphy
for non-empty compact \(K\subset \overline{{\mathbb {R}}}\) under some assumptions on K, \(\beta\) and \((a_{n})_{n\in {\mathbb {N}}}\). Since we have to deal with functions having some growth given by our exponential weights, we have to use the adapted fundamental solution \(z\mapsto e^{-z^{2}}/(\pi z)\) of the Cauchy-Riemann operator.
Proposition 9
Let \(\gamma _{K,n,r}\) be the path from Definition 7. The map
given by
for \(f=[F]\in {\mathcal {O}}^{\beta }_{(a_n)}(\overline{{\mathbb {C}}}\setminus K,E)/{\mathcal {O}}^{\beta }_{(a_n)}(\overline{{\mathbb {C}}},E)\) and \(\varphi \in {\mathcal {O}}_{a_n}^{-\beta } \left( {\overline{{U_{n} (K)}} } \right)\), \(n\in {\mathbb {N}}\), is well-defined, linear and continuous. For all non-empty compact sets \(K_{1}\subset K\) it holds that
on \({\mathcal {O}}^{-\beta }_{(a_n)}(K)\).
Proof
In the following we omit the index K of \(H_{K}\) if no confusion seems to be likely. Let \(f=[F]\in {\mathcal {O}}^{\beta }_{(a_n)}(\overline{{\mathbb {C}}}\setminus K,E)/{\mathcal {O}}^{\beta }_{(a_n)}(\overline{{\mathbb {C}}},E)\) and \(\varphi \in {\mathcal {O}}^{-\beta }_{(a_n)}(K)\). Then there is \(n\in {\mathbb {N}}\) such that \(\varphi \in {\mathcal {O}}_{a_n}^{-\beta } \left( {\overline{{U_{n} (K)}} } \right)\). Due to Proposition 8 (a) and (d) \(H(f)(\varphi )\in E\) and H(f) is independent of the representative F of f. From Proposition 8 (c) it follows that H(f) is well-defined on \({\mathcal {O}}^{-\beta }_{(a_n)}(K)\), i.e. for all \(k\in {\mathbb {N}}\), \(k\ge n\), and \(\varphi \in {\mathcal {O}}_{a_n}^{-\beta } \left( {\overline{{U_{n} (K)}} } \right)\) it holds that
For all \(n\in {\mathbb {N}}\) there are \(m\in {\mathbb {N}}\) and \(C>0\) such that
for all \(f=[F]\in {\mathcal {O}}^{\beta }_{(a_n)}(\overline{{\mathbb {C}}}\setminus K,E)/{\mathcal {O}}^{\beta }_{(a_n)}(\overline{{\mathbb {C}}},E)\), \(\varphi \in {\mathcal {O}}_{a_n}^{-\beta } \left( {\overline{{U_{n} (K)}} } \right)\) and \(\alpha \in {\mathfrak {A}}\) by Proposition 8 (b), which implies that \(H(f)\in L\left({\mathcal {O}}_{a_n}^{-\beta } \left( {\overline{{U_{n} (K)}} } \right) ,E\right)\) for every \(n\in {\mathbb {N}}\). We deduce that \(H(f)\in L({\mathcal {O}}^{-\beta }_{(a_n)}(K),E)\) by [9, 3.6 Satz, p. 117]. Let
denote the quotient map. We equip the quotient space with its usual quotient topology generated by the system of quotient seminorms given by
for \(l\in {\mathbb {N}}\) and \(\alpha \in {\mathfrak {A}}\). Then the quotient space, equipped with these seminorms, is a locally convex space (but maybe not Hausdorff). Since (6) holds for every representative F of f, we obtain for every \(f\in {\mathcal {O}}^{\beta }_{(a_n)}(\overline{{\mathbb {C}}}\setminus K,E)/{\mathcal {O}}^{\beta }_{(a_n)}(\overline{{\mathbb {C}}},E)\), \(\varphi \in {\mathcal {O}}_{a_n}^{-\beta } \left( {\overline{{U_{n} (K)}} } \right)\), \(n\in {\mathbb {N}}\), and \(\alpha \in {\mathfrak {A}}\) that
Now, let \(M\subset {\mathcal {O}}^{-\beta }_{(a_n)}(K)\) be a bounded set. Since the sequence \((B_{n})_{n\in {\mathbb {N}}}\) of closed unit balls \(B_n\) of \({\mathcal {O}}_{a_n}^{-\beta } \left( {\overline{{U_{n} (K)}} } \right)\) is a fundamental system of bounded sets in \({\mathcal {O}}^{-\beta }_{(a_n)}(K)\) by [25, Proposition 25.19, p. 303], there exist \(n\in {\mathbb {N}}\) and \(\lambda >0\) with \(M\subset \lambda B_{n}\). We derive from (7) that
proving the continuity of H.
Moreover, let \(K_{1}\subset \overline{{\mathbb {R}}}\) be compact and \(K_{1}\subset K\). We observe that for every \(F\in {\mathcal {O}}^{\beta }_{(a_n)}(\overline{{\mathbb {C}}}\setminus K_{1},E)\) and \(\varphi \in {\mathcal {O}}_{a_n}^{-\beta } \left( {\overline{{U_{n} (K)}} } \right)\), \(n\in {\mathbb {N}}\), it holds that
by Cauchy’s integral theorem and the Hahn-Banach theorem like in Proposition 8 (c) and (d). This yields to
on \({\mathcal {O}}^{-\beta }_{(a_n)}(K)\). \(\square\)
Now, we take a closer look at the potential inverse of \(H_{K}\).
Proposition 10
The map
given by
is well-defined, linear and continuous.
Proof
We start with the proof that the map \(\varTheta _{K}\) is well-defined and take a closer look at its components. For \(z,\zeta \in {\mathbb {C}}\) we set \(G(z,\zeta ):=e^{-(z-\zeta )^2}\) and note that \(\tfrac{\partial }{\partial z}G(z,\zeta )=-2(z-\zeta )G(z,\zeta )\). We remark that for all \(z=z_{1}+iz_{2}\in {\mathbb {C}}\) and all \(n\in {\mathbb {N}}\)
and we deduce that \(G(z,\cdot )\in {\mathcal {O}}_{a_n}^{-\beta } \left( {\overline{{U_{n} (K)}} } \right)\), in particular \(G({\mathbb {B}}_{1/n} (z),\cdot )\subset {\mathcal {O}}_{a_n}^{-\beta } \left( {\overline{{U_{n} (K)}} } \right)\). For \(\zeta =\zeta _{1}+i\zeta _{2}\in \overline{U_{n}(K)}\) and \(h\in {\mathbb {C}}\), \(0<|h|\le 1\), we observe that
yielding to
We conclude that \(\tfrac{\partial }{\partial z}G(z,\cdot ) =-2(z-\cdot )G(z,\cdot )\in {\mathcal {O}}_{a_n}^{-\beta } \left( {\overline{{U_{n} (K)}} } \right)\) (inequality above and triangle inequality) holds.
For \(z\in {\mathbb {C}}\setminus K\) and \(\zeta \in {\mathbb {C}}\setminus \{z\}\) we define
and note that \(g(z,\cdot )\in {\mathcal {O}}({\mathbb {C}}\setminus \{z\})\). For \(z\in {\mathbb {C}}\setminus K\) there is \(k=k(z)\in {\mathbb {N}}\) such that
and we obtain
for all \(w\in {\mathbb {B}}_{1/k}(z)\). We deduce that \(g(w,\cdot )\in {\mathcal {O}}_{a_k}^{-\beta }\left(\overline{U_{k}(K)}\right)\) for all \(w\in {\mathbb {B}}_{1/k}(z)\). Moreover, we observe that
for all \(\zeta \in \overline{U_{k}(K)}\). Let \(h\in {\mathbb {C}}\) with \(0<|h|<1/k\). Then
and
for all \(\zeta \in \overline{U_{k}(K)}\). It follows that
for all \(\zeta \in \overline{U_{k}(K)}\), which implies
We conclude that \(\tfrac{\partial }{\partial z}g(z,\cdot )\in {\mathcal {O}}_{a_k}^{-\beta }\left(\overline{U_{k}(K)}\right)\) and \(\tfrac{g(z+h,\cdot )-g(z,\cdot )}{h}\) converges to \(\tfrac{\partial }{\partial z}g(z,\cdot )\) in the space \({\mathcal {O}}_{a_k}^{-\beta }\left(\overline{U_{k}(K)}\right)\) as \(h\rightarrow 0\) by (9). Hence for all \(T\in L({\mathcal {O}}^{-\beta }_{(a_n)}(K),E)\) the limit
exists in E, meaning that \((z\mapsto \frac{1}{2\pi i}\langle T,\frac{e^{(z-\cdot )^2}}{z-\cdot }\rangle )\in {\mathcal {O}}({\mathbb {C}}\setminus K,E)\).
Let us turn to the continuity of \(\varTheta _{K}\). Let \(n\in {\mathbb {N}}\). We note that for \(\zeta _{1},z_{1}\in {\mathbb {R}}\)
It follows that
which yields, in particular, that \(G(S_{n}(K),\cdot )\subset {\mathcal {O}}_{a_{2n}}^{-\beta }\left(\overline{U_{2n}(K)}\right)\). Moreover, there is \(k\in {\mathbb {N}}\) such that
Again, it follows that \(g(S_{n}(K), \cdot )\subset {\mathcal {O}}_{a_m}^{-\beta }\left(\overline{U_{m}(K)}\right)\) with \(m:=\max (2n,k)\). Furthermore, we observe that \(M:=\{g(z,\cdot )e^{a_{n}|{{\,\mathrm{Re}\,}}(z)|^{\beta }}\;|\;z\in S_{n}(K)\}\subset {\mathcal {O}}_{a_m}^{-\beta }\left(\overline{U_{m}(K)}\right)\) and
showing that M is bounded in \({\mathcal {O}}^{-\beta }_{(a_n)}(K)\) by [25, Proposition 25.19, p. 303]. For every \(\alpha \in {\mathfrak {A}}\) and \(T\in L({\mathcal {O}}^{-\beta }_{(a_n)}(K),E)\) we have
and therefore the map \(\varTheta _{K}:L_{b}({\mathcal {O}}^{-\beta }_{(a_n)}(K),E)\rightarrow {\mathcal {O}}^{\beta }_{(a_n)}(\overline{{\mathbb {C}}}\setminus K,E)/{\mathcal {O}}^{\beta }_{(a_n)}(\overline{{\mathbb {C}}},E)\) is well-defined, clearly linear and continuous. \(\square\)
The map \(\varTheta _{K}\) is sometimes called (weighted) Cauchy transformation for obvious reasons (see [26, p. 84]).
Theorem 11
If \(K\subset {\mathbb {R}}\) or \(K\cap \{\pm \infty \}\) has no isolated points in K, then the map
is a topological isomorphism with inverse \(\varTheta _{K}\).
Proof
As before we omit the index K of \(H_{K}\) and \(\varTheta _{K}\) if it is not necessary. As a consequence of Proposition 9 and Proposition 10 the maps H and \(\varTheta\) are linear and continuous. First, we prove that \(\varTheta \circ H={{\,\mathrm{id}\,}}\) on \({\mathcal {O}}^{\beta }_{(a_n)}(\overline{{\mathbb {C}}}\setminus K,E)/{\mathcal {O}}^{\beta }_{(a_n)}(\overline{{\mathbb {C}}},E)\), which implies the injectivity of H. Let \(p\in {\mathbb {N}}\), \(p\ge 2\). We choose \(n\in {\mathbb {N}}\) such that \(\mathrm{d}(S_{p}(K),\overline{U_{n}(K)})>0\). We define the path \(\varGamma _{p}:=\varGamma _{-}-\varGamma _{+}\) with
Further, we choose \(m\in {\mathbb {N}}\) such that \(1/m<\min _{1\le j\le k}r_{j}<1/n\) and \(m>p\) where \(r=(r_{j})_{1\le j\le k}\) is from the path \(\gamma _{K,n,r}\) in the definition of H. Due to this choice \(\varGamma _{\pm }\) and \(\gamma _{K,n,r}\) are within \(S_{m}(K)\).
Let \(f=[F]\in {\mathcal {O}}^{\beta }_{(a_n)}(\overline{{\mathbb {C}}}\setminus K,E)/{\mathcal {O}}^{\beta }_{(a_n)}(\overline{{\mathbb {C}}},E)\) and \(z=x+iy\in S_{p}(K)\). Let \(u\in {\mathbb {R}}\), \(u\ne x\), and \([t_{0},t_{1}]\subset [-p,p]\) such that the path \(\gamma _{u}:[t_{0},t_{1}]\rightarrow {\mathbb {C}}\), \(\gamma _{u}(t):=u+it\), is within \(S_{m}(K)\). The map \(\zeta \mapsto F(\zeta )\frac{e^{-(z-\zeta )^{2}}}{z-\zeta }\) is holomorphic on \({\mathbb {C}}\setminus \{z\}\) with values in E and like in Proposition 8 (a) and (b) we deduce that it is Pettis-integrable along \(\gamma _{u}\) and \({\varGamma _{\pm }}_{\mid [s_{0},s_{1}]}\) with \([s_{0},s_{1}]\subset {\mathbb {R}}\) using [5, Proposition 2, p. 354] and the Mackey-Arens theorem. Then we have
for all \(e'\in E'\). Hence we derive from Cauchy’s integral formula that
for all \(e'\in E'\) and \(z\in S_{p}(K)\). Thus we have
for all \(z\in S_{p}(K)\). By (the proof) of Proposition 10 the function \(g(z,\cdot )=\frac{e^{-(z-\cdot )^{2}}}{z-\cdot } \in {\mathcal {O}}^{-\beta }_{(a_n)}(K)\) for all \(z\in {\mathbb {C}}\setminus K\) and
is an element of \({\mathcal {O}}^{\beta }_{(a_n)} (\overline{{\mathbb {C}}}\setminus K,E)\) since \(T:=H([F])\in L({\mathcal {O}}^{-\beta }_{(a_n)}(K),E)\) by Proposition 9. It follows that
for all \(z\in S_{p}(K)\). But the right-hand side \(W_{p}\) of (11), as a function in z, is weakly holomorphic on \(S_{p}(\varnothing )=\{z\in {\mathbb {C}}\;|\;|{{\,\mathrm{Im}\,}}(z)|<p\}\), which follows from
and differentiation under the integral sign. The weak holomorphy and the sequential completeness of E imply that \(W_{p}\) is holomorphic on \(S_{p}(\varnothing )\) by [10, Corollary 2, p. 404]. Thus W is extended by \(W_{p}\) to a function in \({\mathcal {O}}({\mathbb {C}},E)\) and the extensions for each \(p\in {\mathbb {N}}\) coincide because of the identity theorem. We denote this extension by W as well.
Then we have for \(z=x+iy\in \overline{S_{1/n}}:=\{w\in {\mathbb {C}}\;|\; |{{\,\mathrm{Im}\,}}(w)|\le (1/n)\}\subset S_{2n}(\varnothing )\)
Moreover, in combination with the estimate
we get for all \(\alpha \in {\mathfrak {A}}\)
yielding to
Hence \(W\in {\mathcal {O}}^{\beta }_{(a_n)}(\overline{{\mathbb {C}}},E)\) and thus
i.e. H is injective.
Second, we prove that \(H\circ \varTheta ={{\,\mathrm{id}\,}}\) on \(L({\mathcal {O}}^{-\beta }_{(a_n)}(K),E)\), which implies the surjectivity of H. Due to the Hahn-Banach theorem this is equivalent to the condition that
holds for all \(T\in L({\mathcal {O}}^{-\beta }_{(a_n)}(K),E)\), \(\varphi \in {\mathcal {O}}^{-\beta }_{(a_n)}(K)\) and \(e'\in E'\). As
for all \(T\in L({\mathcal {O}}^{-\beta }_{(a_n)}(K),E)\), \(\varphi \in {\mathcal {O}}^{-\beta }_{(a_n)}(K)\) and \(e'\in E'\), it suffices to show the result for \(E={\mathbb {C}}.\)
Since the span of the set of point evaluations of complex derivatives \(\{\delta _{x_{0}}^{(n)}\;|\; x_{0}\in K\cap {\mathbb {R}},\,n\in {\mathbb {N}}_{0}\}\) is dense in \({\mathcal {O}}^{-\beta }_{(a_n)}(K)_{b}'\) by virtue of Proposition 4 (b), we only need to show that \((H\circ \varTheta )(\delta _{x_{0}}^{(n)})(\varphi ) =\langle \delta _{x_{0}}^{(n)},\varphi \rangle\) for all \(x_{0}\in K\cap {\mathbb {R}}\), \(n\in {\mathbb {N}}_{0}\) and \(\varphi \in {\mathcal {O}}^{-\beta }_{(a_n)}(K)\). Let \(x_{0}\in K\cap {\mathbb {R}}\) and \(n\in {\mathbb {N}}_{0}\). Now, we have
for all \(\varphi \in {\mathcal {O}}_{a_k}^{-\beta } \left(\overline{U_{k}(K)}\right)\), \(k\in {\mathbb {N}}\). Let us take a closer look at the integral on the right-hand side of (12). Let \(m\in {\mathbb {N}}\), \(m\ge 2\). Then \(\frac{e^{-(z-\cdot )^{2}}}{z-\cdot }\in {\mathcal {O}} ({\mathbb {B}}_{1/m}(x_{0}))\) for every \(z\in S_{m}(\{x_{0}\})\). We fix the notation \(g_{z}(\zeta ):=\frac{e^{-(z-\zeta )^{2}}}{z-\zeta }\) for \(z\in S_{m}(\{x_{0}\})\) and \(\zeta \in {\mathbb {B}}_{1/m}(x_{0})\). Then we get by Cauchy’s inequality
for every \(z\in S_{m}(\{x_{0}\})\). We deduce that
implying \((z\mapsto \langle \delta _{x_{0}}^{(n)}, \frac{e^{-(z-\cdot )^{2}}}{z-\cdot }\rangle ) \in {\mathcal {O}}^{\beta }_{(a_n)}(\overline{{\mathbb {C}}}\setminus \{x_{0}\})\). This means that the path of the integral on the right-hand side of (12) can be deformed using Cauchy’s integral theorem (like in Proposition 8 (a) and (b)) and we get with \(s:=\min _{j} r_{j}>0\) for \(r=(r_{j})\)
for all \(\varphi \in {\mathcal {O}}_{a_k}^{-\beta } \left(\overline{U_{k}(K)}\right)\), \(k\in {\mathbb {N}}\). The Laurent series of \(\frac{e^{-(z-\cdot )^{2}}}{z-\cdot }\) in \(\zeta \ne z\) is
and so we have for the nth complex derivative of \(g_{z}\) at \(x_{0}\)
with an entire function \(h(\cdot ,x_{0})\). By Cauchy’s integral theorem and Cauchy’s integral formula for derivatives we have
for all \(\varphi \in {\mathcal {O}}_{a_k}^{-\beta } \left(\overline{U_{k}(K)}\right)\), \(k\in {\mathbb {N}}\). \(\square\)
Remark 12
If \(K\subset {\mathbb {R}}\), then Theorem 11 is also valid for locally complete E because Proposition 8 still holds due to [5, Proposition 2, p. 354].
If \(K\cap \{\pm \infty \}\) has isolated points in K, e.g. \(K=\{+\infty \}\), then we cannot apply the preceding theorem directly since a counterpart for Proposition 4 (b) is missing. However, we can make use of the relation (5) if \({\mathcal {O}}^{-\beta }_{(a_n)}(\overline{{\mathbb {R}}})\) is dense in \({\mathcal {O}}^{-\beta }_{(a_n)}(K)\).
Corollary 13
If \({\mathcal {O}}^{-\beta }_{(a_n)}(\overline{{\mathbb {R}}})\) dense in \({\mathcal {O}}^{-\beta }_{(a_n)}(K)\), then the map
is a topological isomorphism with inverse \(\varTheta _{K}\) and
Proof
\(H_{K}\) and \(\varTheta _{K}\) are well-defined, linear and continuous maps by Proposition 9 and Proposition 10. \(H_{\overline{{\mathbb {R}}}}\) is a topological isomorphism with inverse \(\varTheta _{\overline{{\mathbb {R}}}}\) by Theorem 11. The embedding of \({\mathcal {O}}^{-\beta }_{(a_n)}(\overline{{\mathbb {R}}})\) into \({\mathcal {O}}^{-\beta }_{(a_n)}(K)\) is continuous and dense, hence defines the embedding of \(L({\mathcal {O}}^{-\beta }_{(a_n)}(K),E)\) into \(L({\mathcal {O}}^{-\beta }_{(a_n)}(\overline{{\mathbb {R}}}),E)\) (the density of the first embedding implies the injectivity of the latter one) and we have
by the definition of \(\varTheta _{K}\) and \(\varTheta _{\overline{{\mathbb {R}}}}\). Furthermore, it follows from (5) that
on \({\mathcal {O}}^{-\beta }_{(a_n)}(\overline{{\mathbb {R}}})\). We conclude for every \(f\in {\mathcal {O}}^{\beta }_{(a_n)}(\overline{{\mathbb {C}}}\setminus K,E)/{\mathcal {O}}^{\beta }_{(a_n)}(\overline{{\mathbb {C}}},E)\) that
and for every \(T\in L({\mathcal {O}}^{-\beta }_{(a_n)}(K),E)\) that
by Theorem 11. Thus \(H_{K}\) is bijective and \(\varTheta _{K}\) its inverse. \(\square\)
Remark 14
Under the conditions of Theorem 11 resp. Corollary 13 it follows that \({\mathcal {O}}^{\beta }_{(a_n)}(\overline{{\mathbb {C}}}\setminus K,E)/{\mathcal {O}}^{\beta }_{(a_n)}(\overline{{\mathbb {C}}},E)\) is Hausdorff since E and thus \(L_{b}({\mathcal {O}}^{-\beta }_{(a_n)}(K),E)\) is Hausdorff. In particular, \({\mathcal {O}}^{\beta }_{(a_n)}(\overline{{\mathbb {C}}},E)\) is closed in \({\mathcal {O}}^{\beta }_{(a_n)}(\overline{{\mathbb {C}}}\setminus K,E)\) by [25, Lemma 22.9, p. 254].
Corollary 15
If \((a_{n})_{n\in {\mathbb {N}}}\) is strictly increasing, \(a_{n}<0\) for all \(n\in {\mathbb {N}}\) and \(\lim _{n\rightarrow \infty }a_{n}=0\), then the map
is a topological isomorphism with inverse \(\varTheta _{K}\).
Proof
We only need to prove that the condition of Corollary 13 is fulfilled. Due to [17, Theorem 2.2.1, p. 474] (and its correction in [28, Remark, p. 247-248]) the space \({\mathcal {O}}^{-1}_{(a_n)}(\overline{{\mathbb {R}}})\) is dense in \({\mathcal {O}}^{-1}_{(a_n)}(K)\) (where \({\mathcal {O}}^{-1}_{(a_n)}(\overline{{\mathbb {R}}})\) is called \({\mathscr {P}}_{*}\)). \(\square\)
The isomorphy \({\mathcal {O}}^{1}_{(a_n)}(\overline{{\mathbb {C}}}\setminus K,E)/{\mathcal {O}}^{1}_{(a_n)}(\overline{{\mathbb {C}}},E) \cong L_{b}({\mathcal {O}}^{-1}_{(a_n)}(K),E)\) in Corollary 15 is already known for special cases like \(E={\mathbb {C}}\) [17, Theorem 3.2.1, p. 480] and Fréchet spaces E [15, 3.9 Satz, p. 41] but the proof is of homological nature. In the special case \(K=[a,\infty ]\), \(a\in {\mathbb {R}}\), and \(E={\mathbb {C}}\) the duality was proved in [26, Theorem 3.3, p. 85-86] and served as an initial point to prove Corollary 15 for complete E in [19, 4.1 Theorem, p. 41].
4 \((\varOmega )\) for \({\mathcal {O}}^{\beta }_{(a_n)}\)-spaces on strips with holes
In this section we derive sufficient conditions on K, \((a_n)_{n\in {\mathbb {N}}}\) and \(\beta\) such that \({\mathcal {O}}^{\beta }_{(a_n)}(\overline{{\mathbb {C}}}\setminus K)\) satisfies \((\varOmega )\). The basic idea is to prove that the strong dual \({\mathcal {O}}^{-\beta }_{(a_n)}(K)_{b}'\) satisifies \((\varOmega )\). Then we use the duality \({\mathcal {O}}^{\beta }_{(a_n)}(\overline{{\mathbb {C}}}\setminus K)/{\mathcal {O}}^{\beta }_{(a_n)}(\overline{{\mathbb {C}}}) \cong {\mathcal {O}}^{-\beta }_{(a_n)}(K)_{b}'\) from the preceding section to obtain \((\varOmega )\) for \({\mathcal {O}}^{\beta }_{(a_n)}(\overline{{\mathbb {C}}}\setminus K)\). Let us recall that a Fréchet space F with an increasing fundamental system of seminorms \(({\left| \!\left| \!\left| {\cdot }\right| \!\right| \!\right| }_{k})_{k\in {\mathbb {N}}}\) satisfies \((\varOmega )\) by [25, Chap. 29, Definition, p. 367] if
where \(U_{k}:=\{x\in F \; | \; {\left| \!\left| \!\left| {x}\right| \!\right| \!\right| }_{k}\le 1\}\).
We start with a helpful observation concerning the inductive limit \({\mathcal {O}}^{-\beta }_{(a_n)}(K)\), namely, that the choice of the sequence \((1/n)_{n\in {\mathbb {N}}}\) for the neighbourhoods \(U_{n}(K)=U_{1/(1/n)}(K)\) is irrelevant.
Remark 16
Let \((c_{n})_{n\in {\mathbb {N}}}\) be a strictly decreasing sequence in \({\mathbb {R}}\) with \(c_{n}\le 1\) for all \(n\in {\mathbb {N}}\) and \(\lim _{n\to \infty }c_{n}=0\). For \(n\in {\mathbb {N}}\) let
where
and the spectral maps for \(n,k\in {\mathbb {N}}\), \(n\le k\), be given by the restrictions
Then
Proof
It follows directly from Proposition 4 (a) and [9, 4.2 Satz, p. 122]. \(\square\)
We recall an equivalent description of the property \((\varOmega )\). By [25, Lemma 29.13, p. 369] a Fréchet space F with an increasing fundamental system of seminorms \(({\left| \!\left| \!\left| {\cdot }\right| \!\right| \!\right| }_{k})_{k\in {\mathbb {N}}}\) satisfies \((\varOmega )\) if and only if
holds where
is the dual norm.
Lemma 17
There is a strictly decreasing sequence \((c_{n})_{n\in {\mathbb {N}}}\) in \({\mathbb {R}}\) with \(c_{n}\le 1\) for all \(n\in {\mathbb {N}}\) and \(\lim _{n\to \infty }c_{n}=0\) such that
with \(\theta :=\frac{\ln (c_{p}/c_{q})}{\ln (c_{p}/c_{k})}\).
Proof
Let \(c_{n}:=\exp (1/a_{n})\) for all \(n\in {\mathbb {N}}\) if \(a_{n}<0\) for all \(n\in {\mathbb {N}}\) and \(c_{n}:=\exp (-a_{n})\) for all \(n\in {\mathbb {N}}\) if \(a_{n}\ge 0\) for all \(n\in {\mathbb {N}}\). Then \((c_{n})_{n\in {\mathbb {N}}}\) is a strictly decreasing sequence, \(c_{n}\le 1\) for all \(n\in {\mathbb {N}}\) and \(\lim _{n\to \infty }c_{n}=0\). Let \(p,q,k\in {\mathbb {N}}\) such that \(p<q<k\) and \(\theta :=\frac{\ln (c_{p}/c_{q})}{\ln (c_{p}/c_{k})}\). Let \(\zeta \in {\mathbb {R}}\) with \(|\zeta |\ge 1+c_{k}^{-1}\). For \(z\in {\mathbb {C}}\) with \(|z-\zeta |\le c_{n}\), \(n\in \{p,q,k\}\), we deduce from the inequalities
and
that
and
if \(a_{n}<0\), as well as
and
if \(a_{n}\ge 0\). Now, we only need to prove that there is \(C>0\) such that
resp.
If \(a_{n}<0\), we observe that
and, if \(a_{n}\ge 0\), that
What remains to be shown is that
because then we are done with \(C:=\exp (|a_{q}|(c_{p}+c_{q})^{\beta })\). If \(a_{n}<0\), then
and (15) is equivalent to
which holds if and only if
as \(a_{q}(a_{k}-a_{p})<0\). Since \(a_{k}-a_{q}>0\) and \(a_{q}-a_{p}>0\), this is equivalent to
which is true. If \(a_{n}\ge 0\), then
and (15) is equivalent to
which holds, as \(a_{k}-a_{p}>0\), if and only if
\(\square\)
We note that \(\theta\) in the lemma above fulfils \(0<\theta <1\) and state the following improvement of [19, 5.21 Lemma, p. 88].
Lemma 18
The following assertions hold.
-
(a)
$$\begin{aligned}&\forall \; p,q,k\in {\mathbb {N}},\,p<q<k\;\exists \; 0<\theta <1,\,C>0\; \forall \;f\in {\mathcal {O}}_{a_p}^{-\beta }\left(\overline{U_{1/c_{p}}(K)}\right):\\&\qquad \Vert f\Vert _{q,c_{q}}\le C\Vert f\Vert ^{1-\theta }_{p,c_{p}} \Vert f\Vert ^{\theta }_{k,c_{k}} \end{aligned}$$
with \(c_{n}\) from Lemma 17 if \(K\cap \{\pm \infty \}\ne \varnothing\) resp. \(c_{n}:=1/n\), \(n\in {\mathbb {N}}\), if \(K\subset {\mathbb {R}}\).
-
(b)
\({\mathcal {O}}^{-\beta }_{(a_n)}(K)_{b}'\) satisfies \((\varOmega )\).
Proof
(a) Let \(p,q,k\in {\mathbb {N}}\), \(p<q<k\), and \(f\in {\mathcal {O}}_{a_p}^{-\beta }\left(\overline{U_{1/c_{p}}(K)}\right)\). Considering the components of \(U_{1/c_{p}}(K)\) we have to distinguish three different cases.
(i) Let \(Z_{p}\) be a bounded component of \(U_{1/c_{p}}(K)\). By Remark 6 (a) there are only finitely many components \(Z_{q}\) of \(U_{1/c_{q}}(K)\) with \(Z_{q}\subset Z_{p}\). For every such component \(Z_{q}\) we choose \(\zeta \in Z_{q}\cap K\), which exists since \(Z_{q}\) is bounded. Let \(Z_{k}\) be the (unique) component of \(U_{1/c_{k}}(K)\) which contains \(\zeta\). \(Z_{p}\) is a proper simply connected subset of \({\mathbb {C}}\). Thus there exists a biholomorphic map \(\widetilde{\psi }:Z_{p}\rightarrow {\mathbb {B}}_{1}(0)\) with \(\widetilde{\psi }(\zeta )=0\) due to the Riemann mapping theorem (and Möbius transformation). In addition, \(Z_{p}\) and \({\mathbb {B}}_{1}(0)\) are Jordan domains (for the definition see [1, 2.8.5 Lemma, p. 193, 1.8.5 Jordan Curve Theorem, p. 68]) and so there exists a homeomorphism \(\psi :\overline{Z_{p}}\rightarrow \overline{{\mathbb {B}}_{1}(0)}\) such that \(\psi _{\mid Z_{p}}=\widetilde{\psi }\) by [1, 2.8.8 Theorem (Caratheodory), p. 195]. Since \(\psi (\overline{Z_{q}})\subset \psi (Z_{p})={\mathbb {B}}_{1}(0)\) and \(\psi (\overline{Z_{q}})\) is compact, as \(\overline{Z_{q}}\) is compact and \(\psi\) continuous, there is \(0<r_{q}<1\) such that \(\psi (\overline{Z_{q}})\subset \overline{{\mathbb {B}}_{r_{q}}(0)}\). Moreover, there exists \(0<r_{k}<r_{q}\) such that \(\overline{{\mathbb {B}}_{r_{k}}(0)}\subset \psi (Z_{k})\) since \(0\in \psi (Z_{k})\), \(\psi (Z_{k})\) is open by the open mapping theorem (from complex analysis) and \(\psi (Z_{k})\subset \psi (Z_{q})\). The function \(u:=f\circ (\psi ^{-1})\) is holomorphic on \({\mathbb {B}}_{1}(0)\) and continuous on \(\overline{{\mathbb {B}}_{1}(0)}\), in particular, |u| is subharmonic on \({\mathbb {B}}_{1}(0)\) and continuous on \(\overline{{\mathbb {B}}_{1}(0)}\). Setting
we obtain by virtue of [1, 4.4.32 Proposition (Hadamard’s Three Circles Theorem), p. 338]
and hence
with \(\theta :=\frac{\ln (1/r_{q})}{\ln (1/r_{k})}\). We note that \(0<\theta <1\) because \(0<r_{k}<r_{q}<1\). By the maximum principle we have
as well as
and therefore
(ii) Let \(K\cap \{\pm \infty \}\ne \varnothing\). Let \(Z_{p}\) be an unbounded component of \(U_{1/c_{p}}(K)\), w.l.o.g. the real part of \(Z_{p}\) is bounded from below and unbounded from above. Let \(\zeta \in {\mathbb {R}}\) such that \(\zeta \ge 1+c_{k}^{-1}\). Then we have \(\overline{{\mathbb {B}}_{c_{j}}(\zeta )}\subset ([c_{j}^{-1}, \infty )+i[-c_{j},c_{j}])\) for \(j\in \{p,q,k\}\) since \(c_{p}^{-1}<c_{q}^{-1}<c_{k}^{-1}\) and \(c_{j}\le 1\). Applying Hadamard’s Three Circles Theorem to \(u:=|f|\), we get \(M(c_{q})\le M(c_{k})^{\theta }M(c_{p})^{1-\theta }\) with \(\theta :=\frac{\ln (c_{p}/c_{q})}{\ln (c_{p}/c_{k})}\) fulfilling \(0<\theta <1\). Like in (i) we obtain
and
Due to Lemma 17 there is \(C_{2}>0\), independent of \(\zeta\), such that
and thus
(iii) Let \(K\cap \{\pm \infty \}\ne \varnothing\) and \(Z_{p}\) be w.l.o.g. like in (ii). We define \(\widetilde{Z}_{p}:=Z_{p}\cap ((-\infty ,1+c_{k}^{-1})+i{\mathbb {R}})\). By Remark 6 (a) there are only finitely many components \(\widetilde{Z}_{q}\) of \(U_{1/c_{q}}(K)\cap ((-\infty ,1+c_{k}^{-1})+i{\mathbb {R}})\) with \(\widetilde{Z}_{q}\subset \widetilde{Z}_{p}\). For every such component \(\widetilde{Z}_{q}\) we choose \(\zeta \in \widetilde{Z}_{q}\cap (K\cup \{x\in {\mathbb {R}}\;|\;x>c_{k}^{-1}\})\). Let \(\widetilde{Z}_{k}\) be the (unique) component of \(U_{1/c_{k}}(K)\cap ((-\infty ,1+c_{k}^{-1})+i{\mathbb {R}})\) which contains \(\zeta\). The rest is analogous to (i) and thus there are \(\widetilde{C}_{0}\), \(\widetilde{C}_{1}>0\) and \(0<\theta <1\) such that
(iv) First, let us remark the following. Let B be a set, \(B_{0}\subset B\), \(0<\theta _{0}<\theta _{1}<1\), \(h:B_{0} \rightarrow [0,\infty )\), \(g:B\rightarrow [0,\infty )\) and \(h\le g\) on \(B_{0}\). Then
Now, we take the minimum of all the \(\theta\)s which appear in (i)-(iii). There are finitely many of them and denote their minimum again with \(\theta\). Take the maximum of the constants \(\frac{C_{1}}{C_{0}}\), \(C_{2}\) and \(\frac{\widetilde{C}_{1}}{\widetilde{C}_{0}}\) which appear in (i)-(iii). There are again finitely many of them and denote their maximum with C. We apply the remark above to \(B_{0}:=\overline{U_{1/c_{k}}(K)}\), \(B:=\overline{U_{1/c_{p}}(K)}\), \(h(z):=|f(z)|e^{-a_{k}|{{\,\mathrm{Re}\,}}(z)|^{\beta }}\) and \(g(z):=|f(z)|e^{-a_{p}|{{\,\mathrm{Re}\,}}(z)|^{\beta }}\). Then we deduce from (16), (17) and (18) that
(b) We recall Remark 16 and identify both inductive limits. Let \(p\in {\mathbb {N}}\) and choose \(q\in {\mathbb {N}}\), \(q>p\). Let \(k\in {\mathbb {N}}\). If \(k\le p\), then we get for any \(0<\theta <1\) and all \(y\in ({\mathcal {O}}^{-\beta }_{(a_n)}(K)_{b}')'\) by definition of the dual norm
Let \(k>p\). If \(k\le q\), we have for any \(0<\theta <1\) and all \(y\in ({\mathcal {O}}^{-\beta }_{(a_n)}(K)_{b}')'\) by definition of the dual norm
Let \(k>q\) and \(y\in ({\mathcal {O}}^{-\beta }_{(a_n)}(K)_{b}')'\). If \(\Vert y\Vert ^{*}_{p,c_{p}}=\infty\), then (14) is obviously fulfilled. Let \(\Vert y\Vert ^{*}_{p,c_{p}}<\infty\). As \({\mathcal {O}}^{-\beta }_{(a_n)}(K)\) is a DFS-space by Proposition 4 (a), the sets
are a fundamental system of bounded sets of \({\mathcal {O}}^{-\beta }_{(a_n)}(K)\) by [25, Proposition 25.19, p. 303] and hence the seminorms
form a fundamental system of seminorms of \({\mathcal {O}}^{-\beta }_{(a_n)}(K)_{b}'\). Furthermore, \({\mathcal {O}}^{-\beta }_{(a_n)}(K)\) is reflexive and thus there is a unique \(f\in {\mathcal {O}}^{-\beta }_{(a_n)}(K)\) such that \(y(x)=x(f)\) for all \(x\in {\mathcal {O}}^{-\beta }_{(a_n)}(K)'\). Then we obtain by [25, Proposition 22.14, p. 256] for all \(n\in {\mathbb {N}}\), \(n\ge p\),
In particular, this means that \(\{t>0\;|\;f\in tB_{n}\}\ne \varnothing\) and thus we have \(f\in {\mathcal {O}}_{a_n}^{-\beta }\left(\overline{U_{1/c_{n}}(K)}\right)\) as well as
for all \(n\ge p\). So by part (a), there are \(C>0\) and \(0<\theta <1\), only depending on p, q and k, such that
\(\square\)
The idea to use Hadamard’s Three Circles Theorem in the proof of Lemma 18 (a) is taken from the proof of [30, Lemma 5.2 (a)(3), p. 263-264]. If \(K\subset {\mathbb {R}}\) is non-empty and compact, Lemma 18 (b) is already known. Indeed, the space \({\mathcal {O}}({\mathbb {C}}\setminus K)\) satisfies \((\varOmega )\) by [31, Proposition 2.5 (b), p. 173] and thus the quotient space \({\mathcal {O}}({\mathbb {C}}\setminus K)/{\mathcal {O}}({\mathbb {C}})\) as well by [25, Lemma 29.11 (2), p. 368]. Since \((\varOmega )\) is a linear-topological invariant by [25, Lemma 29.11 (1), p. 368], it follows from \({\mathcal {O}}^{-\beta }_{(a_n)}(K)_{b}'\cong {\mathscr {A}}(K)_{b}' \cong {\mathcal {O}}({\mathbb {C}}\setminus K)/{\mathcal {O}}({\mathbb {C}})\) by (2) that \({\mathcal {O}}^{-\beta }_{(a_n)}(K)_{b}'\) also satisfies \((\varOmega )\). Combining our duality result with the preceding lemma, we get a generalisation of [19, 5.22 Theorem, p. 92].
Corollary 19
If
-
(i)
\(K\subset {\mathbb {R}}\), or \(K\cap \{\pm \infty \}\) has no isolated points in K, or
-
(ii)
K is arbitrary, \(a_{n}< 0\) for all \(n\in {\mathbb {N}}\), \(\lim _{n\to \infty }a_{n}=0\) and \(\beta =1\),
then \({\mathcal {O}}^{\beta }_{(a_n)}(\overline{{\mathbb {C}}}\setminus K)\) satisfies \((\varOmega )\).
Proof
The spaces \({\mathcal {O}}^{\beta }_{(a_n)}(\overline{{\mathbb {C}}}\setminus K)\) and \({\mathcal {O}}^{\beta }_{(a_n)}(\overline{{\mathbb {C}}})\) are Fréchet spaces which is easily checked (similar to [20, 3.7 Proposition, p. 240]). By Theorem 11 in (i) resp. Corollary 15 in (ii) \({\mathcal {O}}^{\beta }_{(a_n)}(\overline{{\mathbb {C}}}\setminus K)/{\mathcal {O}}^{\beta }_{(a_n)}(\overline{{\mathbb {C}}})\) is topologically isomorphic to \({\mathcal {O}}^{-\beta }_{(a_n)}(K)_{b}'\), in particular, the quotient is a Fréchet space as \({\mathcal {O}}^{-\beta }_{(a_n)}(K)\) is a DFS-space by Proposition 4 (a). Since \((\varOmega )\) is a linear-topological invariant by [25, Lemma 29.11 (1), p. 368], \({\mathcal {O}}^{\beta }_{(a_n)}(\overline{{\mathbb {C}}}\setminus K)/{\mathcal {O}}^{\beta }_{(a_n)}(\overline{{\mathbb {C}}})\) satisfies \((\varOmega )\) due to Lemma 18 (b). The sequence
is an exact sequence of Fréchet spaces where i means the inclusion and q the quotient map. \({\mathcal {O}}^{\beta }_{(a_n)}(\overline{{\mathbb {C}}})\) satisfies \((\varOmega )\) by [22, Corollary 14, p. 18] combined with Assumption 3 (iii)+(iv) and \({\mathcal {O}}^{\beta }_{(a_n)}(\overline{{\mathbb {C}}}\setminus K)/{\mathcal {O}}^{\beta }_{(a_n)}(\overline{{\mathbb {C}}})\) as well, thus \({\mathcal {O}}^{\beta }_{(a_n)}(\overline{{\mathbb {C}}}\setminus K)\) by [33, 1.7 Lemma, p. 230], too. \(\square\)
5 Surjectivity of the Cauchy-Riemann operator
In our last section we prove our main result on the surjectivity of the Cauchy-Riemann operator on \({\mathcal {E}}^{\beta }_{(a_n)} (\overline{{\mathbb {C}}}\setminus K,E)\). This is done by using the results obtained so far and splitting theory. We recall that a Fréchet space \((F,({\left| \!\left| \!\left| {\cdot }\right| \!\right| \!\right| }_{k})_{k\in {\mathbb {N}}})\) satisfies (DN) by [25, Chap. 29, Definition, p. 359] if
A PLS-space is a projective limit \(X = \lim\limits_{\substack{\longleftarrow\\N\in\mathbb{N}}} X_{N}\), where the \(X_{N} = \lim\limits_{\substack{\longrightarrow\\N\in\mathbb{N}}}\left( {X_{{N,n}} ,\left| {\left| {\left| \cdot \right|} \right|} \right|_{{N,n}} } \right)\) are DFS-spaces, and it satisfies (PA) if
where \({\left| \!\left| \!\left| {\cdot }\right| \!\right| \!\right| }^{*}\) denotes the dual norm of \({\left| \!\left| \!\left| {\cdot }\right| \!\right| \!\right| }\) and \(i^{M}_{N}\), \(i^{K}_{N}\) the linking maps (see [4, Sect. 4, Eq. (24), p. 577]).
Theorem 20
Let \((a_{n})_{n\in {\mathbb {N}}}\) be strictly increasing, \(a_{n}<0\) for all \(n\in {\mathbb {N}}\) and \(\lim _{n\to \infty }a_{n}=0\). If
-
(i)
\(K\subset {\mathbb {R}}\), or \(K\cap \{\pm \infty \}\) has no isolated points in K, or
-
(ii)
K is arbitrary and \(\beta =1\),
and
-
(a)
\(E:=F_{b}'\) where F is a Fréchet space over \({\mathbb {C}}\) satisfying (DN), or
-
(b)
E is an ultrabornological PLS-space over \({\mathbb {C}}\) satisfying (PA),
then
is surjective.
Proof
We only need to check that the conditions of Theorem 1 are fulfilled. \({\mathcal {E}}^{\beta }_{(a_n)}(\overline{{\mathbb {C}}}\setminus K)\) is nuclear, in particular a Schwartz space, and thus its subspace \({\mathcal {E}}^{\beta }_{(a_n),\overline{\partial }}(\overline{{\mathbb {C}}}\setminus K)\) as well by [21, Theorem 3.1, p. 188], [21, 2.8 Example (ii), p. 179], [21, Remark 2.7, p. 178-179] and [21, Remark 2.3 (b), p. 177]. Furthermore, \({\mathcal {E}}^{\beta }_{(a_n),\overline{\partial }}(\overline{{\mathbb {C}}}\setminus K) ={\mathcal {O}}^{\beta }_{(a_n)}(\overline{{\mathbb {C}}}\setminus K)\) by Remark 2. Due to Corollary 19 the space \({\mathcal {O}}^{\beta }_{(a_n)}(\overline{{\mathbb {C}}}\setminus K)\) satisfies \((\varOmega )\). The Cauchy-Riemann operator \(\overline{\partial } :{\mathcal {E}}^{\beta }_{(a_n)}(\overline{{\mathbb {C}}}\setminus K) \rightarrow {\mathcal {E}}^{\beta }_{(a_n)}(\overline{{\mathbb {C}}}\setminus K)\) in the \({\mathbb {C}}\)-valued case is surjective by [23, Corollary 5.6, p. 27] which follows from [23, Example 5.7 (a), p. 27-28] in the case that \(K\subset {\mathbb {R}}\) or \(K\cap \{\pm \infty \}\) has no isolated points in K. If \(K\cap \{\pm \infty \}\) has isolated points in K, then the proof that the conditions of [23, Corollary 5.6, p. 27] are fulfilled is verbatim as in [23, Example 5.7 (a), p. 27-28]. Hence all conditions of Theorem 1 are fulfilled. \(\square\)
Theorem 20, together with [22, Corollary 18, p. 21] (\(K=\varnothing\)), generalises [19, 5.24 Theorem, p. 95] which is case (ii) above.
References
Berenstein, C.A., Gay, R.: Complex variables. In: Graduate Texts in Mathematics, vol. 125. Springer, New York (1991) https://doi.org/10.1007/978-1-4612-3024-3
Bierstedt, K.D., Gramsch, B., Meise, R.: Lokalkonvexe Garben und gewichtete induktive Limites \({\mathfrak{F}}\)-morpher Funktionen. In: J. Blatter, J.B. Prolla, W. Rueß (eds.) Function spaces and dense approximation (Proc., Bonn, 1974), Bonner Math. Schriften 81, pp. 59–72. Inst. Angew. Math., Univ. Bonn, Bonn (1975)
Bonet, J., Domański, P.: Parameter dependence of solutions of differential equations on spaces of distributions and the splitting of short exact sequences. J. Funct. Anal. 230(2), 329–381 (2006). https://doi.org/10.1016/j.jfa.2005.06.007
Bonet, J., Domański, P.: The splitting of exact sequences of PLS-spaces and smooth dependence of solutions of linear partial differential equations. Adv. Math. 217, 561–585 (2008). https://doi.org/10.1016/j.aim.2007.07.010
Bonet, J., Jordá, E., Maestre, M.: Vector-valued meromorphic functions. Arch. Math. (Basel) 79(5), 353–359 (2002). https://doi.org/10.1007/PL00012457
Dierolf, B.: Splitting theory for PLH spaces. Ph.D. thesis, Universität Trier (2014). https://doi.org/10.25353/ubtr-xxxx-4b2b-53a5
Dierolf, B., Sieg, D.: Splitting and parameter dependence in the category of PLH spaces. RACSAM Rev. R. Acad. Cienc. Exactas Fís. Nat. Ser. A Mat 113(1), 59–93 (2019). https://doi.org/10.1007/s13398-017-0424-5
Domański, P., Langenbruch, M.: Vector valued hyperfunctions and boundary values of vector valued harmonic and holomorphic functions. Publ. RIMS, Kyoto Univ 44(4), 1097–1142 (2008). https://doi.org/10.2977/prims/1231263781
Floret, K., Wloka, J.: Einführung in die Theorie der lokalkonvexen Räume. Lecture Notes in Math, vol. 56. Springer, Berlin (1968)
Grosse-Erdmann, K.G.: A weak criterion for vector-valued holomorphy. Math. Proc. Camb. Phil. Soc. 136(2), 399–411 (2004). https://doi.org/10.1017/S0305004103007254
Grothendieck, A.: Sur certains espaces de fonctions holomorphes. I. J. Reine Angew. Math. 192, 35–64 (1953). https://doi.org/10.1515/crll.1953.192.35
Grothendieck, A.: Produits Tensoriels Topologiques et Espaces Nucléaires, Mem. Amer. Math. Soc., vol. 16, 4th edn. AMS, Providence (1966). https://doi.org/10.1090/memo/0016
Ion, P.D.F., Kawai, T.: Theory of vector-valued hyperfunctions. Publ. RIMS Kyoto Univ. 11, 1–19 (1975)
Ito, Y., Nagamachi, S.: Theory of \(H\)-valued Fourier hyperfunctions. Proc. Japan Acad. Ser. A Math. Sci 51(7), 558–561 (1975). https://doi.org/10.3792/pja/1195518523
Junker, K.: Vektorwertige Fourierhyperfunktionen und ein Satz vom Bochner-Schwartz-Typ. Ph.D. thesis, Universität Düsseldorf (1979)
Kalmes, T.: Surjectivity of differential operators and linear topological invariants for spaces of zero solutions. Rev. Mat. Complut. 32, 37–55 (2019). https://doi.org/10.1007/s13163-018-0266-5
Kawai, T.: On the theory of Fourier hyperfunctions and its applications to partial differential equations with constant coefficients. J. Fac. Sci. Univ. Tokyo, Sect. I A 17, 467–517 (1970)
Köthe, G.: Topological Vector Spaces I. Grundlehren Math. Wiss, vol. 159. Springer, Berlin (1969). https://doi.org/10.1007/978-3-642-64988-2
Kruse, K.: Vector-valued Fourier hyperfunctions. Ph.D. thesis, Universität Oldenburg (2014)
Kruse, K.: The approximation property for weighted spaces of differentiable functions. In: M. Kosek (ed.) Function Spaces XII (Proc., Kraków, 2018), Banach Center Publ., vol. 119, pp. 233–258. Inst. Math., Polish Acad. Sci., Warszawa (2019). https://doi.org/10.4064/bc119-14
Kruse, K.: On the nuclearity of weighted spaces of smooth functions. Ann. Polon. Math. 124(2), 173–196 (2020). https://doi.org/10.4064/ap190728-17-11
Kruse, K.: Parameter dependence of solutions of the Cauchy-Riemann equation on spaces of weighted smooth functions. RACSAM Rev. R. Acad. Cienc. Exactas Fís. Nat. Ser. A Mat 114(3), 1–24 (2020). https://doi.org/10.1007/s13398-020-00863-x
Kruse, K.: Surjectivity of the \(\overline{\partial }\)-operator between weighted spaces of smooth vector-valued functions. Complex Var. Elliptic Equ. pp. 1–32 (2021). https://doi.org/10.1080/17476933.2021.1945587
Langenbruch, M.: Asymptotic Fourier and Laplace transformations for hyperfunctions. Studia Math. 205(1), 41–69 (2011). https://doi.org/10.4064/sm205-1-4
Meise, R., Vogt, D.: Introduction to functional analysis. Oxford Graduate Texts in Mathematics, vol. 2. Clarendon Press, Oxford (1997)
Morimoto, M.: Analytic functionals with non-compact carrier. Tokyo J. Math. 1(1), 77–103 (1978). https://doi.org/10.3836/tjm/1270216594
Morimoto, M.: An Introduction to Satos Hyperfunctions. Translations of Mathematical Monographs, vol. 129. AMS, Providence (1992)
Saburi, Y.: Fundamental properties of modified Fourier hyperfunctions. Tokyo J. Math. 8(1), 231–273 (1985). https://doi.org/10.3836/tjm/1270151582
Sebastião e Silva, J.: As funções analíticas e a análise funcional. Port. Math. 9(1–2), 1–130 (1950)
Vogt, D.: Charakterisierung der Unterräume eines nuklearen stabilen Potenzreihenraumes von endlichem Typ. Studia Math. 71(3), 251–270 (1982). https://doi.org/10.4064/sm-71-3-251-270
Vogt, D.: On the solvability of \(P(D)f=g\) for vector valued functions. In: H. Komatsu (ed.) Generalized Functions and Linear Differential Equations VIII (Proc., Kyoto, 1982), RIMS Kôkyûroku, vol. 508, pp. 168–181. RIMS, Kyoto (1983)
Vogt, D.: On the functors \(\text{ Ext}^{1}(E, F)\) for Fréchet spaces. Studia Math. 85(2), 163–197 (1987). https://doi.org/10.4064/sm-85-2-163-197
Vogt, D., Wagner, M.J.: Charakterisierung der Quotientenräume von \(s\) und eine Vermutung von Martineau. Studia Math. 67(3), 225–240 (1980). https://doi.org/10.4064/sm-67-3-225-240
Acknowledgements
The present paper is a generalisation of parts of Chapter 4 and 5 of the author’s PhD thesis [19], written under the supervision of M. Langenbruch. The author is deeply grateful to him for his support and advice. Further, it is worth to mention that some of the results appearing in the PhD thesis and thus their generalised counterparts in this work are essentially due to him.
Funding
Open Access funding enabled and organized by Projekt DEAL.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Kruse, K. The inhomogeneous Cauchy-Riemann equation for weighted smooth vector-valued functions on strips with holes. Collect. Math. 74, 81–112 (2023). https://doi.org/10.1007/s13348-021-00337-2
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s13348-021-00337-2