1 Introduction

The theory of the neural network (NN) operators arise since 1992 with the pioneer work of Cardaliaguet and Euvrard [15], and then in the next years, they have been largely studied by several authors under different aspects, see, e.g., [12, 13, 32, 33]; the main advantage of the above theory lies on its connection with the artificial neural networks and their applications to Approximation Theory. For a complete overview concerning applications of neural networks and learning theory, see, e.g., the very complete monograph of Cucker and Zhou [29], and also [9, 37, 42, 43, 46,47,48,49, 53, 56].

A generalization to the \(L^p\)-setting of the above NN operators has been proved in [21]; here, the authors showed that any multivariate \(L^p\)-data can be approximated in the \(L^p\)-norm by means of the NN operators of the Kantorovich-type. However, even if their natural settings are the \(L^p\)-spaces, the above operators converge also pointwise and uniformly when continuous functions are considered.

Such operators are called “of Kantorovich-type”, since their coefficients are defined by means of suitable averages of the functions f that is approximated.

Usually, the activation functions of the NN operators are a sigmodal function ([30]); the reason is that a sigmoidal curve allows to simulate the two states of the biological neurons, that are, the activated and the non-activated ones, see, e.g., [9, 38, 39, 44].

Recently, also a new unbounded activation functions has been investigated, that is the so-called ReLu (rectified linear unit) activation function, defined by the positive part of x, for every \(x \in {\mathbb {R}}\). The ReLu activation function has a linear grow as x goes to \(+\infty \) and it revealed to be very suitable in order to train deep (i.e., the multi-layers) neural networks, see, e.g., [31, 51].

Due to its definition, it is easy to show that the ReLu activation function can be used to express the well-known ramp (or cut) sigmoidal function (see [36]); furthermore, it is also well known that the ramp function can be considered as the activation function in the NN operators. Then, the above relation implies that also the ReLu activation function can be used in NN operators.

The main purpose of this paper is to study the pointwise rate of approximation for the NN operators of the Kantorovich type. The above aim is pursuit by adopting the following strategy: first of all, an asymptotic expansion for the above operators is established, and then, a Voronovskaja type theorem is proved.

The asymptotic formula allows to expand the above approximation operators, when they are evaluated for a sufficiently smooth functions f, in terms of derivatives of the approximated function f evaluated at suitable nodes. A central role in the asymptotic expansion is played by the truncated algebraic moments of the density functions \(\phi _{\sigma }\left( x\right) \); the density function is generated by suitable sigmoidal functions and it can be considered as the kernel of the operators.

The asymptotic formula can be used to prove a Voronovskaja-type theorem (see, e.g., [6,7,8]), from which we establish the rate of pointwise approximation of the operators under investigation.

In general, Voronovskaja formulas are widely studied in Approximation Theory (see, e.g., [4, 10, 34, 54]), both from the qualitative and quantitative point of view (see, e.g., [1, 50]), also for their relations with the saturation phenomenon for families of linear operators (see [27, 35]).

Furthermore, to improve the above convergence results and to obtain a family of NN operators with an higher order of approximation, here, we also considered suitable families of finite linear combination of the above NN operators of the Kantorovich type. Also for these families of operators, we derive asymptotic and Voronovskaja type formulas, following the same steps above described.

Finally, we discuss in details several examples of sigmoidal functions for which the above results hold. In particular, we consider the cases of the logistic and the hyperbolic tangent sigmoidal functions, which are of crucial importance in the theory of learning artificial neural networks, and the case of the sigmoidal functions generated by the central B-splines, which are useful to construct high-order convergence NN operators.

2 Notations and Preliminary Results

In this paper, we denote by \(C\left( I\right) \) the space of all functions \(f\,:\,I\rightarrow {\mathbb {R}}\) which are continuous on \(I:=\left[ -1,1\right] \) and we denote by \(C^{r}\left( I\right) \), \(r\in {\mathbb {N}}^{+}\) the space of functions of \(C\left( I\right) \) which have continuous derivative \(f^{\left( s\right) }\) on I, for every \(1\le s\le r,\,s\in {\mathbb {N}}^{+}.\) The above spaces will be considered endowed by the usual max-norm \(\left\| \cdot \right\| _{\infty }\). Now, denoting by \(\Phi \,:\,{\mathbb {R}}\rightarrow {\mathbb {R}}\) a given function, we can recall the following definitions.

Definition 1

Let \(h \in {\mathbb {N}}\) be fixed. We define the truncated algebraic moment of \(\Phi \) order h, by:

$$\begin{aligned} m_{h}^{n}\left( \Phi ,u\right) :=\sum _{k=-n}^{n-1}\Phi \left( u-k\right) \left( k-u\right) ^{h},\,\,\,u\in {\mathbb {R}}, \end{aligned}$$
(1)

for every \(n\in {\mathbb {N}}^{+}.\)

Definition 2

Let \(h \ge 0\) be fixed. We call discrete absolute moment of \(\Phi \) of order h what follows:

$$\begin{aligned} M_{h}\left( \Phi \right) :=\sup _{u\in {\mathbb {R}}}\sum _{k\in {\mathbb {Z}}}\left| \Phi \left( u-k\right) \right| \left| u-k\right| ^{h}. \end{aligned}$$

The discrete absolute moments of a given function are widely used tools very useful to establish the convergence of families of linear operators, see, e.g., [6, 7, 55].

It is well known that, if \(\Phi \) is bounded on \({\mathbb {R}}\) and has a sufficiently fast decay to 0 as \(x\rightarrow \pm \infty \), then \(M_{h}\left( \phi \right) <+\infty \), for suitable h, see, e.g., [19].

Now, we recall the definition of sigmoidal function (see, e.g., [26, 30]).

Definition 3

Let \(\sigma \,:\,{\mathbb {R}}\rightarrow {\mathbb {R}}\) be a measurable function. We call \(\sigma \) a sigmoidal function if:

$$\begin{aligned} \lim _{x\rightarrow -\infty }\sigma \left( x\right) =0,\ \ \ \ \ \ \ \ \ \ \mathrm {and}\ \ \ \ \ \ \ \ \ \ \lim _{x\rightarrow +\infty }\sigma \left( x\right) =1. \end{aligned}$$

In what follows, we consider non-decreasing sigmoidal functions \(\sigma \) which satisfy the following conditions:

(\(\Sigma \)1):

\(\sigma \left( x\right) -1/2\) is an odd function;

(\(\Sigma \)2):

\(\sigma \in C^{2}\left( {\mathbb {R}}\right) \) is concave for \(x\ge 0\);

(\(\Sigma \)3):

\(\sigma \left( x\right) =O\left( \left| x\right| ^{-\alpha -1}\right) \) as \(x\rightarrow -\infty \) for some \(\alpha >0\).

We now recall the definition of the following density function:

$$\begin{aligned} \phi _{\sigma }\left( x\right) :=\frac{1}{2}\left[ \sigma \left( x+1\right) -\sigma \left( x-1\right) \right] ,\,x\in {\mathbb {R}}. \end{aligned}$$

The following lemma summarize some useful properties of the function \(\phi _{\sigma }\).

Lemma 4

(i) \(\phi _{\sigma }\left( x\right) \ge 0\) for every \(x\in {\mathbb {R}}\), with \(\phi _{\sigma }\left( 2\right) >0\), and moreover, \(\lim _{x\rightarrow \pm \infty }\phi _{\sigma }\left( x\right) =0\);

(ii) \(\phi _{\sigma }\left( x\right) \) is an even function;

(iii) \(\phi _{\sigma }\left( x\right) \) is non-decreasing for \(x<0\) and non-increasing for \(x\ge 0\);

(iv) \(\phi _{\sigma }\left( x\right) =O\left( \left| x\right| ^{-1-\alpha }\right) \) as \(x\rightarrow \pm \infty \) where \(\alpha \) is the positive constant of condition \(\left( \Sigma 3\right) \);

(v) Let \(x\in I\) and \(n\in {\mathbb {N}}^{+}.\) Then:

$$\begin{aligned} m_{0}^{n}\left( \phi _{\sigma },nx\right) =\sum _{k=-n}^{n-1}\phi _{\sigma }\left( nx-k\right) \ge \phi _{\sigma }\left( 2\right) >0. \end{aligned}$$

Furthermore, if \(\sigma \) is a sigmoidal function which satisfies \(\left( \Sigma 3\right) \) for \(\alpha >r,\) for some \(r\in {\mathbb {N}}^{+}\), then:

(vi) \(M_{h}\left( \phi _{\sigma }\right) <+\infty \), for every \(0\le h \le r\);

(vii) for every fixed \(\gamma >0\), it turns out that:

$$\begin{aligned} \lim _{n\rightarrow +\infty }\sum _{\left| u-k\right| >\gamma n}\phi _{\sigma }\left( u-k\right) \left| u-k\right| ^{h}=0, \end{aligned}$$

uniformly with respect to \(u\in {\mathbb {R}},\) for every \(0\le h \le r;\)

(viii) the sequences \(\left( m_{h}^{n}\left( \phi _{\sigma },u\right) _{n}\right) _{n\in {\mathbb {N}}^{+}}\) of the truncated algebraic moments of order h are equibounded on \({\mathbb {R}}\), for every \(h=0,1,\dots ,r.\)

Remark 5

Note that, if we remove condition \((\Sigma 2)\) on \(\sigma \), and we assume directly that \(\phi _{\sigma }\) satisfies assertion (iii) of Lemma 4, the theory still holds, see, e.g., [25]. The consequence of the above observation is that, we can apply the above theory to \(C^2\) as well as to non-smooth sigmoidal functions, such that the corresponding \(\phi _{\sigma }\) satisfies (iii) of Lemma 4, and \(\phi _{\sigma }(2)>0\).

For a proof of the properties \(\left( i\right) \) - \(\left( v\right) \) see [24]; for the properties \(\left( vi\right) \) - \(\left( viii\right) \), see Lemma 2.6 of [28].

Now, we recall the definition of the NN operators of the Kantorovich type.

Definition 6

Let \(f\,:\,I\rightarrow {\mathbb {R}}\) be a locally integrable function. The Kantorovich-type NN operators \(K_{n}\left( f,\cdot \right) \), activated by a sigmoidal function \(\sigma \), and acting on f, are defined by:

$$\begin{aligned} K_{n}\left( f,x\right) :=\frac{{\displaystyle \sum _{k=-n}^{n-1}\phi _{\sigma }\left( nx-k\right) n \int _{k/n}^{\left( k+1\right) /n}f\left( u\right) du}}{{\displaystyle \sum _{k=-n}^{n-1}\phi _{\sigma }\left( nx-k\right) }},\,x\in I. \end{aligned}$$
(2)

Clearly, for every \(n\in {\mathbb {N}}^{+}\) and \(k\in {\mathbb {Z}}\) such that \(-n\le k\le n-1\), it turns out that \(-1\le \frac{k}{n}<\frac{k+1}{n}\le 1\); the latter inequality, together with condition \(\left( v\right) \) of Lemma 4, implies that the operators are well defined, e.g., in case of locally integrable and bounded functions on I. Furthermore, it turns out that:

$$\begin{aligned} \left| K_{n}\left( f,x\right) \right| \le \left\| f\right\| _{\infty }, \end{aligned}$$

for all \(x\in I\).

Remark 7

It is well known that (see, e.g., [21]) the family \(K_{n}\left( f,\cdot \right) \) converges pointwise at each point of continuity of any bounded f. The convergence turns out to be uniform on I if f is continuous on the whole I.

3 Asymptotic Formulas for the NN Operators of the Kantorovich Type

The main aim of this section is to study the order of pointwise approximation for the operators \(K_{n}\) by means of Voronovskaja type theorem.

From now on, when we refer to a sigmoidal function \(\sigma \), we always consider a sigmoidal function \(\sigma \) satisfying conditions \((\Sigma 1)\), \((\Sigma 2)\), and \((\Sigma 3)\) introduced in Sect. 2.

We begin establishing the following asymptotic expansion for the operators \(K_{n}\).

Theorem 8

Let \(\sigma \) be a sigmoidal function witch satisfies assumption \(\left( \Sigma 3\right) \) with \(\alpha >r,\) for some \(r\in {\mathbb {N}}^{+}\). Moreover, let \(f\in C^{r}\left( I\right) \) be fixed. Then, the following asymptotic formula holds:

$$\begin{aligned}&K_{n}\left( f,x\right) =f\left( x\right) +\sum _{\nu =1}^{r}\frac{f^{\left( \nu \right) }\left( x\right) }{\nu !n^{\nu }}\sum _{h=0}^{\nu }\genfrac(){0.0pt}0{\nu }{h}\frac{m_{h}^{n}\left( \phi _{\sigma },nx\right) }{\left( \nu -h+1\right) m_{0}^{n}\left( \phi _{\sigma },nx\right) }+o\left( n^{-r}\right) ,\\&\quad n \rightarrow \infty , \end{aligned}$$

for every \(x\in I\), where \(m_{0}^{n}\left( \phi _{\sigma },nx\right) >0\), for every \(x\in I\), and \(n\in {\mathbb {N}}^{+}\).

Proof

From the local Taylor formula (for details, see, e.g., [8, p. 283]), we have:

$$\begin{aligned} f\left( u\right) =\sum _{\nu =0}^{r}\frac{f^{\left( \nu \right) }\left( x\right) }{\nu !}\left( u-x\right) ^{\nu }+h\left( u-x\right) \left( u-x\right) ^{r} \end{aligned}$$

for every \(x,u\in I\), where \(h\left( y\right) \) is a suitable boundedFootnote 1 function, such that \(h\left( y\right) \rightarrow 0\) as \(y\rightarrow 0\). Then, for every fixed \(x\in I\), we can write what follows:

$$\begin{aligned} K_{n}\left( f,x\right) =&\frac{{\displaystyle \sum _{k=-n}^{n-1}\phi _{\sigma }\left( nx-k\right) n \int _{k/n}^{\left( k+1\right) /n}f\left( u\right) du}}{{\displaystyle \sum _{k=-n}^{n-1}\phi _{\sigma }\left( nx-k\right) }}\\ =&\frac{{\displaystyle \sum _{k=-n}^{n-1}\phi _{\sigma }\left( nx-k\right) n \int _{k/n}^{\left( k+1\right) /n}\left[ \sum _{\nu =0}^{r}\frac{f^{\left( \nu \right) }\left( x\right) }{\nu !}\left( u-x\right) ^{\nu }\right] du}}{{\displaystyle \sum _{k=-n}^{n-1}\phi _{\sigma }\left( nx-k\right) }}\\&+ \frac{{\displaystyle \sum _{k=-n}^{n-1}\phi _{\sigma }\left( nx-k\right) n \int _{k/n}^{\left( k+1\right) /n}\left[ h\left( u-x\right) \left( u-x\right) ^{r}\right] du}}{{\displaystyle \sum _{k=-n}^{n-1}\phi _{\sigma }\left( nx-k\right) }}\\ =:&I_{1}+I_{2}. \end{aligned}$$

Let us analyze the term \(I_{1}\). Using the binomial theorem and recalling that \({\displaystyle {\displaystyle \sum _{k=-n}^{n-1}\phi _{\sigma }\left( nx-k\right) }}=m_{0}^{n}\left( \phi _{\sigma },nx\right) \), we have that:

$$\begin{aligned} I_{1}=&\left[ \sum _{k=-n}^{n-1}\phi _{\sigma }\left( nx-k\right) n \sum _{\nu =0}^{r}\frac{f^{\left( \nu \right) }\left( x\right) }{\nu !}\int _{k/n}^{\left( k+1\right) /n}\left( u-x\right) ^{\nu }du\right] \frac{{\displaystyle 1}}{{\displaystyle m_{0}^{n}\left( \phi _{\sigma },nx\right) }}\\ =&\left[ \sum _{k=-n}^{n-1}\phi _{\sigma }\left( nx-k\right) n \sum _{\nu =0}^{r}\frac{f^{\left( \nu \right) }\left( x\right) }{\nu !}\right. \\&\left. \int _{k/n}^{\left( k+1\right) /n}\left( u-k/n+k/n-x\right) ^{\nu }du\right] \frac{{\displaystyle 1}}{{\displaystyle m_{0}^{n}\left( \phi _{\sigma },nx\right) }}\\ =&\left[ \sum _{k=-n}^{n-1}\phi _{\sigma }\left( nx-k\right) n \sum _{\nu =0}^{r}\frac{f^{\left( \nu \right) }\left( x\right) }{\nu !}\sum _{h=0}^{\nu }\genfrac(){0.0pt}0{\nu }{h}\left( k/n-x\right) ^{h}\right. \\&\left. \int _{k/n}^{\left( k+1\right) /n}\left( u-k/n\right) ^{\nu -h}du\right] \frac{{\displaystyle 1}}{{\displaystyle m_{0}^{n}\left( \phi _{\sigma },nx\right) }}, \end{aligned}$$

so

$$\begin{aligned} I_{1}=&\frac{1}{m_{0}^{n}\left( \phi _{\sigma },nx\right) }\sum _{k=-n}^{n-1} \phi _{\sigma }\left( nx-k\right) \sum _{\nu =0}^{r}\frac{f^{\left( \nu \right) }\left( x\right) }{\nu !}\sum _{h=0}^{\nu }\genfrac(){0.0pt}0{\nu }{h}\frac{\left( k/n-x\right) ^{h}}{\left( \nu -h+1\right) n^{\nu -h}}\\ =&\frac{1}{m_{0}^{n}\left( \phi _{\sigma },nx\right) }\sum _{\nu =0}^{r}\frac{f^{\left( \nu \right) }\left( x\right) }{\nu !n^{\nu }}\sum _{h=0}^{\nu }\genfrac(){0.0pt}0{\nu }{h}\frac{1}{\nu -h+1}\sum _{k=-n}^{n-1}\left( k-nx\right) ^{h}\phi _{\sigma }\left( nx-k\right) \\ =&\sum _{\nu =0}^{r}\frac{f^{\left( \nu \right) }\left( x\right) }{\nu !n^{\nu }}\sum _{h=0}^{\nu }\genfrac(){0.0pt}0{\nu }{h}\frac{m_{h}^{n}\left( \phi _{\sigma },nx\right) }{\left( \nu -h+1\right) m_{0}^{n}\left( \phi _{\sigma },nx\right) }. \end{aligned}$$

Now, let us analyze the term \(I_{2}\). Let \(\varepsilon >0\) be fixed. Since \(h\left( y\right) \rightarrow 0\) as \(y\rightarrow 0\), then there exists a \(\gamma >0\), such that \(\left| h\left( y\right) \right| <\varepsilon \) if \(\left| y\right| \le \gamma .\) Hence, we can write:

$$\begin{aligned} I_{2}=&\frac{1}{m_{0}^{n}\left( \phi _{\sigma },nx\right) }\sum _{\underset{{\scriptstyle \left| nx-k\right| <\gamma n/2}}{k=-n}}^{n-1}\phi _{\sigma }\left( nx-k\right) n \int _{k/n}^{\left( k+1\right) /n}h\left( u-x\right) \left( u-x\right) ^{r}du\\&+ \frac{1}{m_{0}^{n}\left( \phi _{\sigma },nx\right) }\sum _{\underset{{\scriptstyle \left| nx-k\right| \ge \gamma n/2}}{k=-n}}^{n-1}\phi _{\sigma }\left( nx-k\right) n \int _{k/n}^{\left( k+1\right) /n}h\left( u-x\right) \left( u-x\right) ^{r}du\\ =&I_{2,1}+I_{2,2}. \end{aligned}$$

As concerns \(I_{2,1}\), we observe that, if \(u\in \left[ k/n,\left( k+1\right) /n\right] \), we have:

$$\begin{aligned} \left| u-x\right| \le \left| u-k/n\right| +\left| x-k/n\right| \le 1/n+\gamma /2<\gamma \end{aligned}$$

for every sufficiently large n, and hence:

$$\begin{aligned} \left| I_{2,1}\right| \le&\frac{\varepsilon }{m_{0}^{n}\left( \phi _{\sigma },nx\right) }\sum _{\underset{{\scriptstyle \left| nx-k\right|<\gamma n/2}}{k=-n}}^{n-1} \phi _{\sigma }\left( nx-k\right) n \int _{k/n}^{\left( k+1\right) /n}\left| u-x\right| ^{r}du\\ \le&\frac{\varepsilon }{m_{0}^{n}\left( \phi _{\sigma },nx\right) }\sum _{\underset{{\scriptstyle \left| nx-k\right| <\gamma n/2}}{k=-n}}^{n-1}\phi _{\sigma }\left( nx-k\right) n \\&\int _{k/n}^{\left( k+1\right) /n}\sum _{m=0}^{r}\left( {\begin{array}{c}r\\ m\end{array}}\right) \left( u-k/n\right) ^{r-m}\left| k/n-x\right| ^{m}du\\ \le&\frac{\varepsilon }{m_{0}^{n}\left( \phi _{\sigma },nx\right) n^{r}}\sum _{k=-n}^{n-1}\sum _{m=0}^{r}\left( {\begin{array}{c}r\\ m\end{array}}\right) \frac{\left| k-nx\right| ^{m}}{r-m+1}\phi _{\sigma }\left( nx-k\right) \\ \le&\frac{\varepsilon }{m_{0}^{n}\left( \phi _{\sigma },nx\right) n^{r}}\sum _{m=0}^{r}\left( {\begin{array}{c}r\\ m\end{array}}\right) \frac{M_{m}\left( \phi _{\sigma }\right) }{r-m+1}. \end{aligned}$$

We now consider \(I_{2,2}\). By the boundedness of \(h\left( y\right) \) and arguing as in \(I_{2,1}\), we get:

$$\begin{aligned} \left| I_{2,2}\right| \le&\frac{\left\| h\right\| _{\infty }}{m_{0}^{n}\left( \phi _{\sigma },nx\right) }\sum _{\underset{{\scriptstyle \left| nx-k\right| \ge \gamma n/2}}{k=-n}}^{n-1}\phi _{\sigma }\left( nx-k\right) n \int _{k/n}^{\left( k+1\right) /n}\left| u-x\right| ^{r}du\\ \le&\frac{\left\| h\right\| _{\infty }}{m_{0}^{n}\left( \phi _{\sigma },nx\right) n^{r}}\sum _{m=0}^{r}\left( {\begin{array}{c}r\\ m\end{array}}\right) \frac{1}{r-m+1}\sum _{\underset{{\scriptstyle \left| nx-k\right| \ge \gamma n/2}}{k=-n}}^{n-1}\phi _{\sigma }\left( nx-k\right) \left| k-nx\right| ^{m}\\ \le&\frac{\left\| h\right\| _{\infty }}{m_{0}^{n}\left( \phi _{\sigma },nx\right) n^{r}}\frac{2^{r+1}-1}{r+1}\max _{m=0,\dots ,r} \sum _{\left| nx-k\right| \ge \gamma n/2} \phi _{\sigma }\left( nx-k\right) \left| k-nx\right| ^{m}\\ \le&\frac{\left\| h\right\| _{\infty }}{m_{0}^{n}\left( \phi _{\sigma },nx\right) n^{r}}\frac{2^{r+1}-1}{r+1}\varepsilon \end{aligned}$$

for n sufficiently large, by the property \(\left( vii\right) \) of Lemma 4, and the trivial identity:

$$\begin{aligned} {\displaystyle \sum _{m=0}^{r}\left( {\begin{array}{c}r\\ m\end{array}}\right) \frac{x^{r-m+1}}{r-m+1}=\frac{\left( 1+x\right) ^{r+1}-1}{r+1}}. \end{aligned}$$

This concludes the proof. \(\square \)

As a consequence of the previous result, we can prove the following Voronovskaja type theorem.

Theorem 9

Let \(\sigma \) be a sigmoidal function which satisfies assumption \(\left( \Sigma 3\right) \) with \(\alpha >1\). Suppose that, for every \(x\in {\mathbb {R}}\):

$$\begin{aligned} m_{h}^{n}\left( \phi _{\sigma },x\right) =m_{h}+o\left( n^{-\theta _{h}}\right) ,\,n\rightarrow +\infty ,\,h=0,1, \end{aligned}$$
(3)

where \(m_{h}\in {\mathbb {R}}\), \(\theta _{h}>0,\) \(h=0,1\), and the “o-term” tends to zero uniformly with respect to \(x\in {\mathbb {R}}\). Then, for any \(f\in C^{1}\left( I\right) \), we have:

$$\begin{aligned} \lim _{n\rightarrow +\infty }n\left[ K_{n}\left( f,x\right) -f\left( x\right) \right] =f^{\prime }\left( x\right) \left( \frac{1}{2}+\frac{m_{1}}{m_{0}}\right) , \end{aligned}$$

where \(m_{0}>0\) in view of Lemma 4\(\left( v\right) \).

Proof

From the asymptotic formula of Theorem 8, we have:

$$\begin{aligned} n\left[ K_{n}\left( f,x\right) -f\left( x\right) \right] =&n\left[ \frac{f^{\prime }\left( x\right) }{n}\left( \frac{1}{2}+\frac{m_{1}+o\left( n^{-\theta _{1}}\right) }{m_{0}+o\left( n^{-\theta _{0}}\right) }\right) +o\left( n^{-1}\right) \right] , \end{aligned}$$

and the result follows taking the limit as \(n\rightarrow +\infty \). \(\square \)

Remark 10

The previous theorem shows that the order of pointwise approximation by means of the Kantorovich NN operators is at least of order \(O\left( n^{-1}\right) \) when \(n\rightarrow +\infty \) and \(f\in C^{1}\left( I\right) \).

Moreover, we can observe that, under the assumption of Theorem 9, it is not hard to show that, if \(f\in C^{1}\left( I\right) \), we have:

$$\begin{aligned} \left\| K_{n}\left( f,\cdot \right) -f\left( \cdot \right) \right\| _{\infty }=O\left( n^{-1}\right) \end{aligned}$$

as \(n\rightarrow +\infty \).

Thus, it seems clear that the best possible order of uniform approximation that can be achieved by the operators \(K_{n}\) is O(1/n), as \(n \rightarrow + \infty \). This shows that, in general, a better order of approximation cannot be obtained; indeed, in the main examples of sigmoidal functions (see Section 5 below) \(m_{1}=0\), then the limit of Theorem 9 gives the exact order of approximation. The order is also less rapid than that achieved in case of the classical NN operators, (see [28]), that is \(O(1/n^{2})\), as \(n \rightarrow +\infty \).

4 High-Order Convergence of NN Operators of the Kantorovich Type

To construct NN operators of the Kantorovich type with higher order of approximation than \(K_{n}\), we adopt the following strategy.

Let \(r \in {\mathbb {N}}^{+},\,r>1\) and \(\alpha _{j}\in {\mathbb {R}}\setminus \left\{ 0\right\} ,\,j=1,\dots ,r\) fixed, such that:

$$\begin{aligned} \sum _{j=1}^{r}\alpha _{j}=1. \end{aligned}$$
(4)

Let us define:

$$\begin{aligned} {\mathcal {K}}_{n}^{r}\left( f,x\right) :=\sum _{j=1}^{r}\alpha _{j}K_{nj}\left( f,x\right) ,\,x\in I, \end{aligned}$$

where f is any bounded locally integrable function. It is clear that condition (4) is such that \({\mathcal {K}}_{n}^{r}\) preserves the approximation properties of \(K_{n}\).

Obviously, also in this section, when we refer to \(\sigma \), we always consider sigmoidal functions satisfying \((\sigma i)\), \(i=1, 2, 3\).

Now, we can prove the following asymptotic and Voronovskaja type formula for \({\mathcal {K}}_{n}^{r}\).

Theorem 11

Let \(\sigma \) be a sigmoidal function which satisfies assumption \(\left( \Sigma 3\right) \) with \(\alpha>r>1\), for some \(r\in {\mathbb {N}}^{+}\). Moreover, let \(f\in C^{r}\left( I\right) \) be fixed. Then:

$$\begin{aligned}&{\mathcal {K}}_{n}^{r}\left( f,x\right) =f\left( x\right) +\sum _{\nu =1}^{r}\frac{f^{\left( \nu \right) }\left( x\right) }{\nu !n^{\nu }}\sum _{h=0}^{\nu }\genfrac(){0.0pt}0{\nu }{h}\frac{1}{\nu -h+1}\sum _{j=1}^{r}\frac{\alpha _{j}}{j^{\nu }}\frac{m_{h}^{nj}\left( \phi _{\sigma },njx\right) }{m_{0}^{nj}\left( \phi _{\sigma },njx\right) }\nonumber \\&\quad +o\left( n^{-r}\right) , \end{aligned}$$
(5)

as \(n \rightarrow + \infty \) and for every \(x \in I\). Furthermore, if we suppose that:

$$\begin{aligned} m_{h}^{n}\left( \phi _{\sigma },x\right) =m_{h},\,h=0,\dots ,r \end{aligned}$$
(6)

for \(n\in {\mathbb {N}}^{+}\) sufficiently large, where \(m_{h}\in {\mathbb {R}}\), such that \(\alpha _{j},\,j=1,\dots ,r\) satisfies the following linear algebraic system:

$$\begin{aligned} \sum _{j=1}^{r}\alpha _{j}=1,\,\,\,\,\,\,\,\,\ \ \ \ \ \ \ \ \ \ \ \ \ \ \sum _{j=1}^{r}\frac{\alpha _{j}}{j^{\nu }}=0,\ \ \ \ \ \ \ \ \ \nu =1,\dots ,r-1 \end{aligned}$$
(7)

then

$$\begin{aligned} \lim _{n\rightarrow +\infty }n^{r}\left[ {\mathcal {K}}_{n}^{r}\left( f,x\right) -f\left( x\right) \right] =\frac{f^{\left( r\right) }\left( x\right) }{r!}\sum _{h=0}^{r}\genfrac(){0.0pt}0{r}{h}\frac{1}{r-h+1}\frac{m_{h}}{m_{0}}\sum _{j=1}^{r}\frac{\alpha _{j}}{j^{r}}. \end{aligned}$$
(8)

Proof

We simply observe that, proceeding as in Theorem 8, we can write:

$$\begin{aligned} {\mathcal {K}}_{n}^{r}\left( f,x\right) =&\sum _{j=1}^{r}\alpha _{j}K_{nj}\left( f,x\right) \\ =&\sum _{j=1}^{r}\alpha _{j}\left( \frac{{\displaystyle \sum _{k=-nj}^{nj-1}\phi _{\sigma }\left( njx-k\right) nj \int _{k/\left( nj\right) }^{\left( k+1\right) /\left( nj\right) }f\left( u\right) du}}{{\displaystyle \sum _{k=-nj}^{nj-1}\phi _{\sigma }\left( njx-k\right) }}\right) \\ =&\sum _{j=1}^{r}\alpha _{j}\left( f\left( x\right) +\sum _{\nu =1}^{r}\frac{f^{\left( \nu \right) }\left( x\right) }{\nu !n^{\nu }j^{\nu }}\sum _{h=0}^{\nu }\genfrac(){0.0pt}0{\nu }{h}\frac{1}{\nu -h+1}\frac{m_{h}^{nj}\left( \phi _{\sigma },njx\right) }{m_{0}^{nj}\left( \phi _{\sigma },njx\right) }\right) \\&+ \sum _{j=1}^{r}\alpha _{j}\left( \frac{{\displaystyle \sum _{k=-nj}^{nj-1}\phi _{\sigma }\left( njx-k\right) nj \int _{k/\left( nj\right) }^{\left( k+1\right) /\left( nj\right) }\left[ h\left( u-x\right) \left( u-x\right) ^{r}\right] du}}{{\displaystyle m_{0}^{nj}\left( \phi _{\sigma },njx\right) }}\right) ; \end{aligned}$$

hence, the asymptotic formula (5) follows arguing as for \(I_{2,1}\) and \(I_{2,2,}\) in the proof of Theorem 8. Now, to prove the second part of the theorem, it is sufficient to observe that, under the additional assumptions on the truncated algebraic moments, we have:

$$\begin{aligned} {\mathcal {K}}_{n}^{r}\left( f,x\right) -f\left( x\right) =&\sum _{\nu =1}^{r}\frac{f^{\left( \nu \right) }\left( x\right) }{\nu !n^{\nu }}\sum _{h=0}^{\nu }\genfrac(){0.0pt}0{\nu }{h}\frac{1}{\nu -h+1}\frac{m_{h}}{m_{0}}\sum _{j=1}^{r}\frac{\alpha _{j}}{j^{\nu }}+o\left( n^{-r}\right) \\ =&\frac{f^{\left( r\right) }\left( x\right) }{r!n^{r}}\sum _{h=0}^{r}\genfrac(){0.0pt}0{r}{h}\frac{1}{r-h+1}\frac{m_{h}}{m_{0}}\sum _{j=1}^{r}\frac{\alpha _{j}}{j^{r}}+o\left( n^{-r}\right) \end{aligned}$$

for \(n\in {\mathbb {N}}^{+}\) sufficiently large, \(x\in I\). Then:

$$\begin{aligned} n^{r}\left[ {\mathcal {K}}_{n}^{r}\left( f,x\right) -f\left( x\right) \right] = \frac{f^{\left( r\right) }\left( x\right) }{r!}\sum _{h=0}^{r}\genfrac(){0.0pt}0{r}{h}\frac{1}{r-h+1}\frac{m_{h}}{m_{0}}\sum _{j=1}^{r}\frac{\alpha _{j}}{j^{r}}+n^{r}o\left( n^{-r}\right) \nonumber \\ \end{aligned}$$
(9)

and passing to the limit as \(n\rightarrow +\infty \), the proof of the Voronovskaja formula (8) follows. \(\square \)

The previous theorem shows that the order of pointwise approximation by the NN operators \({\mathcal {K}}_{n}^{r}\left( f,x\right) \) is at least \(O\left( n^{-r}\right) \) as \(n\rightarrow +\infty \) when functions that belong to \(C^{r}\left( I\right) ,\,r \in {\mathbb {N}}\) are approximated. Again, it is quite simple to observe that, under the assumption of Theorem 11 and for \(f\in C^{r}\left( I \right) \), we have:

$$\begin{aligned} \left\| {\mathcal {K}}_{n}^{r}\left( f,\cdot \right) -f\left( \cdot \right) \right\| _{\infty }=O\left( n^{-r}\right) \end{aligned}$$

as \(n\rightarrow +\infty \).

5 Applications to Special Cases

In this section, we discuss the results proved above for some concrete cases of sigmoidal functions.

5.1 Applications with the Logistic Function

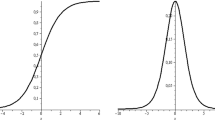
First of all, we consider the case of the Kantorovich NN type operators activated by the well-known logistic function (see, e.g., [20, 40, 41] and Fig. 1):

$$\begin{aligned} \sigma _{\ell }\left( x\right) :=\left( 1+e^{-x}\right) ^{-1},\,x\in {\mathbb {R}}. \end{aligned}$$

NN operators activated by logistic functions have been widely studied, e.g., in [12, 32].

Obviously, \(\sigma _{\ell }\) is a smooth function and it satisfies all the assumptions \(\left( \Sigma i\right) ,\,i=1,2,3.\) Furthermore, by its exponential decay to zero as \(x\rightarrow -\infty ,\) condition \(\left( \Sigma 3\right) \) is satisfied for every \(\alpha >0\). Hence, it turns out that \(M_{h}\left( \phi _{\sigma _{\ell }}\right) <+\infty \) for every \(h \ge 0\) in view of Lemma 4, (vi). The above function is very useful in the theory of artificial neural network, since it is used as activation function in neuronal models when training algorithms would applied, see, e.g., [14, 16, 45, 48, 52].

Fig. 1
figure 1

The logistic function \(\sigma _{\ell }\left( x\right) \) (left) and the corresponding density function \(\phi _{\sigma _{\ell }}\left( x\right) \) (right)

Full size image

Now, to apply the results proved in the previous sections, the truncated algebraic moments of the function \(\phi _{\sigma _{\ell }}\left( x\right) \) must be computed. In general, it is possible to compute the truncated algebraic moments of a given function exploiting a well-known result of Fourier analysis, i.e., the so-called Poisson summation formula (see, e.g., [11]). In particular, since \(\left( \Sigma 3\right) \) holds for every \(\alpha >0\), by Lemma 4 (iv), we have that \(\phi _{\sigma _{\ell }} \in L^{1}\left( {\mathbb {R}} \right) \), and then, the usual \(L^{1}\)-Fourier transform can be used to apply the above mentioned Poisson summation formula. In particular, following the procedure given in [28], it turns out that \(\phi _{\sigma _{\ell }}\) satisfies assumption (3) with \(m_{0}=1\), \(m_{1}=0\) and \(\theta _{0},\theta _{1}>1\). Then, from Theorem 9, we can obtain what follows.

Corollary 12

Let \(\sigma _{\ell }\left( x\right) \) be the logistic function, and \(f\in C^{1}\left( I\right) \) be fixed. Then, for every \(x\in I,\) we have:

$$\begin{aligned} \lim _{n\rightarrow +\infty }n\left[ K_{n}^{\sigma _{\ell }}\left( f,x\right) -f\left( x\right) \right] =\frac{f^{\prime }\left( x\right) }{2}. \end{aligned}$$

Moreover, \(\phi _{\sigma _{\ell }}\left( x\right) \) does not satisfy assumption (6) of Theorem 11, which, hence, cannot be used to construct the operators \({\mathcal {K}}_{n}^{r}\).

5.2 Applications with Hyperbolic Tangent Sigmoidal Function

In this section, we study the case of the Kantorovich NN type operators activated by the well-known hyperbolic tangent sigmoidal function (see, e.g., [25]):

$$\begin{aligned} \sigma _{h}\left( x\right) :=\frac{\tanh \left( x\right) +1}{2},\,x\in {\mathbb {R}}. \end{aligned}$$

The graph of \(\sigma _{h}\left( x\right) \) together with its density function \(\phi _{h}\left( x\right) \) is plotted in Fig. 2.

Fig. 2
figure 2

The hyperbolic tangent sigmoidal function\(\sigma _{h}\left( x\right) \) (left) and the corresponding density function \(\phi _{\sigma _{h}}\left( x\right) \) (right)

Full size image

The NN operators activated by the hyperbolic tangent sigmoidal functions have been widely studied, see, e.g., [22, 23, 33]. Again, we can observe that \(\sigma _{h}\) is a smooth function that satisfies \(\left( \Sigma i\right) ,\,i=1,2,3\), it tends to zero exponentially as \(x\rightarrow -\infty \), and so \(\left( \Sigma 3\right) \) holds for all \(\alpha >0\). Now, computing again the truncated algebraic moments of \(\phi _{\sigma _{h}}\) using the Poisson summation formula (as in the case of logistic function), it turns out that \(m_{0}=1\), \(m_{1}=0\), and \(\theta _{0},\theta _{1}>1\) (see [28] again). Hence, we can obtain the following corollary.

Corollary 13

Let \(\sigma _{h}\left( x\right) \) be the hyperbolic tangent sigmoidal function, and \(f\in C^{1}\left( I\right) \) be fixed. Then, for every \(x\in I,\) we have:

$$\begin{aligned} \lim _{n\rightarrow +\infty }n\left[ K_{n}^{\sigma _{h}}\left( f,x\right) -f\left( x\right) \right] =\frac{f^{\prime }\left( x\right) }{2}. \end{aligned}$$

Also in this case, assumption (6) of Theorem 11 is not satisfied.

To provide examples of sigmoidal functions useful to construct high-order NN type operators, we can consider what follows.

5.3 Applications with Sigmoidal Functions Generated by B-splines

In [22], the well-known central B-splines of order \(d\ge 1\), defined by (see, e.g., [5, 17, 19, 27, 31]):

$$\begin{aligned} M_{d}\left( x\right) :=\frac{1}{\left( d-1\right) !}\sum _{i=0}^{d}\left( -1\right) ^{i}\genfrac(){0.0pt}0{d}{i}\left( \frac{d}{2}+x-i\right) _{+}^{d-1},\,x\in {\mathbb {R}}, \end{aligned}$$

have been used to introduce a class of sigmoidal functions. Here, \(\left( x\right) _{+}:=\max \left\{ x,0\right\} \) denotes the “positive part” of \(x\in {\mathbb {R}}\). The sigmoidal function \(\sigma _{M_{d}}\left( x\right) \) associated with the central B-spline \(M_{d}\), is defined by the following formula:

$$\begin{aligned} \sigma _{M_{d}}\left( x\right) :=\int _{-\infty }^{x}M_{d}\left( t\right) dt,\,x\in {\mathbb {R}}. \end{aligned}$$

Consequently, the corresponding density function has the following expression:

$$\begin{aligned} \phi _{\sigma _{M_{d}}}\left( x\right) :=\frac{1}{2}\int _{x-1}^{x+1}M_{d}\left( t\right) dt,\,x\in {\mathbb {R}} . \end{aligned}$$
(10)

By simple computations it is easy to prove that, also for \(\sigma _{M_{d}}\), assumptions \(\left( \Sigma i\right) ,\,i=1,2,3\) are satisfied. In particular, since the central B-splines have compact support, then \(\left( \Sigma 3\right) \) is satisfied by \(\sigma _{M_{d}}\left( x\right) \) for every \(\alpha >0\). Exploiting the relation (10), it is easy to obtain that:

$$\begin{aligned} m_{h}^{n}\left( \phi _{\sigma _{M_{d}}},x\right) =\frac{1}{2}\sum _{j=0}^{h}\genfrac(){0.0pt}0{h}{j}\frac{\gamma _{j}^{d}}{h-j+1}\left[ 1-\left( -1\right) ^{h-j+1}\right] , \end{aligned}$$

where

$$\begin{aligned} \gamma _{j}^{d}:=m_{j}^{n}\left( M_{d},x\right) =i^{-j}\frac{d^{j}}{dx^{j}}\left( \frac{\sin \left( \frac{x}{2}\right) ^{d}}{\left( \frac{x}{2}\right) ^{d}}\right) (0),\,j \in {\mathbb {N}} \end{aligned}$$

with i the imaginary unit, then, for n sufficiently large, we obtain that \(m_{0}^{n}\left( \phi _{\sigma _{M_{d}}},x\right) =1\) and \(m_{1}^{n}\left( \phi _{\sigma _{M_{d}}},x\right) =0\). Hence:

Corollary 14

Let \(\sigma _{M_{d}}\left( x\right) ,\,d\in {\mathbb {N}}^{+},\) be the sigmoidal function generated by the central B-spline \(M_{d}\left( x\right) \), and \(f\in C^{1}\left( I\right) \) be fixed. Then, for every \(x\in I,\) we have:

$$\begin{aligned} \lim _{n\rightarrow +\infty }n\left[ K_{n}^{\sigma _{M_{d}}}\left( f,x\right) -f\left( x\right) \right] =\frac{f^{\prime }\left( x\right) }{2}. \end{aligned}$$

Remark 15

As showed in Remark 5, the previous results still hold also in case of the well-known (not differentiable) ramp function:

$$\begin{aligned} \sigma _R(x)\, :=\, \left\{ \begin{array}{l} 0, \quad \quad \quad x<-3/2\\ x/3 + 1/2, \quad -3/2 \le x \le 3/2,\\ 1, \quad \quad \quad x > 3/2, \end{array} \right. \end{aligned}$$

since the corresponding density function satisfies the condition (iii) of Lemma 4.

Note that (see [18, 26]) the sigmoidal function \(\sigma _{M_1}(3\, \cdot )\) coincides with the ramp function \(\sigma _R\). Then, if we recall the definition of the well-known ReLu activation function (see, e.g., [36]):

$$\begin{aligned} \psi _{ReLu}(x)\ :=\ (x)_+, \quad \quad x \in {\mathbb {R}}, \end{aligned}$$

it turns out that:

$$\begin{aligned} \sigma _{M_1}(3\, x)\ :=\ \psi _{ReLu}(3\, x+1/2)-\psi _{ReLu}(3\, x-1/2), \end{aligned}$$

then the corresponding density function can be expressed in term of ReLu activation function:

$$\begin{aligned} \phi _{\sigma _{R}}(x)\ =\ \phi _{\sigma _{M_1}(3\, \cdot )}(x)\ =\ \psi _{ReLu}(3\, x+1) - 2\, \psi _{ReLu}(3\, x) + \psi _{ReLu}(3\, x-1). \end{aligned}$$

As a consequence of the above relation, the NN operators \(K_n^{\sigma _{M_1}(3\, \cdot )}\) can be considered as an NN activated by the above linear combination of ReLu activation function. For more details concerning the usefulness of \(\psi _{ReLu}\), see, e.g., [2, 3].

As showed above, the truncated algebraic moments of \(\phi _{\sigma _{M_{d}}}\) are exactly equal to suitable constants. Then, the sigmoidal functions \(\sigma _{M_{d}}\) can be used to generate the high-order convergence operators \({\mathcal {K}}_{n}^{r}\). Here, we consider the linear combination of \(\alpha _{j}^{\left( 1\right) },\,j=1,2\), and of \(\alpha _{j}^{\left( 2\right) },\,j=1,2,3\), which satisfy respectively:

$$\begin{aligned} \sum _{j=1}^{2}\alpha _{j}^{\left( 1\right) }=1,\quad \quad \sum _{j=1}^{2}\frac{\alpha _{j}^{\left( 1\right) }}{j}=0 \end{aligned}$$

and

$$\begin{aligned} \sum _{j=1}^{3}\alpha _{j}^{\left( 2\right) }=1,\quad \quad \sum _{j=1}^{3}\frac{\alpha _{j}^{\left( 2\right) }}{j}=0,\quad \quad \sum _{j=1}^{3}\frac{\alpha _{j}^{\left( 2\right) }}{j^{2}}=0. \end{aligned}$$

In this way, we obtain the following operators:

$$\begin{aligned}&{\mathcal {K}}_{n}^{2,d}\left( f,x\right) :=-K_{n}^{\sigma _{M_{d}}}\left( f,x\right) +2K_{2n}^{\sigma _{M_{d}}}\left( f,x\right) \\&{\mathcal {K}}_{n}^{3,d}\left( f,x\right) :=\frac{1}{2}K_{n}^{\sigma _{M_{d}}}\left( f,x\right) -4K_{2n}^{\sigma _{M_{d}}}\left( f,x\right) +\frac{9}{2}K_{3n}^{\sigma _{M_{d}}}\left( f,x\right) . \end{aligned}$$

Thus, we obtain:

Corollary 16

Let \(\sigma _{M_{d}}\left( x\right) ,\,d\in {\mathbb {N}}^{+},\) be the sigmoidal function generated by the central B-spline \(M_{d}\left( x\right) \), and let \(x \in I\) be fixed.

For any \(f\in C^{2}\left( I\right) \), there holds:

$$\begin{aligned} \lim _{n\rightarrow +\infty }n^{2}\left[ {\mathcal {K}}_{n}^{2,d}\left( f,x\right) -f\left( x\right) \right] =-\frac{f^{\left( 2\right) }\left( x\right) }{4}\left( \frac{2}{3}+\gamma _{2}^{d}\right) , \end{aligned}$$

while for any \(f\in C^{3}\left( I\right) \), we have:

$$\begin{aligned} \lim _{n\rightarrow +\infty }n^{3}\left[ {\mathcal {K}}_{n}^{3,d}\left( f,x\right) -f\left( x\right) \right] =\frac{3f^{\left( 3\right) }\left( x\right) }{72}\left( \frac{1}{2}+\gamma _{2}^{d}\right) . \end{aligned}$$

Clearly, an analogous of Corollary 16 can be reformulated also for a finite linear combination of Kantorovich NN type operators \(K_{n}\) with \(r>3\) to achieve a faster convergence.