Bifurcation and Dynamic Analyses of Non-monotonic Predator–Prey System with Constant Releasing Rate of Predators

Abstract

In this paper, we systematical study the rich dynamics and complex bifurcations of a non-monotonic predator–prey system with a constant releasing rate for the predator. We prove that the system can have at most three positive equilibria, and can undergo a sequence of bifurcations, including transcritical, saddle-node, Hopf, degenerate Hopf, double limit cycle, saddle-node homoclinic bifurcation (or homoclinic loop with a saddle-node), cusp bifurcation of codimension 2, and Bogdanov–Takens bifurcation of codimension 2 and 3. And the system can generate very rich dynamics, such as the existence of a semi-stable limit cycle, multiple coexistent periodic orbits, homoclinic loops, etc. Moreover, our results show that the dynamical behaviors highly rely on the constant releasing rate of predators and the initial conditions. That is, there exists a critical value of the constant releasing rate of predators such that (i) when the constant releasing rate is greater than the critical value, the prey goes to extinction for all admissible initial populations of both species; (ii) when the constant releasing rate is less than the critical value, the prey can always coexist with the predator. Numerical simulations are presented to verify the main results.

Appendices

Appendix A: Proof of Lemma 3.1

Proof

Considering the function

$$\begin{aligned} H(x)=3ax^{3}-(2a-ac)x^{2}-(b-1)x+c. \end{aligned}$$

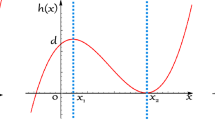
It follows from $H(x_{1})=0$ that $x_{1}$ is a positive real root of the cubic equation $H(x)=0$. Moreover, since H(x) passes the point (0, c), and $H(+\infty )=+\infty$ and $H(-\infty )=-\infty$, the cubic equation $H(x)=0$ always has a negative real root. Hence, the cubic equation $H(x)=0$ has three real roots (a negative real root and two positive real roots), as shown in Fig. 10. Denote the roots of the cubic equation $H(x)=0$ as follows:

$$\begin{aligned} x_{01}<0, \ \ x_{02}>0 \ \ \mathrm {and} \ \ x_{03}>0, \end{aligned}$$

where $x_{1}$ is equal to one of $x_{02}$ and $x_{03}$. Especially, when $H'(x)|_{x=x_{1}}=0$, we have

$$\begin{aligned} x_{1}=x_{02}=x_{03}=\frac{(2a-ac)+\sqrt{\Delta _{*}}}{9a}, \end{aligned}$$

where $\Delta _{*}=(2a-ac)^{2}+9a(b-1)>0$. Thus, we have $H'(x_{1})= 0$ if and only if $x_{1}=\frac{(2a-ac)+\sqrt{\Delta _{*}}}{9a}$. The proof is completed. $\square$

Fig. 10

The existence of the positive real roots of the cubic equation $H(x)=0$. The Hopf bifurcation occurs when $x_{1}=x_{02}$, $x_{1}=x_{03}$ or $x_{1}=x^{2}_{*}$

Appendix B: Coefficients in the proof of Theorem 3.4

Here we provide the expressions of some coefficients that were used in the proof of Theorem 3.4.

• $m_{11}= \frac{(1-x^{*}_{1})(x^{*}_{1})^{2}}{1+a_{0}(x^{*}_{1})^{2}}$, $m_{12}=(x^{*}_{1}-1)x^{*}_{1}$, $m_{13}=\frac{x^{*}_{1}}{1+a_{0}(x^{*}_{1})^{2}}$,

• $m_{21}=\frac{[12(x^{*}_{1})^{2}-15x^{*}_{1}+4][7(x^{*}_{1})^{2}-8x^{*}_{1}+2][-24(x^{*}_{1})^{3}+33(x^{*}_{1})^{2}-15x^{*}_{1}+2]}{2(x^{*}-1)(5x^{*}_{1}-2)[6(x^{*}_{1})^{2}-6x^{*}_{1}+1](3x^{*}_{1}-1)^{2}}$,

• $m_{22}=\frac{[7(x^{*}_{1})^{2}-8x^{*}_{1}+2][24(x^{*}_{1})^{3}-33(x^{*}_{1})^{2}+15x^{*}_{1}-2]}{x^{*}_{1}[6(x^{*}_{1})^{2}-6x^{*}_{1}+1](3x^{*}_{1}-1)^{2}}$,

• $m_{23}=\frac{(2x^{*}_{1}-1)[12(x^{*}_{1})^{2}-15x^{*}_{1}+4][57(x^{*}_{1})^{3}-81 (x^{*}_{1})^{2}+33x^{*}_{1}-4]}{x^{*}_{1}(x^{*}_{1}-1)(5x^{*}_{1}-2)[6(x^{*}_{1})^{2}-6x^{*}_{1}+1](3x^{*}_{1}-1)^{2}}$,

• $m_{31}=\frac{[12 (x^{*}_{1})^{2}-15 x^{*}_{1}+4] [-15060(x^{*}_{1})^{10}+72837(x^{*}_{1})^{9}-154485(x^{*}_{1})^{8}+189370 (x^{*}_{1})^{7}-148793(x^{*}_{1})^{6}+78459(x^{*}_{1})^{5}-28182(x^{*}_{1})^{4}+6825(x^{*}_{1})^{3} -1069(x^{*}_{1})^{2}+98x^{*}_{1} -4]}{2(3x^{*}_{1}-1)^{3}(5x^{*}_{1}-2)^{2}(x^{*}_{1}-1)^{2}[6(x^{*}_{1})^{2}-6x^{*}_{1}+1]^{2}x^{*}_{1}}$,

• $m_{32}=\frac{-6108(x^{*}_{1})^{10}+32877(x^{*}_{1})^{9}-78921 (x^{*}_{1})^{8}+110363 (x^{*}_{1})^{7}-98839(x^{*}_{1})^{6}+58890(x^{*}_{1})^{5}-23540(x^{*}_{1})^{4}+6215(x^{*}_{1})^{3} -1035(x^{*}_{1})^{2}+98x^{*}_{1} -4}{(3x^{*}_{1}-1)^{3}(5x^{*}_{1}-2)(x^{*}_{1}-1)[6(x^{*}_{1})^{2}-6x^{*}_{1}+1]^{2}(x^{*}_{1})^{2}}$,

• $m_{33}= \frac{(1-2x^{*}_{2})[57(x^{*}_{1})^{3}-81(x^{*}_{1})^{2}+33 x^{*}_{1}-4][12 (x^{*}_{1})^{2}-15 x^{*}_{1}+4][73(x^{*}_{1})^{5}-180(x^{*}_{1})^{4}+166(x^{*}_{1})^{3}-71(x^{*}_{1})^{2}+14x^{*}_{1}-1]}{2(3x^{*}_{1}-1)^{3}(5x^{*}_{1}-2)^{2}(x^{*}_{1}-1)^{2}[6(x^{*}_{1})^{2}-6x^{*}_{1}+1]^{2}(x^{*}_{1})^{2}}$.