Skip to main content
SpringerLink
Log in

Traveling Wave Solution of Bad and Good Modified Boussinesq Equations with Conformable Fractional-Order Derivative

  • Published:
Qualitative Theory of Dynamical Systems Aims and scope Submit manuscript

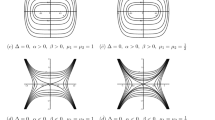
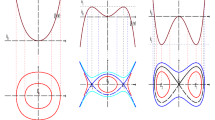
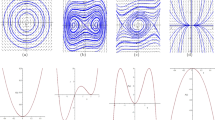
Abstract

In this paper we investigate the fractional order derivative Bad and Good modified equations via the bifurcation theory of dynamical systems method. To convert the fractional order derivative equations into ODEs, we utilize the transformation \( u(x,t)=\phi (\xi ),\,\,\, \xi =x-c t^\alpha \), instead of the commonly use \(\xi =x-c\frac{t^\alpha }{\alpha } \). Bright and dark solitons, kink and anti-kink solutions, as well as periodic wave solutions are obtained. We show that the wavelength and amplitude of the traveling wave solutions depend on the fractional-order \(\alpha \).

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12

Similar content being viewed by others

References

  1. Boussinesq, J.: Theorie des ondes et des remous qui se propagent le long d’un canal rectangulaire horizontal, en communiquant au liquide contenu dans ce canal des vitesses sensiblement pareilles de la surface au fond. J. Math. Pures Appl. 17, 55–108 (1872)

  2. Darvishi, M.T., Najafi, M., Wazwaz, A.M.: Soliton solutions for Boussinesq-like equations with spatio-temporal dispersion. Ocean Eng. 130, 228–240 (2017)

    Google Scholar 

  3. Wazwaz, A.M.: Solitons and singular solitons for a variety of Boussinesq-like equations. Ocean Eng. 53, 1–5 (2012)

    MathSciNet  Google Scholar 

  4. Barostichi, R.F., Figueira, R.O., Himonas, A.A.: Well-posedness of the good Boussinesq equation in analytic Gevrey spaces and time regularity. J. Differ. Equ. 267, 3181–3198 (2019)

    MathSciNet  MATH  Google Scholar 

  5. Zakharov, V.E.: On stochastization of one-dimensional chains of nonlinear oscillators. Sov. Phys. JETP 38(1), 108–110 (1974)

    Google Scholar 

  6. Bekir, A.: Application of the \(\left(\frac{G^{\prime }}{G}\right)\)-expansion method for nonlinear evolution equations. Phys. Lett. A 372(19), 3400–3406 (2008)

    MathSciNet  MATH  Google Scholar 

  7. Eslami, M.: Exact traveling wave solutions to the fractional coupled nonlinear Schrodinger equations. Appl. Math. Comput. 285, 141–148 (2016)

    MathSciNet  MATH  Google Scholar 

  8. Bogdanov, L.V., Zakharov, V.E.: The Boussinesq equation revisited. Phys. D 165(3–4), 137–162 (2002)

    MathSciNet  MATH  Google Scholar 

  9. Zuo, J., Zhang, Y.: The Hirota bilinear method for the coupled Burgers equation and the high-order Boussinesq–Burgers equation. Chin. Phys. B 20(1), 010205 (2011)

    Google Scholar 

  10. Liu, W., Yu, W., Yang, C., Liu, M., Zhang, Y., Lei, M.: Analytic solutions for the generalized complex Ginzburg–Landau equation in fiber lasers. Nonlinear Dyn. 89(4), 2933–2939 (2017)

    MathSciNet  Google Scholar 

  11. Feng, D., Li, J., Lu, J., He, T.: The improved Fan sub-equation method and its application to the Boussinseq wave equation. Appl. Math. Comput. 194(2), 309–320 (2007)

    MathSciNet  MATH  Google Scholar 

  12. Wazwaz, A.M.: Multiple-soliton solutions for the Boussinesq equation. Appl. Math. Comput. 192(2), 479–486 (2007)

    MathSciNet  MATH  Google Scholar 

  13. Ma, Y., Li, B.: Analytic rogue wave solutions for a generalized fourth-order Boussinesq equation in fluid mechanics. Math. Methods Appl. Sci. 42, 39–48 (2019)

    MathSciNet  MATH  Google Scholar 

  14. Lu, X., Wang, J., Lin, F., Zhou, X.: Lump dynamics of a generalized two-dimensional Boussinesq equation in shallow water. Nonlinear Dyn. 91(2), 1249–1259 (2017)

    Google Scholar 

  15. Zheng, H., Xia, Y., Bai, Y., Wu, L.: Travelling wave Solutions of the general regularized long wave equation. Qual. Theory Dyn. Syst. 20, 8 (2021). https://doi.org/10.1007/s12346-020-00442-w

    Article  MathSciNet  MATH  Google Scholar 

  16. Zhu, W., Xia, Y., Bai, Y.: Traveling wave solutions of the complex Ginzburg–Landau equation. Appl. Math. Comput. 382, 125342 (2020)

    MathSciNet  MATH  Google Scholar 

  17. Liu, H., Zhang, L., Li, X., Chang, L.: Equivalent transformations, bifurcations and exact solutions to a class of variable-coefficient PDE. Nuclear Phys. B 960, 115172 (2020)

    MathSciNet  MATH  Google Scholar 

  18. Ray, S.S.: Lie symmetry analysis and reduction for exact solution of (2+1)-dimensional Bogoyavlensky–Konopelchenko equation by geometric approach. Modern Phys. Lett. B 32(11), 1850127 (2018)

    MathSciNet  Google Scholar 

  19. Darvishi, M.T., Najafi, M., Wazwaz, A.M.: New extended rational trigonometric methods and applications. Waves Random Complex Media 30, 1–22 (2018)

    MathSciNet  Google Scholar 

  20. Rezazadeh, H., Younis, M., Rehman, S.U., Eslami, M., Bilal, M., Younas, U.: New exact traveling wave solutions to the (2+ 1)-dimensional Chiral nonlinear Schrödinger equation. Math. Model. Nat. Phenom. 16, 38 (2021)

    MATH  Google Scholar 

  21. Fan, X., Qu, T., Huang, S., Chen, X., Cao, M., Zhou, Q., Liu, W.: Analytic study on the influences of higher-order effects on optical solitons in fiber laser. Optik 184, 370–376 (2019)

    Google Scholar 

  22. Liu, W., Zhu, Y.N., Liu, M., Wen, B., Fang, S., Teng, H., Lei, M., Liu, L.M., Wei, Z.: Optical properties and applications for MoS\(_2\)-Sb\(_2\)Te\(_3\)-MoS\(_2\) heterostructure material. Photonics Res. 6(3), 220–227 (2018)

    Google Scholar 

  23. Liu, W., Pang, L., Han, H., Shen, Z., Lei, M., Teng, H., Wei, Z.: Dark solitons in WS\(_2\) erbium-doped fiber lasers. Photonics Res. 4(3), 111–114 (2016)

    Google Scholar 

  24. Liu, W., Pang, L., Han, H., Liu, M., Lei, M., Fang, S., Teng, H., Wei, Z.: Tungsten disulfide saturable absorbers for 67 fs mode-locked erbium-doped fiber lasers. Opt. Express 25(3), 2950–2959 (2017)

    Google Scholar 

  25. Yan, Y., Liu, W., Zhou, Q., Biswas, A.: Dromion-like structures and periodic wave solutions for variable-coefficients complex cubic-quintic Ginzburg–Landau equation influenced by higher-order effects and nonlinear gain. Nonlinear Dyn. 99(2), 1313–1319 (2020)

    Google Scholar 

  26. Liu, W., Pang, L., Han, H., Bi, K., Lei, M., Wei, Z.: Tungsten disulphide for ultrashort pulse generation in all-fiber lasers. Nanoscale 9(18), 5806–5811 (2017)

    Google Scholar 

  27. Fan, X., Qu, T., Huang, S., Chen, S.X., Cao, M., Zhou, Q., Liu, W.: Analytic study on the influences of higher-order effects on optical solitons in fiber laser. Optik 186, 326–331 (2019)

    Google Scholar 

  28. Ross, B.: The development of fractional calculus 1695–1900. Hist. Math. 4, 75–89 (1977)

    MathSciNet  MATH  Google Scholar 

  29. Podlubny, I.: Fractional Differential Equations. Academic, San Diego (1999)

    MATH  Google Scholar 

  30. Wu, Q., Huang, J.: Fractional Differential Equations. Qinghua University, Beijing (2015)

    Google Scholar 

  31. Khalil, R., Al Horani, M., Yousef, A., Sababheh, M.: A new definition of fractional derivative. J. Comput. Appl. Math. 264, 65–70 (2014)

    MathSciNet  MATH  Google Scholar 

  32. Liu, C.: Counterexamples on Jumarie’s two basic fractional calculus formulae. Commun. Nonl. Sci. Numer. Simul. 22(1–3), 92–94 (2015)

  33. Zhang, B., Zhu, W., Xia, Y., Bai, Y.: A unified analysis of exact traveling wave solutions for the fractional-order and integer-order Biswas–Milovic equation: via bifurcation theory of dynamical system. Qual. Theory Dyn. Syst. 19(11), 1–28 (2020)

    MathSciNet  MATH  Google Scholar 

  34. Zhu, W., Xia, Y., Zhang, B., Bai, Y.: Exact traveling wave solutions and bifurcations of the time fractional differential equations with applications. Int. J. Bifur. Chaos 29(3), 1950041 (2019)

    MathSciNet  MATH  Google Scholar 

  35. Inc, M., Rezazadeh, H., Vahidi, J., Eslami, M., Akinlar, M.A., Ali, M.N., Chu, Y.: New solitary wave solutions for the conformable Klein-Gordon equation with quantic nonlinearity. AIMS Math. 5(6), 6972–6984 (2020)

    MathSciNet  Google Scholar 

  36. Eslami, M., Rezazadeh, H.: The first integral method for Wu–Zhang system with conformable time-fractional derivative. Calcolo 53(3), 475–485 (2016)

    MathSciNet  MATH  Google Scholar 

  37. Su, N.: The fractional Boussinesq equation of groundwater flow and its applications. J. Hydrol. 547, 403–412 (2017)

    Google Scholar 

  38. El-Wakil, S.A., Abulwafa, E.M.: Formulation and solution of space-time fractional Boussinesq equation. Nonlinear Dyn. 80(1–2), 167–175 (2015)

    MathSciNet  Google Scholar 

  39. Ji, F., He, C., Zhang, J., He, J.: A fractal Boussinesq equation for nonlinear transverse vibration of a nanofiber-reinforced concrete pillar. Appl. Math. Model. 82, 437–448 (2020)

    MathSciNet  MATH  Google Scholar 

  40. Yadav, M.P., Agarwal, R.: Numerical investigation of fractional-fractal Boussinesq equation. Chaos Interdiscip. J. Nonlinear Sci. 29(1), 013109 (2019)

    MathSciNet  MATH  Google Scholar 

  41. Durur, H., Tasbozan, O., Kurt, A.: New analytical solutions of conformable time fractional Bad and Good modified Boussinesq equations. Appl. Math. Nonlinear Sci. 5(1), 447–454 (2020)

    MathSciNet  Google Scholar 

  42. Li, J.: Bifurcations and Exact Solutions in Invariant Manifolds for Nonlinear Wave Equations. Science Press, Beijing (2019)

    Google Scholar 

  43. Zhang, B., Xia, Y., Zhu, W., Bai, Y.: Explicit exact traveling wave solutions and bifurcations of the generalized combined double sinh–cosh-Gordon equation. Appl. Math. Comput. 363, 124576 (2019)

    MathSciNet  MATH  Google Scholar 

  44. Zhang, H., Xia, Y., N’gbo, P.: Global existence and uniqueness of a periodic wave solution of the generalized Burgers–Fisher equation. Appl. Math. Lett. 121, 107353 (2021)

  45. Zhang, Y., Xia, Y.: Traveling wave solutions of generalized Dullin–Gottwald–Holm equation with parabolic law nonlinearity. Qual. Theory Dyn. Syst. 20(67), 1–38 (2021)

    MathSciNet  MATH  Google Scholar 

  46. Byrd, P.F., Fridman, M.D.: Handbook of Elliptic Integrals for Engineers and Sciensists. Springer, Berlin (1971)

    Google Scholar 

Download references

Funding

Funding was provided by National Natural Science Foundation of China (Grand No. 11671176).

Author information

Authors and Affiliations

  1. Department of Mathematics, Zhejiang Normal University, Jinhua, 321004, China

    N’Gbo N’Gbo & Yonghui Xia

Authors
  1. N’Gbo N’Gbo
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Yonghui Xia
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Yonghui Xia.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

N’Gbo, N., Xia, Y. Traveling Wave Solution of Bad and Good Modified Boussinesq Equations with Conformable Fractional-Order Derivative. Qual. Theory Dyn. Syst. 21, 14 (2022). https://doi.org/10.1007/s12346-021-00541-2

Download citation

  • Received:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s12346-021-00541-2

Keywords

Search

Navigation