1 Introduction

With the rapid development of modern network technology, the way of rumor spreading has changed from word of mouth to more flexible and convenient Internet transmission. The interactivity of social network makes everyone a receiver of rumors and a disseminator of rumors [1]. Rumors spread all over the world. Some rumors harm personal reputation, cause mental distress and damage to health. Some rumors even endanger the security and stability of the society and the reputation of the government [2].

In early 2020, COVID-19 outbreak occurred, and there were many rumors. For example, “the probability of new coronavirus infection among smokers is much lower than that of non-smokers”, “The cause of COVID-19 is that the people of Wuhan eat bats”, “COVID-19 is a biochemical weapon made by a laboratory”, which has caused great harm to Wuhan people, caused panic to the society, and even damaged the image of the country [3]. Social security and stability is the primary condition for rapid development. Therefore, how to effectively control the spread of rumors has become an important issue faced by many governments and scholars.

There are many similarities between the spread of rumors and the spread of infectious diseases, so many scholars use the theory of infectious disease dynamics to study the spread of rumors. According to the characteristics of rumor spreading, many mathematical models of rumor spreading are considered, and their dynamic properties are analyzed. In 1965–1985, classical DK model [4] and MT model [5] are presented. Then many scholars improved the model according to different factors [6,7,8,9,10,11,12,13,14,15]. Kandhway and Kuri [6] used the MT rumor model to simulate the information dissemination in a homogeneous mixed population. Through the analysis of rumor spreading, Zhao et al. [7] revised the flow chart of rumor spreading process and established an IRS mathematical model. Chen et al. [8] studies a new delayed susceptible-exposed-infected-recovered (SEIR) rumor spreading model with saturation incidence on heterogeneous networks. Huo et al. [9] considered the use of media information as a measure of control to suppress the spread of rumors. Recently, Tian and Ding [10] considered the influence of debunking behavior on rumor dynamics. The authors believe that an ignorant person can become latent by receiving rumors or counter-rumors. Driven by complicated psychology, he will become a rumor spreader, a rumor debunker or a stifler. Then, the authors established an ILRDS rumor spreading model to analyze the spread of rumors, analyzed the stability of the equilibria, and studied the influence of different parameters on the rumor propagation process in numerical simulation.

In recent decades, the optimal control theory is more and more used in the field of biological mathematics, which provides a strong theoretical basis for solving the problem of disease transmission [16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31]. Based on the reported tuberculosis data, a mathematical control model of tuberculosis transmission dynamics in South Korea was established [16]. Through the optimal control theory, the authors put forward the optimal TB control strategy, estimated the TB budget of the government, and worked out the optimal TB elimination plan. Lemos-Paião et al. [17] developed a model of cholera transmission with isolation and treatment, proposed and analyzed the optimal control problem of the model, and carried out numerical simulation of the local cholera outbreak. The results show that when the optimal control strategy is applied, the number of infected individuals will be significantly reduced. In order to control the spread of dengue fever in Peshawar, Pakistan, Agusto and Khan [18] added insecticide use and vaccination to control the spread of dengue fever in a deterministic model of dengue virus transmission. The results showed that the same number of infections were avoided regardless of how the cost was weighted. This is due to the reciprocal relationship between the cost of pesticide use and the cost of vaccination. Li and Guo [19] established an online game addiction model with positive and negative media reports to analyze the influence of media in the spread of online game addiction. The results of numerical simulation showed that the control of media coverage through the optimal control conclusion can greatly alleviate the serious situation of game addiction.

The harm of rumor spread can affect individuals, society and country. Nowadays, information dissemination is more convenient, it is particularly important to control the spread of rumors. Our main contributions and innovations are as follows.

  1. (i)

    The innovation of rumor spreading model. In the study of rumor spread, most of the previous studies only considered the influence of a single control measure in the rumor spreading model, ignoring the dynamic influence of multiple control measures on rumor spread [8,9,10]. In order to simulate the rumor spread more truly, it is necessary to consider the actual measures to control the rumor spread in real life [32, 33], as shown below. (1) In the background of the network, we can intelligently screen and evaluate the news or posts with a certain amount of dissemination on the network; (2) We can resist rumors by increasing the public’s scientific literacy and popularizing common sense; (3) The government publishes rumor refuting information through official channels for specific rumors; (4) There are some relevant laws to punish those who maliciously create and spread rumors. We develop a new rumor spreading model, which considers these control measures in reality. This makes up for the deficiency of previous literatures.

  2. (ii)

    Innovation in the proof of stability. The proof of the global asymptotic stability of the equilibria is an important and difficult point in the study of the properties of the dynamic model [7, 10]. In this paper, we provide a new way to prove the global asymptotic stability of equilibria, which is different from the proof in Ref. [10]. This provides a new perspective for the study of the dynamics of rumor propagation and enriches its research methods.

  3. (iii)

    Innovation in numerical simulation. In the previous literatures on the control of rumor propagation, some scholars observed and compared the results under this static state by changing the parameter values [6, 7, 10]. Some scholars study the dynamic optimal control of rumor spreading model with single control measure [9, 11]. In this paper, we not only study the dynamic optimal control problem of multiple control measures, but also further study its cost-effectiveness analysis. Through the quantitative comparative analysis, the results are more clear.

The next organizational structure of this paper is as follows: the description of the model is shown in Sect. 2. The stability of the equilibria are proved in Sect. 3. The optimal control problem is discussed in Sect. 4. The numerical simulation with discussion is analyzed in Sect. 5. Finally the conclusion is shown in Sect. 6.

2 Formulation of the Model

2.1 Model Description

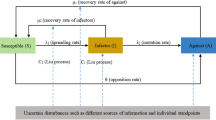
In 2019, Tian and Ding [10] proposed a new rumor spreading model with debunking behavior. In the model, the whole population is divided into five compartments, which are named as: Ignorants (I), Latents (L), Rumor Spreaders (R), Debunkers (D) and Stiflers (S). The ILRDS rumor spreading model was established as follows:

$$\begin{aligned} \left\{ \begin{array}{l} \frac{dI(t)}{dt}=\varepsilon -\mu IR-kID-\rho I, \\ \frac{dL(t)}{dt}=\mu IR+kID -(\alpha +\beta +\gamma +\rho )L, \\ \frac{dR(t)}{dt}=\alpha L-(\delta +\xi +\rho )R, \\ \frac{dD(t)}{dt}=\beta L+\xi R-(\theta +\rho )D, \\ \frac{dS(t)}{dt}=\delta R+\theta D+\gamma L-\rho S, \\ \end{array} \right. \end{aligned}$$
(1)

where \(\varepsilon \) is the immigration rate; \(\mu \) is the rumor-contacting rate; k denotes the debunker-contacting rate; \(\rho \) denotes the emigration rate; \(\alpha \) represents the rumor-spreading rate; \(\beta \) represents the debunking rate; \(\gamma \) represents the silent rate; \(\delta \) represents the rumor-stifling rate; \(\xi \) denotes the reversal rate; \(\theta \) denotes the debunking-stifling rate. \(N(t)=I(t)+L(t)+R(t)+D(t)+S(t)\) denotes the whole population at time t.

In general, an infected person can only be exposed to a limited number of people per unit of time, so we choose to use the standard incidence rate \(\mu \frac{ IR}{N}\), which would be more appropriate [34]. In the above model, we will further consider the influence of the following four control means on rumor spread: \(u_{1}\) background detection; \(u_{2}\) public education; \(u_{3}\) official debunking; \(u_{4}\) legal punishment. Thus, the population flow of each warehouse is shown in Fig. 1.

Fig. 1
figure 1

Transfer diagram of controlled model

Full size image

Then, we propose a controlled rumor spreading model as follows:

$$\begin{aligned} \left\{ \begin{array}{l} \frac{dI(t)}{dt}=\varepsilon -(1-u_{1})\mu \frac{IR}{N}-k\frac{ID}{N}-\rho I, \\ \frac{dL(t)}{dt}=(1-u_{1})\mu \frac{IR}{N}+k\frac{ID}{N} -(1-u_{4})\alpha L-(\beta +\gamma +\rho +u_{2}\tau )L, \\ \frac{dR(t)}{dt}=(1-u_{4})\alpha L-(\delta +\xi +\rho +u_{3}\varphi )R, \\ \frac{dD(t)}{dt}=(\beta +u_{2}\tau k_{1}) L+(\xi +u_{3}\varphi (1-k_{2})) R-(\theta +\rho )D, \\ \frac{dS(t)}{dt}=(\delta +u_{3}\varphi k_{2}) R+\theta D+(\gamma +u_{2}\tau (1-k_{1})) L-\rho S , \\ \end{array} \right. \end{aligned}$$
(2)

where

  1. 1.

    \(u_{1}\), namely, background detection represents the effect of preventing rumors spread due to the intelligent detection of data by the network background.

  2. 2.

    \(u_{2}\), namely, public education denotes the effect of science education on preventing rumors spreading. \(\tau \) represents the efficiency of restraining rumor spreading, and \(k_{1}\) is the proportion of people who turn into debunker due to this measure.

  3. 3.

    \(u_{3}\), namely, official debunking denotes the effect of that the government publish debunking news through the official channels to reduce the spread of rumors. \(\varphi \) represents the efficiency of official debunking, and \(k_{2}\) is the proportion of people who turn into stiflers due to this measure.

  4. 4.

    \(u_{4}\), namely, legal punishment represents the effect of that the government punishes those who maliciously create and spread rumors through laws and regulations.

2.2 Positivity and Boundedness

Lemma 1

Let \(P(0)\ge 0\) denotes the initial information, \(P(t)=(I,L,R,D,S)\) are the model variables, and the solutions of the model (2) will be non-negative for all \(t>0\).

Proof

Suppose \(\lambda (t)=(1-u_{1})\mu \frac{R}{N}+k\frac{D}{N}\), then the first equation of model (2) yields

$$\begin{aligned} \frac{dI}{dt}=\varepsilon -[\lambda (t)+\rho ] I. \end{aligned}$$

By the integrating factor method, the solution of the above equation is as follows.

$$\begin{aligned} I(t)= & {} I(0)\exp \Big (-\rho t-\int _{0}^{t}\lambda (u)du\Big )\\&+\exp \Big (-\rho t-\int _{0}^{t}\lambda (u)du\Big ) \int _{0}^{t}\varepsilon \Big [\rho x+ \int _{0}^{x}\lambda (z)dz\Big ]dx\ \\> & {} 0. \end{aligned}$$

Similarly, we can get the rest of the variables to be positive. \(\square \)

Lemma 2

The feasible region defined in the closed set \(\Omega \subset R_{+}^{5}\), is positive invariant for the system (2) with non-negative initial conditions in \(R_{+}^{5}\).

Proof

We add all the equations of system (2) and get that

$$\begin{aligned} \frac{dN(t)}{dt}=\frac{dI(t)}{dt}+\frac{dL(t)}{dt}+\frac{dR(t)}{dt}+\frac{dD(t)}{dt}+\frac{dS(t)}{dt}=\varepsilon -\rho N(t). \end{aligned}$$

By solving the above equation, we can get:

$$\begin{aligned} N(t)=\frac{\varepsilon }{\rho }+N(0)e^{-\rho t}. \end{aligned}$$

Therefore,

$$\begin{aligned} \lim _{t\rightarrow +\infty }N(t)=\frac{\varepsilon }{\rho }. \end{aligned}$$

So we can analyse the system (2) in the feasible region \(\Omega \) that is defined by:

$$\begin{aligned} \Omega =\left\{ (I,L,R,D,S)\in R_{+}^{5}: 0\le N(t)\le \frac{\varepsilon }{\rho } \right\} . \end{aligned}$$

Therefore, \(\Omega \) is a positive invariant set, and we will discuss the dynamics of the model (2) in \(\Omega \) later. \(\square \)

3 Stability Analysis

3.1 Basic Reproduction Number

The basic reproductive number \(R_{0}\) represents “the average number of new infections directly caused by infected cases in the whole infection period in the fully susceptible population” [34]. It is an important concept in epidemiology. Its significance in this paper is the average number of new rumor spreaders directly caused by a rumor spreader in ignorants. By using the next generation matrix [35], we can obtain the basic reproduction number \(R_{0}\). It’s easy to know that system (2) has a rumor-free equilibrium \(E_{0}=(I^{0},0,0,0,0)\), where \(I^{0}=N^{0}=\frac{\varepsilon }{\rho }\). Thus we choose the matrix F and V as

$$\begin{aligned} \quad \quad F_{3\times {3}}=\left( \begin{array}{ccc} 0 &{}\quad (1-u_{1})\mu &{}\quad k\\ 0 &{}\quad 0 &{}\quad 0\\ 0 &{}\quad 0 &{}\quad 0\\ \end{array} \right) , \quad \end{aligned}$$

and

$$\begin{aligned} V_{3\times {3}}=\left( \begin{array}{ccc} (1-u_{4})\alpha +(\beta +\gamma +\rho +u_{2}\tau ) &{}\quad 0&{}\quad 0 \\ -(1-u_{4})\alpha &{}\quad \delta +\xi +\rho +u_{3}\varphi &{}\quad 0\\ -(\beta +u_{2}\tau k_{2}) &{}\quad -(\xi +u_{3}\varphi (1-k_{2})) &{}\quad \theta +\rho \\ \end{array} \right) . \end{aligned}$$

For the convenience of calculation, we use some substitutions to make the equations more concise. We can get the following system.

$$\begin{aligned} \left\{ \begin{array}{l} \frac{dI(t)}{dt}=\varepsilon -d_{1}\mu \frac{IR}{N}-k\frac{ID}{N}-\rho I, \\ \frac{dL(t)}{dt}=d_{1}\mu \frac{IR}{N}+k\frac{ID}{N} -d_{2}\alpha L-d_{3}L, \\ \frac{dR(t)}{dt}=d_{2}\alpha L-d_{4}R, \\ \frac{dD(t)}{dt}=d_{5} L+d_{6} R-d_{7}D, \\ \frac{dS(t)}{dt}=d_{9} R+\theta D+d_{8} L-\rho S, \\ \end{array} \right. \end{aligned}$$
(3)

where the coefficients are \(d_{1}=1-u_{1}\), \(d_{2}=1-u_{4}\), \(d_{3}=\beta +\gamma +\rho +u_{2}\tau \), \(d_{4}=\delta +\xi +\rho +u_{3}\varphi \), \(d_{5}=\beta +u_{2}\tau k_{1}\), \(d_{6}=\xi +u_{3}\varphi (1-k_{2})\), \(d_{7}=\theta +\rho \), \(d_{8}=\gamma +u_{2}\tau (1-k_{1})\), \(d_{9}=\delta +u_{3}\varphi k_{2}\).

Through the spectral radius of \(FV^{-1}\), the expression of the basic reproduction number is:

$$\begin{aligned} R_{0}=\rho (FV^{-1})=\frac{kd_{4}d_{5}+\alpha k d_{2}d_{6}+\alpha \mu d_{1}d_{2}d_{7}}{d_{4}d_{7}(d_{3}+\alpha d_{2})}. \end{aligned}$$
(4)

3.2 Globally Asymptotically Stable (GAS) of Rumor-Free Equilibrium

In system (3), we know that it always has the rumor-free equilibrium \(E_{0}=(I^{0}, L^{0}, R^{0}, D^{0}, S^{0})\). Then we can get the follow theorem.

Theorem 1

For the system (3), the rumor-free equilibrium \(E_{0}=(I^{0}, L^{0}, R^{0}, D^{0}, S^{0})\) is globally asymptotically stable if \(0<R_{0}<1\).

Proof

When \(R_{0}\) is less than 1, we get \(kd_{4}d_{5}<d_{3}d_{4}d_{7}+\alpha d_{2}d_{4}d_{7}\). So we can construct the following Lyapunov function:

$$\begin{aligned} G=\frac{\alpha d_{2}d_{7}}{\alpha d_{2}d_{7}+d_{3}d_{7}-kd_{5}}L+R+\frac{\alpha kd_{2}}{\alpha d_{2}d_{7}+d_{3}d_{7}-kd_{5}}D \end{aligned}$$

The derivative of G is:

$$\begin{aligned} \frac{dG}{dt}= & {} \frac{\alpha d_{2}d_{7}}{\alpha d_{2}d_{7}+d_{3}d_{7}-kd_{5}}\left[ d_{1}\mu \frac{IR}{N}+k\frac{ID}{N} -d_{2}\alpha L-d_{3}L\right] +(d_{2}\alpha L-d_{4}R) \\&+\frac{\alpha kd_{2}}{\alpha d_{2}d_{7}+d_{3}d_{7}-kd_{5}}(d_{5} L+d_{6} R-d_{7}D) \\\le & {} \frac{\alpha d_{2}d_{7}}{\alpha d_{2}d_{7}+d_{3}d_{7}-kd_{5}}[d_{1}\mu R+kD -d_{2}\alpha L-d_{3}L]+(d_{2}\alpha L-d_{4}R) \\&+\frac{\alpha kd_{2}}{\alpha d_{2}d_{7}+d_{3}d_{7}-kd_{5}}(d_{5} L+d_{6} R-d_{7}D) \\= & {} L\left[ \frac{-\alpha d_{2}d_{7}(d_{2}\alpha +d_{3})}{\alpha d_{2}d_{7}+d_{3}d_{7}-kd_{5}}+d_{2}\alpha +\frac{\alpha d_{2}kd_{5}}{\alpha d_{2}d_{7}+d_{3}d_{7}-kd_{5}}\right] \\&+R\left( \frac{\alpha d_{2}d_{7}d_{1}\mu }{\alpha d_{2}d_{7}+d_{3}d_{7}-kd_{5}}-d_{4}+\frac{\alpha kd_{2}d_{6}}{\alpha d_{2}d_{7}+d_{3}d_{7}-kd_{5}}\right) \\&+D\left( \frac{\alpha d_{2}d_{7}}{\alpha d_{2}d_{7}+d_{3}d_{7}-kd_{5}}k-\frac{\alpha kd_{2}}{\alpha d_{2}d_{7}+d_{3}d_{7}-kd_{5}}d_{7}\right) \\= & {} Rd_{4}\left( \frac{\alpha \mu d_{1}d_{2}d_{7}+\alpha kd_{2}d_{6}}{\alpha d_{2}d_{4}d_{7}+d_{3}d_{4}d_{7}-kd_{4}d_{5}}-1\right) \end{aligned}$$

Due to \(d_{i}\in [0,1], (i=1,2,\dots ,9)\) and \(0<R_{0}<1\), the following inequality holds.

$$\begin{aligned} \alpha \mu d_{1}d_{2}d_{7}<d_{4}d_{7}(d_{3}+\alpha d_{2})-kd_{4}d_{5}-\alpha k d_{2}d_{6}. \end{aligned}$$

Thus when \(0<R_{0}<1\), \(\frac{dG}{dt}\) is negative. Through the asymptotic stability theorem [36], the rumor-free equilibrium \(E_{0}\) is globally asymptotically stable on \(\Omega \). \(\square \)

3.3 Globally Asymptotically Stable of Rumor-Spreading Equilibrium

In this subsection, we first prove the existence of rumor-spreading equilibrium, and then prove that rumor-spreading equilibrium is GAS. Let all equations of system (3) be equal to 0, and the expression of rumor-spreading equilibrium \(E^{*}=(I^{*}, L^{*}, R^{*}, D^{*}, S^{*})\) is obtained as follows:

$$\begin{aligned}&I^{*}=\frac{Nd_{4}d_{7}(d_{2}\alpha +d_{3})}{\mu \alpha d_{1}d_{2}d_{7}+k(d_{4}d_{5}+d_{2}d_{6}\alpha )}, \\&L^{*}=\frac{\varepsilon -\rho I^{*}}{d_{2}\alpha +d_{3}}, \\&R^{*}=\frac{d_{2}\alpha }{d_{4}}L^{*}, \\&D^{*}=\left( \frac{d_{5}}{d_{7}}+\frac{d_{6}d_{2}\alpha }{d_{7}d_{4}}\right) L^{*}, \\&S^{*}=\left( \frac{d_{8}}{\rho }+\frac{d_{9}d_{2}\alpha }{\rho d_{4}}+\frac{\theta d_{5}}{\rho d_{7}}+\frac{\theta d_{6}d_{2}\alpha }{\rho d_{7}d_{4}}\right) L^{*}. \end{aligned}$$

Theorem 2

For the system (3), the rumor-spreading equilibrium \(E^{*}=(I^{*},L^{*},R^{*},D^{*},S^{*})\) is globally asymptotically stable if \(R_{0}>1\).

Proof

In order to make the later combination of variables more convenient, we do the following transformation. By denoting

$$\begin{aligned} x=\frac{I}{I^{*}},\,\,\, y=\frac{L}{L^{*}},\,\,\, z=\frac{R}{R^{*}},\,\,\, u=\frac{D}{D^{*}},\,\,\, w=\frac{S}{S^{*}}, \end{aligned}$$

we have

$$\begin{aligned} \frac{dx}{dt}= & {} x\left[ \frac{\varepsilon }{I^{*}}\left( \frac{1}{x}-1\right) -d_{1}\mu \frac{R^{*}}{N}(z-1)-k\frac{D^{*}}{N}(u-1)\right] , \nonumber \\ \frac{dy}{dt}= & {} y\left[ d_{1}\mu \frac{I^{*}R^{*}}{L^{*}N}\left( \frac{xz}{y}-1\right) +k\frac{I^{*}D^{*}}{L^{*}N}\left( \frac{xu}{y}-1\right) \right] , \nonumber \\ \frac{dz}{dt}= & {} z\left[ d_{2}\alpha \frac{L^{*}}{R^{*}}\left( \frac{y}{z}-1\right) \right] , \nonumber \\ \frac{du}{dt}= & {} u\left[ d_{5}\frac{L^{*}}{D^{*}}\left( \frac{y}{u}-1\right) +d_{6} \frac{R^{*}}{D^{*}}\left( \frac{z}{u}-1\right) \right] , \nonumber \\ \frac{dw}{dt}= & {} w\left[ d_{8}\frac{L^{*}}{S^{*}}\left( \frac{y}{w}-1\right) +d_{9}\frac{R^{*}}{S^{*}}\left( \frac{z}{w}-1\right) +\theta \frac{D^{*}}{S^{*}}\left( \frac{u}{w}-1\right) \right] . \end{aligned}$$
(5)

Therefore, we can see that the rumor-spreading equilibrium \(E^{*}\) of system (3) is transformed into \({\bar{E}}^{*}=(1,1,1,1,1)\) of the new system (5).

Setting a Lyapunov function V as follows:

$$\begin{aligned}&V=a_{1}I^{*}(x-1-lnx)+a_{2}L^{*}(y-1-lny)+a_{3}R^{*}(z-1-lnz) \\&\qquad \ +a_{4}D^{*}(u-1-lnu)+a_{5}S^{*}(w-1-lnw), \end{aligned}$$

where \(a_{1}\), \(a_{2}\), \(a_{3}\), \(a_{4}\) and \(a_{5}\) are undetermined positive coefficients. We obtain the derivative of V as follows:

$$\begin{aligned}&V'=a_{1}I^{*}\left( 1-\frac{1}{x}\right) x'+a_{2}L^{*}\left( 1-\frac{1}{y}\right) y'+a_{3}R^{*}\left( 1-\frac{1}{z}\right) z' \\&\qquad \ +a_{4}D^{*}\left( 1-\frac{1}{u}\right) u'+a_{5}S^{*}\left( 1-\frac{1}{w}\right) w' \\&\quad \ =a_{1}\left( 2\varepsilon -d_{1}\mu \frac{I^{*}R^{*}}{N}-k\frac{I^{*}D^{*}}{N}\right) +a_{2}\left( d_{1}\mu \frac{I^{*}R^{*}}{N}+k\frac{I^{*}D^{*}}{N}\right) +a_{3}d_{2}\alpha L^{*} \\&\qquad \ +a_{4}(d_{5}L^{*}+d_{6}R^{*})+a_{5}(d_{8}L^{*}+d_{9}R^{*}+\theta D^{*})\nonumber \\&\qquad -\left( a_{1}\varepsilon -a_{1}\mu d_{1}\frac{I^{*}R^{*}}{N}-a_{1}k\frac{I^{*}D^{*}}{N}\right) x \\&\qquad \ -a_{1}\varepsilon \frac{1}{x}-\left( a_{2}d_{1}\mu \frac{I^{*}R^{*}}{N}+a_{2}k\frac{I^{*}D^{*}}{N}-a_{4}d_{5}L^{*}-a_{5}d_{8}L^{*}-a_{3}d_{2}\alpha L^{*}\right) y\nonumber \\&\qquad -a_{2}k\frac{I^{*}D^{*}}{N}\frac{xu}{y} \\&\qquad \ -a_{2}d_{1}\mu \frac{I^{*}R^{*}}{N}\frac{xz}{y}-\left( -a_{1}d_{1}\mu \frac{I^{*}R^{*}}{N}+a_{3}d_{2}\alpha L^{*}-a_{4}d_{6}R^{*}-a_{5}d_{9}R^{*}\right) z\nonumber \\&\qquad -a_{3}d_{2}\alpha L^{*}\frac{y}{z} \\&\qquad \ -\left( -a_{1}k\frac{I^{*}D^{*}}{N}+a_{4}d_{5}L^{*}+a_{4}d_{6}R^{*}-a_{5}\theta D^{*}\right) u-a_{4}d_{6}R^{*}\frac{z}{u}-a_{4}d_{5}L^{*}\frac{y}{u} \\&\qquad \ -(a_{5}d_{8}L^{*}+a_{5}d_{9}R^{*}+a_{5}\theta D^{*})w-a_{5}d_{8}L^{*}\frac{y}{w}-a_{5}d_{9}R^{*}\frac{z}{w}-a_{5}\theta D^{*}\frac{u}{w} \\&\qquad \ +\left( -a_{1}\mu d_{1}\frac{I^{*}R^{*}}{N}+a_{2}d_{1}\mu \frac{I^{*}R^{*}}{N}\right) xz+\left( -a_{1}k\frac{I^{*}D^{*}}{N}+a_{2}k\frac{I^{*}D^{*}}{N}\right) xu. \end{aligned}$$

According to the characteristics of arithmetic geometric mean inequality, the above variables are combined. Let’s assume that

$$\begin{aligned} F(x,y,z,u,w)=: & {} b_{1}\left( 2-x-\frac{1}{x}\right) +b_{2}\left( 3-\frac{1}{x}-\frac{xu}{y}-\frac{y}{u}\right) \nonumber \\&+b_{3}\left( 3-\frac{1}{x}-\frac{xz}{y}-\frac{y}{z}\right) \nonumber \\&+b_{4}\left( 4-\frac{1}{x}-\frac{y}{z}-\frac{z}{u}-\frac{xu}{y}\right) . \end{aligned}$$
(6)

Variables that are not successfully combined will not appear in the final formula, so we let the coefficients of these terms be 0.

$$\begin{aligned}&a_{2}d_{1}\mu \frac{I^{*}R^{*}}{N}+a_{2}k\frac{I^{*}D^{*}}{N}-a_{4}d_{5}L^{*}-a_{5}d_{8}L^{*}-a_{3}d_{2}\alpha L^{*}=0, \\&-a_{1}d_{1}\mu \frac{I^{*}R^{*}}{N}+a_{3}d_{2}\alpha L^{*}-a_{4}d_{6}R^{*}-a_{5}d_{9}R^{*}=0, \\&-a_{1}k\frac{I^{*}D^{*}}{N}+a_{4}d_{5}L^{*}+a_{4}d_{6}R^{*}-a_{5}\theta D^{*}=0, \\&a_{5}d_{8}L^{*}+a_{5}d_{9}R^{*}+a_{5}\theta D^{*}=0, \\&a_{5}d_{8}L^{*}=0, \\&a_{5}d_{9}R^{*}=0, \\&a_{5}\theta D^{*}=0, \\&-a_{1}\mu d_{1}\frac{I^{*}R^{*}}{N}+a_{2}d_{1}\mu \frac{I^{*}R^{*}}{N}=0, \\&-a_{1}k\frac{I^{*}D^{*}}{N}+a_{2}k\frac{I^{*}D^{*}}{N}=0. \end{aligned}$$

We can obtain that

$$\begin{aligned} a_{1}=a_{2}=1, a_{3}=\frac{(d_{1}d_{7}\mu +kd_{6})I^{*}R^{*}}{d_{2}d_{7}\alpha L^{*}N}, \,\,\,a_{4}=\frac{kI^{*}}{d_{7}N},\,\,\, a_{5}=0. \end{aligned}$$

Substituting the above coefficients into \(V'\),

$$\begin{aligned} V'= & {} 2\varepsilon +\frac{(d_{1}d_{7}\mu +kd_{6})I^{*}R^{*}}{d_{7}N}+k\frac{I^{*}D^{*}}{N}-\left( \varepsilon -\mu d_{1}\frac{I^{*}R^{*}}{N}-k\frac{I^{*}D^{*}}{N}\right) x-\varepsilon \frac{1}{x} \nonumber \\&-k\frac{I^{*}D^{*}}{N}\frac{xu}{y}-d_{1}\mu \frac{I^{*}R^{*}}{N}\frac{xz}{y}-\frac{(d_{1}d_{7}\mu +kd_{6})I^{*}R^{*}}{d_{7}N}\frac{y}{z}\nonumber \\&-\frac{d_{6}kI^{*}R^{*}}{d_{7}N}\frac{z}{u}-\frac{d_{5}kI^{*}L^{*}}{d_{7}N}\frac{y}{u}.\end{aligned}$$
(7)

Letting the coefficients of all variables of F(x, y, z, u, w) and that of \(V'\) be equal, we can get the following equations.

$$\begin{aligned}&b_{1}=\varepsilon -\mu d_{1}\frac{I^{*}R^{*}}{N}-k\frac{I^{*}D^{*}}{N}, \\&b_{1}+b_{2}+b_{3}+b_{4}=\varepsilon , \\&b_{2}+b_{4}=k\frac{I^{*}D^{*}}{N}, \\&b_{2}=\frac{d_{5}kI^{*}L^{*}}{d_{7}N}, \\&b_{3}=d_{1}\mu \frac{I^{*}R^{*}}{N}, \\&b_{3}+b_{4}=\frac{(d_{1}d_{7}\mu +kd_{6})I^{*}R^{*}}{d_{7}N}, \\&b_{4}=\frac{d_{6}kI^{*}R^{*}}{d_{7}N}. \end{aligned}$$

By solving the above equations, we can get the following conclusions.

$$\begin{aligned}&b_{1}=\rho I^{*},\quad b_{2}=\frac{d_{5}kI^{*}L^{*}}{d_{7}N},\quad b_{3}=d_{1}\mu \frac{I^{*}R^{*}}{N},\quad b_{4}=\frac{d_{6}kI^{*}R^{*}}{d_{7}N}. \end{aligned}$$

Finally, we only need to verify that the constant terms of \(V'\) and that of F(x, y, z, u, w) are equal.

$$\begin{aligned} 2b_{1}+3b_{2}+3b_{3}+4b_{4}= & {} 2\rho I^{*}+3\frac{d_{5}kI^{*}L^{*}}{d_{7}N}+3d_{1}\mu \frac{I^{*}R^{*}}{N}+4\frac{d_{6}kI^{*}R^{*}}{d_{7}N} \\= & {} 2\varepsilon +\frac{(d_{1}d_{7}\mu +kd_{6})I^{*}R^{*}}{d_{7}N}+k\frac{I^{*}D^{*}}{N}. \end{aligned}$$

Through the arithmetic geometric mean inequality, we can get the conclusion that

$$\begin{aligned} V'= & {} F(x,y,z,u,w) \\= & {} b_{1}\left( 2-x-\frac{1}{x}\right) +b_{2}\left( 3-\frac{1}{x}-\frac{xu}{y}-\frac{y}{u}\right) +b_{3}\left( 3-\frac{1}{x}-\frac{xz}{y}-\frac{y}{z}\right) \\&+b_{4}\left( 4-\frac{1}{x}-\frac{y}{z}-\frac{z}{u}-\frac{xu}{y}\right) \\\le & {} 0. \end{aligned}$$

Therefore, we can know that rumor-spreading equilibrium is globally asymptotically stable through LaSalle’s Invariable Principle [36]. \(\square \)

4 Optimal Control Problem

In this section, we’re to study the control problem of system (2) for a period of time. We consider the influence of the following four control measures on rumor spread: \(u_{1}\) background detection; \(u_{2}\) public education; \(u_{3}\) official debunking; \(u_{4}\) legal punishment. Our goal is to reduce the number of the latents and the rumor spreaders as much as possible, while keeping the cost of its control strategy as low as possible. Therefore, we design the following objective function to ensure that our goal can be achieved.

$$\begin{aligned} J( u_{1},u_{2},u_{3},u_{4})=\int _{0}^{t_{f}}\left[ A_{1}L+A_{2}R+\frac{B_{1}}{2} u_{1}^{2}+\frac{B_{2}}{2}u_{2}^{2}+\frac{B_{3}}{2}u_{3}^{2}+\frac{B_{4}}{2}u_{4}^{2}\right] dt,\nonumber \\ \end{aligned}$$
(8)

where \(A_{1}, A_{2}\) are the weight coefficients associated with the latents and the rumor spreaders, \(B_{1}, B_{2}, B_{3}, B_{4}\) are the weight coefficients of four control variables. So we want to obtain the optimal control \((u_{1}^{*}, u_{2}^{*}, u_{3}^{*}, u_{4}^{*})\) such that

$$\begin{aligned} J(u_{1}^{*}, u_{2}^{*}, u_{3}^{*}, u_{4}^{*})=\min J(u_{1}, u_{2}, u_{3}, u_{4}),\qquad (u_{1}, u_{2}, u_{3}, u_{4})\in U. \end{aligned}$$
(9)

where U is the admissible space of control variables given by

$$\begin{aligned} U=\{(u_{1},u_{2},u_{3},u_{4})|u_{i}(t)\ \textit{is}\ \textit{Lebesgue}\ \textit{measurable}\ \textit{on}\,\, [0,1],\ i=1,2,3,4 \}. \end{aligned}$$

The Pontryagin maximum principle [37] is used to solve the problem. It is easy to know that the necessary conditions for the existence of optimal control are satisfied. Next, we will solve the optimal control solution. The Hamiltonian function H subject to the system (2) is

$$\begin{aligned}&H=A_{1}L+A_{2}R+\frac{1}{2}(B_{1}u_{1}^{2}+B_{2}u_{2}^{2}+B_{3}u_{3}^{2}+B_{4}u_{4}^{2}) \nonumber \\&\qquad +\lambda _{1}\left[ \varepsilon -(1-u_{1})\mu \frac{IR}{N}-k\frac{ID}{N}-\rho I \right] \nonumber \\&\qquad +\lambda _{2}\left[ (1-u_{1})\mu \frac{IR}{N}+k\frac{ID}{N} -(1-u_{4})\alpha L-(\beta +\gamma +\rho +u_{2}\tau )L\right] \nonumber \\&\qquad +\lambda _{3}[(1-u_{4})\alpha L-(\delta +\xi +\rho +u_{3}\varphi )R] \nonumber \\&\qquad +\lambda _{4}[(\beta +u_{2}\tau k_{1}) L+(\xi +u_{3}\varphi (1-k_{2})) R-(\theta +\rho )D] \nonumber \\&\qquad +\lambda _{5}[(\delta +u_{3}\varphi k_{2}) R+\theta D+(\gamma +u_{2}\tau (1-k_{1})) L-\rho S], \end{aligned}$$
(10)

where \(\lambda _{i}\ (i=1,2,3,4,5)\) are the adjoint variables.

The equation of the adjoint system corresponding to the state system (2) is as follows:

$$\begin{aligned} \left\{ \begin{array}{l} \lambda '_{1}(t)=-\frac{\partial H}{\partial I}=\lambda _{1}\left[ (1-u_{1})\mu \frac{R}{N}+k\frac{D}{N}+\rho \right] -\lambda _{2}\left[ (1-u_{1})\mu \frac{R}{N}+k\frac{D}{N}\right] , \\ \lambda '_{2}(t)=-\frac{\partial H}{\partial L}=-A_{1}+\lambda _{2}[(1-u_{4})\alpha +(\beta +\gamma +\rho +u_{2}\tau )]-\lambda _{3}(1-u_{4})\alpha \\ \qquad \qquad \qquad \quad \quad \,\, -\lambda _{4}(\beta +u_{2}k_{1}\tau )-\lambda _{5}[\gamma +u_{2}\tau (1-k_{1})], \\ \lambda '_{3}(t)=-\frac{\partial H}{\partial R}=-A_{2}+(\lambda _{1}-\lambda _{2})(1-u_{1})\mu \frac{I}{N}+\lambda _{3}(\delta +\xi +\rho +u_{3}\varphi ) \\ \qquad \qquad \qquad \quad \quad \,\, -\lambda _{4}[\xi +u_{3}\varphi (1-k_{2})]-\lambda _{5}(\delta +u_{3}\varphi k_{2}), \\ \lambda '_{4}(t)=-\frac{\partial H}{\partial D}=\lambda _{1}k\frac{I}{N}-\lambda _{2}k\frac{I}{N}+\lambda _{4}(\theta +\rho )-\lambda _{5}\theta ,\\ \lambda '_{5}(t)=-\frac{\partial H}{\partial S}=\lambda _{5}\rho . \end{array} \right. \end{aligned}$$

The transversality conditions of the adjoint system are

$$\begin{aligned} \lambda _{i}(t_{f})=0, \qquad i=1,2,3,4,5. \end{aligned}$$

According to Pontryagin maximum principle, we can know that the optimal control \((u_{1}^{*}\), \(u_{2}^{*}\), \(u_{3}^{*}\), \(u_{4}^{*})\) needs to satisfy the following conditions

$$\begin{aligned} \frac{\partial H}{\partial u_{i}}=0, \qquad i=1,2,3,4. \end{aligned}$$

So we have

$$\begin{aligned}&\frac{\partial H}{\partial u_{1}}=B_{1}u_{1}+\lambda _{1}\mu \frac{IR}{N}-\lambda _{2}\mu \frac{IR}{N}=0, \\&\frac{\partial H}{\partial u_{2}}=B_{2}u_{2}+\lambda _{4}\tau k_{1}L-\lambda _{2}\tau L+\lambda _{5}\tau (1-k_{1})L=0, \\&\frac{\partial H}{\partial u_{3}}=B_{3}u_{3}-\lambda _{3}\varphi R+\lambda _{4}\varphi (1-k_{2})R+\lambda _{5}\varphi k_{2}R=0, \\&\frac{\partial H}{\partial u_{4}}=B_{4}u_{4}+\lambda _{2}\alpha L-\lambda _{3}\alpha L=0. \end{aligned}$$

Thus, we get the expression of the optimal control \((u_{1}^{*}, u_{2}^{*}, u_{3}^{*}, u_{4}^{*})\),

$$\begin{aligned} \left\{ \begin{array}{l} u_{1}^{*}=max\left\{ 0,min\left\{ 1,\frac{(\lambda _{2}-\lambda _{1})\mu IR}{B_{1}N}\right\} \right\} , \\ u_{2}^{*}=max\left\{ 0,min\left\{ 1,\frac{\tau L(\lambda _{2}-\lambda _{4}k_{1}-\lambda _{5}(1-k_{1}))}{B_{2}}\right\} \right\} , \\ u_{3}^{*}=max\left\{ 0,min\left\{ 1,\frac{\varphi R(\lambda _{3}-\lambda _{4}(1-k_{2})-\lambda _{5}k_{2})}{B_{3}}\right\} \right\} , \\ u_{4}^{*}=max\left\{ 0,min\left\{ 1,\frac{\alpha L(\lambda _{3}-\lambda _{2})}{B_{4}}\right\} \right\} . \end{array} \right. \end{aligned}$$
(11)

5 The Control Strategies and Cost-Effectiveness Analysis

5.1 Various Control Strategies

In this section, we use the forward backward sweep method to find the optimal control under each strategy [38,39,40,41,42,43,44]. The specific algorithm process is as follows.

Step 1 In the admissible space of control variables, a guess initial values are selected. Combined with the initial conditions of the state system, the fourth-order Runge–Kutta method is used to simulate the system from front to back in time, and the state solution and control variable expressions are obtained.

Step 2 The new state solution and control expressions are substituted into the adjoint system. Combined with the transversality conditions, according to the time point from back to front, the expressions of the adjoint variables are obtained by using the fourth-order Runge–Kutta method.

Step 3 The state variables and adjoint variables are used to update the control variables. Then the new state variables and control variables are taken as the new initial values, and the iteration continues.

Step 4 The iterative process continues until the values of two adjacent states, adjoint and control variables are close enough.

In order to explore and analyze the effectiveness of the control measures in system (2), we set up different control schemes, the combination of double, triple and quadruple control variables. The reason why we don’t consider a single control measure is that people usually choose to take multiple measures in parallel to prevent rumors spreading.

Scenario 1: Double control strategies

   Strategy A: background detection \(+\) public education (\(u_{1}\), \(u_{2}\)).

   Strategy B: background detection \(+\) official debunking (\(u_{1}\), \(u_{3}\)).

   Strategy C: background detection \(+\) legal punishment (\(u_{1}\), \(u_{4}\)).

   Strategy D: public education \(+\) official debunking (\(u_{2}\), \(u_{3}\)).

   Strategy E: public education \(+\) legal punishment (\(u_{2}\), \(u_{4}\)).

   Strategy F: official debunking \(+\) legal punishment (\(u_{3}\), \(u_{4}\)).

Scenario 2: Triple control strategies

   Strategy G: background detection \(+\) public education \(+\) official debunking (\(u_{1}\), \(u_{2}\), \(u_{3}\)).

   Strategy H: background detection \(+\) public education \(+\) legal punishment (\(u_{1}\), \(u_{2}\), \(u_{4}\)).

   Strategy I: background detection \(+\) official debunking \(+\) legal punishment (\(u_{1}\), \(u_{3}\), \(u_{4}\)).

   Strategy J: public education \(+\) official debunking \(+\) legal punishment (\(u_{2}\), \(u_{3}\), \(u_{4}\)).

Scenario 3: Quadruple control strategies

   Strategy K: background detection \(+\) public education \(+\) official debunking \(+\) legal punishment (\(u_{1}\), \(u_{2}\), \(u_{3}\), \(u_{4}\)).

The research object of this paper is the long-term residents in mainland China. According to some relevant survey data [45], the initial population of each warehouse we selected is as follows: \(I(0)=500\), \(L(0)=250\), \(R(0)=20\), \(D(0)=9\), \(S(0)=50\) (units in million). Combined with some literatures [9, 10] about rumor spreading, we choose the value of parameters as follows: \(\rho =0.08\), \(\mu =0.5\), \(k=0.5\), \(\alpha =0.35\), \(\beta =0.1\), \(\theta =0.15\), \(\delta =0.05\), \(\gamma =0.23\), \(\xi =0.05\), \(\tau =0.4\), \(\varphi =0.6\), \(k_{1}=0.2\), \(k_{2}=0.5\). The weight coefficients of objective function are \(A_{1}=1\), \(A_{2}=2\), \(B_{1}=1\), \(B_{2}=10\), \(B_{3}=10\), \(B_{4}=5\). Due to the influence of many human factors in real life, the efficiency of control measures is difficult to reach 100%, so we set the maximum value of control variables (\(u_{1}\), \(u_{2}\), \(u_{3}\), \(u_{4}\)) as 0.8 [46]. The final time \(t_{f}\) is set to 100 days.

Fig. 2
figure 2

Simulation of the strategy A to F in scenario 1 for: a total number of rumor spreaders; b total number of the latents

Full size image

Under strategy A to F, the number of rumor spreaders and the latents are shown in (a) and (b) of Fig. 2 respectively. Because we are more concerned about the number of rumor spreaders and the latents than other warehouses, we only show the population change chart of these two warehouses under each strategy. As can be seen from Fig. 2a, in strategy A to F the number of rumor spreaders almost reaches its peak in 3 days. Among these strategies, the peak value of strategy A is the largest, about 74. This is an unsatisfactory result. The peak value of strategy F is the smallest, about 22. In the next 30 days or so, they dropped rapidly to about 5, and then slowly to the end.

But the number of the latents in Fig. 2b is different from that of rumor spreaders in Fig. 2a. We can see that the number of the latents in strategy A decreases the fastest, while the number of the latents in strategy F decreases the slowest. This result seems to be contrary to the result in Fig. 2a, which is mainly due to different strategies and different objects.

Fig. 3
figure 3

Optimal control strategies in scenario 1

Full size image

Figure 3 shows the optimal control of strategy A to F in scenario 1. What they have in common is that at the beginning of control, the control intensity of all non-zero control variables should be kept at the maximum intensity. In the optimal control of different strategies, the time point of gradual decline to 0 is different, as shown in Fig. 3.

Fig. 4
figure 4

Simulation of the strategy G to J in scenario 2 for: a total number of rumor spreaders; b total number of the latents

Full size image
Fig. 5
figure 5

Optimal control strategies in scenario 2

Full size image

In scenario 2, the changes in the number of rumor spreaders and the latents of strategy G to J are shown in (a) and (b) of Fig. 4, respectively. It is easy to see that the number of rumor spreaders in strategy G reaches the peak after 2 days, and the maximum is 48. And it’s the highest in strategy G to J. This shows that under the combination of three control measures the control effect of rumor spreading may be better than that of the two control measures. The optimal control under Strategies G to J are shown in Fig. 5. At the beginning of the control, the maximum control force should be maintained, and then gradually reduced to 0.

Fig. 6
figure 6

Simulation of the strategy K and without control in scenario 3 for: a total number of rumor spreaders; b total number of the latents

Full size image
Fig. 7
figure 7

Optimal control strategy in scenario 3

Full size image

Figure 6 shows the change trend of the number of rumor spreaders and the latents under the strategy of quadruple control measure and without control measure. It can be seen from Fig. 6a that the number of rumor spreaders will rapidly increase to 110 in 5 days without using control measure. Then it gradually decreased to 78 in the next 30 days and remained stable. Figure 6 verifies the correctness of Theorem 2 in the previous theory from the image. And from this we can see that if the rumors are not effectively controlled, the result is very bad.

Under the quadruple control strategies, the number of rumor spreaders increased in one day, but the increase was less. And it decreased rapidly in the next 7 days. As can be seen from Fig. 6b, the number of the latents will also drop very fast under the quadruple control strategies. This is a good result.

From Fig. 7, we can see the change in the control strength of the quadruple control measures. The four control measures should be maintained at a maximum control intensity of 0.8 at the beginning and continue for 67 days, 12 days, 99 days and 28 days respectively. And then they gradually go down to zero. Among them, we have noticed that control measure \(u_{3}\) needs to be maintained at the maximum intensity all the time, while the remaining control measures do not need to be maintained at the maximum intensity from the beginning to the end, so as to avoid a lot of waste in human and financial resources.

From the above simulation results, some control strategies are better, but the difference among them is difficult to distinguish from the graphs. Therefore, we need to further distinguish them from the cost-effectiveness analysis.

5.2 Cost-Effectiveness Analysis

Cost-effectiveness analysis is an effective method to evaluate different control measures in public health intervention. In general, incremental cost-effectiveness ratio (ICER) [47] of strategy A relative to strategy B is selected as an important index for evaluation,

$$\begin{aligned} ICER=\frac{TC(B)-TC(A)}{TA(B)-TA(A)}. \end{aligned}$$
(12)

The definition expression of the total averted cases (TA) is as follows

$$\begin{aligned} TA=\int _{0}^{t_{f}}[L+R-({\tilde{L}}+{\tilde{R}})]dt , \end{aligned}$$
(13)

where L, R denote the latents and the rumor spreaders of without control respectively, \({\tilde{L}}, {\tilde{R}}\) denote the latents and the rumor spreaders of a control strategy respectively. \(\int _{0}^{t_{f}}(L+R)dt\) is the total number of people infected (TI) in the whole process without control. The definition expression of the total cost (TC) is as follows

$$\begin{aligned} TC=\int _{0}^{t_{f}}[B_{1}u_{1}I+B_{2}u_{2}L+B_{3}u_{3}R+B_{4}u_{4}L]dt, \end{aligned}$$
(14)

where \(B_{i}, (i=1, 2, 3, 4)\) are the cost per person for each control measure \(u_{i}, (i=1, 2, 3, 4)\). We show the values of TA and TC under all control strategies (A to K) and without control strategy in Table 1.

Table 1 Cost-effectiveness analysis
Full size table

Table 1 shows the data (TI, IAR, TC, ICER) of each strategy. Compared with the data in the last column, from the optimal incremental cost-effectiveness ratio (ICER) analysis, strategy F is the optimal control strategy and ICER(F) \(= 0.546\). It shows that if the optimal control under the strategy is implemented, it only costs 0.546 for each less infected person. But at the same time, we note that strategy K is the optimal control strategy if analyzed from the optimal infection averted ratio (IAR). IAR(K) \(= 94.4465\%\), which indicates that 94.4465% of people can be reduced by rumor attack if the measures are implemented according to the optimal control of the strategy, but the ICER of this strategy is higher. We also need to pay attention to strategy J, IAR(J) \(= 94.0264\%\), ICER(J) \(=0.68595\). In strategy J, the values of IAR and ICER are satisfactory.

Therefore, we suggest that when the budget is sufficient, we can choose control strategy K to achieve the optimal proportion of total averted infectious. If the budget is limited and not enough, we can choose strategy F to achieve the optimal incremental cost-effectiveness ratio. If we want to take IAR and ICER into account, we should consider strategy J as the optimal control strategy.

6 Conclusion

In the era of rapid information dissemination, the harm of rumor spread is greater than before, and the research on the control of rumor spread is more urgent. This paper extended the rumor model by adding four control variables. The main findings were as follows.

  1. (i)

    Through the analysis of rumor propagation, a new extended rumor spreading model with comprehensive interventions (\(u_{1}\) background detection, \(u_{2}\) public education, \(u_{3}\) official debunking, \(u_{4}\) legal punishment) was obtained. The basic reproduction number \(R_{0}\) was calculated by the next generation matrix. Then we proved the globally asymptotically stable (GAS) of rumor-free equilibrium and rumor-spreading equilibrium by using the Lyapunov function. It provides a framework and method for proving GAS in stability analysis.

  2. (ii)

    In the theoretical analysis of optimal control, we used Pontryagin maximum principle to get the state system and adjoint system, and obtain the expression of the optimal solution.

  3. (iii)

    In the simulation, we divided the control variables into three scenarios, a total of 11 control strategies. Then we used the forward backward sweep method to simulate all the control strategies. Through the analysis of ICER and IAR data of all control strategies, different optimal strategies should be determined from different perspectives.

Through the above theoretical and numerical analysis, we can use some control strategies to effectively curb the spread of rumors and reduce the harm to people and society. These results can also be used as suggestions for safety management departments.

Rumors usually have a certain timeliness. Over time, many rumors are automatically dispelled. This is an important difference between the spread of rumors and the spread of disease. When we consider this factor, the law of rumor propagation will change, and the corresponding model will also become different. This will also be an interesting question. We leave it for future work.