1 Introduction

It is well-known that isoperimetric inequalities are of interest in applied and pure mathematics [22, 48]. The Cheeger isoperimetric inequality is related with many conformal invariants in Riemannian manifolds and graphs, namely the exponent of convergence, the bottom of the spectrum of the Laplace–Beltrami operator, Poincaré–Sobolev inequalities, and the Hausdorff dimensions of the sets of both escaping and bounded geodesics in negatively curved surfaces [4, 13, 18, p. 228], [23, 27,28,29,30,31, 43, 46, 52, p. 333]. Isoperimetric inequality is also closely related to Ancona’s project on the space of positive harmonic functions of Gromov-hyperbolic graphs and manifolds [7,8,9]. In fact, in the study of the Laplace operator on a hyperbolic manifold or graph X, Ancona obtained in those three last papers several interesting results, under the hypothesis that the bottom of the spectrum of the Laplace spectrum \(\lambda _1(X)\) is positive. If we denote by h(X) the isoperimetric constant of X, the well-known Cheeger’s inequality \(\lambda _1(X) \ge \frac{1}{4} \,h(X)^2\) guarantees that \(\lambda _1(X)>0\) when \(h(X) > 0\) (see [17] for a converse inequality). Therefore, the results in this paper are useful in order to apply these Ancona’s results: We provide the minimal hypotheses in order to guarantee \(h(X) > 0\) (in fact, we have a characterization of this fact), then \(\lambda _1(X)>0\) and we can apply Ancona’s results to ensure the existence of solutions for elliptic partial differential equations in graphs and manifolds, among many other results (also, recall that in fact \(h(X) > 0\) and \(\lambda _1(X)>0\) are equivalent conditions for a large kind of graphs and manifolds).

There is a natural connection between isoperimetric inequality and hyperbolicity. Recall that one of the definitions of Gromov hyperbolicity involves some kind of isoperimetric inequality (see [3, 34]).

The Cayley graph of the group \(\mathbb {Z}\) is an example of hyperbolic graph without isoperimetric inequality. Cao proved in [21] that hyperbolicity implies isoperimetric inequality (with an extra hypothesis on the Gromov boundary).

In [41] we studied the relationship of hyperbolicity and Cheeger isoperimetric inequality in the context of graphs and Riemannian manifolds with bounded local geometry.

A celebrated theorem of Kanai [37] gives that quasi-isometries preserve several interesting properties (including isoperimetric inequalities) between Riemannian manifolds and graphs with bounded local geometry. The isoperimetric inequality is also preserved with weaker hypotheses in the context of Riemann surfaces [20, 33].

Mikhail Gromov started the theory of Gromov hyperbolic spaces in [34] in order to study finitely generated groups. The concept of Gromov hyperbolicity is very interesting since it grasps the essence of negatively curved Riemannian manifolds and discrete spaces like trees and the Cayley graphs of many finitely generated groups. Besides, Gromov hyperbolic spaces are an important class of metric spaces [14, 16, 19, 32, 54]. Gromov hyperbolicity has been thoroughly studied not only in Cayley graphs, but also in general graphs (see, e.g., [5, 6, 11, 12, 15, 39, 40, 47, 49,50,51, 55] and the references therein). Also, hyperbolicity has been applied in several areas such as the secure transmission of information and virus propagation on networks [35, 36], real networks [1, 2, 24, 38, 45], or phylogenetics [25, 26].

In [41] we characterized, in terms of their Gromov boundary, the uniform hyperbolic graphs and a large class of hyperbolic manifolds satisfying isoperimetric inequality (see, respectively, Theorems 2 and 4). In Theorems 2, 4 and [21, Theorem 1.1] it is used the hypothesis of the existence of a pole (in fact, although [21, Theorem 1.1] apparently uses a different hypothesis, actually, in hyperbolic spaces, it is equivalent to the existence of a pole). The hypothesis on Gromov hyperbolicity is natural (we need it in order to deal with the Gromov boundary). However, although the hypothesis on the pole is technically needed in the proofs, it does not look natural. The goal of this paper is to remove this hypothesis in the statements of Theorems 2 and 4. Thus, in Theorems 7 and 8 we prove that having a pole is not needed as an hypothesis but it is also a necessary condition of the characterization; this characterization appears in Theorems 5 and 6.

2 Background

We include in this section the definitions and results that we will need in Sect. 3.

Definition 1

Given any Riemannian n-manifold M, the Cheeger isoperimetric constant of M is defined as

$$\begin{aligned} h(M) = \inf _U \frac{{{\,\mathrm{Vol}\,}}_{n-1}(\partial U)}{{{\,\mathrm{Vol}\,}}_{n}(U)} , \end{aligned}$$

where U ranges over all non-empty bounded open subsets of M, and \({{\,\mathrm{Vol}\,}}_{m}(S)\) denotes the m-dimensional Riemannian volume of S.

Along this paper we consider any graph \(G=(V,E)=(V(G),E(G))\) endowed with its natural metric \(d_{G}\) obtained by considering shortest paths (we always assume that every edge has length 1). Given any vertex \(v\in V(G)\) and \(m\in \mathbb {N}\) we denote, as usual, by \(B_{\,G}(v,m)\), \({\bar{B}}_{\,G}(v,m)\) and \(S_{\,G}(v,m)\) the open ball, the closed ball and the sphere in G with center v and radius m, respectively.

Definition 2

The combinatorial Cheeger isoperimetric constant of G is defined to be

$$\begin{aligned} h(G) = \inf _U \frac{|\partial U|}{|U|} , \end{aligned}$$

where U ranges over all non-empty finite subsets of vertices in G, \(\partial U = \{v \in G \, | \, d_{\,G}(v,U) = 1\}\) and |U| denotes the cardinality of the set U.

A graph or Riemannian manifold X satisfies the (Cheeger) isoperimetric inequality if \(h(X)>0\), since this means that

$$\begin{aligned} |U| \le h(X)^{-1} |\partial U| , \end{aligned}$$

for every finite set of vertices U if X is a graph, and

$$\begin{aligned} {{\,\mathrm{Vol}\,}}_{n}(U) \le h(X)^{-1} {{\,\mathrm{Vol}\,}}_{n-1}(\partial U) , \end{aligned}$$

for every bounded open set U in the Riemannian n-manifold X.

We just consider graphs and manifolds X which are connected (recall that if X has connected components \(\{X_m\}\), then \(h(X)=\inf _m h(X_m)\)).

Let \((X,d_X)\) and \((Y,d_Y)\) be two metric spaces, and \(a,\ b\) constants satisfying \(a\ge 1,\ b\ge 0\). A function \(g: X\longrightarrow Y\) is an (a, b)-quasi-isometric embedding if

$$\begin{aligned} \frac{1}{a} \,d_X(x_1,x_2)-b \le d_{\,Y}(g(x_1),g(x_2))\le a \, d_X(x_1,x_2)+b, \end{aligned}$$

for every \(x_1, x_2\in X\). We say that the function g is c-full if for each y in Y there exists a point x in X with \(d_Y(g(x),y)\le c\).

A map \(g: X\longrightarrow Y\) is a quasi-isometry, if there are constants \(a\ge 1,\ b,c \ge 0\) such that g is a c-full (a, b)-quasi-isometric embedding. Two metric spaces X and Y are said quasi-isometric if there is a quasi-isometry \(g:X\longrightarrow Y\). It is easy to see that to be quasi-isometric is an equivalence relation.

Definition 3

Given a graph G and \(v \in V(G)\), we denote by N(v) the set of neighbors of v. The graph G is \(\mu \)-uniform if each vertex v of V has at most \(\mu \) neighbors, i.e., \(\sup \big \{|N(v)| \, : \,\, v\in V(G)\big \}\le \mu \). We say that G is uniform or that G has bounded local geometry if it is \(\mu \)-uniform for some constant \(\mu \).

We say that a Riemannian n-manifold M has bounded local geometry if there exist positive constants r, a,  satisfying the following property: for each \(p \in M\) there exists a diffeomorphism \(F_p : B_M(p,r) \rightarrow \mathbb {R}^n\) such that

$$\begin{aligned} \frac{1}{a}\,d(p_1,p_2) \le \Vert F_p(p_1) - F_p(p_2) \Vert \le a\,d(p_1,p_2) \end{aligned}$$

for every \(p_1,p_2 \in B_M(p,r)\).

If M is a complete Riemannian manifold, the injectivity radius inj(x) of \(x\in M\) is the largest radius for which the exponential map at x is a diffeomorphism. If M has non-positive sectional curvatures, then the injectivity radius can be defined, also, as the supremum of those \(r>0\) such that \(B_M(x,r)\) is simply connected or, equivalently, as half the infimum of the lengths of the (homotopically non-trivial) loops based at x. The injectivity radius inj(M) of M is defined as

$$\begin{aligned} \text {inj}(M) = \inf _{x\in M} \text {inj}(x). \end{aligned}$$

One can check that M has bounded local geometry if it has a lower bound on its Ricci curvature and positive injectivity radius [10].

Given a metric space X and \(x,y,w\in X\), we define the Gromov product of x, y with respect to w as

$$\begin{aligned} (x|y)_w=\frac{1}{2}\big (d(x,w)+d(y,w)-d(x,y)\big ). \end{aligned}$$

Definition 4

Given \(\delta \ge 0\) and a metric space X, we say that X is \(\delta \)-(Gromov) hyperbolic if

$$\begin{aligned} (x|y)_w\ge \min \{(x|z)_w,(z|y)_w\}-\delta \end{aligned}$$

for every \(x,y,z,w \in X\). We say that X is hyperbolic if it is \(\delta \)-hyperbolic for some \(\delta \ge 0\).

If X is hyperbolic, we denote by \(\delta (X)\) the sharp hyperbolicity constant of X:

$$\begin{aligned} \delta (X)= \inf \big \{ \delta : \, X \, \text { is } \delta -\text {hyperbolic} \, \big \}. \end{aligned}$$

If X is not hyperbolic, then we define \(\delta (X)=\infty \).

Recall that a geodesic metric space X is a metric space such that for every \(x_1,x_2 \in X\) there exists a geodesic joining them. A geodesic ray \(\gamma \) emanating from \(v \in X\) is a geodesic \(\gamma : [0,\infty ) \rightarrow X\) with \(\gamma (0)=v\).

Definition 5

A geodesic metric space X has a pole in a point v if there exists \(M > 0\) such that each point of X lies in an M-neighborhood of some geodesic ray emanating from v.

Definition 6

If X is a geodesic metric space and \(x_1,x_2,x_3\in X\), the union of three geodesics \([x_1 x_2]\), \([x_2 x_3]\) and \([x_3 x_1]\) is a geodesic triangle that will be denoted by \(T=\{x_1,x_2,x_3\}\). We say that \(x_1,x_2,x_3\) are the vertices of T. The geodesic triangle T is \(\delta \)-thin if any side of T is contained in the \(\delta \)-neighborhood of the union of the two other sides. We denote by \(\delta _{th}(T)\) the sharp thin constant of T, i.e., \( \delta _{th}(T):=\inf \{\delta \ge 0: \, T \, \text { is } \delta -\text {thin}\,\}. \) We say that the space X satisfies the Rips condition with constant \(\delta \) (or is \(\delta \)-thin) if every geodesic triangle in X is \(\delta \)-thin. We denote by \(\delta _{th}(X)\) the sharp thin constant of X, i.e., \( \delta _{th}(X):=\sup \{\delta _{th}(T): \, T \, \text { is a geodesic triangle in } X\,\}. \)

It is well-known that a geodesic metric space is hyperbolic if and only if it satisfies the Rips condition for some constant [3, 32]. Although there are many different definitions of Gromov hyperbolicity (see, e.g., [3, 32]), they are equivalent in the following sense: if X is \(\delta \)-hyperbolic with respect to one definition, then it is \(\delta '\)-hyperbolic with respect to another definition (for some \(\delta '\) related to \(\delta \)).

Since we consider any graph G as a geodesic metric space, we need to identify any edge \(uv\in E(G)\) with the interval [0, 1] in \(\mathbb {R}\). Thus, the points in G are the vertices and, also, the points in the interior of any edge of G. Therefore, any connected graph G has a natural distance defined on its points (vertices and interior points), induced by taking shortest paths in G, and we can see G as a metric graph.

Definition 7

Given a metric space (X, d) and a constant \(A>1\), we say that (X, d) is A-uniformly perfect if there exists some \(\varepsilon _0>0\) such that for every \(0<\varepsilon \le \varepsilon _0\) and every \(x\in X\) there exist a point \(y\in X\) such that \(\varepsilon /A <d(x,y) \le \varepsilon \). We say that (X, d) is uniformly perfect if there exists some A such that (X, d) is A-uniformly perfect.

Let us recall the concept of boundary of a hyperbolic space. For further information we refer the reader to [14, 19, 32, 34].

Let X be a hyperbolic space and fix \(w\in X\).

A sequence of points \(\{x_i\}\subset X\) converges to infinity if

$$\begin{aligned} \lim _{i,j\rightarrow \infty } (x_i|x_j)_w=\infty . \end{aligned}$$

One can check that this property is independent from the choice of w. Two sequences \(\{x_i\},\{x'_i\}\) that converge to infinity are equivalent if

$$\begin{aligned} \lim _{i\rightarrow \infty } (x_i|x'_i)_w=\infty . \end{aligned}$$

One can check that this defines an equivalence relation for sequences in X converging to infinity. The sequential boundary at infinity \(\partial _\infty X\) of X is the set of equivalence classes of sequences converging to infinity.

For every \(\xi , \xi ' \in \partial _\infty X\), its Gromov product with respect to \(w\in X\) is defined as

$$\begin{aligned} (\xi |\xi ')_w = \inf \ \liminf _{i\rightarrow \infty } (x_i|x'_i)_w, \end{aligned}$$

where the infimum is taken over all sequences \(\{x_i\} \in \xi \), \(\{x'_i\} \in \xi ' \).

A metric d on \(\partial _\infty X\) is visual if there exist \(w\in X\), \(A > 1\) and positive constants \(k_1\), \(k_2\), such that

$$\begin{aligned} k_1A^{-(\xi |\xi ')_w} \le d(\xi , \xi ') \le k_2A^{-(\xi |\xi ')_w} \end{aligned}$$

for all \(\xi , \xi ' \in \partial _\infty X\). In this case, we say that d is a visual metric with respect to w and A.

Theorem 1

[19, Theorem 2.2.7] If X is a hyperbolic space, then for every \(w \in X\), there exists \(A_0 > 1\) such that for each \(A \in (1, A_0]\) there is a metric \(d_A\) on \(\partial _\infty X\), which is visual with respect to w and A.

Note that \(\partial _\infty X\) is a bounded and complete metric space for any visual metric.

Theorem 2

[41, Theorem 4.15] If G is a hyperbolic uniform infinite graph with a pole, then \(h(G)>0\) if and only if \(\partial _\infty G\) is uniformly perfect for some visual metric.

Let (X, d) be a metric space, \(Y \subset X\) and \(t>0\). The subset Y is t-separated in X if \(d(y_1,y_2)\ge t\) for any \(y_1,y_2\in Y\) with \(y_1 \ne y_2\). A t-approximation of X is a maximal (with respect to the inclusion) t-separated set in X.

Let X be a complete Riemannian manifold with induced metric d. If \(A_\varepsilon \) is an \(\varepsilon \)-approximation of X, the graph \(\varGamma _{A_\varepsilon }=(A_\varepsilon ,E)\) with \(E:=\{xy \, : \, x,y \in A_\varepsilon , \, 0<d(x,y)\le 2\varepsilon \}\) is called an \(\varepsilon \)-net of X.

Proposition 1

[37, Lemmas 2.5 and 4.5] If X is a complete Riemannian manifold with bounded local geometry and \(\varGamma \) is an \(\varepsilon \)-net in X, then \(\varGamma \) and X are quasi-isometric, and \(h(X)>0\) if and only if \(h(\varGamma )>0\).

Theorem 3

[32, p.88] If X and Y are quasi-isometric geodesic metric spaces, then X is hyperbolic if and only if Y is hyperbolic.

Proposition 2

[41, Proposition 5.6] If X and Y are quasi-isometric hyperbolic proper geodesic metric spaces, then X has a pole if and only if Y has a pole.

Lemma 1

[37, Lemma 2.3] Any \(\varepsilon \)-net in a complete Riemannian manifold with bounded local geometry is uniform.

Theorem 4

[41, Theorem 5.12] If X is a hyperbolic non-compact complete Riemannian manifold with bounded local geometry and a pole, then \(h(X)>0\) if and only if \(\partial _\infty X\) is uniformly perfect.

In [21] appear several sufficient conditions that guarantee that a Riemannian n-manifold is hyperbolic. Besides, see [53] for the case \(n=2\) of Riemannian surfaces.

3 Main results

In this section we prove that having a pole is a necessary condition for a hyperbolic uniform graph or a complete Riemannian manifold with bounded local geometry satisfying isoperimetric inequality. Therefore, it can be removed as hypothesis in the statements of Theorems 2 and 4.

In fact, we are going to prove the following results.

Theorem 5

Given a hyperbolic uniform graph \(\varGamma \), then \(h(\varGamma )>0\) if and only if \(\varGamma \) is an infinite graph with a pole and \(\partial _\infty \varGamma \) is uniformly perfect for some visual metric.

Theorem 6

Let X be a hyperbolic complete Riemannian manifold with bounded local geometry. Then, \(h(X)>0\) if and only if X is non-compact and has a pole and \(\partial _\infty X\) is uniformly perfect.

These results are a consequence of Theorems 2, 4, and the two following results.

Theorem 7

Let \(\varGamma \) be a uniform graph. If \(\varGamma \) is hyperbolic and \(h(\varGamma )>0\), then \(\varGamma \) is an infinite graph with a pole.

Theorem 8

Let X be a complete Riemannian manifold with bounded local geometry. If X is hyperbolic and \(h(X)>0\), then X is non-compact and has a pole.

Let us now proceed with the proof of Theorem 7.

Proof

Seeking for a contradiction assume that \(\varGamma \) is a finite graph. Since \(h(\varGamma )>0\), if we consider the set \(U= V(\varGamma )\), then

$$\begin{aligned} 0 < h(\varGamma ) \le \frac{|\partial V(\varGamma )|}{|V(\varGamma )|} = 0, \end{aligned}$$

a contradiction. Therefore, \(\varGamma \) is an infinite graph.

Seeking for a contradiction assume that \(\varGamma \) does not have a pole. Let \(\mu \) be a constant such that \(\varGamma \) is \(\mu \)-uniform.

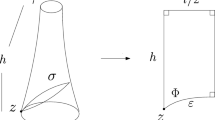
Fix \(v\in V(\varGamma )\) and denote by K the union of the geodesic rays starting from v. Note that there exists at least a geodesic ray, since \(\varGamma \) is an infinite graph, and so \(K \ne \emptyset \). Since \(\varGamma \) does not have a pole, for each n there exists \(v_n\in V(\varGamma )\) with \(d_\varGamma (v_n,K) \ge 4n\). Let \(\eta _n : [0,\ell _n] \rightarrow \varGamma \) be a geodesic joining \(v_n\) with K and such that \(\eta _n(0)= v_n\) and \(d_\varGamma (v_n,K) = L(\eta _n) = \ell _n \ge 4n\).

Given \(s \in \mathbb {R}\), denote by \(\lfloor s \rfloor \) the lower integer part of s, i.e., the largest integer not greater than s. Assume that the ball \(B_\varGamma \big (\eta _n(t),\lfloor \delta _{th}(\varGamma ) \rfloor +1 \big )\) intersects every geodesic joining \(v_n\) with some point of K, for some \(t \in \mathbb {Z}^+\) with \(\lfloor \delta _{th}(\varGamma ) \rfloor < t \le 4n \le \ell _n\). Thus, the connected component \(A_n\) of \(\varGamma {\setminus } B_\varGamma \big (\eta _n(t),\lfloor \delta _{th}(\varGamma ) \rfloor +1 \big )\) containing \(v_n\) satisfies that its boundary \(\partial A_n\) is contained in the sphere \(S_\varGamma \big (\eta _n(t),\lfloor \delta _{th}(\varGamma ) \rfloor \big )\) since \(\varGamma \) is a graph.

Since \(\varGamma \) is \(\mu \)-uniform,

$$\begin{aligned} | \partial A_n | \le \big | S_\varGamma \big (\eta _n(t),\lfloor \delta _{th}(\varGamma ) \rfloor \big ) \big | \le \mu ^{\lfloor \delta _{th}(\varGamma ) \rfloor } . \end{aligned}$$

Thus

$$\begin{aligned}&t - \lfloor \delta _{th}(\varGamma ) \rfloor = \big | V(\varGamma ) \cap \eta _n \big (\big [ 0, t - \lfloor \delta _{th}(\varGamma ) \rfloor - 1 \big ] \big ) \big | \\&\quad \le | A_n | \le h(\varGamma )^{-1} | \partial A_n | \le h(\varGamma )^{-1} \mu ^{\lfloor \delta _{th}(\varGamma ) \rfloor } , \end{aligned}$$

and we conclude that

$$\begin{aligned} t \le \lfloor \delta _{th}(\varGamma ) \rfloor + h(\varGamma )^{-1} \mu ^{\lfloor \delta _{th}(\varGamma ) \rfloor } =: M . \end{aligned}$$

Hence, if \(2n> M\), there exists a geodesic \(\sigma _n\) from \(v_n\) to K such that \(\sigma _n \cap B_\varGamma \big (\eta _n(2n),\lfloor \delta _{th}(\varGamma ) \rfloor +1 \big ) = \emptyset \). Note that \(d_\varGamma (\eta _n(2n),K) = \ell _n - 2n \ge 2n\). Let \(x_n\) and \(y_n\) be the endpoints of \(\eta _n\) and \(\sigma _n\) in K, respectively, and consider the geodesic triangle \(T^n=\{v_n,x_n,y_n\}\) in \(\varGamma \). Since \(\delta _{th}(\varGamma ) < \lfloor \delta _{th}(\varGamma ) \rfloor +1\), we have

$$\begin{aligned} d_\varGamma (\eta _n(2n),\sigma _n) \ge \lfloor \delta _{th}(\varGamma ) \rfloor +1 > \delta _{th}(\varGamma ), \end{aligned}$$

and so, there exists \(z_n \in [x_ny_n]\) with \(d_\varGamma (\eta _n(2n),z_n) \le \delta _{th}(\varGamma )\) (see Fig. 1).

Fig. 1
figure 1

If there is a geodesic \(\sigma _n=[v_ny_n]\) from \(v_n\) to K which does not intersect the ball \(B_\varGamma \big (\eta _n(2n),\delta ' \big )\), where \(\delta ':=\lfloor \delta _{th}(\varGamma ) \rfloor +1\), then there is a point \(z_n\in [x_ny_n]\) which is far from K

Full size image

Consider now the geodesic triangle \(T_n=\{v,x_n,y_n\}\) in \(\varGamma \), and \(z_n \in [x_ny_n]\). Since \([vx_n]\cup [vy_n] \subset K\), we have

$$\begin{aligned}&\delta _{th}(\varGamma ) \ge d_\varGamma (z_n,[vx_n]\cup [vy_n]) \ge d_\varGamma (z_n,K) \\&\quad \ge d_\varGamma (\eta _n(2n),K) - d_\varGamma (\eta _n(2n),z_n) \ge 2n - \delta _{th}(\varGamma ), \end{aligned}$$

and so, \(\delta _{th}(\varGamma ) \ge n\) for every n. This is the contradiction we were looking for, since \(\varGamma \) is hyperbolic, and we conclude that \(\varGamma \) has a pole. \(\square \)

Finally, let us now proceed with the proof of Theorem 8.

Proof

Seeking for a contradiction assume that X is a compact manifold. Since \(h(X)>0\), if we consider the set \(U= X\), then

$$\begin{aligned} 0 < h(X) \le \frac{{{\,\mathrm{Vol}\,}}_{n-1}(\partial X)}{{{\,\mathrm{Vol}\,}}_{n}(X)} = 0, \end{aligned}$$

a contradiction. Hence, X is non-compact.

Let \(\varGamma \) be an \(\varepsilon \)-net in X. Since \(h(X)>0\), Proposition 1 gives that \(h(\varGamma )>0\).

Note that X is a proper geodesic metric space since it is a complete Riemannian manifold. Also, \(\varGamma \) is a proper geodesic metric space since it is a uniform graph by Lemma 1.

By Proposition 1, X and \(\varGamma \) are quasi-isometric and so, \(\varGamma \) is hyperbolic by Theorem 3. Theorem 7 gives that \(\varGamma \) has a pole, and by Proposition 2, X has a pole. \(\square \)

Remark 1

Theorem 5 also allows to improve Theorem 4.12 in [42] which is based in the same results. In the same way, having a pole is a necessary condition and can be removed as hypothesis.

Remark 2

Theorem 5.11 in [44] states that for geodesic, visual, Gromov hyperbolic spaces, having uniformly perfect boundary at infinity is equivalent to being uniformly equilateral. Thus, Theorems 5 and 6 can also be written using this property and without using the boundary at infinity.