Abstract
We prove a functorial correspondence between a category of logarithmic \(\mathfrak {sl}_2\)-connections on a curve \({\mathsf {X}}\) with fixed generic residues and a category of abelian logarithmic connections on an appropriate spectral double cover  . The proof is by constructing a pair of inverse functors \(\pi ^\text {ab}, \pi _\text {ab}\), and the key is the construction of a certain canonical cocycle valued in the automorphisms of the direct image functor \(\pi _*\).
. The proof is by constructing a pair of inverse functors \(\pi ^\text {ab}, \pi _\text {ab}\), and the key is the construction of a certain canonical cocycle valued in the automorphisms of the direct image functor \(\pi _*\).
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
This paper describes an approach to analysing meromorphic connections on Riemann surfaces. The technique, called abelianisation, is to introduce a decorated graph \(\Gamma \) on a Riemann surface \({\mathsf {X}}\) in order to establish a correspondence between meromorphic connections on vector bundles of higher rank over \({\mathsf {X}}\) and meromorphic connections on line bundles (which we call abelian connections) over a multi-sheeted ramified cover  . Namely, given a flat vector bundle \({{\mathcal {E}}}\) on \({\mathsf {X}}\), an application of the standard local theory of singular differential equations near each pole allows one to extract valuable asymptotic information in the form of locally defined flat filtrations on \({{\mathcal {E}}}\), first discovered by Levelt [18]. These filtrations, often called Levelt filtrations, can be organised into a single flat line bundle \({{\mathcal {L}}}\) over
. Namely, given a flat vector bundle \({{\mathcal {E}}}\) on \({\mathsf {X}}\), an application of the standard local theory of singular differential equations near each pole allows one to extract valuable asymptotic information in the form of locally defined flat filtrations on \({{\mathcal {E}}}\), first discovered by Levelt [18]. These filtrations, often called Levelt filtrations, can be organised into a single flat line bundle \({{\mathcal {L}}}\) over  , and \({{\mathcal {E}}}\) can be recovered from \({{\mathcal {L}}}\) using the combinatorial data encoded in \(\Gamma \).
, and \({{\mathcal {E}}}\) can be recovered from \({{\mathcal {L}}}\) using the combinatorial data encoded in \(\Gamma \).
1.1 Main result
In this paper, we restrict our attention to the simplest case of \(\mathfrak {sl}_2\)-connections with logarithmic singularities and generic residues. Our main result (Theorem 3.3) is a natural equivalence between a category of \(\mathfrak {sl}_2\)-connections on \({\mathsf {X}}\) and a category of logarithmic abelian connections on a double cover  of \({\mathsf {X}}\). More precisely, fix \(({\mathsf {X}},{\mathsf {D}})\) a compact smooth complex curve with a finite set of marked points, fix the data of generic residues along \({\mathsf {D}}\), and choose an appropriate meromorphic quadratic differential \(\varphi \) on \({\mathsf {X}}\) with double poles along \({\mathsf {D}}\). Then \(\varphi \) gives rise to a double cover
of \({\mathsf {X}}\). More precisely, fix \(({\mathsf {X}},{\mathsf {D}})\) a compact smooth complex curve with a finite set of marked points, fix the data of generic residues along \({\mathsf {D}}\), and choose an appropriate meromorphic quadratic differential \(\varphi \) on \({\mathsf {X}}\) with double poles along \({\mathsf {D}}\). Then \(\varphi \) gives rise to a double cover  (called the spectral curve) ramified at
(called the spectral curve) ramified at  , a graph \(\Gamma \) on \({\mathsf {X}}\) (called the Stokes graph), and a transversality condition on the Levelt filtrations extracted at nearby poles as dictated by \(\Gamma \). Then there is a natural equivalence of categories:
, a graph \(\Gamma \) on \({\mathsf {X}}\) (called the Stokes graph), and a transversality condition on the Levelt filtrations extracted at nearby poles as dictated by \(\Gamma \). Then there is a natural equivalence of categories:

Given a flat vector bundle \({{\mathcal {E}}}\) on \({\mathsf {X}}\), the abelianisation functor \(\pi ^\text {ab}_\Gamma \) extracts Levelt filtrations along \({\mathsf {D}}\) and glues them into a flat line bundle \({{\mathcal {L}}}\) over  . In order to recover \({{\mathcal {E}}}\) from \({{\mathcal {L}}}\), the main difficulty is that the naive guess that \({{\mathcal {E}}}\) is the pushforward \(\pi _*{{\mathcal {L}}}\) is incorrect because \(\pi _*{{\mathcal {L}}}\) necessarily has logarithmic singularities along the branch locus. The solution is to realise the combinatorial content of the Stokes graph \(\Gamma \) in cohomology: we construct a canonical cocycle \(\mathbb {V}\) on \({\mathsf {X}}\) (called the Voros cocycle) which deforms the pushforward functor \(\pi _*\), as a functor, and this deformation is the nonabelianisation functor \(\pi _\text {ab}^\Gamma \). The Voros cocycle is constructed in a completely standardised and combinatorial way from the Stokes graph \(\Gamma \). This is significant because it means \(\mathbb {V}\) is constructed without reference to any specific choice of \({{\mathcal {E}}}\) or \({{\mathcal {L}}}\), thereby setting up an equivalence of categories.
. In order to recover \({{\mathcal {E}}}\) from \({{\mathcal {L}}}\), the main difficulty is that the naive guess that \({{\mathcal {E}}}\) is the pushforward \(\pi _*{{\mathcal {L}}}\) is incorrect because \(\pi _*{{\mathcal {L}}}\) necessarily has logarithmic singularities along the branch locus. The solution is to realise the combinatorial content of the Stokes graph \(\Gamma \) in cohomology: we construct a canonical cocycle \(\mathbb {V}\) on \({\mathsf {X}}\) (called the Voros cocycle) which deforms the pushforward functor \(\pi _*\), as a functor, and this deformation is the nonabelianisation functor \(\pi _\text {ab}^\Gamma \). The Voros cocycle is constructed in a completely standardised and combinatorial way from the Stokes graph \(\Gamma \). This is significant because it means \(\mathbb {V}\) is constructed without reference to any specific choice of \({{\mathcal {E}}}\) or \({{\mathcal {L}}}\), thereby setting up an equivalence of categories.
1.2 Context: spectral networks and exact WKB
Analysis of higher rank connections using abelian connections over a multi-sheeted cover has previously appeared in the context of spectral networks [7,8,9,10, 14], and even earlier from a different point of view in the context of the exact WKB analysis; e.g., [4, 16, 21]. The purpose of our work is to give a mathematical formulation of abelianisation of connections, and this paper is the first and important step in this direction. Our point of view, via the deformation theory of the pushforward functor, sheds light on the mathematical content of the methods of spectral networks and the exact WKB analysis, unifying the insights coming from these theories. Indeed, the local expressions for the Voros cocycle \(\mathbb {V}\) involve precisely the same type of unipotent matrices that appear in the pioneering work of Voros on the exact WKB analysis [21] (we call \(\mathbb {V}\) the Voros cocycle exactly for this reason). At the same time, the off-diagonal terms of \(\mathbb {V}\) are given in terms of abelian parallel transports along canonically defined paths on the spectral curve. These appeared in the work of Gaiotto–Moore–Neitzke [8] which inspired the current project. In fact, one of the main achievements of this paper is giving a clear mathematical explanation that the path-lifting rule appearing in [8] emerges simply from the repeated application of the Voros cocycle.
1.3 Outlook
Abelianisation of connections can be seen as generalising the abelianisation of Higgs bundles [1, 13] (a.k.a. the spectral correspondence, which is a key step in the analysis of Hitchin integrable systems and the geometric Langlands programme) to flat bundles. Indeed, Proposition 3.6 shows that the abelianisation line bundle \({{\mathcal {L}}}\) is the correct analogue of the spectral line bundle. It was also conjectured in the work of Gaiotto–Moore–Neitzke [8] that such a procedure of abelianisation of connections should yield symplectic cluster coordinates on moduli spaces of meromorphic connections. This article (which is an extension of the work the author completed in his thesis [19]) is thus the first important step in realising this programme in mathematical terms.
1.4 Content
The article is dedicated to the proof of Theorem 3.3, which proceeds by constructing the functors \(\pi ^\text {ab}_\Gamma , \pi _\text {ab}^\Gamma \) and showing that they form an inverse equivalence. Propositions 3.5 and 3.6 give a summary of the main properties of the relationship between \(({{\mathcal {E}}}, \nabla )\) and its abelianisation  . We also make the curious observation that the nonabelian Voros cocycle may itself be abelianised: there is an abelian cocycle
. We also make the curious observation that the nonabelian Voros cocycle may itself be abelianised: there is an abelian cocycle  on the spectral curve
on the spectral curve  which completely determines the Voros cocycle \(\mathbb {V}\) in the sense of Proposition 3.16.
which completely determines the Voros cocycle \(\mathbb {V}\) in the sense of Proposition 3.16.
2 Logarithmic connections and spectral curves
Throughout this paper, let \({\mathsf {X}}\) be a compact smooth complex curve and \({\mathsf {D}} \subset {\mathsf {X}}\) a finite set of marked points. We assume that \({\mathsf {D}}\) is nonempty with \(|{\mathsf {D}}| > \chi ({\mathsf {X}}) = 2 - 2g_{\mathsf {X}}\), where \(g_{\mathsf {X}}\) is the genus of \({\mathsf {X}}\). The Lie algebra \(\mathfrak {sl} (2, \mathbb {C})\) is denoted by \(\mathfrak {sl}_2\).
2.1 Logarithmic connections and Levelt filtrations
2.1. A logarithmic \(\mathfrak {sl}_2\)- connection on \(({\mathsf {X}}, {\mathsf {D}})\) is the data \(({{\mathcal {E}}}, \nabla , M )\) of a holomorphic rank-two vector bundle \({{\mathcal {E}}}\) on \({\mathsf {X}}\), a \({\underline{\mathbb {C}}}_{\mathsf {X}}\)-linear map of sheaves
satisfying the Leibniz rule  for all \(e \in {{\mathcal {E}}}, f \in {{\mathcal {O}}}_{\mathsf {X}}\), and a trivialisation
for all \(e \in {{\mathcal {E}}}, f \in {{\mathcal {O}}}_{\mathsf {X}}\), and a trivialisation  such that
such that  . They form a category, which we denote by \(Conn ^2_{\mathfrak {sl}} ({\mathsf {X}},{\mathsf {D}})\). We will often omit “\( M \)” from the notation.
. They form a category, which we denote by \(Conn ^2_{\mathfrak {sl}} ({\mathsf {X}},{\mathsf {D}})\). We will often omit “\( M \)” from the notation.
2.2. Generic Levelt exponents and residue data. The residue sequence for \(\Omega ^1_{\mathsf {X}} ({\mathsf {D}})\) implies that the restriction of \(\nabla \) to \({\mathsf {D}}\) is a well-defined \({{\mathcal {O}}}_{\mathsf {D}}\)-linear endomorphism  , called the residue of \(\nabla \) along \({\mathsf {D}}\). A further restriction of \({\text {Res}}\nabla \) to any point \(\mathsf {p}\in {\mathsf {D}}\) is an endomorphism of the fibre
, called the residue of \(\nabla \) along \({\mathsf {D}}\). A further restriction of \({\text {Res}}\nabla \) to any point \(\mathsf {p}\in {\mathsf {D}}\) is an endomorphism of the fibre  whose eigenvalues \(\pm \lambda _\mathsf {p}\in \mathbb {C}\) are called the Levelt exponents of \(\nabla \) at \(\mathsf {p}\). The determinant map
whose eigenvalues \(\pm \lambda _\mathsf {p}\in \mathbb {C}\) are called the Levelt exponents of \(\nabla \) at \(\mathsf {p}\). The determinant map  sends \({\text {Res}}\nabla \) to a global section of \({{\mathcal {O}}}_{\mathsf {D}}\):
sends \({\text {Res}}\nabla \) to a global section of \({{\mathcal {O}}}_{\mathsf {D}}\):

2.3 Definition
(Generic residue data) The Levelt exponents \(\pm \lambda _\mathsf {p}\) at \(\mathsf {p}\) are called generic if \({\text {Re}}(\lambda _\mathsf {p}) \ne 0\) and \(\lambda _\mathsf {p}\notin \tfrac{1}{2} {\mathbb {Z}}\). We will refer to any section \(a \in {\mathsf {H}}^0_{\mathsf {X}} ({{\mathcal {O}}}_{\mathsf {D}})\) as residue data, and say it is generic if for each \(\mathsf {p}\in {\mathsf {D}}\), the two square roots \(\pm \lambda _\mathsf {p}\) of \(a_\mathsf {p}\) define generic Levelt exponents.
2.4. Thus, a is generic if and only if each complex number \(a_\mathsf {p}\) is not purely negative real or a quarter square \(n^2/4\) for some \(n \in {\mathbb {Z}}\). We will always order the generic Levelt exponents by their increasing real part: \(- \lambda _\mathsf {p}\prec \lambda _\mathsf {p}\) if and only if \({\text {Re}}(\lambda _\mathsf {p}) > 0\). The assumption that \({\text {Re}}(\lambda _\mathsf {p}) \ne 0\) is necessary for the construction in this paper because we will use the ordering \(\prec \), but the assumption that \(\lambda _\mathsf {p}\notin \tfrac{1}{2} {\mathbb {Z}}\) (usually called non-resonance) can be removed without a great deal of difficulty; in this paper, however, we restrict ourselves to this simplest situation and generalisations will appear elsewhere.
2.5 Example
Perhaps the most familiar explicit example is the following. Take \({\mathsf {X}} \mathrel {\mathop :}=\mathbb {P}^1\), fix \(d \geqslant 3\) distinct points \({\mathsf {D}} \mathrel {\mathop :}=\left\{ u_1, \ldots , u_{d} \right\} \subset \mathbb {P}^1\), and d constant matrices \( A _1, \ldots , A _d \in \mathfrak {sl}_2\) with \( A _1 + \cdots + A _d = 0\). We usually choose an affine coordinate z on \(\mathbb {P}^1 =\mathrel {\mathop :}\mathbb {P}^1_z\) such that \(u_d\) is the point at infinity. Then the trivial rank-two vector bundle \({{\mathcal {E}}} = {{\mathcal {O}}}_{\mathbb {P}^1} \oplus {{\mathcal {O}}}_{\mathbb {P}^1}\) is equipped with a logarithmic connection \(\nabla \) defined with respect to the standard basis for \({{\mathcal {E}}}\) by the following formula in the affine coordinate charts z and \(w = z^{-1}\):

Evidently, \(\nabla \) has logarithmic singularities at each point \(u_i\) with residue \({\text {Res}}_{u_i} \nabla = A _i\). The residue \({\text {Res}}\nabla \) along \({\mathsf {D}}\) is then simply the full collection of the chosen matrices \(\left\{ A _1, \ldots , A _d \right\} \). The eigenvalues \(\pm \lambda _i \in \mathbb {C}\) of each \( A _i\) are the Levelt exponents of \(\nabla \), so the residue data of \(\nabla \) is \(a = \left\{ \lambda _1^2, \ldots , \lambda _d^2 \right\} \).
2.6. The central object of study in this paper is the category of logarithmic \(\mathfrak {sl}_2\)-connections on \(({\mathsf {X}},{\mathsf {D}})\) with fixed generic residue data a, for which we shall use the following shorthand notation:

2.7. Local diagonal decomposition. Fix a point \(\mathsf {p}\in {\mathsf {D}}\), and consider a connection germ \(({{\mathcal {E}}}_\mathsf {p}, \nabla _\mathsf {p})\) at \(\mathsf {p}\) with generic Levelt exponents \(\pm \lambda _\mathsf {p}\) at \(\mathsf {p}\), where \({\text {Re}}(\lambda ) > 0\). A coordinate trivialisation  transforms \(\nabla _\mathsf {p}\) to a logarithmic \(\mathfrak {sl}_2\)-differential system
transforms \(\nabla _\mathsf {p}\) to a logarithmic \(\mathfrak {sl}_2\)-differential system  , where
, where  is some \(\mathfrak {sl}_2\)-matrix of holomorphic function germs. By [22, Theorems 5.1, 5.4], there exists a holomorphic \({\mathsf {SL}}_2\) gauge transformation which transforms the given differential system into the diagonal system
is some \(\mathfrak {sl}_2\)-matrix of holomorphic function germs. By [22, Theorems 5.1, 5.4], there exists a holomorphic \({\mathsf {SL}}_2\) gauge transformation which transforms the given differential system into the diagonal system  which depends only on \(\lambda _\mathsf {p}\) and z. This classical theorem about singular ordinary differential equations admits vast generalisations, but we do not need them here. Together with the fixed ordering on the Levelt exponents, it induces a graded decomposition of \({{\mathcal {E}}}_\mathsf {p}\) with respect to which \(\nabla _\mathsf {p}\) is diagonal.
which depends only on \(\lambda _\mathsf {p}\) and z. This classical theorem about singular ordinary differential equations admits vast generalisations, but we do not need them here. Together with the fixed ordering on the Levelt exponents, it induces a graded decomposition of \({{\mathcal {E}}}_\mathsf {p}\) with respect to which \(\nabla _\mathsf {p}\) is diagonal.
2.8 Proposition
(Local diagonal decomposition) Let \(({{\mathcal {E}}}_\mathsf {p}, \nabla _\mathsf {p}, M _\mathsf {p})\) be the germ of a logarithmic \(\mathfrak {sl}_2\)-connection at \(\mathsf {p}\in {\mathsf {D}}\) with generic Levelt exponents \(\pm \lambda _\mathsf {p}\). Then there is a canonical ordered decomposition

where  is a rank-one logarithmic connection germ at \(\mathsf {p}\) with residue \(\pm \lambda _\mathsf {p}\). Moreover, \( M \) induces a flat skew-symmetric isomorphism
is a rank-one logarithmic connection germ at \(\mathsf {p}\) with residue \(\pm \lambda _\mathsf {p}\). Moreover, \( M \) induces a flat skew-symmetric isomorphism  .
.
Here, “skew-symmetric” means that \( M _\mathsf {p}\) is multiplied by \(-1\) under the switching map. The order on the Levelt exponents \(- \lambda _\mathsf {p}\prec + \lambda _\mathsf {p}\) determines a \(\nabla _\mathsf {p}\)-invariant filtration \({{\mathcal {E}}}_\mathsf {p}^\bullet \mathrel {\mathop :}=\big ( \Lambda ^-_\mathsf {p}\subset {{\mathcal {E}}}_\mathsf {p}\big )\) on the vector bundle germ \({{\mathcal {E}}}_\mathsf {p}\), which we will refer to as the Levelt filtration in reference to the more general such concept studied by Levelt in his thesis [18].
We will refer to the \(\nabla _\mathsf {p}\)-invariant filtration \({{\mathcal {E}}}_\mathsf {p}^\bullet \mathrel {\mathop :}=\big ( \Lambda ^-_\mathsf {p}\subset {{\mathcal {E}}}_\mathsf {p}\big )\), given by the order on the Levelt exponents \(- \lambda _\mathsf {p}\prec + \lambda _\mathsf {p}\), as the Levelt filtration on the vector bundle germ \({{\mathcal {E}}}_\mathsf {p}\). Clearly, any pair of logarithmic \(\mathfrak {sl}_2\)-connection germs \(({{\mathcal {E}}}_\mathsf {p}, \nabla _\mathsf {p}), ({{\mathcal {E}}}'_\mathsf {p}, \nabla '_\mathsf {p})\) with the same generic Levelt exponents \(\pm \lambda _\mathsf {p}\) at \(\mathsf {p}\) are isomorphic and any such isomorphism is necessarily diagonal with respect to the diagonal decompositions. Any morphism \(({{\mathcal {E}}}_\mathsf {p}, \nabla _\mathsf {p}) \rightarrow ({{\mathcal {E}}}'_\mathsf {p}, \nabla '_\mathsf {p})\) necessarily preserves the Levelt filtration.
2.9 Example
Continuing Example 2.5, assume that \(\nabla \) has generic residue data, and restrict our attention to the disc germ of, say, the singularity \(u_1\). There is an \({\mathsf {SL}}_2\) matrix \( G = G (z)\), holomorphic at \(z = u_1\), such that

Then the line subbundles \(\Lambda _{1}^-, \Lambda _1^+\) are generated by \(e_- \mathrel {\mathop :}= G ^{-1} {\tiny \begin{bmatrix}1\\ 0\end{bmatrix}}\) and \(e_+ \mathrel {\mathop :}= G ^{-1} {\tiny \begin{bmatrix}0\\ 1\end{bmatrix}}\).
2.2 Logarithmic connections and double covers
Logarithmic connections can be pulled back and pushed forward along ramified covers. In this section we describe these operations, restricting ourselves to the simplest case of double covers  with simple ramification and which are trivial over the polar divisor \({\mathsf {D}}\). Thus, let \({\mathsf {C}} \mathrel {\mathop :}=\pi ^{-1} ({\mathsf {D}})\) and let
with simple ramification and which are trivial over the polar divisor \({\mathsf {D}}\). Thus, let \({\mathsf {C}} \mathrel {\mathop :}=\pi ^{-1} ({\mathsf {D}})\) and let  be the ramification divisor. Here and everywhere, we assume that \({\mathsf {R}}\) has no higher multiplicity and that the branch locus \({\mathsf {B}} \mathrel {\mathop :}=\pi ({\mathsf {R}}) \subset {\mathsf {X}}\) is disjoint from \({\mathsf {D}}\). We denote by
be the ramification divisor. Here and everywhere, we assume that \({\mathsf {R}}\) has no higher multiplicity and that the branch locus \({\mathsf {B}} \mathrel {\mathop :}=\pi ({\mathsf {R}}) \subset {\mathsf {X}}\) is disjoint from \({\mathsf {D}}\). We denote by  the canonical involution.
the canonical involution.
2.10. Odd abelian connections. Connections on line bundles are sometimes called abelian connections. The line bundle  carries a canonical logarithmic connection
carries a canonical logarithmic connection  , defined to be the connection for which the canonical map
, defined to be the connection for which the canonical map  is flat. Explicitly, if z is a local coordinate on
is flat. Explicitly, if z is a local coordinate on  vanishing at \(\mathsf {r}\in {\mathsf {R}}\), then the local section
vanishing at \(\mathsf {r}\in {\mathsf {R}}\), then the local section  gives a trivialisation, in which
gives a trivialisation, in which  is given by
is given by

2.11 Definition
(Odd abelian connection) An odd abelian logarithmic connection on  is the data
is the data  consisting of an abelian logarithmic connection on
consisting of an abelian logarithmic connection on  equipped with a skew-symmetric isomorphism
equipped with a skew-symmetric isomorphism  intertwining
intertwining  and
and  .
.
Here, “skew-symmetric” means \(\mu \) satisfies \(\sigma ^*\mu = - \mu \). Abelian connections with a similar structure but over the punctured curve  have appeared in [14, §4.2] under the name equivariant connections. We refer to the isomorphism \(\mu \) as the odd structure on
have appeared in [14, §4.2] under the name equivariant connections. We refer to the isomorphism \(\mu \) as the odd structure on  . Odd abelian connections form a category
. Odd abelian connections form a category

where morphisms are morphisms of connections \(\phi : {{\mathcal {L}}} \rightarrow {{\mathcal {L}}}'\) that intertwine the odd structures \(\mu , \mu '\) in the sense that \(\mu ' \circ (\phi \otimes \sigma ^*\phi ) = \mu \). It is easy to check that if \(\mu _1, \mu _2\) are any two odd structures on the same abelian connection  , then
, then  , and there are exactly two such isomorphisms.
, and there are exactly two such isomorphisms.
2.12 Proposition
(Residues of odd connections) The residue of any odd abelian connection  at a ramification point is \(-1/2\). In particular, the monodromy of
at a ramification point is \(-1/2\). In particular, the monodromy of  around a ramification point is \(-1\). Furthermore, if \(\mathsf {p}\in {\mathsf {D}}\) and \(\mathsf {p}_\pm \in {\mathsf {C}}\) are the two preimages of \(\mathsf {p}\), then the residues of
around a ramification point is \(-1\). Furthermore, if \(\mathsf {p}\in {\mathsf {D}}\) and \(\mathsf {p}_\pm \in {\mathsf {C}}\) are the two preimages of \(\mathsf {p}\), then the residues of  at \(\mathsf {p}_\pm \) satisfy
at \(\mathsf {p}_\pm \) satisfy

Proof
The residue of  at \(\mathsf {r}\in {\mathsf {R}}\) is \(-1\). If
at \(\mathsf {r}\in {\mathsf {R}}\) is \(-1\). If  , then the residue of the connection
, then the residue of the connection  at \(\mathsf {r}\) is \(2 \lambda \), so the odd structure on \({{\mathcal {L}}}\) forces \(\lambda = -1/2\). Next, since \(\sigma (\mathsf {p}_-) = \mathsf {p}_+\), the residue at \(\mathsf {p}_-\) of
at \(\mathsf {r}\) is \(2 \lambda \), so the odd structure on \({{\mathcal {L}}}\) forces \(\lambda = -1/2\). Next, since \(\sigma (\mathsf {p}_-) = \mathsf {p}_+\), the residue at \(\mathsf {p}_-\) of  is equal to the residue of
is equal to the residue of  at \(\mathsf {p}_+\). This means
at \(\mathsf {p}_+\). This means  has residue
has residue  at \(\mathsf {p}_-\). But the residue of
at \(\mathsf {p}_-\). But the residue of  at \(\mathsf {p}_-\) is 0, so the odd structure on \({{\mathcal {L}}}\) forces the identity. \(\square \)
at \(\mathsf {p}_-\) is 0, so the odd structure on \({{\mathcal {L}}}\) forces the identity. \(\square \)
By using the residue theorem for connections [6, Cor. (B.3), p.186], it is easy to compute the degree of a line bundle carrying an odd connection.
2.13 Proposition
(Degree of odd connections) If  , then
, then  .
.
2.14. Pullback and pushforward of connections. The pullback of \({{\mathcal {O}}}_{\mathsf {X}}\)-modules along \(\pi \) extends to a pullback functor on connections

by the rule \(\pi ^*\nabla (\pi ^*e) = \pi ^*(\nabla e)\) for any local section \(e \in {{\mathcal {E}}}\). Clearly, the Levelt exponents of \(\nabla \) at \(\mathsf {p}\in {\mathsf {D}}\) and the Levelt exponents of \(\pi ^*\nabla \) at any preimage \(\tilde{\mathsf {p}} \in {\mathsf {C}}\) of \(\mathsf {p}\) are the same. More interesting is pushing connections forward along \(\pi \). The direct image functor \(\pi _*\) of  -modules can be used to pushforward connections from
-modules can be used to pushforward connections from  down to \({\mathsf {X}}\), but the relationship between the polar divisors is more complicated (see [11, proposition 2.17] for more generality).
down to \({\mathsf {X}}\), but the relationship between the polar divisors is more complicated (see [11, proposition 2.17] for more generality).
2.15 Proposition
(Pushforward of odd abelian connections) The direct image \(\pi _*\) extends to a functor

Moreover, for any  , if \(\pm \lambda \in \mathbb {C}\) are its residues at the two preimages \(\mathsf {p}_\pm \in {\mathsf {C}}\) of a point \(\mathsf {p}\in {\mathsf {D}}\), then the Levelt exponents of
, if \(\pm \lambda \in \mathbb {C}\) are its residues at the two preimages \(\mathsf {p}_\pm \in {\mathsf {C}}\) of a point \(\mathsf {p}\in {\mathsf {D}}\), then the Levelt exponents of  at \(\mathsf {p}\) are \(\pm \lambda \).
at \(\mathsf {p}\) are \(\pm \lambda \).
Proof
A logarithmic connection on  is a map
is a map  , and its direct image is therefore
, and its direct image is therefore  . We claim that there is a canonical isomorphism
. We claim that there is a canonical isomorphism  . First, \(\pi ^*\Omega ^1_{\mathsf {X}} ({\mathsf {B}} \cup {\mathsf {D}}) = \big ( \pi ^*\Omega ^1_{\mathsf {X}} \big ) ( \pi ^*({\mathsf {B}} \cup {\mathsf {D}}))\), where \(\pi ^*({\mathsf {B}} \cup {\mathsf {D}}) = 2{\mathsf {R}} \cup {\mathsf {C}}\) (pulled back as a divisor). The derivative map
. First, \(\pi ^*\Omega ^1_{\mathsf {X}} ({\mathsf {B}} \cup {\mathsf {D}}) = \big ( \pi ^*\Omega ^1_{\mathsf {X}} \big ) ( \pi ^*({\mathsf {B}} \cup {\mathsf {D}}))\), where \(\pi ^*({\mathsf {B}} \cup {\mathsf {D}}) = 2{\mathsf {R}} \cup {\mathsf {C}}\) (pulled back as a divisor). The derivative map  drops rank along \({\mathsf {R}}\); i.e., it is a nonvanishing section of the line bundle
drops rank along \({\mathsf {R}}\); i.e., it is a nonvanishing section of the line bundle  , thereby inducing an isomorphism
, thereby inducing an isomorphism  . Dualising, we get
. Dualising, we get  . Thus, the projection formula implies
. Thus, the projection formula implies  . To check that
. To check that  satisfies the Leibniz rule, let \(e \in \pi _*{{\mathcal {L}}}\) be a local section on some open set \({\mathsf {U}} \subset {\mathsf {X}}\), and \(f \in {{\mathcal {O}}}_{\mathsf {X}} ({\mathsf {U}})\). Then
satisfies the Leibniz rule, let \(e \in \pi _*{{\mathcal {L}}}\) be a local section on some open set \({\mathsf {U}} \subset {\mathsf {X}}\), and \(f \in {{\mathcal {O}}}_{\mathsf {X}} ({\mathsf {U}})\). Then  . Now it is clear that the Leibniz rule for
. Now it is clear that the Leibniz rule for  follows from the Leibniz rule for
follows from the Leibniz rule for  . Therefore,
. Therefore,  is a rank-two logarithmic connection on \(({\mathsf {X}}, {\mathsf {B}} \cup {\mathsf {D}})\).
is a rank-two logarithmic connection on \(({\mathsf {X}}, {\mathsf {B}} \cup {\mathsf {D}})\).
To show that the odd structure on \({{\mathcal {L}}}\) induces an \(\mathfrak {sl}_2\)-structure on \(\pi _*{{\mathcal {L}}}\), recall that there is a canonical isomorphism  , where \({\text {Nm}}({{\mathcal {L}}})\) is the norm of \({{\mathcal {L}}}\) [12, Cor. 3.12]. For a double cover, there is a canonical isomorphism \(\pi ^*{\text {Nm}}({{\mathcal {L}}}) \cong {{\mathcal {L}}} \otimes \sigma ^*{{\mathcal {L}}}\). Moreover, it is easy to see that
, where \({\text {Nm}}({{\mathcal {L}}})\) is the norm of \({{\mathcal {L}}}\) [12, Cor. 3.12]. For a double cover, there is a canonical isomorphism \(\pi ^*{\text {Nm}}({{\mathcal {L}}}) \cong {{\mathcal {L}}} \otimes \sigma ^*{{\mathcal {L}}}\). Moreover, it is easy to see that  is canonically isomorphic to
is canonically isomorphic to  . The statement about the residues is obvious because \(\pi \) is unramified over \({\mathsf {D}}\). \(\square \)
. The statement about the residues is obvious because \(\pi \) is unramified over \({\mathsf {D}}\). \(\square \)
2.16. Image of \(\pi _*\). One can show that the monodromy of  around the branch locus \({\mathsf {B}}\) is a quasi-permutation representation of the double cover
around the branch locus \({\mathsf {B}}\) is a quasi-permutation representation of the double cover  [17]. As a result, no connection on \(({\mathsf {X}},{\mathsf {D}})\) is the pushforward of an abelian connection on
[17]. As a result, no connection on \(({\mathsf {X}},{\mathsf {D}})\) is the pushforward of an abelian connection on  . In other words, the image of the pushforward functor \(\pi _*\) in \(Conn ^2_{\mathfrak {sl}} ({\mathsf {X}}, {\mathsf {B}} \cup {\mathsf {D}})\) does not even intersect the subcategory \(Conn ^2_{\mathfrak {sl}} ({\mathsf {X}}, {\mathsf {D}})\). Abelianisation fixes this problem: in Sect. 3.3, we will explicitly construct a deformation of the pushforward functor \(\pi _*\) which does map into \(Conn ^2_{\mathfrak {sl}} ({\mathsf {X}}, {\mathsf {D}})\).
. In other words, the image of the pushforward functor \(\pi _*\) in \(Conn ^2_{\mathfrak {sl}} ({\mathsf {X}}, {\mathsf {B}} \cup {\mathsf {D}})\) does not even intersect the subcategory \(Conn ^2_{\mathfrak {sl}} ({\mathsf {X}}, {\mathsf {D}})\). Abelianisation fixes this problem: in Sect. 3.3, we will explicitly construct a deformation of the pushforward functor \(\pi _*\) which does map into \(Conn ^2_{\mathfrak {sl}} ({\mathsf {X}}, {\mathsf {D}})\).
2.3 Spectral curves for quadratic differentials
Let \(\varphi \) be a quadratic differential on \(({\mathsf {X}},{\mathsf {D}})\), by which we mean a meromorphic quadratic differential on \({\mathsf {X}}\) with at most order-two poles along \({\mathsf {D}}\); i.e., it is a global holomorphic section of \({\mathsf {S}}^2 \Omega ^1_{\mathsf {X}} (2{\mathsf {D}})\). The standard reference is [20]; see also [3, §§2,3]. By the Riemann–Roch Theorem,

2.17. Quadratic residue. In any local coordinate x centred at \(\mathsf {p}\in {\mathsf {D}}\), a quadratic differential \(\varphi \) with a double pole at \(\mathsf {p}\) is expanded as  . The coefficient \(a_\mathsf {p}\in \mathbb {C}\) is a coordinate-independent quantity, called the (quadratic) residue of \(\varphi \) at \(\mathsf {p}\) and denoted \({\text {Res}}_\mathsf {p}(\varphi )\). The residue of \(\varphi \) along \({\mathsf {D}}\) is thus a global section \(a = {\text {Res}}(\varphi ) \in {\mathsf {H}}^0_{\mathsf {X}} ({{\mathcal {O}}}_{\mathsf {D}})\), same as what we called residue data in Sect. 2.1. There is a quadratic residue short exact sequence:
. The coefficient \(a_\mathsf {p}\in \mathbb {C}\) is a coordinate-independent quantity, called the (quadratic) residue of \(\varphi \) at \(\mathsf {p}\) and denoted \({\text {Res}}_\mathsf {p}(\varphi )\). The residue of \(\varphi \) along \({\mathsf {D}}\) is thus a global section \(a = {\text {Res}}(\varphi ) \in {\mathsf {H}}^0_{\mathsf {X}} ({{\mathcal {O}}}_{\mathsf {D}})\), same as what we called residue data in Sect. 2.1. There is a quadratic residue short exact sequence:

2.18 Lemma
For any \(a \in {\mathsf {H}}^0_{\mathsf {X}} ({{\mathcal {O}}}_{\mathsf {D}})\), there is a quadratic differential \(\varphi \) on \(({\mathsf {X}},{\mathsf {D}})\) with \({\text {Res}}(\varphi ) = a\).
Proof
By the Kodaira Vanishing Theorem, \({\mathsf {H}}^1_{\mathsf {X}} \big ( {\mathsf {S}}^2 \Omega ^1_{\mathsf {X}} ({\mathsf {D}}) \big ) = 0\), which implies that the residue map \({\text {Res}}: {\mathsf {H}}^0_{\mathsf {X}} \big ( {\mathsf {S}}^2 \Omega ^1_{\mathsf {X}} (2{\mathsf {D}}) \big ) \rightarrow {\mathsf {H}}^0_{\mathsf {X}} \big ( {{\mathcal {O}}}_{\mathsf {D}} \big )\) is surjective. This means that any residue data a decorating the divisor \({\mathsf {D}}\) can be lifted to a quadratic differential \(\varphi \). \(\square \)
2.19. In view of (3), the only configuration \(({\mathsf {X}},{\mathsf {D}})\) for which there is a unique quadratic differential \(\varphi \) with specified residues is \((g_{\mathsf {X}}, |{\mathsf {D}}|) = (0,3)\) (i.e., \(\mathbb {P}^1\) with three marked points). In this case, the three-dimensional vector space of quadratic differentials \({\mathsf {H}}^0_{\mathsf {X}} \big ( {\mathsf {S}}^2 \Omega ^1_{\mathsf {X}} (2{\mathsf {D}}) \big )\) can be parameterised by the residues \(\alpha , \beta , \gamma \) at the three points of \({\mathsf {D}}\). Identifying \(({\mathsf {X}}, {\mathsf {D}})\) with \((\mathbb {P}^1, \left\{ 0,1,\infty \right\} )\), one can show that the unique quadratic differential with residues \(\alpha , \beta , \gamma \) at the double poles \(0,1, \infty \) is

2.20. Generic quadratic differentials. We will say that a quadratic differential \(\varphi \) is generic if all zeroes are simple. The subspace of generic quadratic differentials in \({\mathsf {H}}^0_{\mathsf {X}} \big ( {\mathsf {S}}^2 \Omega ^1_{\mathsf {X}} (2{\mathsf {D}}) \big )\) is obviously open dense given as the complement of a hypersurface. If \((g_{\mathsf {X}}, |{\mathsf {D}}|) \ne (0,3)\), then the space of quadratic differentials is at least one-dimensional; but if \((g_{\mathsf {X}}, |{\mathsf {D}}|) = (0,3)\), this is a condition on the residues of \(\varphi \). One can use (5) to calculate that the open subspace of generic quadratic differentials for \((g_{\mathsf {X}}, |{\mathsf {D}}|) = (0,3)\) is the complement of the quadratic hypersurface

2.21 Lemma
Let \(a \in {\mathsf {H}}^0_{\mathsf {X}} ({{\mathcal {O}}}_{\mathsf {D}})\) be generic residue data. If \((g_{\mathsf {X}}, |{\mathsf {D}}|) = (0, 3)\), assume in addition that a is contained in the complement of the hypersurface (6). Then there exists a generic quadratic differential \(\varphi \) on \(({\mathsf {X}},{\mathsf {D}})\) such that \({\text {Res}}(\varphi ) = a\).
2.22 Example
Consider the following examples of meromorphic quadratic differentials on \({\mathsf {X}} \mathrel {\mathop :}=\mathbb {P}^1_z\):

The quadratic differential \(\varphi _1\) is of the form (6) with \(\alpha = \beta = \gamma = 1/9\). They respectively have double poles along \({\mathsf {D}}_1 \mathrel {\mathop :}=\left\{ 0, 1, \infty \right\} \), \({\mathsf {D}}_2 \mathrel {\mathop :}=\left\{ 0, \pm 1, \infty \right\} \), and \({\mathsf {D}}_3 \mathrel {\mathop :}=\left\{ e^{\pm \pi i /4}, e^{\pm 3\pi i /4} \right\} \). Each quadratic residue of \(\varphi _1\) and \(\varphi _2\) is 1/9; each quadratic residue of \(\varphi _3\) is \(e^{\pi i /4}\). The quadratic differential \(\varphi _1\) has two simple zeros at \(e^{\pm \pi i/3}\). The quadratic differentials \(\varphi _2, \varphi _3\) both have four simple zeros; they are respectively \(e^{\pm \pi i/4}, e^{\pm 3\pi i/4}\) and \(\pm \tfrac{1}{2} e^{\pi i/4}, \pm 2 e^{3\pi i/4}\). Consequently, all three of these quadratic differentials are generic with generic residues.
2.23. The log-cotangent bundle. Let \({\mathsf {Y}}\) be the total space of \(\Omega ^1_{\mathsf {X}} ({\mathsf {D}})\), sometimes called the log-cotangent bundle, and let \(p : {\mathsf {Y}} \rightarrow {\mathsf {X}}\) be the projection map. Like the usual cotangent bundle, the log-cotangent bundle \({\mathsf {Y}}\) has a canonical one-form, which can be constructed as follows. Let \(\theta \in {\mathsf {H}}^0 \big ({\mathsf {Y}}, p^*\Omega ^1_{\mathsf {X}} ({\mathsf {D}}) \big )\) be the tautological section. Then the fibre product

exists in the category of vector bundles, because \(p : {\mathsf {Y}} \rightarrow {\mathsf {X}}\) is a surjective submersion. Unravelling the definition of the fibre product, we find that \({{\mathcal {A}}}\) consists of all vector fields on \({\mathsf {Y}}\) that are tangent to the divisor \(p^*{\mathsf {D}} \subset {\mathsf {Y}}\); i.e., \({{\mathcal {A}}} \cong {{\mathcal {T}}}_{\mathsf {Y}} (- \log p^*{\mathsf {D}})\). Finally, dualising the surjective map \({{\mathcal {A}}} \rightarrow p^*{{\mathcal {T}}}_{\mathsf {X}} (-{\mathsf {D}})\) yields an injective morphism  . The canonical one-form \(\eta _{\mathsf {Y}} \in {\mathsf {H}}^0 \big ( {\mathsf {Y}}, \Omega ^1_{\mathsf {Y}} (\log p^*{\mathsf {D}}) \big )\) on \({\mathsf {Y}}\) is then defined as the image of the tautological section \(\theta \) under this map.
. The canonical one-form \(\eta _{\mathsf {Y}} \in {\mathsf {H}}^0 \big ( {\mathsf {Y}}, \Omega ^1_{\mathsf {Y}} (\log p^*{\mathsf {D}}) \big )\) on \({\mathsf {Y}}\) is then defined as the image of the tautological section \(\theta \) under this map.
2.24 Example
Take \({\mathsf {X}} = \mathbb {P}^1_z\) with \({\mathsf {D}} = \left\{ 0,1,\infty \right\} \). Then \(\Omega ^1_{\mathbb {P}^1} ({\mathsf {D}})\) has a trivialisation over the affine z-chart given by the logarithmic one-form  . With respect to this trivialisation, the canonical one-form \(\eta _ Y \) is simply
. With respect to this trivialisation, the canonical one-form \(\eta _ Y \) is simply  where y is the linear coordinate in the fibre.
where y is the linear coordinate in the fibre.
2.25. The spectral curve. If \(\varphi \) is a quadratic differential on \(({\mathsf {X}},{\mathsf {D}})\), then \(p^*\varphi \) is a section of \({\mathsf {S}}^2 \big ( \Omega ^1_{\mathsf {Y}} (\log p^*{\mathsf {D}}) \big )\) via  . The spectral curve of \(\varphi \) is the zero locus in \({\mathsf {Y}}\) of the section \(\eta ^2_{\mathsf {Y}} - p^*\varphi \in {\mathsf {S}}^2 \big ( \Omega ^1_{\mathsf {Y}} (\log p^*{\mathsf {D}}) \big )\):
. The spectral curve of \(\varphi \) is the zero locus in \({\mathsf {Y}}\) of the section \(\eta ^2_{\mathsf {Y}} - p^*\varphi \in {\mathsf {S}}^2 \big ( \Omega ^1_{\mathsf {Y}} (\log p^*{\mathsf {D}}) \big )\):

We denote by  the restriction to
the restriction to  of the canonical projection \(p : {\mathsf {Y}} \rightarrow {\mathsf {X}}\). We also denote the ramification divisor by
of the canonical projection \(p : {\mathsf {Y}} \rightarrow {\mathsf {X}}\). We also denote the ramification divisor by  and the branch divisor by \({\mathsf {B}} \subset {\mathsf {X}}\). As a double cover,
and the branch divisor by \({\mathsf {B}} \subset {\mathsf {X}}\). As a double cover,  is equipped with a canonical involution
is equipped with a canonical involution  .
.
If \(\varphi \) is generic, then  is embedded in \({\mathsf {Y}}\) as a smooth divisor, and the projection
is embedded in \({\mathsf {Y}}\) as a smooth divisor, and the projection  is a simply ramified double cover, branched exactly at the zeroes of \(\varphi \), and trivial over the points of \({\mathsf {D}}\). Its genus is
is a simply ramified double cover, branched exactly at the zeroes of \(\varphi \), and trivial over the points of \({\mathsf {D}}\). Its genus is  . (see, e.g., [1, remark 3.2]). Using the Riemann–Hurwitz formula, the number of ramification points \(|{\mathsf {R}}|\) of \(\pi \), which is the same as the number of zeroes \(|{\mathsf {B}}|\) of \(\varphi \), is
. (see, e.g., [1, remark 3.2]). Using the Riemann–Hurwitz formula, the number of ramification points \(|{\mathsf {R}}|\) of \(\pi \), which is the same as the number of zeroes \(|{\mathsf {B}}|\) of \(\varphi \), is

2.26 Example
For the quadratic differential \(\varphi _1\) from Example 2.22, the spectral curve  has genus 0, hence is a copy of \(\mathbb {P}^1\). If we trivialise \(\Omega ^1_{\mathbb {P}^1} ({\mathsf {D}})\) over the affine z-chart using the differential form
has genus 0, hence is a copy of \(\mathbb {P}^1\). If we trivialise \(\Omega ^1_{\mathbb {P}^1} ({\mathsf {D}})\) over the affine z-chart using the differential form  , then
, then  is given by the equation \(y^2 = \tfrac{1}{9} (z^2 - z + 1)\). For both quadratic differentials \(\varphi _2\) and \(\varphi _3\), the spectral curve has genus 1, so it is an elliptic curve over \(\mathbb {P}^1\), and it is given by \(y^2 = \tfrac{1}{9} (z^4 + 1)\).
is given by the equation \(y^2 = \tfrac{1}{9} (z^2 - z + 1)\). For both quadratic differentials \(\varphi _2\) and \(\varphi _3\), the spectral curve has genus 1, so it is an elliptic curve over \(\mathbb {P}^1\), and it is given by \(y^2 = \tfrac{1}{9} (z^4 + 1)\).
Notice that, although the quadratic differential \(\varphi _1\) is singular at the points 0, 1 in the affine z-chart, its spectral curve  is perfectly well-behaved above these points (see Fig. 1). This is a manifestation of the fact that our spectral curve
is perfectly well-behaved above these points (see Fig. 1). This is a manifestation of the fact that our spectral curve  is embedded inside the total space of the logarithmic cotangent bundle rather than the usual cotangent bundle. In contrast, constructing a spectral curve of \(\varphi _1\) using the same equations but in the usual cotangent bundle yields a curve which escapes from the total space above the points 0, 1 (see Fig. 2).
is embedded inside the total space of the logarithmic cotangent bundle rather than the usual cotangent bundle. In contrast, constructing a spectral curve of \(\varphi _1\) using the same equations but in the usual cotangent bundle yields a curve which escapes from the total space above the points 0, 1 (see Fig. 2).
A real slice of the total space of \(\Omega ^1_{\mathbb {P}^1} ({\mathsf {D}})\) over the real line in \(\mathbb {P}^1_z\). In blue is the spectral curve  of the quadratic differential \(\varphi _1\) from Example 2.22
of the quadratic differential \(\varphi _1\) from Example 2.22
A real slice of the total space of \(\Omega ^1_{\mathbb {P}^1}\) over the real line in \(\mathbb {P}^1_z\). In blue is the curve given by the equation  , where \(\varphi _1\) is the quadratic differential from Example 2.22
, where \(\varphi _1\) is the quadratic differential from Example 2.22
2.27. The canonical one-form. Pulling back the canonical one-form \(\eta _{\mathsf {Y}}\) to  yields a differential form \(\eta \) with logarithmic poles along \({\mathsf {C}} \mathrel {\mathop :}=\pi ^{-1} ({\mathsf {D}})\), called the canonical one-form on
yields a differential form \(\eta \) with logarithmic poles along \({\mathsf {C}} \mathrel {\mathop :}=\pi ^{-1} ({\mathsf {D}})\), called the canonical one-form on  . It satisfies \(\eta ^2 = \pi ^*\varphi \) and \(\sigma ^*\eta = - \eta \), and can therefore be thought of as the ‘canonical square root’ of the quadratic differential \(\varphi \). It has zeroes along the ramification locus \({\mathsf {R}}\), and its residues at the two preimages \(\mathsf {p}_\pm \in {\mathsf {C}}\) of any point \(\mathsf {p}\in {\mathsf {D}}\) satisfy \({\text {Res}}_{\mathsf {p}_-} \eta = - {\text {Res}}_{\mathsf {p}_+} \eta \) and \(\big ( {\text {Res}}_{\mathsf {p}_\pm } \eta \big )^2 = {\text {Res}}_\mathsf {p}\varphi \). If the residue data \(a = {\text {Res}}(\varphi )\) is generic, we can fix an order on the preimages of \(\mathsf {p}\):
. It satisfies \(\eta ^2 = \pi ^*\varphi \) and \(\sigma ^*\eta = - \eta \), and can therefore be thought of as the ‘canonical square root’ of the quadratic differential \(\varphi \). It has zeroes along the ramification locus \({\mathsf {R}}\), and its residues at the two preimages \(\mathsf {p}_\pm \in {\mathsf {C}}\) of any point \(\mathsf {p}\in {\mathsf {D}}\) satisfy \({\text {Res}}_{\mathsf {p}_-} \eta = - {\text {Res}}_{\mathsf {p}_+} \eta \) and \(\big ( {\text {Res}}_{\mathsf {p}_\pm } \eta \big )^2 = {\text {Res}}_\mathsf {p}\varphi \). If the residue data \(a = {\text {Res}}(\varphi )\) is generic, we can fix an order on the preimages of \(\mathsf {p}\):

If \(\mathsf {p}_- \prec \mathsf {p}_+\), we shall call \(\mathsf {p}_-\) a sink pole and \(\mathsf {p}_+\) a source pole. The divisor \({\mathsf {C}}\) is thus decomposed equally into sinks and sources \({\mathsf {C}} = {\mathsf {C}}^- \sqcup {\mathsf {C}}^+\).
2.4 Logarithmic connections and spectral curves
In general, connections do not have an invariant notion of eigenvalues or eigenvectors. However, in the presence of a spectral curve, we can make sense of these notions as follows.
2.28.
Let  be the spectral curve of a generic quadratic differential \(\varphi \) with generic residue data a along \({\mathsf {D}}\). Suppose \(({{\mathcal {E}}}, \nabla ) \in Conn _{\mathsf {X}}^2\) is a logarithmic \(\mathfrak {sl}_2\)-connection on \(({\mathsf {X}},{\mathsf {D}})\) with residue data a. If \(\mathsf {p}\in {\mathsf {D}}\), let \(\pm \lambda _\mathsf {p}\) be the Levelt exponents at \(\mathsf {p}\), which by construction are the residues of \(\eta \) at the preimages \(\mathsf {p}_\pm \in {\mathsf {C}}\). Consider the local diagonal decomposition \({{\mathcal {E}}}_\mathsf {p}\cong \Lambda _\mathsf {p}^- \oplus \Lambda _\mathsf {p}^+\).
be the spectral curve of a generic quadratic differential \(\varphi \) with generic residue data a along \({\mathsf {D}}\). Suppose \(({{\mathcal {E}}}, \nabla ) \in Conn _{\mathsf {X}}^2\) is a logarithmic \(\mathfrak {sl}_2\)-connection on \(({\mathsf {X}},{\mathsf {D}})\) with residue data a. If \(\mathsf {p}\in {\mathsf {D}}\), let \(\pm \lambda _\mathsf {p}\) be the Levelt exponents at \(\mathsf {p}\), which by construction are the residues of \(\eta \) at the preimages \(\mathsf {p}_\pm \in {\mathsf {C}}\). Consider the local diagonal decomposition \({{\mathcal {E}}}_\mathsf {p}\cong \Lambda _\mathsf {p}^- \oplus \Lambda _\mathsf {p}^+\).
Let z be a local coordinate on  centred at \(\mathsf {p}_\pm \) in which \(\eta \) is in normal form
centred at \(\mathsf {p}_\pm \) in which \(\eta \) is in normal form  . Since
. Since  is unramified over \(\mathsf {p}\), we also use z as a local coordinate on \({\mathsf {X}}\) centred at \(\mathsf {p}\). If we fix a basepoint \(\mathsf {p}_*\) near \(\mathsf {p}\), then examining the Levelt normal form of \(\nabla _\mathsf {p}\) with respect to the coordinate z we obtain germs of (multivalued) flat sections \(\psi ^\pm _\mathsf {p}\) which can be expressed as \(\psi ^\pm _\mathsf {p}= f^\pm _\mathsf {p}e^\pm _\mathsf {p}\), where \(e^\pm _\mathsf {p}\) is a (univalued) generator of \(\Lambda _\mathsf {p}^\pm \), and \(f^\pm _\mathsf {p}\) is the germ of a (multivalued) function defined in the coordinate z by The observation is that the integrand in this expression is precisely the canonical one-form \(\eta \) thought of as written in the local coordinate z near \(\mathsf {p}\).
is unramified over \(\mathsf {p}\), we also use z as a local coordinate on \({\mathsf {X}}\) centred at \(\mathsf {p}\). If we fix a basepoint \(\mathsf {p}_*\) near \(\mathsf {p}\), then examining the Levelt normal form of \(\nabla _\mathsf {p}\) with respect to the coordinate z we obtain germs of (multivalued) flat sections \(\psi ^\pm _\mathsf {p}\) which can be expressed as \(\psi ^\pm _\mathsf {p}= f^\pm _\mathsf {p}e^\pm _\mathsf {p}\), where \(e^\pm _\mathsf {p}\) is a (univalued) generator of \(\Lambda _\mathsf {p}^\pm \), and \(f^\pm _\mathsf {p}\) is the germ of a (multivalued) function defined in the coordinate z by The observation is that the integrand in this expression is precisely the canonical one-form \(\eta \) thought of as written in the local coordinate z near \(\mathsf {p}\).
2.29.
To express this in a coordinate-free way, let \({\mathsf {U}} \subset {\mathsf {X}}\) be any simply connected open neighbourhood of \(\mathsf {p}\) disjoint from \({\mathsf {B}}\) and all other points of \({\mathsf {D}}\). Then \({\mathsf {U}}\) has two disjoint preimages \({\mathsf {U}}_\pm \) on  where \({\mathsf {U}}_\pm \) contains \(\mathsf {p}_\pm \). Let \(\eta _\pm \) be the restriction of \(\eta \) to \({\mathsf {U}}_\pm \), and we can think of \(\eta _\pm \) as being defined on \({\mathsf {U}}\). Define (multivalued) functions on the punctured neighbourhood \({\mathsf {U}}^\circ \mathrel {\mathop :}={\mathsf {U}} \setminus \left\{ \mathsf {p} \right\} \) by \( f_\pm (\mathsf {q}) \mathrel {\mathop :}=\exp \left( - \int _{\mathsf {p}_*}^\mathsf {q}\eta _\pm \right) . \) Note that the germ of \(f_\pm \) at \(\mathsf {p}\) is precisely \(f_\mathsf {p}^\pm \), and that \(f_\pm \) satisfies the differential equation
where \({\mathsf {U}}_\pm \) contains \(\mathsf {p}_\pm \). Let \(\eta _\pm \) be the restriction of \(\eta \) to \({\mathsf {U}}_\pm \), and we can think of \(\eta _\pm \) as being defined on \({\mathsf {U}}\). Define (multivalued) functions on the punctured neighbourhood \({\mathsf {U}}^\circ \mathrel {\mathop :}={\mathsf {U}} \setminus \left\{ \mathsf {p} \right\} \) by \( f_\pm (\mathsf {q}) \mathrel {\mathop :}=\exp \left( - \int _{\mathsf {p}_*}^\mathsf {q}\eta _\pm \right) . \) Note that the germ of \(f_\pm \) at \(\mathsf {p}\) is precisely \(f_\mathsf {p}^\pm \), and that \(f_\pm \) satisfies the differential equation  ; moreover, \(f_\pm \) is nowhere-vanishing on \({\mathsf {U}}^\circ \). Analytically continue the solutions \(\psi ^\pm _\mathsf {p}\) to multivalued flat sections \(\psi _\pm \) of \({{\mathcal {E}}}\) over \({\mathsf {U}}^\circ \), and define \( e_\pm \mathrel {\mathop :}=f_\pm ^{-1} \psi _\pm . \) These sections of \({{\mathcal {E}}}\) form a basis of holomorphic generators over \({\mathsf {U}}\) satisfying:
; moreover, \(f_\pm \) is nowhere-vanishing on \({\mathsf {U}}^\circ \). Analytically continue the solutions \(\psi ^\pm _\mathsf {p}\) to multivalued flat sections \(\psi _\pm \) of \({{\mathcal {E}}}\) over \({\mathsf {U}}^\circ \), and define \( e_\pm \mathrel {\mathop :}=f_\pm ^{-1} \psi _\pm . \) These sections of \({{\mathcal {E}}}\) form a basis of holomorphic generators over \({\mathsf {U}}\) satisfying:

Thus, we can think of \(e_\pm \) as an eigensection of \(\nabla \) with eigenvalue \(\eta _\pm \), and the line subbundles  that they generate determine the flat eigen-decomposition of \(({{\mathcal {E}}}, \nabla )\) over \({\mathsf {U}}\) that uniquely continues the local diagonal decomposition of \({{\mathcal {E}}}_\mathsf {p}\):
that they generate determine the flat eigen-decomposition of \(({{\mathcal {E}}}, \nabla )\) over \({\mathsf {U}}\) that uniquely continues the local diagonal decomposition of \({{\mathcal {E}}}_\mathsf {p}\):

2.30.
More invariantly, let  be any simply connected neighbourhood of a pole
be any simply connected neighbourhood of a pole  which is disjoint from \({\mathsf {R}}\) and all other points of \({\mathsf {C}}\). Let f be any (multivalued) solution of the differential equation
which is disjoint from \({\mathsf {R}}\) and all other points of \({\mathsf {C}}\). Let f be any (multivalued) solution of the differential equation  defined over the punctured neighbourhood \(\tilde{{\mathsf {U}}}^*\mathrel {\mathop :}=\tilde{{\mathsf {U}}} \setminus \left\{ \mathsf {p} \right\} \). Then the same calculation as above shows that the pullback \(\pi ^*{{\mathcal {E}}}\) over \(\tilde{{\mathsf {U}}}\) has a section e which is an eigensection of \(\pi ^*\nabla \) with eigenvalue \(\eta \):
defined over the punctured neighbourhood \(\tilde{{\mathsf {U}}}^*\mathrel {\mathop :}=\tilde{{\mathsf {U}}} \setminus \left\{ \mathsf {p} \right\} \). Then the same calculation as above shows that the pullback \(\pi ^*{{\mathcal {E}}}\) over \(\tilde{{\mathsf {U}}}\) has a section e which is an eigensection of \(\pi ^*\nabla \) with eigenvalue \(\eta \):

2.5 The Stokes graph
Fix some generic residue data a. If \((g_{\mathsf {X}}, |{\mathsf {D}}|) = (0, 3)\), assume in addition that a is contained in the complement of the hypersurface (6). For any generic quadratic differential \(\varphi \) on \(({\mathsf {X}},{\mathsf {D}})\) with residues a, let  be its spectral curve with canonical one-form \(\eta \).
be its spectral curve with canonical one-form \(\eta \).
2.31. The horizontal foliation. The curves \({\mathsf {X}}\) and  , viewed as real two-dimensional surfaces, are naturally equipped with singular foliations \(\mathfrak {F}\) and
, viewed as real two-dimensional surfaces, are naturally equipped with singular foliations \(\mathfrak {F}\) and  , respectively, with the property that
, respectively, with the property that  is the orientation double cover of \(\mathfrak {F}\). These foliations are well-known (see, e.g., [15, 20]), and we only recall what is necessary (see [3, §3] for a concise survey). The foliation
is the orientation double cover of \(\mathfrak {F}\). These foliations are well-known (see, e.g., [15, 20]), and we only recall what is necessary (see [3, §3] for a concise survey). The foliation  can be defined as the integration of the real distribution \({ker} \big ( {\text {Im}}(\eta ) \big )\) inside the real tangent bundle of
can be defined as the integration of the real distribution \({ker} \big ( {\text {Im}}(\eta ) \big )\) inside the real tangent bundle of  . Concretely, the local equation for a leaf passing through a point \(\mathsf {p}\) is given by \({\text {Im}}\left( \, \int _{\mathsf {p}}^{\mathsf {z}} \eta \, \right) = 0\). Evidently, this foliation is singular at the poles \({\mathsf {C}} = \pi ^{-1} ({\mathsf {D}})\) and at the ramification points \({\mathsf {R}}\). The foliation \(\mathfrak {F}\), defined as the image of
. Concretely, the local equation for a leaf passing through a point \(\mathsf {p}\) is given by \({\text {Im}}\left( \, \int _{\mathsf {p}}^{\mathsf {z}} \eta \, \right) = 0\). Evidently, this foliation is singular at the poles \({\mathsf {C}} = \pi ^{-1} ({\mathsf {D}})\) and at the ramification points \({\mathsf {R}}\). The foliation \(\mathfrak {F}\), defined as the image of  under \(\pi \), is often called the horizontal foliation for the quadratic differential \(\varphi \); it is singular at the poles \({\mathsf {D}}\) and the branch points \({\mathsf {B}}\). A leaf of \(\mathfrak {F}\) (or
under \(\pi \), is often called the horizontal foliation for the quadratic differential \(\varphi \); it is singular at the poles \({\mathsf {D}}\) and the branch points \({\mathsf {B}}\). A leaf of \(\mathfrak {F}\) (or  ) is critical if one of its endpoints belongs to \({\mathsf {B}}\) (or \({\mathsf {R}}\)). A critical leaf of \(\mathfrak {F}\) is a saddle trajectory if both of its endpoints belong to \({\mathsf {B}}\).
) is critical if one of its endpoints belongs to \({\mathsf {B}}\) (or \({\mathsf {R}}\)). A critical leaf of \(\mathfrak {F}\) is a saddle trajectory if both of its endpoints belong to \({\mathsf {B}}\).
2.32.
If the horizontal foliation \(\mathfrak {F}\) has no saddle trajectories, then by [3, Lemma 3.1] the open real surface \({\mathsf {X}} \setminus ({\mathsf {D}} \cup {\mathsf {B}} \cup \Gamma )\), where \(\Gamma \) is the union of all critical leaves of \(\mathfrak {F}\), decomposes into a finite disjoint union of topological open discs, called horizontal strips (Fig. 3). Similarly, the open real surface  , where
, where  is the union of all critical leaves of
is the union of all critical leaves of  , is also a finite disjoint union of horizontal strips (Fig. 3).
, is also a finite disjoint union of horizontal strips (Fig. 3).
A horizontal strip on \({\mathsf {X}}\) (left) and on  (right). Topologically an open disc, the boundary consists of exactly four critical leaves of \(\mathfrak {F}\) or
(right). Topologically an open disc, the boundary consists of exactly four critical leaves of \(\mathfrak {F}\) or  , two points in \({\mathsf {D}}\) or \({\mathsf {C}}\) (not necessarily distinct), and two points in \({\mathsf {B}}\) or \({\mathsf {R}}\) (necessarily distinct). The preimage of a horizontal strip on \({\mathsf {X}}\) is a pair of horizontal strips on
, two points in \({\mathsf {D}}\) or \({\mathsf {C}}\) (not necessarily distinct), and two points in \({\mathsf {B}}\) or \({\mathsf {R}}\) (necessarily distinct). The preimage of a horizontal strip on \({\mathsf {X}}\) is a pair of horizontal strips on  . Notation: points in \({\mathsf {B}}\) or \({\mathsf {R}}\) are denoted by
. Notation: points in \({\mathsf {B}}\) or \({\mathsf {R}}\) are denoted by


2.33. Saddle-free quadratic differentials and very generic residues. If the horizontal foliation \(\mathfrak {F}\) has no saddle trajectories, then the quadratic differential \(\varphi \) is said to be saddle-free. It follows from [3, Lemma 4.11] that the subset of quadratic differentials which are saddle-free is open dense. Note that “saddle-free” may be a condition on the residue data a. For example, if \((g_{\mathsf {X}}, |{\mathsf {D}}|) = (0, 3)\), the quadratic differential \(\varphi \) with given residues a is unique (given by (5)) and may fail to be saddle-free. In this case, there are only two ramification points  , so a saddle trajectory occurs if and only if the canonical one-form \(\eta \) satisfies \({\text {Im}}\left( \, \int _{\mathsf {r}_-}^{\mathsf {r}_+} \eta \, \right) = 0\) for a path of integration in
, so a saddle trajectory occurs if and only if the canonical one-form \(\eta \) satisfies \({\text {Im}}\left( \, \int _{\mathsf {r}_-}^{\mathsf {r}_+} \eta \, \right) = 0\) for a path of integration in  . If \(\mathsf {b}_\pm \in {\mathsf {B}}\) are the two branch points, then upon identifying \({\mathsf {X}} \cong \mathbb {P}^1\) and choosing a branch cut in order to write \(\eta \) with \(\sqrt{\varphi }\), where \(\varphi \) is given by (5), this integral can be explicitly computed in terms of logarithms and it defines a closed real-analytic subset of \(\mathbb {C}^3_{\alpha \beta \gamma }\). It therefore determines an explicit condition on the residues \(a = \left\{ \alpha , \beta , \gamma \right\} \) for the unique \(\varphi \) to be saddle-free. We will say that residue data a is very generic if there exists a generic saddle-free quadratic differential \(\varphi \) with residues a.
. If \(\mathsf {b}_\pm \in {\mathsf {B}}\) are the two branch points, then upon identifying \({\mathsf {X}} \cong \mathbb {P}^1\) and choosing a branch cut in order to write \(\eta \) with \(\sqrt{\varphi }\), where \(\varphi \) is given by (5), this integral can be explicitly computed in terms of logarithms and it defines a closed real-analytic subset of \(\mathbb {C}^3_{\alpha \beta \gamma }\). It therefore determines an explicit condition on the residues \(a = \left\{ \alpha , \beta , \gamma \right\} \) for the unique \(\varphi \) to be saddle-free. We will say that residue data a is very generic if there exists a generic saddle-free quadratic differential \(\varphi \) with residues a.
Ultimately, however, this apparent rigidity in our construction is artificial and can be removed by using a more topological argument. We will study this as well as other non-generic situations elsewhere.
From left to right: plot of critical trajectories of quadratic differentials \(\varphi _1, \varphi _2, \varphi _3\) from Example 2.22. In plots 1 and 2, the trajectories that escape the picture frame tend to infinity
2.34 Example
All three quadratic differentials \(\varphi _1, \varphi _2, \varphi _3\) from Example 2.22 are saddle-free. The true plots of their critical trajectories are presented in Fig. 4.
2.35. The Stokes and spectral graphs Now we define the main combinatorial gadgets in our construction. Let \(\varphi \) be a generic and saddle-free quadratic differential.
2.36 Definition
(Stokes graph, spectral graph) The Stokes graph \(\Gamma \) is the graph on \({\mathsf {X}}\) whose vertices are \({\mathsf {D}} \cup {\mathsf {B}}\) and whose edges are the critical leaves of \(\mathfrak {F}\). The spectral graph  is the oriented graph on
is the oriented graph on  whose vertices are \({\mathsf {C}} \cup {\mathsf {R}}\) and whose edges are the critical leaves of
whose vertices are \({\mathsf {C}} \cup {\mathsf {R}}\) and whose edges are the critical leaves of  .
.
Thus,  is a (ramified) orientation double cover of graphs. Each face of \(\Gamma \) and
is a (ramified) orientation double cover of graphs. Each face of \(\Gamma \) and  is a horizontal strip. We refer to the edges and the faces of \(\Gamma \) as Stokes rays and Stokes regions; and to the edges and the faces of
is a horizontal strip. We refer to the edges and the faces of \(\Gamma \) as Stokes rays and Stokes regions; and to the edges and the faces of  as spectral rays and spectral regions. The graphs
as spectral rays and spectral regions. The graphs  are bipartite with bipartitions \(\Gamma _0 = {\mathsf {D}} \cup {\mathsf {B}}\) and
are bipartite with bipartitions \(\Gamma _0 = {\mathsf {D}} \cup {\mathsf {B}}\) and  .
.
The polar vertices \({\mathsf {C}}\) are further divided into sinks and sources (cf. 2.27):
-
sink vertices \(\mathrm{{\mathsf {C}}_-}\): those where \({\text {Re}}({\text {Res}}\eta ) < 0\);
-
source vertices \(\mathrm{{\mathsf {C}}_+}\): those where \({\text {Re}}({\text {Res}}\eta ) > 0\).
If \(\mathsf {p}\in {\mathsf {D}}\), we will always denote its preimages in \({\mathsf {C}}\) by \(\mathsf {p}_-, \mathsf {p}_+\) where \(\mathsf {p}_\pm \in {\mathsf {C}}_\pm \). They satisfy the relation \(\sigma (\mathsf {p}_\pm ) = \mathsf {p}_\mp \). All spectral rays incident to a sink/source are oriented into/out of the sink/source, so spectral rays  are divided by parity:
are divided by parity:
-
positive spectral rays
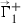 : polar vertex is a source;
: polar vertex is a source; -
negative spectral rays
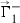 : polar vertex is a sink.
: polar vertex is a sink.
2.37.
Spectral rays always occur in pairs: the involution \(\sigma \) maps a spectral ray to a spectral ray of opposite parity. Stokes rays have no natural notion of parity; instead, the preimage of every Stokes ray \(\alpha \in \Gamma _1\) is a pair of opposite spectral rays  (see Fig. 5). The graphs
(see Fig. 5). The graphs  are squaregraphs: every Stokes region is a quadrilateral with two branch vertices and two polar vertices, and its boundary is made up of four Stokes rays (Fig. 6).
are squaregraphs: every Stokes region is a quadrilateral with two branch vertices and two polar vertices, and its boundary is made up of four Stokes rays (Fig. 6).
Every spectral ray and every Stokes ray has a polar vertex and a ramification/branch vertex. Depicted are the pair of opposite spectral rays \(\alpha _+, \alpha _-\) on  in the preimage of the Stokes ray \(\alpha \) on \({\mathsf {X}}\). Notation: We index Stokes rays by \(\alpha , \beta , \ldots \); the corresponding positive spectral rays are denoted by \(\alpha _+, \beta _+, \ldots \) and the negative ones by \(\alpha _-, \beta _-, \ldots \)
in the preimage of the Stokes ray \(\alpha \) on \({\mathsf {X}}\). Notation: We index Stokes rays by \(\alpha , \beta , \ldots \); the corresponding positive spectral rays are denoted by \(\alpha _+, \beta _+, \ldots \) and the negative ones by \(\alpha _-, \beta _-, \ldots \)
Two spectral regions \(i, i'\) in the preimage of the Stokes region \( I = \left\{ i, i' \right\} \). Here, \(\mathsf {r}_1, \mathsf {r}_2 \in {\mathsf {R}}\) are the ramification points above the branch points \(\mathsf {b}_1, \mathsf {b}_2 \in {\mathsf {B}}\). Notation: We index faces of  by letters \(i, j, k, \ldots \), though if two faces are both preimages of the same Stokes region \( I \), we will usually call them \(i, i'\). A face of \(\Gamma \), whose preimage consists of faces \(i, i'\) of
by letters \(i, j, k, \ldots \), though if two faces are both preimages of the same Stokes region \( I \), we will usually call them \(i, i'\). A face of \(\Gamma \), whose preimage consists of faces \(i, i'\) of  , is indexed by the unordered pair \( I = \left\{ i, i' \right\} \). Notice that if a Stokes region \( I = \left\{ i,i' \right\} \) has polar vertices \(\mathsf {p}, \mathsf {q}\in {\mathsf {D}}\), and if the spectral region i has polar vertices \(\mathsf {p}_+, \mathsf {q}_-\), then the spectral region \({i'}\) has polar vertices \(\mathsf {p}_-, \mathsf {q}_+\)
, is indexed by the unordered pair \( I = \left\{ i, i' \right\} \). Notice that if a Stokes region \( I = \left\{ i,i' \right\} \) has polar vertices \(\mathsf {p}, \mathsf {q}\in {\mathsf {D}}\), and if the spectral region i has polar vertices \(\mathsf {p}_+, \mathsf {q}_-\), then the spectral region \({i'}\) has polar vertices \(\mathsf {p}_-, \mathsf {q}_+\)
Similarly, every spectral region is a quadrilateral with two ramification vertices and two polar vertices (one of which is a source and one is a sink), and its boundary is made up of four spectral rays (two of which are positive and two are negative). We index them as described in Fig. 6:

Each branch point has three incident Stokes rays and three incident Stokes regions, but each Stokes region has two branch vertices, so there are \(3|{\mathsf {B}}|\) Stokes rays and \(\tfrac{3}{2}|{\mathsf {B}}|\) Stokes regions in total. So, using (8),


Note also that  .
.
2.38 Example
Figure 4 shows a plot of the Stokes graph of the quadratic differential \(\varphi _1\) from Example 2.22. Figure 7 shows a more schematic rendering.
Right: a schematic picture of the Stokes graph \(\Gamma \) (orange) of the quadratic differential \(\varphi _1\) from Example 2.22. The point at infinity has been blown up to an orange bounding circle. Left: the corresponding spectral graph  on the spectral curve
on the spectral curve  . The preimages of the points \(0,1,\infty \) carry a label according to whether the vertex is a sink or a source
. The preimages of the points \(0,1,\infty \) carry a label according to whether the vertex is a sink or a source
2.39. The Stokes open cover. The graphs  define canonical acyclic open covers (i.e., every finite intersection is either empty or a disjoint union of contractible open sets) of the punctured curves
define canonical acyclic open covers (i.e., every finite intersection is either empty or a disjoint union of contractible open sets) of the punctured curves

by enlarging all edges and faces as follows. For every face \( I \in \Gamma _2\) and every edge \(\alpha \in \Gamma _1\), let \({\mathsf {U}}_{ I }\) and \({\mathsf {U}}_{\alpha }\) be the germs of open neighbourhoods in \({\mathsf {X}}^\circ \) of the face \( I \) and the edge \(\alpha \), respectively. We continue calling them Stokes regions and Stokes rays. We define spectral regions \({\mathsf {U}}_i\) and spectral rays \({\mathsf {U}}_\alpha ^\pm \) for all  in the same way. We obtain what we call Stokes open covers of \({\mathsf {X}}^\circ \) and
in the same way. We obtain what we call Stokes open covers of \({\mathsf {X}}^\circ \) and  , respectively:
, respectively:

If \(\mathsf {p}\) is a vertex of \({\mathsf {U}}_ I \), then intersecting \({\mathsf {U}}_ I \) with the infinitesimal disc \({\mathsf {U}}_\mathsf {p}\) around \(\mathsf {p}\) can be seen as the germ of a sectorial neighbourhood of \(\mathsf {p}\) (or a disjoint union of two). In fact, the infinitesimal punctured disc \({\mathsf {U}}_\mathsf {p}^*\) centred at \(\mathsf {p}\) is covered by such sectorial neighbourhoods whose double intersections are the Stokes rays incident to \(\mathsf {p}\).
2.40.
Any double intersection \({\mathsf {U}}_ I \cap {\mathsf {U}}_ J \) of Stokes regions is either a single Stokes ray or a pair of disjoint Stokes rays with the same polar vertex but necessarily different branch vertices, and there are no nonempty triple intersections. So we define the nerves of these covers by

We adopt the following notational convention: if \({\mathsf {U}}_{\alpha }\) is a Stokes ray contained in the double intersection \({\mathsf {U}}_ I \cap {\mathsf {U}}_ J \), then \({\mathsf {U}}_ I , {\mathsf {U}}_ J \) are ordered such that going from \({\mathsf {U}}_ I \) to \({\mathsf {U}}_ J \) the Stokes ray \(\alpha \) is crossed anti-clockwise around the branch vertex of \({\mathsf {U}}_{\alpha }\).
2.41.
The restriction of the projection  to any spectral region \({\mathsf {U}}_i\), any spectral ray \({\mathsf {U}}_\alpha ^\pm \), or any infinitesimal disc \({\mathsf {U}}_\mathsf {p}^\pm \) around a pole \(\mathsf {p}_\pm \) is an isomorphism respectively onto its image Stokes region \({\mathsf {U}}_ I = {\mathsf {U}}_{\left\{ i, i' \right\} }\), Stokes ray \({\mathsf {U}}_\alpha \), or infinitesimal disc \({\mathsf {U}}_\mathsf {p}\) around the pole \(\mathsf {p}\); we denote these restrictions as follows:
to any spectral region \({\mathsf {U}}_i\), any spectral ray \({\mathsf {U}}_\alpha ^\pm \), or any infinitesimal disc \({\mathsf {U}}_\mathsf {p}^\pm \) around a pole \(\mathsf {p}_\pm \) is an isomorphism respectively onto its image Stokes region \({\mathsf {U}}_ I = {\mathsf {U}}_{\left\{ i, i' \right\} }\), Stokes ray \({\mathsf {U}}_\alpha \), or infinitesimal disc \({\mathsf {U}}_\mathsf {p}\) around the pole \(\mathsf {p}\); we denote these restrictions as follows:

2.42 Example
For the differential \(\varphi _1\) from Example 2.22, the Stokes open covers of \({\mathsf {X}}^\circ = \mathbb {P}^1 \setminus \left\{ 0,1,\infty \right\} \) and  are illustrated in Fig. 8.
are illustrated in Fig. 8.
The Stokes and spectral regions from Fig. 7 are appropriately coloured to show which pair of spectral regions lie in the preimage of which Stokes region
2.6 Transverse connections
2.43.
If \({\mathsf {U}}_ I \) is a Stokes region with \( I = \left\{ i, i' \right\} \), denote its polar vertices by \(\mathsf {p}, \mathsf {p}' \in {\mathsf {D}}\). Given a connection \(({{\mathcal {E}}}, \nabla ) \in Conn _{\mathsf {X}}^2\), consider its local diagonal decompositions \({{\mathcal {E}}}_\mathsf {p}\cong \Lambda _\mathsf {p}^- \oplus \Lambda _\mathsf {p}^+\) and \({{\mathcal {E}}}_{\mathsf {p}'} \cong \Lambda _{\mathsf {p}'}^- \oplus \Lambda _{\mathsf {p}'}^+\). Let us analytically continue the flat abelian connection germs \(\Lambda _\mathsf {p}^-, \Lambda _{\mathsf {p}'}^-\) to \({\mathsf {U}}_ I \) using the flat structure on \({{\mathcal {E}}}\):

2.44. Transversality of Levelt filtrations. These continuations equip the vector bundle \({{\mathcal {E}}}\) over \({\mathsf {U}}_ I \) with a pair of flat filtrations \({{\mathcal {E}}}_{\mathsf {p}, I }^\bullet = \big ( \Lambda _i \subset {{\mathcal {E}}}_ I \big )\) and \({{\mathcal {E}}}_{\mathsf {p}', I }^\bullet = \big ( \Lambda _{i'} \subset {{\mathcal {E}}}_ I \big )\), where \({{\mathcal {E}}}_{\mathsf {p}, I }^\bullet , {{\mathcal {E}}}_{\mathsf {p}', I }^\bullet \) are the unique continuations to the Stokes region \({\mathsf {U}}_ I \) of the Levelt filtrations \({{\mathcal {E}}}_{\mathsf {p}}^\bullet = \big ( \Lambda _{\mathsf {p}}^- \subset {{\mathcal {E}}}_\mathsf {p}\big ), {{\mathcal {E}}}_{\mathsf {p}'}^\bullet = \big ( \Lambda _{\mathsf {p}'}^- \subset {{\mathcal {E}}}_{\mathsf {p}'} \big )\).
2.45 Definition
(Transversality with respect to \(\Gamma \)) We will say that a connection \(({{\mathcal {E}}}, \nabla ) \in Conn _{\mathsf {X}}^2\) is transverse with respect to \(\Gamma \) if for every Stokes region \({\mathsf {U}}_{ I }\) the two filtrations \({{\mathcal {E}}}_{\mathsf {p}, I }^\bullet , {{\mathcal {E}}}_{\mathsf {p}', I }^\bullet \) are transverse: \({{\mathcal {E}}}_{\mathsf {p}, I }^\bullet \pitchfork {{\mathcal {E}}}_{\mathsf {p}', I }^\bullet \).
In other words, the two flat line subbundles \(\Lambda _i, \Lambda _{i'} \subset {{\mathcal {E}}}_ I \) are required to be distinct. Such transverse connections form a full subcategory \(Conn _{\mathsf {X}}^2 (\Gamma ) \subset Conn _{\mathsf {X}}^2\).
That such connections exist is obvious: one can, for example, choose a point in each Stokes region \({\mathsf {U}}_ I \) and connect it to some fixed basepoint by an arbitrary path that avoids \({\mathsf {D}}\). Then \(\Gamma \)-transversality is equivalent to avoiding finitely many algebraic conditions. In fact, the same argument shows that (with respect to an appropriate topology) the subset of \(\Gamma \)-transverse connections is open dense. We do not need these details here, and only mention that these and other moduli-theoretic considerations will be described in great detail in a future publication.
2.46 Proposition
(Semilocal diagonal decomposition of transverse connections) If \(({{\mathcal {E}}}, \nabla , M ) \in Conn _{\mathsf {X}}^2 (\Gamma )\), then the restriction  to any Stokes region \({\mathsf {U}}_ I \) has a canonical flat decomposition
to any Stokes region \({\mathsf {U}}_ I \) has a canonical flat decomposition

where  and
and  are defined by (14). Moreover, the \(\mathfrak {sl}_2\)-structure \( M \) defines a flat skew-symmetric isomorphism
are defined by (14). Moreover, the \(\mathfrak {sl}_2\)-structure \( M \) defines a flat skew-symmetric isomorphism  .
.
The main construction in this paper (Theorem 3.3) is an equivalence between \(Conn _{\mathsf {X}}^2 (\Gamma )\) and a certain category of odd abelian connections on the spectral curve  .
.
A Stokes region \({\mathsf {U}}_ I \) whose polar vertices coincide. The subset of \({\mathsf {X}}\) bounded by the Stokes rays \(\alpha , \beta \) in the complement of \({\mathsf {U}}_ I \) must contain another point \(\mathsf {q}\in {\mathsf {D}}\), for otherwise all Stokes rays incident to the branch point \(\mathsf {b}\) are also incident to \(\mathsf {p}\). But then the complement of \(\Gamma \) has a connected component which is not a horizontal strip contradicting [3, Lemma 3.1]. Generically, the monodromy of \(\nabla \) around the pole \(\mathsf {q}\) does not preserve the Levelt filtration coming from \(\mathsf {p}\)
2.47. Transversality over Stokes rays. Suppose \({\mathsf {U}}_\alpha \) is a Stokes ray contained in the double intersection \({\mathsf {U}}_ I \cap {\mathsf {U}}_ J \) of two adjacent Stokes regions. Then \({{\mathcal {E}}}\) has two diagonal decompositions over \({\mathsf {U}}_{\alpha }\):

Let \(\mathsf {p}' \in {\mathsf {D}}\) be the common polar vertex of \({\mathsf {U}}_ I , {\mathsf {U}}_ J \). Then \(\Lambda _{i'}, \Lambda _{j'}\) are continuations of the same line bundle germ \(\Lambda _{\mathsf {p}'}^- \subset {{\mathcal {E}}}_\mathsf {p}\), so \(\Lambda _{i'} = \Lambda _{j'}\) over the Stokes ray \({\mathsf {U}}_{\alpha }\). With respect to this pair of decompositions, the identity map on \({{\mathcal {E}}}\) has the following upper-triangular expression, which will be exploited throughout our construction in this paper:

2.48 Remark
Note that in the definition of transversality with respect to \(\Gamma \), it is not required that the two polar vertices \(\mathsf {p}, \mathsf {p}'\) of \({\mathsf {U}}_ I \) be different. If \(\mathsf {p}= \mathsf {p}'\) it may seem that no connection \(\nabla \) can be transverse with respect to \(\Gamma \) for such a Stokes graph, but this is not the case. This is because the Stokes region \({\mathsf {U}}_ I \) defines two disjoint sectorial neighbourhoods of \(\mathsf {p}\), so the two analytic continuations \(\Lambda _i, \Lambda _{i'} \subset {{\mathcal {E}}}_ I \) of the same germ \(\Lambda _\mathsf {p}^-\) are generically not the same, as explained in Fig. 9.
3 Abelianisation
3.1.
As before, let \(({\mathsf {X}},{\mathsf {D}})\) be a smooth compact curve equipped with a nonempty set of marked points \({\mathsf {D}}\) such that \(|{\mathsf {D}}| > 2 - 2g_{\mathsf {X}}\). Suppose \({\mathsf {D}}\) is decorated with very generic residue data a in the sense of Definition 2.3 and 2.33. We are studying the category
of logarithmic \(\mathfrak {sl}_2\)-connections on \(({\mathsf {X}},{\mathsf {D}})\) with residue data a.
Our method is to choose a generic saddle-free quadratic differential \(\varphi \) on \(({\mathsf {X}},{\mathsf {D}})\) with residues a. Let  be the spectral curve of \(\varphi \), and let \(\Gamma \) be the corresponding Stokes graph on \({\mathsf {X}}\). Consider the subcategory of connections that are transverse with respect to \(\Gamma \) in the sense of Definition 2.45:
be the spectral curve of \(\varphi \), and let \(\Gamma \) be the corresponding Stokes graph on \({\mathsf {X}}\). Consider the subcategory of connections that are transverse with respect to \(\Gamma \) in the sense of Definition 2.45:

3.2. The main result of this paper is that \(Conn _{\mathsf {X}}^2 (\Gamma )\) is equivalent to a category of odd abelian connections on the spectral curve  as follows. For every \(\mathsf {p}\in {\mathsf {D}}\), let \(\pm \lambda _\mathsf {p}\in \mathbb {C}\) be the Levelt exponents of the residue data a at \(\mathsf {p}\) (arranged such that \({\text {Re}}(\lambda _\mathsf {p}) > 0\)). Put \({\mathsf {C}} \mathrel {\mathop :}=\pi ^{-1} ({\mathsf {D}})\), let \({\mathsf {C}}_\pm \) be as in 2.35, let
as follows. For every \(\mathsf {p}\in {\mathsf {D}}\), let \(\pm \lambda _\mathsf {p}\in \mathbb {C}\) be the Levelt exponents of the residue data a at \(\mathsf {p}\) (arranged such that \({\text {Re}}(\lambda _\mathsf {p}) > 0\)). Put \({\mathsf {C}} \mathrel {\mathop :}=\pi ^{-1} ({\mathsf {D}})\), let \({\mathsf {C}}_\pm \) be as in 2.35, let  be the ramification divisor of \(\pi \), and define abelian residue data along \({\mathsf {C}} \cup {\mathsf {R}}\) as follows:
be the ramification divisor of \(\pi \), and define abelian residue data along \({\mathsf {C}} \cup {\mathsf {R}}\) as follows:

Consider the category of odd abelian logarithmic connections on  with residues \({\underline{\lambda }}\), for which we use the following shorthand notation:
with residues \({\underline{\lambda }}\), for which we use the following shorthand notation:

3.3 Theorem
(Abelianisation of logarithmic \(\mathfrak {sl}_2\)-connections) There is a natural equivalence of categories  .
.
Expressed more explicitly, this equivalence is

We will prove this theorem by constructing a pair functors,

called abelianisation and nonabelianisation with respect to \(\Gamma \); they are constructed in Sects. 3.1 and 3.3, respectively. In Proposition 3.21, we prove that they form an equivalence of categories.
3.1 The abelianisation functor
In this subsection, given an \(\mathfrak {sl}_2\)-connection \(({{\mathcal {E}}}, \nabla , M ) \in Conn _{\mathsf {X}}^2 (\Gamma )\), we construct an abelian connection  , and show that this construction is functorial. The idea is to extract the diagonal decompositions of \({{\mathcal {E}}}\) at the poles of \(\nabla \), analytically continue them to the spectral regions on the spectral curve, and then glue them into a flat line bundle using canonical isomorphisms that arise due to transversality.
, and show that this construction is functorial. The idea is to extract the diagonal decompositions of \({{\mathcal {E}}}\) at the poles of \(\nabla \), analytically continue them to the spectral regions on the spectral curve, and then glue them into a flat line bundle using canonical isomorphisms that arise due to transversality.
Definition at the poles. Given \(\mathsf {p}\in {\mathsf {D}}\), consider the local diagonal decomposition  from Proposition 2.8. We define
from Proposition 2.8. We define  over the infinitesimal disc \({\mathsf {U}}_\mathsf {p}^\pm \) around \(\mathsf {p}_\pm \) to be the pullback of the connection germ
over the infinitesimal disc \({\mathsf {U}}_\mathsf {p}^\pm \) around \(\mathsf {p}_\pm \) to be the pullback of the connection germ  :
:

Thus,  is the germ of a logarithmic abelian connection at \(\mathsf {p}_\pm \) with residue \(\pm \lambda _\mathsf {p}\). It also follows that \((\pi _\mathsf {p}^\mp )^*\Lambda ^\pm _\mathsf {p}= \sigma ^*{{\mathcal {L}}}_\mathsf {p}^\pm \), so the pullback of the flat skew-symmetric isomorphism
is the germ of a logarithmic abelian connection at \(\mathsf {p}_\pm \) with residue \(\pm \lambda _\mathsf {p}\). It also follows that \((\pi _\mathsf {p}^\mp )^*\Lambda ^\pm _\mathsf {p}= \sigma ^*{{\mathcal {L}}}_\mathsf {p}^\pm \), so the pullback of the flat skew-symmetric isomorphism  to the disc \({\mathsf {U}}_\mathsf {p}^\pm \) defines a flat skew-symmetric isomorphism
to the disc \({\mathsf {U}}_\mathsf {p}^\pm \) defines a flat skew-symmetric isomorphism

Definition on spectral regions. Let  be a spectral region, and let \(\mathsf {p}_-\) be its sink vertex. We define
be a spectral region, and let \(\mathsf {p}_-\) be its sink vertex. We define  by uniquely continuing the germ \({{\mathcal {L}}}_\mathsf {p}^-\) using the flat structure on \(\pi ^*{{\mathcal {E}}}\):
by uniquely continuing the germ \({{\mathcal {L}}}_\mathsf {p}^-\) using the flat structure on \(\pi ^*{{\mathcal {E}}}\):

Evidently,  for \(\Lambda _i\) defined by (14). Furthermore, if \({\mathsf {U}}_{i'} = \sigma ({\mathsf {U}}_i)\), then \(\pi ^*_i \Lambda _{i'} = \sigma ^*{{\mathcal {L}}}_{i'}\) for \(\Lambda _{i'}\) defined by (14). So if \( I = \left\{ i,i' \right\} \), the pullback to \({\mathsf {U}}_i\) of the \(\mathfrak {sl}_2\)-structure \( M _ I \) from Proposition 2.46 defines a flat skew-symmetric isomorphism
for \(\Lambda _i\) defined by (14). Furthermore, if \({\mathsf {U}}_{i'} = \sigma ({\mathsf {U}}_i)\), then \(\pi ^*_i \Lambda _{i'} = \sigma ^*{{\mathcal {L}}}_{i'}\) for \(\Lambda _{i'}\) defined by (14). So if \( I = \left\{ i,i' \right\} \), the pullback to \({\mathsf {U}}_i\) of the \(\mathfrak {sl}_2\)-structure \( M _ I \) from Proposition 2.46 defines a flat skew-symmetric isomorphism

Gluing over spectral rays. For every \(\alpha \in \Gamma _1\), consider the pair of opposite spectral rays  , and let \(\mathsf {p}_\pm \in {\mathsf {C}}^\pm \) be their respective polar vertices. Let \({\mathsf {U}}_ I = {\mathsf {U}}_{\left\{ i,i' \right\} }, {\mathsf {U}}_ J = {\mathsf {U}}_{\left\{ j,j' \right\} } \subset {\mathsf {X}}\) be the pair of adjacent Stokes regions which intersect along the Stokes ray \({\mathsf {U}}_\alpha \) as described in Fig. 10.
, and let \(\mathsf {p}_\pm \in {\mathsf {C}}^\pm \) be their respective polar vertices. Let \({\mathsf {U}}_ I = {\mathsf {U}}_{\left\{ i,i' \right\} }, {\mathsf {U}}_ J = {\mathsf {U}}_{\left\{ j,j' \right\} } \subset {\mathsf {X}}\) be the pair of adjacent Stokes regions which intersect along the Stokes ray \({\mathsf {U}}_\alpha \) as described in Fig. 10.
\({\mathsf {U}}_\mathsf {p}^\pm \) is a pair of opposite spectral rays, \(\mathsf {r}\) is their common ramification vertex, and \(\mathsf {p}_\pm \) are their respective polar vertices. \({\mathsf {U}}_i, {\mathsf {U}}_j\) are a pair of oriented Stokes regions which have \({\mathsf {U}}_\alpha ^+\) in their intersection, arranged such that the ordered pair \(({\mathsf {U}}_i, {\mathsf {U}}_j)\) respects the cyclic anti-clockwise order around \(\mathsf {r}\). Let \({\mathsf {U}}_{i'} \mathrel {\mathop :}=\sigma ({\mathsf {U}}_i), {\mathsf {U}}_{j'} \mathrel {\mathop :}=\sigma ({\mathsf {U}}_j)\), so \({\mathsf {U}}_{\alpha }^-\) is a connected component of \({\mathsf {U}}_{i'} \cap {\mathsf {U}}_{j'}\)
By transversality with respect to \(\Gamma \), the vector bundle \({{\mathcal {E}}}\) has two diagonal decompositions over the Stokes ray \({\mathsf {U}}_\alpha \):

Then \(\Lambda _{i'}, \Lambda _{j'}\) are continuations of the same line bundle germ \(\Lambda _{\mathsf {p}'}^- \subset {{\mathcal {E}}}_\mathsf {p}\), so \(\Lambda _{i'} = \Lambda _{j'}\) over the Stokes ray \({\mathsf {U}}_{\alpha }\). The identity map on \({{\mathcal {E}}}\), written with respect to this pair of decompositions, is the upper triangular matrix (16). We therefore define

The upper-triangular form (16) of the identity map on \({{\mathcal {E}}}\) also implies that the gluing maps \(g_\alpha ^-, g_\alpha ^+\) intertwine the pullbacks \(\mu _i, \mu _j\) and \(\mu _{i'}, \mu _{j'}\), respectively.
Gluing near the poles. For every \(\mathsf {p}\in {\mathsf {D}}\), let  be the infinitesimal disc neighbourhoods of \(\mathsf {p}_\pm \). Consider a Stokes region \({\mathsf {U}}_ I = {\mathsf {U}}_{\left\{ i,i' \right\} }\) such that \({\mathsf {U}}_i\) is incident to \(\mathsf {p}_+\) and \({\mathsf {U}}_{i'}\) is incident to \(\mathsf {p}_-\). First, the intersection of \({\mathsf {U}}_{i'}\) with \({\mathsf {U}}_\mathsf {p}^-\) is a sectorial neighbourhood of \(\mathsf {p}_-\), and the line bundle \({{\mathcal {L}}}_{i'}\) is the unique continuation of the germ \({{\mathcal {L}}}_\mathsf {p}^-\), so identity is the gluing map here. On the other hand, the intersection of \({\mathsf {U}}_{i}\) with \({\mathsf {U}}_\mathsf {p}^+\) is a sectorial neighbourhood of \(\mathsf {p}_+\), over which by Propositions 2.8 and 2.46 we have two decompositions
be the infinitesimal disc neighbourhoods of \(\mathsf {p}_\pm \). Consider a Stokes region \({\mathsf {U}}_ I = {\mathsf {U}}_{\left\{ i,i' \right\} }\) such that \({\mathsf {U}}_i\) is incident to \(\mathsf {p}_+\) and \({\mathsf {U}}_{i'}\) is incident to \(\mathsf {p}_-\). First, the intersection of \({\mathsf {U}}_{i'}\) with \({\mathsf {U}}_\mathsf {p}^-\) is a sectorial neighbourhood of \(\mathsf {p}_-\), and the line bundle \({{\mathcal {L}}}_{i'}\) is the unique continuation of the germ \({{\mathcal {L}}}_\mathsf {p}^-\), so identity is the gluing map here. On the other hand, the intersection of \({\mathsf {U}}_{i}\) with \({\mathsf {U}}_\mathsf {p}^+\) is a sectorial neighbourhood of \(\mathsf {p}_+\), over which by Propositions 2.8 and 2.46 we have two decompositions  and
and  . Then the obvious isomorphism
. Then the obvious isomorphism  over this double intersection implies
over this double intersection implies

The pullback of this map is the desired gluing map  . These gluing maps satisfy the cocycle condition, because if \({\mathsf {U}}_i\) and \({\mathsf {U}}_j\) are two adjacent spectral regions incident to \(\mathsf {p}_+\), then the identity map
. These gluing maps satisfy the cocycle condition, because if \({\mathsf {U}}_i\) and \({\mathsf {U}}_j\) are two adjacent spectral regions incident to \(\mathsf {p}_+\), then the identity map  over the intersection of Stokes regions \({\mathsf {U}}_ I = {\mathsf {U}}_{\left\{ i,i' \right\} }\) and \({\mathsf {U}}_{ J } = {\mathsf {U}}_{\left\{ j,j' \right\} }\) has the upper-triangular form (16), and therefore induces an isomorphism
over the intersection of Stokes regions \({\mathsf {U}}_ I = {\mathsf {U}}_{\left\{ i,i' \right\} }\) and \({\mathsf {U}}_{ J } = {\mathsf {U}}_{\left\{ j,j' \right\} }\) has the upper-triangular form (16), and therefore induces an isomorphism  . The isomorphism
. The isomorphism  given by the identity on \({{\mathcal {E}}}\) is unipotent. So its determinant
given by the identity on \({{\mathcal {E}}}\) is unipotent. So its determinant  intertwines \( M _ I \) and \( M _\mathsf {p}\), and therefore also \(\mu _i\) and \(\mu _\mathsf {p}^+\) as well as \(\mu _{i'}\) and \(\mu _\mathsf {p}^-\).
intertwines \( M _ I \) and \( M _\mathsf {p}\), and therefore also \(\mu _i\) and \(\mu _\mathsf {p}^+\) as well as \(\mu _{i'}\) and \(\mu _\mathsf {p}^-\).
Extension over ramification. This completes the construction of  on the spectral curve
on the spectral curve  away from the ramification divisor \({\mathsf {R}}\). Deligne’s construction [5, pp. 91–96] gives an extension over \({\mathsf {R}}\) with logarithmic poles and residues \(-1/2\), and it is easy to check that for any such extension, \(\mu \) extends uniquely to an odd structure. Deligne extensions are unique only up to a unique isomorphism (see also [2, Theorem IV.4.4]), but it is possible to fix this ambiguity as follows (details are not important for us here and will appear elsewhere). If \(\mathsf {r}\in {\mathsf {R}}\) is any ramification point and \(\mathsf {b}= \pi (\mathsf {r})\) is the corresponding branch point, let \({\mathsf {U}}_ I , {\mathsf {U}}_ J , {\mathsf {U}}_ K \) be the three Stokes regions incident to \(\mathsf {b}\). Then the germ \({{\mathcal {L}}}_r\) of \({{\mathcal {L}}}\) at \(\mathsf {r}\) is the pullback of the line bundle germ \(\Lambda _\mathsf {b}\) at \(\mathsf {b}\) which is defined as the kernel of the canonical map \(\Lambda _ I \oplus \Lambda _ J \oplus \Lambda _ K \longrightarrow {{\mathcal {E}}}_\mathsf {b}\). As a result, we obtain an abelian connection
away from the ramification divisor \({\mathsf {R}}\). Deligne’s construction [5, pp. 91–96] gives an extension over \({\mathsf {R}}\) with logarithmic poles and residues \(-1/2\), and it is easy to check that for any such extension, \(\mu \) extends uniquely to an odd structure. Deligne extensions are unique only up to a unique isomorphism (see also [2, Theorem IV.4.4]), but it is possible to fix this ambiguity as follows (details are not important for us here and will appear elsewhere). If \(\mathsf {r}\in {\mathsf {R}}\) is any ramification point and \(\mathsf {b}= \pi (\mathsf {r})\) is the corresponding branch point, let \({\mathsf {U}}_ I , {\mathsf {U}}_ J , {\mathsf {U}}_ K \) be the three Stokes regions incident to \(\mathsf {b}\). Then the germ \({{\mathcal {L}}}_r\) of \({{\mathcal {L}}}\) at \(\mathsf {r}\) is the pullback of the line bundle germ \(\Lambda _\mathsf {b}\) at \(\mathsf {b}\) which is defined as the kernel of the canonical map \(\Lambda _ I \oplus \Lambda _ J \oplus \Lambda _ K \longrightarrow {{\mathcal {E}}}_\mathsf {b}\). As a result, we obtain an abelian connection  .
.
Finally, functoriality of our construction readily follows from the fact that morphisms of connections necessarily preserve diagonal decompositions.
3.4 Proposition
The assignment  extends to a functor
extends to a functor

We call \(\pi ^\text {ab}_\Gamma \) the abelianisation functor, and the image  of \(({{\mathcal {E}}}, \nabla , M )\) under \(\pi ^\text {ab}_\Gamma \) the abelianisation of \(({{\mathcal {E}}}, \nabla , M )\) with respect to \(\Gamma \). The following proposition summarises some properties of abelianisation all of which are immediate consequences of the construction.
of \(({{\mathcal {E}}}, \nabla , M )\) under \(\pi ^\text {ab}_\Gamma \) the abelianisation of \(({{\mathcal {E}}}, \nabla , M )\) with respect to \(\Gamma \). The following proposition summarises some properties of abelianisation all of which are immediate consequences of the construction.
3.5 Proposition
(Properties of abelianisation) Let \(({{\mathcal {E}}}, \nabla , M ) \in Conn _{\mathsf {X}}^2 (\Gamma )\), and let  be its abelianisation.
be its abelianisation.
-
(1)
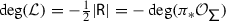 .
.
For any \(\mathsf {p}\in {\mathsf {D}}\), let \({\mathsf {U}}_\mathsf {p}\) be the infinitesimal disc around \(\mathsf {p}\). Let  be the local diagonal decomposition (Proposition 2.8). Then there is a canonical flat isomorphism
be the local diagonal decomposition (Proposition 2.8). Then there is a canonical flat isomorphism
-
(2)
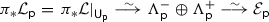 .
.
Let \({\mathsf {U}}_\mathsf {p}^\pm \) be the infinitesimal disc around the preimage \(\mathsf {p}_\pm \in {\mathsf {C}}\) of \(\mathsf {p}\). Recall the notation  . Then there are canonical flat isomorphisms
. Then there are canonical flat isomorphisms
-
(3)
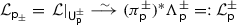 .
.
Let \({\mathsf {U}}_ I \subset {\mathsf {X}}\) be a Stokes region with polar vertices \(\mathsf {p}, \mathsf {p}' \in {\mathsf {D}}\), and let  be the semilocal diagonal decomposition of \({{\mathcal {E}}}\) over \({\mathsf {U}}_ I \) (Proposition 2.46), where \(\Lambda _i, \Lambda _{i'}\) are as in (14). Then there is a canonical flat isomorphism
be the semilocal diagonal decomposition of \({{\mathcal {E}}}\) over \({\mathsf {U}}_ I \) (Proposition 2.46), where \(\Lambda _i, \Lambda _{i'}\) are as in (14). Then there is a canonical flat isomorphism
-
(4)
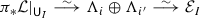 .
.
Let \({\mathsf {U}}_i, {\mathsf {U}}_{i'}\) be the spectral regions above \({\mathsf {U}}_{ I }\) incident to \(\mathsf {p}_-, \mathsf {p}'_- \in {\mathsf {C}}\), respectively, and recall the notation  . Then there are canonical flat isomorphisms
. Then there are canonical flat isomorphisms
-
(5)
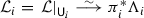 and
and 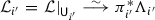 .
.
Finally, recall that \(\eta \) is the canonical one-form on the spectral curve  .
.
-
(6)
The abelian connection
 on the abelianisation line bundle \({{\mathcal {L}}}\) is holomorphic along \({\mathsf {C}}\); it has logarithmic poles only along the ramification divisor \({\mathsf {R}}\) with residues \(-1/2\).
on the abelianisation line bundle \({{\mathcal {L}}}\) is holomorphic along \({\mathsf {C}}\); it has logarithmic poles only along the ramification divisor \({\mathsf {R}}\) with residues \(-1/2\).
The following proposition, which readily follows from the discussion in Sect. 2.4, expresses the sense in which the abelianisation of connections is the analogue of abelianisation of Higgs bundles.
3.6 Proposition
(Spectral properties of abelianisation) For any simply connected open subset  , the abelianisation line bundle \({{\mathcal {L}}}\) has a generator e which is an eigensection for
, the abelianisation line bundle \({{\mathcal {L}}}\) has a generator e which is an eigensection for  with eigenvalue \(\eta \) (in the sense of Sect. 2.4); i.e., it satisfies the following equation:
with eigenvalue \(\eta \) (in the sense of Sect. 2.4); i.e., it satisfies the following equation:

Moreover, over any spectral region  , there is a canonical flat inclusion
, there is a canonical flat inclusion  with respect to which this section e is an eigensection for \(\pi ^*\nabla \) with eigenvalue \(\eta \):
with respect to which this section e is an eigensection for \(\pi ^*\nabla \) with eigenvalue \(\eta \):

3.7 Example
Let us illustrate the above construction in the simplest possible explicit example. Consider a logarithmic \(\mathfrak {sl}_2\)-connection \(({{\mathcal {E}}}, \nabla )\) from Example 2.5 with \(d = 3\). Namely, \({\mathsf {X}} = \mathbb {P}^1\), \({{\mathcal {E}}} = {{\mathcal {O}}}_{\mathbb {P}^1}^{\oplus 2}\), and \({\mathsf {D}} \mathrel {\mathop :}=\left\{ 0, 1, \infty \right\} \). Let \( A _1, A _2\) be any pair of \(\mathfrak {sl} (2, \mathbb {C})\)-matrices, both with eigenvalues \(\pm 1/3\), and let \(\nabla \) be given by the formula (1). Then the \(\nabla \) has Levelt exponents \(\pm 1/3\) at each pole.
To abelianise \(\nabla \), we must choose a generic saddle-free quadratic differential on \(({\mathsf {X}}, {\mathsf {D}})\) with residues 1/9 at each point of \({\mathsf {D}}\). One such choice is the quadratic differential \(\varphi _1\) from Example 2.22. Its spectral curve  was described in Example 2.26, its Stokes and spectral graphs were detailed in Fig. 7, and the relevant Stokes open cover was presented in Fig. 8. Finally, in Fig. 11, we illustrate the abelianisation construction by displaying which Levelt line subbundle is considered on which Stokes and spectral region.
was described in Example 2.26, its Stokes and spectral graphs were detailed in Fig. 7, and the relevant Stokes open cover was presented in Fig. 8. Finally, in Fig. 11, we illustrate the abelianisation construction by displaying which Levelt line subbundle is considered on which Stokes and spectral region.
3.2 The Voros cocycle
This section introduces the main ingredient in constructing the deablianisation functor \(\pi _\text {ab}^\Gamma \), the Voros cocycle. Let  be its abelianisation of \(({{\mathcal {E}}}, \nabla , M ) \in Conn _{\mathsf {X}}^2 (\Gamma )\).
be its abelianisation of \(({{\mathcal {E}}}, \nabla , M ) \in Conn _{\mathsf {X}}^2 (\Gamma )\).
3.8. The canonical nonabelian cocycle \( V \). Let \({\mathsf {U}}_\alpha \in \Gamma _1\) be a Stokes ray on \({\mathsf {X}}\) with polar vertex \(\mathsf {p}\in {\mathsf {D}}\) and branch vertex \(\mathsf {b}\in {\mathsf {B}}\). It is a component of the intersection of exactly two Stokes regions \({\mathsf {U}}_ I , {\mathsf {U}}_ J \) (see Fig. 12). Consider the pair of canonical identifications given by Proposition 3.5(4):

Over the Stokes ray \({\mathsf {U}}_{\alpha }\), their ratio yields a flat automorphism of  :
:

where \(\pi _* L \) denotes the associated local system  on \({\mathsf {X}}^\circ \). The nerve of the cover \(\mathfrak {{{U}}}_\Gamma \) of \({\mathsf {X}}^\circ \) consists of Stokes rays, so we obtain aČech 1-cocycle \( V \) with values in the local system \(\mathcal {A}ut (\pi _* L )\):
on \({\mathsf {X}}^\circ \). The nerve of the cover \(\mathfrak {{{U}}}_\Gamma \) of \({\mathsf {X}}^\circ \) consists of Stokes rays, so we obtain aČech 1-cocycle \( V \) with values in the local system \(\mathcal {A}ut (\pi _* L )\):

3.9 Lemma
If \(({{\mathcal {E}}}, \nabla , M ) \in Conn _{\mathsf {X}}^2 (\Gamma )\), let  be its abelianisation, and consider the pushforward \(\pi _*{{\mathcal {L}}} = \pi _*\pi ^\text {ab}_\Gamma {{\mathcal {E}}}\). If \( V \) is the cocycle (26), then there is a canonical isomorphism
be its abelianisation, and consider the pushforward \(\pi _*{{\mathcal {L}}} = \pi _*\pi ^\text {ab}_\Gamma {{\mathcal {E}}}\). If \( V \) is the cocycle (26), then there is a canonical isomorphism

Proof
The action of the cocycle \( V \) on the pushforward bundle \(\pi _*{{\mathcal {L}}}\) is a new bundle \({{\mathcal {E}}}' \mathrel {\mathop :}= V \cdot \pi _*{{\mathcal {L}}}\). Explicitly, the local piece \({{\mathcal {E}}}'_{ I }\) over a Stokes region \({\mathsf {U}}_{ I }\) is defined to be  , and the gluing data over a Stokes ray \({\mathsf {U}}_{\alpha } \subset {\mathsf {U}}_ I \cap {\mathsf {U}}_ J \) is given by \( V _{\alpha }\):
, and the gluing data over a Stokes ray \({\mathsf {U}}_{\alpha } \subset {\mathsf {U}}_ I \cap {\mathsf {U}}_ J \) is given by \( V _{\alpha }\):

But this commutative square together with (24) and (25) imply that \({{\mathcal {E}}}\) and \({{\mathcal {E}}}'\) are canonically isomorphic. \(\square \)
3.10. Transposition paths. Let us explicitly compute each automorphism \( V _{\alpha }\) with respect to a pair of canonical decompositions of \(\pi _*{{\mathcal {L}}}\) over the Stokes ray \({\mathsf {U}}_\alpha \). Through the isomorphisms  and
and  , the automorphism \( V _{\alpha } = \varphi _ J \circ \varphi _ I ^{-1}\) over \({\mathsf {U}}_\alpha \) is just the identity on \({{\mathcal {E}}}\) written as a map \(\Lambda _i \oplus \Lambda _{i'} \rightarrow \Lambda _j \oplus \Lambda _{j'}\). Notice that \(\Lambda _{i'} = \Lambda _{j'}\) because they are continuations of the same line bundle germ at \(\mathsf {p}\), so using (16) we find:
, the automorphism \( V _{\alpha } = \varphi _ J \circ \varphi _ I ^{-1}\) over \({\mathsf {U}}_\alpha \) is just the identity on \({{\mathcal {E}}}\) written as a map \(\Lambda _i \oplus \Lambda _{i'} \rightarrow \Lambda _j \oplus \Lambda _{j'}\). Notice that \(\Lambda _{i'} = \Lambda _{j'}\) because they are continuations of the same line bundle germ at \(\mathsf {p}\), so using (16) we find:

Now, we can decompose the map \(\Delta _\alpha : \Lambda _i \rightarrow \Lambda _{j'}\) through canonical inclusions, projections, and the upper-triangular expressions (16) for the identity on \({{\mathcal {E}}}\) as follows:

We interpret the first and second upper-triangular expressions as the identity maps on \({{\mathcal {E}}}\) over \({\mathsf {U}}_\gamma \) and \({\mathsf {U}}_\beta \), respectively. Since all these bundle maps are \(\nabla \)-flat, the map \(\Delta _\alpha \) can be interpreted as the endomorphism of the fibre of \({{\mathcal {E}}}\) over a point in \({\mathsf {U}}_\alpha \) obtained as the composition of \(\nabla \)-parallel transports \( P _ I , P _ K , P _ J \) along paths \(\delta _ I \) contained in \({\mathsf {U}}_ I \) from \({\mathsf {U}}_\alpha \) to \({\mathsf {U}}_\gamma \), followed by \(\delta _ K \) contained in \({\mathsf {U}}_ K \) from \({\mathsf {U}}_\gamma \) to \({\mathsf {U}}_\beta \), followed by \(\delta _ J \) contained in \({\mathsf {U}}_ J \) from \({\mathsf {U}}_\beta \) back to \({\mathsf {U}}_\alpha \) (see Fig. 12).
\({\mathsf {U}}_ I , {\mathsf {U}}_ J , {\mathsf {U}}_ K \subset {\mathsf {X}}\) are the Stokes regions with \( I = \left\{ i,i' \right\} , J = \left\{ j,j' \right\} , K = \left\{ k,k' \right\} \). The stokes rays \({\mathsf {U}}_\alpha , {\mathsf {U}}_\gamma , {\mathsf {U}}_\gamma \) are indicated by \(\alpha , \beta , \gamma \) (same for the spectral rays). \(\mathsf {b}\in {\mathsf {B}}\) is the branch point and \(\mathsf {r}\in {\mathsf {R}}\) is the ramification point above \(\mathsf {b}\)
Explicitly:

The key idea, which goes back to Gaiotto–Moore–Neitzke [8], is to notice that this expression has an interpretation as a parallel transport for the abelian connection  on the spectral curve. Indeed, if we fix points \(\mathsf {p}, \mathsf {p}', \mathsf {p}''\) in \({\mathsf {U}}_\alpha , {\mathsf {U}}_\gamma , {\mathsf {U}}_\beta \) as shown in Fig. 12, then through the canonical identification of fibres using Proposition 3.5(4), we have:
on the spectral curve. Indeed, if we fix points \(\mathsf {p}, \mathsf {p}', \mathsf {p}''\) in \({\mathsf {U}}_\alpha , {\mathsf {U}}_\gamma , {\mathsf {U}}_\beta \) as shown in Fig. 12, then through the canonical identification of fibres using Proposition 3.5(4), we have:

Here, \(\Delta ^+_\alpha \) is defined by the diagram; we used (22), and \(p_i, p_k, p_{j'}\) are  -parallel transports along the paths \(\delta _i, \delta _k, \delta _{j'}\) which are the lifts of \(\delta _ I , \delta _ K , \delta _ J \) as shown in Fig. 12. Since \(g^+_{\beta }, g^-_{\gamma }\) are precisely the gluing maps for \({{\mathcal {L}}}\), we find that \(\Delta ^+_\alpha \) is nothing but the parallel transport of
-parallel transports along the paths \(\delta _i, \delta _k, \delta _{j'}\) which are the lifts of \(\delta _ I , \delta _ K , \delta _ J \) as shown in Fig. 12. Since \(g^+_{\beta }, g^-_{\gamma }\) are precisely the gluing maps for \({{\mathcal {L}}}\), we find that \(\Delta ^+_\alpha \) is nothing but the parallel transport of  along the clockwise semicircular path \(\delta _\mathsf {p}^+ \mathrel {\mathop :}=\delta _{j'} \delta _k \delta _{i}\) (our paths compose the same way as maps: from right to left) around the ramification point \(\mathsf {r}\) starting at \(\mathsf {p}_+\) and ending at \(\mathsf {p}_-\). The Stokes graph determines such sheet transposition paths on all Stokes rays: i.e., for any \(\mathsf {p}\in {\mathsf {U}}_\alpha \), the path \(\delta _\mathsf {p}^+\) on
along the clockwise semicircular path \(\delta _\mathsf {p}^+ \mathrel {\mathop :}=\delta _{j'} \delta _k \delta _{i}\) (our paths compose the same way as maps: from right to left) around the ramification point \(\mathsf {r}\) starting at \(\mathsf {p}_+\) and ending at \(\mathsf {p}_-\). The Stokes graph determines such sheet transposition paths on all Stokes rays: i.e., for any \(\mathsf {p}\in {\mathsf {U}}_\alpha \), the path \(\delta _\mathsf {p}^+\) on  is the unique lift starting at \(\mathsf {p}_+\) of a clockwise loop \(\delta _\mathsf {p}\) based at \(\mathsf {p}\in {\mathsf {U}}_\alpha \) around the branch point \(\mathsf {b}\) (see Fig. 13).
is the unique lift starting at \(\mathsf {p}_+\) of a clockwise loop \(\delta _\mathsf {p}\) based at \(\mathsf {p}\in {\mathsf {U}}_\alpha \) around the branch point \(\mathsf {b}\) (see Fig. 13).
3.11 Lemma
For every Stokes ray \({\mathsf {U}}_\alpha \subset {\mathsf {X}}\) and every point \(\mathsf {p}\in {\mathsf {U}}_{\alpha }\), the automorphism \( V _{\alpha , \mathsf {p}}\) of the fibre  is:
is:

The correspondence \(\mathsf {p}_+ \mapsto \delta ^+_{\mathsf {p}}\) is a well-defined map  , where
, where  is the fundamental groupoid of the punctured spectral curve, which is the set of paths on
is the fundamental groupoid of the punctured spectral curve, which is the set of paths on  considered up to homotopy with fixed endpoints. If we define a flat bundle isomorphism
considered up to homotopy with fixed endpoints. If we define a flat bundle isomorphism

then \(\Delta _\alpha = \pi _*\Delta ^+_\alpha \) defines an endomorphism of \(\pi _*{{\mathcal {L}}}\) over the Stokes ray \({\mathsf {U}}_{\alpha }\). So Lemma 3.11 may be expressed in terms of bundle maps as follows.
3.12 Lemma
For every \(\alpha \in \Gamma _1\), the automorphism \( V _{\alpha }\) of  is \( V _{\alpha } = \text {id}+ \pi _*\Delta ^+_\alpha \).
is \( V _{\alpha } = \text {id}+ \pi _*\Delta ^+_\alpha \).
3.13. The Voros cocycle. One of the central observations in this paper is that formula (28) does not depend on the fact that  is the abelianisation of \(({{\mathcal {E}}}, \nabla )\). Indeed, this formula is written purely in terms of the parallel transport along canonically defined paths on
is the abelianisation of \(({{\mathcal {E}}}, \nabla )\). Indeed, this formula is written purely in terms of the parallel transport along canonically defined paths on  and the pushforward functor \(\pi _*\). In other words, if
and the pushforward functor \(\pi _*\). In other words, if  is any abelian connection (i.e., not a priori the abelianisation of some connection on \({\mathsf {X}}\)), then for each Stokes ray \(\alpha \in \Gamma _1\), we can consider the automorphism \( V _{\alpha }\) of \(\pi _*{{\mathcal {L}}}\) over \({\mathsf {U}}_{\alpha }\) defined by
is any abelian connection (i.e., not a priori the abelianisation of some connection on \({\mathsf {X}}\)), then for each Stokes ray \(\alpha \in \Gamma _1\), we can consider the automorphism \( V _{\alpha }\) of \(\pi _*{{\mathcal {L}}}\) over \({\mathsf {U}}_{\alpha }\) defined by

for each \(\mathsf {p}\in {\mathsf {U}}_{\alpha }\) with preimages \(\mathsf {p}_\pm \in {\mathsf {U}}_{\alpha }^\pm \). As a bundle automorphism over \({\mathsf {U}}_{\alpha }\),

where  and
and  . This yields a cocycle
. This yields a cocycle

Now, if  is a morphism in
is a morphism in  , and \( V , V '\) are respectively the cocycles for \({{\mathcal {L}}}, {{\mathcal {L}}}'\) defined by the formula (29), then the identity
, and \( V , V '\) are respectively the cocycles for \({{\mathcal {L}}}, {{\mathcal {L}}}'\) defined by the formula (29), then the identity  immediately implies the following commutative square for every \(\alpha \):
immediately implies the following commutative square for every \(\alpha \):

In other words, for every Stokes ray \(\alpha \in \Gamma _1\), the collection

indexed by abelian connections  , forms a natural transformation
, forms a natural transformation

of the pushforward functor (2), defined over \({\mathsf {U}}_{\alpha }\). We obtain a cocycle valued in the local system \(\mathcal {A}ut (\pi _*)\) of nonabelian groups on the punctured base curve \({\mathsf {X}}^\circ \) consisting of natural automorphisms of \(\pi _*\).
3.14 Definition
(Voros cocycle) The Voros cocycle is the nonabelian Čech 1-cocycle

\(\square \)
3.15. Abelianisation of the Voros cocycle. The parallel transports \(\Delta _\alpha \) can also be arranged into a cocycle as follows. If  is any abelian connection, then
is any abelian connection, then  , where
, where  and
and  for each \(\alpha \in \Gamma ^+_1\). The sheaf \(\mathcal {H}om ( L , \sigma ^* L )\) is a local system of abelian groups, and we can define an abelian Čech 1-cocycle on
for each \(\alpha \in \Gamma ^+_1\). The sheaf \(\mathcal {H}om ( L , \sigma ^* L )\) is a local system of abelian groups, and we can define an abelian Čech 1-cocycle on  by
by

by  and
and  is a morphism in
is a morphism in  , and \(\Delta , \Delta '\) are the corresponding cocycles, then the identity
, and \(\Delta , \Delta '\) are the corresponding cocycles, then the identity  implies for every \(\alpha \) a pair of commutative squares:
implies for every \(\alpha \) a pair of commutative squares:

In other words, for every \(\alpha \), the collection of flat homomorphisms

indexed by abelian connections  , forms a natural transformation
, forms a natural transformation

defined over \({\mathsf {U}}_{\alpha }^\pm \). Here,  is the pullback functor by the canonical involution \(\sigma \). Thus, we obtain a cocycle valued in the local system \(\mathcal {H}om (\text {id}, \sigma ^*)\) of abelian groups on the punctured spectral curve
is the pullback functor by the canonical involution \(\sigma \). Thus, we obtain a cocycle valued in the local system \(\mathcal {H}om (\text {id}, \sigma ^*)\) of abelian groups on the punctured spectral curve  consisting of natural transformations from the identity functor \(\text {id}\) to the pullback functor \(\sigma ^*\):
consisting of natural transformations from the identity functor \(\text {id}\) to the pullback functor \(\sigma ^*\):

Formula (30) makes it apparent that the Voros cocycle \(\mathbb {V}\) is completely determined by the cocycle  ; let us make this precise. Suppose
; let us make this precise. Suppose  , and choose a point \(\mathsf {p}\in {\mathsf {U}}_{\alpha }\) for some \(\alpha \). If \(\mathsf {p}_\pm \in {\mathsf {U}}_{\alpha }^\pm \) are the two preimages of \(\mathsf {p}\), then the canonical isomorphism
, and choose a point \(\mathsf {p}\in {\mathsf {U}}_{\alpha }\) for some \(\alpha \). If \(\mathsf {p}_\pm \in {\mathsf {U}}_{\alpha }^\pm \) are the two preimages of \(\mathsf {p}\), then the canonical isomorphism  on stalks induces a canonical inclusion of \(\mathcal {H}om ( L , \sigma ^* L )_{\mathsf {p}_\pm }\) into \({\mathcal {End}} (\pi _* L )_\mathsf {p}\) via
on stalks induces a canonical inclusion of \(\mathcal {H}om ( L , \sigma ^* L )_{\mathsf {p}_\pm }\) into \({\mathcal {End}} (\pi _* L )_\mathsf {p}\) via

Given any \(c \in \mathcal {H}om ( L , \sigma ^* L )_{\mathsf {p}_\pm }\), we denote its image in \(\mathcal {E}nd (\pi _* L )_\mathsf {p}\) by \(\pi _*c\).
3.16 Proposition
The Voros cocycle \(\mathbb {V}\) and the abelian cocycle  satisfy
satisfy  , where
, where  is the identity cocycle.
is the identity cocycle.
That is to say, the nonabelian Voros cocycle \(\mathbb {V}\) is actually ‘in disguise’ the data of an abelian cocycle  but on a different curve. In other words,
but on a different curve. In other words,  should be thought of as the abelianisation of the Voros cocycle.
should be thought of as the abelianisation of the Voros cocycle.
Proof
Notice that \(\pi \) induces a double cover  , yielding a map on cocycles:
, yielding a map on cocycles:

Then formula (30) implies that \(\mathbb {V}\) is the image of  . \(\square \)
. \(\square \)
3.3 The nonabelianisation functor
In this section, we construct the nonabelianisation functor \(\pi _\text {ab}^\Gamma \) and prove that it is an inverse equivalence to the abelianisation functor \(\pi _\Gamma ^\text {ab}\). The main ingredient is the Voros cocycle \(\mathbb {V}\), and the construction proceeds in two steps. If  is an abelian connection on
is an abelian connection on  , we first use the the pushforward functor \(\pi _*\) to obtain a rank-two connection
, we first use the the pushforward functor \(\pi _*\) to obtain a rank-two connection  on \(({\mathsf {X}}, {\mathsf {D}} \cup {\mathsf {B}})\). But
on \(({\mathsf {X}}, {\mathsf {D}} \cup {\mathsf {B}})\). But  does not holomorphically extend over the branch locus \({\mathsf {B}}\), because it has nontrivial monodromy around \({\mathsf {B}}\), as we remarked after the proof of Proposition 2.15. Therefore, \(\pi _*\) cannot invert \(\pi ^\text {ab}_\Gamma \), because its image is not even contained in \(Conn _{\mathsf {X}}^2\). Instead, step two is to use the Voros cocycle \(\mathbb {V}\) to deform \(\pi _*\) as a functor. The result is the nonabelianisation functor \(\pi _\text {ab}^\Gamma \).
does not holomorphically extend over the branch locus \({\mathsf {B}}\), because it has nontrivial monodromy around \({\mathsf {B}}\), as we remarked after the proof of Proposition 2.15. Therefore, \(\pi _*\) cannot invert \(\pi ^\text {ab}_\Gamma \), because its image is not even contained in \(Conn _{\mathsf {X}}^2\). Instead, step two is to use the Voros cocycle \(\mathbb {V}\) to deform \(\pi _*\) as a functor. The result is the nonabelianisation functor \(\pi _\text {ab}^\Gamma \).
3.17. Construction of \(\nabla \). Given any abelian connection  , we construct \(({{\mathcal {E}}}, \nabla , M ) \in Conn _{\mathsf {X}}^2 (\Gamma )\). Consider the pushforward
, we construct \(({{\mathcal {E}}}, \nabla , M ) \in Conn _{\mathsf {X}}^2 (\Gamma )\). Consider the pushforward  . The Voros cocycle \(\mathbb {V}\) determines a cocycle \( V \mathrel {\mathop :}=\mathbb {V}({{\mathcal {L}}}) \in {\check{Z}}^1 \big (\mathfrak {{{U}}}_\Gamma , \mathcal {A}ut (\pi _*{{\mathcal {L}}}) \big )\).
. The Voros cocycle \(\mathbb {V}\) determines a cocycle \( V \mathrel {\mathop :}=\mathbb {V}({{\mathcal {L}}}) \in {\check{Z}}^1 \big (\mathfrak {{{U}}}_\Gamma , \mathcal {A}ut (\pi _*{{\mathcal {L}}}) \big )\).
Definition over Stokes regions. The main step in the construction is to use \( V \) to reglue \(\pi _*{{\mathcal {L}}}\) over Stokes rays. For each Stokes region \({\mathsf {U}}_ I \), let

and if \({\mathsf {U}}_\alpha \) is a Stokes ray in the ordered double intersection \({\mathsf {U}}_ I \cap {\mathsf {U}}_ J \), then the gluing over \({\mathsf {U}}_\alpha \) is given by  . If \({\mathsf {U}}_i\) is a spectral region in the preimage of \({\mathsf {U}}_ I \), then since \({{\mathcal {E}}}_ I ({\mathsf {U}}_ I ) = {{\mathcal {L}}} ({\mathsf {U}}_i) \oplus \sigma ^*{{\mathcal {L}}} ({\mathsf {U}}_i)\), the map \( M _ I \) defines an \(\mathfrak {sl}_2\)-structure on each local piece \({{\mathcal {E}}}_{ I }\). Moreover, \( M _ I \) and \( M _ J \) glue over \({\mathsf {U}}_\alpha \) because \( V _{\alpha }\) is unipotent with respect to the corresponding decompositions.
. If \({\mathsf {U}}_i\) is a spectral region in the preimage of \({\mathsf {U}}_ I \), then since \({{\mathcal {E}}}_ I ({\mathsf {U}}_ I ) = {{\mathcal {L}}} ({\mathsf {U}}_i) \oplus \sigma ^*{{\mathcal {L}}} ({\mathsf {U}}_i)\), the map \( M _ I \) defines an \(\mathfrak {sl}_2\)-structure on each local piece \({{\mathcal {E}}}_{ I }\). Moreover, \( M _ I \) and \( M _ J \) glue over \({\mathsf {U}}_\alpha \) because \( V _{\alpha }\) is unipotent with respect to the corresponding decompositions.
Definition at the poles. Recall that the infinitesimal punctured disc \({\mathsf {U}}_\mathsf {p}^*\) centred at a point \(\mathsf {p}\in {\mathsf {D}}\) is covered by sectorial neighbourhoods coming from the Stokes regions incident to \(\mathsf {p}\). Thanks to the upper-triangular nature of the Voros cocycle \( V \), we obtain a flat bundle \({{\mathcal {E}}}_\mathsf {p}^*\) over \({\mathsf {U}}_\mathsf {p}^*\) equipped with a filtration \(({{\mathcal {E}}}_\mathsf {p}^*)^\bullet \) whose associated graded is canonically isomorphic to  . Now, it is a simple fact that if the associated graded of a filtered connection extends over a point, then the filtered connection itself extends with the same Levelt exponents. Thus, \({{\mathcal {E}}}_\mathsf {p}^*\) has a canonical extension over \({\mathsf {U}}_\mathsf {p}\) to a bundle \({{\mathcal {E}}}_\mathsf {p}\) with connection \(\nabla _\mathsf {p}\) that has logarithmic poles at \(\mathsf {p}\) and Levelt exponents \(\pm \lambda _\mathsf {p}\). It remains to define \(\nabla \) over the branch locus \({\mathsf {B}}\).
. Now, it is a simple fact that if the associated graded of a filtered connection extends over a point, then the filtered connection itself extends with the same Levelt exponents. Thus, \({{\mathcal {E}}}_\mathsf {p}^*\) has a canonical extension over \({\mathsf {U}}_\mathsf {p}\) to a bundle \({{\mathcal {E}}}_\mathsf {p}\) with connection \(\nabla _\mathsf {p}\) that has logarithmic poles at \(\mathsf {p}\) and Levelt exponents \(\pm \lambda _\mathsf {p}\). It remains to define \(\nabla \) over the branch locus \({\mathsf {B}}\).
Definition at the branch points. We will first compute the monodromy of \(\nabla \) around each branch point directly to show that it is trivial, and then use Deligne’s canonical extension [5, pp. 91–96].
3.18 Lemma
The monodromy of \(\nabla \) around any branch point is trivial. Therefore, the connection \(({{\mathcal {E}}}, \nabla , M )\) on \({\mathsf {X}}^\circ \) has a canonical holomorphic extension over \({\mathsf {B}}\).
The technique is to express the parallel transport of \(\nabla \) along paths on \({\mathsf {X}}\) in terms of the parallel transport of  along their lifts to
along their lifts to  as well as the sheet transposition paths. We adopt the following notation for the parallel transports of
as well as the sheet transposition paths. We adopt the following notation for the parallel transports of  , respectively:
, respectively:

It follows immediately from the construction of \({{\mathcal {E}}}\) that if \(\wp \) is a path on \({\mathsf {X}}^\circ \) contained in a Stokes region, then \( P (\wp ) = \pi _*p (\wp )\). Explicitly, let \(\wp ', \wp ''\) be the two lifts of \(\wp \) to  . Let \(\mathsf {x}, \mathsf {y}\) be the startpoint and the endpoint of \(\wp \), and similarly for \(\wp ', \wp ''\). Then, for example, the fibre
. Let \(\mathsf {x}, \mathsf {y}\) be the startpoint and the endpoint of \(\wp \), and similarly for \(\wp ', \wp ''\). Then, for example, the fibre  is the direct sum of fibres \(L_{\mathsf {x}'} \oplus L_{\mathsf {x}''}\) of \({{\mathcal {L}}}\). With respect to these decompositions, the parallel transport \( P (\wp ) : E_{\mathsf {x}} \longrightarrow E_{\mathsf {y}}\) is expressed as
is the direct sum of fibres \(L_{\mathsf {x}'} \oplus L_{\mathsf {x}''}\) of \({{\mathcal {L}}}\). With respect to these decompositions, the parallel transport \( P (\wp ) : E_{\mathsf {x}} \longrightarrow E_{\mathsf {y}}\) is expressed as

We say that a path \(\wp \) on \({\mathsf {X}}^\circ \) (or  ) is a short path if its endpoints do not belong to the Stokes graph \(\Gamma \) (or to the spectral graph
) is a short path if its endpoints do not belong to the Stokes graph \(\Gamma \) (or to the spectral graph  ) and it intersects at most one Stokes ray (or spectral ray). If \(\wp \) is a short path on \({\mathsf {X}}^\circ \) that intersects a Stokes ray \({\alpha } \in \Gamma _1\), then \(\wp \) is divided into two segments \(\wp _-, \wp _+\) (Fig. 14).
) and it intersects at most one Stokes ray (or spectral ray). If \(\wp \) is a short path on \({\mathsf {X}}^\circ \) that intersects a Stokes ray \({\alpha } \in \Gamma _1\), then \(\wp \) is divided into two segments \(\wp _-, \wp _+\) (Fig. 14).
Each \(\wp _\pm \) is contained in a Stokes region, so \( P (\wp _\pm ) = \pi _*p (\wp _\pm )\). On the other hand, the vector bundle \({{\mathcal {E}}}\) is constructed by gluing \(\pi _*{{\mathcal {L}}}\) to itself over \({\mathsf {U}}_{\alpha }\) by the automorphism \( V _{\alpha }\), so we obtain the following formula for \( P (\wp )\):

Explicitly, let \(\wp ', \wp ''\) denote the two lifts of \(\wp \) to  , where \(\wp '\) intersects \(\alpha _-\) and \(\wp ''\) intersects \(\alpha _+\) (Fig. 14). The parallel transport \( P (\wp ) : E_{\mathsf {x}} \longrightarrow E_{\mathsf {y}}\) can be expressed as
, where \(\wp '\) intersects \(\alpha _-\) and \(\wp ''\) intersects \(\alpha _+\) (Fig. 14). The parallel transport \( P (\wp ) : E_{\mathsf {x}} \longrightarrow E_{\mathsf {y}}\) can be expressed as

The off-diagonal term \(p (\wp '_+) \Delta _{\alpha }^+ p (\wp ''_-)\) is the parallel transport of  along the concatenated path \(\wp ^+_\alpha \mathrel {\mathop :}=\wp '_+ \delta ^+_\alpha \wp ''_-\) (Fig. 15), so
along the concatenated path \(\wp ^+_\alpha \mathrel {\mathop :}=\wp '_+ \delta ^+_\alpha \wp ''_-\) (Fig. 15), so

Proof of Lemma 3.18
Fix a branch point \(\mathsf {b}\in {\mathsf {B}}\), and let \({\mathsf {U}}_{\alpha }, {\mathsf {U}}_{\beta }, {\mathsf {U}}_{\gamma }\) be the three Stokes rays incident to \(\mathsf {b}\). Fix a basepoint \(\mathsf {x}\) in the Stokes region \({\mathsf {U}}_ I \) as shown in Fig. 16, and also fix a loop \(\wp \) around \(\mathsf {b}\). We calculate the monodromy \( P (\wp )\). Fix two more basepoints \(\mathsf {y}, \mathsf {z}\) in the other two Stokes regions, thus dividing the loop \(\wp \) into three short paths denoted by \(\wp _\alpha , \wp _\beta , \wp _\gamma \), as explained in Fig. 17. Then \( P (\wp ) = P (\wp _\gamma ) P (\wp _\beta ) P (\wp _\alpha )\). Each \( P (\wp _\bullet )\) (where \(\bullet = \alpha , \beta , \gamma \)) can be expressed via (39) as

Now, let \(\wp ', \wp ''\) be the two lifts of \(\wp \) to  , as explained in Fig. 18. The lifts \(\wp ''_\alpha , \wp '_\beta , \wp ''_\gamma \) intersect the positive spectral rays \(\alpha _+, \beta _+, \gamma _+\), giving rise to three sheet transposition paths \(\wp ^+_\alpha , \wp ^+_\beta , \wp ^+_\gamma \) as shown in Fig. 19. By inspection,
, as explained in Fig. 18. The lifts \(\wp ''_\alpha , \wp '_\beta , \wp ''_\gamma \) intersect the positive spectral rays \(\alpha _+, \beta _+, \gamma _+\), giving rise to three sheet transposition paths \(\wp ^+_\alpha , \wp ^+_\beta , \wp ^+_\gamma \) as shown in Fig. 19. By inspection,

The loop \(\wp \) from Fig. 16 is homotopic to the concatenated path \(\wp _\gamma \wp _\beta \wp _\alpha \) as shown
Left: Let \(\mathsf {x}', \mathsf {x}''\) be the two preimages of \(\mathsf {x}\) on  as shown. Right: Let \(\mathsf {y}', \mathsf {y}'', \mathsf {z}', \mathsf {z}''\) be the lifts of \(\mathsf {y}, \mathsf {z}\) as shown, \(\wp ' = \wp '_\gamma \wp '_\beta \wp '_\alpha \) and \(\wp '' = \wp ''_\gamma \wp ''_\beta \wp ''_\alpha \)
as shown. Right: Let \(\mathsf {y}', \mathsf {y}'', \mathsf {z}', \mathsf {z}''\) be the lifts of \(\mathsf {y}, \mathsf {z}\) as shown, \(\wp ' = \wp '_\gamma \wp '_\beta \wp '_\alpha \) and \(\wp '' = \wp ''_\gamma \wp ''_\beta \wp ''_\alpha \)
The explicit formula (40) gives three expressions:

Notice that \( P (\wp _\beta )\) is lower-triangular in the given decompositions of  and
and  , because it is the lift \(\wp '_\beta \) of \(\wp _\beta \) starting at \(\mathsf {y}'\) that intersects the positive spectral ray \(\beta _+\). Also notice that the source fibre of \( P (\wp _\alpha )\) is decomposed as \(L_{\mathsf {x}'} \oplus L_{\mathsf {x}''}\), whilst the target fibre of \( P (\wp _\gamma )\) is decomposed as \(L_{\mathsf {x}''} \oplus L_{\mathsf {x}'}\), so the monodromy \( P (\wp ) \in {\mathsf {Aut}}\big (L_{\mathsf {x}'} \oplus L_{\mathsf {x}''} \big )\) is given by
, because it is the lift \(\wp '_\beta \) of \(\wp _\beta \) starting at \(\mathsf {y}'\) that intersects the positive spectral ray \(\beta _+\). Also notice that the source fibre of \( P (\wp _\alpha )\) is decomposed as \(L_{\mathsf {x}'} \oplus L_{\mathsf {x}''}\), whilst the target fibre of \( P (\wp _\gamma )\) is decomposed as \(L_{\mathsf {x}''} \oplus L_{\mathsf {x}'}\), so the monodromy \( P (\wp ) \in {\mathsf {Aut}}\big (L_{\mathsf {x}'} \oplus L_{\mathsf {x}''} \big )\) is given by

Applying relations (41), we find that \(\wp ''_\gamma \wp ^+_{\beta } \wp '_\alpha = \wp ''_\gamma (\wp '_\alpha \wp ''_\gamma )^{-1} \wp '_\alpha = 1\), which is a constant path at \(\mathsf {x}'\), so the top-left entry of \( P (\wp )\) is 1. Next, the path \(\wp ^+_{\gamma } \wp ^+_{\beta } \wp '_\alpha \) appearing in the bottom-left entry, simplifies to \((\wp ''_\gamma \wp ''_\beta \wp ''_\alpha )^{-1}\), so \(p(\wp ^+_{\gamma } \wp ^+_{\beta } \wp ^+_{\alpha }) = p (\wp '_\gamma \wp '_\beta \wp '_\alpha )^{-1}\). Now, \(\wp ''_\gamma \wp ''_\beta \wp ''_\alpha \wp '_\gamma \wp '_\beta \wp '_\alpha \) is a loop around the ramification point \(\mathsf {r}\) based at \(\mathsf {x}'\), and since the connection  has monodromy \(-1\) around \(\mathsf {r}\) by Proposition 2.12, we find:
has monodromy \(-1\) around \(\mathsf {r}\) by Proposition 2.12, we find:

It follows that \(p (\wp '_\gamma \wp '_\beta \wp '_\alpha )^{-1} = - p (\wp ''_\gamma \wp ''_\beta \wp ''_\alpha )\), and so the bottom-left entry of \( P (\wp )\) is 0. Similarly, we can calculate the other entries of \( P (\wp )\) and find that \( P (\wp ) = \text {id}\). \(\square \)
3.19. Diagonal decompositions and transversality. The fact that the connection \(\nabla \) is transverse with respect to \(\Gamma \) is deduced from the fact that the local and semilocal diagonal decompositions of \({{\mathcal {E}}}\) (Propositions 2.8 and 2.46) can be easily recovered from our construction as follows. Let \({\mathsf {U}}_\mathsf {p}\) be the infinitesimal disc around a pole \(\mathsf {p}\in {\mathsf {D}}\). If \({\mathsf {U}}_\mathsf {p}^\pm \) are respectively the infinitesimal discs around \(\mathsf {p}_\pm \), let  and \(\Lambda _\mathsf {p}^\pm \mathrel {\mathop :}=\pi _*{{\mathcal {L}}}_\mathsf {p}^\pm \). Then it follows from the construction of \({{\mathcal {E}}}\) over \({\mathsf {U}}_\mathsf {p}\) that the local diagonal decomposition of \({{\mathcal {E}}}_\mathsf {p}\) is precisely
and \(\Lambda _\mathsf {p}^\pm \mathrel {\mathop :}=\pi _*{{\mathcal {L}}}_\mathsf {p}^\pm \). Then it follows from the construction of \({{\mathcal {E}}}\) over \({\mathsf {U}}_\mathsf {p}\) that the local diagonal decomposition of \({{\mathcal {E}}}_\mathsf {p}\) is precisely  . As a result, the local Levelt filtration of \({{\mathcal {E}}}\) at \(\mathsf {p}\) is \({{\mathcal {E}}}_\mathsf {p}^\bullet = \big ( \Lambda _\mathsf {p}^- \subset {{\mathcal {E}}}^\mathsf {p}\big )\).
. As a result, the local Levelt filtration of \({{\mathcal {E}}}\) at \(\mathsf {p}\) is \({{\mathcal {E}}}_\mathsf {p}^\bullet = \big ( \Lambda _\mathsf {p}^- \subset {{\mathcal {E}}}^\mathsf {p}\big )\).
Let \({\mathsf {U}}_ I \) be a Stokes region with \( I = \left\{ i,i' \right\} \) and with polar vertices \(\mathsf {p}, \mathsf {p}'\) such that the spectral regions \({\mathsf {U}}_i, {\mathsf {U}}_{i'}\) are respectively incident to the preimages \(\mathsf {p}_-, \mathsf {p}'_-\). By construction, if  and \(\smash {\Lambda _{i^{(\prime )}} \mathrel {\mathop :}=\pi _*{{\mathcal {L}}}_{i^{(\prime )}}}\), then \({{\mathcal {E}}}_ I = \Lambda _i \oplus \Lambda _{i'}\). Of course, \({{\mathcal {L}}}_{i}\) is the unique continuation of \({{\mathcal {L}}}_{\mathsf {p}}^-\) from \({\mathsf {U}}_{\mathsf {p}}^-\) to \({\mathsf {U}}_i\), and therefore \(\Lambda _i\) is the unique continuation of \(\Lambda _\mathsf {p}^-\) from \({\mathsf {U}}_\mathsf {p}\) to \({\mathsf {U}}_ I \). Same for \(\Lambda _{i'}\). As a result, the direct sum \(\Lambda _i \oplus \Lambda _{i'}\) is nothing but the transverse intersection \({{\mathcal {E}}}_{\mathsf {p}, I }^\bullet \pitchfork {{\mathcal {E}}}_{\mathsf {p}', I }^\bullet \) of Levelt filtrations \({{\mathcal {E}}}_\mathsf {p}^\bullet , {{\mathcal {E}}}_{\mathsf {p}'}^\bullet \) continued to \({\mathsf {U}}_ I \). This demonstrates the fact that \(\nabla \) is transverse with respect to \(\Gamma \), so \(({{\mathcal {E}}}, \nabla , M ) \in Conn _{\mathsf {X}}^2 (\Gamma )\).
and \(\smash {\Lambda _{i^{(\prime )}} \mathrel {\mathop :}=\pi _*{{\mathcal {L}}}_{i^{(\prime )}}}\), then \({{\mathcal {E}}}_ I = \Lambda _i \oplus \Lambda _{i'}\). Of course, \({{\mathcal {L}}}_{i}\) is the unique continuation of \({{\mathcal {L}}}_{\mathsf {p}}^-\) from \({\mathsf {U}}_{\mathsf {p}}^-\) to \({\mathsf {U}}_i\), and therefore \(\Lambda _i\) is the unique continuation of \(\Lambda _\mathsf {p}^-\) from \({\mathsf {U}}_\mathsf {p}\) to \({\mathsf {U}}_ I \). Same for \(\Lambda _{i'}\). As a result, the direct sum \(\Lambda _i \oplus \Lambda _{i'}\) is nothing but the transverse intersection \({{\mathcal {E}}}_{\mathsf {p}, I }^\bullet \pitchfork {{\mathcal {E}}}_{\mathsf {p}', I }^\bullet \) of Levelt filtrations \({{\mathcal {E}}}_\mathsf {p}^\bullet , {{\mathcal {E}}}_{\mathsf {p}'}^\bullet \) continued to \({\mathsf {U}}_ I \). This demonstrates the fact that \(\nabla \) is transverse with respect to \(\Gamma \), so \(({{\mathcal {E}}}, \nabla , M ) \in Conn _{\mathsf {X}}^2 (\Gamma )\).
3.20 Proposition
The correspondence  extends to a functor
extends to a functor

This follows immediately from the commutative square (32). We call \(\pi _\text {ab}^\Gamma \) the nonabelianisation functor, and the image  under \(\pi _\text {ab}^\Gamma \) the nonabelianisation of
under \(\pi _\text {ab}^\Gamma \) the nonabelianisation of  with respect to the Stokes graph \(\Gamma \). Finally, our Main Theorem 3.3 follows from the following proposition.
with respect to the Stokes graph \(\Gamma \). Finally, our Main Theorem 3.3 follows from the following proposition.
3.21 Proposition
The functors \(\pi ^\text {ab}_\Gamma , \pi _\text {ab}^\Gamma \) form a pair of inverse equivalences of categories.
Proof
Given \(({{\mathcal {E}}}, \nabla , M ) \in Conn _{\mathsf {X}}^2 (\Gamma )\), let  be its image under \(\pi ^\text {ab}_\Gamma \). By construction, the Voros cocycle \(\mathbb {V}\) applied to \({{\mathcal {L}}}\) is the cocycle \( V \) from (26). Lemma 3.9 gives a canonical isomorphism
be its image under \(\pi ^\text {ab}_\Gamma \). By construction, the Voros cocycle \(\mathbb {V}\) applied to \({{\mathcal {L}}}\) is the cocycle \( V \) from (26). Lemma 3.9 gives a canonical isomorphism  , so \(\pi _\text {ab}^\Gamma \pi ^\text {ab}_\Gamma \Rightarrow \text {Id}\).
, so \(\pi _\text {ab}^\Gamma \pi ^\text {ab}_\Gamma \Rightarrow \text {Id}\).
The converse is clear from the discussion above of diagonal decompositions and transversality (3.3), so we will be brief. Given  , let \(({{\mathcal {E}}}, \nabla , M )\) in \(Conn _{\mathsf {X}}^2 (\Gamma )\) be its nonabelianisation, and suppose \({{\mathcal {L}}}'\) is the abelianisation of \({{\mathcal {E}}}\). First, we have
, let \(({{\mathcal {E}}}, \nabla , M )\) in \(Conn _{\mathsf {X}}^2 (\Gamma )\) be its nonabelianisation, and suppose \({{\mathcal {L}}}'\) is the abelianisation of \({{\mathcal {E}}}\). First, we have  for every \(\mathsf {p}\in {\mathsf {D}}\). If
for every \(\mathsf {p}\in {\mathsf {D}}\). If  is a spectral region with sink polar vertex \(\mathsf {p}_-\), then \(\Lambda _i = \pi _*{{\mathcal {L}}}_i\) is the unique continuation of \(\Lambda _\mathsf {p}^-\). Both \({{\mathcal {L}}}_i\) and \({{\mathcal {L}}}'_i\) are the unique continuations of \((\pi _\mathsf {p}^-)^*\Lambda _\mathsf {p}^-\) to \({\mathsf {U}}_i\), we get
is a spectral region with sink polar vertex \(\mathsf {p}_-\), then \(\Lambda _i = \pi _*{{\mathcal {L}}}_i\) is the unique continuation of \(\Lambda _\mathsf {p}^-\). Both \({{\mathcal {L}}}_i\) and \({{\mathcal {L}}}'_i\) are the unique continuations of \((\pi _\mathsf {p}^-)^*\Lambda _\mathsf {p}^-\) to \({\mathsf {U}}_i\), we get  . Thus, \({{\mathcal {L}}}, {{\mathcal {L}}}'\) are canonically isomorphic over
. Thus, \({{\mathcal {L}}}, {{\mathcal {L}}}'\) are canonically isomorphic over  , and because their extensions over \({\mathsf {R}}\) are unique, this isomorphism also extends over
, and because their extensions over \({\mathsf {R}}\) are unique, this isomorphism also extends over  . So
. So  , and hence \(\text {id}\Rightarrow \pi ^\text {ab}_\Gamma \pi _\text {ab}^\Gamma \). \(\square \)
, and hence \(\text {id}\Rightarrow \pi ^\text {ab}_\Gamma \pi _\text {ab}^\Gamma \). \(\square \)
References
Beauville, A., Narasimhan, M.S., Ramanan, S.: Spectral curves and the generalised theta divisor. J. Reine Angew. Math. 398, 169–179 (1989)
Borel, A., Grivel, P.-P., Kaup, B., Haefliger, A., Malgrange, B., Ehlers, F.: Algebraic \(D\)-Modules. Perspectives in Mathematics, vol. 2. Academic Press Inc., Boston (1987)
Bridgeland, T., Smith, I.: Quadratic differentials as stability conditions. Publ. Math. Inst. Hautes Études Sci. 121, 155–278 (2015)
Delabaere, É., Dillinger, H., Pham, F.: Résurgence de Voros et périodes des courbes hyperelliptiques. Ann. Inst. Fourier (Grenoble) 43(1), 163–199 (1993)
Deligne, P.: Équations différentielles à points singuliers réguliers. Lecture Notes in Mathematics, vol. 163. Springer, Berlin (1970)
Esnault, H., Viehweg, E.: Logarithmic De Rham complexes and vanishing theorems. Invent. Math. 86, 161 (1986)
Gabella, M.: Quantum holonomies from spectral networks and framed BPS states. Commun. Math. Phys. 351(2), 563–598 (2017)
Gaiotto, D., Moore, G.W., Neitzke, A.: Spectral networks. Ann. Henri Poincaré 14(7), 1643–1731 (2013)
Gaiotto, D., Moore, G.W., Neitzke, A.: Wall-crossing, Hitchin systems, and the WKB approximation. Adv. Math. 234, 239–403 (2013)
Gaiotto, D., Moore, G.W., Neitzke, A.: Spectral networks and snakes. Ann. Henri Poincaré 15(1), 61–141 (2014)
Gualtieri, M., Li, S., Pym, B.: The Stokes groupoids. J. Reine Angew. Math. 739, 81–119 (2018)
Hausel, T., Pauly, C.: Prym varieties of spectral covers. Geom. Topol. 16(3), 1609–1638 (2012)
Hitchin, N.J.: The self-duality equations on a Riemann surface. Proc. London Math. Soc. 55(1), 59–126 (1987). https://doi.org/10.1112/plms/s3-55.1.59
Hollands, L., Neitzke, A.: Spectral networks and Fenchel–Nielsen coordinates. Lett. Math. Phys. 106(6), 811–877 (2016)
Hubbard, J., Masur, H.: Quadratic differentials and foliations. Acta Math. 142(3–4), 221–274 (1979)
Kawai, T., Takei,Y.: Algebraic analysis of singular perturbation theory. Translations of Mathematical Monographs, vol. 227. American Mathematical Society, Providence (2005). Translated from the 1998 Japanese original by Goro Kato, Iwanami Series in Modern Mathematics
Korotkin, D.: Solution of matrix Riemann–Hilbert problems with quasi-permutation monodromy matrices. Math. Ann. 329(2), 335–364 (2004)
Levelt, A.H.M.: Hypergeometric functions. Doctoral thesis, University of Amsterdam. Drukkerij Holland N. V., Amsterdam (1961)
Nikolaev, N.: Abelianisation of logarithmic connections. Ph.D. thesis, University of Toronto (2018)
Strebel, K.: Quadratic Differentials. Ergebnisse der Mathematik und ihrer Grenzgebiete (3) [Results in Mathematics and Related Areas (3)], vol. 5. Springer, Berlin (1984)
Voros, A.: The return of the quartic oscillator. The complex WKB method. Ann l’I.H.P. Phys. théorique 39(3), 211–338 (1983)
Wasow,W.: Asymptotic expansions for ordinary differential equations. Robert E. Krieger Publishing Co., Huntington (1976). Reprint of the 1965 edition
Acknowledgements
The author thanks Francis Bischoff, Aaron Fenyes, Alberto García-Raboso, Kohei Iwaki, Omar Kidwai, Andrew Neitzke, Steven Rayan, and Shinji Sasaki for helpful and enlightening discussions. Many thanks also go to the anonymous referee for their very thoughtful and helpful comments. The author expresses special gratitude to Marco Gualtieri, who suggested the problem and provided so much invaluable input, support, and encouragement as the author’s thesis advisor. At various stages, this work was supported by the Ontario Graduate Scholarship and by the NCCR SwissMAP of the SNSF.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Nikolaev, N. Abelianisation of logarithmic \(\mathfrak {sl}_2\)-connections. Sel. Math. New Ser. 27, 78 (2021). https://doi.org/10.1007/s00029-021-00688-5
Accepted:
Published:
DOI: https://doi.org/10.1007/s00029-021-00688-5
Keywords
- Meromorphic connections
- Spectral curves
- Spectral networks
- Stokes graph
- Exact WKB
- Abelianisation
- Levelt filtrations
- Singular differential equations







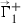 : polar vertex is a source;
: polar vertex is a source;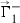 : polar vertex is a sink.
: polar vertex is a sink.





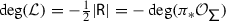 .
.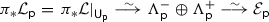 .
.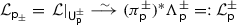 .
.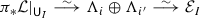 .
.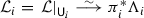 and
and 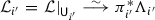 .
. on the abelianisation line bundle
on the abelianisation line bundle 








