Local Langlands correspondence for even orthogonal groups via theta lifts

Abstract

Using theta correspondence, we obtain a classification of irreducible representations of an arbitrary even orthogonal group (i.e. the local Langlands correspondence) by deducing it from the local Langlands correspondence for symplectic groups due to Arthur. Moreover, we show that our classifications coincide with the local Langlands correspondence established by Arthur and formulated precisely by Atobe–Gan for quasi-split even orthogonal groups.

Appendices

Appendix A: Local Langlands correspondence for special even orthogonal groups

In [3], Arthur established a weaker version LLC for quasi-split special even orthogonal groups from the LLC for quasi-split even orthogonal groups. This was explicated by Atobe–Gan [2]. Since we now construct the LLC for even orthogonal groups, following Arthur’s idea, we can deduce a weaker version LLC for special even orthogonal groups. We shall do it in this appendix.

Let $V=V_{2n}$ be a 2n-dimensional orthogonal space and $\chi _V$ be the discriminant character of V. By [9, §8] and [2, §3], we define

$$\begin{aligned} \Phi ({{\,\mathrm{SO}\,}}(V_{2n}))=\{\phi : {{\,\mathrm{WD}\,}}_{F} \rightarrow \text {O}(2n, {\mathbb {C}}) | \det (\phi )=\chi _{V}\} /({{\,\mathrm{SO}\,}}(2n, {\mathbb {C}})\text{-conjugacy }). \end{aligned}$$

and call an element $\phi \in \Phi ({{\,\mathrm{SO}\,}}(V_{2n}))$ an L-parameter for ${{\,\mathrm{SO}\,}}(V_{2n})$. Note that $\Phi ({{\,\mathrm{SO}\,}}(V_{2n}))$ is different from $\Phi ({\text {O}}(V_{2n}))$ since we consider the ${{\,\mathrm{SO}\,}}(2n,\mathbb C)$-conjugacy rather than ${\text {O}}(2n,{\mathbb {C}})$-conjugacy here. There is a natural surjective map

$$\begin{aligned} \Phi ({{\,\mathrm{SO}\,}}(V_{2n}))\twoheadrightarrow \Phi ({\text {O}}(V_{2n})). \end{aligned}$$

(A.1)

We define $\Phi ^\epsilon ({{\,\mathrm{SO}\,}}(V_{2n}))$ to be the preimage of $\Phi ^\epsilon ({\text {O}}(V_{2n}))$. It is easy to check that the map (A.1) is bijective on the subset $\Phi ^\epsilon ({{\,\mathrm{SO}\,}}(V_{2n}))$ and is a two-to-one map on $\Phi ({{\,\mathrm{SO}\,}}(V_{2n})){\setminus } \Phi ^\epsilon ({{\,\mathrm{SO}\,}}(V_{2n}))$.

Next we state the local Langlands correspondence for special even orthogonal groups. The reader can consult [2, §3.3] for a detailed description.

Desideratum 10.6

Fix $(d,c)\in (F^\times )^2$. Let $V_{2n}=V_{2n}^+$ be the orthogonal space associated to (d, c), and $\chi _V=(\cdot , d)_F$ be the discriminant character of $V_{2n}$.

• (1) There exists a surjective map

  $$\begin{aligned} {\mathcal {L}}: \bigsqcup _{\delta \in \{\pm 1\}} {{\,\mathrm{Irr}\,}}\left( {{\,\mathrm{SO}\,}}(V_{2n}^\delta )\right) \longrightarrow \Phi ({{\,\mathrm{SO}\,}}(V_{2n})) \end{aligned}$$

  which is finite-to-one. For any $\phi \in \Phi ({{\,\mathrm{SO}\,}}(V_{2n}))$, we denote ${\mathcal {L}}^{-1}(\phi )$ by $\Pi _{\phi }$ and call it the L-packet of $\phi$. We also write $\Pi _{\phi }({{\,\mathrm{SO}\,}}(V_{2n}))=\Pi _{\phi }\cap {{\,\mathrm{Irr}\,}}\left( {{\,\mathrm{SO}\,}}(V_{2n})\right)$.

• (2) For each Whittaker datum ${\mathfrak {W}}_{c^\prime }$, there exists a canonical bijection

  $$\begin{aligned} {\mathcal {J}}_{{\mathfrak {W}}_{c^\prime }} : \Pi _{\phi } \longrightarrow \widehat{{\mathcal {S}}^+_{\phi }}. \end{aligned}$$

  (A.2)

• (3) The L-packet $\Pi _{\phi }$ and the bijection ${\mathcal {J}}_{{\mathfrak {W}}_{c^\prime }}$ satisfy the analogues of Theorem 4.4 (3)-(12).

Desideratum 10.6 has not been established. However, following what Arthur did in [3], we can deduce a weaker version of Desideratum 10.6 as follows.

We introduce an equivalence relation $\sim _{\epsilon }$ on ${{\,\mathrm{Irr}\,}}({{\,\mathrm{SO}\,}}(V_{2n}^\delta ))$. Choose an element $\epsilon \in \text {O}(V_{2n}^\delta )$ such that $\det (\epsilon )=-1$. For $\pi _0\in {{\,\mathrm{Irr}\,}}({{\,\mathrm{SO}\,}}(V_{2n}^\delta ))$, we define its conjugate $\pi _0^\epsilon$ by

$$\begin{aligned} \pi _0^\epsilon (h)=\pi _0(\epsilon ^{-1}h\epsilon ) \quad \text{ for } h\in {\text {O}}(V_{2n}^\delta ). \end{aligned}$$

Then the equivalence relation $\sim _{\epsilon }$ on ${{\,\mathrm{Irr}\,}}({{\,\mathrm{SO}\,}}(V_{2n}^\delta ))$ is defined by

$$\begin{aligned} \pi _0 \sim _{\epsilon } \pi _0^\epsilon . \end{aligned}$$

We denote by $[\pi _0]$ the image of a representation $\pi _0\in {{\,\mathrm{Irr}\,}}({{\,\mathrm{SO}\,}}(V_{2n}^\delta ))$ under the canonical map ${{\,\mathrm{Irr}\,}}({{\,\mathrm{SO}\,}}(V_{2n}^\delta ))\rightarrow {{\,\mathrm{Irr}\,}}({{\,\mathrm{SO}\,}}(V_{2n}^\delta ))/\sim _{\epsilon }$. We say that $[\pi _0]\in {{\,\mathrm{Irr}\,}}({{\,\mathrm{SO}\,}}(V_{2n}^\delta ))/\sim _{\epsilon }$ is tempered (resp. discrete) if some (and hence any) representative $\pi _0$ is tempered (resp. discrete). We also define an equivalence relation $\sim _{\det }$ on ${{\,\mathrm{Irr}\,}}(\text {O}(V_{2n}^\delta ))$ by

$$\begin{aligned} \pi \sim _{\det } \pi \otimes \det \quad \text{ for } \pi \in {{\,\mathrm{Irr}\,}}(\text {O}(V_{2n}^\delta )). \end{aligned}$$

Then the restriction and the induction gives a canonical bijection

$$\begin{aligned} {{\,\mathrm{Irr}\,}}({\text {O}}(V_{2n}^\delta ))/\sim _{\det } \longleftrightarrow {{\,\mathrm{Irr}\,}}({{\,\mathrm{SO}\,}}(V_{2n}^\delta ))/\sim _{\epsilon }. \end{aligned}$$

We state the weaker version of LLC for ${{\,\mathrm{SO}\,}}(V_{2n})$ as follows:

Theorem A.1

(Weak LLC for special even orthogonal groups) Fix $(d,c)\in (F^\times )^2$. Let $V_{2n}=V_{2n}^+$ be the orthogonal space associated to (d, c), and $\chi _V=(\cdot , d)_F$ be the discriminant character of $V_{2n}$.

• (1). There exists a surjective map

  $$\begin{aligned} {\mathcal {L}}: \bigsqcup _{\delta \in \{\pm 1\}} \left( {{\,\mathrm{Irr}\,}}\left( {{\,\mathrm{SO}\,}}(V_{2n}^\delta )\right) /\sim _{\epsilon }\right) \longrightarrow \Phi ({\mathrm{O}}(V_{2n})), \end{aligned}$$

  which is finite-to-one. For $\phi \in \Phi ({\mathrm{O}}(V_{2n}))$, we denote $\mathcal L^{-1}(\phi )$ by $\Pi ^0_{\phi }$ and call it the L-packet of $\phi$. We also write $\Pi ^0_{\phi }({{\,\mathrm{SO}\,}}(V_{2n}))=\Pi ^0_{\phi }\cap {{\,\mathrm{Irr}\,}}\left( {{\,\mathrm{SO}\,}}(V_{2n})\right)$.

• (2). For each Whittaker datum ${\mathfrak {W}}_{c^\prime }$, there exist a canonical bijection

  $$\begin{aligned} {\mathcal {J}}^0_{{\mathfrak {W}}_{c^\prime }} : \Pi ^0_{\phi } \longrightarrow \widehat{{\mathcal {S}}^+_{\phi }}. \end{aligned}$$

  (A.3)

• (3). The L-packet $\Pi ^0_{\phi }$ and the bijection ${\mathcal {J}}^0_{{\mathfrak {W}}_{c^\prime }}$ satisfy the analogues of Theorem 4.4 (3)-(12).

• (4). For $\phi \in \Phi ({\mathrm{O}}(V_{2n})),$ let $\Pi _{\phi }$ be the L-packet defined in Theorem 4.4. Then the image of $\Pi _{\phi }$ under the map

  $$\begin{aligned} {{\,\mathrm{Irr}\,}}({\mathrm{O}}(V_{2n}^\delta ))\longrightarrow \left( {{\,\mathrm{Irr}\,}}(\mathrm{O}(V_{2n}^\delta ))/\sim _{\det } \right) \longrightarrow \left( {{\,\mathrm{Irr}\,}}({{\,\mathrm{SO}\,}}(V_{2n}^\delta ))/\sim _{\epsilon }\right) \end{aligned}$$

  is the packet $\Pi _{\phi }^0$ and the diagram

  

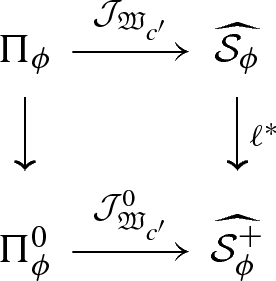
  is commutative for any Whittaker datum ${\mathfrak {W}}_{c^\prime }$, where $\ell :{\mathcal {S}}^+_{\phi }\rightarrow {\mathcal {S}}_{\phi }$ is the natural embedding.

Proof

This follows from Theorem 4.4; see also Atobe–Gan [2, §3.5] for an explication. $\square$

Appendix B: The Plancherel measures and normalized intertwining operators

We recall the definition of Plancherel measures and prove Lemma 7.2 in this Appendix.

We retain the notation in Sect. 7.1. Let ${\overline{P}}=M_{P} U_{{{\overline{P}}}}$ be the opposite parabolic subgroup to P of ${\text {O}}(V)$ and consider the induced representation

$$\begin{aligned} {{\,\mathrm{Ind}\,}}_{{\overline{P}}}^{{\text {O}}\left( V\right) }\left( \tau _{s} \otimes \pi _0 \right) . \end{aligned}$$

Similarly to those of Sect. 7.1, they are realized on the space of smooth functions

$$\begin{aligned} {\overline{\Psi }}_{s} : {\text {O}}(V) \rightarrow {\mathscr {V}}_{\tau } \otimes {\mathscr {V}}_{\pi _0} \end{aligned}$$

such that

$$\begin{aligned} {\overline{\Psi }}_{s}\left( u_{{{\overline{P}}}} m_{P}(a) h_0 h\right)&=|\det (a)|_{F}^{s+\rho _{{{\overline{P}}}}} \tau (a) \pi _0(h_0) {\overline{\Psi }}_{s}\left( h\right) \end{aligned}$$

for any $u_{{{\overline{P}}}} \in U_{{{\overline{P}}}}, a\in {{\,\mathrm{GL}\,}}(X), h_0\in \text {O}(V_0), h \in \text {O}(V)$. As in [10, §12], we define the standard intertwining operator

$$\begin{aligned} J_{{\overline{P}}|P}(\tau _{s}\otimes \pi _0): {{\,\mathrm{Ind}\,}}_{P}^{\text {O}(V)}(\tau _{s}\otimes \pi _0)&\longrightarrow {{\,\mathrm{Ind}\,}}_{{\overline{P}}}^{{\text {O}}(V)}(\tau _{s}\otimes \pi _0) \end{aligned}$$

by (the meromorphic continuations of) the integrals

$$\begin{aligned} J_{{\overline{P}}|P}(\tau _{s}\otimes \pi _0)\Psi _s(h)&= \int _{U_{{{\overline{P}}}}} \Psi _s({\bar{u}}h)d{\bar{u}} \end{aligned}$$

for $\Psi _s\in {{\,\mathrm{Ind}\,}}_{P}^{{\text {O}}(V)}(\tau _{s}\otimes \pi _0)$. Similarly, we have the standard intertwining operator

$$\begin{aligned} J_{P|{{\overline{P}}}}(\tau _{s}\otimes \pi _0): {{\,\mathrm{Ind}\,}}_{\overline{P}}^{{\text {O}}(V)}(\tau _{s}\otimes \pi _0)&\longrightarrow {{\,\mathrm{Ind}\,}}_{P}^{{\text {O}}(V)}(\tau _{s}\otimes \pi _0). \end{aligned}$$

By [10, §12], the Plancherel measure associated to ${{\,\mathrm{Ind}\,}}_{ P}^{{\text {O}}(V)}(\tau _{s}\otimes \pi _0)$ is a rational function $\mu (\tau _{s}\otimes \pi _0)$ such that

$$\begin{aligned} J_{P|{\overline{P}}}(\tau _{s}\otimes \pi _0)\circ J_{{\overline{P}}|P}(\tau _{s}\otimes \pi _0)= \mu (\tau _{s}\otimes \pi _0)^{-1}. \end{aligned}$$

At this point, the Plancherel measure $\mu (\tau _{s}\otimes \pi _0)$ is only well-defined up to a scalar since it depends on the choice of Haar measures on $U_P$ and $U_{{{\overline{P}}}}$. We refer the reader to [10, Appendix B.2] for the choice of these Haar measures we used here.

Fix a Whittaker datum ${\mathfrak {W}}_{c^\prime }$. Let ${\widetilde{w}}_{c^\prime }$ be the lift of w in (7.1). Then there is a intertwining isomorphism

$$\begin{aligned} \ell (w_{c^\prime },\tau _s\otimes \pi _0): {{\,\mathrm{Ind}\,}}_{{{\overline{P}}}}^{\text {O}(V)}(\tau _{s}\otimes \pi _0)\rightarrow {{\,\mathrm{Ind}\,}}_P^{\text {O}(V)}(w(\tau _{s}\otimes \pi _0)) \end{aligned}$$

given by left translation

$$\begin{aligned} \left( \ell (w_{c^\prime },\tau _s\otimes \pi _0){\overline{\Psi }}_{s}\right) (h) ={\overline{\Psi }}_s({\widetilde{w}}_{c^\prime }^{-1}h) \end{aligned}$$

for ${\overline{\Psi }}_s\in {{\,\mathrm{Ind}\,}}_{{{\overline{P}}}}^{\text {O}(V)}(\tau _{s}\otimes \pi _0)$ and $h\in {\text {O}}(V)$. It is easy to check that the following diagram

(B.1)

is commutative, where $\mathcal M({\widetilde{w}}_{c^\prime },\tau _{s}\otimes \pi _0)$ is the unnormalized intertwining operator defined in Sect. 7.1.

Note that

$$\begin{aligned} {\widetilde{w}}_{c^\prime }^2= m_P((-\mathbf{1 })^{k-1})\cdot \mathbf{1} _{V_0}. \end{aligned}$$

Hence ${\widetilde{w}}_{c^\prime }^2$ lies in the center of $M_P$. We have an intertwining isomorphism

$$\begin{aligned} \ell (w^2_{c^\prime },\tau _s\otimes \pi _0): {{\,\mathrm{Ind}\,}}_{P}^{\text {O}(V)}(\tau _{s}\otimes \pi _0)\rightarrow {{\,\mathrm{Ind}\,}}_P^{\text {O}(V)}(w^2(\tau _{s}\otimes \pi _0))={{\,\mathrm{Ind}\,}}_P^{\text {O}(V)}(\tau _{s}\otimes \pi _0) \end{aligned}$$

given by left translation

$$\begin{aligned} \left( \ell (w_{c^\prime }^2,\tau _s\otimes \pi _0)\Psi _{s}\right) (h) = \Psi _s(({\widetilde{w}}_{c^\prime })^{-2}h)=\omega _{\tau }(-1)^{k-1}\Psi _s(h). \end{aligned}$$

(B.2)

for $\Psi _s\in {{\,\mathrm{Ind}\,}}_{P}^{{\text {O}}(V)}(\tau _{s}\otimes \pi _0)$ and $h\in {\text {O}}(V)$. Here $\omega _\tau$ is the central character of $\tau$. Then we have the following commutative diagram

(B.3)

Combining (B.1), (B.2) and (B.3), we have

$$\begin{aligned}&{\mathcal {M}}({\widetilde{w}}_{c^\prime },w(\tau _{s}\otimes \pi _0))\circ {\mathcal {M}}({\widetilde{w}}_{c},\tau _{s}\otimes \pi _0)\nonumber \\&\quad = \ell (w^2_{c^\prime },\tau _s\otimes \pi _0)\circ J_{P|{{\overline{P}}}}(\tau _{s}\otimes \pi _0)\circ J_{{{\overline{P}}}|P}(\tau _{s}\otimes \pi _0)\nonumber \\&\quad = \omega _{\tau }(-1)^{k-1}\times \mu (\tau _{s}\otimes \pi _0)^{-1}. \end{aligned}$$

(B.4)

Now we begin to prove Lemma 7.2 for even orthogonal groups.

Proposition B.1

Let ${\mathcal {R}}_{{\mathfrak {W}}_{c^\prime }}\left( w, \tau _{s} \otimes \pi _0\right)$ and be the normalized intertwining operator defined in Sect. 7.1. Then we have

• (i) ${\mathcal {R}}_{{\mathfrak {W}}_{c^\prime }}\left( w, w(\tau _{s} \otimes \pi _0)\right) \circ {\mathcal {R}}_{{\mathfrak {W}}_{c^\prime }}\left( w, \tau _{s} \otimes \pi _0\right) =1$;

• (ii) ${\mathcal {R}}_{{\mathfrak {W}}_{c\prime }}\left( w, w(\tau _{-{\bar{s}}} \otimes \pi _0)\right) ^*={\mathcal {R}}_{{\mathfrak {W}}_{c^\prime }}\left( w,\tau _{s} \otimes \pi _0 \right)$.

In particular, ${\mathcal {R}}_{{\mathfrak {W}}_{c^\prime }}\left( w,\tau _{s} \otimes \pi _0 \right)$ is unitary when s is purely imaginary. Hence ${\mathcal {R}}_{{\mathfrak {W}}_{c^\prime }}\left( w,\tau _{s} \otimes \pi _0 \right)$ is holomorphic at $s=0$.

Proof

We first prove (i). Let $\phi _\tau$ and $\phi _{0}$ be the L-parameters of $\tau$ and $\pi _0$. Then by (B.4) and Corollary 8.10, we have

$$\begin{aligned}&\quad {\mathcal {R}}_{{\mathfrak {W}}_{c^\prime }}\left( w, w(\tau _{s} \otimes \pi _0)\right) \circ {\mathcal {R}}_{{\mathfrak {W}}_{c^\prime }}\left( w, \tau _{s} \otimes \pi _0\right) \\&=\epsilon (V)^{2k}\times \chi _{V}(c^\prime /c)^{2k}\times r(w,w(\tau _s\otimes \pi _{0}))^{-1}\times r(w,\tau _s\otimes \pi _{0})^{-1}\\&\quad \times |c^\prime |_F^{k\rho _P}\times |c^\prime |_F^{k\rho _{{{\overline{P}}}}}\times {\mathcal {M}}({\widetilde{w}}_{c^\prime },w(\tau _{s}\otimes \pi _0))\circ {\mathcal {M}}({\widetilde{w}}_{c^\prime },\tau _{s}\otimes \pi _0)\\&=r(w,w(\tau _s\otimes \pi _{0}))^{-1}\times r(w,\tau _s\otimes \pi _{0})^{-1}\times \omega _{\tau }(- 1)^{k-1}\times \mu (\tau _{s}\otimes \pi _0)^{-1}\\&=r(w,w(\tau _s\otimes \pi _{0}))^{-1}\times r(w,\tau _s\otimes \pi _{0})^{-1}\times \omega _{\tau }(- 1)^{k-1}\times \gamma (s,\phi _{\tau }\otimes \phi _{0}^{\vee },\psi )^{-1}\\&\quad \times \gamma (-s,\phi _{\tau }^{\vee }\otimes \phi _0, \psi _{-1} )\times \gamma (2s, \wedge ^2\circ \phi _{\tau }, \psi )^{-1}\times \gamma (-2s, \wedge ^{2} \circ \phi _{\tau }^{\vee },\psi _{-1})^{-1}\\&=1, \end{aligned}$$

where the last equality follows from (7.3), (7.4) and the following formulas

$$\begin{aligned} \gamma (s,\phi ,\psi )&= \frac{\varepsilon (s,\phi ,\psi )\times L(1-s,\phi ^\vee )}{L(s,\phi )},\\ \varepsilon (s,\phi ,\psi _{-1})&=\det (\phi )(-1)\times \varepsilon (s,\phi ,\psi ) \end{aligned}$$

for any representation $\phi$ of ${{\,\mathrm{WD}\,}}_F$.

The second statement follows from a similar argument in [3, Proposition 2.3.1], we omit the details here.$\square$