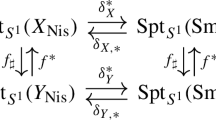Étale cohomology of rank one $\ell$-adic local systems in positive characteristic

Abstract

We show that in positive characteristic special loci of deformation spaces of rank one $\ell$-adic local systems are quasi-linear. From this we deduce the Hard Lefschetz theorem for rank one $\ell$-adic local systems and a generic vanishing theorem.

1 Introduction

In this note we study the cohomology of étale rank one $\ell$-adic local systems on algebraic varieties in terms of $\ell$-adic analysis applied to the deformation space of local systems. One feature of our approach is that we apply non-archimedean techniques (formal Lie groups, affinoid algebras etc.) that were originally developed as tools in the study of p-adic cohomology theories. Before we explain our new non-archimedean methods in Sect. 1.4 we sketch some applications in the most simple form. The general form is described in Sects. 5 and 6.

1.1 Hard Lefschetz

One of the applications of our $\ell$-adic technique is a new case of the Hard Lefschetz isomorphism in positive characteristic. Let $\ell$ be a prime number and let X be a smooth projective variety over an algebraically closed field F of characteristic different from $\ell$. Let d be the dimension of X. Let $\eta \in H^2(X,{\mathbb {Z}}_\ell )$ be a polarization in étale cohomology, i.e. the first Chern class of an ample line bundle on X, where we omit Tate twists as F is algebraically closed.

Theorem 1.1

(Hard Lefschetz) Let ${\mathcal {L}}$ be a rank one étale $\overline{{\mathbb {Q}}}_\ell$-local system on X. Then for any $i\in {\mathbb {N}},$ the cup-product map

$$\begin{aligned} \cup \eta ^i :H^{-i}(X, {\mathcal {L}}[d]) \xrightarrow {\sim } H^{i}(X, {\mathcal {L}}[d]) \end{aligned}$$

on étale cohomology is an isomorphism.

More generally, we also obtain the isomorphism $\cup \eta ^i$ for ${\mathcal {L}}[d]$ replaced by ${\mathcal {F}}\otimes {\mathcal {L}}$, where ${\mathcal {F}}\in D^b_c(X,\overline{{\mathbb {Q}}}_{\ell })$ is an arithmetic semi-simple perverse sheaf, see Theorem 5.4. Here we call a sheaf arithmetic if it is fixed by the action of a Galois group of a finitely generated field, see Definition 5.1 and Remark 5.2. In particular, semi-simple objects ${\mathcal {F}}\in D^b_c(X,\overline{{\mathbb {Q}}}_{\ell })$ of geometric origin [2, p. 163] are arithmetic.

Remark 1.2

In characteristic zero, Theorem 1.1 in the more general case where ${\mathcal {L}}$ is a semi-simple local system of arbitrary rank was first shown by complex analytic techniques in [27, Lem. 2.6]. In fact in characteristic zero we know the Hard Lefschetz isomorphism for any semi-simple perverse sheaf, see [2, Thm. 5.4.10], [7, Thm. 1.4], [24, MainThm. 1] and [20, Thm. 19.47].

In positive characteristic, Theorem 1.1 was shown for a torsion rank one local system ${\mathcal {L}}$ by Deligne [6, Thm. 4.1.1] relying on arithmetic weight arguments. More generally the Hard Lefschetz isomorphism for an arithmetic semi-simple perverse sheaf was known from combining [2, Thm. 6.2.10] and the Langlands correspondence for $\mathrm{GL}_r$ over function fields [18, Thm. 7.6], see [7, 1.8].

1.2 Jumping loci

Jumping loci in the moduli space of line bundles or rank one local systems on complex varieties have been studied extensively, see [14] for the initial approach. As a second application we show that jumping loci in the deformation space of étale rank one $\overline{{\mathbb {Q}}}_{\ell }$-local systems satisfy a strong linearity condition analogous to the well-understood situation in characteristic zero, see Sect. 6.1 for details.

Let $\pi$ be a finitely generated free ${\mathbb {Z}}_\ell$-module. Let

$$\begin{aligned} {\mathcal {G}}(\overline{{\mathbb {Q}}}_{\ell }) :=\mathrm{Hom}_\mathrm{cont}(\pi , \overline{{\mathbb {Q}}}_{\ell }^\times ) \end{aligned}$$

be the set of continuous homomorphisms $\pi \rightarrow E^\times$, where $E\subset \overline{{\mathbb {Q}}}_{\ell }$ is any finite extension of ${\mathbb {Q}}_\ell$ endowed with the $\ell$-adic topology. We endow ${\mathcal {G}}(\overline{{\mathbb {Q}}}_{\ell })$ with a noetherian Zariski topology such that $\dim ({\mathcal {G}}(\overline{{\mathbb {Q}}}_{\ell }))=\mathrm{rank}(\pi )$. This Zariski topology originates from the observation that the elements of ${\mathcal {G}}(\overline{{\mathbb {Q}}}_{\ell })$ are the $\overline{{\mathbb {Q}}}_{\ell }$-points of a multiplicative formal Lie group ${\mathcal {G}}$, see Sect. 3.1.

For a torsion free quotient ${\mathbb {Z}}_\ell$-module $\pi /\pi '$, we call

$$\begin{aligned} {\mathcal {H}}(\overline{{\mathbb {Q}}}_{\ell })=\mathrm{Hom}_\mathrm{cont}(\pi /\pi ', \overline{{\mathbb {Q}}}_{\ell }^\times ) \end{aligned}$$

a formal Lie subgroup of ${\mathcal {G}}(\overline{{\mathbb {Q}}}_{\ell })$, or more precisely the $\overline{{\mathbb {Q}}}_{\ell }$-points of a formal Lie subgroup ${\mathcal {H}}$. Note that $\mathrm{codim}_{{\mathcal {G}}(\overline{{\mathbb {Q}}}_{\ell })}({\mathcal {H}}(\overline{{\mathbb {Q}}}_{\ell }))=\mathrm{rank}(\pi ')$.

Let X be either a smooth proper variety or the torus ${\mathbb {G}}_m^d$ over an algebraically closed field F of characteristic different from $\ell$. In the following we let the free ${\mathbb {Z}}_\ell$-module $\pi$ be a quotient of the abelian étale fundamental group $\pi _1^\mathrm{ab}( X)$. Then with the group of characters ${\mathcal {G}}(\overline{{\mathbb {Q}}}_{\ell })$ as above, any $s\in {\mathcal {G}}(\overline{{\mathbb {Q}}}_{\ell })$ gives rise to an étale rank one $\overline{{\mathbb {Q}}}_{\ell }$-local system ${\mathcal {L}}_s$ on X.

For ${\mathcal {F}}\in D^b_c(X ,\overline{{\mathbb {Q}}}_{\ell })$ and $i,j \in {\mathbb {Z}}$, we consider the jumping locus of étale cohomology

$$\begin{aligned} \Sigma ^i({\mathcal {F}},j) := \{ s\in {\mathcal {G}}(\overline{{\mathbb {Q}}}_{\ell }) \, |\, \mathrm{dim} \ H^i(X ,{\mathcal {F}}\otimes {\mathcal {L}}_s ) > j \} \end{aligned}$$

which one can show to be Zariski closed in ${\mathcal {G}}(\overline{{\mathbb {Q}}}_{\ell })$. Our second application is a structure theorem for those loci, see Theorem 6.2.

Theorem 1.3

For an arithmetic sheaf ${\mathcal {F}}\in D^b_c (X,\overline{{\mathbb {Q}}}_{\ell })$ we have

$$\begin{aligned} \Sigma ^i({\mathcal {F}},j) = \bigcup _{r\in I} s_r {\mathcal {H}}_r( \overline{{\mathbb {Q}}}_{\ell }) , \end{aligned}$$

where I is finite, $s_r\in {\mathcal {G}}(\overline{{\mathbb {Q}}}_{\ell })$ are torsion points and ${\mathcal {H}}_r$ are formal Lie subgroups of ${\mathcal {G}}$.

Remark 1.4

As far as we are aware of, Theorem 1.3 is the first result on jumping loci of $\ell$-adic cohomology in positive characteristic.

For $\mathrm{ch}(F)=0$ and ${\mathcal {F}}$ of geometric origin in the sense of [2, p. 163], Theorem 1.3 is shown in [14, Thm. 0.1], [28, Thm. 4.2], [25, Thm. 2.2], [17, Sec. 11], [3, Thm. 1.1] using complex analytic techniques. Arithmetic methods for understanding jumping loci in characteristic zero are developed in [22, Thm. 1.1] for coherent cohomology and [11, Thm. 1.5] for $\ell$-adic sheaves.

We expect Theorem 1.3 to hold for non-arithmetic ${\mathcal {F}}\in D^b_c (X,\overline{{\mathbb {Q}}}_{\ell })$ without the conclusion on the $s_r$ being torsion points. This holds for $\mathrm{ch}(F)=0$.

1.3 Generic vanishing

The study of generic vanishing was initiated by Green–Lazarsfeld for the cohomology of line bundles [13, Thm. 1]. As a third application we prove a generic vanishing result for étale rank one $\overline{{\mathbb {Q}}}_{\ell }$-local systems. For this we formulate a new abstract approach to generic vanishing based on the Hard Lefschetz isomorphism and the study of jumping loci, see Sect. 6.2. For simplicity of exposition in the introduction, we confine the presentation to the most important special case of abelian varieties.

Let X be an abelian variety of dimension d over the algebraically closed field F of characteristic different from $\ell$. Let $\pi$ be the $\ell$-adic completion of the abelian étale fundamental group $\pi _1^\mathrm{ab}(X)$ and let the notation be as in Sect. 1.2.

Theorem 1.5

Assume that ${\mathcal {F}}\in D^b_c( X, \overline{{\mathbb {Q}}}_{\ell })$ is arithmetic and perverse. Then

$$\begin{aligned} \mathrm{codim}_{{\mathcal {G}}( \overline{{\mathbb {Q}}}_{\ell })}(\Sigma ^i({\mathcal {F}},0)) \ge |2i| \end{aligned}$$

for all $i\in {\mathbb {Z}}$.

This is Corollary 6.10.

Remark 1.6

For $\mathrm{ch}(F)=0$ Theorem 1.5 is equivalent to [25, Thm. 4.1] and [1, Thm. 1.3], who do not need the arithmeticity assumption, see also [17, Thm. 1.1]. For $\mathrm{ch}(F)>0$, the inequality

$$\begin{aligned} \mathrm{codim}(\Sigma ^i({\mathcal {F}},0)) >0 \ \mathrm{for} \ i\ne 0 \end{aligned}$$

is shown in [30, Intro].

Our proof of Theorem 1.5 relies on a study of a Galois tower

$$\begin{aligned} \cdots \rightarrow X_{n+1} \rightarrow X_n \rightarrow \cdots \rightarrow X_0 =X \end{aligned}$$

which is “isotropic” with respect to the Weil pairing associated to a polarization $\eta$. Here $\mathrm{Gal}(X_n/X) = ({\mathbb {Z}}_\ell /\ell ^n{\mathbb {Z}}_\ell )^r$, $r\le d$. This tower gives rise to a “tautological” rank one étale ${\mathfrak {R}}$-local system ${\mathcal {L}}_{{\mathfrak {R}}}$ on X. Here the noetherian Jacobson ring ${\mathfrak {R}}={\mathbb {Z}}_\ell \llbracket \pi \rrbracket \otimes _{{\mathbb {Z}}_\ell } \overline{{\mathbb {Q}}}_{\ell }$ is defined in terms of the completed group ring ${\mathbb {Z}}_\ell \llbracket \pi \rrbracket$, see Sect. 3.1.

The idea for the proof of Theorem 1.5 is to use on the one hand an isomorphism property of the Lefschetz operator on finitely generated ${\mathfrak {R}}$-modules

$$\begin{aligned} \cup \eta ^i:H^{-i}(X,{\mathcal {F}}\otimes {\mathcal {L}}_{{\mathfrak {R}}}) \rightarrow H^i(X,{\mathcal {F}}\otimes {\mathcal {L}}_{{\mathfrak {R}}}) . \end{aligned}$$

On the other hand the choice of the tower leads to a vanishing result for the Lefschetz operator $\cup \eta ^i$ for $i\ge 1+d-r$, see Proposition 4.6 and Lemma 6.14.

1.4 Main Theorem

The three theorems presented in this introduction all rely on the Main Theorem which does not refer to any variety X. It describes a Zariski closed locus of the space of $\overline{{\mathbb {Q}}}_{\ell }$-points of a multiplicative formal Lie group under the condition that the locus is invariant under a specific type of linear automorphism.

We use the notation introduced in 1.2, i.e. let $\pi$ be a finitely generated free ${\mathbb {Z}}_\ell$-module with corresponding character group ${\mathcal {G}}(\overline{{\mathbb {Q}}}_{\ell })=\mathrm{Hom}_\mathrm{cont} (\pi ,\overline{{\mathbb {Q}}}_{\ell }^\times )$. As before we endow ${\mathcal {G}}(\overline{{\mathbb {Q}}}_{\ell })$ with a Zariski topology via the canonical bijection

$$\begin{aligned} {{\,\mathrm{Spm}\,}}({\mathfrak {R}}) \xrightarrow {\sim } {\mathcal {G}}(\overline{{\mathbb {Q}}}_{\ell }) \quad J\mapsto \left( \pi \rightarrow ({\mathfrak {R}}/J)^\times =\overline{{\mathbb {Q}}}_{\ell }^\times \right) \end{aligned}$$

where ${\mathfrak {R}}={\mathbb {Z}}_\ell \llbracket \pi \rrbracket \otimes _{{\mathbb {Z}}_\ell } \overline{{\mathbb {Q}}}_{\ell }$ receives the tautological character $\pi \rightarrow {\mathfrak {R}}^\times$, see Sect. 3.1. The following is Theorem 3.4.

Theorem 1.7

(Main Theorem) Let $\sigma$ be a ${\mathbb {Z}}_\ell$-linear automorphism of $\pi$ such that $\sigma$ acts semi-simply on $\pi \otimes _{{\mathbb {Z}}_\ell } {\mathbb {Q}}_\ell$ and such that for a given complex embedding $\iota :\overline{{\mathbb {Q}}}_{\ell }\hookrightarrow {\mathbb {C}}$, its eigenvalues $\alpha _i$ verify $|\iota (\alpha _i)|=|\iota (\alpha _j)|\ne 1$ for all i, j. Let $S\subset {\mathcal {G}}(\overline{{\mathbb {Q}}}_{\ell })$ be a Zariski closed subset. Then, if $\sigma (S)= S$ we have

$$\begin{aligned} S = \bigcup _{r\in I} s_r {\mathcal {H}}_r( \overline{{\mathbb {Q}}}_{\ell }) , \end{aligned}$$

where I is finite, $s_r\in {\mathcal {G}}(\overline{{\mathbb {Q}}}_{\ell })$ are torsion points and ${\mathcal {H}}_r$ are formal Lie subgroups of ${\mathcal {G}}$.

We briefly describe how we apply the Main Theorem.

The idea of our proof of Theorem 1.1 comes from [7]. We use a deformation space of rank one $\overline{{\mathbb {Q}}}_{\ell }$-local systems on X isomorphic to ${\mathcal {G}}(\overline{{\mathbb {Q}}}_{\ell })$ as above. Inside of this deformation space we define the bad locus to be the set of rank one local systems ${\mathcal {L}}$ for which Theorem 1.1 fails to hold. The bad locus is constructible in ${\mathcal {G}}(\overline{{\mathbb {Q}}}_{\ell })$ and we let S be its Zariski closure. Then S is stabilized by a suitable Frobenius action $\sigma$ satisfying the conditions of the Main Theorem. So it implies that S is a union of torsion translated Lie subgroups. Consequently, the torsion rank one local systems are dense in S. In view of Deligne’s Hard Lefschetz theorem the bad locus cannot contain a torsion local system, so it is empty.

For Theorem 1.3 we use that the jumping loci, which are closed subsets of ${\mathcal {G}}(\overline{{\mathbb {Q}}}_{\ell })$, satisfy the assumption of the Main Theorem with respect to a suitable Frobenius action $\sigma$. The proof of Theorem 1.5 combines Theorem 1.1 and Theorem 6.2 as sketched at the end of Sect. 1.3.

We now describe the idea of the proof of the Theorem 1.7. We can assume that S is irreducible. The conclusion in particular implies that the torsion points are Zariski dense in S (see Lemma 3.1). So we first construct one torsion point on S. To this aim, we replace S by the closed subset $\ell ^n S$ of the group ${\mathcal {G}}(\overline{{\mathbb {Q}}}_{\ell })$ for some $n\gg 0$ so as make sure that it cuts non-trivially a small $\ell$-adic neighborhood of $1\in {\mathcal {G}}(\overline{{\mathbb {Q}}}_{\ell })$ on which the $\ell$-adic logarithm map is an isomorphism. This enables one to transfer the problem to a closed $\ell$-adic polydisc in the Lie algebra of ${\mathcal {G}}$, i.e. to a Tate algebra on which $\sigma$ acts linearly.

Proposition 2.1 and 2.5, proven using $\ell$-adic analysis, show that in our logarithmic coordinate chart S contains the origin and moreover is conical. This implies that $\ell S\subset S$ by a density argument. We can then apply a theorem of de Jong [5, Prop. 1.2(1)] to finish the proof. Alternatively, what was our initial proof, one can use the Weierstrass preparation theorem to find another torsion point on S contained in its regular locus, in case $1\in S$ was singular. Then one shows using simple $\ell$-adic analysis that if S contains a torsion point in its regular locus such that S is conical around this point then S is linear. This is similar to the approach in [11, Section 4]. As de Jong’s argument shortens our initial argument, we do not give the details of it in this note.

2 Tate algebras

Let E be a finite extension of ${\mathbb {Q}}_\ell$ with residue field k and uniformizer $\lambda \in {\mathcal {O}}_E$. We always fix an embedding $E\hookrightarrow \overline{{\mathbb {Q}}}_{\ell }$ into an algebraic closure of ${\mathbb {Q}}_\ell$. We let $|-|:E\rightarrow {\mathbb {R}}$ be the $\ell$-adic absolute value normalized by $|\ell |=1/\ell$. Let $A=E\langle T_1, \ldots , T_b \rangle$ be the Tate algebra, see [12, Sec. 3.1]. Let $| - |$ be the Gauss norm on A, i.e. $|g|=\mathrm{sup}_n |g^{(n)}|$ where $g^{(n)}$ is the coefficient of $\underline{T}^n, \ n\in {\mathbb {N}}^b$ in the expansion of g. We denote by M the maximal ideal $(T_1, \ldots , T_b)\subset A$.

Let $\sigma \in \mathrm{Mat}_b({\mathcal {O}}_E)$ be the diagonal matrix $\sigma = \mathrm{diag}(\alpha _1, \ldots , \alpha _b )$. Then $\sigma$ induces an endomorphism of A as an E-algebra by the rule $T_j\mapsto \sum _{i=1}^b \sigma _{i j} T_i$, which we also denote by $\sigma$.

Proposition 2.1

Assume that $\underline{\alpha }^{ n}\ne 1$ for all $n\in {\mathbb {N}}^b{\setminus } \{ 0\}$. Let $I\subset A$ be an ideal with $\sigma (I)\subset I$ which is not contained in the maximal ideal M. Then $I=A$.

Proof

As I does not lie in M, there is a $g_\circ \in I$ with $g_\circ (0)=1$, which we fix for the rest of the proof. The basic idea of the proof is simple: successively apply linear expressions in $\sigma$ to $g_\circ$ in order to kill the coefficients of degree $>0$ without changing the constant coefficient 1. The problem is to make such a sequence of elements of I converge.

As any ideal in A is closed [12, Thm. 3.2.1], so is the subset

$$\begin{aligned} \tilde{I}= \{ g\in I\,|\, g(0)=1, |g^{(n)}|\le |g_\circ ^{(n)} | \} \end{aligned}$$

of A.

Lemma 2.2

$\tilde{I}$ is compact.

Proof

As a Banach space, A is isomorphic to $c_0$, the set of sequences $g=(g^{(n)})_{n\in {\mathbb {N}}^b}$ in E with $|g^{(n)}|\rightarrow 0$ as $|n|\rightarrow \infty$. It is endowed with the supremum norm $|g|=\mathrm{sup}_n |g^{(n)}|$. One has an injective map

$$\begin{aligned} \varphi :\prod _{n\in {\mathbb {N}}^b, g_\circ ^{(n)}\ne 0} {\mathcal {O}}_E \rightarrow J\subset c_0, \ (u^{(n)}) \mapsto (u^{(n)}g_\circ ^{(n)}), \end{aligned}$$

defining J as its image. As $\tilde{I}=J\cap I\cap \{(g^{(n)})_n, \ g^{(0)}=1\}$, I is closed and the map $c_0\rightarrow E, \ (g^{(n)})\mapsto g^{(0)}$ is continuous, we just have to prove that J is compact. The map $\varphi$ is continuous for the product topology on the left and the restriction of the topology of A to J on the right. Indeed, for $\rho >0$, the inverse image

$$\begin{aligned}&\varphi ^{-1} (\{ |g|<\rho \})\\&\quad =\prod _{ n\in {\mathbb {N}}^b, 0< |g_\circ ^{(n)}|< \rho }{\mathcal {O}}_E \times \prod _{ n\in {\mathbb {N}}^b, |g_\circ ^{(n)}| \ge \rho } \{u^{(n)}, |u^{(n)}| <| g_\circ ^{(n)}|^{-1}\rho \} \end{aligned}$$

is open as the index set $\{n\in {\mathbb {N}}^b, |g_\circ ^{(n)}| \ge \rho \}$ on the right is finite.

As ${\mathcal {O}}_E$ is compact, so is $\prod _{n\in {\mathbb {N}}^b, g_\circ ^{(n)}\ne 0} {\mathcal {O}}_E$ by Tychonoff’s theorem. So its image J by the continuous map $\varphi$ is compact as well. This finishes the proof. $\square$

For $i\ge -1,$ set

$$\begin{aligned} N_i= \{ n\in {\mathbb {N}}^b{\setminus }\{0 \}\, |\, |1-\underline{\alpha }^n| \ge |\lambda ^i|\}. \end{aligned}$$

This is an ascending chain of subsets of ${\mathbb {N}}^b{\setminus }\{0 \}$ such that

$$\begin{aligned} N_{i+1}{\setminus } N_i=\{ n\in {\mathbb {N}}^b{\setminus }\{0 \}\, |\, |1 -\underline{\alpha }^n| = |\lambda ^{i+1}|\}. \end{aligned}$$

Because $\alpha _i\in {\mathcal {O}}$ and $\underline{\alpha }^n\ne 1$ for all $n\in {\mathbb {N}}^b{\setminus } \{0\}$, one has

$$\begin{aligned} N_{-1}=\varnothing , \ \ \cup _i N_i={\mathbb {N}}^b{\setminus }\{0 \}. \end{aligned}$$

We define closed subsets

$$\begin{aligned} \tilde{I}_i= \{ g\in \tilde{I}\,|\, g^{(n)}=0 \text { for all } n\in N_i \}\subset I. \end{aligned}$$

In particular, $\tilde{I}_{-1}= \tilde{I}$ contains $g_\circ$, so it is non-empty. The $\tilde{I}_i$ form a descending chain of subsets of $\tilde{I}$.

Claim 2.3

For all $i\ge 0$ the set $\tilde{I}_i$ is non-empty.

Proof

It suffices to show that if $\tilde{I}_i$ is non-empty, so is $\tilde{I}_{i+1}$. In the following we fix $i\ge -1$. We set ${\mathcal {M}}=N_{i+1}{\setminus } N_i \subset N_{i+1}$, which we assume to be non-empty else the problem is solved. We choose a linear order $m_1\prec m_2 \prec \ldots$ of ${\mathcal {M}}=\{m_1, m_2,\ldots \}$. For $\mathrm{card}({\mathcal {M}})\ge j\ge 1$ we define a closed subset

$$\begin{aligned} \tilde{I}^{j}_i=\{ g\in \tilde{I}_i\,|\, g^{(m)}=0 \text { for } m\prec m_j, m\in {\mathcal {M}}\} \subset \tilde{I}. \end{aligned}$$

Set $\tilde{I}^j_i=\tilde{I}_{i+1}$ for $j> \mathrm{card}({\mathcal {M}})$. This is a decreasing sequence of subsets of $\tilde{I}_i$ such that

$$\begin{aligned} \cap _{ j\ge 1 } \tilde{I}^{j}_i =\tilde{I}_{i+1}. \end{aligned}$$

Thus we reduce the problem to showing that if $\tilde{I}^{j}_i \ne \varnothing$ for some $j\ge 1$, then $\tilde{I}^{j+1}_i \ne \varnothing$ for by Lemma 2.2 we then conclude $\tilde{I}_{i+1} \ne \varnothing .$

We define a map $\Phi ^m:I\rightarrow I$ by

$$\begin{aligned} \Phi ^m(g)= \frac{\sigma (g)- \underline{\alpha }^{ m }g}{1- \underline{\alpha }^{m}} \end{aligned}$$

for $m\in {\mathbb {N}}^b {\setminus }\{ 0 \}$. Then we obviously have $\Phi ^{m}( g)^{(m)}=0, \ \Phi ^{m}( g)(0)=1.$ In order to conclude the proof of the Claim 2.3, it remains to prove Claim 2.4. Indeed, we then get $\Phi ^{m_j} (\tilde{I}^j_i )\subset \tilde{I}^{j+1}_i$. $\square$

Claim 2.4

$|\Phi ^{m}( g)^{( n)} | \le |g^{( n)} |$ for $g\in \tilde{I}_i$, $n\in {\mathbb {N}}^b$ and $m\in {\mathcal {M}}$.

Proof

As $\Phi ^m(g)^{(n)}=g^{(n)}=0$ for $n \in N_i$ we assume that $n \notin N_i$. This implies $|1-\underline{\alpha }^{n}| \le |1-\underline{\alpha }^{m} |$. We have

$$\begin{aligned} \Phi ^m(g)^{( n)} = \frac{\underline{\alpha }^{ n} -\underline{\alpha }^{ m}}{1- \underline{\alpha }^{m}} g^{( n)}. \end{aligned}$$

So

$$\begin{aligned} |\Phi ^{m}(g)^{( n)} |= & {} \left| \frac{\underline{\alpha }^{ n} -\underline{\alpha }^{m}}{1-\underline{\alpha }^{ m}} \right| |g^{(n)}| \\\le & {} \frac{\max ( |1- \underline{\alpha }^{n}|, |1 - \underline{\alpha }^{ m}|)}{|1- \underline{\alpha }^{ m}|}|g^{(n)}| \le |g^{(n)}|. \end{aligned}$$

This finishes the proof. $\square$

Lemma 2.2 and Claim 2.3 imply that $\cap _{i} \tilde{I}_i$ is non-empty, say it contains h. Then $h^{(n)}=0$ for all $n\in {\mathbb {N}}^b{\setminus }\{ 0 \}$, so $h \in I$ is a constant and hence $1\in I$. This finishes the proof of Proposition 2.1. $\square$

In the next proposition we combine Proposition 2.1 with a “weight” argument in order to deduce that I is homogeneous under suitable assumptions. We fix a complex embedding $\iota :\overline{{\mathbb {Q}}}_{\ell }\hookrightarrow {\mathbb {C}}$.

Proposition 2.5

Let $\sigma \in \mathrm{GL}_b({\mathcal {O}}_E)$ be the diagonal matrix $\sigma =\mathrm{diag}(\alpha _1, \ldots , \alpha _b )$. We assume that $|\iota (\alpha _i)|=|\iota (\alpha _j)| \ne 1$ for all $1\le i,j \le b$. Let $I\subset A$ be a radical ideal with $\sigma (I)=I$. Then I is homogeneous.

Proof

To start with we observe that as a consequence of our assumption on the eigenvalues $\alpha _i$ we obtain the implication

$$\begin{aligned} \underline{\alpha }^{n} =1 \quad \Rightarrow \quad n_1 + \cdots + n_b=0 \end{aligned}$$

(1)

for $n\in {\mathbb {Z}}^b$.

As I is the intersection of finitely many minimal prime ideals containing it and as $\sigma$ permutes these prime ideals, we can assume without loss of generality that I itself is a prime ideal. The assumptions on the eigenvalues $\alpha _i$ in Proposition 2.1 are satisfied by (1), so we see that $I\subset M=(T_1, \ldots , T_b)$.

One has to check that the homogeneous components of an element $g\in I$ are in I. Denote by $\hat{A}$ and $\hat{I}$ the completion at the maximal ideal $M=(T_1, \ldots , T_b)$. As the map $A/I\rightarrow \hat{A}/\hat{I}$ is injective, it suffices to show that the homogeneous components of g are in $\hat{I}$. This is equivalent to saying that the homogeneous components of g are in the ideal $I+M^n/ M^n\subset A/ M^n$ for all $n>0$, i.e. that $I+M^n/ M^n$ is graded by degree.

Let $D\hookrightarrow \mathrm{GL}_{b,E}$ be the smallest linear algebraic subgroup (over E) containing $\sigma ^m$ for all $m\in {\mathbb {Z}}$. We can determine the diagonalizable group D a follows. Let $T\hookrightarrow \mathrm{GL}_{b,E}$ be the standard maximal torus. Then D is the intersection of the kernels of all characters $\chi _n:T\rightarrow {\mathbb {G}}_m$ with $\chi _n(\underline{\alpha })=1$. Here $n\in {\mathbb {Z}}^b$ and $\chi _n(\underline{\alpha }) =\underline{\alpha }^n$. By (1) we see that those $\chi _n$ are trivial on the diagonal torus ${\mathbb {G}}_m$, so D contains the diagonal ${\mathbb {G}}_m$.

But D acts on $A/M^n$ for any $n>0$ and this action preserves $I+M^n/M^n$. The weight decomposition with respect to the action of the diagonal ${\mathbb {G}}_m\subset T$ implies that $I+M^n/M^n$ is graded by degree. $\square$

3 Multiplicative formal groups

In this section we prove our main theorem on multiplicative formal Lie groups, Theorem 3.4.

3.1 Basics

We recall some basic results on multiplicative formal groups and we define a Zariski topology on its group of $\overline{{\mathbb {Q}}}_{\ell }$-points.

Let E be a finite extension of ${\mathbb {Q}}_\ell$ and fix an embedding $E\hookrightarrow \overline{{\mathbb {Q}}}_{\ell }$. For an abelian pro-finite group $\pi$ we let

$$\begin{aligned} R={\mathcal {O}}_E \llbracket \pi \rrbracket = \lim _\Lambda {\mathcal {O}}_E [\Lambda ] = \lim _{m, \Lambda } ({\mathcal {O}}_E/ (\lambda ^m)) [\Lambda ] \end{aligned}$$

where $\Lambda$ runs through the system of finite quotients of $\pi$ and $(\lambda )\subset {\mathcal {O}}_E$ is the maximal ideal. The quotient $({\mathcal {O}}_E/ (\lambda ^m)) [\Lambda ]$ is finite and is endowed with the discrete topology. Then ${\mathcal {O}}_E \llbracket \pi \rrbracket$ is endowed with the limit topology.

On ${\mathcal {O}}_E \llbracket \pi \rrbracket$ we consider the usual completed Hopf algebra structure over ${\mathcal {O}}_E$, for example the multiplication is given by

$$\begin{aligned} {\mathcal {O}}_E \llbracket \pi \rrbracket \, \widehat{\otimes }_{{\mathcal {O}}_E} {\mathcal {O}}_E \llbracket \pi \rrbracket \rightarrow {\mathcal {O}}_E \llbracket \pi \rrbracket \quad [e_1]\otimes [e_2]\mapsto [e_1+ e_2]. \end{aligned}$$

For another pro-finite group $\pi '$ the continuous Hopf algebra homomorphisms ${\mathcal {O}}_E \llbracket \pi \rrbracket \rightarrow {\mathcal {O}}_E \llbracket \pi ' \rrbracket$ are in bijection with the continuous homomorphisms $\pi \rightarrow \pi '$. One can show this by reducing to $\pi$ and $\pi '$ finite and then applying Cartier duality [32, Exp. VIIB, 2.2.2 Prop.]. We denote the prime ideal generated by $1-[e]$ for all $e\in \pi$ by M, i.e. M is the kernel of the counit ${\mathcal {O}}_E \llbracket \pi \rrbracket \rightarrow {\mathcal {O}}_E$, $[e]\mapsto 1$ for $e \in \pi$.

In the following we assume that $\pi$ is a finitely generated free ${\mathbb {Z}}_\ell$-module of rank b. In this situation one says that the associated formal group ${\mathcal {G}}={{\,\mathrm{Spf}\,}}({\mathcal {O}}_E \llbracket \pi \rrbracket )$ is a multiplicative b-dimensional formal Lie group over ${\mathcal {O}}_E$. A closed formal subgroup ${\mathcal {H}}\hookrightarrow {\mathcal {G}}$ is called a formal Lie subgroup if it corresponds to a quotient morphism of ${\mathcal {O}}_E$-algebras ${\mathcal {O}}_E \llbracket \pi \rrbracket \rightarrow {\mathcal {O}}_E \llbracket \pi /\pi ' \rrbracket$, where $\pi /\pi '$ is a torsion free quotient ${\mathbb {Z}}_\ell$-module of $\pi$.

Once we choose a ${\mathbb {Z}}_\ell$-basis $e_1,\ldots , e_b$ of $\pi$ we obtain an isomorphism

$$\begin{aligned} {\mathcal {O}}_E\llbracket \pi \rrbracket \cong {\mathcal {O}}_E \llbracket X_1,\ldots , X_b \rrbracket \end{aligned}$$

defined by

$$\begin{aligned} {[}e_i] \mapsto 1+X_i \end{aligned}$$

and the comultiplication becomes

$$\begin{aligned} {\mathcal {O}}_E \llbracket X_1,\ldots , X_b \rrbracket \rightarrow {\mathcal {O}}_E\llbracket Y_1, \ldots , Y_b, Y'_1,\ldots , Y'_b \rrbracket \\&\quad X_i\mapsto Y_i+Y'_i+ Y_i Y'_i. \end{aligned}$$

We identify ${\mathcal {G}}(\overline{{\mathbb {Q}}}_{\ell })=\mathrm{Hom}_{{\mathcal {O}}_E}( {\mathcal {O}}_E \llbracket \pi \rrbracket ,\overline{{\mathbb {Q}}}_{\ell })$ with the group of continuous homomorphisms $\mathrm{Hom}_\mathrm{cont}(\pi , \overline{{\mathbb {Q}}}_{\ell }^\times )$. Recall that by [15, Prop.A.2.2.3], ${\mathcal {G}}(\overline{{\mathbb {Q}}}_{\ell })$ can also be identified with the maximal spectrum ${{\,\mathrm{Spm}\,}}({\mathfrak {R}})$ of ${\mathfrak {R}} = R \otimes _{{\mathcal {O}}_E} \overline{{\mathbb {Q}}}_{\ell }$. Furthermore, ${\mathfrak {R}}$ is a noetherian Jacobson ring of dimension b (loc.cit.).

As a maximal spectrum, ${\mathcal {G}}(\overline{{\mathbb {Q}}}_\ell )$ is endowed with a Zariski topology, which is the topology on ${\mathcal {G}}(\overline{{\mathbb {Q}}}_\ell )$ we use in the sequel.

Lemma 3.1

The subset of torsion points of ${\mathcal {G}}(\overline{{\mathbb {Q}}}_\ell )$ is dense.

Proof

We have to show that if $g\in {\mathfrak {R}}$ vanishes on all torsion points then $g=0$. Without loss of generality $g\in {\mathcal {O}}_E \llbracket \pi \rrbracket$. Let $[\ell ^n ]: {\mathcal {O}}_E \llbracket \pi \rrbracket \rightarrow {\mathcal {O}}_E \llbracket \pi \rrbracket$ be the morphism induced by $\ell ^n$-multiplication on $\pi$. Let $J_n$ be the ideal generated by $[\ell ^n](M)$. For all $n>0$ the ring

$$\begin{aligned} {\mathcal {O}}_E \llbracket \pi \rrbracket /J_n= {\mathcal {O}}_E [ \pi /\ell ^n \pi ] \end{aligned}$$

(2)

is flat over ${\mathcal {O}}_E$ and its tensor product with E is reduced. As the finite group ${{\,\mathrm{Spm}\,}}({\mathcal {O}}_E [ \pi /\ell ^n \pi ]\otimes _{{\mathcal {O}}_E} \overline{{\mathbb {Q}}}_{\ell })$ identifies with the $\ell ^n$-torsion points of ${\mathcal {G}}(\overline{{\mathbb {Q}}}_{\ell })$, we see that the image of g in the rings (2) vanishes for all $n>0$. As the limit over n of the rings (2) is ${\mathcal {O}}_E \llbracket \pi \rrbracket$ by definition, we get $g=0$. $\square$

3.2 Exponential map

We recall some well-known facts on the $\ell$-adic exponential map, see [4, Ch. 12]. We consider the $\ell$-adic absolute value $|-|$ on $\overline{{\mathbb {Q}}}_{\ell }$ with $|\ell | =1/\ell$. For $\rho \in (0,1)\cap |\overline{{\mathbb {Q}}}_{\ell }^\times |$ we have extensions of rings

$$\begin{aligned} {\mathcal {O}}_E \llbracket X_1,\ldots , X_b \rrbracket \otimes _{{\mathcal {O}}_E} E \subset E\langle X_1,\ldots , X_b \rangle _{\rho } \end{aligned}$$

where the Tate ring on the right is the completion of the polynomial ring with respect to the $\rho$-Gauss norm. Recall that the $\rho$-Gauss norm of $g=\sum _{n} g^{(n)} \underline{X}^n$ is defined by $|g|=\sup _n | g^{(n)}| \rho ^n$.

Under the additional assumption $\rho <\ell ^{-1/(\ell -1)}$, we have an exponential isomorphism

$$\begin{aligned} E\langle X_1,\ldots , X_b \rangle _{\rho } \xrightarrow {\sim } E \langle T_1,\ldots , T_b \rangle _{\rho } , \ X_i \mapsto \exp (T_i)-1. \end{aligned}$$

Let $B(\rho )\subset \overline{{\mathbb {Q}}}_{\ell }^b$ be the polydisc consisting of points with maximum norm $\le \rho$, where $\rho \in |\overline{{\mathbb {Q}}}_{\ell }^\times |$. As $B(\rho )$ can be identified with the maximal spectrum of

$$\begin{aligned} \overline{{\mathbb {Q}}}_{\ell }\langle T_1,\ldots , T_b \rangle _{\rho } ={{\,\mathrm{colim}\,}}_E E\langle T_1, \ldots , T_b\rangle _\rho , \end{aligned}$$

we can endow it with a Zariski topology.

Independently of the choice of coordinates one can identify $B(\rho )$ with $\mathrm{Hom}_{\overline{{\mathbb {Z}}}_{\ell }} (\pi \otimes _{{\mathbb {Z}}_\ell } \beta \overline{{\mathbb {Z}}}_{\ell }, \overline{{\mathbb {Z}}}_{\ell })$, where $\beta \in \overline{{\mathbb {Q}}}_{\ell }$ is such that $|\beta | =1/\rho$. So more generally for any finitely generated $\overline{{\mathbb {Z}}}_{\ell }$-submodule $\pi '\subset \pi \otimes _{{\mathbb {Z}}_\ell } \overline{{\mathbb {Q}}}_{\ell }$ containing $\pi$, there exists a closed polydisc $B_{\pi '} \subset B(1)$.

Similarly, we let ${\mathcal {G}}(\overline{{\mathbb {Q}}}_{\ell })(\rho )$ be the subgroup of ${\mathcal {G}}(\overline{{\mathbb {Q}}}_{\ell })$ which consists of the continuous homomorphisms $\chi :\pi \rightarrow \overline{{\mathbb {Q}}}_{\ell }^\times$ with $|\chi (e)-1|\le \rho$ for all $e \in \pi$. We then obtain an injective group homomorphism

$$\begin{aligned} \exp _\rho :B(\rho ) \rightarrow {\mathcal {G}}(\overline{{\mathbb {Q}}}_{\ell }) \quad \text { for } \rho <\ell ^{-1/(\ell -1)} \end{aligned}$$

which is continuous with respect to the Zariski topology and the image of which is ${\mathcal {G}}(\overline{{\mathbb {Q}}}_{\ell })(\rho )$.

Lemma 3.2

Let $S\subset {\mathcal {G}}(\overline{{\mathbb {Q}}}_{\ell })$ be an irreducible closed subset and $\rho \in (0,1)\cap | \overline{{\mathbb {Q}}}_{\ell }^\times |$ be such that the subset $S \cap {\mathcal {G}}(\overline{{\mathbb {Q}}}_{\ell })(\rho )$ is non-empty. Then $S \cap {\mathcal {G}}(\overline{{\mathbb {Q}}}_{\ell })(\rho )$ is dense in S.

Proof

After replacing E by a finite extension we can assume that S is given by an integral quotient ring A of ${\mathcal {O}}_E \llbracket \pi \rrbracket$ which is flat over ${\mathcal {O}}_E$. The map $A\rightarrow A\otimes _{{\mathcal {O}}_E \llbracket \pi \rrbracket } \overline{{\mathbb {Q}}}_{\ell }\langle X_1,\ldots , X_b \rangle _{\rho }$ is injective since it is flat and non-zero. The codomain of this map is a reduced Jacobson ring [11, Prop. 2.2] and its maximal ideals correspond to $S \cap {\mathcal {G}}(\overline{{\mathbb {Q}}}_{\ell })(\rho )$. As the closure of $S \cap {\mathcal {G}}(\overline{{\mathbb {Q}}}_{\ell })(\rho )$ corresponds to the intersection of these maximal ideals inside A, which is the zero ideal, we deduce Lemma 3.2. $\square$

3.3 Main Theorem

This subsection contains the technically central result of our note. Let E be a finite extension of ${\mathbb {Q}}_\ell$ together with a fixed embedding $E\hookrightarrow \overline{{\mathbb {Q}}}_{\ell }$ and let ${\mathcal {G}}={{\,\mathrm{Spf}\,}}( {\mathcal {O}}_E \llbracket \pi \rrbracket )$ be a multiplicative b-dimensional formal Lie group over ${\mathcal {O}}_E$. Let $\sigma :\pi \rightarrow \pi$ be an automorphism such that the ${\mathbb {Q}}_\ell$-linear map $\sigma :\pi \otimes _{{\mathbb {Z}}_\ell } {\mathbb {Q}}_\ell \rightarrow \pi \otimes _{{\mathbb {Z}}_\ell } {\mathbb {Q}}_\ell$ is semi-simple with eigenvalues $\alpha _1, \ldots , \alpha _b\in \overline{{\mathbb {Q}}}_{\ell }$. We also denote by $\sigma :{\mathcal {G}}\rightarrow {\mathcal {G}}$ the corresponding automorphism of formal groups. Recall that we fix a complex embedding $\iota :\overline{{\mathbb {Q}}}_\ell \hookrightarrow {\mathbb {C}}$.

We define quasi-linearity following de Jong [5, Def. 1.1].

Definition 3.3

A closed subset $S\subset {\mathcal {G}}(\overline{{\mathbb {Q}}}_{\ell })$ is called quasi-linear if it can be written in the form

$$\begin{aligned} S=\bigcup _{r\in I} s_r {\mathcal {H}}_r(\overline{{\mathbb {Q}}}_{\ell }), \end{aligned}$$

where I is finite, the elements $s_r\in {\mathcal {G}}(\overline{{\mathbb {Q}}}_\ell )$ are torsion and the ${\mathcal {H}}_r$ are formal Lie subgroups of ${\mathcal {G}}$.

Theorem 3.4

Assume that for all $i,j\in \{1,\ldots , b \}$ we have $|\iota (\alpha _i)|=|\iota (\alpha _j)| \ne 1$. Let $S\subset {\mathcal {G}}(\overline{{\mathbb {Q}}}_{\ell })$ be a Zariski closed subset with $\sigma (S)=S$. Then S is quasi-linear.

Proof

We can assume that S is non-empty and irreducible. We fix $\rho \in (0, \ell ^{-1/(\ell -1)})\cap |\overline{{\mathbb {Q}}}_{\ell }^\times |$. There exist $\overline{{\mathbb {Z}}}_{\ell }$-linear independent eigenvectors $e'_1,\ldots , e'_b\in \pi \otimes _{{\mathbb {Z}}_\ell } \overline{{\mathbb {Z}}}_{\ell }$ of $\sigma$ such that $\pi$ is contained in $\pi '=\overline{{\mathbb {Z}}}_{\ell }e'_1 + \cdots +\overline{{\mathbb {Z}}}_{\ell }e'_b$. We also fix an integer $w>0$ with $\ell ^w\pi '\subset \pi \otimes _{{\mathbb {Z}}_\ell } \overline{{\mathbb {Z}}}_{\ell }$.

There exists $n>0$ such that $[\ell ^n]( S)\cap {\mathcal {G}}(\rho /\ell ^w)$ is non-empty. As $[\ell ^n]:{\mathcal {O}}_E \llbracket \pi \rrbracket \rightarrow {\mathcal {O}}_E \llbracket \pi \rrbracket$ is a finite, faithfully flat ring homomorphism, we deduce that $[\ell ^n]( S)$ is closed in ${\mathcal {G}}(\overline{{\mathbb {Q}}}_{\ell })$. So $\exp _\rho ^{-1}( [\ell ^n](S) )\cap B_{\pi '}$ is closed and non-empty in the polydisc $B_{\pi '}$. The choice of $e'_1, \ldots , e'_b$ above allows us to identify $B_{\pi '}$ with the maximal spectrum of the Tate algebra $\overline{{\mathbb {Q}}}_{\ell }\langle T'_1 , \ldots , T'_b \rangle$. So after replacing E by a finite extension the Zariski closed subset $\exp _\rho ^{-1}( [\ell ^n](S) )\cap B_{\pi '}$ of $B_{\pi '}$ corresponds to a radical ideal $I\subset E\langle T'_1,\ldots , T'_b \rangle$.

We can apply Proposition 2.5 in order to see that I is homogeneous. Consequently, $\exp _\rho ^{-1}( [\ell ^n](S) )\cap B_{\pi '}$ and therefore also its subset $\exp _{\rho /\ell ^w}^{-1}( [\ell ^n](S) )$ is stabilized by the homothety $\ell$, which is equivalent to the fact that $[\ell ^n](S)\cap {\mathcal {G}}(\rho /\ell ^w)$ is stabilized by $[\ell ]$. As $[\ell ^m](S)\cap {\mathcal {G}}(\rho /\ell ^w)$ is Zariski dense in $[\ell ^m](S)$ for all $m\ge n$ by Lemma 3.2, we deduce that $[\ell ]$ also stabilizes $[\ell ^n](S)$. By a result of de Jong [5, Prop. 1.2(1)] this implies the theorem. $\square$

4 Generalized Fourier–Mellin transform

In this section we consider a generalization of $\ell$-adic cohomology which for tori is called Mellin transform in [15, Prop. 3.1.3] and which for complex abelian varieties is a completion of the Fourier–Mellin transform in [1, Section 1]. The use of this “Fourier–Mellin transform” is limited by the fact that we do not know any sort of inversion formula at the moment. The only really new result in this section is Proposition 4.6 which provides a simple direct approach to generic vanishing.

4.1 Definition and basic properties

Let X be a separated, connected scheme of finite type over the algebraically closed field F. All cohomology groups we consider will be with respect to the étale topology. In the sequel, a tensor product involving a derived object (module or sheaf) means a derived tensor product.

Let E be a finite extension of ${\mathbb {Q}}_\ell$ with a fixed embedding $E\hookrightarrow \overline{{\mathbb {Q}}}_{\ell }$. Let R be a complete noetherian local ${\mathcal {O}}_E$-algebra with finite residue field and maximal ideal ${\mathfrak {m}}$. Then ${\mathfrak {R}}=R\otimes _{{\mathcal {O}}_E} \overline{{\mathbb {Q}}}_{\ell }$ is a noetherian Jacobson ring by [15, Prop.A.2.2.3].

Let ${\mathcal {F}}$ be in $D^b_c(X, {\mathcal {O}}_E)$ and let $\rho :\pi _1(X)\rightarrow R^\times$ be a continuous character. We define ${\mathfrak {m}}$-adic étale cohomology as

$$\begin{aligned} R \Gamma (X,{\mathcal {F}}\otimes _{{\mathcal {O}}_E} {\mathcal {L}}_{R} ) := R \lim _n R \Gamma (X,{\mathcal {F}}\otimes _{{\mathcal {O}}_E} {\mathcal {L}}_{R/{\mathfrak {m}}^n} ), \end{aligned}$$

where ${\mathcal {L}}_{R/{\mathfrak {m}}^n}$ is the étale local system on X associated to the finite character $\pi _1(X)\xrightarrow {\rho } R^\times \rightarrow (R/{\mathfrak {m}}^n)^\times$. We denote the cohomology of this complex by $H^i(X, {\mathcal {F}}\otimes _{{\mathcal {O}}_E} {\mathcal {L}}_{R})$. The corresponding cohomology with compact support is defined in the usual way. Let $\omega _X \in D^b_c(X,{\mathcal {O}}_E )$ be the dualizing complex $f^!({\mathcal {O}}_E )$, where $f:X\rightarrow \mathrm{Spec}\,(F)$ is the canonical map.

We collect some properties of this ${\mathfrak {m}}$-adic cohomology, which follow from [9].

Proposition 4.1

• (1) [Finiteness] The complex $R \Gamma (X,{\mathcal {F}}\otimes _{{\mathcal {O}}_E} {\mathcal {L}}_{R} )$ has bounded, coherent cohomology groups, i.e. it is in $D^b_\mathrm{coh}(R)$.

• (2) [Base change] For any quotient ring $R'$ of R we have a base change isomorphism

  $$\begin{aligned} R \Gamma (X,{\mathcal {F}}\otimes _{{\mathcal {O}}_E} {\mathcal {L}}_{R} ) \otimes _{R} R' \xrightarrow {\simeq } R \Gamma (X,{\mathcal {F}}\otimes _{{\mathcal {O}}_E} {\mathcal {L}}_{R'} )\in D^b_\mathrm{coh}(R' ). \end{aligned}$$

• (3) [Limit property] We have an isomorphism of R-modules

  $$\begin{aligned} H^i(X, {\mathcal {F}}\otimes _{{\mathcal {O}}_E} {\mathcal {L}}_{R} ) \xrightarrow {\simeq } \lim _n H^i(X, {\mathcal {F}}\otimes _{{\mathcal {O}}_E} {\mathcal {L}}_{ R/ {\mathfrak {m}}^n}). \end{aligned}$$

• (4) [Duality] There is a canonical isomorphism

  $$\begin{aligned} R \mathrm{Hom}_R ( R \Gamma _c(X,{\mathcal {F}}\otimes _{{\mathcal {O}}_E} {\mathcal {L}}_{R} ),R ) \simeq R \Gamma (X,{\mathcal {F}}^\vee \otimes _{{\mathcal {O}}_E} {\mathcal {L}}^\vee _{R} ) \end{aligned}$$

  in $D^b_\mathrm{coh}(R)$, where ${\mathcal {F}}^\vee = R\mathrm{Hom}({\mathcal {F}}, \omega _X)$ and where ${\mathcal {L}}^\vee _R$ is the local system associated to the dual character $\rho ^{-1}$.

Part (1), (2) and (4) follow from [9, Thm. 6.3, Thm. 7.2], part (3) follows from the fact that $\lim _n^1 H^i(X,R/ {\mathfrak {m}}^n)$ vanishes for all $i\in {\mathbb {Z}}$ as these R-modules are artinian. Note that Ekedahl assumes that R has finite global dimension, which is sufficient for our application. It is however not difficult to show the general case.

Note that for ${\mathcal {F}}\in D^b_c(X,\overline{{\mathbb {Q}}}_{\ell })$ we get a corresponding complex

$$\begin{aligned} R \Gamma (X,{\mathcal {F}}\otimes {\mathcal {L}}_{{\mathfrak {R}}} ) \ \mathrm{in} \ D^b_\mathrm{coh}({\mathfrak {R}} ), \end{aligned}$$

associated to the character $\pi _1(X)\xrightarrow {\rho } R^\times \rightarrow \mathfrak {R}^\times$.

One way in which this étale ${\mathfrak {m}}$-adic cohomology is useful is the following isomorphism criterion for a cup-product. Let ${\mathcal {F}}$ and ${\mathcal {K}}$ be in $D^b_c(X,\overline{{\mathbb {Q}}}_{\ell })$ and assume that R is an integral domain in which $\ell$ does not vanish.

Lemma 4.2

For $\xi \in H^j(X,{\mathcal {K}})$ and $i\in {\mathbb {Z}}$ the following are equivalent:

• (1) The cup-product

  $$\begin{aligned} H^i(X, {\mathcal {F}}\otimes {\mathcal {L}}_{{\mathfrak {R}}} ) \xrightarrow {\cup \xi } H^{i+j}(X, {\mathcal {F}}\otimes {\mathcal {K}}\otimes {\mathcal {L}}_{{\mathfrak {R}}} ) \end{aligned}$$

  is an isomorphism (resp. not an isomorphism) after tensoring with ${{\,\mathrm{Frac}\,}}({\mathfrak {R}} )$.

• (2) $H^i(X,{\mathcal {F}}\otimes {\mathcal {L}}_s ) \xrightarrow {\cup \xi } H^{i+j}(X,{\mathcal {F}}\otimes {\mathcal {K}}\otimes {\mathcal {L}}_s)$ is an isomorphism (resp. not an isomorphism) for all $s\in U$, where $U\subset {{\,\mathrm{Spm}\,}}({\mathfrak {R}} )$ is a dense open subset.

Here ${\mathcal {L}}_s$ for $s\in {{\,\mathrm{Spm}\,}}({\mathfrak {R}} )$ is the local system on X corresponding to the character $\pi _1(X)\rightarrow {\mathfrak {R}}^\times \rightarrow k(s)^\times$, which is given by reduction modulo the maximal ideal associated to s. Note that the residue field k(s) is equal to $\overline{{\mathbb {Q}}}_{\ell }$, see Sect. 3.1.

Proof

It suffices to prove (1) $\Rightarrow$ (2). By Proposition 4.1(1) there exists a dense open subset $U\subset {{\,\mathrm{Spm}\,}}({\mathcal {R}})$ such that the following ${\mathfrak {R}}$-modules are flat over U:

$$\begin{aligned}&H^*(X, {\mathcal {F}}\otimes {\mathcal {L}}_{{\mathfrak {R}}}), \ H^*(X, {\mathcal {F}}\otimes {\mathcal {K}}\otimes {\mathcal {L}}_{{\mathfrak {R}}} )\text { and} \\&\quad {{\,\mathrm{coker}\,}}( H^*(X, {\mathcal {F}}\otimes {\mathcal {L}}_{{\mathfrak {R}}} ) \xrightarrow {\cup \xi } H^*(X, {\mathcal {F}}\otimes {\mathcal {K}}\otimes {\mathcal {L}}_{{\mathfrak {R}}} ) ) . \end{aligned}$$

Note that then also the kernel of $\cup \xi$ is flat over U. Then the conclusion follows from Proposition 4.1(2) and the Tor-spectral sequence. $\square$

Combining Lemma 4.2 with [31, Prop. 0.9.2.3] we obtain:

Corollary 4.3

The set of $s\in {{\,\mathrm{Spm}\,}}({\mathfrak {R}} )$ with the property that

$$\begin{aligned} H^i(X,{\mathcal {F}}\otimes {\mathcal {L}}_s ) \xrightarrow {\cup \xi } H^{i+j}(X,{\mathcal {F}}\otimes {\mathcal {K}}\otimes {\mathcal {L}}_s) \end{aligned}$$

is an isomorphism (resp. not an isomorphism) is constructible.

Now we consider a special ring R. Let $\pi$ be a torsion free $\ell$-adic quotient of $\pi _1^\mathrm{ab}(X )$ and let R be the completed group ring

$$\begin{aligned} R = {\mathcal {O}}_E \llbracket \pi \rrbracket = \lim _n {\mathcal {O}}_E [\pi / \ell ^n \pi ] \end{aligned}$$

as in Sect. 3. We let $\rho :\pi _1(X) \rightarrow R^\times$ be the canonical character $e\mapsto [e ]$. Set $\mathfrak {R}=R \otimes _{{\mathcal {O}}_E} \overline{{\mathbb {Q}}}_{\ell }$.

Definition 4.4

The integral Fourier-Mellin transform of ${\mathcal {F}}\in D^b_c(X, {\mathcal {O}}_E )$ is defined as

$$\begin{aligned} {{\,\mathrm{FM}\,}}_\pi (X,{\mathcal {F}}) = R \Gamma (X,{\mathcal {F}}\otimes _{{\mathcal {O}}_E} {\mathcal {L}}_{R} )\in D^b_\mathrm{coh}(R). \end{aligned}$$

Up to isogeny we get an induced Fourier-Mellin transform

$$\begin{aligned} {\mathfrak {FM}}_\pi (X,{\mathcal {F}}) \in D^b_\mathrm{coh}({\mathfrak {R}}) \end{aligned}$$

for ${\mathcal {F}}\in D^b_c(X,\overline{{\mathbb {Q}}}_{\ell })$. The corresponding cohomology modules are denoted by ${{\,\mathrm{FM}\,}}^i_\pi (X,{\mathcal {F}})$ resp. ${\mathfrak {FM}}^i_\pi (X,{\mathcal {F}})$.

In case the group $\pi$ is clear from the context we omit it in the notation.

Remark 4.5

For $R={\mathcal {O}}_E \llbracket \pi \rrbracket$ and for an R-module (sheaf) ${\mathcal {M}}$ we denote by ${\mathcal {M}}'$ the same abelian group (sheaf) with the R-module structure twisted by the automorphism $[-1]:R \xrightarrow {\sim } R$, $[-1]([e]) = [-e]$ for $e\in \pi$. Then the dual R-module sheaf ${\mathcal {L}}_R^\vee$ is isomorphic to ${\mathcal {L}}'_R$.

4.2 A vanishing result

Again we fix a finitely generated free ${\mathbb {Z}}_\ell$-module quotient $\pi$ of $\pi _1^\mathrm{ab}(X)$ and we set $R = {\mathcal {O}}_E\llbracket \pi \rrbracket$. We have an induced tower of Galois coverings of X

$$\begin{aligned} \cdots \rightarrow X_{n+1} \rightarrow X_n \rightarrow \cdots \rightarrow X_0=X \end{aligned}$$

with $\mathrm{Gal}(X_n/X)=\pi /\ell ^n \pi$. We denote this tower by $X_\infty$ and we use the notation

$$\begin{aligned} H^j(X_\infty , {\mathcal {K}})={{\,\mathrm{colim}\,}}_n H^j(X_n , {\mathcal {K}}) \end{aligned}$$

for ${\mathcal {K}}\in D^b_c(X,{\mathcal {O}}_E)$.

The following vanishing proposition is our key new technical result which allows us to obtain a short proof of the generic vanishing theorem. The analog for complex analytic varieties could be used to give an alternative direct proof of  [1, Thm. 1.3], [25, Cor. 7.5], [17, Thm. 1.1].

Proposition 4.6

Let ${\mathcal {F}}$ and ${\mathcal {K}}$ be in $D^b_c(X,{\mathcal {O}}_E)$. If $\xi \in H^j(X,{\mathcal {K}})$ becomes divisible in $H^j(X_\infty ,{\mathcal {K}})$, then the cup-product map

$$\begin{aligned} {{\,\mathrm{FM}\,}}^i(X,{\mathcal {F}}) \xrightarrow {\cup \xi } {{\,\mathrm{FM}\,}}^{i+j}(X,{\mathcal {F}}\otimes _{{\mathcal {O}}_E} {\mathcal {K}}) \end{aligned}$$

vanishes for all $i\in {\mathbb {Z}}$.

Proof

Recall that $R={\mathcal {O}}_E \llbracket \pi \rrbracket$ and that this ring is identified with ${\mathcal {O}}_E \llbracket X_1, \ldots , X_b \rrbracket$ by sending $[e_i]$ to $1+X_i$, see Sect. 3.1. The key observation is that we have an isomorphism of pro-rings

$$\begin{aligned} \{ R / {\mathfrak {m}}^n \}_n \simeq \{{\mathcal {O}}_E/\ell ^m {\mathcal {O}}_E [\pi / \ell ^n \pi ] \}_{m,n}. \end{aligned}$$

(3)

One easily sees the two isomorphisms of pro-rings

$$\begin{aligned} \{ R / {\mathfrak {m}}^n \}_n \simeq \{ R /(\ell ^m R + X_1^n R + \cdots + X_b^n R) \}_{m,n} \end{aligned}$$

(4)

and

$$\begin{aligned} \{ {\mathcal {O}}_E/\ell ^m [\pi / \ell ^n \pi ] \}_{m,n} =\{ R/(\ell ^m R + ((X_1+1)^{\ell ^n}-1) R + \cdots ) \}_{m,n} . \end{aligned}$$

(5)

So to prove the isomorphism of pro-rings  (3) we have to show that for fixed $m>0$ the right sides of (4) and of (5) are isomorphic as pro-systems in n. As the ring on the right side of (5) is artinian, $X_i$ is nilpotent in it, which shows one direction.

Conversely, it suffices to show that $(X_i+1)^{\ell ^r}-1$ vanishes in the ring on the right side of (4) for $r\gg 0$ depending on m and n. We verify this by observing that in the ring $R/\ell ^m$ for any $n\ge m>0$ we have $X_i^{\ell ^{n-m+1}} | (X_i+1)^{\ell ^n}-1$. In order to verify this divisibility one has to show that all coefficients of the integral polynomial $(X_i+1)^{\ell ^n}-1 = \sum _{r=1}^{\ell ^n} \left( {\begin{array}{c}\ell ^n\\ r\end{array}}\right) X_i^r$ are divisible by $\ell ^m$ in degrees $< \ell ^{n-m+1}$. This follows from $\mathrm{ord}_\ell \left( \left( {\begin{array}{c}\ell ^n\\ r\end{array}}\right) \right) = n-\mathrm{ord}_\ell (r)$ for $r>0$.

From Proposition 4.1(3) and from the isomorphism (3) we deduce that

$$\begin{aligned} {{\,\mathrm{FM}\,}}^i(X,{\mathcal {F}})= \mathrm{lim}_{m,n} H^i(X, {\mathcal {F}}\otimes _{{\mathcal {O}}_E} {\mathcal {L}}_{{\mathcal {O}}_E/\ell ^m [\pi / \ell ^n \pi ] } ). \end{aligned}$$

We have

$$\begin{aligned} H^i(X, {\mathcal {F}}\otimes _{{\mathcal {O}}_E} {\mathcal {L}}_{{\mathcal {O}}_E/\ell ^m [\pi / \ell ^n \pi ] } ) \cong H^i(X_n, p_n^*({\mathcal {F}})\otimes _{{\mathcal {O}}_E}{\mathcal {O}}_E/\ell ^m ) \end{aligned}$$

(6)

and similarly for ${{\,\mathrm{FM}\,}}^{i+j}(X,{\mathcal {F}}\otimes _{{\mathcal {O}}_E} {\mathcal {K}})$, where $p_{n}:X_n \rightarrow X$ is the canonical finite étale map. For the isomorphism (6) one uses that $p_{n\, *} \,{\mathcal {O}}_E /\ell ^m \cong {\mathcal {L}}_{{\mathcal {O}}_E/\ell ^m [\pi / \ell ^n \pi ] }$ and the projection formula. Here ${\mathcal {O}}_E /\ell ^m$ is the constant sheaf on $X_n$.

Our assumption on $\xi$ says that if n is large enough, depending on m, then $\xi$ is $\ell ^m$-divisible in $H^j(X_n,{\mathcal {K}})$. In this situation the cup-product

$$\begin{aligned} H^i(X_n, p_n^*({\mathcal {F}})\otimes _{{\mathcal {O}}_E}{\mathcal {O}}_E/\ell ^m ) \xrightarrow {\cup \xi } H^{i+j}(X_n, p_n^*({\mathcal {F}}) \otimes _{{\mathcal {O}}_E}{\mathcal {K}}\otimes _{{\mathcal {O}}_E}{\mathcal {O}}_E/\ell ^m ) \end{aligned}$$

(7)

vanishes. So taking the limit over m and n in (7) and using the projection formula we finish the proof of Proposition 4.6. $\square$

5 Hard Lefschetz theorem

5.1 Formulation of the theorems

Let X be a separated scheme of finite type over an algebraically closed field F of characteristic different from $\ell$.

Definition 5.1

A complex ${\mathcal {F}}\in D^b_c(X , \overline{{\mathbb {Q}}}_{\ell })$ is called arithmetic, if there exists a finitely generated field $F_0\subset F$ such that

• (1) X descends to a separated scheme of finite type $X_0/F_0$;

• (2) ${\mathcal {F}}$ lies in the full subcategory

  $$\begin{aligned} D^b_c(X_0\otimes _{F_0}\overline{F}_0 , \overline{{\mathbb {Q}}}_{\ell }) \hookrightarrow D^b_c(X , \overline{{\mathbb {Q}}}_{\ell }), \end{aligned}$$

  where $F_0\subset \overline{F_0}$ is the algebraic closure of $F_0$ in F;

• (3) For each element $\sigma \in \mathrm{Gal}(\overline{F}_0 /F_0)$, one has

  $$\begin{aligned} \sigma ({\mathcal {F}})\simeq {\mathcal {F}}\in D^b_c(X_0\otimes _{F_0}\overline{F}_0 , \overline{{\mathbb {Q}}}_{\ell }) . \end{aligned}$$

In particular if $F=\overline{{\mathbb {F}}}_p$ then ${\mathcal {F}}$ is arithmetic if and only if it is stabilized by a non-trivial power of the Frobenius.

Remark 5.2

The notion of arithmeticity in Definition 5.1 is the same as the one in in [11, Defn. 1.4], replacing ${\mathbb {C}}$ by F. In [2, p. 163] semi-simple ${\mathcal {F}}\in D^b_c(X, \overline{{\mathbb {Q}}}_\ell )$ of geometric origin are defined (over $F={\mathbb {C}}$, but this is irrelevant for the discussion) and one easily checks that these ${\mathcal {F}}$ are arithmetic.

In fact wherever we impose the arithmeticity condition in this note a slightly weaker condition would be sufficient, which is however quite technical to formulate precisely. Recall that the condition labeled (P) in [2, Lem. 6.2.6] says that after a spreading of X,  a suitable specialization of ${\mathcal {F}}$ to ${\mathcal {F}}_{\bar{s}}$ is fixed by a Frobenius, where $\bar{s}$ is a sufficiently generic $\overline{{\mathbb {F}}}_p$-point. The specialization depends on the choice of a strictly henselian discrete valuation ring V with $V \subset F$ such that the closed point of $\mathrm{Spec}\,(V)$ is $\bar{s}$. In our use of the arithmeticity condition, all we shall need is precisely this invariance of ${\mathcal {F}}$ under one generic Frobenius action.

The Lefschetz isomorphism is shown for mixed semi-simple perverse sheaves defined over a finite field in [2, Thm. 5.4.10] and for semi-simple perverse sheaves of geometric origin over the complex numbers in [2, Thm. 6.2.10]. Combining this with the Langlands correspondence for function fields [18] one can show Theorem 5.3 by first specializing to an algebraic closure of a finite field F similarly to [7, Rmk. 1.7] and then using the method of the proof of [7, 1.8]. In the next two theorems, X is a smooth projective variety over an algebraic closed field F of characteristic different from $\ell$, and $\eta \in H^2(X, {\mathbb {Z}}_\ell )$ is the first Chern class of an ample line bundle.

Theorem 5.3

(Hard Lefschetz) Let ${\mathcal {F}}\in D^b_c(X, \overline{{\mathbb {Q}}}_\ell )$ be an arithmetic semi-simple perverse sheaf. Then for any $i\in {\mathbb {N}},$ the cup-product map

$$\begin{aligned} \cup \eta ^{ i}:H^{-i}(X, {\mathcal {F}}) \xrightarrow {\sim } H^{i}(X, {\mathcal {F}}) \end{aligned}$$

is an isomorphism.

The aim of this section is to prove Theorem 5.4 for which weights are not available.

Theorem 5.4

(Hard Lefschetz) Let ${\mathcal {L}}$ be an étale rank one $\overline{{\mathbb {Q}}}_{\ell }$-local system on X. Let ${\mathcal {F}}\in D^b_c(X, \overline{{\mathbb {Q}}}_{\ell })$ be an arithmetic semi-simple perverse sheaf. Then for any $i\in {\mathbb {N}},$ the cup-product map

$$\begin{aligned} \cup \eta ^{ i}:H^{-i}(X, {\mathcal {F}}\otimes {\mathcal {L}}) \xrightarrow {\sim } H^{i}(X, {\mathcal {F}}\otimes {\mathcal {L}}) \end{aligned}$$

is an isomorphism. $\square$

Remark 5.5

One conjectures the Hard Lefschetz isomorphism to hold for any semi-simple perverse $\overline{{\mathbb {Q}}}_{\ell }$-sheaf on a projective scheme X over an algebraically closed field F of characteristic different from $\ell$, see [7].

5.2 Proof of Hard Lefschetz

We now prove Theorem 5.4. We follow the general strategy of Drinfeld in [7, Lem. 2.5].

We first make the reduction to the case $F=\overline{{\mathbb {F}}}_p$. To this aim we quote [2, Lem. 6.1.9] which unfortunately is only written for the passage from the field of complex numbers to positive characteristic, so we quote in addition [7, Rmk. 1.7] where it is observed that the spreading and specialization also work in positive characteristic with only minor changes.

From now on, we assume that $F=\overline{{\mathbb {F}}}_p$. Then X descends to a variety over a finite subfield $F_0\subset F$. With the notation of Sect. 3 we let $\pi$ be the $\ell$-adic completion of the abelian étale fundamental group $\pi _1(X)^\mathrm{ab}$ modulo torsion.

We first show that if the Hard Lefschetz theorem is true for all ${\mathcal {L}}$ which factor through $\pi$, then it is true in general. Indeed, write $\chi :\pi (X)^\mathrm{ab}\rightarrow {\mathcal {O}}_E^\times$ for the character corresponding to ${\mathcal {L}}$ where $\pi _1(X)^\mathrm{ab}$ is the maximal abelian quotient. We can decomposte $\pi _1(X)^\mathrm{ab}$ into a product $\pi \times \pi '$, where $\pi '$ is itself a product of a finite $\ell$-group and a pro-finite prime to $\ell$ group. As $\chi (\pi ')$ is finite this leads to a decomposition ${\mathcal {L}}= {\mathcal {L}}' \otimes {\mathcal {M}}$ such that ${\mathcal {L}}'$ is a torsion rank one $\overline{{\mathbb {Q}}}_{\ell }$-local system and such that the character of ${\mathcal {M}}$ factors through $\pi$. The sheaf ${\mathcal {F}}\otimes {\mathcal {L}}'$ is still semi-simple perverse and arithmetic, so by our assumption, Hard Lefschetz holds for $({\mathcal {F}}\otimes {\mathcal {L}}' )\otimes {\mathcal {M}}={\mathcal {F}}\otimes {\mathcal {L}}$.

We now prove Hard Lefschetz under the assumption that the character of ${\mathcal {L}}$ factors through $\pi$. We consider the multiplicative formal Lie group ${\mathcal {G}}=\mathrm{Spf} ({\mathbb {Z}}_\ell \llbracket \pi \rrbracket )$. So ${\mathcal {G}}(\overline{{\mathbb {Q}}}_{\ell })$ parametrizes the $\overline{{\mathbb {Q}}}_{\ell }$-local systems whose character factors through $\pi$. We define $S_\circ \subset {\mathcal {G}}(\overline{{\mathbb {Q}}}_{\ell })$ to correspond to those $\overline{{\mathbb {Q}}}_{\ell }$-local systems ${\mathcal {L}}$ such that Theorem 5.4 fails. By Corollary 4.3, $S_\circ$ is constructible. We define $S\subset {\mathcal {G}}(\overline{{\mathbb {Q}}}_{\ell })$ to be the Zariski closure of $S_\circ$.

The geometric Frobenius $\sigma \in \mathrm{Gal}(F/F_0)$ induces an automorphism $\sigma :{\mathcal {G}}\rightarrow {\mathcal {G}}$ of the formal Lie group. As ${\mathcal {F}}$ is assumed to be arithmetic, we can replace $F_0$ by a finite extension and assume that $\sigma$ fixes ${\mathcal {F}}$ up to quasi-isomorphism. Thus we obtain a (non-canonical) isomorphism

$$\begin{aligned} \sigma :H^*(X,{\mathcal {F}}\otimes {\mathcal {L}}) \xrightarrow {\sim } H^*(X,{\mathcal {F}}\otimes \sigma ({\mathcal {L}})) \end{aligned}$$

compatible with the cup-product with $\eta ^i$. So $\sigma (S_\circ ) =S_\circ$ and $\sigma (S)=S$.

The Frobenius $\sigma$ acts ${\mathbb {Z}}_\ell$-linearly and semi-simply on $\pi \otimes _{{\mathbb {Z}}_\ell }{\mathbb {Q}}_\ell$, use [29, Thm. 2] and note that the Albanese map $X\rightarrow \mathrm{Alb}(X)$ induces an isomorphism with the Tate module $\pi \cong T_\ell (\mathrm{Alb}(X))$ [26, Ann. II]. Furthermore, the Frobenius $\sigma$ acts with weight $-1$ on $\pi$, see [6, Thm. 1]. Therefore Theorem 3.4 is applicable and says that S is quasi-linear.

By Lemma 3.1, the torsion points are dense in S. If $S_\circ$ were non-empty it would contain a torsion point corresponding to an arithmetic rank one $\overline{{\mathbb {Q}}}_{\ell }$-local system ${\mathcal {L}}$. But then ${\mathcal {F}}\otimes {\mathcal {L}}$ would be perverse, semi-simple, arithmetic and Hard Lefschetz would fail for it. This contradicts Theorem 5.3. So $S_\circ$ is empty. This finishes the proof.

6 Jumping loci and generic vanishing

In this section we discuss further applications of our main Theorem 3.4.

6.1 Flat locus of the Fourier-Mellin transform and the cohomological jumping locus

Let X be a separated, connected scheme of finite type over the algebraically closed field F of characteristic different from $\ell$. Let E be a finite extension of ${\mathbb {Q}}_\ell$ with a fixed embedding $E\hookrightarrow \overline{{\mathbb {Q}}}_{\ell }$. Let $\pi$ be a finitely generated free ${\mathbb {Z}}_\ell$-module which is a quotient of $\pi _1^\mathrm{ab}(X)$. Set

$$\begin{aligned} R = {\mathcal {O}}_E\llbracket \pi \rrbracket , \quad {\mathfrak {R}}=R\otimes _{{\mathcal {O}}_E} \overline{{\mathbb {Q}}}_{\ell }\end{aligned}$$

and let ${\mathcal {G}}= {{\,\mathrm{Spf}\,}}({\mathcal {O}}_E \llbracket \pi \rrbracket )$ be the associated multiplicative formal Lie group. For ${\mathcal {F}}\in D^b_c(X,\overline{{\mathbb {Q}}}_{\ell })$ and $i,j\in {\mathbb {Z}}$ consider the subset

$$\begin{aligned} \Sigma ^i_\pi ({\mathcal {F}},j) := \{ {\mathcal {L}}\in {\mathcal {G}}(\overline{{\mathbb {Q}}}_{\ell }) \, | \, \mathrm{dim} \ H^i(X ,{\mathcal {F}}\otimes {\mathcal {L}}) > j \}. \end{aligned}$$

of ${\mathcal {G}}(\overline{{\mathbb {Q}}}_{\ell })$, where we omit the index $\pi$ if it is clear from the context. It is Zariski closed as one easily sees from combining Proposition 4.1 and [31, Thm. 7.6.9].

As $\pi \otimes _{{\mathbb {Z}}_\ell } {\mathbb {Q}}_\ell$ is dual to a subgroup of $H^1(X,{\mathbb {Q}}_\ell )$, it has a canonical weight filtration ([16, Sec. 2]). The weight zero part of $H^1(X,{\mathbb {Q}}_\ell )$ is equal to the kernel $H^1(X,{\mathbb {Q}}_\ell )\rightarrow H^1(X^\mathrm{reg},{\mathbb {Q}}_\ell )$, where $X^\mathrm{reg}$ is the regular locus of the reduced scheme $X_\mathrm{red}$.

Example 6.1

• (1) For X proper, integral and geometrically unibranch the group $H^1(X,{\mathbb {Q}}_\ell )$ is pure of weight one.

• (2) For $X\subset Y$ an open subscheme of a smooth variety Y over F with $H^1(Y,{\mathbb {Q}}_\ell )=0$ the cohomology group $H^1(X,{\mathbb {Q}}_\ell )$ is pure of weight two. Indeed,

  $$\begin{aligned} H^1(X,{\mathbb {Q}}_\ell ) \rightarrow H^2_{Y\setminus X}(Y,{\mathbb {Q}}_\ell ) = {\mathbb {Q}}_\ell (-1)^{\oplus b} \end{aligned}$$

  is injective and the group on the right side is pure of weight two, where b is the number of irreducible components of $Y{\setminus } X$ which are of codimension one. This holds for example for $X={\mathbb {G}}_m^d\subset Y={\mathbb {P}}^d_F$.

Theorem 6.2

Assume that $\pi$ is pure of weight different from zero. Let ${\mathcal {F}}\in D^b_c(X,\overline{{\mathbb {Q}}}_{\ell })$ be arithmetic.

• (1) Then $\Sigma ^i({\mathcal {F}},j)$ is quasi-linear for all $i,j\in {\mathbb {Z}}$.

• (2) The non-flat locus $S\subset {{\,\mathrm{Spm}\,}}({\mathfrak {R}}) ={\mathcal {G}}(\overline{{\mathbb {Q}}}_{\ell })$ of the ${\mathfrak {R}}$-module ${\mathfrak {FM}}^i(X,{\mathcal {F}})$ is quasi-linear.

Remark 6.3

Conjecturally, the theorem remains true if we only assume that $\pi$ is mixed of non-zero weights instead of pure. Indeed, for $\mathrm{ch}(F)=0$, this is true by [11, Thm. 1.5] and the general case would follow along the same lines from a “mixed version” of [5].

If ${\mathcal {F}}\in D^b_c(X,\overline{{\mathbb {Q}}}_{\ell })$ is not assumed to be arithmetic we can still conjecture the theorem to hold without the part that the translation is by torsion points $s_r\in {\mathcal {G}}(\overline{{\mathbb {Q}}}_{\ell })$ in the Definition 3.3 of quasi-linearity.

Remark 6.4

Results related to Theorem 6.2 for $\mathrm{ch}(F)=0$ have been extensively studied using complex analytic techniques, see [14, 28, Thm. 3.1,Cor. 6.4], [23, Thm. 3.1], [17, Sec. 11] and [3, Thm. 1.1]. For the torus $X={\mathbb {G}}_m^d$ part (1) of Theorem 6.2 proves part of a conjecture of Loeser [19, Intro. p.9] under our arithmeticity assumption.

Proof of Theorem 6.2

For simplicity of notation we stick to part (1), as part (2) is proved almost verbatim the same way. By the same technique as in the proof of Hard Lefschetz in Sect. 5, we can assume that F is the algebraic closure of a finite field $F_0$ and that the scheme X descends to a scheme $X_0$ of finite type over $F_0$. By the arithmeticity condition on ${\mathcal {F}}$, after replacing $F_0$ by a finite extension, for any $\sigma \in {\mathrm{Gal}}(F/F_0)$ we have ${\mathcal {F}}\simeq \sigma ({\mathcal {F}})\in D^b_c(X ,\overline{{\mathbb {Q}}}_{\ell })$. Without loss of generality we can assume that $\pi$ is the $\ell$-adic completion of $\pi _1^\mathrm{ab}(X)$ modulo torsion. Then ${\mathrm{Gal}}(F /F_0)$ acts on $\pi$. It follows that $\Sigma ^i({\mathcal {F}},j)$ is stabilized by any $\sigma \in {\mathrm{Gal}}(F/F_0)$ for $i,j\in {\mathbb {Z}}$. We claim that we can apply Theorem 3.4 with $\sigma \in {\mathrm{Gal}}(F /F_0)$ the Frobenius, to see that $\Sigma ^i({\mathcal {F}},j)$ is quasi-linear. For this we have to see that the Frobenius $\sigma$ acts semi-simply on $\pi \otimes {\mathbb {Q}}_\ell$.

We may assume that X has dimension $\ge 1$. Choose a regular closed subscheme $Y\hookrightarrow X$ of dimension one such that the composition $\pi _1(Y)\rightarrow \pi _1(X)\rightarrow \pi$ is surjective, for example by using [8, App. C]. By [26, Ann. II] the Albanese map $\pi _1(Y)\rightarrow T_\ell ( \mathrm{Alb}(Y))$ identifies $T_\ell ( \mathrm{Alb}(Y))$ with the $\ell$-adic completion of $\pi _1(Y)$ modulo the torsion subgroup. So $\pi \otimes _{{\mathbb {Z}}_\ell }{\mathbb {Q}}_\ell$ is isomorphic to a quotient of the torus part or of the abelian part of the Tate module $V_\ell ( \mathrm{Alb}(Y))$. By Tate [29, Thm. 2] the Frobenius action on the Tate module of an abelian variety is semi-simple. The Frobenius action on the Tate module of the torus is a scalar multiplication after replacing $F_0$ by a finite extension. This finishes the proof. $\square$

6.2 Generic vanishing

This section is motivated by [1, Thm. 1.1]. Except for the proof of Theorem 6.8, what we say is only an $\ell$-adic translation of loc.cit. The classical question on a lower bound for the codimension of the jumping loci $\Sigma ^i({\mathcal {F}},0)$ has been initiated by Green-Lazarsfeld for line bundles [14].

We consider a smooth projective variety X over the algebraically closed field F of characteristic different from $\ell$. As before $\pi$ is a free ${\mathbb {Z}}_\ell$-module quotient of $\pi _1^\mathrm{ab}(X )$. Our criterion on generic vanishing depends on properties of the tower of Galois coverings

$$\begin{aligned} \cdots \rightarrow X_{n+1} \rightarrow X_n \rightarrow \cdots \rightarrow X_0 =X \end{aligned}$$

with Galois groups $\mathrm{Gal}(X_n/X)=\pi /\ell ^n\pi$. We then write $X_\infty$ for this tower and $H^i(X_\infty ,{\mathbb {Z}}_\ell )$ for ${{\,\mathrm{colim}\,}}_n H^i(X_n , {\mathbb {Z}}_\ell )$. Let $\eta \in H^2(X , {\mathbb {Z}}_\ell )$ be a polarization, i.e. the first Chern class of an ample line bundle, where we omit Tate twists for simplicity of notation. We consider a situation in which $\eta$ becomes divisible in $H^2(X_\infty ,{\mathbb {Z}}_\ell )$. Note that a class $z\in H^i(X, {\mathbb {Z}}_\ell )$ becomes divisible in $H^i(X_\infty , {\mathbb {Z}}_\ell )$ if

$$\begin{aligned} \forall m, \exists n \ \text {such that} \ p_n^* ( z) \in \ell ^m H^i(X_n, {\mathbb {Z}}_\ell ) \subset H^i(X_n, {\mathbb {Z}}_\ell ), \end{aligned}$$

where $p_n :X_n\rightarrow X$ is the covering map.

We describe now two kinds of Examples 6.5 and 6.6.

Example 6.5

Let X be an abelian variety of dimension d with polarization $\eta$. Let V be a maximal isotropic subspace of the Tate module $T_\ell (X)\otimes _{{\mathbb {Z}}_\ell } {\mathbb {Q}}_\ell$ with respect to the Weil pairing associated to $\eta$, so $\dim _{{\mathbb {Q}}_\ell }(V)=d$. Note that $T_\ell (X)$ can be identified with the $\ell$-adic completion of $\pi _1^\mathrm{ab}(X)$. We set $\pi =T_\ell (X)/ T_\ell (X)\cap V$ which is a free ${\mathbb {Z}}_\ell$-module of rank d. Then $\eta$ becomes divisible in $H^2(X_\infty ,{\mathbb {Z}}_\ell )$ by [21, Thm. 23.3].

Example 6.6

Let $X=X^{(1)}\times \cdots \times X^{(d)}$ be a product of smooth proper curves with polarizations $\eta ^{(1)},\ldots , \eta ^{(d)}$ and let $X_\infty ^{(j)}\rightarrow X^{(j)}$ be towers with Galois group ${\mathbb {Z}}_\ell$. We consider the tower $X_n = X^{(1)}_n \times \cdots \times X^{(d)}_n$ and the polarization $\eta = \eta ^{(1)} +\cdots + \eta ^{(d)}$ of X. Then $\eta$ becomes divisible in $H^2(X_\infty ,{\mathbb {Z}}_\ell )$.

Remark 6.7

The tower in Example 6.6 is used in [2, Prop.4.5.1] to prove via [2, Cor.4.5.5] the purity theorem for the intermediate perverse extension in [2, Cor. 5.3.3].

Theorem 6.8

Let X be a smooth projective variety over the algebraically closed field F. Assume that ${\mathcal {F}}\in {}^p\! D^{\le 0}_c(X,\overline{{\mathbb {Q}}}_{\ell })$ is arithmetic and that the pullback to $H^2(X_\infty , {\mathbb {Z}}_\ell )$ of a polarization $\eta \in H^2(X , {\mathbb {Z}}_\ell )$ becomes divisible. Then

$$\begin{aligned} \mathrm{codim}_{{{\,\mathrm{Spm}\,}}({\mathfrak {R}} )}(\Sigma ^i({\mathcal {F}},0)) \ge i \end{aligned}$$

for all $i\ge 0$.

The proof of Theorem 6.8 is given at the end of this section. It uses Proposition 4.6, Theorems 5.4 and 6.2.

Corollary 6.9

For ${\mathcal {F}}\in {} ^{p}\! D^{\ge 0}_c(X,\overline{{\mathbb {Q}}}_{\ell })$ the Fourier-Mellin transform satisfies ${\mathfrak {FM}}^i(X,{\mathcal {F}})=0$ for $i<0$.

Proof

Using Proposition 4.1(4) on duality together with Remark 4.5, we see that

$$\begin{aligned} {\mathfrak {FM}}(X,{\mathcal {F}})' \simeq R\mathrm{Hom}_{{\mathfrak {R}}}({\mathfrak {FM}}(X,{\mathcal {F}}^\vee ) , {\mathfrak {R}}). \end{aligned}$$

We prove by descending induction on i that

$$\begin{aligned} \mathrm{codim}\big (\mathrm{supp} ( {\mathfrak {FM}}^i(X,{\mathcal {F}}^\vee ) )\big ) \ge i . \end{aligned}$$

(8)

In fact, Corollary 6.9 follows from (8) and the above duality by support estimates for dual complexes [1, Lem. 2.8].

For $i>\dim (X)$ we have ${\mathfrak {FM}}^i(X,{\mathcal {F}}^\vee )=0$ for cohomological dimension reasons that, i.e. $\mathrm{supp} ( {\mathfrak {FM}}^i(X,{\mathcal {F}}^\vee ) )$ is empty. This starts the induction. Now we fix $i>0$ and we assume that (8) is known in degrees bigger than i. From Proposition 4.1(2) and the Tor-spectral sequence we deduce that for $s\notin \mathrm{supp} ( {\mathfrak {FM}}^j(X,{\mathcal {F}}^\vee ))$ for all $j>i$, i.e. for s outside of a closed subset of codimension $\ge i+1$, we have

$$\begin{aligned} {\mathfrak {FM}}^i(X,{\mathcal {F}}^\vee )\otimes _{{\mathfrak {R}}} k(s) \cong H^i(X,{\mathcal {F}}^\vee \otimes {\mathcal {L}}_s ). \end{aligned}$$

The right hand side vanishes for s outside of a closed subset of codimension $\ge i$ by Theorem 6.8. This shows (8). $\square$

Corollary 6.10

Assume that X is an abelian variety and that $\pi =T_\ell (X)$. Let ${\mathcal {F}}\in {}^p\! D^{\le 0}_c(X,\overline{{\mathbb {Q}}}_{\ell })$ be arithmetic. Then

$$\begin{aligned} \mathrm{codim}_{{{\,\mathrm{Spm}\,}}({\mathfrak {R}} )}(\Sigma ^i({\mathcal {F}},0)) \ge 2i \end{aligned}$$

for all $i\ge 0$.

Proof

By Theorem 6.2 we know that up to a translation by a torsion character, which we can assume to be trivial in the following, each irreducible component S of $\Sigma ^i_\pi ({\mathcal {F}},0)$ corresponds to a free ${\mathbb {Z}}_\ell$-module quotient $\pi /\pi '$ of $\pi$. In particular, $\mathrm{codim}(S)=\mathrm{rank} (\pi ')$. Let $\pi ^\mathrm{half}$ be a quotient of $\pi =T_\ell (X)$ by an isotropic subgroup $V\cap \pi$ as in Example 6.5, where V is chosen such that $2\, \mathrm{rank} (\pi '\cap V)\ge \mathrm{rank} (\pi ')$. Clearly, $\mathrm{rank}(\pi ^\mathrm{half})= \dim (X)$. We have an exact sequence

$$\begin{aligned} 0\rightarrow V\cap \pi '\rightarrow \pi ' \rightarrow \mathrm{im}(\pi '\rightarrow \pi ^\mathrm{half})\rightarrow 0. \end{aligned}$$

So

$$\begin{aligned} \mathrm{rank}(\pi ')/2\ge \mathrm{rank} \left( \mathrm{im}(\pi '\rightarrow \pi ^\mathrm{half} ) \right) \ge \mathrm{codim} (\Sigma ^i_{\pi ^\mathrm{half}}({\mathcal {F}},0))\ge i. \end{aligned}$$

Here the right inequality follows from Theorem 6.8 applied to the setup of Example 6.5 where $X_\infty /X$ has automorphism group $\pi ^\mathrm{half}$. $\square$

Remark 6.11

One can expect the theorem and its corollaries to hold for non-arithmetic ${\mathcal {F}}$. In fact, for $\mathrm{ch}(F)=0$ this can be shown by essentially the same technique using that Hard Lefschetz is known in general [27, Lem.2.6] (and more generally [20, Cor.1.1]) and using [28, Thm. 3.1 (c)] instead of Theorem 3.4.

Remark 6.12

For $\mathrm{ch}(F)=0$ Corollary 6.10 is equivalent to  [25, Thm. 4.1] and [1, Thm. 1.3], who do not need the arithmeticity assumption, compare Remark 6.11, see also [17]. For $\mathrm{ch}(F)>0$, the inequality $\mathrm{codim}(\Sigma ^i({\mathcal {F}},0)) >0$ for $i> 0$ is shown in [30, Intro].

Remark 6.13

In case of Example 6.6, the theorem and its corollaries can be easily deduced from [10, Thm. 1.1], even for non-arithmetic ${\mathcal {F}}$. In fact in this situation we deduce from loc. cit. that Corollary 6.9 even holds integrally, i.e. for ${\mathcal {F}}\in {} ^p \!D^{\ge 0}_c(X,{\mathbb {F}}_\ell )$ we have $H^i(X, {\mathcal {F}}\otimes _{{\mathbb {F}}_\ell } {\mathcal {L}}_{{\mathbb {F}}_\ell \llbracket \pi \rrbracket } )=0$ for $i<0$. Bhatt–Schnell–Scholze ask [1, Rmk. 2.11] whether the analog of the latter integral result is true in the situation of Example 6.5.

In the proof of Theorem 6.8 the following lemma is crucial.

Lemma 6.14

Let $\pi '$ is a closed subgroup of $\pi$ with $\pi /\pi '$ torsion free. Let $X'_\infty \rightarrow X$ be the Galois tower of $\pi /\pi '$ and $r=\mathrm{rank} ( \pi ' )+1$. Then $\eta ^r$ becomes divisible in $H^{2r}(X'_\infty , {\mathbb {Z}}_\ell )$.

Proof

The lemma is equivalent to saying that for all $m>0$, the image of $\eta ^r$ in $H^{2r}(X'_\infty , {\mathbb {Z}}/\ell ^m)$ vanishes. The Hochschild-Serre spectral sequence of the covering $X_\infty \rightarrow X'_\infty$ yields a spectral sequence

$$\begin{aligned} E^{pq}_2 = H^p(\pi ', H^q(X_\infty , {\mathbb {Z}}/\ell ^m ) ) \Rightarrow H^{p+q}(X'_\infty , {\mathbb {Z}}/\ell ^m ), \end{aligned}$$

with associated filtration $F^* H^{p+q}(X'_\infty ),$ which is compatible with cup-product. As $\eta$ vanishes in

$$\begin{aligned} E_2^{0 2}\subset H^2(X_\infty ,{\mathbb {Z}}/\ell ^m ), \end{aligned}$$

the image of $\eta$ in $H^{2}(X'_\infty , {\mathbb {Z}}/\ell ^m)$ lies in $F^1 H^{2}(X'_\infty , {\mathbb {Z}}/\ell ^m)$. So the image of $\eta ^r$ lies in $F^r H^{2r}(X'_\infty , {\mathbb {Z}}/\ell ^m) .$ As $\mathrm{cd}_\ell (\pi ')=r-1$, $E^{pq}_2=0$ for $p>r-1$. Thus

$$\begin{aligned} F^r H^{2r}(X'_\infty , {\mathbb {Z}}/\ell ^m)=0 . \end{aligned}$$

This finishes the proof. $\square$

Proof of Theorem 6.8

If ${\mathcal {F}}_1 \rightarrow {\mathcal {F}}_2 \rightarrow {\mathcal {F}}_3 \rightarrow {\mathcal {F}}_1[1]$ is an exact triangle in $D^b_c(X,\overline{{\mathbb {Q}}}_{\ell })$ such that Theorem 6.8 holds for ${\mathcal {F}}={\mathcal {F}}_1$ and for ${\mathcal {F}}={\mathcal {F}}_3$ then it also holds for ${\mathcal {F}}_2$. By [2, Thm. 4.3.1] we can therefore assume that ${\mathcal {F}}$ is a simple perverse sheaf.

Assume that the theorem fails in some degree $i>0$. Let S be an irreducible component of $\Sigma ^i({\mathcal {F}},0)$ of codimension $<i$ in ${{\,\mathrm{Spm}\,}}({\mathcal {R}})={\mathcal {G}}(\overline{{\mathbb {Q}}}_{\ell })$. By Theorem 6.2(1) we see that S is the translation by a torsion point s of a closed subset of the form ${{\,\mathrm{Spm}\,}}({\mathfrak {R}}' )$, where ${\mathfrak {R}}' = {\mathbb {Z}}_\ell \llbracket \pi /\pi '\rrbracket \otimes _{{\mathbb {Z}}_\ell } \overline{{\mathbb {Q}}}_{\ell }$. Replacing ${\mathcal {F}}$ by ${\mathcal {F}}\otimes {\mathcal {L}}_s$ we can assume without loss of generality that $s=1$, i.e. $S= {{\,\mathrm{Spm}\,}}({\mathfrak {R}}')$.

In terms of the Fourier-Mellin transform we see that

$$\begin{aligned} {\mathfrak {FM}}_{\pi /\pi '}^i(X,{\mathcal {F}})\otimes _{{\mathfrak {R}}'} \mathrm{Frac}({{\mathfrak {R}}'}) \ne 0, \end{aligned}$$

(9)

because for a generic point $s\in {{\,\mathrm{Spm}\,}}({\mathfrak {R}}' )$ we have

$$\begin{aligned} {\mathfrak {FM}}_{\pi /\pi '}^i(X,{\mathcal {F}})\otimes _{{\mathfrak {R}}'} k(s)\cong H^i(X, {\mathcal {F}}\otimes {\mathcal {L}}_s ) \end{aligned}$$

by Proposition 4.1 and because the cohomology group on the right does not vanish.

By Theorem 5.4 and Lemma 4.2 we see that the Lefschetz map

$$\begin{aligned} {\mathfrak {FM}}_{\pi /\pi '}^{-i}(X,{\mathcal {F}}) \xrightarrow {\cup \eta ^i} {\mathfrak {FM}}_{\pi /\pi '}^i(X,{\mathcal {F}}) \end{aligned}$$

(10)

becomes an isomorphism when tensored with $\mathrm{Frac}({{\mathfrak {R}}'})$, so the map (10) is non-vanishing according to (9). But by Proposition 4.6 and Lemma 6.14 we see that the map (10) vanishes, since $\mathrm{rank}(\pi ')= \mathrm{codim}(S) <i$. This is a contradiction and finishes the proof. $\square$