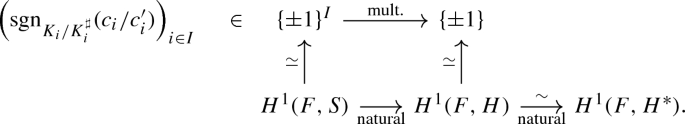Correction to: Stable conjugacy and epipelagic L-packets for Brylinski–Deligne covers of ${\text {Sp}}(2n)$

1 Correction to: Selecta Mathematica (2020) 26:12 https://doi.org/10.1007/s00029-020-0537-0

The computations of the toral invariants $f_{(G, S)}(\alpha )$ in Sect. 7.2 of the paper Stable conjugacy and epipelagic L-packets for Brylinski–Deligne covers of ${\text {Sp}}(2n)$ in Selecta Mathematica (N.S.), Vol. 26, (2020), no. 1 (ditto for the arXiv version) are flawed when the root $\alpha$ takes the form $\alpha = \epsilon _i \pm \epsilon _j$, in both the symplectic and the odd orthogonal case. The resulting $f_{(G, S)}(\alpha )$ can vary within a stable conjugacy class ${\mathcal {E}}$ of embeddings $j: S \hookrightarrow G$ of maximal tori. The main impacts of this mistake are listed below.

• The proof of Lemma 7.2.2 no longer works for general tori S. This lemma is used to prove the key Theorem 7.6.3 on the stability of epipelagic L-packets.

• Theorem 8.3.1 is directly built upon Sect. 7.2. Its aim is interpret the stable system (a notion of obstruction to stability, see Definition 7.3.3) constructed in Sect. 8.2 for $m \equiv 2 \pmod {4}$, as a ratio $\epsilon _j(\gamma ) / \epsilon _k(\gamma )$. This is used in Sect. 9.3 to show the compatibility with $\Theta$-lifting when $m=2$.

The goal here is to show that

• Lemma 7.2.2 still holds for a restricted class of maximal tori, which suffices for our purposes;

• Theorem 8.3.1 can be turned into a definition for the stable system when $m \equiv 2 \pmod {4}$, in order to force the results in Sect. 9.3 to be true. The new definition is more transparent.

The impacted results can thus be restored with reasonable modifications. Remarkably, this is a reversion to the strategy in an early draft of this work.

The author is grateful to Chuijia Wang for kindly pointing our these mistakes.

2 Correction to Lemma 7.2.2

One should assume in Lemma 7.2.2 that S is a maximal torus of type (ER) in $G = \mathrm {Sp}(W)$, as in Definition 6.1.1. This is all what one needs for the epipelagic supercuspidals studied in Sect. 7.3–7.6. The corrected arguments are given below.

Retain the notation in the original proof. The goal is to show $\epsilon _j(\gamma _0)$ depends only on the stable conjugacy class of $j: S \hookrightarrow G$ and $\gamma _0 \in S(F)_{p'}$. Given j, define the sign

$$\begin{aligned} E_j(S, G) = \prod _{\alpha \in R(G, jS)_{\mathrm {sym}}({\overline{F}}) / \Gamma _F} f_{G, jS}(\alpha ). \end{aligned}$$

Set $G_{j \gamma _0} := Z_G(j(\gamma _0))^\circ$. By [1, Lemma 4.12], which applies to S since it is of type (ER),

$$\begin{aligned} \epsilon _j(\gamma _0) = \prod _{\begin{array}{c} \alpha \in R(G, jS)_{\mathrm {sym}}({\overline{F}}) / \Gamma _F \\ \alpha (\gamma _0) \ne 1 \end{array}} f_{G, jS}(\gamma _0) = \frac{E_j(S, G)}{E_j(S, G_{j \gamma _0})}. \end{aligned}$$

(1)

Fix any additive character $\psi$ of F. Kottwitz’s formula [1, Corollary 4.11] gives

$$\begin{aligned} E_j(S, G) = \dfrac{e(G) \epsilon (X^*(S)_{{\mathbb {C}}} - X^*(T)_{{\mathbb {C}}}, \psi )}{\displaystyle \prod _{\alpha \in R(G, jS)_{\mathrm {sym}}({\overline{F}}) / \Gamma _F} \lambda _{F_\alpha / F_{\pm \alpha }}(\psi \circ \mathrm {Tr}_{F_\alpha / F_{\pm \alpha }}) }; \end{aligned}$$

(2)

• e(G) is the Kottwitz sign of G;

• T is a minimal Levi subgroup in the quasisplit inner form $G^*$ of G;

• $\epsilon (\cdots , \psi )$ is the $\epsilon$-factor with Langlands’ normalization associated with the virtual $\Gamma _F$-representation $X^*(S)_{{\mathbb {C}}} - X^*(T)_{{\mathbb {C}}}$ of degree zero;

• $F_\alpha /F_{\pm \alpha }$ are the quadratic extensions associated with symmetric roots $\alpha$, and $\lambda _{F_\alpha / F_{\pm \alpha }}(\cdots )$ are Langlands’ constants.

Formulas (1) and (2) apply to connected reductive F-groups in general. In particular, we have the formula for $E_j(S, G_{\gamma _0})$ by replacing T with a minimal Levi subgroup $T_j \subset G^*_{j\gamma _0}$. The denominator of (2) only depends on the stable conjugacy class of j.

Return to our setting that S is of type (ER) and $G = {\text {Sp}}(W)$. It remains to show that

$$\begin{aligned} e(G_{j\gamma _0}) \epsilon (X^*(S)_{{\mathbb {C}}} - X^*(T_j)_{{\mathbb {C}}}, \psi ) \end{aligned}$$

depends only on the stable conjugacy class of j.

Using Theorem 6.2.2 we know that $j\gamma _0$ can only have eigenvalues $\pm \,1$, with multiplicities $2n_\pm$ respectively. Hence

$$\begin{aligned} G_{j\gamma _0} = \mathrm {Sp}(W_+) \times \mathrm {Sp}(W_-) \end{aligned}$$

where $W_\pm \subset W$ are symplectic vector subspaces of dimension $2n_\pm$. The stable conjugacy class of j and $\gamma _0$ determine the isomorphism class of $G_{j\gamma _0}$, hence determines $e(G_{j\gamma _0})$ and $X^*(T_j)_{{\mathbb {C}}}$. The proof is now complete.

3 Correction to Section 8.2 and Theorem 8.3.1

The obscure construction in Sect. 8.2 should be abandoned. Theorem 8.3.1 should instead be turned into a definition for the stable system when $m \equiv 2 \pmod {4}$. Specifically, we shall define

$$\begin{aligned} \theta _j^\dagger (\gamma _0) := \frac{\epsilon _k(\gamma _0)}{\epsilon _j(\gamma _0)}, \end{aligned}$$

where $\gamma _0 \in S(F)_{p'}$. Then we put $\theta _j := \theta _j^\circ \theta _j^\dagger$ to obtain a stable system as in Theorem 8.2.6.

Let us recall the notation from Sect. 8.2 and 8.3 briefly.

• Fix an additive character $\psi$ of the non-Archimedean local field F. Fix a symplectic F-vector space $(W, \langle \cdot |\cdot \rangle$ to define $G = \mathrm {Sp}(W)$ and its m-fold BD-cover ${\tilde{G}}$.

• Consider an inducing datum $({\mathcal {E}}, S, \theta ^\flat )$ (Definition 7.3.1) and pick any $Y = Y_\psi \in {\mathfrak {s}}(F)$ as in (8.3).

• For each conjugacy class of embeddings $j: S \hookrightarrow G$ in ${\mathcal {E}}$, we plug Y into the moment map correspondence to produce $H = \mathrm {SO}(V,q)$ and the conjugacy class of embeddings $k: S \hookrightarrow H$.

This will guarantee the compatibility with $\Theta$-lifting of epipelagic representations [3] when $m = 2$. All the statements in Sect. 9.3 remain valid.

To achieve this, we must check the conditions SS.1–SS.3 in Definition 7.3.3, and show that $\theta _j^\dagger$ is independent of the choice of Y.

Suppose Y is chosen. We begin with SS.2. It cannot be reduced to $\dim W = 2$ like in the original arguments for Theorem 8.2.6. However, we can still

• parameterize j by a datum $(K, K^\sharp , \vec {c})$ with $K = \prod _{i \in I} K_i$ an étale F-algebra, $K^\sharp = \prod _{i \in I} K_i^\sharp$ the subalgebra fixed by an involution $\tau$, and $\vec {c} = (c_i)_{i \in I} \in K^\times$ with $\tau (\vec {c}) = -\vec {c}$;

• parameterize $jY \in j{\mathfrak {s}}(F)$ by $(K, K^\sharp , \vec {c}, \vec {y})$ where $\vec {y} = (y_i)_{i \in I} \in K^\times$ with $\tau (\vec {y}) = -\,\vec {y}$; the part $\vec {y}$ depends only on the stable conjugacy class of j.

This gives $S(F) \simeq \prod _{i \in I} K_i^1$ where $K_i^1$ is the norm-one subtorus of $K_i^\times$. A similar parameterization for conjugacy classes of maximal tori and their elements exists for H and its pure inner forms. See for example [2, Sect. 3.1].

By Theorem 6.2.2, $\gamma _0 = (\gamma _{0, i})_{i \in I} \in \{\pm \, 1\}^I$. Accordingly,

$$\begin{aligned} I = I_+ \sqcup I_-, \quad I_{\pm } := \{i \in I: \gamma _{0, i} = \pm \,1\}. \end{aligned}$$

The analysis of stable conjugacy in ${\tilde{G}}$ in the proof of Theorem 8.2.6 reduces SS.2 to the equality

$$\begin{aligned} \theta ^\dagger _{j'}(\gamma _0) = \theta ^\dagger _j(\gamma _0) \prod _{\begin{array}{c} i \in I \\ \gamma _{0,i} = -\,1 \end{array}} \mathrm {sgn}_{K_i/K_i^\sharp }\left( c_i / c'_i \right) \end{aligned}$$

(3)

for all $j, j' \in {\mathcal {E}}$, parameterized by $(K, K^\sharp , \vec {c})$ and $(K, K^\sharp , \vec {c}')$ respectively.

Denote by $k': S \hookrightarrow H' = \mathrm {SO}(V', q')$ the embedding arising from $j'$ by moment map correspondence. It is stably conjugate to k (possibly across pure inner forms). By definition of the moment map correspondence in Sect. 8.1, k (resp. $k'$) is parameterized by $(K, K^\sharp , \vec {c}\vec {y})$ (resp. $(K, K^\sharp , \vec {c}'\vec {y})$).

Let $V_\pm \subset V$ and $V'_\pm \subset V'$ are the quadratic subspaces on which $k\gamma _0$ and $k'\gamma _0$ act by $\pm \,1$, respectively. Note that $\dim V_+ = \dim V'_+$ (resp. $\dim V_- = \dim V'_-$) are odd (resp. even). We have

$$\begin{aligned} H_{k\gamma _0} \simeq {\text {SO}}(V_+) \times {\text {SO}}(V_-), \quad H'_{k' \gamma _0} \simeq {\text {SO}}(V'_+) \times {\text {SO}}(V'_-). \end{aligned}$$

Note that k and $k'$ are related by a pure inner twist from H to $H'$ coming from $H^1(F, S)$. In turn, this restricts to a pure inner twists from $H_{j\gamma _0}$ to $H'_{j'\gamma _0}$, and similarly on their ±-factors. The parameter of $kS_+$ in $kS = kS_+ \times kS_-$ is carved out from that of kS by $I_+ \subset I$. Ditto for $k'S_+$.

We have shown that $\epsilon _j(\gamma _0) = \epsilon _{j'}(\gamma _0)$, so (3) reduces into

$$\begin{aligned} \epsilon _{k'}(\gamma _0) = \epsilon _k(\gamma _0) \prod _{\begin{array}{c} i \in I \\ \gamma _{0,i} = -\,1 \end{array}} \mathrm {sgn}_{K_i/K_i^\sharp }\left( c_i / c'_i \right) . \end{aligned}$$

(4)

We shall prove it by Kottwitz’s formula. The Langlands constants are stably invariant and $T_k \simeq T'_{k'}$ since $(H_{k\gamma _0})^* = (H'_{k'\gamma _0})^*$. Thus (1) and (2) imply

$$\begin{aligned} \frac{\epsilon _{k'}(\gamma _0)}{\epsilon _k(\gamma _0)} = \frac{E_{k'}(S, H') / E_{k'}(S, H'_{k'\gamma _0})}{E_k(S, H) / E_k(S, H_{k\gamma _0})} = \frac{e(H')e(H_{k'\gamma _0})}{e(H)e(H_{k\gamma _0})} \end{aligned}$$

• 1. First, we claim that

  $$\begin{aligned} \frac{e(H')}{e(H)} = \prod _{i \in I} \mathrm {sgn}_{K_i/K_i^\sharp }(c_i/c'_i). \end{aligned}$$

  Indeed, e(H) is computed by the diagonal arrow below.

  

  where $Z = {\text {ker}}[H^*_{\text {SC}} \rightarrow H^*]$, and $\rho$ is induced by the half-sum of positive roots. The diagonal arrow is non-trivial since there does exist a pure inner form $H^{**}$ of $H^*$ with $e(H^{**}) = -\,1$. Hence the bottom arrow is the identity map.

  The pure inner twist from H to $H'$ in question comes from

  

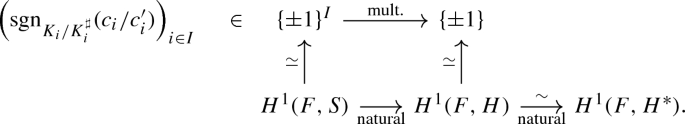
  The claim follows.

• 2. Since $\dim V_+ = \dim V'_+$ is odd, the same arguments yield

  $$\begin{aligned} \frac{e({\text {SO}}(V'_+))}{e({\text {SO}}(V_+))} = \prod _{i \in I_+} \mathrm {sgn}_{K_i/K_i^\sharp }(c_i/c'_i). \end{aligned}$$

• 3. To establish (4), it suffices to show $e({\text {SO}}(V'_-)) = e({\text {SO}}(V_-))$. Apart from the trivial case $\dim V_- = 2$, there are exactly two pure inner forms of ${\text {SO}}(V_-)$: the other one arises from a quadratic vector space $V_{-, \diamond }$ with the same dimension and discriminant, but opposite Hasse invariant. Denote by $V^{\mathrm {an}}_-$ and $V^{\mathrm {an}}_{-,\diamond }$ their anisotropic kernels. It is known that

  $$\begin{aligned} \{ \dim V^{\mathrm {an}}_-, \dim V^{\mathrm {an}}_{-, \diamond } \} = \{0, 4\} \;\text {or}\; \{2\}. \end{aligned}$$

  In either case, the split ranks of ${\text {SO}}(V_-)$ and ${\text {SO}}(V_{-,\diamond })$ have the same parity, hence $e({\text {SO}}(V_-)) = e({\text {SO}}(V_{-,\diamond }))$. This establishes SS.2.

For SS.1, one has $\theta _j = \theta _j^\circ \theta _j^\dagger$ by construction. Rescaling $\psi$ or $\langle \cdot |\cdot \rangle$ by some $a \in F^\times$ amounts to a similar rescaling of Y. This amounts to rescale the $q\langle Y \rangle$ in Remark 8.1.2 by a. This also amounts to replacing the parameter $(K, K^\sharp , \vec {c})$ (see Sect. 3.1) of j by $(K, K^\sharp , a\vec {c})$, corresponding to some $j' \in {\mathcal {E}}$. The required sign-change is already predicated by SS.2.

Now consider SS.3. Following the proof of Theorem 8.2.6, one should show that $\theta ^\dagger _j$ depends only on the pro-p part of the datum $\theta ^\flat$. Granting this fact, one shows $\theta _j^\dagger = \theta _{{\text {Ad}}(w)j}^\dagger$ for any $w \in \Omega (G,jS)(F)$ by repeating the original arguments.

To prove this, assume for convenience that the $a(\psi )$ in (8.2) is zero. The only ambiguity is that $Y \in {\mathfrak {s}}(F)_{-1/e}$ can be replaced by any $Y' \in Y + {\mathfrak {s}}(F)_0$. Consider the parameter $\vec {y}' = (y'_i)_{i \in I}$ of $jY'$. Then

$$\begin{aligned} \frac{y'_i}{y_i} - 1 \; \text {is topologically nilpotent in}\; K_i^\sharp \end{aligned}$$

for all $i \in I$. Since we assumed $p \ne 2$ from Sect. 7.3 onward, the group of 1 + topological nilpotents is 2-divisible in $(K_i^\sharp )^\times$, hence $\mathrm {sgn}_{K_i/K_i^\sharp } = 1$ on them. The resulting $k: S \hookrightarrow H$, etc. are thus unaltered up to conjugacy.

The above also shows that $\theta ^\dagger _j(\gamma _0)$ depends only on the pro-p part of $\theta ^\flat$ determined by Y, not on Y itself.