Stochastic modelling of operational quality of k-out-of-n systems

Abstract

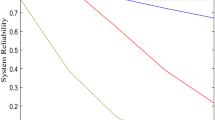
In this paper, we study some operational quality measures of the k-out-of-n systems. Performance of these systems is characterized by a quality (output) function that is decreasing in the absence of components’ failures. Moreover, it decreases (downward jump) with each failure of a component in a system as well. We employ the point processes approach for description of the corresponding failure process and derivation of the main results. Expectations (unconditional and conditional on survival) and variability for the system’s quality function are derived and analyzed. The corresponding ‘future quality process’ is defined and described. Some illustrative examples are presented.

Appendix

1.1 Proof of Lemma 1

Let $s_{0} \equiv 0$, $s_{m + 1} \equiv t$, $\Delta t_{0} \equiv 0$, and $\Delta t_{j}$ is infinitesimally small so that $s_{j} + \Delta t_{j} < s_{j + 1}$, $j = 1,2, \ldots ,m$. Then, using the notion of stochastic intensity,

$$\begin{aligned} P(s_{j} \le S_{j} \le s_{j} + \Delta t_{j} ,j = 1, \ldots ,m,N(t) = m) = P(\{ {\text{No}}\,\,{\text{events}}\,\,{\text{in}}\,\,(s_{j - 1} + \Delta t_{j - 1} ,s_{j} ),\,\,1\,\,{\text{event}}\,\,{\text{in}}\,[s_{j} ,\,s_{j} + \Delta t_{j} ]\} ,j = 1,2, \ldots ,m,\, \hfill \\ \quad \quad {\text{no}}\,\,{\text{events}}{\kern 1pt} \,\,{\text{in}}\,\,(s_{m} + \Delta t_{m} ,t))\, \hfill \\ \quad \quad = \left[ {\exp \{ - \varLambda_{0} (0,s_{1} )\} (\lambda_{0} (s_{1} )\Delta t_{1} + o(\Delta t_{1} ))} \right. \times \exp \{ - \varLambda_{1} (s_{1} + \Delta t_{1} ,s{}_{2})\} (\lambda_{1} (s_{2} |s_{1} )\Delta t_{2} + o(\Delta t_{2} )) \times \cdots \hfill \\ \quad \quad \quad \times \exp \{ - \varLambda_{m - 1} (s_{m - 1} + \Delta t_{m - 1} ,s_{m} )\} (\lambda_{m - 1} (s_{m} |s_{1} ,s_{2} , \ldots ,s_{m - 1} )\Delta t_{m} + o(\Delta t_{m} ))\left. {\exp \{ - \varLambda_{m} (s_{m} + \Delta t_{m} ,t)\} } \right] \hfill \\ \quad \quad = \prod\limits_{j = 0}^{m} {\left( {\lambda_{j} (s_{j + 1} |s_{1} ,s_{2} , \ldots ,s_{j} )\Delta t_{j + 1} + o(\Delta t_{j + 1} )} \right)} \cdot \exp \left\{ { - \sum\limits_{j = 0}^{m} {\varLambda_{j} (s_{j} + \Delta t_{j} ,s_{j + 1} )} } \right\}. \hfill \\ \end{aligned}$$

Denote by $f_{{S_{1} ,S_{2} , \ldots ,S_{N(t)} ,N(t)}} (s_{1} ,s_{2} , \ldots ,s_{m} ,m)$ the joint distribution of $(S_{1} = s_{1} ,S_{2} = s_{2} , \ldots ,S_{m} = s_{m} ,N(t) = m)$. Then

$$\begin{aligned} f_{{S_{1} ,S_{2} , \ldots ,S_{N(t)} ,N(t)}} (s_{1} ,s_{2} , \ldots ,s_{m} ,m) = \lim_{{\Delta t_{j} \to 0,j = 1,2, \ldots ,m}} \frac{{P(s_{j} \le S_{j} \le s_{j} + \Delta t_{j} ,j = 1, \ldots ,m,N(t) = m)}}{{\left( {\prod\nolimits_{j = 1}^{m} {\Delta t_{j} } } \right)}} \hfill \\ \quad = \left[ {\prod\limits_{j = 0}^{m - 1} {\lambda_{j} } (s_{j + 1} |s_{1} ,s_{2} , \ldots ,s_{j} )\exp \{ - \varLambda_{j} (s_{j} ,s_{j + 1} )\} } \right] \cdot \exp \{ - \varLambda_{m} (s_{m} ,t)\} ,\quad 0 \le s_{1} \le s_{2} \le \cdots \le s_{m} \le t,\quad m = 1,2, \ldots ,n - k. \hfill \\ \end{aligned}$$

1.2 Proof of Theorem 4

Denote by $\{ s_{1} ,s_{2} , \ldots ,s_{n(s)} ,n(s)\}$ the realization of $\{ S_{1} ,S_{2} , \ldots ,S_{N(s)} ,N(s)\}$. By definition,

$$\begin{aligned} Q_{E} & (t|\{ s_{1} ,s_{2} , \ldots ,s_{n(s)} ,n(s)\} ,T > s) = E[\tilde{Q}(s + t)I(s + t)|\{ s_{1} ,s_{2} , \ldots ,s_{n(s)} ,n(s)\} ,T > s] \hfill \\ & = E\left[ {Q(s + t)\prod\limits_{i = 1}^{n(s)} {\exp \{ - \psi_{i} (s_{i} )\} } \prod\limits_{j = N(s) + 1}^{N(s + t)} {\exp \{ - \psi_{j} (S_{j} )\} } \cdot I(s + t)|\{ s_{1} ,s_{2} , \ldots ,s_{n(s)} ,n(s)\} ,T > s} \right] \hfill \\ & = Q(s + t)\prod\limits_{i = 1}^{n(s)} {\exp \{ - \psi_{i} (s_{i} )\} } E\left[ {\prod\limits_{j = N(s) + 1}^{N(s + t)} {\exp \{ - \psi_{j} (S_{j} )\} } \cdot I(s + t)|\{ t_{1} ,t_{2} , \ldots ,t_{n(s)} ,n(s)\} } \right] \hfill \\ & = Q(s + t)\prod\limits_{i = 1}^{n(s)} {\exp \{ - \psi_{i} (s_{i} )\} } E\left[ {\prod\limits_{j = 1}^{{N_{s} (t)}} {\exp \{ - \psi_{n(s) + j} (s + S_{j}^{*} )\} } \cdot I(s + t)|\{ t_{1} ,t_{2} , \ldots ,t_{n(s)} ,n(s)\} } \right], \hfill \\ \end{aligned}$$

where $n(s) \le n - k$, $N_{s} (t) = N(s + t) - N(s)$, $S_{j}^{*}$ is the time from $s$ to the $j$ th component’s failure occurred in $(s,s + t]$, $j = 1,2, \ldots ,N_{s} (t)$. Note that, given $\{ s_{1} ,s_{2} , \ldots ,s_{n(s)} ,n(s)\}$, at time $s$ the system is the $k$-out-of $n - n(s)$ system with the common components failure rate $\lambda (s + u)$, $u \ge 0$. Thus, applying similar procedure as that in the proof of Theorem 1,

$$\begin{aligned} & E \left[ {\prod\limits_{j = 1}^{{N_{s} (t)}} {\exp \{ - \psi_{n(s) + j} (s + S_{j}^{*} )\} } \cdot I(s + t)|\{ t_{1} ,t_{2} , \ldots ,t_{n(s)} ,n(s)\} } \right] \hfill \\ & \quad = \exp \{ - (n - n(s))\varLambda_{s} (t)\} + \sum\limits_{m = 1}^{n - n(s) - k} {\int\limits_{0}^{t} {\int\limits_{0}^{{v_{m} }} \cdots } } \int\limits_{0}^{{v_{2} }} {\prod\limits_{i = 1}^{m} {\exp \{ - \psi_{n(s) + i} (s + v_{i} )\} } } \hfill \\ & \quad \;\; \times \left[ {\prod\limits_{j = 0}^{m - 1} {\lambda_{sj} } (v_{j + 1} |v_{1} ,v_{2} , \ldots ,v_{j} )\exp \{ - \varLambda_{sj} (v_{j} ,v_{j + 1} )\} } \right] \cdot \exp \{ - \varLambda_{sm} (v_{m} ,t)\} dv_{1} dv_{2} \ldots dv_{m} , \hfill \\ \end{aligned}$$

where $\varLambda_{s} (t) = \int_{0}^{t} {\lambda (s + w)} dw$, $\lambda_{sj} (t|v_{1} ,v_{2} , \ldots ,v_{j} ) = (n - n(s) - j)\lambda (s + t)$, $j = 0,1,2, \ldots ,n - n(s) - k$, $\varLambda_{sj} (u_{1} ,u_{2} ) = \int_{{u_{1} }}^{{u_{2} }} {\lambda_{sj} (w|v_{1} ,v_{2} , \ldots ,v_{j} )} dw$.

Observe that

$$\begin{aligned} & Q_{E} (t|\{ s_{1} ,s_{2} , \ldots ,s_{n(s)} ,n(s)\} ,T > s) = E[\tilde{Q}(s + t)I(s + t)|\{ s_{1} ,s_{2} , \ldots ,s_{n(s)} ,n(s)\} ,T > s] \hfill \\ & = E[\tilde{Q}(s + t)I(s + t)|\{ s_{1} ,s_{2} , \ldots ,s_{n(s)} ,n(s)\} ,T > s,T > s + t]P(T > s + t|\{ s_{1} ,s_{2} , \ldots ,s_{n(s)} ,n(s)\} ,T > s) \hfill & \\ + E[\tilde{Q}(s + t)I(s + t)|\{ s_{1} ,s_{2} , \ldots ,s_{n(s)} ,n(s)\} ,T > s,T \le s + t]P(T \le s + t|\{ s_{1} ,s_{2} , \ldots ,s_{n(s)} ,n(s)\} ,T > s) \hfill & \\ = E[\tilde{Q}(s + t)I(s + t)|\{ s_{1} ,s_{2} , \ldots ,s_{n(s)} ,n(s)\} ,T > s + t]P(T > s + t|\{ s_{1} ,s_{2} , \ldots ,s_{n(s)} ,n(s)\} ,T > s) \hfill & \\ = Q_{ES} (t|\{ t_{1} ,t_{2} , \ldots ,t_{n(s)} ,n(s)\} ,T > s)P(T > s + t|\{ s_{1} ,s_{2} , \ldots ,s_{n(s)} ,n(s)\} ). \hfill \\ \end{aligned}$$

Again, given $\{ s_{1} ,s_{2} , \ldots ,s_{n(s)} ,n(s)\}$ at time $s$, the system is the $k$-out-of $n - n(s)$ system with the common components failure rate $\lambda (s + u)$, $u \ge 0$. Thus,

$$P(T > s + t|\{ s_{1} ,s_{2} , \ldots ,s_{n(s)} ,n(s)\} ) = \sum\limits_{l = k}^{n - n(s)} {} \left( {\begin{array}{*{20}c} {n - n(s)} \\ l \\ \end{array} } \right)(\exp \{ - \varLambda_{s} (t)\} )^{l} (1 - \exp \{ - \varLambda_{s} (t)\} )^{n - n(s) - l} ,$$

and

$$Q_{ES} (t|\{ t_{1} ,t_{2} , \ldots ,t_{n(s)} ,n(s)\} ,T > s) = \frac{{Q_{E} (t|\{ s_{1} ,s_{2} , \ldots ,s_{n(s)} ,n(s)\} ,T > s)}}{{P(T > s + t|\{ s_{1} ,s_{2} , \ldots ,s_{n(s)} ,n(s)\} )}}.$$

1.3 Proof of Theorem 5

Observe that

$$\begin{aligned} Q_{E} (t|T > s) & = E[\tilde{Q}(s + t)I(s + t)|T > s] \hfill \\ & = E_{{(\{ S_{1} ,S_{2} , \ldots ,S_{N(s)} ,N(s)\} |T > s)}} [E[\tilde{Q}(s + t)I(s + t)|\{ S_{1} ,S_{2} , \ldots ,S_{N(s)} ,N(s)\} ,T > s]], \hfill \\ \end{aligned}$$

where $E_{{(\{ S_{1} ,S_{2} , \ldots ,S_{N(s)} ,N(s)\} |T > s)}} [ \cdot ]$ stands for the expectation with respect to the conditional joint distribution $(\{ S_{1} ,S_{2} , \ldots ,S_{N(s)} ,N(s)\} |T > s)$. From Theorem 4

$$\begin{aligned} & E[\tilde{Q}(s + t)I(s + t)|\{ T_{1} ,T_{2} , \ldots ,T_{N(s)} ,N(s)\} ,T > s] \hfill \\ & = Q(s + t)\prod\limits_{i = 1}^{n(s)} {\exp \{ - \psi (s_{i} )\} } \times \left\{ {\exp \{ - (n - n(s))\varLambda_{s} (t)\} } \right. \hfill \\ & \quad + \sum\limits_{m = 1}^{n - n(s) - k} {\int\limits_{0}^{t} {\int\limits_{0}^{{v_{m} }} \cdots } } \int\limits_{0}^{{v_{2} }} {\prod\limits_{i = 1}^{m} {\exp \{ - \psi_{n(s) + i} (s + v_{i} )\} } } \hfill \\ & \;\; \times \left. {\left[ {\prod\limits_{j = 0}^{m - 1} {\lambda_{sj} } (v_{j + 1} |v_{1} ,v_{2} , \ldots ,v_{j} )\exp \{ - \varLambda_{sj} (v_{j} ,v_{j + 1} )\} } \right] \cdot \exp \{ - \varLambda_{sm} (v_{m} ,t)\} dv_{1} dv_{2} \ldots dv_{m} } \right\}, \hfill \\ \end{aligned}$$

and the conditional joint distribution $(\{ S_{1} ,S_{2} , \ldots ,S_{N(s)} ,N(s)\} |T > s)$ is given by

$$\begin{aligned} & \frac{1}{P(T > s)}\left[ {\prod\limits_{j = 0}^{m - 1} {\lambda_{j} } (s_{j + 1} |s_{1} ,s_{2} , \ldots ,s_{j} )\exp \{ - \varLambda_{j} (s_{j} ,s_{j + 1} )\} } \right] \cdot \exp \{ - \varLambda_{m} (s_{m} ,t)\} \hfill \\ & \quad 0 \le s_{1} \le s_{2} \le \cdots \le s_{m} \le s,m = 1,2, \ldots ,n - k. \hfill \\ \end{aligned}$$

Let

$$\begin{aligned} \varPhi (r) & \equiv \left\{ {\exp \{ - (n - r)\varLambda_{s} (t)\} + \sum\limits_{m = 1}^{n - r - k} {\int\limits_{0}^{t} {\int\limits_{0}^{{v_{m} }} \cdots } } \int\limits_{0}^{{v_{2} }} {\prod\limits_{i = 1}^{m} {\exp \{ - \psi_{r + i} (s + v_{i} )\} } } } \right. \hfill \\ & \quad \left. { \times \left[ {\prod\limits_{j = 0}^{m - 1} {\lambda_{sj} } (v_{j + 1} |v_{1} ,v_{2} , \ldots ,v_{j} )\exp \{ - \varLambda_{sj} (v_{j} ,v_{j + 1} )\} } \right] \cdot \exp \{ - \varLambda_{sm} (v_{m} ,t)\} dv_{1} dv_{2} \ldots dv_{m} } \right\}. \hfill \\ \end{aligned}$$

Then

$$\begin{aligned} Q_{E} (t|T > s) & = \frac{{\exp \{ - n\varLambda (s)\} }}{{\sum\nolimits_{l = k}^{n} {\left( {\begin{array}{*{20}c} n \\ l \\ \end{array} } \right)} (\exp \{ - \varLambda (s)\} )^{l} (1 - \exp \{ - \varLambda (s)\} )^{n - l} }}Q(s + t)\varPhi (0) \hfill \\ & \; + \frac{Q(s + t)}{{\sum\nolimits_{l = k}^{n} {\left( {\begin{array}{*{20}c} n \\ l \\ \end{array} } \right)} (\exp \{ - \varLambda (s)\} )^{l} (1 - \exp \{ - \varLambda (s)\} )^{n - l} }} \hfill \\ & \times \sum\limits_{r = 1}^{n - k} {\int\limits_{0}^{s} {\int\limits_{0}^{{s_{r} }} \cdots \int\limits_{0}^{{s_{2} }} {\left[ {\prod\limits_{i = 1}^{r} {\exp \{ - \psi (s_{i} )\} } } \right]\varPhi (r)} } } \hfill \\ & \times \left[ {\prod\limits_{j = 0}^{r - 1} {\lambda_{j} } (s_{j + 1} |s_{1} ,s_{2} , \ldots ,s_{j} )\exp \{ - \varLambda_{j} (s_{j} ,s_{j + 1} )\} } \right] \cdot \exp \{ - \varLambda_{r} (s_{r} ,t)\} ds_{1} \ldots ds_{r - 1} ds_{r} . \hfill \\ \end{aligned}$$

On the other hand, by definition, $Q_{ES} (t|T > s) = E[\tilde{Q}(s + t)|T > s + t] = Q_{ES} (s + t)$