Abstract
In this work, we establish a categorification of the classical Dold-Kan correspondence in the form of an equivalence between suitably defined \(\infty \)-categories of simplicial stable \(\infty \)-categories and connective chain complexes of stable \(\infty \)-categories. The result may be regarded as a contribution to the foundations of an emerging subject that could be termed categorified homological algebra.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
A central tool in classical homological algebra is the construction of a chain complex from a simplicial abelian group via the formula
The fact that a large number of interesting complexes arise via this procedure is not a coincidence—the classical Dold-Kan correspondence [6, 10] states that the passage to normalized chains establishes an equivalence of categories:
Theorem
(Dold, Kan). The normalized chains functor \({\text {C}}\) provides an equivalence
between the category \({\text {Ab}}_{\Delta }\) of simplicial abelian groups and the category \({\text {Ch}}_{\ge 0}({\text {Ab}})\) of connective chain complexes with inverse given explicitly by the Dold-Kan nerve \({\text {N}}\).
In this work, we establish a categorification of the classical Dold-Kan correspondence where the category \({\text {Ab}}\) of abelian groups gets replaced by the \((\infty ,2)\)-category \(\mathcal {S}t\) of stable \(\infty \)-categories.
Theorem
The categorified normalized chains functor \(\mathcal {C}\) furnishes an equivalence

between the  of 2-simplicial stable \(\infty \)-categories and the \(\infty \)-category \({\text {Ch}}_{\ge 0}(\mathcal {S}t)\) of connective chain complexes of stable \(\infty \)-categories with explicit inverse given by the categorified Dold-Kan nerve \(\mathcal {N}\).
of 2-simplicial stable \(\infty \)-categories and the \(\infty \)-category \({\text {Ch}}_{\ge 0}(\mathcal {S}t)\) of connective chain complexes of stable \(\infty \)-categories with explicit inverse given by the categorified Dold-Kan nerve \(\mathcal {N}\).
We refer the reader to Sects. 3.1 and 3.2 for an explication of the terminology and a precise statement of the theorem. A key ingredient of the proof is an explicit construction of the categorified Dold-Kan nerve \(\mathcal {N}\). Its classical counterpart \({\text {N}}\) associates to a chain complex \(B_{\bullet }\) of abelian groups the simplicial abelian group \({\text {N}}(B_{\bullet })\) which can be described as follows: the group of n-simplices is given by collections \(\{x_{\sigma }\}\), parametrized by monotone maps \(\sigma : [k] \hookrightarrow [n]\), of elements \(x_{\sigma } \in B_{k}\) subject to the equations
Example
A 2-simplex in \({\text {N}}(B_{\bullet })\) consists of
-
elements \(x_{012} \in B_2\), \(x_{01},x_{02},x_{12} \in B_1\), and \(x_{0},x_{1},x_{2} \in B_{0}\),
-
satisfying the equations
-
(1)
\(d(x_{012}) = x_{12} - x_{02} + x_{01}\),
-
(2)
\(d(x_{ij}) = x_{j} - x_{i}\).
-
(1)
As a foretaste, we provide an informal description of the data comprising a 2-simplex in the categorified Dold-Kan nerve \(\mathcal {N}(\mathcal {B}_{\bullet })\) associated to a complex
of stable \(\infty \)-categories:
-
objects \(X_{012} \in \mathcal {B}_2\), \(X_{01},X_{02},X_{12} \in \mathcal {B}_1\), and \(X_0,X_1,X_2 \in \mathcal {B}_0\),
-
a chain of morphisms \(X_{0} \rightarrow X_{1} \rightarrow X_{2}\) in \(\mathcal {B}_0\),
-
a 3-term complex
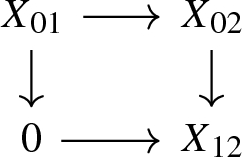
in \(\mathcal {B}_1\),
-
together with coherent data that exhibits
-
(1)
\(d(X_{012})\) as the totalization of the complex \(X_{01} \rightarrow X_{02} \rightarrow X_{12}\),
-
(2)
\(d(X_{ij})\) as the cofiber of \(X_{i} \rightarrow X_{j}\).
-
(1)
Note that the data of a 2-simplex in \(\mathcal {N}(\mathcal {B}_{\bullet })\) defines, upon passage to classes in the respective Grothendieck groups, a 2-simplex in \({\text {N}}(K_0(\mathcal {B}_{\bullet }))\). This observation generalizes to simplices in all dimensions and is a justification for the use of the term categorification.
The categorified Dold-Kan nerve \(\mathcal {N}\) unifies various known constructions from algebraic K-theory:
-
(I)
Let \(\mathcal {B}\) be a stable \(\infty \)-category and let \(\mathcal {B}[1]\) denote the chain complex
$$\begin{aligned} 0 \longleftarrow \mathcal {B}\longleftarrow 0 \longleftarrow 0 \longleftarrow \dots \end{aligned}$$concentrated in degree 1. Then \(\mathcal {N}(\mathcal {B}[1])\) is an \(\infty \)-categorical version of Waldhausen’s \(S_{\bullet }\)-construction (cf. [17]). Waldhausen’s \(S_{\bullet }\)-construction is usually considered as a simplicial object in the category \({\text {Cat}}\) (or \({\text {Cat}}_{\infty }\)). While the additional 2-functoriality present in our treatment does not seem to appear explicitly in the literature, it does feature implicitly, yet crucially, in Waldhausen’s proof of the additivity theorem [17] and its modification for stable \(\infty \)-categories presented in [15]. This observation will be explored in detail elsewhere.
-
(II)
Let \(f:\mathcal {B}_1 \rightarrow \mathcal {B}_0\) be an exact functor of stable \(\infty \)-categories. Then applying \(\mathcal {N}\) to the complex
$$\begin{aligned} \mathcal {B}_{0} \overset{f}{\longleftarrow } \mathcal {B}_{1} \longleftarrow 0 \longleftarrow 0 \longleftarrow \dots \end{aligned}$$concentrated in degrees \(\{0,1\}\) yields an \(\infty \)-categorical version of Waldhausen’s relative \(S_{\bullet }\)-construction. Besides its appearance in Waldhausen’s own work, this construction also features prominently in [5] where it provides a local description of perverse schobers (cf. [11]).
-
(III)
Let \(\mathcal {B}\) be a stable \(\infty \)-category and let \(\mathcal {B}[2]\) denote the chain complex
$$\begin{aligned} 0 \longleftarrow 0 \longleftarrow \mathcal {B}\longleftarrow 0 \longleftarrow \dots \end{aligned}$$concentrated in degree 2. Then \(\mathcal {N}(\mathcal {B}[2])\) is an \(\infty \)-categorical version of Hesselholt-Madsen’s \(S^{2,1}_{\bullet }\)-construction. As explained in [8], a duality on the category \(\mathcal {B}\) furnishes \(\mathcal {N}(\mathcal {B}[2])\) with the structure of a real object which can then be utilized to upgrade the K-theory spectrum of \(\mathcal {B}\) to a genuine \(\mathbb {Z}/(2)\)-equivariant spectrum.
-
(IV)
Let \(\mathcal {B}\) be a stable \(\infty \)-category and let \(\mathcal {B}[k]\) denote the chain complex with \(\mathcal {B}\) concentrated in degree k. Then \(\mathcal {N}(\mathcal {B}[k])\) is an \(\infty \)-categorical version of the k-dimensional \(S^{\langle k \rangle }_{\bullet }\)-construction introduced for abelian categories in [16]. These higher-dimensional Waldhausen constructions have an interesting interpretation in the context of higher algebraic K-theory: Let us denote by \(\mathcal {A}^{\simeq }\) the Kan complex obtained from an \(\infty \)-category \(\mathcal {A}\) by discarding noninvertible morphisms. Then, for every \(k \ge 1\), there is a canonical weak equivalence of spaces
$$\begin{aligned} \Omega ^k |\mathcal {N}(\mathcal {B}[k])^{\simeq }| \simeq K(\mathcal {B}) \end{aligned}$$(1.1)which exhibits \(|\mathcal {N}(\mathcal {B}[k])^{\simeq }|\) as a k-fold delooping of the K-theory space of \(\mathcal {B}\). In fact, the sequence of spaces \(\{|\mathcal {N}(\mathcal {B}[k])^{\simeq }|\}_{k \ge 1}\) can be augmented to a spectrum which models the connective algebraic K-theory spectrum of \(\mathcal {B}\). Interpreting the simplicial object \(\mathcal {N}(\mathcal {B}([k]))\) as a categorification of the Eilenberg-MacLane space \({\text {N}}(B[k])\), we observe that (1.1) may be regarded as a categorification of the description of the Eilenberg-MacLane spectrum associated to an abelian group B in terms of the sequence \(\{{\text {N}}(B[k])\}_{k \ge 1}\). A more detailed study of the \(S^{\langle k \rangle }_{\bullet }\)-constructions in the context of stable \(\infty \)-categories are the subject of [3] where we explore relations to higher Auslander-Reiten theory as introduced by Iyama [9].
The kth cohomology group of a topological space X with coefficients in an abelian group B can be described as homotopy classes of maps from X to K(B, k). The interpretation of the 2-simplicial stable \(\infty \)-category \(\mathcal {N}(\mathcal {B}[k])\) as a categorified Eilenberg-MacLane space predicts the existence of a categorified notion of cohomology. This circle of ideas will be explored in future work with a view towards applications to topological Fukaya categories. For \(k=1\), the results of [4, 7] can be interpreted as describing the topological Fukaya category of a marked Riemann surface as a categorified relative 1st cohomology group.
2 The classical Dold-Kan correspondence
Let \({\text {Ab}}\) denote the category of abelian groups. The Dold-Kan correspondence establishes an equivalence between the category \({\text {Ab}}_{\Delta }\) of simplicial abelian groups and the category \({\text {Ch}}_{\ge 0}({\text {Ab}})\) of connective chain complexes of abelian groups. We present a particular proof of this result which is designed so that the proof of our main result, provided in Sect. 3, can be regarded as a step-by-step categorification of the arguments involved.
Let \(A_{\bullet }\) be a simplicial abelian group. The associated chain complex \((A_{\bullet },d)\) with differential \(d = \sum _{i = 0}^n (-1)^i d_i\) admits two subcomplexes \((\overline{A}_{\bullet },d)\) and \((D_{\bullet },d)\) where, for \(n \ge 0\), we have
and \(D_n \subset A_n\) is the subgroup generated by the degenerate n-simplices. For each element \(\underline{j} = (j_1,\dots ,j_n)\) of the cube \(\{0,1\}^n\), we consider
setting \(j_0 = 1\), and introduce the map
where \(|\underline{j}| = \sum _i j_i\).
Proposition 2.2
Let \(n \ge 0\), and let \(D_n \subset A_n\) be the subgroup generated by the degenerate simplices. Then the map \(\pi : A_n \rightarrow A_n\) is a retraction onto \(\overline{A}_n\) with kernel \(D_n\). In particular, it induces an isomorphism
Proof
To show that \({\text {im}}(\pi ) \subset \overline{A}_n\), we observe that, for \(0 < i \le n\), the face map \(d_i\) maps the two faces of the cube \(\{f_{\underline{j}}^*a\}\) that are orthogonal to the ith coordinate direction to the same \((n-1)\)-dimensional cubes in \(A_{n-1}\). Since the contributions of these faces in the formula for \(\pi \) appear with opposite signs, we obtain, for every \(a \in A_n\), \(d_i \pi (a) = 0\). A similar argument shows that \(D_n \subset \ker (\pi )\): for \(a = s_i a'\), we have \(\pi (a) = 0\) since the opposing faces orthogonal to the ith coordinate direction of the cube \(\{f_{\underline{j}}^*a\}\) cancel in formula (2.1). We show that \(\pi \) is a retraction. Let \(a \in \overline{A}_n\). For \(\underline{j} \ne (1,\dots ,1)\), the map \(f_{\underline{j}}\) factors through some face map \(\partial _i: [n-1] \rightarrow [n]\), \(i >0\), so that \(f_{\underline{j}}^*a = 0\). Since \(f_{(1,\dots ,1)} = {\text {id}}\), we have \(\pi (a) = a\) so that \(\pi \) is a retraction. Finally, by formula (2.1) and \(f_{(1,\dots ,1)}(a) = a\), we may write, for every \(a \in A_n\), \(\pi (a) = a + r\) with \(r \in D_n\), which implies that \(A_n = \overline{A}_n + D_n\). In combination with the statements established above, we obtain \(A_n = \overline{A}_n \oplus D_n\) so that \(D_n = \ker (\pi )\). \(\square \)
Corollary 2.3
We have an isomorphism of complexes
where the projection onto the first summand is given by \(\pi \).
Proof
Immediate from Proposition 2.2. \(\square \)
We consider the functor
referring to \({\text {C}}(A_{\bullet })\) as the normalized chain complex associated to \(A_{\bullet }\). The functor \({\text {C}}\) is part of an adjunction
where the right adjoint \({\text {N}}\) is, for formal reasons, given as follows: For a chain complex \(B_{\bullet }\), we have
where \({\text {C}}(\mathbb {Z}\Delta ^{n})\) denotes the normalized chain complex of the n-simplex. More explicitly, an n-simplex in \({\text {N}}(B_{\bullet })\) is given by a collection \(\{b_{\sigma }\}\) where \(\sigma \) runs over all inclusions \(\sigma : [m] \hookrightarrow [n]\) and \(b_{\sigma } \in B_m\) subject to the equations
Theorem 2.4
The adjunction
is a pair of inverse equivalences.
Proof
We analyze the counit of the adjunction \({\text {C}}({\text {N}}(B_{\bullet })) \rightarrow B_{\bullet }\). An n-simplex in \({\text {N}}(B_{\bullet })\) is given by a collection \(\{b_{\sigma }\}\) and the counit maps this collection to \(b_{{\text {id}}} \in B_n\). The condition that \(\{b_{\sigma }\}\) be a normalized chain translates to the requirement that \(b_{\sigma } = 0\) for all \(\sigma \) that factor through one of the face maps \(\partial _i\), \(i>0\). But this implies that the only possibly nonzero elements are \(b_{{\text {id}}}\) and \(b_{\partial _0}\). Further, the element \(b_{\partial _0}\) is determined as the image of \(b_{{\text {id}}}\) under d. Therefore, the counit is an isomorphism.
The unit \(u: A_{\bullet } \rightarrow {\text {N}}({\text {C}}(A_{\bullet }))\) is given by associating to a in \(A_n\) the n-simplex in \({\text {N}}((A_{\bullet }, d))\) given by the collection \(\{a_{\sigma }\}\) with \(a_{\sigma } = \sigma ^*a\) and then postcomposing with the map
By an argument similar as for the counit, it is immediate that \({\text {C}}(u)\) is an isomorphism. We conclude the proof in virtue of Proposition 2.5 below. \(\square \)
Proposition 2.5
The normalized chains functor \({\text {C}}\) is conservative: a morphism \(f: A_{\bullet } \rightarrow A'_{\bullet }\) of simplicial abelian groups is an isomorphism if and only if \({\text {C}}(f)\) is an isomorphism of chain complexes.
Proof
Given a simplicial abelian group \(A_{\bullet }\), we denote by \({\text {P}}(A_{\bullet })\) the simplicial abelian group obtained by pullback of \(A_{\bullet }\) along the functor
so that \({\text {P}}(A_{\bullet })_n = A_{n+1}\). The collection of omitted face maps
defines a map of simplicial abelian groups \(d: {\text {P}}(A_{\bullet }) \rightarrow A_{\bullet }\). We denote the kernel of d by \(\Omega (A_{\bullet })\). Similarly, we define for a connective chain complex \(B_{\bullet }\) the chain complex \(\Omega (B_{\bullet })\) as the shift
ommitting \(B_0\). It is immediate from the definitions that we have a natural isomorphism
induced by the termwise identification
We show by induction on \(n \ge 0\) that, for every map \(f: A_{\bullet } \rightarrow A'_{\bullet }\) such that C(f) is an isomorphism of chain complexes, the map \(f_n: A_n \rightarrow A'_n\) is an isomorphism. For \(n = 0\), the claim is apparent. Assume the induction hypothesis holds for a fixed \(n \ge 0\) and all maps of simplicial abelian groups. For a given map \(f: A_{\bullet } \rightarrow A'_{\bullet }\), consider the diagram of simplicial abelian groups

where the horizontal sequences are short exact. Then the induction hypothesis implies that \(\overline{f}_n\) and \(f_n\) are isomorphisms so that \({\text {P}}(f)_n = f_{n+1}\) is an isomorphism as well. \(\square \)
3 The categorified Dold-Kan correspondence
In this section, we prove the main result of this work: a categorification of the Dold-Kan correspondence relating simplicial objects and connective chain complexes with values in the category of stable \(\infty \)-categories. We begin by defining these notions in detail.
3.1 Basic definitions
3.1.1 Model for \((\infty ,2)\)-categories
Let \( {{{\text {Set}}}_{\Delta }}\) denote the category of simplicial sets. Following [12], we define an \(\infty \)-category to be a simplicial set satisfying the inner horn filling conditions. We define \({\text {Cat}}_{\infty }\) to be the full subcategory of \( {{{\text {Set}}}_{\Delta }}\) spanned by the \(\infty \)-categories. Note that we really treat \({\text {Cat}}_{\infty }\) as an ordinary 1-category (and later as an enriched category) and not as an \(\infty \)-category. \(\infty \)-categories are the fibrant objects of a model structure on the category of marked simplicial sets \( {{{\text {Set}}}^{+}_{\Delta }}\) with marked edges given by the equivalences. As explained in [13], the category of \( {{{\text {Set}}}^{+}_{\Delta }}\)-enriched categories carries a model structure which can be regarded as a model for the theory of \((\infty ,2)\)-categories. The \((\infty ,2)\)-categorical structures that appear in this work will be organized within this model and related to other models via the theory developed in [13]. The fibrant objects within this model structure can be identified with the \({\text {Cat}}_{\infty }\)-enriched categories.
3.1.2 Stable \(\infty \)-categories
The simplicial set of functors between a pair of \(\infty \)-categories forms another \(\infty \)-category so that \({\text {Cat}}_{\infty }\) becomes a \({\text {Cat}}_{\infty }\)-enriched category with respect to the Cartesian monoidal structure. Marking equivalences in the various functor \(\infty \)-categories, \({\text {Cat}}_{\infty }\) becomes a fibrant object in the model category of \( {{{\text {Set}}}^{+}_{\Delta }}\)-enriched categories from Sect. 3.1.1. We may therefore interpret \({\text {Cat}}_{\infty }\) as a specific model for the \((\infty ,2)\)-category of \(\infty \)-categories. We further denote by \(\mathcal {S}t\subset {\text {Cat}}_{\infty }\) the \({\text {Cat}}_{\infty }\)-enriched subcategory with stable \(\infty \)-categories as objects and functor \(\infty \)-categories spanned by the exact functors in the sense of [14, Chapter 1].
3.1.3 The simplex 2-category
By a 2-category, we mean a category enriched in categories. A 2-category defines a \( {{{\text {Set}}}^{+}_{\Delta }}\)-enriched category by passing to nerves of the enriched mapping categories and marking equivalences. We will typically leave this passage implicit so that, referring to 3.1.1, we may consider any 2-category as an \((\infty ,2)\)-category. We denote by \(\mathbb {C}{\text {at}}\) the 2-category of small categories and by  the full 2-subcategory spanned by the standard ordinals \(\{[n]\}\), considered as categories.
the full 2-subcategory spanned by the standard ordinals \(\{[n]\}\), considered as categories.
3.1.4 Localization
We will construct \(\infty \)-categories via localization: Given a small category \(\mathcal {C}\) and a set of morphisms W, there is an associated \(\infty \)-category \({\text {L}}_{W}\mathcal {C}\), equipped with a functor \({\text {N}}(\mathcal {C}) \rightarrow {\text {L}}_{W}\mathcal {C}\) universal among all functors that send W to equivalences (cf. [14, 1.3.4]).
3.1.5 2-simplicial stable \(\infty \)-categories
We denote by  the category of \({\text {Cat}}_{\infty }\)-enriched functors from the opposite 2-simplex category
the category of \({\text {Cat}}_{\infty }\)-enriched functors from the opposite 2-simplex category  to \(\mathcal {S}t\). Here, the superscript \(({{\text {op}}},-)\) signifies that we reverse the direction of the 1-morphisms but not the 2-morphisms (cf. Sect. 3.3.2 for more details). This category comes equipped with a collection of weak equivalences given by those \({\text {Cat}}_{\infty }\)-enriched natural transformations that are levelwise equivalences of stable \(\infty \)-categories. Via localization, we obtain a corresponding \(\infty \)-category
to \(\mathcal {S}t\). Here, the superscript \(({{\text {op}}},-)\) signifies that we reverse the direction of the 1-morphisms but not the 2-morphisms (cf. Sect. 3.3.2 for more details). This category comes equipped with a collection of weak equivalences given by those \({\text {Cat}}_{\infty }\)-enriched natural transformations that are levelwise equivalences of stable \(\infty \)-categories. Via localization, we obtain a corresponding \(\infty \)-category  of 2-simplicial stable \(\infty \)-categories.
of 2-simplicial stable \(\infty \)-categories.
Remark 3.1
Let  , and let \(n \ge 1\). The functor of 1-categories \(\Delta ^{{{\text {op}}}} \rightarrow \mathcal {S}t_{\infty }\) underlying \(\mathcal {A}_{\bullet }\) provides us with exact functors
, and let \(n \ge 1\). The functor of 1-categories \(\Delta ^{{{\text {op}}}} \rightarrow \mathcal {S}t_{\infty }\) underlying \(\mathcal {A}_{\bullet }\) provides us with exact functors

The additional data captured by the 2-functoriality of \(\mathcal {A}_{\bullet }\) contains unit and counit transformations which exhibit a sequence of adjunctions
For example, for \(n=1\), the units and (resp. counits) of the adjunctions \(d_0 \vdash s_0\) and \(s_0 \vdash d_1\) are induced by the 2-morphisms in 
and
respectively. Here, \(\partial _0,\partial _1\) denote the face maps and \(\sigma _0\) the degeneracy map and we further note that the orders of composition get swapped due to the contravariance of \(\mathcal {A}_{\bullet }\) with respect to 1-morphisms.
3.1.6 Connective chain complexes of stable \(\infty \)-categories
We denote by \({\mathbb {N}}\) the poset of nonnegative integers, considered as a category. We denote by \({\text {Fun}}({\mathbb {N}}^{{{\text {op}}}},\mathcal {S}t)\) the category of (strict) functors from the opposite category of \({\mathbb {N}}\) to the category \(\mathcal {S}t\) of stable \(\infty \)-categories. We introduce the full subcategory
given by those diagrams
of stable \(\infty \)-categories that satisfy the following condition: for every \(i \ge 0\), the functor \(d^2: \mathcal {B}_{i+2} \rightarrow \mathcal {B}_i\) is a zero object of the \(\infty \)-category \({\text {Fun}}_{{\text {ex}}}(\mathcal {B}_{i+2},\mathcal {B}_i)\) of exact functors. The category \({\text {Ch}}_{\ge 0}(\mathcal {S}t)\) comes equipped with a class of weak equivalences given by those natural transformations that are levelwise equivalences. We refer to the corresponding localization \({\text {L}}{\text {Ch}}_{\ge 0}(\mathcal {S}t)\) as the \(\infty \)-category of connective chain complexes of stable \(\infty \)-categories.
Remark 3.2
At first sight, our definition of a complex of stable \(\infty \)-categories may seem too naive. For example, the analogous definition of a connective complex of objects in a stable \(\infty \)-category \(\mathcal {A}\) as a functor
satisfying the condition \(d^2 \simeq 0\) really is too naive. The reason is that, for every \(i \ge 0\), there is a potentially nontrivial space of paths in the Kan complex \({\text {Map}}_{\mathcal {A}}(X_{i+2},X_i)\) from \(d^2\) to 0. Following general principles, the condition \(d^2 \simeq 0\) should be replaced by the choice of a path in \({\text {Map}}_{\mathcal {A}}(X_{i+2},X_i)\) between \(d^2\) and 0. Further, these choices are supposed to be part of a coherent system of trivializations \(d^n \simeq 0\), \(n \ge 2\), corresponding to trivializations of higher Massey products. This coherence data is important: it is, for example, needed to form the totalization of a complex. One way to codify all this data is to remember the complex in terms of the filtered object formed by the totalizations of its various truncations. This is the point of view taken in [14, Chapter 1] where a connective complex of objects in a stable \(\infty \)-category corresponds to a functor
without any further conditions. The actual terms of the complex captured by such a datum are then given as shifts of the cofibers of the maps \(Y_i \rightarrow Y_{i+1}\). One concrete justification for this being a reasonable notion of a complex is provided by a Dold-Kan correspondence relating simplicial objects and connective chain complexes with values in a given stable \(\infty \)-category ([14, 1.2.4]).
In contrast, given a chain complex of stable \(\infty \)-categories in our sense, the space of identifications \(d^2 \simeq 0\) is contractible, since it is the space of equivalences between \(d^2\) and the zero object 0 in the \(\infty \)-category \({\text {Fun}}_{{\text {ex}}}(\mathcal {B}_{i+2},\mathcal {B}_i)\). Therefore, in this context, there is no analog of the coherent system of trivializations captured by (3.3).
3.2 Statement of the theorem
Using the terminology introduced in Sect. 3.1, we may formulate the main theorem.
Theorem 3.4
There exist functors

and

which induce a pair of inverse equivalences

of \(\infty \)-categories.
Remark 3.7
The classical Dold-Kan correspondence generalizes to categories that are additive and idempotent complete. While the \((\infty ,2)\)-category \(\mathcal {S}t\) does not have direct analogs of these two properties, it does admit certain categorified variants:
-
(i)
Given two functors f and g between stable \(\infty \)-categories \(\mathcal {A}\) and \(\mathcal {A}'\), equipped with a natural transformation \(\eta : f \Rightarrow g\), we may form the cone of \(\eta \) as a replacement for the difference of two maps.
-
(ii)
Given an idempotent \(e: \mathcal {A}\rightarrow \mathcal {A}\) that arises from a fully faithful embedding \(i: \mathcal {A}' \subset \mathcal {A}\) with right adjoint \(q: \mathcal {A}\rightarrow \mathcal {A}'\) as \(e = i \circ q\), then there is a canonical natural transformation \(e \Rightarrow {\text {id}}_{\mathcal {A}}\) whose cone will be a projector onto the subcategory \(\ker (q) \subset \mathcal {A}\). Together, the subcategories \(\ker (q)\) and \(\mathcal {A}'\) form a semiorthogonal decomposition of \(\mathcal {A}\) (cf. [2]).
Our proof of Theorem 3.4 relies on a systematic utilization of these features of \(\mathcal {S}t\). Abelian categories form a pleasant class of categories for which the Dold-Kan correspondence holds. It is an interesting task to introduce a suitable categorified axiomatic framework of “2-abelian” \((\infty ,2)\)-categories. One basic requirement would be that the proof of the categorified Dold-Kan correspondence generalizes to this context.
Before we construct the functors in Theorem 3.4 and provide its proof, we need some preliminaries on Grothendieck constructions.
3.3 Grothendieck constructions
Let C be a category and let \({\text {Grp}}\) denote the category of small groupoids. Recall that, given a functor
the classical Grothendieck construction of F is the category \(\chi (F)\) defined as follows:
-
objects are pairs (c, x) where \(c \in C\) and \(x \in F(c)\),
-
a morphism from (c, x) to \((c',x')\) consists of a morphism \(f: c \rightarrow c'\) in C together with a morphism \(x \rightarrow F(f)(x')\) in F(c).
The construction provides a functor
into the category \({\text {Fib}}_{/C}\) of categories fibered in groupoids over C. The functor \(\chi \) has a left adjoint \(\Xi \) given by
and a right adjoint \(\Gamma \) provided by
Upon localizing the categories \({\text {Fun}}(C^{{{\text {op}}}},{\text {Grp}})\) and \({\text {Fib}}_{/C}\) along natural equivalences and equivalences, respectively, the functor \(\chi \) becomes an equivalence with inverse provided by both \(\Xi \) and \(\Gamma \). As a central tool in his approach to higher category theory, Lurie has introduced various generalizations of the adjunction
in the context of Quillen’s theory of model categories. In this work, we will use various explicit versions of these Grothendieck constructions and a description of their inverses in terms of generalizations of the right adjoint functor \(\Gamma \). In this section, we survey the theory in the form it will be applied below.
3.3.1 The \((\infty ,1)\)-categorical Grothendieck construction
Let C be an ordinary category and let
be a functor into the category \({\text {Cat}}_{\infty }\) of \(\infty \)-categories, considered as a full subcategory of the category \({{\text {Set}}}_{\Delta }\) of simplicial sets.
Definition 3.8
We define a simplicial set \(\chi (F)\) as follows: An n-simplex of \(\chi (F)\) consists of
-
(1)
an n-simplex \(\sigma : [n] \rightarrow C\) of the nerve of C,
-
(2)
for every \(I \subset [n]\), a functor
$$\begin{aligned} \Delta ^I \longrightarrow F(\sigma (\min (I))) \end{aligned}$$such that, for every \(I \subset J \subset [n]\), the diagram
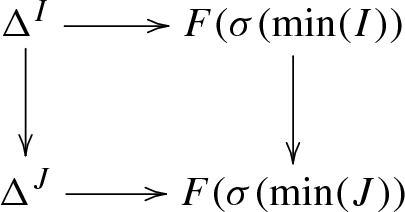
commutes.
The simplicial set \(\chi (F)\) comes equipped with an apparent forgetful map \(\chi (F) \rightarrow {\text {N}}(C)\). We consider \(\chi (F)\) as an object of \( {{{\text {Set}}}^{+}_{\Delta }}_{/{\text {N}}(C)}\) marking the Cartesian edges, and refer to it as the Grothendieck construction of F.
As a consequence of results in [12], the Grothendieck construction induces an equivalence of \(\infty \)-categories
obtained by localizing along levelwise and fiberwise categorical equivalences. The right-hand symbol \(\circ \) signifies that we restrict to the full subcategory of Cartesian fibrations with Cartesian edges marked.
We will use an explicit model for an inverse equivalence to \(\chi \) which we now construct. For an object \(c \in C\), we denote by \(C_{/c}\) the overcategory of c. Keeping track of the forgetful functor \(C_{/c} \rightarrow C\), the various overcategories organize to define a functor
Given an object \(X \in {{{\text {Set}}}^{+}_{\Delta }}_{/{\text {N}}(C)}\), we thus obtain a functor
Here, and in what follows, we adopt the notation for marked simplicial sets from [12]: Given a simplicial set K, we denote by \(K^{\sharp }\) (resp. \(K^{\flat }\)) the marked simplicial sets with all (resp. degenerate) edges marked.
Proposition 3.9
There is a natural transformation
which is a levelwise weak equivalence. In particular, upon localization, the functor \(\Gamma \) defines an inverse to \(\chi \).
Proof
For a functor \(F: C^{{{\text {op}}}} \longrightarrow {\text {Cat}}_{\infty }\) and \(c \in C\), we provide a map of simplicial sets
which, by adjunction, can be identified with a map
of simplicial sets over \({\text {N}}(C)\). We define this map by associating to an n-simplex \((x, c_0 \rightarrow c_1 \rightarrow \dots \rightarrow c_n \rightarrow c)\) of \(F(c) \times {\text {N}}(C_{/c})\) the n-simplex of \(\chi (F)\) that is given by
-
(1)
the n-simplex \(\sigma = c_0 \rightarrow \dots \rightarrow c_n\) in \({\text {N}}(C)\)
-
(2)
for \(I \subset [n]\), the I-simplex of \(F(\sigma (\min (I)))\) obtained as the composite
$$\begin{aligned} \Delta ^I \rightarrow \Delta ^n \overset{x}{\rightarrow } F(c) \rightarrow F(\sigma (\min (I))). \end{aligned}$$
This association is natural in c and provides the value of the transformation \(\eta \) at F.
To show that \(\eta \) is a weak equivalence, we need to show that, for every \(F: C^{{{\text {op}}}} \rightarrow {\text {Cat}}_{\infty }\) and for every \(c \in C\), the map \(\eta _F(c)\) from (3.11) is an equivalence of \(\infty \)-categories. To this end, we note that there is a natural evaluation map
obtained by pullback along the map \(\Delta ^0 \rightarrow {\text {N}}(C_{/c})\) corresponding to the vertex \({\text {id}}: c \rightarrow c\). The composite \({\text {ev}}_c \circ \eta _F(c)\) equals the identity. The map \({\text {ev}}_c\) is an equivalence by [12, 4.3.2.15], since the requirement to map all edges in \({\text {N}}(C_{/c})\) to Cartesian edges is equivalent to being a relative right Kan extension along \(\Delta ^0 \rightarrow {\text {N}}(C_{/c})\). We conclude in virtue of the two-out-of-three property of equivalences of \(\infty \)-categories. \(\square \)
3.3.2 2-Categorical terminology
Let \(\mathbb {C}\) be a 2-category. We denote the category of morphisms between objects x and y by \(\mathbb {C}(x,y)\). We denote by \(\mathbb {C}^{({{\text {op}}},-)}\) the 2-category with
and by \(\mathbb {C}^{(-,{{\text {op}}})}\) the 2-category with
and further \(\mathbb {C}^{({{\text {op}}},{{\text {op}}})} = (\mathbb {C}^{({{\text {op}}},-)})^{(-,{{\text {op}}})}\).
Example 3.12
The 2-category \(\mathbb {C}{\text {at}}\) of small categories admits a self-duality
We introduce 2-categorical versions of undercategories and overcategories. Since there is potential confusion with the orientation of the 2-morphisms, we provide explicit descriptions of both. For an object c in a 2-category \(\mathbb {C}\), we define the lax undercategory \(\mathbb {C}_{c/}\) with
-
objects given by 1-morphisms \(c \rightarrow x\),
-
a 1-morphism from \(\varphi :c \rightarrow x\) to \(\psi :c \rightarrow y\) consists of a 2-commutative triangle
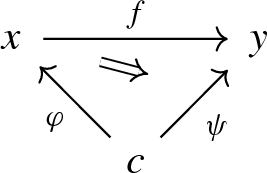
where f is a 1-morphism in \(\mathbb {C}\),
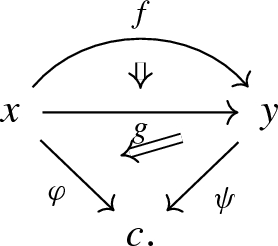
-
a 2-morphism \(\gamma \) from f to g is given by a 2-commutative diagram
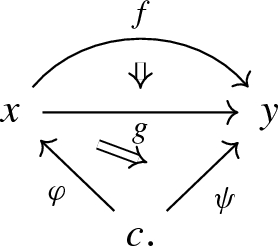
For every object c in \(\mathbb {C}\), we define the lax overcategory \(\mathbb {C}_{/c}\) with
-
objects given by 1-morphisms \(x \rightarrow c\),
-
a 1-morphism from \(\varphi :x \rightarrow c\) to \(\psi :y \rightarrow c\) consists of a 2-commutative triangle
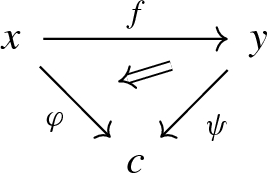
where f is a 1-morphism in \(\mathbb {C}\),
-
a 2-morphism \(\gamma \) from f to g is given by a 2-commutative diagram
For a 2-category \(\mathbb {C}\), we define its homotopy category \(|\mathbb {C}|_1\) to be the category with
-
the same objects as \(\mathbb {C}\),
-
for objects \(c,c' \in \mathbb {C}\), the set
$$\begin{aligned} |\mathbb {C}|_1(c,c') = \pi _0 |\mathbb {C}(c,c')|, \end{aligned}$$of morphisms, where \(|-|\) denotes the geometric realization.
3.3.3 The \((\infty ,2)\)-categorical Grothendieck construction
In this section, we introduce a combinatorial variant of the unstraightening functor for \((\infty ,2)\)-categories introduced in [13]. It can be applied to any strict 2-functor
where \(\mathbb {C}\) is a 2-category. It is a lax analog of the relative nerve construction, provided in [12] as a combinatorial alternative to the straightening construction applicable to strict functors \({\text {C}}\rightarrow {\text {Cat}}_{\infty }\) where \({\text {C}}\) is an ordinary category.
For every nonempty finite linearly ordered set I, we define a 2-category  as follows:
as follows:
-
The set of objects of
 is I,
is I, -
The category
 of morphisms between objects i and j is the poset consisting of those subsets \(S \subset I\) satisfying \(\min S = i\) and \(\max S = j\).
of morphisms between objects i and j is the poset consisting of those subsets \(S \subset I\) satisfying \(\min S = i\) and \(\max S = j\). -
The composition law is given by the formula
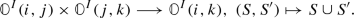
The various 2-categories  , \(n \ge 0\), assemble to a functor
, \(n \ge 0\), assemble to a functor
into the category \({\text {Cat}}_2\) of 2-categories.
Definition 3.14
Let \(\mathbb {C}\) be a 2-category. We define the nerve \({\text {N}}^{{\text {sc}}}(\mathbb {C})\) of \(\mathbb {C}\) to be the scaled simplicial set with

with functoriality in n provided by (3.13). The thin 2-simplices are the ones that correspond to invertible natural transformations.
For \(n \ge 0\), and \(\emptyset \ne I \subset [n]\), we define the category

where \(|-|_1\) denotes the homotopy category as introduced in Sect. 3.3.2. For \(\emptyset \ne I \subset J\), we have a pullback functor

Definition 3.16
Let
be a \({\text {Cat}}_{\infty }\)-enriched functor where we interpret \(\mathbb {C}^{({{\text {op}}}, {{\text {op}}})}\) as \({\text {Cat}}_{\infty }\)-enriched via passage to nerves of the morphism categories. We introduce a simplicial set  , called the lax Grothendieck construction of F as follows: An n-simplex in
, called the lax Grothendieck construction of F as follows: An n-simplex in  consists of
consists of
-
(1)
a functor
 of 2-categories,
of 2-categories, -
(2)
for every \(\emptyset \ne I \subset [n]\), a functor \({\text {N}}(G(I)) \rightarrow F(\sigma (\min (I)))\) so that, for every \( \emptyset \ne J \subset I \subset [n]\), the diagram
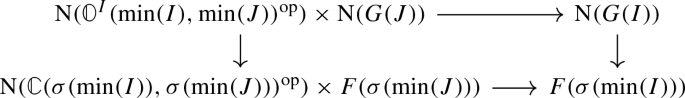
commutes where the top row is obtained from (3.15) by passing to nerves.
By construction, the lax Grothendieck construction comes equipped with a forgetful functor  . We further introduce a marking on
. We further introduce a marking on  consisting of the \(\pi \)-Cartesian edges so that we have
consisting of the \(\pi \)-Cartesian edges so that we have  .
.
We summarize some basic properties which are proven in [1] where the functor  is called the relative 2-nerve.
is called the relative 2-nerve.
Proposition 3.17
Let \(\mathbb {C}\) be a 2-category, and let
be a \({\text {Cat}}_{\infty }\)-enriched functor. Then
-
(1)
The lax Grothendieck construction
 is a locally Cartesian fibration which is Cartesian over every thin 2-simplex of \({\text {N}}^{{\text {sc}}}(\mathbb {C})\).
is a locally Cartesian fibration which is Cartesian over every thin 2-simplex of \({\text {N}}^{{\text {sc}}}(\mathbb {C})\). -
(2)
For every \({\text {Cat}}\)-enriched functor \(\mathbb {D}\rightarrow \mathbb {C}\), we have

-
(3)
Suppose that \(\mathbb {C}\) is a 2-category with discrete morphism categories which we may therefore identify with a 1-category. Then restriction along the functor
$$\begin{aligned} G(I) \rightarrow I, (\min (I) \rightarrow j) \mapsto j \end{aligned}$$induces a map
 (3.18)
(3.18)between the ordinary and lax Grothendieck constructions which is a fiberwise equivalence of Cartesian fibrations.
Let \(\mathbb {C}\) be a 2-category and c an object of \(\mathbb {C}\). Consider the lax overcategory \(\mathbb {C}_{/c}\) as defined in Sect. 3.3.2. The forgetful functor \(\mathbb {C}_{/c} \rightarrow \mathbb {C}\) induces a map \({\text {N}}^{{\text {sc}}}(\mathbb {C}_{/c}) \rightarrow {\text {N}}^{{\text {sc}}}(\mathbb {C})\) of simplicial sets. We further introduce a marking on \({\text {N}}^{{\text {sc}}}(\mathbb {C}_{/c})\) given by those edges where the corresponding 2-morphism is an isomorphism. Thus, we have \({\text {N}}^{{\text {sc}}}(\mathbb {C}_{/c}) \in {{{\text {Set}}}^{+}_{\Delta }}_{/{\text {N}}^{{\text {sc}}}(\mathbb {C})}\). The functoriality of this construction in c is captured by a \({\text {Cat}}_{\infty }\)-enriched functor
We now define for \(X \in {{{\text {Set}}}^{+}_{\Delta }}_{/{\text {N}}^{{\text {sc}}}(\mathbb {C})}\) and \(c \in \mathbb {C}\), the marked simplicial set

Pulling back (3.19), this construction is functorial in c and defines a functor

The additional functoriality in X provides

Proposition 3.20
There is a natural weak equivalence

of endofunctors of \({\text {Fun}}(\mathbb {C}^{({{\text {op}}},{{\text {op}}})}, {\text {Cat}}_{\infty })\).
Proof
The argument is similar to the proof of Proposition 3.9: For every \(F: \mathbb {C}^{({{\text {op}}},{{\text {op}}})} \rightarrow {\text {Cat}}_{\infty }\), there is an explicit natural map

constructed as follows: For every \(c \in \mathbb {C}\), we have to provide a map of simplicial sets

over \({\text {N}}^{{\text {sc}}}(\mathbb {C})\). Let \((\sigma ,\tau )\) be an n-simplex of \(F(c) \times {\text {N}}^{{\text {sc}}}(\mathbb {C}_{/c})\), and denote by \(\alpha \) the n-simplex in \({\text {N}}^{{\text {sc}}}(\mathbb {C})\) obtained by postcomposing \(\tau \) with the map \({\text {N}}^{{\text {sc}}}(\mathbb {C}_{/c}) \rightarrow {\text {N}}^{{\text {sc}}}(\mathbb {C})\). Note that for \(I \subset [n]\), we have an induced functor of categories

given by postcomposition with the given map \(\alpha (j) \rightarrow c\). Further, the \({\text {Cat}}_{\infty }\)-enriched functor F provides a map
evaluation at \(\sigma \) then provides a map

via pullback of the image of \(\sigma \) in \(F(\alpha (\min (I)))\) along the map \([k] \rightarrow I \subset [n]\) corresponding to a k-simplex in  . The collection of these maps for the various nonempty subsets \(I \subset [n]\) defines the desired n-simplex in
. The collection of these maps for the various nonempty subsets \(I \subset [n]\) defines the desired n-simplex in  .
.
To see that the resulting map  is a weak equivalence, we argue as follows. For every object \(c \in \mathbb {C}\), we consider the evaluation map
is a weak equivalence, we argue as follows. For every object \(c \in \mathbb {C}\), we consider the evaluation map

given by pullback along \(\{c \overset{{\text {id}}}{\rightarrow } c\} \rightarrow {\text {N}}(\mathbb {C}_{/c})\). By the argument of [13, 4.1.8], the opposite of this map is \({\mathfrak P}_{{\text {N}}^{{\text {sc}}}(\mathbb {C})^{{{\text {op}}}}}\)-anodyne, so that \({\text {ev}}(c)\) is an equivalence of \(\infty \)-categories. Further, the composite \({\text {ev}}(c) \circ \eta _F(c)\) is the map  induced by (3.18) applied to the restriction \(F|\{c\}\) along \(\{c\} \subset \mathbb {C}\) (noting that \(\chi (F)_c = \chi (F|\{c\})\) and
induced by (3.18) applied to the restriction \(F|\{c\}\) along \(\{c\} \subset \mathbb {C}\) (noting that \(\chi (F)_c = \chi (F|\{c\})\) and  ). Hence, by Proposition 3.17(3), it is an equivalence of \(\infty \)-categories. We conclude by two-out-of-three. \(\square \)
). Hence, by Proposition 3.17(3), it is an equivalence of \(\infty \)-categories. We conclude by two-out-of-three. \(\square \)
3.4 The categorified normalized chains functor \(\mathcal {C}\)
We provide the definition of the functor \(\mathcal {C}\) from Theorem 3.4 whose construction is a mutatis mutandis modification of the normalized chains functor appearing in the classical Dold-Kan correspondence.
Definition 3.21
Given a 2-simplicial stable \(\infty \)-category \(\mathcal {A}_{\bullet }\), we define, for \(n \ge 0\), the stable \(\infty \)-category
as the full subcategory spanned by those vertices a of \(\mathcal {A}_n\) such that, for every \(1 \le i \le n\), the object \(d_i(a)\) is a zero object in \(\mathcal {A}_{n-1}\). As a result of the relations among the face maps in \(\Delta \), the various functors \(d_0: \mathcal {A}_n \rightarrow \mathcal {A}_{n-1}\), \(n > 0\), restrict to define a chain complex
of stable \(\infty \)-categories. We denote this chain complex by \(\mathcal {C}(\mathcal {A}_{\bullet })\) and refer to it as the categorified normalized chain complex associated to \(\mathcal {A}_{\bullet }\).
A morphism  induces a strictly commutative diagram
induces a strictly commutative diagram

so that the construction \(\mathcal {A}_{\bullet } \mapsto \mathcal {C}(\mathcal {A}_{\bullet })\) extends to define a functor

Further, given a weak equivalence \(\mathcal {A}_{\bullet } \rightarrow \mathcal {B}_{\bullet }\), we obtain, for every n, an exact equivalence \(\mathcal {A}_n \rightarrow \mathcal {B}_n\) which further induces an exact equivalence on subcategories \(\overline{A_n} \rightarrow \overline{B_n}\). We conclude that \(\mathcal {C}\) preserves weak equivalences.
3.5 The categorified Dold-Kan nerve \(\mathcal {N}\)
We provide a definition of the functor \(\mathcal {N}\) from Theorem 3.4. It can be regarded as a categorification of the classical Dold-Kan nerve appearing in Sect. 2.
Let \(n \ge 0\). We denote by \({\mathbb {N}}_{/[n]}\) the following lax version of the comma category of  with respect to the embedding
with respect to the embedding  :
:
-
The objects of \({\mathbb {N}}_{/[n]}\) are given by morphisms \(\varphi : [m] \rightarrow [n]\) in
 .
. -
A morphism from \(\varphi :[m] \rightarrow [n]\) to \(\varphi ':[m'] \rightarrow [n]\) consists of a 2-commutative triangle
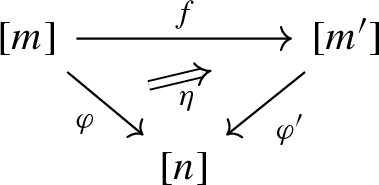
where f is the image of a morphism in \({\mathbb {N}}\), i.e., an iteration of face maps \(\partial _0\).
We equip the category \({\mathbb {N}}_{/[n]}\) with the forgetful functor to \({\mathbb {N}}\) and thus obtain a \({\text {Cat}}\)-enriched functor

Remark 3.23
The category \({\mathbb {N}}_{/[n]}\) is in fact a poset.
Definition 3.24
Let \(k \ge 0\). We define corresponding cubes in the poset \({\mathbb {N}}_{/[n]}\) by specifying the images of the vertices:
-
(1)
\(f: [1]^k \rightarrow {\mathbb {N}}_{/[k]}\) with \(f(j_1,\dots ,j_k)\) given by
$$\begin{aligned}{}[k] \rightarrow [k], \; i \mapsto i - 1 + j_i, \end{aligned}$$where we set \(j_0 = 1\),
-
(2)
\(b: [1]^k \rightarrow {\mathbb {N}}_{/[k]}\) with \(b(j_1,\dots ,j_k)\) given by
$$\begin{aligned}{}[k-1] \rightarrow [k], \; i \mapsto i + j_{i+1} \end{aligned}$$so that \(b = \partial _0^* f\),
-
(3)
and \(q: [1]^{k+1} \rightarrow {\mathbb {N}}_{/[k]}\) with
$$\begin{aligned} q(j_0,\dots ,j_k) = {\left\{ \begin{array}{ll} b(j_1,\dots ,j_k) &{} \text {if } j_0 = 0,\\ f(j_1,\dots ,j_k) &{} \text {if } j_0 = 1. \end{array}\right. } \end{aligned}$$
Example 3.25
For \(k=2\), the cube q may be depicted as

Here, and in what follows, we have highlighted the nondegenerate simplices by boldfaced letters. Below, this will help recognize the indices of nonzero objects (which correspond precisely to nondegenerate simplices).
Definition 3.26
Let \(\mathcal {B}_{\bullet }: {\mathbb {N}}^{{{\text {op}}}} \rightarrow \mathcal {S}t\) be a chain complex of stable \(\infty \)-categories with corresponding Grothendieck construction (Sect. 3.3.1)
We define, for every \(n \ge 0\), the \(\infty \)-category
as the full subcategory spanned by the diagrams
that satisfy the following conditions:
-
N1
For every \(k \ge 1\) and every degenerate k-simplex \(\tau : [k] \rightarrow [n]\) of \(\Delta ^n\), the object \(A_\tau \) is a zero object in the \(\infty \)-category \(\mathcal {B}_k\).
-
N2
For every \(k \ge 1\) and every nondegenerate k-simplex \(\sigma : [k] \rightarrow [n]\), the corresponding cube
$$\begin{aligned} A|q^*\sigma : (\Delta ^1)^{k+1} \longrightarrow \chi (\mathcal {B}_{\bullet }), \end{aligned}$$obtained by restricting A to the pullback of \(\sigma \) along the canonical cube from Definition 3.24, is a \(\pi \)-limit diagram with limit vertex \((0,0,\dots ,0)\).
It follows from [12, 5.1.2.2] that the \(\infty \)-category \({\text {Map}}_{{\text {N}}({\mathbb {N}})}({\text {N}}({\mathbb {N}}_{/[n]}), \chi (\mathcal {B}_{\bullet }))\) and, since limits commute with limits, the subcategory \(\mathcal {N}(\mathcal {B}_{\bullet })_n\) is stable as well. The various stable \(\infty \)-categories \(\mathcal {N}(\mathcal {B}_{\bullet })_n\) assemble to define a 2-simplicial stable \(\infty \)-category with 2-functoriality determined by (3.22). We refer to

as the categorified Dold-Kan nerve of \(\mathcal {B}_{\bullet }\).
To gain familiarity with the categorified Dold-Kan nerve, we provide an explicit description of the low-dimensional simplices of \(\mathcal {N}(\mathcal {A}_{\bullet })\) for a given chain complex \(\mathcal {B}_{\bullet }\) of stable \(\infty \)-categories:
-
(0)
We have \(\mathcal {N}(\mathcal {B}_{\bullet })_0 \cong \mathcal {B}_0\).
-
(1)
The \(\infty \)-category of 1-simplices of \(\mathcal {N}(\mathcal {B}_{\bullet })\) is equivalent to the \(\infty \)-category of diagrams of the form
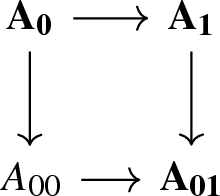
in \(\chi (\mathcal {B}_{\bullet })\) where
-
(a)
\(\{A_i\}\) are objects of \(\mathcal {B}_0\), \(\{A_{ij}\}\) are objects of \(\mathcal {B}_1\),
-
(b)
\(A_{00}\) is a zero object in \(\mathcal {B}_1\),
-
(c)
the square
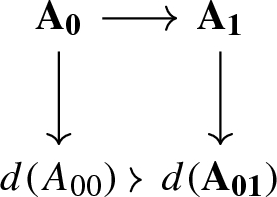
in \(\mathcal {B}_0\) induced by A is biCartesian so that it exhibits the object \(d(A_{01})\) as the cofiber of the map \(A_0 \rightarrow A_1\).
-
(a)
-
(2)
The \(\infty \)-category \(\mathcal {N}(\mathcal {B}_{\bullet })_2\) is equivalent to the \(\infty \)-category of diagrams in \(\chi (\mathcal {B}_{\bullet })\) of the form
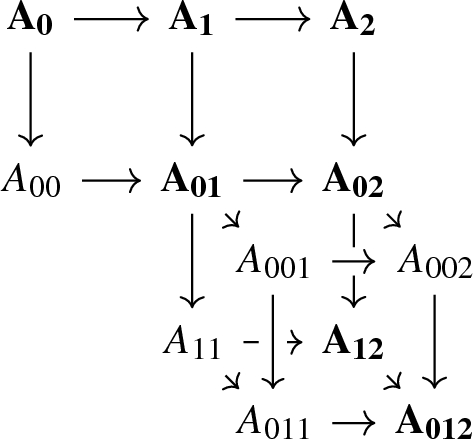
with
-
(a)
\(\{A_i\}\) objects of \(\mathcal {B}_0\), \(\{A_{ij}\}\) objects of \(\mathcal {B}_1\), \(\{A_{ijk}\}\) objects of \(\mathcal {B}_2\),
-
(b)
\(A_{00}\) and \(A_{11}\) are zero objects in \(\mathcal {B}_1\), \(A_{001}\), \(A_{011}\), and \(A_{002}\) are zero objects in \(\mathcal {B}_2\),
-
(c)
the diagram A exhibits the objects \(d(A_{01})\), \(d(A_{02})\), and \(d(A_{12})\) as cofibers of the morphisms \(A_0 \rightarrow A_1\), \(A_0 \rightarrow A_2\), and \(A_1 \rightarrow A_2\), respectively, as detailed in (1). In particular, by the octahedral lemma, the square
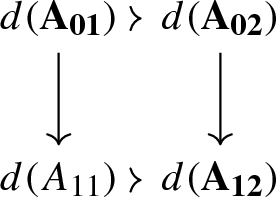
is biCartesian.
-
(d)
The cube
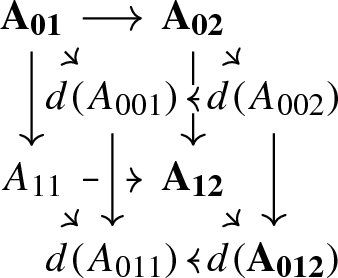
in \(\mathcal {B}_1\) induced by the diagram A is biCartesian so that it exhibits the object \(d(A_{012})\) as a totalization of the 3-term complex \(A_{01} \rightarrow A_{02} \rightarrow A_{12}\).
-
(a)
-
(n)
Similarly, the higher-dimensional simplices of \(\mathcal {N}(\mathcal {B}_{\bullet })\) consist of collections of diagrams in \(\mathcal {B}_k\) parametrized by the various posets of k-simplices of \(\Delta ^n\), together with additional compatibility data that, for every nondegenerate k-simplex \(\sigma \) in \(\Delta ^n\), exhibits the object \(d(A_{\sigma })\) as the totalization of a \((k+1)\)-term complex with underlying sequence of maps
$$\begin{aligned} A_{\partial _k\sigma } \rightarrow A_{\partial _{k-1}\sigma } \rightarrow \dots \rightarrow A_{\partial _0\sigma }. \end{aligned}$$
Our next goal is to study special cases of the categorified Dold-Kan nerve and exhibit how they relate to previously studied constructions.
Example 3.27
Let
be a 2-term chain complex of stable \(\infty \)-categories concentrated in degrees 0, 1. Then the \(\infty \)-category of n-simplices of \(\mathcal {N}(\mathcal {B}_{\bullet })\) consists of diagrams

in \(\chi (\mathcal {B}_{\bullet })\) where
-
\(\{A_i\}\) are objects of \(\mathcal {B}_0\), \(\{A_{ij}\}\) are objects of \(\mathcal {B}_1\),
-
the objects \(\{A_{ii}\}\) are zero objects in \(\mathcal {B}_1\),
-
for every \(0 \le i < j \le n\), the diagram
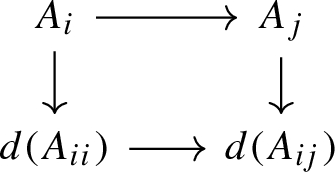
in \(\mathcal {B}_0\) induced by A is biCartesian,
-
for every \(0 \le i< j < k \le n\), the diagram
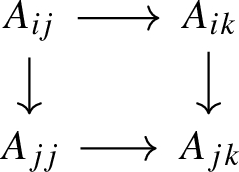
in \(\mathcal {B}_0\) induced by A is biCartesian.
In this special case, the categorified Dold-Kan nerve \(\mathcal {N}(\mathcal {B}_{\bullet })\) can thus be regarded as an \(\infty \)-categorical variant of Waldhausen’s relative \(S_{\bullet }\)-construction associated to the functor \(d: \mathcal {B}_1 \rightarrow \mathcal {B}_0\) of stable \(\infty \)-categories. In particular, for \(\mathcal {B}_0 = 0\), we recover Waldhausen’s \(S_{\bullet }\)-construction of the stable \(\infty \)-catgeory \(\mathcal {B}_1\).
Example 3.28
Let \(\mathcal {B}\) be a stable \(\infty \)-category, \(k \ge 0\), and let \(\mathcal {B}[k]\) denote the chain complex of stable \(\infty \)-categories that has \(\mathcal {B}\) in degree k and the zero category \(\Delta ^0\) in all other degrees. We describe the categorified Dold-Kan nerve \(\mathcal {N}(\mathcal {B}[k])\). Consider the cube
from Definition 3.24. In dimensions 1, 2, and 3, the respective cubes can be depicted as follows:

The n-simplices of \(\mathcal {N}(\mathcal {B}[k])\) are then given by diagrams
subject to the following conditions:
-
(1)
For every degenerate k-simplex \(\tau :[k] \rightarrow [n]\), the object \(A_\tau \) is a zero object in \(\mathcal {B}\).
-
(2)
For every nondegenerate \((k+1)\)-simplex \(\sigma :[k+1] \rightarrow [n]\), the cube \((\sigma \circ b)^*A\) is an exact cube in \(\mathcal {B}\).
As already explained in Example 3.27, \(\mathcal {N}(\mathcal {B}[1])\) is an \(\infty \)-categorical variant of Waldhausen’s \(S_{\bullet }\)-construction. The simplicial object \(\mathcal {N}(\mathcal {B}[2])\) can be regarded as an \(\infty \)-categorical version of the \(S^{2,1}_{\bullet }\)-construction due to Hesselholt-Madsen [8]. For \(k \ge 3\), the simplicial object underlying \(\mathcal {N}(\mathcal {B}[k])\) is an \(\infty \)-categorical version of the k-dimensional \(S^{\langle k \rangle }_{\bullet }\)-construction as recently introduced and studied for abelian categories in [16].
4 Proof of Theorem 3.4
Our strategy for the proof of Theorem 3.4 is to produce a step-by-step categorification of the proof of the classical Dold-Kan correspondence presented in Sect. 2.
4.1 The equivalence \(\mathcal {C}\circ \mathcal {N}\simeq {\text {id}}\)
Proposition 4.1
There is a natural weak equivalence
where \((\Gamma , \chi )\) denote the functors comprising the Grothendieck construction from Sect. 3.3.1.
Proof
Let \(\mathcal {B}_{\bullet }\) be a chain complex of stable \(\infty \)-categories. For \(n \ge 0\), the \(\infty \)-category \(\mathcal {C}(\mathcal {N}(\mathcal {B}_{\bullet }))_n\) consists of diagrams
subject to the conditions spelled out in Definition 3.26 and additionally satisfying, for every \(1 \le i \le n\),
These conditions imply that the only nonzero objects in the diagram comprising A are the ones parametrized by the n-simplex \({\text {id}}: [n] \rightarrow [n]\) and the \((n-1)\)-simplex \(\partial _0: [n-1] \rightarrow [n]\). In particular, restriction along the functor
where \({\mathbb {N}}_{/n}\) denotes the overcategory \(0 \rightarrow 1 \rightarrow \dots \rightarrow n\) of n in the poset \({\mathbb {N}}\), induces an equivalence \(\mathcal {C}(\mathcal {N}(\mathcal {B}_{\bullet }))_n \simeq \Gamma (\chi (\mathcal {B}_{\bullet }))_n\). Since this map is functorial in n and \(\mathcal {B}_{\bullet }\), we obtain a natural weak equivalence
\(\square \)
Corollary 4.2
There is a natural equivalence \(\mathcal {C}\circ \mathcal {N}\simeq {\text {id}}\) as endofunctors of the \(\infty \)-category \({\text {L}}{\text {Ch}}_{\ge 0}(\mathcal {S}t)\) of connective chain complexes of stable \(\infty \)-categories.
Proof
Immediate from Proposition 4.1 and Proposition 3.9. \(\square \)
4.2 The equivalence \(\mathcal {N}\circ \mathcal {C}\simeq {\text {id}}\)
We proceed by showing \(\mathcal {N}\circ \mathcal {C}\simeq {\text {id}}\). To this end, we produce a zigzag diagram

of endofunctors of  and show that all maps in the diagram are weak equivalences. The resulting equivalence \({\text {id}}\simeq \mathcal {N}\circ \mathcal {C}\) of endofunctors of the \(\infty \)-categorical localization
and show that all maps in the diagram are weak equivalences. The resulting equivalence \({\text {id}}\simeq \mathcal {N}\circ \mathcal {C}\) of endofunctors of the \(\infty \)-categorical localization  can be interpreted as a categorification of the unit transformation \(u: {\text {id}}\rightarrow {\text {N}}\circ {\text {C}}\) constructed in the proof of Theorem 2.4.
can be interpreted as a categorification of the unit transformation \(u: {\text {id}}\rightarrow {\text {N}}\circ {\text {C}}\) constructed in the proof of Theorem 2.4.
4.2.1 The lax version \(\widetilde{\mathcal {N}}\) of \(\mathcal {N}\)
In the definition of the categorified Dold-Kan nerve of a connective chain complex \(\mathcal {B}_{\bullet }\) of stable \(\infty \)-categories, we have used the Grothendieck construction \(\pi : \chi (\mathcal {B}_{\bullet }) \rightarrow {\text {N}}({\mathbb {N}})\). We denote by \(\widetilde{\mathcal {N}}(\mathcal {B}_{\bullet })\) the mutatis mutandis definition obtained by using the lax Grothendieck construction  instead, where we interpret \({\mathbb {N}}\) as a 2-category with discrete morphism categories.
instead, where we interpret \({\mathbb {N}}\) as a 2-category with discrete morphism categories.
Proposition 4.4
There is a weak equivalence
of functors  .
.
Proof
This is an immediate consequence Proposition 3.17(3). \(\square \)
4.2.2 The functor \(\mathcal {F}\)
To simplify notation, we introduce  . For \(n \ge 0\), we introduce the pushout
. For \(n \ge 0\), we introduce the pushout

along the inclusion \(\{0\} \times {\text {id}}: {\text {N}}({\mathbb {N}}_{/[n]}) \subset \Delta ^1 \times {\text {N}}({\mathbb {N}}_{/[n]})\). We further denote the inclusions

where \(s = \{1\} \times {\text {id}}\). We introduce a functor

as follows: Given a 2-simplicial stable \(\infty \)-category \(\mathcal {A}_{\bullet }\), we define

to be the full subcategory spanned by the diagrams

satisfying the following conditions:
-
(F1)
The functor
 maps edges corresponding to strictly commutative triangles to \(\pi \)-Cartesian edges in
maps edges corresponding to strictly commutative triangles to \(\pi \)-Cartesian edges in  .
. -
(F2)
The functor \(s^*X\) maps every vertex of \({\text {N}}({\mathbb {N}}_{/[n]})\) corresponding to a degenerate simplex \(\tau :[k] \rightarrow [n]\) to a zero object in the fiber \(\pi ^{-1}([k])\).
-
(F3)
For every nondegenerate simplex \(\sigma : [k] \hookrightarrow [n]\), the composite

is a biCartesian cube in the fiber \(\pi ^{-1}([k])\) where f denotes the cube from Definition 3.24.
Proposition 4.5
Restriction along  defines a functor
defines a functor

which is a weak equivalence.
Proof
Let  , let
, let  denote the lax Grothendieck construction, and let \(n \ge 0\). Let \(K \subset \Delta ^1 \times {\text {N}}({\mathbb {N}}_{/[n]})\) be the full subcategory spanned by the vertices of \(\{0\} \times {\text {N}}({\mathbb {N}}_{/[n]})\) and those vertices of \(\{1\} \times {\text {N}}({\mathbb {N}}_{/[n]})\) that correspond to degenerate simplices \([k] \rightarrow [n]\) of \(\Delta ^n\). We then have the following statements which are direct consequences of the pointwise formula for relative Kan extensions (cf. [12, 4.3.2.2]):
denote the lax Grothendieck construction, and let \(n \ge 0\). Let \(K \subset \Delta ^1 \times {\text {N}}({\mathbb {N}}_{/[n]})\) be the full subcategory spanned by the vertices of \(\{0\} \times {\text {N}}({\mathbb {N}}_{/[n]})\) and those vertices of \(\{1\} \times {\text {N}}({\mathbb {N}}_{/[n]})\) that correspond to degenerate simplices \([k] \rightarrow [n]\) of \(\Delta ^n\). We then have the following statements which are direct consequences of the pointwise formula for relative Kan extensions (cf. [12, 4.3.2.2]):
-
(1)
For a functor

over \({\text {N}}({\mathbb {N}})\), the following conditions are equivalent:
-
(a)
For every degenerate simplex \([k] \rightarrow [n]\), the functor Y maps the corresponding vertex of \(\{1\} \times {\text {N}}({\mathbb {N}}_{/[n]})\) to a zero object in the fiber \(\pi ^{-1}([k])\).
-
(b)
Y is a \(\pi \)-right Kan extension of its restriction \(Y|\{0\} \times {\text {N}}({\mathbb {N}}_{/[n]})\).
-
(a)
-
(2)
For a functor

over \({\text {N}}({\mathbb {N}})\), the following conditions are equivalent:
-
(a)
For every nondegenerate simplex \(\sigma : [k] \hookrightarrow [n]\), the composite

is a biCartesian cube in the fiber \(\pi ^{-1}([k])\).
-
(b)
Z is a \(\pi \)-left Kan extension of its restriction Z|K.
-
(a)
Now let  denote the full subcategory spanned by those vertices that satisfy conditions (F2) and (F3). Then, by [12, 4.3.1.15] and (1), (2), the restriction map
denote the full subcategory spanned by those vertices that satisfy conditions (F2) and (F3). Then, by [12, 4.3.1.15] and (1), (2), the restriction map

is a trivial Kan fibration. Let  denote the full subcategory spanned by the vertices that satisfy condition (F1). By definition, we have
denote the full subcategory spanned by the vertices that satisfy condition (F1). By definition, we have  . Then we have a pullback diagram of simplicial sets
. Then we have a pullback diagram of simplicial sets

so that  is a trivial Kan fibration and hence an equivalence of \(\infty \)-categories. \(\square \)
is a trivial Kan fibration and hence an equivalence of \(\infty \)-categories. \(\square \)
Proposition 4.6
Restriction along \(s: {\text {N}}({\mathbb {N}}_{/[n]}) \hookrightarrow \mathcal {M}_n\) defines a natural transformation
of endofunctors of  which is a pointwise weak equivalence.
which is a pointwise weak equivalence.
Proof
Let  and \(n \ge 0\). Let \(X \in \mathcal {F}(\mathcal {A}_{\bullet })_n\) and let
and \(n \ge 0\). Let \(X \in \mathcal {F}(\mathcal {A}_{\bullet })_n\) and let

be its restriction along s. We show the following:
-
(1)
For \(0 < i \le k\), let

denote a functor obtained by lifting the morphism \(\partial _i: [k-1] \rightarrow [k]\) of
 with respect to the locally Cartesian fibration
with respect to the locally Cartesian fibration  . Then, for every \(\sigma : [k] \rightarrow [n]\), we have \(\partial _i^*(A_{\sigma }) \simeq 0\).
. Then, for every \(\sigma : [k] \rightarrow [n]\), we have \(\partial _i^*(A_{\sigma }) \simeq 0\). -
(2)
For every \(k \ge 0\) and every nondegenerate \((k+1)\)-simplex \(\sigma : [k+1] \rightarrow [n]\), the corresponding cube

obtained by restricting A to the pullback of \(\sigma \) along the cube from Definition 3.24, is a \(\pi \)-limit diagram with limit vertex \((0,0,\dots ,0)\).
To verify (1), we first note that, by definition, for every degenerate simplex \([k] \rightarrow [n]\), the corresponding object \(A_{\tau }\) is a zero object so that there is nothing to show. The value of A at a nondegenerate simplex \(\sigma : [k] \hookrightarrow [n]\) is given by the totalization of the cube \(X|f^*\sigma \). Due to condition (F1), this cube has the property that every edge parallel to the ith coordinate axis of the cube gets mapped under \(\partial _i^*\) to an equivalence in  . Since totalization commutes with the functor \(\partial _i^*\), it follows that the totalization of \(X|f^*\sigma \) is zero by Lemma 4.7 showing (1).
. Since totalization commutes with the functor \(\partial _i^*\), it follows that the totalization of \(X|f^*\sigma \) is zero by Lemma 4.7 showing (1).
We prove (2). Let  denote the Cartesian fibration obtained by restricting
denote the Cartesian fibration obtained by restricting  . We first show the following claim:
. We first show the following claim:
-
(I)
For every nondegenerate simplex \(\sigma : [k] \hookrightarrow [n]\), the cube \(X|\Delta ^1 \times q^*\sigma \) is a \(\pi \)-limit cube.
Note that (F3) implies that the front face \(X|\Delta ^1 \times f^*\sigma \) of this cube is biCartesian in the fiber  so that it suffices to show that the back face \(C {:}{=} X|\Delta ^1 \times b^*\sigma \) is biCartesian in the fiber
so that it suffices to show that the back face \(C {:}{=} X|\Delta ^1 \times b^*\sigma \) is biCartesian in the fiber  . Again by property (F3), the face \(F {:}{=} X|\Delta ^1 \times f^*(\sigma \circ \partial _0)\) of C is biCartesian in
. Again by property (F3), the face \(F {:}{=} X|\Delta ^1 \times f^*(\sigma \circ \partial _0)\) of C is biCartesian in  . We need to show that the face of C opposite to F is biCartesian as well. To see this, we argue as follows: Consider the restriction R of X to the inclusion
. We need to show that the face of C opposite to F is biCartesian as well. To see this, we argue as follows: Consider the restriction R of X to the inclusion  . Let \(K \subset \Delta ^1 \times {\text {N}}({\text {Fun}}([k-1],[n]))\) denote the nerve of the poset spanned by \(\{0\} \times {\text {Fun}}([k-1],[n])\) together with all elements of \(\{1\} \times {\text {Fun}}([k-1],[n])\) whose second component is a degenerate simplex. Then property (F3), applied to the simplices \(\sigma \circ \partial _i\), \(i > 0\), implies that X|R is a left Kan extension of X|K where we consider both functors with values in the fiber
. Let \(K \subset \Delta ^1 \times {\text {N}}({\text {Fun}}([k-1],[n]))\) denote the nerve of the poset spanned by \(\{0\} \times {\text {Fun}}([k-1],[n])\) together with all elements of \(\{1\} \times {\text {Fun}}([k-1],[n])\) whose second component is a degenerate simplex. Then property (F3), applied to the simplices \(\sigma \circ \partial _i\), \(i > 0\), implies that X|R is a left Kan extension of X|K where we consider both functors with values in the fiber  . Now let \(K' \subset R\) denote the nerve of the subposet spanned by all elements except \(\{1\} \times \sigma \circ \partial _1\). The fact that X|R is a left Kan extension of \(X|K'\) translates via the pointwise formula for Kan extensions to the statement that the face of C opposite of F is biCartesian, proving the claim (I).
. Now let \(K' \subset R\) denote the nerve of the subposet spanned by all elements except \(\{1\} \times \sigma \circ \partial _1\). The fact that X|R is a left Kan extension of \(X|K'\) translates via the pointwise formula for Kan extensions to the statement that the face of C opposite of F is biCartesian, proving the claim (I).
Now (I) implies our desired statement as follows: The cube \(A|q^*\sigma \) is the face of the larger cube \(X|\Delta ^1 \times q^*\sigma \) obtained by restriction along \(\{1\} \times q^* \sigma \). Since this cube is a \(\pi \)-limit cube, it suffices to show that the cube \(X|\{0\} \times q^*\sigma \) is a \(\pi \)-limit. But this is clear, since all edges of the arrow \(X|\{0\} \times b^*\sigma \rightarrow X|\{0\} \times f^*\sigma \) (which comprises the cube \(X|\{0\} \times q^*\sigma \)) are \(\pi \)-Cartesian.
By Proposition 4.9 below, to show that \(s^*\) is a weak equivalence, it suffices to verify that \(\mathcal {C}(s^*)\) is a weak equivalence. This is easily seen by direct inspection: Namely, unravelling the definitions, the \(\infty \)-category \(\mathcal {C}(\mathcal {F}(\mathcal {A}_{\bullet }))_n\) is equivalent to the \(\infty \)-category of diagrams in  of the form
of the form

where the horizontal arrows are equivalences and the vertical arrows are \(\pi \)-Cartesian covers of \(\partial _0\). Similarly, the \(\infty \)-category \(\mathcal {C}(\widetilde{\mathcal {N}}(\mathcal {C}(\mathcal {A}_{\bullet }))_n\) is equivalent to the \(\infty \)-category of diagrams in  of the form
of the form

with vertical arrow \(\pi \)-Cartesian. The functor \(\mathcal {C}(s^*)_n\) is simply the forgetful functor which is thus clearly an equivalence. \(\square \)
Lemma 4.7
Let \(\mathcal {A}\) be a stable \(\infty \)-category and let \(C: (\Delta ^1)^k \rightarrow \mathcal {A}\) be a cube in \(\mathcal {A}\). Let B and F denote the restrictions of the cube C to \(\{0\} \times (\Delta ^1)^{k-1}\) and \(\{1\} \times (\Delta ^1)^{k-1}\), respectively. Then the following are equivalent:
-
(1)
\({\text {tot}}(C)\) and \({\text {tot}}(B)\) are zero objects in \(\mathcal {A}\).
-
(2)
\({\text {tot}}(C)\) and \({\text {tot}}(F)\) are zero objects in \(\mathcal {A}\).
-
(3)
\({\text {tot}}(F)\) and \({\text {tot}}(B)\) are zero objects in \(\mathcal {A}\).
Proof
This follows immediately from the fact that there exists an exact triangle

in \(\mathcal {A}\). \(\square \)
Collecting all results of this section, we obtain the following main result:
Theorem 4.8
There is a natural equivalence
of endofunctors of the \(\infty \)-category  of 2-simplicial stable \(\infty \)-categories.
of 2-simplicial stable \(\infty \)-categories.
Proof
The various results of this section imply the existence of a diagram of natural weak equivalences

which leads to the desired conclusion after localization. \(\square \)
4.2.3 The functor \(\mathcal {C}\) is conservative
The following proposition is used in final argument of the proof of Proposition 4.5:
Proposition 4.9
The categorified normalized chains functor

is conservative: a morphism f in  is a weak equivalence if and only if \(\mathcal {C}(f)\) is a weak equivalence.
is a weak equivalence if and only if \(\mathcal {C}(f)\) is a weak equivalence.
Proof
The proof is a step-by-step categorification of the proof of Proposition 2.5. Given a 2-simplicial stable \(\infty \)-category \(\mathcal {A}_{\bullet }\), we introduce its path object \(\mathcal {P}(\mathcal {A}_{\bullet })\), which is the 2-simplicial object obtained by pullback along the 2-functor

The values of the path object are given by \(\mathcal {P}(\mathcal {A}_{\bullet })_n = \mathcal {A}_{n+1}\). The various omitted face maps \(d_n: \mathcal {A}_n \rightarrow \mathcal {A}_{n-1}\) define a natural map of 2-simplicial stable \(\infty \)-categories \(d: \mathcal {P}(\mathcal {A}_{\bullet }) \rightarrow \mathcal {A}_{\bullet }\) which can be described more formally as the pullback along a natural transformation \({\text {id}}\Rightarrow \alpha \). For every \(n \ge 0\), we denote by \(\Omega (\mathcal {A}_{\bullet })_n\) the full subcategory of \(\mathcal {A}_{n+1}\) spanned by the objects X such that \(d_{n+1}(X)\) is a zero object in \(\mathcal {A}_{n}\). We obtain a 2-simplicial stable \(\infty \)-category \(\Omega (\mathcal {A}_{\bullet })\) which is part of a sequence
in  , functorial in \(\mathcal {A}_{\bullet }\), with composite equivalent to the zero map.
, functorial in \(\mathcal {A}_{\bullet }\), with composite equivalent to the zero map.
For a connective chain complex \(\mathcal {B}_{\bullet }\) of stable \(\infty \)-categories, we define \(\Omega (\mathcal {B}_{\bullet })\) as the shifted chain complex
omitting \(\mathcal {B}_0\). It is immediate from the definitions that we have an equality
of functors from  to \({\text {Ch}}_{\ge 0}(\mathcal {S}t)\).
to \({\text {Ch}}_{\ge 0}(\mathcal {S}t)\).
We now proceed by showing the following statement by induction on n:
-
(I)
Let \(n \ge 0\). Then, for every map \(f: \mathcal {A}_{\bullet } \rightarrow \mathcal {A}'_{\bullet }\) of 2-simplicial stable \(\infty \)-categories, such that \(\mathcal {C}(f)\) is a weak equivalence, the map \(f_n: \mathcal {A}_n \rightarrow \mathcal {A}'_n\) is an equivalence of stable \(\infty \)-categories.
The statement is obvious for \(n = 0\), since \(\mathcal {C}(f)_0 = f_0\). Assume that (I) holds for a fixed \(n \ge 0\). Given a map \(\mathcal {A}_{\bullet } \rightarrow \mathcal {A}'_{\bullet }\), we consider the commutative diagram

in  . Evaluating the diagram at
. Evaluating the diagram at  , we obtain the diagram
, we obtain the diagram

of stable \(\infty \)-categories. By induction hypothesis, the functor \(f_n\) is an equivalence. Further, by (4.10), we have that \(\mathcal {C}(\Omega (f)) = \Omega (\mathcal {C}(f))\) is a weak equivalence so that, again by induction hypothesis, the functor \(\Omega (f)_n\) is an equivalence. Note that the right square in (4.11) can be completed to a commutative diagram

where \(d_n\) and \(s_n\) denote the respective face and degeneracy maps and we leave the 2-categorical data implicit. We deduce that \(f_{n+1}\) is an equivalence by Lemma 4.13. This concludes the proof of (I) and the lemma. \(\square \)
Lemma 4.13
Consider a diagram

of stable \(\infty \)-categories with \(sp = sq = {\text {id}}_{\mathcal {A}}\), \(s'p' = s'q' = {\text {id}}_{\mathcal {A}'}\) so that these identities are counits and units, respectively, of adjunctions
and
Set \(\mathcal {B}= \ker (q)\) and \(\mathcal {B}' = \ker (q')\). Suppose that the induced functors \(f: \mathcal {A}\rightarrow \mathcal {A}'\) and \(\overline{g}: \mathcal {B}\rightarrow \mathcal {B}'\) are equivalences. Then the functor g is an equivalence.
Proof
Consider the relative nerve \(\pi : {\text {N}}_s(\Delta ^1) \longrightarrow \Delta ^1\) of the functor \(\Delta ^1 \rightarrow {\text {Cat}}_{\infty }\) determined by \(s: \mathcal {A}\rightarrow \mathcal {X}\) (cf. [12, 3.2.5.12]). Since s has the right adjoint q, the coCartesian fibration \(\pi \) is Cartesian as well so that we have an equivalence \(\mathcal {X}\simeq {\text {Map}}^{\#}_{\Delta ^1}(\Delta ^1, {\text {N}}_s(\Delta ^1))\) with the \(\infty \)-category of Cartesian sections of \({\text {N}}_s(\Delta ^1)\). The latter \(\infty \)-category can be identified with the full subcategory of \({\text {Fun}}(\Delta ^1, \mathcal {X})\) spanned by the counit edges, i.e., edges equivalent to \(s(q(X)) \rightarrow X\). Here, an edge e is a counit edge if and only if q(e) is an equivalence in \(\mathcal {A}\). But this is in turn equivalent to the statement that the cofiber of e lies in \(\mathcal {B}= \ker (q)\). Consider the \(\infty \)-category \(\mathcal {X}(\mathcal {B},\mathcal {A})\) of diagrams

in \(\mathcal {X}\) where \(A \in \mathcal {A}\), \(B \in \mathcal {B}\), and both squares are biCartesian (which implies \(A' \in \mathcal {A}\)). The above discussion implies that the evaluation map at X establishes an equivalence of \(\infty \)-categories \(\mathcal {X}(\mathcal {B},\mathcal {A}) \simeq \mathcal {X}\). Let \({\text {Map}}_{\mathcal {X}}(\mathcal {B},\mathcal {A}) \subset {\text {Fun}}(\Delta ^1, \mathcal {X})\) denote the full subcategory spanned by those edges e in \(\mathcal {X}\) so that \(d_1(e)\) is a vertex in \(\mathcal {B}\) and \(d_0(e)\) is a vertex in \(\mathcal {A}\). Clearly, projection onto the bottom right edge provides an equivalence
We now construct an \(\infty \)-category \(\mathcal {Y}\) equipped with a map \(\theta : \mathcal {Y}\rightarrow \Delta ^1\) as follows: an n-simplex in \(\mathcal {Y}\) consists of
-
(i)
a map \(f: [n] \rightarrow [1]\) in \(\Delta \),
-
(ii)
an n-simplex \(\sigma : \Delta ^n \rightarrow \mathcal {X}\) such that \(\sigma |\Delta ^{f^{-1}(0)} \subset \mathcal {B}\) and \(\sigma |\Delta ^{f^{-1}(1)} \subset \mathcal {A}\).
Note that \({\text {Map}}_{\mathcal {X}}(\mathcal {B},\mathcal {A})\) can be identified with the \(\infty \)-category of sections of \(\theta \). The assumption that p is a left adjoint to s implies that the map \(\theta \) is a coCartesian fibration where a section e is a coCartesian edge if and only if p(e) is an equivalence in \(\mathcal {A}\).
We have thus produced a diagram of equivalences of \(\infty \)-categories

The diagram (4.14) induces a map \(t: \mathcal {Y}\rightarrow \mathcal {Y}'\) that preserves coCartesian edges and is a fiberwise equivalence. By [12, 3.3.1.5], it follows that t itself is an equivalence. We conclude by noting the commutative diagram

where all horizontal arrows are equivalences and, since t is an equivalence, the rightmost vertical map is an equivalence. By the two-out-of-three property the leftmost arrow f is an equivalence as well. \(\square \)
Remark 4.15
The equivalence
appearing in the proof of Lemma 4.13 admits the following interpretation: the stable \(\infty \)-category \(\mathcal {X}\) comes equipped with a semiorthogonal decomposition \(\mathcal {X}= \langle \mathcal {B}, \mathcal {A}\rangle \) satisfying a certain admissibility condition. In this situation, the equivalence (4.16) shows that the \(\infty \)-category \(\mathcal {X}\) can be recovered from the two components \(\mathcal {B}\) and \(\mathcal {A}\) of the decomposition together with the gluing functor \(\overline{p}: \mathcal {B}\rightarrow \mathcal {A}\), using the terminology of [2].
References
Abellán García, F., Dyckerhoff, T., Stern, W.: A relative 2-nerve. (2019) arXiv:1910.06223 to appear in Algebr. Geom. Topol
Bondal, A., Kapranov, M.: Representable functors, Serre functors, and mutations. Izvestiya Rossiiskoi Akademii Nauk. Seriya Matematicheskaya 53(6), 1183–1205 (1989)
Dyckerhoff, Tobias, Jasso, Gustavo, Walde, Tashi: Simplicial structures in higher Auslander-Reiten theory. Adv. Math. 355, 106762 (2019)
Dyckerhoff, Tobias, Kapranov, Mikhail: Triangulated surfaces in triangulated categories. J. Eur. Math. Soc. (JEMS) 20(6), 1473–1524 (2018)
Dyckerhoff, T., Kapranov, M., Schechtman, V., Soibelman, Y.: Topological Fukaya categories with coefficients. in preparation (2017)
Dold, A.: Homology of symmetric products and other functors of complexes. Ann Math, pp 54–80 (1958)
Dyckerhoff, T.: \(\mathbb{A}^1\) -homotopy invariants of topological Fukaya categories of surfaces. Compos. Math. 153(8), 1673–1705 (2017)
Hesselholt, L., Madsen, I.: Real algebraic K-theory. to appear, (2013)
Iyama, O.: Higher-dimensional Auslander-Reiten theory on maximal orthogonal subcategories. Adv. Math. 210(1), 22–50 (2007)
Kan, Daniel M.: Functors involving css complexes. Trans. Am. Math. Soc. 87(2), 330–346 (1958)
Kapranov, M., Schechtman, V.: Perverse schobers. (2014). arXiv preprint arXiv:1411.2772
Lurie, J.: Higher topos theory. Annals of Mathematics Studies, vol. 170. Princeton University Press, Princeton, NJ (2009)
Lurie, J.: (Infinity,2)-Categories and the Goodwillie Calculus I. ArXiv e-prints, May (2009)
Lurie, J.: Higher Algebra. preprint, May (2011)
Lurie, J.: Algebraic K-Theory and Manifold Topology. Lecture notes available the author’s website, (2014)
Poguntke, T.: Higher Segal structures in algebraic \( K \)-theory. (2017) arXiv preprint arXiv:1709.06510
Waldhausen, F.: Algebraic \(K\)-theory of spaces. In Algebraic and geometric topology (New Brunswick, N.J., 1983), volume 1126 of Lecture Notes in Math., pp. 318–419. Springer, Berlin (1985)
Acknowledgements
It is a pleasure to thank Rune Haugseng, Gustavo Jasso, Dima Kaledin, Mikhail Kapranov, Jacob Lurie, Thomas Nikolaus, Thomas Poguntke, Vadim Schechtman, Ed Segal, and Nicolo Sibilla for inspiring conversations that helped shape my perspective on the material presented in this work. Specifically, I would like to thank Mikhail Kapranov and Vadim Schechtman for many discussions on perverse schobers, which are one of the sources of inspiration for this work, and I am indebted to Thomas Nikolaus for conversations which convinced me to focus on 2-categorical methods. Finally, I am very grateful to an anonymous referee for the careful reading and many comments which helped improve the text.
Funding
Open Access funding enabled and organized by Projekt DEAL.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.





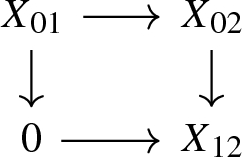
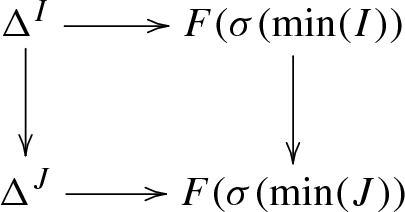




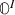 is I,
is I, of morphisms between objects i and j is the poset consisting of those subsets
of morphisms between objects i and j is the poset consisting of those subsets 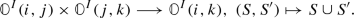
 of 2-categories,
of 2-categories,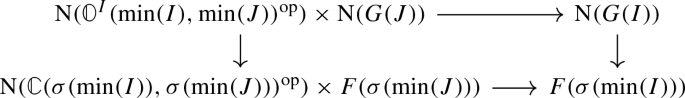
 is a locally Cartesian fibration which is Cartesian over every thin 2-simplex of
is a locally Cartesian fibration which is Cartesian over every thin 2-simplex of 

 .
.



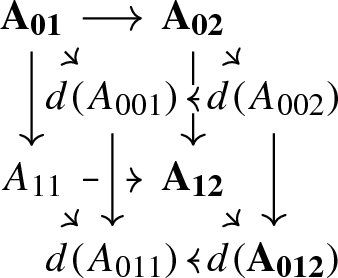
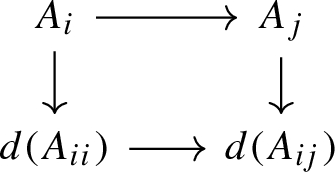
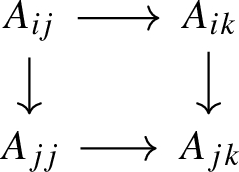
 maps edges corresponding to strictly commutative triangles to
maps edges corresponding to strictly commutative triangles to  .
.




 with respect to the locally Cartesian fibration
with respect to the locally Cartesian fibration  . Then, for every
. Then, for every 