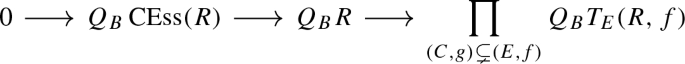The topological nilpotence degree of a Noetherian unstable algebra

Abstract

We investigate the topological nilpotence degree, in the sense of Henn–Lannes–Schwartz, of a connected Noetherian unstable algebra R. When R is the mod p cohomology ring of a compact Lie group, Kuhn showed how this invariant is controlled by centralizers of elementary abelian p-subgroups. By replacing centralizers of elementary abelian p-subgroups with components of Lannes’ T-functor, and utilizing the techniques of unstable algebras over the Steenrod algebra, we are able to generalize Kuhn’s result to a large class of connected Noetherian unstable algebras. We show how this generalizes Kuhn’s result to more general classes of groups, such as groups of finite virtual cohomological dimension, profinite groups, and Kac–Moody groups. In fact, our results apply much more generally, for example, we establish results for p-local compact groups in the sense of Broto–Levi–Oliver, for connected H-spaces with Noetherian mod p cohomology, and for the Borel equivariant cohomology of a compact Lie group acting on a manifold. Along the way we establish several results of independent interest. For example, we formulate and prove a version of Carlson’s depth conjecture in the case of a Noetherian unstable algebra of minimal depth.

1 Introduction

1.1 Motivation and overview

When G is a compact Lie group, or even just a finite group, the mod p cohomology ring $H_{G}^* {:}{=} H^*(BG;\mathbb {F}_p)$ can be extremely complicated. Nonetheless, the global structure of the ring is better understood. This has its origin in Quillen’s work on equivariant cohomology [52, 53]. Quillen introduced the category $\mathbf{A} _G$ of elementary abelian p-subgroups of G, with morphisms those group homomorphisms induced by conjugation in G. He then proved that the restriction maps induced a morphism

which is an $\mathcal {F}$-isomorphism, that is, each element in the kernel of $q_1$ is nilpotent, and for each element y in the inverse limit, there exists an integer n with $y^{p^n}$ in the image of $q_1$. Using this, Quillen showed that the Krull dimension of $H_G^*$ is the maximal rank of an elementary abelian p-subgroup of G.

The cohomology $H_G^*$ has an action of the Steenrod algebra $\mathcal {A}$, and is in fact an unstable $\mathcal {A}$-module (see Sect. 2.2). Quillen’s theorem can be restated internally in the category of unstable modules over the Steenrod algebra. In fact, Henn et al. [34] do much more than this. The category of unstable modules $\mathcal {U}$ has a filtration (the nilpotent filtration)

$$\begin{aligned} \mathcal {U} \supseteq {{\,\mathrm{Nil}\,}}_1 \supseteq {{\,\mathrm{Nil}\,}}_2 \supseteq \cdots \end{aligned}$$

first introduced by Schwartz [56]. In general, the category ${{\,\mathrm{Nil}\,}}_n$ is the smallest localizing subcategory of $\mathcal {U}$ containing all n-fold suspensions of unstable modules (we refer the reader to Sect. 2.3 for more details, and further characterizations of ${{\,\mathrm{Nil}\,}}_n$).

Using the general theory of localization in abelian categories, for any unstable module M over the Steenrod algebra there is an associated localization functor $\lambda _n :M \rightarrow L_nM$ which is localization away from ${{\,\mathrm{Nil}\,}}_n$. Quillen’s map is precisely localization away from ${{\,\mathrm{Nil}\,}}_1$ for $M = H_G^*$. Henn, Lannes, and Schwartz introduced the following invariant, which we call the topological nilpotence degree of M.

Definition 1.1

Let M be an unstable module, then the topological nilpotence degree of M is

$$\begin{aligned} d_0(M) = \inf \{ k \in \mathbb {N} | \lambda _{k+1}M \text { is a monomorphism}\}. \end{aligned}$$

For example, $d_0(H_G^*) = 0$ when the cohomology is detected by elementary abelian subgroups, for example, in the case of the mod 2 cohomology of symmetric groups. We note that if R is a Noetherian unstable algebra, then Henn, Lannes, and Schwartz prove that $d_0(R)$ is a finite number.

In [34] Henn, Lannes, and Schwartz gave a rough upper bound for $d_0(H_G^*(X))$, the mod p Borel-equivariant cohomology of a compact Lie group G acting on a manifold X. More recently, the case where X is a point has been considered by Kuhn, who proved the following result [36, 37]. In this, if G is a compact Lie group with maximal central elementary abelian p-subgroup C(G), we let e(G) denote the top degree of a generator (with respect to a minimal generating set) of the finitely generated $H_G^*$-module $H_{C(G)}^*$, i.e., the top degree of $\mathbb {F}_p \otimes _{H_G^*}H^*_{C(G)}$.

Theorem 1.2

(Kuhn) Let G be a compact Lie group, then

$$\begin{aligned} d_0(H_G^*) \le \max _{E < G}\{ e(C_G(E)) - \dim (C_G(E))\}. \end{aligned}$$

The theorem is actually a combination of several results. Kuhn first defines the central essential ideal, ${{\,\mathrm{CEss}\,}}(G)$, of a compact Lie group as the kernel of the map

Here the product is taken over those elementary abelian p-subgroups E of G for which C(G) is strictly contained in E, and the map is the map induced by the inclusions $C_G(E) \le G$. He then shows that

$$\begin{aligned} d_0(H_G^*) = \max \{ d_0({{\,\mathrm{CEss}\,}}(C_G(E))) \mid E < G\} \end{aligned}$$

(1.3)

and

$$\begin{aligned} d_0({{\,\mathrm{CEss}\,}}(G)) \le e(G) - \dim (G). \end{aligned}$$

(1.4)

for any compact Lie group G. Combining these two results gives Theorem 1.2.

We make the following remarks about this theorem.

• (1) As noted by Kuhn, it suffices in Theorem 1.2 to only consider those E which contain C(G).

• (2) By [37, Theorem 2.30] the central essential ideal ${{\,\mathrm{CEss}\,}}(G)$ is non-zero if and only the cohomology $H_G^*$ has depth equal to the rank c(G) of the maximal central elementary abelian p-group C(G).

• (3) The appearance of $-\dim (G)$ in the theorem comes from Symonds’ theorem [58] that the Castelnuovo–Mumford regularity ${{\,\mathrm{Reg}\,}}(H_G^*)$ (see Sect. 4.3) is less than or equal to $-\dim (G)$.

Using these three remarks, one could restate Kuhn’s theorem in the following way:

$$\begin{aligned} d_0(H_G^*) \le \underset{\begin{array}{c} C(G) \le E < G \\ {{\,\mathrm{depth}\,}}(H_{C_G(E)}^*) = c(C_G(E)) \end{array}}{\max }\{ e(C_G(E)) + {{\,\mathrm{Reg}\,}}(H_{C_G(E)}^*)\}. \end{aligned}$$

We state it in this way, as this is closer to the generalization we prove below.

1.2 Unstable algebras and the topological nilpotence degree

In the previous section we saw that the topological nilpotence degree of $H_G^*$ can be bounded by invariants coming from the cohomology of elementary abelian p-subgroups of G. In order to generalize this to an arbitrary unstable Noetherian algebra R we need to explain what plays the role of the centralizer of R. For this, we use Lannes’ T-functor [39].

We recall in Sect. 2.2 that for any pair (E, f) such that E is an elementary abelian group and f is a finite morphism $R \rightarrow H_E^*$ of unstable algebras, we can produce a new unstable algebra $T_E(R;f)$, along with a canonical map $\rho = \rho _{R,(E,f)} :R \rightarrow T_E(R;f)$. If $R = H_G^*$, and $E < G$ is an elementary abelian p-subgroup, then the fundamental computation of Lannes is that $T_E(H_G^*;{{\,\mathrm{res}\,}}_{G,E}^*) \cong H_{C_G(E)}^*$, where ${{\,\mathrm{res}\,}}_{G,E}^* :H_G^* \rightarrow H_E^*$ is the induced map, and $\rho :H_G^* \rightarrow H_{C_G(E)}^*$ is simply the map induced by the inclusion $C_G(E) \rightarrow G$. Inspired, by this Dwyer and Wilkerson [22] used the components of the T-functor to define centrality in a Noetherian unstable algebra. In particular, we say that (E, f) is central if $\rho _{R,(E,f)} :R \rightarrow T_E(R;f)$ is an isomorphism.

Pairs (E, f) (not necessarily central) as considered above naturally assemble into a category $\mathbf{A} _R$, known as Rector’s category (see Sect. 2.1). This category has the property that every endomorphism is an isomorphism, and as such the set of isomorphism classes of objects forms a poset, where

$$\begin{aligned}{}[(E,f)] \le [(V,g)] \quad \text { if and only if } \quad {{\,\mathrm{Hom}\,}}_\mathbf{A _R}((E,f),(V,g)) \ne \emptyset \end{aligned}$$

Using work of Dwyer and Wilkerson, we prove the following result.

Theorem A

(Theorem 3.13) Let R be a connected Noetherian unstable algebra, then there exists a unique (up to isomorphism) maximal central element $(C,g) \in \mathbf{A} _R$ with respect to the above poset structure.

If $R = H_G^*$ for a finite p-group G with group-theoretic center C(G), then $C = C(G)$, however this does not hold in general for a compact Lie group. Instead, there is a monomorphism $C(G) \rightarrow C$, which need not be an isomorphism in general, see Example 3.15 for an example due to Mislin. We refer to a choice of representative for the central element as the center of R, and write $(E,f) \subseteq (V,g)$ if $[(E,f)] \le [(V,g)]$.

We now have the following dictionary between the usual group-theoretic notions and their analogs in the theory of unstable algebras.

Group theory	Unstable algebra
Group cohomology $H_G^*$	Noetherian unstable algebra R
Quillen category $\mathbf{A} _G$	Rector’s category $\mathbf{A} _R$
Cohomology of the centralizer $H^*_{C_G(E)}$	Component of Lannes T-functor $T_E(R;f)$
Maximal central elementary abelian p-subgroup, $C(G) <G$	Center of R, $(C,g) \in \mathbf{A} _R$

Inspired by Kuhn’s work, the following is the main result of this paper, and is a generalization of Theorem 1.2 to certain Noetherian connected unstable algebras. We note that the technical hypothesis mentioned in the theorem is always satisfied if $p = 2$ or if R is concentrated in even degrees. Here, if R is an unstable algebra with center (C, g) we let c(R) denote the rank of the C, and let e(R) denote the top degree of $\mathbb {F}_p \otimes _{R}T_E(R;f)$.

Theorem B

(Theorem 5.1) Let R be a connected Noetherian unstable algebra with center (C, g), and suppose that $T_E(R;f)$ satisfies the assumptions of Hypothesis 4.20 for all $(C,g) \subseteq (E,f)$, then

$$\begin{aligned} d_0(R) \le \underset{\begin{array}{c} (C,g) \subseteq (E,f) \in \mathbf{A} _R \\ {{\,\mathrm{depth}\,}}(T_E(R;f)) = c(T_E(R;f)) \end{array}}{\max }\{e(T_E(R;f)) + {{\,\mathrm{Reg}\,}}(T_E(R;f)) \}. \end{aligned}$$

1.3 The central essential ideal of a Noetherian unstable algebra

The proof of Theorem B is given by proving the analogs of (1.3) and (1.4) for an arbitrary connected Noetherian unstable algebra. To do this, we first define the central essential ideal of a Noetherian unstable algebra R with center (C, g) as the unstable algebra fitting in the left exact sequence

$$\begin{aligned} 0 \rightarrow {{\,\mathrm{CEss}\,}}(R) \rightarrow R \rightarrow \prod _{(C,g) \subsetneq (E,f)} T_E(R;f) \end{aligned}$$

where the product is taken over the maps $\rho _{R,(E,f)}$. This does not depend on the choice of representative for the center of R.

For G a finite group, Kuhn has proved that the Krull dimension of ${{\,\mathrm{CEss}\,}}(G)$ is at most the rank of C. The proof uses a result about transfers due to Carlson [16] that is not available for a general unstable algebra. We instead use $\mathcal {U}$-technology to prove the following result, which is crucial in the sequel.

Theorem C

(Theorem 4.3) Let R be a connected Noetherian unstable algebra with center (C, g), then the Krull dimension of ${{\,\mathrm{CEss}\,}}(R)$ is at most the rank of C.

This theorem is used crucially in the next result, with is the analog of (1.4). If R is a Noetherian unstable algebra with center (C, g), then the image of $g :R \rightarrow H_C^*$ is either a polynomial algebra (when $p = 2$) or a polynomial tensor an exterior algebra (when $p >2$). In particular, there always exists a subalgebra $B \subset R$ such that $B \rightarrow {{\,\mathrm{Im}\,}}(g)$ is an isomorphism. Borrowing terminology from Kuhn, we call such a B a Duflot algebra. The technical hypothesis Hypothesis 4.20 mentioned previously is that the Duflot algebra is polynomial which, as noted, is automatic if $p = 2$ of if R is concentrated in even degrees. Our analog of (1.4) is the following.

Theorem D

(Theorems 4.24 and 4.25) Let R be a connected Noetherian unstable algebra at the prime p with center (C, g) satisfying Hypothesis 4.20, then if ${{\,\mathrm{CEss}\,}}(R) \ne 0$ we have

$$\begin{aligned} d_0({{\,\mathrm{CEss}\,}}(R)) \le e(R) + {{\,\mathrm{Reg}\,}}(R). \end{aligned}$$

Moreover, ${{\,\mathrm{CEss}\,}}(R) \ne 0$ if and only if ${{\,\mathrm{depth}\,}}(R) = {{\,\mathrm{rank}\,}}(C)$. In this case, ${{\,\mathrm{CEss}\,}}(R)$ is a Cohen–Macaulay R-module of dimension ${{\,\mathrm{rank}\,}}(C)$.

The statement that if ${{\,\mathrm{depth}\,}}(R) = {{\,\mathrm{rank}\,}}(C)$, then ${{\,\mathrm{CEss}\,}}(R) \ne 0$ can be considered a form of Carlson’s depth conjecture (see [19, Question 12.5.7]) in the case of a Noetherian unstable algebra of minimal depth, see also the discussion in Sect. 4.3. Indeed, we always have ${{\,\mathrm{depth}\,}}(R) \ge {{\,\mathrm{rank}\,}}(C)$ by the author’s generalized version of Duflot’s theorem [29], see also Corollary B.7 in this paper (Carlson considers the case $R = H_G^*$ for G a finite group).

The proof of Theorem B then follows the same strategy as Kuhn; we show in Proposition 5.17 that for any connected Noetherian unstable algebra R with center (C, g) we have

$$\begin{aligned} d_0(R) \le \max _{(C,g) \subseteq (E,f) \in \mathbf{A} _R}\{d_0({{\,\mathrm{CEss}\,}}(T_E(R;f))) \}. \end{aligned}$$

Combining this with the bound coming from Theorem D then gives the result.

1.4 The topological nilpotence degree for the mod p cohomology of groups

The components of Lannes T-functor have been computed for the mod p cohomology of a large number of classes of groups, not just for compact Lie groups. In all these cases, Rector’s category $\mathbf{A} _{H_G^*}$ can be identified with Quillen’s category $\mathbf{A} _G$ with objects the elementary abelian p-subgroups of G, and central elements in $\mathbf{A} _{H_G^*}$ correspond to elementary abelian p-subgroups $E < G$ for which $C_G(E) \rightarrow E$ is a mod p cohomology isomorphism. Borrowing terminology from Mislin [45], we call such subgroups cohomologically p-central. Our results imply that there is (up to isomorphism) a unique maximal cohomologically p-central subgroup $C_p(G)$, whose rank may be greater than the rank of the usual group-theoretic center of G.

Theorem B then gives rise to the following computation of the topological nilpotence degree of the mod p cohomology of these groups.

Theorem E

(Theorem 6.7) Assume we are in one of the following cases:

• (1) G is a compact Lie group.

• (2) G is a discrete group for which there exists a mod p acyclic G-CW complex with finitely many G-cells and finite isotropy groups.

• (3) G is a profinite group such that the continuous mod p cohomology $H_G^*$ is finitely generated as an $\mathbb {F}_p$-algebra.

• (4) G is a group of finite virtual cohomological dimension such that $H_G^*$ is finite generated as an $\mathbb {F}_p$-algebra.

• (5) G is a Kac–Moody group.

Then, for any prime p we have

$$\begin{aligned} d_0(H_G^*) \le \underset{\begin{array}{c} C_p(G) \le E \in \mathbf{A} _G \\ {{\,\mathrm{depth}\,}}(H_{C_{{G}}(E)}^*) = c(C_{{G}}(E)) \end{array}}{\max }\{e(H_{C_{{G}}(E)}^*) + {{\,\mathrm{Reg}\,}}(H_{C_{{G}}(E)}^*)\} \end{aligned}$$

where $c(C_G(E))$ is the rank of the maximal cohomologically p-central subgroup of G.

Of course, by including additional summands, one can rewrite this as

$$\begin{aligned} d_0(H_G^*) \le \max _{E < G}\{ e(H^*_{C_G(E)}) + {{\,\mathrm{Reg}\,}}(H^*_{C_G(E))})\} \end{aligned}$$

to give a result analogous to Theorem 1.2.

We have similar results in the case of the mod p cohomology of p-local compact groups [10], see Sect. 6.2.

Example 1.5

In Example 6.10, we compute that $1 \le d_0(H^*_{{{\,\mathrm{GL}\,}}_2(\mathbb {Z}_3)}) \le 2$ when $p = 3$. Similarly, in Example 6.11 we compute that $d_0(H^*_{S_2}) = 2$ at the prime 3, where $S_2$ is the Morava stabilizer group which features prominently in the chromatic approach to stable homotopy theory. $\square$

Finally, in an appendix, we show that a slight variation of our methods shows the following.

Theorem F

(Theorem A.2) Let G be a compact Lie group, X a manifold, and suppose that the Duflot algebra for $H_{C_G(E)}^*(X^E)$ is polynomial for all $C(G;X) \le E$, then

$$\begin{aligned} d_0(H_G^*(X)) \le \max _{C(G,X) \le E < G}\{e(C_G(E),X^E) + \dim (X^E) - \dim (C_G(E)) \} \end{aligned}$$

1.5 Notation

The following is some of the notation used in this paper.

$\mathcal {U}$	The category of unstable modules over the Steenrod algebra (Sect. 2.1)
$\mathcal {K}$	The category of unstable algebras over the Steenrod algebra (Sect. 2.1)
R	Generic unstable algebra (Sect. 2.1)
E	Elementary abelian p-group
$\mathbf{A} _R$	Rector’s category associated to a Noetherian unstable algebra R (Sect. 2.1)
(E, f)	Element of Rector’s category $\mathbf{A} _R$ (Sect. 2.1)
$T_E$	Lannes’ T-functor (Sect. 2.2)
$d_0M$	Topological nilpotence degree of an unstable module (Sect. 2.3)
${{\,\mathrm{CEss}\,}}(R)$	The central essential ideal of a Noetherian unstable algebra (Sect. 4.1)
$P_CM$	The module of primitives for a comodule (Sect. 4.2)
$Q_BM$	The space of indecomposables for a B-module M (Sect. 4.2)
${{\,\mathrm{Reg}\,}}(M)$	The regularity of a module M (Sect. 4.3)
$\mathcal {F}$	Fusion system associated to a discrete p-toral group S (Sect. 6.2)
$\mathcal {F}^e$	Full subcategory of $\mathcal {F}$ consisting of fully centralized
	elementary abelian p-subgroups of S (Sect. 6.2)
$H_{\mathfrak m}^i(M)$	The local cohomology of a module M (Appendix B)

1.6 Conventions

We will always write $H_G^*(X)$ for the mod p G-equivariant cohomology of a space X. In particular, taking X to be a point, then $H_G^*$ denotes the group cohomology of G. For a space X we will always write $H^*(X)$ for the mod p cohomology of X; thus $H_G^* = H^*(BG)$. If R is an augmented $\mathbb {F}_p$-algebra we will write $\epsilon _R :R \rightarrow \mathbb {F}_p$ for the canonical map; in the case of $R=H^*(X)$, we will often abbreviate this to $\epsilon _X$, or even $\epsilon _G$ if $X = BG$ .

2 Noetherian unstable modules, unstable algebras, and Lannes’ T-functor

We being with a review of the theory of unstable modules, unstable algebras, and Lannes’ T-functor. We introduce the fundamental category $\mathbf{A} _R$, also known as Rector’s category, of a Noetherian unstable algebra R. Finally, we review Schwartz’s nilpotent filtration of the category of unstable modules.

2.1 Unstable modules, unstable algebras and Rector’s category

Much of this section is well-known, and a useful reference is [57]. We first start with the definition of the categories of unstable modules and unstable algebras over the mod p Steenrod algebra. We let $\mathcal {A}$ denote the mod p Steenrod algebra, for which we assume the reader is familiar with.

Definition 2.1

An unstable $\mathcal {A}$-module M is a graded $\mathcal {A}$-module such that for all $x \in M$

• (1) ${{\,\mathrm{Sq}\,}}^ix = 0$ for $i > |x|$, if $p = 2$;

• (2) $\beta ^eP^ix = 0$ for all $2i+e > |x|$, if p is odd and $e \in \{ 0, 1\}$.

We let $\mathcal {U} \subset {{\,\mathrm{Mod}\,}}_{\mathcal {A}}$ denote the full subcategory of graded $\mathcal {A}$-modules whose objects are unstable $\mathcal {A}$-modules.

We observe that if $M \in \mathcal {U}$, then M is trivial in negative degrees. If $M^0 \cong \mathbb {F}_p$, then we say the M is connected. The category of unstable modules has a suspension functor $\Sigma :\mathcal {U} \rightarrow \mathcal {U}$: given an $\mathcal {A}$-module M, we define $(\Sigma M)^n \cong M^{n-1}$, with $\mathcal {A}$-module structure given by $\theta (\Sigma m) = (-1)^{|\theta |}\Sigma \theta (m)$ for all $m \in M, \theta \in \mathcal {A}$.

The mod p cohomology of a space $H^*(X)$ is always an unstable module. In fact, it also has an algebra structure satisfying certain properties, which leads to the following definition.

Definition 2.2

An unstable $\mathcal {A}$-algebra R is an unstable $\mathcal {A}$-module, together with maps $\mu :R \otimes R \rightarrow R$ and $\eta :\mathbb {F}_p \rightarrow R$ which determine a commutative, unital, $\mathbb {F}_p$-algebra structure on R and such that the Cartan formula holds (equivalently, $\phi$ is $\mathcal {A}$-linear) and

$$\begin{aligned} {{\,\mathrm{Sq}\,}}^nx = x^2&\text { if } p = 2 \text { and } n = |x|, \nonumber \\ P^nx = x^p&\text { if } p > 2 \text { and } 2n = |x|. \end{aligned}$$

(2.3)

We let $\mathcal {K}$ denote the category of unstable algebras over $\mathcal {A}$. This is the category with objects unstable algebras, and morphisms degree preserving maps which are both $\mathcal {A}$-linear and maps of graded algebras.

Finally, we say that R is a Noetherian unstable algebra if R is finitely generated as an algebra.

Example 2.4

The mod-p cohomology of an elementary abelian p-group E of rank n is of fundamental importance in the theory of unstable algebras over the Steenrod algebra. We recall that

$$\begin{aligned} H_E^* \cong \mathbb {F}_2[x_1,\ldots ,x_n] \end{aligned}$$

with $|x_i| = 1$ when $p = 2$, and

$$\begin{aligned} H_E^* \cong \mathbb {F}_p[\beta (y_1),\ldots ,\beta (y_n)] \otimes \Lambda _{\mathbb {F}_p}(y_1,\ldots ,y_n) \end{aligned}$$

where $|y_i| = 1$ and $\beta$ denotes the Bockstein homomorphism associated to the sequence $0 \rightarrow \mathbb {Z}/p \rightarrow \mathbb {Z}/p^2 \rightarrow \mathbb {Z}/p \rightarrow 0$. In particular, $H_E^*$ is a Gorenstein ring of dimension n. Its importance comes from the fact that it is an injective object in the category $\mathcal {U}$, see [15, 43, 44].

Finally, we note that the group homomorphism $E \times E \rightarrow E$ given by multiplication induces a homomorphism $H_E^* \rightarrow H^*_{E \times E} \cong H_E^* \otimes H_E^*$, making $H_E^*$ into a primitively generated Hopf algebra. $\square$

Given an unstable algebra R, we can also define a category $R-\mathcal {U}$, whose objects are unstable ${{\,\mathrm{\mathcal {A}}\,}}$-modules M together with $\mathcal {A}$-linear structure maps $R \otimes M \rightarrow M$ which make M into an R-module, and whose morphisms are the $\mathcal {A}$-linear maps which are also R-linear. The full subcategory of $R-\mathcal {U}$ consisting of the finitely generated R-modules will be denoted $R_{fg}-\mathcal {U}$.

Example 2.5

Let G be a compact Lie group and X a manifold, then the Borel equivariant cohomology $H_G^*(X)$ is an object of $R_{fg}-\mathcal {U}$ for $R = H_G^*$, see [52, 53].

The following categories, first studied by Rector [54], will play a crucial role in the sequel.

Definition 2.6

Let R be a Noetherian unstable algebra, then the category $\mathbf{V} _R$ is the category with objects (E, f) where E is an elementary abelian p-group, and $f :R \rightarrow H_E^*$ is a homomorphism of unstable algebras. A morphism $\alpha :(E,f) \rightarrow (V,g)$ is a morphism $\alpha ^* :H_V^* \rightarrow H_E^*$ of unstable algebras (equivalently, a group homomorphism $\alpha :E \rightarrow V$) such that the diagram

commutes.

Rector’s category $\mathbf{A} _R$ is the full subcategory of $\mathbf{V} _R$ consisting of those (E, f) where $f :R \rightarrow H_E^*$ is a finite morphism, i.e., $H_E^*$ is a finitely generated R-module via f.

We observe that if $\alpha :(E,f) \rightarrow (V,g)$ is a morphism in $\mathbf{A} _R$, then $\alpha ^* :H_E^* \rightarrow H_V^*$ necessarily arises form a monomorphism $E \rightarrow V$ of elementary abelian p-groups. We have the following properties of $\mathbf{A} _R$, where we recall that a Noetherian unstable algebra always has finite Krull dimension.

Proposition 2.7

Let R be a Noetherian unstable algebra of Krull dimension d.

• (1) The category $\mathbf{A} _R$ has a finite skeleton.

• (2) For each $(E,f) \in \mathbf{A} _R$ we have ${{\,\mathrm{rank}\,}}(E) \le d$. In fact,

  $$\begin{aligned} d = \max \{ {{\,\mathrm{rank}\,}}(E) \mid (E,f) \in \mathbf{A} _R \}. \end{aligned}$$

Proof

Part (1) is due to Rector [54, Proposition 2.3(1)], while (2) is an algebraic consequence of Rector’s $\mathcal {F}$-isomorphism theorem [54, Theorem 1.4], as extended to the case $p >2$ by Broto and Zarati [13]. $\square$

Remark 2.8

Given a pair $(E,f) \in \mathbf{V} _R$, choosing an element $e \in E$ is equivalent to giving a homomorphism $\chi _e :\mathbb {Z}/p \rightarrow E$ with $\chi _e(1) = e$. Let $f_e :R \rightarrow H_{\mathbb {Z}/p}^*$ denote the composite $R \xrightarrow {f} H_E^* \xrightarrow {\chi _e^*} H_{\mathbb {Z}/p}^*$. Then, the kernel of f, denoted $\ker (f)$, is the set consisting of all $e \in E$ with the property that $f_e$ is trivial above dimension 0 [22, Definition 4.3]. By [22, Proposition 4.4], the pair $(E,f) \in \mathbf{A} _R$ (that is, the morphism $f :R \rightarrow H_E^*$ is finite) if and only if $\ker (f) = \{ 0 \}$.

Moreover, if R is connected and Noetherian, then for any pair $(E,f) \in \mathbf{V} _R$, $\ker (f)$ is a subgroup of E, and $f :R \rightarrow H_E^*$ extends uniquely to a map $\tilde{f} :R \rightarrow H_{E/\ker (f)}^*$ such that the pair $(E/\ker (f),\tilde{f})$ is in $\mathbf{A} _R$ [22, Proposition 4.8]. Here, ‘extends’ means that the evident diagram

commutes. This construction is functorial; the assignment $(E,f) \mapsto (E/\ker (f),\tilde{f})$ defines a functor $\text {rec} :\mathbf{V} _R \rightarrow \mathbf{A} _R$, see [30, Section 4.6] for further discussion.

Remark 2.9

An extension of the work of Rector to the case of unstable algebras of finite transcendence degree d is given by Henn et al. in [33, Part II]. Let $V_d = (\mathbb {Z}/p)^d$, considered as a profinite right ${{\,\mathrm{End}\,}}V_d$-set i.e., a profinite set with a continuous right action of the monoid ${{\,\mathrm{End}\,}}V_d$. Let $\mathcal {PS}-{{\,\mathrm{End}\,}}V_d$ denote the category whose objects are profinite right ${{\,\mathrm{End}\,}}V_d$-sets, and whose morphisms are maps of profinite sets respecting the ${{\,\mathrm{End}\,}}V_d$-action, and let $\mathcal {K}_d$ denote the category of unstable algebras of transcendence degree d. In [33, Theorem II.2.4] Henn, Lannes, and Schwartz prove that the functor

$$\begin{aligned} s_d :\mathcal {K}_d \rightarrow (\mathcal {PS}-{{\,\mathrm{End}\,}}V_d)^{\text {op}}, \quad R \mapsto {{\,\mathrm{Hom}\,}}_{\mathcal {K}}(R,H_{V_d}^*) \end{aligned}$$

induces an equivalence of categories $\mathcal {K}_d/{{\,\mathrm{Nil}\,}}_1 \rightarrow (\mathcal {PS}-{{\,\mathrm{End}\,}}V_d)^{\text {op}}$, where the inverse equivalence is induced by the functor

$$\begin{aligned} b_d :(\mathcal {PS}-{{\,\mathrm{End}\,}}V_d)^{\text {op}} \rightarrow \mathcal {K}_d, \quad S \mapsto {{\,\mathrm{Hom}\,}}_{\mathcal {PS}-{{\,\mathrm{End}\,}}V_d}(S,H_{V_d}^*). \end{aligned}$$

Here, the category $\mathcal {K}/{{\,\mathrm{Nil}\,}}_1$ is the quotient category of $\mathcal {K}$ given by inverting all the $\mathcal {F}$-isomorphisms. In particular, the natural map $R \rightarrow (b_d \circ s_d)(R)$ is an $\mathcal {F}$-isomorphism for all unstable algebras $R \in \mathcal {K}_d$.

Moreover, if S is a Noetherian ${{\,\mathrm{End}\,}}V_d$-set in the sense of [33, Definition 5.8], then $b_d(S)$ is a Noetherian unstable algebra, and conversely if R is a Noetherian unstable algebra, then $s_d(R)$ is a Noetherian ${{\,\mathrm{End}\,}}V_d$-set [33, Theorem 7.1]. Moreover, to such an S, one can associate a category $\mathcal {R}(S)$ which, in the case where $S = s_d(R)$ for a Noetherian unstable algebra R, is Rector’s category $\mathbf{A} _R$, see the remark on page 1097 of [33]. Finally, Henn, Lannes, and Schwartz define the notion of the kernel of an element of an ${{\,\mathrm{End}\,}}V_d$-set, see [33, Section 5.2]. If R is a connected Noetherian unstable algebra, and $(E,f) \in \mathbf{A} _R$, then f is an element of $s_d(R)$, and the kernel $\ker (f)$ agrees with that considered in Remark 2.8.

2.2 Lannes’ T-functor

In this section we review Lannes’ T-functor, and some standard properties of it. This section overlaps with [29, Section 2].

We recall that Lannes’ T-functor $T_E$ is left adjoint to $- \otimes H_E^*$ on the category of unstable modules, i.e., there is an isomorphism

$$\begin{aligned} {{\,\mathrm{Hom}\,}}_{\mathcal {U}}(T_EM,N) \cong {{\,\mathrm{Hom}\,}}_{\mathcal {U}}(M,H_E^* \otimes N), \end{aligned}$$

for $M,N \in \mathcal {U}$. Although it is relativity elementary to see that such a functor exists (for example, by the adjoint functor theorem), the following results of Lannes [39] are far more surprising.

Theorem 2.10

(Lannes) The functor $T_E :\mathcal {U} \rightarrow \mathcal {U}$ is exact, and commutes with tensor products. Moreover, it restricts to a functor $T_E :\mathcal {K} \rightarrow \mathcal {K}$.

For any unstable algebra R, we write $T^0_ER$ for the $\mathbb {F}_p$-vector space of degree 0 elements of $T_ER$. By (2.3) this is a p-Boolean algebra, i.e., a commutative, unital, $\mathbb {F}_p$-algebra in which $x^p = x$ for any element x.

Given a $\mathcal {K}$-morphism $f :R \rightarrow H_E^*$, the adjoint is a map $T_ER \rightarrow \mathbb {F}_p$. Since $\mathbb {F}_p$ is concentrated in degree 0, we get a map $T^0_ER \rightarrow \mathbb {F}_p$. We can then define

$$\begin{aligned} T_E(R;f) = T_ER \otimes _{T^0_ER} \mathbb {F}_p(f), \end{aligned}$$

where $\mathbb {F}_p(f)$ denotes $\mathbb {F}_p$ with the $T^0_ER$-module structure coming from the above map. If R is Noetherian, then the T-functor decomposes as a finite direct sum of unstable algebras (see for example the discussion around (2.6) of [29])

$$\begin{aligned} T_E(R) = \bigoplus _{f \in {{\,\mathrm{Hom}\,}}_{\mathcal {K}}(R,H_E^*)}T_E(R;f). \end{aligned}$$

The components $T_E(R;f)$ are better behaved than $T_E(R)$ itself, in the sense that if R is connected, then so are the $T_E(R;f)$. If $M \in R-\mathcal {U}$, then we also define

$$\begin{aligned} T_E(M;f) = T_EM \otimes _{T_E^0R} \mathbb {F}_p(f). \end{aligned}$$

The following is [22, Lemma 3.1].

Lemma 2.11

Let $(E,f) \in \mathbf{V} _R$, then the set ${{\,\mathrm{Hom}\,}}_{\mathcal {K}}(T_E(R;f),S)$ is naturally isomorphic to the set of $\mathcal {K}$-maps $g :R \rightarrow H_E^* \otimes S$ making the diagram

commute, where $\epsilon _S :S \rightarrow S^0$ is projection onto the degree 0 component, and $\xi _S :\mathbb {F}_p \rightarrow S^0$ is the unit inclusion.

Given a morphism $\phi :T_E(R;f) \rightarrow S$ in $\mathcal {K}$ as in the previous lemma, we write $\phi ^{\#}$ for the corresponding map $R \rightarrow H_E^* \otimes S$, and call this the adjoint of $\phi$. Likewise, given a map $g :R \rightarrow H_E^* \otimes S$ satisfying the conditions of the lemma, we call the corresponding map $T_E(R;f) \rightarrow H_E^*$ the adjoint of g.

We will need the following maps, where $\epsilon _E :H_E^* \rightarrow \mathbb {F}_p$ is the canonical map.

Definition 2.12

Let R be a unstable algebra, and $(E,f) \in \mathbf{V} _R$. We define maps:

• (1) $\eta _{R,(E,f)} :R \rightarrow H_E^* \otimes T_E(R;f)$ as the adjoint of $\text {id} :T_E(R;f) \rightarrow T_E(R;f)$.

• (2) $\rho _{R,(E,f)} :R \rightarrow T_E(R;f)$ as the composite map $(\epsilon _{E} \otimes 1 )\circ \eta _{R,(E,f)}$.

• (3) $\kappa _{R,(E,f)} :T_E(R;f) \rightarrow H_E^* \otimes T_E(R;f)$ as the adjoint to the composite

  $$\begin{aligned} R \xrightarrow {\eta _{R,(E,f)}} H_E^* \otimes T_E(R;f) \xrightarrow {\Delta \otimes 1} H_E^* \otimes H_E^* \otimes T_E(R;f). \end{aligned}$$

As shown in [34, Section 1.13] for each E, the map $\kappa _{R,(E,f)}$ gives $T_E(R;f)$ the structure of a $H_E^*$-comodule.

Note that any map $g :T_E(R;f) \rightarrow S$ can be written as $T_E(R;f) \xrightarrow {\text {id}} T_E(R;f) \xrightarrow {g} S$, and taking adjoints we see that $g^{\#} :R \rightarrow H_E^* \otimes S$ is isomorphic to the composite $(1 \otimes g) \circ \eta _{R,(E,f)}$. This gives the following, which is the component-wise version of [29, Lemma 2.3].

Lemma 2.13

For any map $g :T_E(R;f) \rightarrow S$ the diagram

commutes.

Proof

As noted, $g^{\#}$ factors as the composite $(1 \otimes g)\circ \eta _{R,(E,f)}$. It follows that

$$\begin{aligned} (\epsilon _E \otimes 1)\circ g^{\#}&\cong (\epsilon _E \otimes 1)\circ (1 \otimes g)\circ \eta _{R,(E,f)}\\&\cong g \circ (\epsilon _E \otimes 1)\circ \eta _{R,(E,f)}\\&\cong g \circ \rho _{R,(E,f)} \end{aligned}$$

as required. $\square$

The next result follows immediately from Lemma 2.13 and the definitions of the maps involved.

Corollary 2.14

We have $\kappa _{R,(E,f)} \circ \rho _{R,(E,f)} \cong \eta _{R,(E,f)}$.

The assignment $(E,f) \mapsto T_E(M;f)$ extends to a functor $\mathbf{V} _R \rightarrow R-\mathcal {U}$; in fact, if R is Noetherian, and $M \in R_{fg}-\mathcal {U}$, then using [30, Corollary 1.12] we even obtain a functor $\mathbf{A} _R \rightarrow R_{fg}-\mathcal {U}$. Given a morphism $\alpha :(E,f) \rightarrow (V,g) \in \mathbf{A} _R$, we will write $T_{\alpha }(g) :T_E(R;f) \rightarrow T_V(R;g)$ for the induced map. By naturality, we deduce the following.

Lemma 2.15

For any morphism $\alpha :(E,f) \rightarrow (V,g) \in \mathbf{A} _R$, there is a commutative diagram

Finally, we have the useful result [34, Lemma 4.8].

Lemma 2.16

(Henn–Lannes–Schwartz) Let R be a Noetherian unstable algebra, $M \in R_{fg}-\mathcal {U}$, and $\alpha :E \rightarrow E'$ an epimorphism. Then for each $f \in {{\,\mathrm{Hom}\,}}_{\mathcal {K}}(R,H_{E'}^*)$ the map $\alpha$ induces an isomorphism

$$\begin{aligned} T_E(M;\alpha ^*f) \xrightarrow {\simeq } T_{E'}(M;f). \end{aligned}$$

Finally, it is worth pointing out the following result, which is a consequence of [39, Proposition 2.1.3].

Lemma 2.17

If R is an unstable algebra concentrated in even degrees, then so are $T_E(R)$ and $T_E(R;f)$ for any $(E,f) \in \mathbf{A} _R$.

Example 2.18

A fundamental computation is that of $T_E(H_G^*)$ where G is a compact Lie group, due to Lannes [38, 39]. More specifically, let $E < G$ be an elementary abelian p-subgroup, with induced map ${{\,\mathrm{res}\,}}_{G,E}^* :H_G^* \rightarrow H_E^*$. The multiplication map $E \times C_E(G) \rightarrow G$ induces a morphism $H_G^* \rightarrow H_E^* \otimes H_{C_E{(G)}}^*$. The adjoint to this gives rise to an isomorphism

$$\begin{aligned} T_E(H_G^*;{{\,\mathrm{res}\,}}_{G,E}^*) \cong H^*_{C_G(E)}. \end{aligned}$$

Moreover, the maps $\eta _{H_G^*,(E,{{\,\mathrm{res}\,}}_{G,E}^*)}$, $\rho _{H_G^*,(E,{{\,\mathrm{res}\,}}_{G,E}^*)}$ and $\kappa _{H_G^*,(E,{{\,\mathrm{res}\,}}_{G,E}^*)}$ are the maps induced on cohomology by the obvious maps

$$\begin{aligned}&E \times C_G(E) \rightarrow G \\&C_G(E) \rightarrow G \\&E \times C_G(E) \rightarrow C_G(E). \end{aligned}$$

Note that the claims of Corollary 2.14 and Lemma 2.16 are clear in this case.

It follows that $T_E(R;f)$ plays the role of the ‘centralizer’ of the pair $(E,f) \in \mathbf{A} _R$. We investigate this analogy further in the following sections. $\square$

2.3 The nilpotent filtration of an unstable algebra

In this section, we review Schwartz’s nilpotent filtration of the category of unstable modules over the Steenrod algebra, and the associated localization functors of Henn, Lannes, and Schwartz. We recall that in the previous section we introduced the categories $\mathcal {U}$ and $\mathcal {K}$ of unstable modules and unstable algebras over the Steenrod algebra respectively. As noted in the introduction, Schwartz [56] introduced a natural filtration on $\mathcal {U}$, known as the nilpotent filtration. We take the following from [34].

Definition 2.19

Let M, N be unstable modules.

• (1) M is called n-nilpotent if and only if every finitely generated submodule admits a filtration such that each filtration quotient is an n-fold suspension.

• (2) The category ${{\,\mathrm{Nil}\,}}_n$ is the full subcategory of $\mathcal {U}$ that contains all n-nilpotent modules.

• (3) N is called ${{\,\mathrm{Nil}\,}}_n$-reduced if and only if ${{\,\mathrm{Hom}\,}}_{\mathcal {U}}(M,N) = 0$ for all $M \in {{\,\mathrm{Nil}\,}}_n$, and ${{\,\mathrm{Nil}\,}}_n$-closed if and only if ${{\,\mathrm{Ext}\,}}_{\mathcal {U}}^i(M,N) = 0$ for $i = 0,1$ and all n-nilpotent modules M.

Further equivalent conditions for n-nilpotent modules, and more information about the nilpotent filtration can be found in [57, Chapter 6], or the fundamental paper of Henn et al. [34].

The nilpotent filtration leads to the following definition [34, Def. 3.5].

Definition 2.20

Let M be an unstable ${{\,\mathrm{\mathcal {A}}\,}}$-module, then the topological nilpotence degree of M is

$$\begin{aligned} d_0M {:}{=} \inf \{ k \in \mathbb {N} | M \text { is } {{\,\mathrm{Nil}\,}}_{k+1}\text {-reduced} \}. \end{aligned}$$

We note that if R is Noetherian, and $M \in R_{fg}-\mathcal {U}$, then $d_0(M)$ is finite [34, Theorem 4.3]. In particular, $d_0(R)$ itself is finite.

There are a number of alternative characterizations of the number $d_0$. For example, the subcategories ${{\,\mathrm{Nil}\,}}_n$ are localizing, and the general theory of localization in abelian categories implies there exists a functor $L_n :\mathcal {U}\rightarrow \mathcal {U}$, and a natural transformation $\lambda _n :1_{\mathcal {U}} \rightarrow L_n$ such that $L_nM$ is ${{\,\mathrm{Nil}\,}}_n$-closed, and $\lambda _n$ has n-nilpotent kernel and cokernel. In this case, we have

$$\begin{aligned} d_0M = \inf \{ k \in \mathbb {N} | \lambda _{k+1}M \text { is a monomorphism}\}. \end{aligned}$$

Further equivalent characterizations can be found in [36, Definition 3.11]. One particular result of interest for us is the following, which is a direct consequence of [34, Theorem 4.9].

Proposition 2.21

Let R be a Noetherian unstable algebra, and $M \in R_{fg}-\mathcal {U}$, then for $n\ge d_0(M)$ there is a monomorphism in $R_{fg}-\mathcal {U}$:

induced by the product of the maps $\eta _{M,(E,f)}$.

Here we write $K^{\le n}$ for the quotient of a graded module K by all elements of degree greater than n. Note that if K is an unstable module, then so is the quotient $K^{\le n}$.

We also have the following properties of $d_0$, which are a combination of [34, Proposition 3.6] and [36, Proposition 3.12].

Proposition 2.22

Let M be an unstable module.

• (1) If M is concentrated in finitely many degrees, then $d_0(M) \le n$, where n is the top degree in which M is non-zero.

• (2) Let $0 \rightarrow M' \rightarrow M \rightarrow M''$ be an exact sequence in $\mathcal {U}$, then $d_0M' \le d_0M$.

• (3) Let $0 \rightarrow M' \rightarrow M \rightarrow M'' \rightarrow 0$ be an exact sequence in $\mathcal {U}$, then $d_0(M) \le \max \{d_0(M'),d_0(M'')\}$.

• (4) $d_0(M \otimes M') = d_0(M) + d_0(M')$.

• (5) $d_0(T_EM) = d_0(M)$.

• (6) If $M \ne 0$, then $d_0(\Sigma ^nM) = d_0(M) + n$.

The topological nilpotence degree of a Noetherian unstable algebra R is related to algebraic nilpotence in the following way, compare [37, Corollary 2.6].

Lemma 2.23

Let R be a connected Noetherian unstable algebra, and define t to be $d_0(R)$ for $p = 2$, or $d_0(R) + \dim (R)$ for p odd. Then t is the maximal integer d such that ${{\,\mathrm{rad}\,}}(R)^d \ne 0$. In particular, for $s > t$, the product of any s nilpotent elements in R is zero.

Proof

Let $d^{{{\,\mathrm{alg}\,}}}(R)$ be the maximal d such that ${{\,\mathrm{rad}\,}}(R)^d \ne 0$, so that our claim is $d^{{{\,\mathrm{alg}\,}}}(R) \le t$. It is clear that

$$\begin{aligned} d^{{{\,\mathrm{alg}\,}}}(H_E^* \otimes T_E(R;f)^{\le d}) \le {\left\{ \begin{array}{ll} d^{{{\,\mathrm{alg}\,}}}(T_E(R;f)^{\le d}) &{} \text { if } p = 2\\ d^{{{\,\mathrm{alg}\,}}}(T_E(R;f)^{\le d}) + {{\,\mathrm{rank}\,}}(E) &{} \text { if } p > 2.\end{array}\right. } \end{aligned}$$

It then follows from Proposition 2.21 that

$$\begin{aligned} d^{{{\,\mathrm{alg}\,}}}(R) \le {\left\{ \begin{array}{ll} \max \limits _{(E,f) \in \mathbf{A} _R}\{d^{{{\,\mathrm{alg}\,}}}(T_E(R;f)^{\le d_0(R)})\} \le d_0(R) &{} \text { if } p = 2\\ \max \limits _{(E,f) \in \mathbf{A} _R}\{d^{{{\,\mathrm{alg}\,}}}(T_E(R;f)^{\le d_0(R)}) +{{\,\mathrm{rank}\,}}(E) \} \le d_0(R) +\dim (R) &{} \text { if } p > 2. \end{array}\right. } \end{aligned}$$

Here we have used that ${{\,\mathrm{rank}\,}}(E) \le \dim (R)$ for each $(E,f) \in \mathbf{A} _R$, see Proposition 2.7(2). It follows that $d^{{{\,\mathrm{alg}\,}}}(R) \le t$ as claimed. $\square$

Remark 2.24

(The case of an odd prime) The cohomology of elementary abelian p-groups (Example 2.4) shows already one significant difference between working at $p = 2$ or working at an odd prime, namely the presence of the exterior classes. Many of the fundamental results of unstable algebras therefore have slightly different forms in the case of odd primes. One way to deal with these problems is to work with the full subcategory $\mathcal {U}' \subseteq \mathcal {U}$ consisting of unstable modules which are non-trivial only in even degrees. There is an obvious forgetful functor $\mathcal {O} :\mathcal {U}' \rightarrow \mathcal {U}$ which has a right adjoint $\widetilde{ \mathcal {O}} :\mathcal {U}\rightarrow \mathcal {U}'$, see [43] for example, which is the largest submodule of M that is concentrated in even degrees, or even more explicitly

$$\begin{aligned} \widetilde{O}M = \bigcap _{\theta \in \mathcal {A}} \ker (\beta \theta :M^{\text {ev}} \rightarrow M). \end{aligned}$$

Similarly, we have the category $\mathcal {K}'$ of unstable algebras concentrated in even degrees. At certain points it will be convenient for us to assume that our unstable algebra comes from $\mathcal {K'}$ (considered naturally as an object in $\mathcal {K}$) when p is odd.

3 The center of a Noetherian unstable algebra

In this section, following Dwyer and Wilkerson, we study central objects of a Noetherian unstable algebra with respect to the objects of $\mathbf{A} _R$. The main new result, given here as Theorem 3.13, is that up to isomorphism there is a maximal such element with respect to a natural poset structure on $\mathbf{A} _R$. We also prove that for each central object $(E,f) \in \mathbf{A} _R$, the unstable algebra R naturally obtains the structure of a $H_E^*$-comodule, which will be crucial for the calculation of $d_0(R)$.

3.1 Central objects of a Noetherian unstable algebra

Throughout this section we assume that R is a connected Noetherian unstable algebra. It would suffice to assume that the module of indecomposables Q(R) is locally finite, i.e., every element of Q(R) is contained in a finite ${{\,\mathrm{\mathcal {A}}\,}}$-submodule, however we have no need for this greater generality.

We observe from Example 2.18 that if $E \le G$ is a central elementary abelian p-subgroup of a compact Lie group, then the map $\rho _{H_G^*,(E,{{\,\mathrm{res}\,}}_{G,E}^*)} :H_G^* \rightarrow T_E(H_G^*;{{\,\mathrm{res}\,}}_{G,E}^*)$ is an isomorphism. Based on this is natural to make the following definition.

Definition 3.1

(Dwyer–Wilkerson) Let R be a connected Noetherian unstable algebra, then a pair $(E,f) \in \mathbf{A} _R$ is called central if $\rho _{R,(E,f)} :R \rightarrow T_E(R;f)$ is an isomorphism.

As noted, given a central elementary abelian p-subgroup E of a compact Lie group G, the pair $(E,{{\,\mathrm{res}\,}}_{G,E}^*)$ is then central inside $\mathbf{A} _{H_G^*}$. We will see later the converse is true if G is a finite p-group, but not in general.

A useful criteria for recognizing central objects is given in [22, Proposition 3.4].

Proposition 3.2

(Dwyer–Wilkerson) A pair $(E,f) \in \mathbf{A} _R$ is central if and only if there exists a $\mathcal {K}$-map $R \rightarrow H_E^* \otimes R$ which, when composed with the projections $H_E^* \otimes R \rightarrow R$ and $H_E^* \otimes R \rightarrow H_E^*$ gives, respectively, the identity map of R and the map f.

We now prove some basic facts about central objects, all of which are analogous to standard statements about central subgroups of groups. We begin with the following result, which is an algebraic analog of the fact that if E is an elementary abelian p-subgroup of a group G, then E is always a central subgroup of $C_G(E)$.

Proposition 3.3

Given $(E,f) \in \mathbf{A} _R$, there is a $\mathcal {K}$-map $h :T_E(R;f) \rightarrow H_E^*$ factoring the map $f :R \rightarrow H_E^*$. Moreover, the pair (E, h) is central in $\mathbf{A} _{T_E(R;f)}$.

Proof

We define the map h as the composite

To see that this factors the map f, note that

$$\begin{aligned} f&\cong (1 \otimes \epsilon _{T_E(R;f)}) \circ \eta _{R,(E,f)} \\&\cong (1 \otimes \epsilon _{T_E(R;f)}) \circ \kappa _{R,(E,f)} \circ \rho _{R,(E,f)} \\&= h \circ \rho _{R,(E,f)}, \end{aligned}$$

where we have used Lemma 2.14. Finally, because f and $\rho _{R,(E,f)}$ are finite morphisms (the latter by [30, Corollary 1.12], for example), so is h. The composite $(\epsilon _{E} \otimes 1) \circ \kappa _{R,(E,f)} :T_E(R;f) \rightarrow T_E(R;f)$ is the identity, and therefore $(E,h) \in \mathbf{A} _{T_E(R;f)}$ is central by Proposition 3.2. $\square$

Remark 3.4

The morphism $h :T_E(R;f) \rightarrow H_E^*$ is in fact a morphism of $H_E^*$-comodules. In fact, unwinding the definitions of the maps involved, this is nothing other than the statement of coassociativity for the $H_E^*$-comodule $T_E(R;f$).

We have the following behavior with respect to tensor products.

Lemma 3.5

Suppose $R_1$ and $R_2$ are Noetherian connected unstable algebras, and $(E_i,f_i) \in \mathbf{A} _{R_i}$ is central for $i=1,2$, then $(E_1 \oplus E_2,f)$ is central in $\mathbf{A} _{R_1 \otimes R_2}$, where $f :R_1 \otimes R_2 \rightarrow H_{E_1 \oplus E_2}^*$ is the composite $R_1 \otimes R_2 \xrightarrow {f_1 \otimes f_2} H_{E_1}^* \otimes H_{E_2}^* \cong H_{E_1 \oplus E_2}^*$.

Proof

This is an almost immediate consequence of the fact that the T-functor commutes with tensor-products; there is a natural isomorphism $T_{E_1 \oplus E_2}(R_1 \otimes R_2;f) \cong T_{E_1}(R_1;f_1) \otimes T_E(R_2;f_2)$, and under this isomorphism $\rho _{R_1 \otimes R_2,(E_1 \oplus E_2,f)}$ corresponds to $\rho _{R_1,(E_1,f_1)} \otimes \rho _{R_2,(E_2,f_2)}$. Alternatively, if $\phi _i :R \rightarrow H_{E_i}^* \otimes R_i$ is the $\mathcal {K}$-map arising via Proposition 3.2, then the $\mathcal {K}$-map $\phi _1 \otimes \phi _2 :R_1 \otimes R_2 \rightarrow H_{E_1 \oplus E_2}^* \otimes R_1 \otimes R_2$ satisfies the conditions of Proposition 3.2, and shows that $(E_1 \oplus E_2,f)$ is central. $\square$

The next two lemmas are due to Dwyer–Wilkerson [22, Lemma 4.5 and Lemma 4.6]; the first is an immediate consequence of Proposition 3.2.

Lemma 3.6

(Dwyer–Wilkerson) Let (C, g) be in $\mathbf{A} _R$, and assume that (C, g) is central. If $C'$ is a subgroup of C, then $(C',g')$ is central where $g :R \xrightarrow {g} H_C^* \xrightarrow {\iota ^*} H_{C'}^*$, and $\iota :C' \rightarrow C$ is the inclusion.

Remark 3.7

Let $(E,f) \in \mathbf{V} _R$ and $(C,g) \in \mathbf{A} _R$ with (C, g) central. Observe that, by adjunction, a map $R \rightarrow H_E^* \otimes H_C^*$ can be specified by giving a $\mathcal {K}$-map $T_C(R;g) \rightarrow H_E^*$, or equivalently, using that (C, g) is central, a $\mathcal {K}$-map $R \rightarrow H_E^*$. We denote by $f \boxplus g:R \rightarrow H_E^* \otimes H_C^*$ the map corresponding to f, so that $(E \oplus C, f \boxplus g) \in \mathbf{V} _R$. Dwyer and Wilkerson show the following.

Lemma 3.8

(Dwyer–Wilkerson) Let $(E,f) \in \mathbf{V} _R$ and $(C,g) \in \mathbf{A} _R$ with (C, g) central. Then $(E \oplus C,f \boxplus g)$ is the unique pair in $\mathbf{V} _R$ which restricts to f (resp. g) along the summand inclusion $E \rightarrow E \oplus C$ (resp. $C \rightarrow E \oplus C$).

We observe that it is not necessarily the case that $(E \oplus C,f \boxplus g) \in \mathbf{A} _R$, i.e., the map $f \boxplus g :R \rightarrow H_{E \oplus C}^*$ is not necessarily finite. As discussed in Remark 2.8, there is a functor ${{\,\mathrm{rec}\,}}:\mathbf{V} _R \rightarrow \mathbf{A} _R$, given by $(V,j) \mapsto (V/\ker (j),\tilde{j})$ and applying this to the construction in Lemma 3.8 leads to the following definition.

Definition 3.9

Let (E, f) and (C, g) be objects of $\mathbf{A} _R$, and assume that (C, g) is central, then we let $(E \circ C,\sigma (f,g)) {:}{=} {{\,\mathrm{rec}\,}}(E \oplus C, f \boxplus g)$ be the object in $\mathbf{A} _R$ corresponding to $(E \oplus C, f \boxplus g) \in \mathbf{V} _R$, i.e., $E \circ C = E \oplus C/\ker (f \boxplus g)$.

As a diagram, we can represent this as

where $q^*$ is induced by $q :E \oplus C \rightarrow E \circ C$, and the composite $q^* \circ \sigma (f,g) \cong f \boxplus g$. Note that the natural maps $E \rightarrow E \circ C$, and $C \rightarrow E \circ C$, induce maps $T_E(R;f) \rightarrow T_{E \circ C}(R;\sigma (f,g))$ and $T_C(R;f) \rightarrow T_{E \circ C}(R;\sigma (f,g))$.

3.2 The poset of central objects

Observe that the category $\mathbf{A} _R$ has the property that every endomorphism is an isomorphism. Such a category is called an EI-category (see [42]), and the set of isomorphism classes of objects is partially ordered by the relation

$$\begin{aligned}{}[(E,f)] \le [(V,g)] \quad \text {if} \quad {{\,\mathrm{Hom}\,}}_\mathbf{A _R}((E,f),(V,g)) \ne \emptyset . \end{aligned}$$

Recall that this implies that there exists a monomorphism $\iota :E \hookrightarrow V$ such that the diagram

We will write $(E,f) \subseteq (V,g)$ if $[(E,f)] \le (V,g)]$.

Consider the full subcategory $\mathbf{A} _R^{\mathrm{central}} \subset \mathbf{A} _R$ consisting of the central objects. This inherits the partial order from $\mathbf{A} _R$. We shall show that, with respect to this partial order, $\mathbf{A} _R^{\mathrm{central}}$ has, up to isomorphism, a unique maximal element, i.e., there is, up to isomorphism, a unique maximal central object in $\mathbf{A} _R$. To do this, we briefly recall the definition of an under category.

Definition 3.10

Given $(E,f) \in \mathbf{A} _R$, the under category $(E,f) \downarrow \mathbf{A} _R$ is the category with objects pairs $(\alpha ,(V,g))$ where $\alpha :(E,f) \rightarrow (V,g)$ is a morphism in $\mathbf{A} _R$, and a morphism $(\alpha ,(V,g)) \rightarrow (\alpha ',(W,h))$ is a morphism $f :(V,g) \rightarrow (W,h)$ in $\mathbf{A} _R$ such that the diagram

commutes.

A crucial observation is the following, which is shown in the proof of Proposition 4.10 of [22].

Proposition 3.11

(Dwyer–Wilkerson) Let (C, g) be central, then for any $(E,f) \in \mathbf{A} _R$ the assignment $(E,f) \mapsto (E \circ C,\sigma (f,g))$ defines a functor $\sigma :\mathbf{A} _R \rightarrow (C,g) \downarrow \mathbf{A} _R$. Moreover, the natural map

$$\begin{aligned} \iota :T_E(R;f) \rightarrow T_{E \circ C}(R;\sigma (f,g)) \end{aligned}$$

induced by $E \rightarrow E \circ C$ is an isomorphism.

Corollary 3.12

If (C, g) and (E, f) are central in $\mathbf{A} _R$, then so is $(E \circ C,\sigma (f,g))$.

Proof

By the previous proposition $\iota :T_E(R;f) \rightarrow T_{E \circ C}(R;\sigma (f,g))$ is an isomorphism. Centrality of $T_E(R;f)$ implies that $\rho _{R,(E,f)} :R \rightarrow T_E(R;f)$ is an isomorphism, and hence so is the composite $\iota \circ \rho _{R,(E,f)}$. Observe that $\rho _{R,\sigma (f,g)} \cong \iota \circ \rho _{R,(E,f)}$. This is clear because the map $\{ e \} \rightarrow E \circ C$ factors through $\{ e \} \rightarrow E$. It follows that $\rho _{R,\sigma (f,g))} :R \rightarrow T_{E \circ C}(R;\sigma (f,g))$ is an isomorphism, and $(E \circ C, \sigma (f,g)) \in \mathbf{A} _R$ is central. $\square$

Theorem 3.13

With respect to the poset structure above, there exists a unique (up to isomorphism) maximal central element $(C,g) \in \mathbf{A} _R$.

Proof

By Proposition 2.7(1) there are only finitely many isomorphism classes of objects in $\mathbf{A} _R$ and hence $\mathbf{A} _R^{\mathrm{central}}$. It follows that there exist maximal isomorphism classes of central objects. We now show that there is a unique such isomorphism class. To that end, suppose we are given two central objects (E, f) and (V, g) in $\mathbf{A} _R$. By Proposition 3.11 the pair $(E \circ V,\sigma (f,g)) \in (E,f) \downarrow \mathbf{A} _R$ and by symmetry $(E \circ V,\sigma (f,g)) \in (V,g) \downarrow \mathbf{A} _R$. In particular, we have $(E,f) \subseteq (E \circ V,\sigma (f,g)) \supseteq (V,g)$. Moreover, by Corollary 3.12$(E \circ V,\sigma (f,g))$ is central in $\mathbf{A} _R$. This implies the result. $\square$

Definition 3.14

Let R be a Noetherian unstable algebra, then the center $(C,g) \in \mathbf{A} _R$ is a choice of representative for the isomorphism class of the maximal central object with respect to the poset structure on $\mathbf{A} _R$. We say that rank of the center is the rank of the elementary abelian p-group C.

Example 3.15

(Mislin) The following example, due to Mislin [45], shows that if $R = H_G^*$ for a compact Lie group, then the center of $H_G^*$ need not agree with the maximal central elementary abelian p-subgroup of G. Let $G = \Sigma _3$ and work at the prime 2, then the inclusion $C_2 \rightarrow \Sigma _3$ of a 2-Sylow subgroup induces an isomorphism $H_{\Sigma _3}^* \cong H_{C_2}^*$. Moreover, we have $T_{C_2}(H_{\Sigma _3}^*;{{\,\mathrm{res}\,}}^*_{\Sigma _3,C_2}) \cong H_{C_{\Sigma _3}(C_2)}^* \cong H_{C_2}^*$. In particular, the map $H_{\Sigma _3}^* \rightarrow T_{C_2}(H_{\Sigma _3}^*;{{\,\mathrm{res}\,}}^*_{\Sigma _3,C_2})$ is an isomorphism. This shows that the pair $(C_2,{{\,\mathrm{res}\,}}_{\Sigma _3,C_2}^*)$ is central in $H_{\Sigma _3}^*$. In fact, $(C_2,{{\,\mathrm{res}\,}}_{\Sigma _3,C_2}^*)$ is the center of $H_{\Sigma _3}^*$. Note that $\Sigma _3$ actually has 3 conjugate elementary abelian subgroups of order 2, and that $\Sigma _3$ has trivial group theoretic center.

Mislin shows more generally that, at the prime p, the center of ${H_G^*}$ is equal to the maximal elementary abelian p-subgroup of the center of $G/\mathcal {O}_{p'}(G)$, where $\mathcal {O}_{p'}(G)$ denote the largest $p'$-normal subgroup of G for $p'$ a prime not equal to p. Thus, if G is a finite p-group, then the center of $H_G^*$ is equal to the maximal central elementary abelian p-subgroup of G, but not in general. In particular, if G is a finite p-group, then the center of $H_G^*$ is always non-trivial. $\square$

Example 3.16

(Modular invariant theory) Let V be a finite-dimensional $\mathbb {F}_p$-vector space, G a finite group such that p divides the order of G, and $\rho :G \rightarrow GL_n(V)$ a faithful modular representation. We let $\mathbb {F}[V]$ denote the graded algebra of polynomial functions on V with generators in degree 2, which is a graded $\mathbb {F}_p$-algebra with a unique action of the Steenrod algebra. These operations commute with the action of G, and define an action on $\mathbb {F}[V]^G$, see [25, Section 5] or [49, Chapter 8] for more details. Moreover, $\mathbb {F}[V]^G$ is a finitely-generated $\mathbb {F}_p$-algebra, see for example, [49, Corollary 2.1.5]. In other words, $\mathbb {F}[V]^G$ defines a connected Noetherian unstable algebra.

Let $i :U \hookrightarrow V$ be the inclusion of an $\mathbb {F}_p$-linear subspace U, then we can define a morphism $f_U :\mathbb {F}[V]^G \hookrightarrow \mathbb {F}[V] \xrightarrow {i^*} \mathbb {F}[U] \rightarrow H_U^*$, which is a $\mathcal {K}$-map. In fact every morphism in $\mathbf{A} _{\mathbb {F}[V]^G}$ arises this way; Rector’s category $\mathbf{A} _{\mathbb {F}[V]^G}$ is equivalent to the category of pairs $(U,f_U)$ such that $H_U^*$ is a finite $\mathbb {F}[V]^G$-module via $f_U$. This can be deduced from the proof of Theorem 1.1 of [25]. Moreover, Dwyer and Wilkerson also prove that

$$\begin{aligned} T_U(\mathbb {F}[V]^G;f_U) \cong \mathbb {F}[V]^{G_U} \end{aligned}$$

where $G_U \le G$ is the pointwise stabilizer of U, i.e., $G_U = \{ g \in G \mid g \cdot u = u \}$.

Let $V^G = \{v \in V \mid g \cdot v = v \}$ denote the G-invariant subspace $V^G \subseteq V$. It follows from the discussion above that the center of $F[V]^G$ is $(V^G,f_{V^G})$. Note that because the representation is faithful, we have $\dim _{\mathbb {F}_p}(V^G) < \dim _{\mathbb {F}_p}(V)$, giving an upper bound for the rank of the center. Moreover, if G is a p-group, then $V^G \ne 0$, so that the center is non-trivial in this case. This is a direct analogue of the fact that (non-trivial) p-groups have non-trivial centers, and hence, in light of the previous example, that the unstable algebra $H_G^*$ always has non-trivial center when G is a p-group. $\square$

Example 3.17

(Noetherian H-spaces) Suppose X is a connected H-space with Noetherian mod p-cohomology. The mod p cohomology is given by

$$\begin{aligned} H^*(X) \cong \mathbb {F}_2[x_1,\ldots ,x_r] \otimes \frac{\mathbb {F}_2[y_1,\ldots ,y_s]}{(y_1^{2^{a_1}},\ldots ,y_s^{2^{a_s}})}, \end{aligned}$$

(3.18)

when $p = 2$ see, for example, [1, Equation (5)] and

$$\begin{aligned} H^*(X;\mathbb {F}_p) \cong \frac{\mathbb {F}_p[y_1,\ldots ,y_s]}{(y_1^2,\ldots ,y_s^2)} \otimes \mathbb {F}_p[\beta y_1,\ldots , \beta y_k,x_{k+1},\ldots ,x_n] \otimes \frac{\mathbb {F}_p[z_1,\ldots ,z_t]}{(z_1^{p^{a_1}},\ldots ,z_t^{p^{a_t}})}, \end{aligned}$$

(3.19)

when p is odd, where $\beta$ is the Bockstein [18, Corollary 2.7]. Note that in both cases the generators cannot take arbitrary degrees, see [1, Theorem 1.6] when $p = 2$ and [18, Proposition 2.8] when p is odd.

We claim that the center of $H^*(X)$ has rank equal to the Krull dimension of $H^*(X)$ (note that this is the maximal possible rank by Proposition 2.7). Indeed, in both cases there exists a map of Hopf algebras $f :H^*(X) \rightarrow H_E^*$ where E is elementary abelian of rank equal to the Krull dimension of $H^*(X)$ - when $p = 2$ this is [1, Theorem 2.2] and when p is odd this is [18, Theorem 2.6]. This map is in fact the localization away from ${{\,\mathrm{Nil}\,}}_1$ of $H^*(X)$ and hence these morphisms are finite [34, Corollary 4.10]. That they are central then follows from [21, Theorem 3.2 and Lemma 4.5], see also the proof of Theorem 2.3 of [1]. $\square$

We now show that the center is well-behaved under tensor products of unstable algebras.

Lemma 3.20

Suppose $R_1$ and $R_2$ are Noetherian connected unstable algebras with center $(C_i,g_i) \in \mathbf{A} _{R_i}$ for $i=1,2$, then $(C_1 \oplus C_2,g)$ is the center of $\mathbf{A} _{R_1 \otimes R_2}$, where $g :R_1 \otimes R_2 \rightarrow H_{C_1 \oplus C_2}^*$ is the composite $C_1 \otimes C_2 \xrightarrow {f_1 \otimes f_2} H_{C_1}^* \otimes H_{C_2}^* \cong H_{C_1 \oplus C_2}^*$.

Proof

By Lemma 3.5$(C_1 \oplus C_2,g) \in \mathbf{A} _{R_1 \otimes R_2}$ is central, so it remains to show that it is maximal. Suppose then that $(C_1 \oplus C_2,g) \subsetneq (V,j)$ for some $(V,j) \in \mathbf{A} _{R_1 \otimes R_2}$. In particular, we have a monomorphism $\alpha :C_1 \oplus C_2 \rightarrow V$. The composition is a monomorphism, and so we may identify $C_1$ with $\iota _1\alpha (C_1) \subset V$ and choose a complement $V_1$ of $C_1$, and similar for $C_2$. We can then produce $(V_i,j_i) \in \mathbf{A} _{R_i}$ for $i = 1,2$ such that $(C_1,g_1) \subseteq (V_1,j_1)$ and $(C_2,g_2) \subseteq (V_2,j_2)$. From centrality of (V, j) we easily see that $(V_i,j_i) \in \mathbf{A} _{R_i}$ is central. We now observe that either $(C_1,g_1) \subsetneq (V_1,j_1)$ or $(C_2,g_2) \subsetneq (V_2,j_2)$ for otherwise we could not have $(C_1 \oplus C_2,g) \subsetneq (V,j)$. This contradicts the assumption that $(C_i,g_i)$ is the center of $R_i$, and so $(C_1 \oplus C_2,g)$ is maximal, and hence is the center of $\mathbf{A} _{R_1 \otimes R_2}$. $\square$

Example 3.21

We now consider three unstable algebras which we shall see have trivial center, as suggested by the referee.

• (1) Consider the square-zero extension $R = \mathbb {F}_2[x] \oplus \Sigma \mathbb {F}_2$ where $|x| =1$, or equivalently $R = H_{\mathbb {Z}/2}^* \oplus \Sigma \mathbb {F}_2$. Let $f :R \rightarrow H_{\mathbb {Z}/2}^*$ denote the projection map. Since $T_{\mathbb {Z}/2}(-;f)$ is exact, we must compute $T_{\mathbb {Z}/2}(\mathbb {F}_2[x];f)$ and $T_{\mathbb {Z}/2}(\Sigma \mathbb {F}_2;f)$. Both are well-known from Lannes’ computations: $T_{\mathbb {Z}/2}(\mathbb {F}_2[x],f) \cong \mathbb {F}_2[x]$, while $T_{\mathbb {Z}/2}(\Sigma \mathbb {F}_2;f) \cong \Sigma T_{\mathbb {Z}/2}(\mathbb {F}_2;f)$ is trivial. In this case, the map $\rho _{R,(\mathbb {Z}/2,f)} :R \rightarrow T_{\mathbb {Z}/2}(R;f)$ is not an isomorphism, so $(\mathbb {Z}/2,f) \in \mathbf{A} _R$ is not central. This is in fact the only non-trivial element in $\mathbf{A} _R$, so we conclude that the center is trivial.

  An alternative way to see that the center must be trivial is to note that the depth (see Appendix B) of R is 0. By Corollary B.7 the depth of R is always at least the rank of the center; in particular, if ${{\,\mathrm{depth}\,}}(R) = 0$, then the center must be trivial.

• (2) Let R denote the sub-algebra of $\mathbb {F}_2[x]$ omitting the class of degree 1. In this case, the category $\mathbf{A} _R$ contains only the trivial subgroup (because R has no class in degree 1), and therefore R has trivial center.

• (3) Let $\overline{\mathbb {F}}_2[x]$ denote the augmentation ideal of $\mathbb {F}_2[x]$, then consider the unstable algebra $R = \mathbb {F}_2 \oplus \overline{ \mathbb {F}_2[x]}^{\oplus 2}$. There are two maps $R \rightarrow H_{\mathbb {Z}/2}^*$ given by the projection onto $\overline{\mathbb {F}_2[x]}$ and the inclusion map. A similar argument to (1) shows that these maps cannot be central, and so R has trivial center.

3.3 Hopf algebras and comodules

One of the key properties of $H_G^*$ used by Kuhn is that for a central elementary abelian subgroup C, $H_G^*$ is a $H_C^*$-comodule, and moreover the restriction map $H_G^* \rightarrow H_C^*$ is a morphism of $H_C^*$-comodules. A similar result occurs for general unstable algebras.

Proposition 3.22

Let R be a connected Noetherian unstable algebra and $(V,j) \in \mathbf{A} _R^{\mathrm{central}}$, then R is a $H_V^*$-comodule, and $j :R \rightarrow H_V^*$ is a morphism of $H_V^*$-comodules. In particular, the image of j is a sub-Hopf algebra of $H_V^*$.

Proof

We recall that $\kappa _{R,(V,j)} :T_V(R;j) \rightarrow H_V^* \otimes T_V(R;j)$ makes $T_V(R;j)$ into a $H_V^*$-comodule; since $\rho _{R,(V,j)}$ is central, it follows that R is also a $H_V^*$-comodule.

That $j :R \rightarrow H_V^*$ is a morphism of $H_V^*$-comodules follows from a diagram chase. Indeed, the diagram

commutes, and the top composite is j, while the bottom composite is $1 \otimes j$. Here $\Psi _{R,(V,j)}$ denotes the comodule structure map.

To see that the image K of j is a sub-Hopf algebra of $H_V^*$ follows as in the proof of Theorem 1.2 of [3]. We recall their argument here: The map j is a morphism of $H_V^*$-comodule algebras, and therefore K is a sub-comodule algebra of $H_V^*$. Because $H_V^*$ is a commutative Hopf algebra, the restriction of the diagonal in $H_V^*$ to K has image in $K \otimes K$, and hence K is a sub-Hopf algebra of $H_V^*$. $\square$

We have the following corollary which, as noted in [3, Remark 1.3], follows from the Borel structure theorem [46, Theorem 7.11].

Corollary 3.23

There is a basis $x_1,\ldots ,x_c$ for $H_V^1$ such that

$$\begin{aligned} K = {\left\{ \begin{array}{ll} \mathbb {F}_2[x_1^{2^{j_1}},\ldots ,x_c^{2^{j_c}}] &{}\text { if } p=2\\ \mathbb {F}_p[y_1^{p^{j_1}},\ldots ,y_b^{p^{j_b}},y_{b+1},\ldots ,y_c] \otimes \Lambda (x_{b+1},\ldots ,x_c) &{} \text { if } p \text { is odd,} \end{array}\right. } \end{aligned}$$

(3.24)

for some natural numbers $j_1 \ge j_2 \ge \cdots$, and where $y_i = \beta x_i$ for $\beta$ the Bockstein homomorphism.

Now suppose we are given (V, j) in $\mathbf{A} ^{\mathrm{central}}_R$ and a non-trivial homomorphism $\alpha :(V,j) \rightarrow (E,f)$ in $\mathbf{A} _R$; in particular, there is a monomorphism $\alpha :V \hookrightarrow E$, and (E, f) need not be central. As discussed previously, $T_V(R;j)$ is a $H_V^*$-comodule via $\kappa _{R,(V,j)}$ and $T_E(R;f)$ is a $H_E^*$-comodule via $\kappa _{R,(E,f)}$. Moreover, if we compose with the coalgebra morphism $\alpha ^* :H_E^* \rightarrow H_V^*$, then $T_E(R;f)$ becomes a $H_V^*$-comodule via $\alpha ^* \circ \kappa _{R,(E,f)}$, and moreover $T_{\alpha }(f) :T_V(R;j) \rightarrow T_E(R;f)$ is a morphism of $H_V^*$-comodules, see the discussion (before passing to components) on the bottom of page 30 of [34]. In particular, the following diagram commutes:

This leads to the following result.

Lemma 3.25

Suppose R is a connected Noetherian unstable algebra, (V, j) is central, and that $(V,j) \subseteq (E,f)$ (so that there is a non-trivial homomorphism $\alpha :(V,j) \rightarrow (E,f)$ in $\mathbf{A} _R$). With the comodule structures as described above, $\rho _{R,(E,f)} :R \rightarrow T_E(R,f)$ is a morphism of $H_V^*$-comodules.

Proof

By definition of the comodule structures, we must show that the diagram

commutes. To see that the top and bottom square commute, we use Lemmas 2.13 and 2.15 and the definition of $T_{\alpha }(f)$ to see that there are isomorphisms

$$\begin{aligned} T_{\alpha }(f) \circ \rho _{R,(V,j)}&\cong (\epsilon _V \otimes 1) \circ (1 \otimes T_{\alpha }(f)) \circ \eta _{R,(V,j)}\\&\cong (\epsilon _V \otimes 1) \circ (\alpha ^* \otimes 1) \circ \eta _{R,(E,f)}\\&\cong (\epsilon _E \otimes 1) \circ \eta _{R,(E,f)} = \rho _{R,(E,f)}. \\ \end{aligned}$$

Finally, the middle square commutes by the fact that $T_{\alpha }(f)$ is a morphism of $H_V^*$-comodules. Thus, the diagram commutes as claimed. $\square$

We also require the following technical lemma. We are grateful to the referee for simplifying the proof. We recall our usual notation: if $(E,f) \in \mathbf{A} _R$, then there exists $h :T_E(R;f) \rightarrow H_E^*$ with $(E,h) \in \mathbf{A} ^{\mathrm{central}}_{T_E(R;f)}$ (Proposition 3.3).

Lemma 3.26

Let R be a Noetherian unstable algebra and suppose $(E,f) \in \mathbf{A} _R$. Suppose furthermore that $(E,h) \subseteq (V,\widetilde{j})$ for $(V,\widetilde{j}) \in \mathbf{A} _{T_E(R;f)}$. Then, $\widetilde{j}^{\#} :R \rightarrow H_E^* \otimes H_V^* \cong H_{E \oplus V}^*$ is equivalent to the composite

$$\begin{aligned} R \xrightarrow {\rho _{R,(E,f)}} T_E(R;f) \xrightarrow {\widetilde{j}} H_V^* \xrightarrow {\mu ^*} H_{E \oplus V}^* \end{aligned}$$

where the last map is induced by $\mu :E \oplus V \rightarrow V$ sending $(e,v) \mapsto \iota (e) + v$, where $\iota :E \rightarrow V$ denotes the inclusion.

Proof

Because $(E,h) \in \mathbf{A} ^{\mathrm{central}}_{T_E(R;f)}$ we can apply Lemma 3.8 to define $(\widetilde{j} \oplus h) :T_E(R;f) \rightarrow H^*_{E \oplus V}$. Moreover, the explicit construction given in Remark 3.7, along with the uniqueness part of Lemma 3.8, show that the following diagram commutes:

Therefore $\widetilde{j}^{\#} = (\widetilde{j} \oplus h) \circ \rho _{E,(E,f)} = \mu ^* \circ \widetilde{j} \circ \rho _{R,(E,f)}$, as claimed. $\square$

This technical lemma is used in the following, which is a T-functor version of the observation that if G is a group and E and V are elementary abelian p-subgroups of G, with $\mathcal {Z}(C_G(E))< V < C_G(E)$, then $C_{C_G(E)}(V) \cong C_G(V)$, where $\mathcal {Z}(-)$ denotes the maximal central elementary abelian p-subgroup of a group.

Proposition 3.27

With assumptions as in the previous lemma, we have

$$\begin{aligned} T_V(T_E(R;f);\tilde{j}) \cong T_V(R; j) \end{aligned}$$

where $j = \rho _{R,(E,f)}\circ \tilde{j}$.

Remark 3.28

The situation of the proposition is displayed in the following diagram:

Proof

Applying [22, Proposition 3.3] and Lemma 3.26 there are isomorphisms

$$\begin{aligned} T_V(T_E(R;f);\tilde{j}) \cong T_{E \oplus V}(R;\tilde{j}^{\#}) \cong T_{E \oplus V}(R; \mu ^{*} \circ j). \end{aligned}$$

Since $\mu$ is an epimorphism we have

$$\begin{aligned} T_{E \oplus V}(R;\mu ^{*}\circ j) \cong T_V(R;j) \end{aligned}$$

by Lemma 2.16. Combining these isomorphisms gives the result. $\square$

3.4 Central elements and the nilpotence degree

The goal of this subsection is to improve the result Proposition 2.21 in the case $M = R$; more specifically, to prove that we only need to consider those $(E,f) \in \mathbf{A} _R$ for which $(C,g) \subseteq (E,f)$. The proof will be based on the corresponding result for finite groups, due to Kuhn [36, Theorem 4.4].

To begin, we recall that given a category ${{\,\mathrm{\mathcal {C}}\,}}$ the twisted arrow category ${{\,\mathrm{\mathcal {C}}\,}}^{\#}$ is the category whose objects are the morphisms of ${{\,\mathrm{\mathcal {C}}\,}}$, and a morphism from $f :C \rightarrow D$ to $f' :C' \rightarrow D'$ is a pair of morphisms $u :C \rightarrow C'$, $v :D' \rightarrow D$ in ${{\,\mathrm{\mathcal {C}}\,}}$ such that the following diagram commutes:

The work of Henn et al. [34] discussed briefly in Sect. 2.3, can be rephrased in terms of the twisted arrow category of $\mathbf{A} _R$. In particular, following the discussion in [34, (1.17.4)] the fundamental result [34, Theorem 4.9] can equivalently be given as the statement that for R a Noetherian unstable algebra and $M \in R-\mathcal {U}$ there is a morphism

(3.29)

which is localization away from ${{\,\mathrm{Nil}\,}}_n$. Here the limit is taken over the twisted arrow category $\mathbf{A} _R^{\#}$, and ${{\,\mathrm{Eq}\,}}$ denotes the equalizer. The maps $\mu (\alpha )$ and $\nu (\alpha )$ are defined in [34, (1.16.2)]; it will not prove important in what follows to have an explicit description of them, so we omit it.

Now let R be a connected Noetherian unstable algebra with center (C, g) and recall that Dwyer–Wilkerson have constructed a functor $\sigma :\mathbf{A} _R \rightarrow (C,g) \downarrow \mathbf{A _R}$, see Proposition 3.11. Generalizing a result of Kuhn about finite groups [36, Theorem 4.4], we now show the following.

Theorem 3.30

In the case $M = R$ of (3.29), the limit can be taken over the category $((C,g) \downarrow \mathbf{A} _R)^{\#}$.

Proof

The proof will be the essentially the same as Kuhn’s, just translated into the language of unstable algebras. To that end, let $\alpha :(E,f) \rightarrow (E',f')$ be a morphism in $\mathbf{A} _R$, and let $\alpha _{C}$ denote the composite morphism in $\mathbf{A} _R$

$$\begin{aligned} \alpha _C :(E,f) \xrightarrow {\alpha } (E',f') \rightarrow (C \circ E',\sigma (f',g)). \end{aligned}$$

Let us now define morphisms $f_{\alpha } :\alpha _C \rightarrow \alpha$ and $g_{\alpha } :\alpha _C \rightarrow \sigma (\alpha )$ in $\mathbf{A} _R^{\#}$ via the following commutative diagram in $\mathbf{A} _R$:

Now [36, Lemma 4.5] goes through with an essentially unchanged proof: for any contravariant functor $F:\mathbf{A} _R \rightarrow {{\,\mathrm{Mod}\,}}_{\mathbb {F}_p}$ such that for all $\alpha :(E,f) \rightarrow (E',f')$, $F(f_{\alpha }) :F(\alpha ) \rightarrow F(\alpha _C)$ is an isomorphism, the canonical map

$$\begin{aligned} \Xi :\lim _{\alpha \in \mathbf{A} _R^{\#}} F(\alpha ) \rightarrow \lim _{\alpha \in ((C,g) \downarrow \mathbf{A} _R)^{\#}}F(\alpha ) \end{aligned}$$

is an isomorphism. This applies in particular to $F(\alpha ) = H_{E}^*$ and $F(\alpha ) = T_{E'}(R;f')$; the first is clear, and the latter follows from Proposition 3.11. As with [36, Theorem 4.4] this completes the proof, as the limit in (3.29) is built from these two examples by constructions that preserve isomorphisms. $\square$

Using [34, (1.17.4)] again, we can improve on their Theorem 4.9.

Theorem 3.31

Let R be a connected Noetherian unstable algebra with center (C, g), then the morphism

induced by the maps $\eta _{R,(E,f)}$ is localization away from ${{\,\mathrm{Nil}\,}}_n$ (the products in this formula are taken over all objects of $(C,g) \downarrow \mathbf{A} _R$ resp. over all morphisms of $(C,g) \downarrow \mathbf{A} _R$).

Finally, we have the following important corollary, which is the promised improvement of Proposition 2.21.

Corollary 3.32

Let R be a connected Noetherian unstable algebra with center (C, g), then for $n \ge d_0(R)$ there is a monomorphism in $R_{fg}-\mathcal {U}$

induced by the product of the maps $\eta _{R,(E,f)}$.

4 The topological nilpotence degree of the central essential ideal

In this section we introduce the central essential ideal ${{\,\mathrm{CEss}\,}}(R)$ of a connected Noetherian algebra R, following the definition of Kuhn for compact Lie groups. We give an upper bound for $d_0({{\,\mathrm{CEss}\,}}(R))$, and prove that ${{\,\mathrm{CEss}\,}}(R)$ is non-zero if and only if the depth of R is equal to the rank of the center of R (Definition 3.14).

4.1 The central essential ideal

We recall that in [37] Kuhn defines the central essential ideal for a compact Lie group G to be the kernel of the map

where the product is taken over those elementary abelian p-subgroups of G strictly containing the maximal central subgroup C(G). The analog for a general unstable algebra R replaces $H_G^*$ with R and $H_{C_G(E)}^*$ with components of the T-functor.

Definition 4.1

Let R be a connected Noetherian unstable algebra with center $(C,g) \in \mathbf{A} _R$, then the central essential ideal ${{\,\mathrm{CEss}\,}}(R)$ is defined by

Note that ${{\,\mathrm{CEss}\,}}(R)$ is independent of the choice of representative for the center. Moreover, by replacing $\mathbf{A} _R$ by a choice of skeleton if necessary, we can assume this product is finite (see Proposition 2.7).

Lemma 4.2

${{\,\mathrm{CEss}\,}}(R)$ is a sub-$H_C^*$-comodule of R.

Proof

This is a consequence of Lemma 3.25. $\square$

The main result of this section is the following. We refer the reader to Appendix B for a brief discussion on the basic commutative algebra needed in this section, in particular, for the definition of the depth and dimension of an R-module.

Theorem 4.3

Let R be a connected Noetherian unstable algebra with center $(C,g) \in \mathbf{A} _R$. Let c(R) be the rank of C, then the Krull dimension of the R-module ${{\,\mathrm{CEss}\,}}(R)$ is at most c(R).

The proof will require some preliminary results. We recall the following definitions, due to Henn [30] and Powell [51].

Definition 4.4

Let R be a Noetherian unstable algebra, and $M \in R-\mathcal {U}$.

• (1) (Henn) The T-support of M is

  $$\begin{aligned} T-{{\,\mathrm{supp}\,}}(M) = \{ (E,f) \in \mathbf{A} _R \mid T_E(M;f) \ne 0 \}. \end{aligned}$$

• (2) (Powell) The $R-\mathcal {U}$ transcendence degree of M is

  $$\begin{aligned} {{\,\mathrm{\mathbf {TrDeg}}\,}}_{R-\mathcal {U}}(M) = \sup \{{{\,\mathrm{rank}\,}}( E) \mid (E,f) \in T-{{\,\mathrm{supp}\,}}(M)\}. \end{aligned}$$

The following result justifies the terminology of the $R-\mathcal {U}$ transcendence degree, see [51, Proposition 7.2.6].

Proposition 4.5

(Powell) Let $M \in R_{fg}-\mathcal {U}$, then

$$\begin{aligned} {{\,\mathrm{\mathbf {TrDeg}}\,}}_{R-\mathcal {U}}(M) = \dim _R(M). \end{aligned}$$

The proof relies on the existence of Brown–Gitler modules $J_R(n)$ in the category $R-\mathcal {U}$ (see [30, Section 1.5]), which represent the functor $M \mapsto (M^n)^*$, where $()^*$ is the vector space dual. Given $(E,f) \in \mathbf{A} _R$, we define an injective object $I_{(E,f)}(n)$ in $R-\mathcal {U}$ as $H_E^* \otimes J_{T_E(R;f)}(n)$ [30, Proposition 1.6]. In fact, if R is a Noetherian unstable algebra, then $I_{(E,f)}(n)$ is even injective in $R_{fg}-\mathcal {U}$. From the definitions (see also [51, Lemma 6.1.7]) we have

$$\begin{aligned} {{\,\mathrm{Hom}\,}}_{R-\mathcal {U}}(M,I_{(E,f)}(n)) \cong (T_E(M;f)^n)^*. \end{aligned}$$

(4.6)

We now present the proof of Proposition 4.5.

Proof

(Powell) Since Powell’s work is not published, we sketch Powell’s proof here. To that end, let $\overline{R} = R/{{\,\mathrm{Ann}\,}}_R(M)$, which is a Noetherian unstable algebra (note that the annihilator ideal is closed under the action of the Steenrod algebra) such that $\alpha :R \rightarrow \overline{R}$ is a morphism of unstable algebras, and let $\overline{M} \in \overline{R}_{fg}-\mathcal {U}$ denote the object obtained by inducing M along the morphism $\alpha$, so that $M \cong \alpha ^* \overline{M}$. Standard base change results about Lannes’ T-functor show that ${{\,\mathrm{\mathbf {TrDeg}}\,}}_{R-\mathcal {U}}(M) = {{\,\mathrm{\mathbf {TrDeg}}\,}}_{\overline{R}-\mathcal {U}}(\overline{M})$ see [51, Proposition 7.2.2(1)] (if the reader prefers a published reference, this is also easily deduced from the formulas on page 1756 of [48]).

Now $\dim _R(M) = \dim (\overline{R}) = \max \{ {{\,\mathrm{rank}\,}}(E) \mid (E,f) \in \mathbf{A} _{\overline{R}}\} \ge {{\,\mathrm{\mathbf {TrDeg}}\,}}_{\overline{R}-\mathcal {U}}(\overline{M})$ by Proposition 2.7, which gives one inequality.

For the reverse inequality, we recall that the Dickson invariants are defined by

$$\begin{aligned} D_n = (H^*_{(\mathbb {Z}/2)^n})^{{{\,\mathrm{GL}\,}}_n(\mathbb {Z}/2)} \text { for } p = 2 \end{aligned}$$

and

$$\begin{aligned} D_n = (P_n)^{{{\,\mathrm{GL}\,}}_n(\mathbb {Z}/p)} \text { for } p > 2 \end{aligned}$$

where $P_n$ is the subalgebra of $H^*_{(\mathbb {Z}/p)^n}$ generated by $\beta H^1_{(\mathbb {Z}/p)^n}$. As is well known, $D_n \cong \mathbb {F}_p[c_1,\ldots ,c_n]$. Then, for s another non-negative integer, one lets $D_{n,s}$ denote the subalgebra of $D_n$ whose elements are the $p^s$-th powers of elements $D_n$, which naturally obtains an action of the Steenrod algebra. Specifically, $D_{n,s} \cong \mathbb {F}_p[c_1^{p^s},\ldots ,c_n^{p^s}]$. Suppose now that $\dim (\overline{R}) = n$, then by [14, Appendix A] there exists a natural number s and a monomorphism of unstable algebras $\iota :D_{n,s} \rightarrow \overline{R}$ for which $\overline{R}$ is a finitely-generated $D_{n,s}$-module. We let $\omega _{\iota }$ denote the image of the top Dickson invariant $c_n^{p^s}$. Because M is Noetherian, the localization $\overline{M}[\omega _{\iota }^{-1}]$ is non-trivial.

By [30, Theorem 1.9] there exists an embedding in $\overline{R} - \mathcal {U}$

$$\begin{aligned} \overline{M} \hookrightarrow \bigoplus _{i \in \mathcal {I}} I_{(E_i,f_i)}(a_i) \end{aligned}$$

where each component is non-trivial, and $(E_i,f_i) \in \mathbf{A} _{\overline{R}}$, so that, in particular by Proposition 2.7(2), ${{\,\mathrm{rank}\,}}(E_i) \le n$. Using exactness of localizations, there exists an $i \in \mathcal {I}$ for which $I_{(E_i,f_i)}(a_i)[\omega _{\iota }^{-1}] \ne 0$. By [51, Lemma 7.1.4] we have ${{\,\mathrm{rank}\,}}(E_i) = n$. By (4.6) $T_{E_i}(\overline{M};f_i) \ne 0$, and hence $T-{{\,\mathrm{supp}\,}}(\overline{M}) \ge n = \dim _R(M)$. In particular, ${{\,\mathrm{\mathbf {TrDeg}}\,}}_{\overline{R}-\mathcal {U}}(\overline{M}) \ge \dim _R(M)$, as required. $\square$

We will need the following computation, which is an almost immediate consequence of [30, Lemma 3.6]. The proof is given in [29, Proposition 3.14].

Proposition 4.7

Let R be a Noetherian unstable algebra and $M \in R_{fg}-\mathcal {U}$, then

$$\begin{aligned} {{\,\mathrm{\mathbf {TrDeg}}\,}}_{R-\mathcal {U}}(H_E^* \otimes T_E(M;f)^{\le n}) \le {{\,\mathrm{rank}\,}}(E). \end{aligned}$$

Finally, we also need the following result, also due to Powell [51, Proposition 7.3.1]. The proof is also given in [29, Proposition 3.17].

Proposition 4.8

(Powell) Let M be non-trivial and $M \hookrightarrow N$ a monomorphism in $R_{fg}-\mathcal {U}$, then

$$\begin{aligned} {{\,\mathrm{\mathbf {TrDeg}}\,}}_{R-\mathcal {U}}(M) \ge {{\,\mathrm{depth}\,}}_R(N). \end{aligned}$$

With these preparations, we can now prove Theorem 4.3.

Proof of Theorem 4.3

If ${{\,\mathrm{CEss}\,}}(R) = 0$ then the result is clear, thus we can assume that ${{\,\mathrm{CEss}\,}}(R) \ne 0$. By Proposition 3.32 we can find n large enough so that

is a monomorphism in $R_{fg}-\mathcal {U}$. We factor $\lambda$ as a product $\lambda = \lambda _{>c} \times \lambda '$ where

and

Recall that $\eta _{R,(E,f)} \cong \kappa _{R,(E,f)} \circ \rho _{R,(E,f)}$ so that we can factor $\lambda _{>c}$:

where $\rho _{>c}$ is the product of the maps $\rho _{R;(E,f)}$ for $(C,g) \subsetneq (E,f)$. In particular, ${{\,\mathrm{CEss}\,}}(R) = \ker (\rho _{>c})$. The factorization shows that ${{\,\mathrm{CEss}\,}}(R)$ is contained in the kernel of $\lambda _{> c}$, and since $\lambda$ is injective, we deduce that the restriction of $\lambda '$ to ${{\,\mathrm{CEss}\,}}(R) \subset R$ is injective. We deduce that ${{\,\mathrm{\mathbf {TrDeg}}\,}}_{R-\mathcal {U}}({{\,\mathrm{CEss}\,}}(R)) \le {{\,\mathrm{\mathbf {TrDeg}}\,}}_{R-\mathcal {U}}(H_C^* \otimes T_C(R;f)^{<n}) \le c(R)$, where the last inequality uses Proposition 4.7. By Proposition 4.5 we have ${{\,\mathrm{\mathbf {TrDeg}}\,}}_{R}({{\,\mathrm{CEss}\,}}(R)) =\dim _R({{\,\mathrm{CEss}\,}}(R)) \le c(R)$, as claimed. $\square$

For the following, we recall that if R is a connected Noetherian unstable algebra with center (C, g) then the depth of R is always at least equal to the rank of C, see Corollary B.7.

Corollary 4.9

Let R be a connected Noetherian algebra with center (C, g) and let $c(R) = {{\,\mathrm{rank}\,}}(C)$. If ${{\,\mathrm{CEss}\,}}(R) \ne 0$, then ${{\,\mathrm{depth}\,}}(R) = c(R)$, and $\dim _R({{\,\mathrm{CEss}\,}}(R)) = c(R)$.

Proof

Assume that ${{\,\mathrm{CEss}\,}}(R) \ne 0$, then by Corollary B.7, the previous result, and Proposition 4.8 we have

$$\begin{aligned} c(R) \le {{\,\mathrm{depth}\,}}(R) \le {{\,\mathrm{\mathbf {TrDeg}}\,}}_{R-\mathcal {U}}({{\,\mathrm{CEss}\,}}(R)) \le c(R). \end{aligned}$$

Thus, ${{\,\mathrm{depth}\,}}(R) = {{\,\mathrm{\mathbf {TrDeg}}\,}}_{R-\mathcal {U}}({{\,\mathrm{CEss}\,}}(R)) = \dim _R({{\,\mathrm{CEss}\,}}(R)) = c(R)$. $\square$

We will prove the converse in Theorem 4.25.

4.2 Primitives and indecomposables

Let R be a connected Noetherian unstable algebra with center (C, g).¹ Since $(C,g) \in \mathbf{A} _R$ the morphism g is finite, and so the following is well defined.

Definition 4.10

Let e(R) denote the maximum degree of a generator (with respect to a minimal generating set) for $H_C^*$ as a R-module, or equivalently the top nonzero degree of the finite dimensional Hopf algebra $H_C^* \otimes _R \mathbb {F}_p$.

We recall from Proposition 3.22 and Corollary 3.23 that $g :R \rightarrow H_C^*$ is a morphism of $H_C^*$-comodules, and that there is a basis $x_1,\ldots ,x_c$ for $H_C^1$ such that

$$\begin{aligned} {{\,\mathrm{Im}\,}}(g) = {\left\{ \begin{array}{ll} \mathbb {F}_2[x_1^{2^{j_1}},\ldots ,x_c^{2^{j_c}}] &{}\text { if } p=2\\ \mathbb {F}_p[y_1^{p^{j_1}},\ldots ,y_b^{p^{j_b}},y_{b+1},\ldots ,y_c] \otimes \Lambda (x_{b+1},\ldots ,x_c) &{} \text { if } p \text { is odd,} \end{array}\right. } \end{aligned}$$

(4.11)

for some natural numbers $j_1 \ge j_2 \ge \cdots$, and where $y_i = \beta x_i$ for $\beta$ the Bockstein homomorphism. We then have

$$\begin{aligned} e(R) = \sum _{i=1}^c (a_i-1). \end{aligned}$$

where

$$\begin{aligned} a_i = {\left\{ \begin{array}{ll} 2^{j_i} &{} p = 2\\ 2p^{j_i} &{} p \text { odd, and } 1 \le i \le b\\ 1 &{} \text {otherwise.} \end{array}\right. } \end{aligned}$$

In order to proceed, we need one more definition, due to Kuhn [37, Definition 2.15].

Definition 4.12

A Duflot algebra of R is a subalgebra $B \subseteq R$ that maps isomorphically to $K = {{\,\mathrm{Im}\,}}(R \rightarrow H_{C}^*)$.

Since the image K is a free graded-commutative algebra over $\mathbb {F}_p$, such Duflot algebras always exist (as the natural epimorphism $R \rightarrow K$ always splits).

Given a Noetherian unstable algebra R, we fix a Duflot algebra $B \subseteq R$.

Definition 4.13

If M is a graded B-module, then the space of indecomposables is

We let $e_{\text {indec}}(M)$ be its largest nonzero degree, or $-\infty$ if $M = 0$.

As shown in Lemma 4.2, ${{\,\mathrm{CEss}\,}}(R)$ is a sub $H_C^*$-comodule of R. Moreover, it is an unstable module, as it is the kernel of a morphism of unstable modules, and the comodule structure map is a morphism of unstable modules. Comodules with this additional structure are called unstable $H_C^*$-comodules in [37].

Definition 4.14

Let M be an unstable $H_C^*$-comodule, then the modules of primitives is

where $\Psi _M :M \rightarrow H_C^* \otimes M$ is the comodule structure map and $i(x) = 1 \otimes x$

We let $e_{{{\,\mathrm{prim}\,}}}({{\,\mathrm{CEss}\,}}(R))$ denote the supremum of the degrees in which $P_C({{\,\mathrm{CEss}\,}}(R))$ is non-zero, with the convention that this is $-\infty$ if ${{\,\mathrm{CEss}\,}}(R) = 0$.

Remark 4.15

If R has trivial center, then the constructions still make sense, where $e(R) = 0$, and $Q_B{{\,\mathrm{CEss}\,}}(R) \cong P_C{{\,\mathrm{CEss}\,}}(R) \cong {{\,\mathrm{CEss}\,}}(R)$.

Remark 4.16

Note that $Q_BM$ will not necessarily be an unstable module because B is not necessarily closed under Steenrod operations. On the other hand $P_CM$ is always an unstable module.

The following lemma is proved by Totaro for Chow rings of finite p-groups [59, Lemma 12.10]–the proof goes through essentially without change here.

Lemma 4.17

Let R be a Noetherian unstable algebra, with center (C, g). Let M be a non-negatively graded R-module that is also a $H_{C}^*$-comodule, such that the morphism $R \otimes M \rightarrow M$ is a morphism of $H_{C}^*$-comodules. Let $B \subseteq R$ be a Duflot algebra. Then,

• (1) M is a free B-module

• (2) The composite $P_CM \hookrightarrow M \twoheadrightarrow Q_BM$ is injective.

Proof

We follow Totaro [59, Lemma 12.10]. To that end, let $L = \ker (g :R \rightarrow H_C^*)$, and let $M_i = L^iM \subset M$ for $i \ge 0$, where $L^i$ denotes the $\mathbb {F}_p$-linear span of all products of i elements of the ideal L. This gives a filtration of M by R-modules.

By Proposition 3.22$g :R \rightarrow H_C^*$ is a morphism of $H_C^*$-comodules, and hence L is a sub-$H_C^*$-comodule of R. Let $\Psi _M :M \rightarrow H_C^* \otimes M$ denote the $H_C^*$-comodule structure map for M, and $\Psi _{R}$ the corresponding comodule structure map for R. By assumption there is a commutative diagram

Since L is a sub-$H_C^*$-comodule, this diagram implies that $LM \subset M$ is a $H_C^*$-comodule. By induction we see that $M_i$ is a sub-$H_C^*$-comodule for all $i \ge 0$.

For each $i \ge 0$ it follows that ${{\,\mathrm{gr}\,}}_iM = M_i/M_{i+1}$ is a $H_C^*$-comodule. It is also a module over $K = {{\,\mathrm{Im}\,}}(R \xrightarrow {g} H_C^*)$, which we have seen is a sub-Hopf algebra of $H_C^*$. By assumption, the $H_C^*$-comodule structure and the R-module structure are compatible. Applying a lemma of Kuhn [36, Lemma 5.2] we deduce that ${{\,\mathrm{gr}\,}}_iM$ is a free B-module, and the composite $P_C({{\,\mathrm{gr}\,}}_iM) \hookrightarrow {{\,\mathrm{gr}\,}}_iM \twoheadrightarrow Q_B({{\,\mathrm{gr}\,}}_iM)$ is injective, for each $i \ge 0$. The filtration of M given by the $M_i$ is separated, and so the fact that each ${{\,\mathrm{gr}\,}}_iM$ is a free B-module implies that M is also a free B-module. $\square$

Theorem 4.18

Let R be a connected Noetherian unstable algebra with center (C, g), and fix a Duflot algebra B of R.

• (1) ${{\,\mathrm{CEss}\,}}(R)$ is a finitely-generated free B-module, i.e., a Cohen–Macaulay module.

• (2) The composite $P_C {{\,\mathrm{CEss}\,}}(R) \hookrightarrow {{\,\mathrm{CEss}\,}}(R) \twoheadrightarrow Q_B {{\,\mathrm{CEss}\,}}(R)$ is monic.

• (3) There is an exact sequence

  

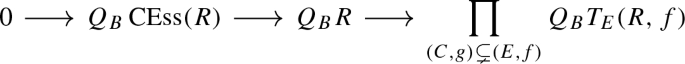
Proof

Everything in (1) and (2) except for the claim that ${{\,\mathrm{CEss}\,}}(R)$ is finitely-generated is a consequence of the previous lemma with $M = {{\,\mathrm{CEss}\,}}(R)$. Now, B has Krull dimension equal to the rank of C, namely c(R). Since we know ${{\,\mathrm{CEss}\,}}(R)$ is a free B-module, it suffices to check that the Krull dimension of ${{\,\mathrm{CEss}\,}}(R)$ is at most c(R), which is Theorem 4.3.

For (3), consider the left exact sequence

Note that these are R-modules and $H_C^*$-comodules in a compatible way. We can apply Lemma 4.17 to the images and cokernels of these maps to deduce that they are free B-modules. It follows that the maps split, and we have an exact sequence as claimed. $\square$

Corollary 4.19

If ${{\,\mathrm{CEss}\,}}(R) \ne 0$, then we have $d_0({{\,\mathrm{CEss}\,}}(R)) = e_{{{\,\mathrm{prim}\,}}}({{\,\mathrm{CEss}\,}}(R))$. In general, $e_{{{\,\mathrm{prim}\,}}}({{\,\mathrm{CEss}\,}}(R)) \le e_{{{\,\mathrm{indec}\,}}}({{\,\mathrm{CEss}\,}}(R)) < \infty$.

Proof

The stated inequality is an immediate consequence of Theorem 4.18(2) applied to $M = {{\,\mathrm{CEss}\,}}(R)$.

For the first claim we use [37, Lemma 2.11] in which Kuhn proves that any unstable $H_C^*$-comodule with $P_CM$ finite-dimensional has the property that $d_0M = e_{{{\,\mathrm{prim}\,}}}(M)$ (under our conventions this is only true if $M \ne 0$). Using Theorem 4.18(2) again, we see that if $Q_A{{\,\mathrm{CEss}\,}}(R)$ is finite-dimensional, then so is $P_C{{\,\mathrm{CEss}\,}}(R)$. But it is clear that if ${{\,\mathrm{CEss}\,}}(R)$ is a finitely-generated B-module, then $Q_B {{\,\mathrm{CEss}\,}}(R)$ is finite-dimensional, and this is a consequence of Theorem 4.18(1). The first part of the corollary then follows by applying Kuhn’s lemma to $M = {{\,\mathrm{CEss}\,}}(R)$. $\square$

4.3 Regularity and $e_{{{\,\mathrm{indec}\,}}}({{\,\mathrm{CEss}\,}}(R))$

We now give the following version of [37, Proposition 2.27]. This proposition is the first point of the paper we need to make some assumptions on the Duflot algebra. In particular, we make the following hypothesis, which is in effect for the rest of this section.

Hypothesis 4.20

R is a connected Noetherian unstable algebra whose Duflot algebra B is polynomial.

Remark 4.21

This always holds if $p = 2$, or if R is concentrated in even degrees (i.e., R is naturally an element of $\mathcal {U}'$, see Remark 2.24).

For the following, we let $\mathfrak m = R^{> 0}$ denote the maximal homogeneous ideal of R, and let

$$\begin{aligned} H_{\mathfrak m}^0(M) = \{ x \in M \mid \text { there exists } n \in \mathbb {N} \text { with } m^{\mathfrak n}x = 0\}. \end{aligned}$$

denote the $\mathfrak m$-torsion functor for an R-module M (see Appendix B). This has right derived functors, $H_{\mathfrak m}^i(M)$, the i-th local cohomology of M. We note that since R and M are graded, so are these local cohomology modules, although we will usually suppress the internal grading.

Proposition 4.22

Let R be a connected Noetherian unstable algebra with Duflot algebra B, then

$$\begin{aligned} Q_B{{\,\mathrm{CEss}\,}}(R) = H_{\mathfrak m}^0(Q_B{{\,\mathrm{CEss}\,}}(R)) = H_{\mathfrak m}^0(Q_BR). \end{aligned}$$

Proof

The first equality follows because $Q_B{{\,\mathrm{CEss}\,}}(R)$ is finite-dimensional. For the second, consider the left exact sequence of Theorem 4.18(3):

This gives a left exact sequence

Thus we must show that whenever $(C,g) \subsetneq (E,f)$, we have $H^0_{\mathfrak m}Q_BT_E(R,f) = 0$. Fix such a pair (E, f).

By assumption, the Duflot algebra B is polynomial, say $B \cong \mathbb {F}_p[f_1,\ldots ,f_c]$, and moreover by Lemma 4.17$H_E^*$ is a free B-module, so that the sequence $f_1,\ldots ,f_c$ is regular by Lemma B.3. The cohomology $H_E^*$ is Cohen–Macaulay, and hence $Q_BH_E^*$ is also Cohen–Macaulay, of Krull dimension $r - c$, where r is the p-rank of E (as the quotient of a Cohen–Macaulay ring by a regular sequence is still Cohen–Macaulay, see [4, Theorem 2.1.3]). We note that $r>c$ by the assumption that $(C,g) \subsetneq (E,f)$. It follows that ${{\,\mathrm{depth}\,}}(Q_BH_E^*) = r-c > 0$.

Because $H_E^*$ is a finitely generated R-module via f so is the quotient ring $Q_BH_E^*$. It follows from Lemma B.5 that

$$\begin{aligned} r - c = {{\,\mathrm{depth}\,}}(Q_BH_E^*) = {{\,\mathrm{depth}\,}}_R(Q_BH_E^*). \end{aligned}$$

In particular, by Lemma B.3 there exists elements $y_i \in \mathfrak m = R^{>0}$ such that $Q_BH_E^*$ is a finitely generated free module over the graded polynomial subring $S \cong k[y_1,\ldots ,y_{r-c}] \subseteq R$.

Since S has dimension $r - c>0$, we can find a non-zero element $\ell$ with positive degree which is a non-zero divisor on $Q_BH_E^*$. It follows that the sequence $f_1,\ldots ,f_c,\ell \in R$ restricts to a regular sequence in $H_E^*$. By Proposition 3.3 there exists a $h :T_E(R;f) \rightarrow H_E^*$ such that (E, h) is central in $T_E(R,f)$, and so Theorem B.6 applies to show that the sequence $f_1,\ldots ,f_c,\ell$ is regular in $T_E(R;f)$. It follows that $\ell \in \mathfrak m$ restricts to a non-zero divisor on $Q_BT_E(R;f)$, and so by [12, Lemma 2.1.1(i)] $H_{\mathfrak m}^0Q_BT_E(R;f) = 0$ , as required. $\square$

Remark 4.23

The proof actually shows that, even when Hypothesis 4.20 does not hold, we still have $Q_B{{\,\mathrm{CEss}\,}}(R) = H_{\mathfrak m}^0(Q_B{{\,\mathrm{CEss}\,}}(R)) \subseteq H_{\mathfrak m}^0(Q_BR)$.

Given an R-module M, we let $a_i(R,M)$ be the maximum degree of a non-zero element of $H^i_{\mathfrak m}(M)$ (with the convention that this is $\infty$ if unbounded, or $-\infty$ if $H_{\mathfrak m}^i(M) = 0$). The Castelnuovo–Mumford regularity of M is defined as

$$\begin{aligned} {{\,\mathrm{Reg}\,}}(R,M) = \sup _i \{a_i(R,M)+i\}, \end{aligned}$$

see [58] for the basic properties of regularity. If $R = M$, then we write ${{\,\mathrm{Reg}\,}}(R)$ and $a_i(R)$. The main result of this section is the following. We remind the reader we work under Hypothesis 4.20.

Theorem 4.24

Let R be a connected Noetherian unstable algebra, then $e_{{{\,\mathrm{indec}\,}}}({{\,\mathrm{CEss}\,}}(R)) \le e(R) + {{\,\mathrm{Reg}\,}}(R)$, and hence if ${{\,\mathrm{CEss}\,}}(R) \ne 0$, we have

$$\begin{aligned} d_0({{\,\mathrm{CEss}\,}}(R)) \le e(R) + {{\,\mathrm{Reg}\,}}(R). \end{aligned}$$

More specifically, we have

$$\begin{aligned} e_{{{\,\mathrm{indec}\,}}}({{\,\mathrm{CEss}\,}}(R)) = e(R) + a_{c(R)}(R) + c(R) \le e(R) + {{\,\mathrm{Reg}\,}}(R). \end{aligned}$$

Proof

We first show that $e_{{{\,\mathrm{indec}\,}}}({{\,\mathrm{CEss}\,}}(R)) = e(R) + a_{c(R)}(R) + c(R)$. This is the claim that the top non-zero degree of $Q_B{{\,\mathrm{CEss}\,}}(R)$ is $e(R) + a_{c(R)}(R) + c(R)$. By Proposition 4.22 it is equivalent to show that the top non-zero degree of $H_{\mathfrak m}^0(Q_BR)$ is $e(R) + a_{c(R)}(R) + c(R)$.

Now, by definition $H_{\mathfrak m}^{c(R),e}(R) = 0$ for all $e > a_{c(R)}(R)$ and $H_{\mathfrak m}^{c(R),a_{c(R)}(R)}(R) \ne 0$ (here we are explicitly writing the internal degree of the local cohomology module). If we choose algebra generators $z_1,\ldots ,z_c$ for the Duflot algebra, then $|z_1| + \cdots |z_c| = c(R) + e(R)$, $Q_BR = R/(z_1,\ldots ,z_c)$ and the long exact sequence in local cohomology shows that $H_{\mathfrak m}^{0,e(R)+c(R)+e}(Q_BR) = 0$ for all $e>a_{C(R)}(R)$ and

$$\begin{aligned} H_{\mathfrak m}^{0,e(R)+c(R)+a_{c(R)}(R)}(Q_BR) = H_{\mathfrak m}^{c(R),a_{c(R)}(R)}(R) \ne 0, \end{aligned}$$

compare [37, Corollary 2.25 and Proposition 2.26]. In particular, $e_{{{\,\mathrm{indec}\,}}}({{\,\mathrm{CEss}\,}}(R)) = e(R) + a_{c(R)}(R) + c(R)$, as claimed. The subsidiary claim about $d_0({{\,\mathrm{CEss}\,}}(R))$ is then a consequence of Corollary 4.19. $\square$

We now turn to a form of Carlson’s depth conjecture [16] or [19, Question 12.5.7]. We recall that, for a finite group G, Carlson has conjectured that if the product of restriction maps

$$\begin{aligned} H_G^* \longrightarrow \prod _{{{\,\mathrm{rank}\,}}(E) = s}H^*_{C_G(E)} \end{aligned}$$

is injective, then ${{\,\mathrm{depth}\,}}(H_G^*) \ge s$. This is Carlson’s depth conjecture. It is a theorem of Duflot [20] that the depth of $H_G^*$ is always equal to at least the p-rank of the center of a Sylow p-subgroup of G. If equality holds, we will say that $H_G^*$ has minimal depth. Suppose that G is a p-group and $H_G^*$ has minimal depth, then Carlson’s depth conjecture is that ${{\,\mathrm{CEss}\,}}(H_G^*) \ne 0$, and has been proven in this case by Green [28] and Kuhn [36, Theorem 2.13].

In [29] the author generalized Duflot’s result on depth for connected Noetherian unstable algebras; the depth is always at least c(R), the rank of the center of R (see Corollary B.7), and we say that R has minimal depth if ${{\,\mathrm{depth}\,}}(R) = c(R)$. One can then ask that if R has minimal depth, then is ${{\,\mathrm{CEss}\,}}(R) \ne 0$? (note that we have already proved the converse of this in Corollary 4.9). This is part of the content of the following.

Theorem 4.25

The central essential ideal ${{\,\mathrm{CEss}\,}}(R)$ is non-zero if and only if the depth of R is minimal, i.e., ${{\,\mathrm{depth}\,}}(R) = c(R)$. Moreover, in this case ${{\,\mathrm{CEss}\,}}(R)$ is a Cohen–Macaulay R-module of dimension c(R).

Proof

The only if direction is Corollary 4.9, so we prove the converse. To this end, suppose that ${{\,\mathrm{depth}\,}}(R) = c(R)$, so that $H_{\mathfrak m}^{c(R)}(R) \ne 0$ by Proposition B.4. By Theorem 4.24 we have $e_{{{\,\mathrm{indec}\,}}}({{\,\mathrm{CEss}\,}}(R)) \ge 0$, and hence ${{\,\mathrm{CEss}\,}}(R) \ne 0$.

For the second claim, observe that we have

$$\begin{aligned} c(R) \le {{\,\mathrm{depth}\,}}_R({{\,\mathrm{CEss}\,}}(R)) \le \dim _R({{\,\mathrm{CEss}\,}}(R)) = c(R) \end{aligned}$$

by Corollary 4.9 and Theorem 4.18. $\square$

5 The topological nilpotence degree of a Noetherian unstable algebra

In this section we introduce the p-central defect of a Noetherian unstable algebra, which is the analog of p-centrality for finite groups. For unstable algebras of p-central defect 0, we have an immediate estimate for $d_0(R)$. In general, we use an inductive argument to prove the following, the main result of the paper.

Theorem 5.1

Let R be a connected Noetherian unstable algebra with center (C, g), and suppose that $T_E(R;f)$ satisfies the assumptions of Hypothesis 4.20 for all $(C,g) \subseteq (E,f)$, then

$$\begin{aligned} d_0(R) \le \underset{\begin{array}{c} (C,g) \subseteq (E,f) \in \mathbf{A} _R \\ {{\,\mathrm{depth}\,}}(T_E(R;f)) = c(T_E(R;f)) \end{array}}{\max }\{e(T_E(R;f)) + {{\,\mathrm{Reg}\,}}(T_E(R;f)) \}. \end{aligned}$$

The proof will be given in Sect. 5.2.

5.1 The p-central defect of a Noetherian unstable algebra

Definition 5.2

Let R be a connected Noetherian unstable algebra with center (C, g). Let c(R) be the rank of C, and

$$\begin{aligned} p(R) = \max \{ {{\,\mathrm{rank}\,}}(E) \mid (E,f) \in \mathbf{A} _R \}. \end{aligned}$$

The p-central defect of R is $p(R)- c(R)$.

Lemma 5.3

We have

$$\begin{aligned} c(R) \le {{\,\mathrm{depth}\,}}(R) \le \dim (R) = p(R) \end{aligned}$$

If particular, the p-central defect is always greater than or equal to zero, and if it is zero, then ${{\,\mathrm{depth}\,}}(R) = \dim (R) = c(R)$, so that R is a Cohen–Macaulay ring.

Proof

We have $c(R) \le {{\,\mathrm{depth}\,}}(R)$ by the author’s generalization of Duflot’s theorem (Corollary B.7), the inclusion ${{\,\mathrm{depth}\,}}(R) \le \dim (R)$ always holds, and $\dim (R) = p(R)$ by Proposition 2.7(2). The result of the lemma is then clear. $\square$

Remark 5.4

The Cohen–Macaulay defect of R is defined as $\dim (R) =p(R) - {{\,\mathrm{depth}\,}}(R)$. By Duflot’s depth theorem (Corollary B.7) ${{\,\mathrm{depth}\,}}(R) \ge c(R)$, so that the Cohen–Macaulay defect is always less than or equal to the p-central defect of R.

Lemma 5.5

Let R be a connected Noetherian unstable algebra with center (C, g). If $(C,g) \subseteq (E,f)$, then the p-central defect of $T_E(R;f)$ is less than or equal to R, with equality if and only if $(C,g) \simeq (E,f)$.

Proof

We first claim that $p(T_E(R;f)) \le p(R)$. Indeed, if $(V,\tilde{g}) \in \mathbf{A} _{T_E(R;f)}$, then we can precompose with $\rho _{R,(E,f)} :R \rightarrow T_E(R;f)$ to get a pair $(V,g) \in \mathbf{A} _R$ for $g = \tilde{g} \circ \rho _{R,(E,f)}$. On the other hand, we recall there exists $h :T_E(R;f) \rightarrow H_E^*$ such that (E, h) is central in $\mathbf{A} _{T_E(R;f)}$, see Proposition 3.3. Thus, $c(R) \le c(T_E(R;f))$, with equality if and only if (E, f) is central in $\mathbf{A} _R$, in which case $(E,f) \simeq (C,g)$. Combining these two inequalities we see that

$$\begin{aligned} p(T_E(R;f)) - c(T_E(R;f)) \le p(R) - c(R), \end{aligned}$$

hence the result. $\square$

Algebras of p-central defect 0 have several nice properties, as we now explain. We note that in this case the product in the definition of ${{\,\mathrm{CEss}\,}}(R)$ is taken oven the empty set, and hence this product trivial algebra, so that in this case ${{\,\mathrm{CEss}\,}}(R) \cong R$.

The following characterization of unstable algebras of p-central defect 0 was suggested by the referee.

Lemma 5.6

Let R be a connected Noetherian unstable algebra with center (C, g), then R has p-central defect 0 if and only if there is an equivalence of categories $\mathbf{A} _R \simeq \mathbf{A} _{H_C^*}$.

Proof

If R has p-central defect greater than 0, then there exists a pair $(E,f) \in \mathbf{A} _R$ with $(C,g) \subsetneq (E,f)$, and such an (E, f) cannot be equivalent to an object $\mathbf{A} _{H_C^*}$ as ${{\,\mathrm{rank}\,}}(C) \lneq {{\,\mathrm{rank}\,}}(E)$. Now suppose that R has p-central defect equal to zero, and let $(E,f) \in \mathbf{A} _R$. Note that $(E,f) \subseteq (C,g)$ as (C, g) is the unique maximal object of $\mathbf{A} _R$. In particular, there is a morphism $\alpha :H_C^* \rightarrow H_E^*$, and clearly the pair $(E,\alpha )$ defines an object of $\mathbf{A} _{H_C^*}$. This defines a functor $F :\mathbf{A} _R \rightarrow \mathbf{A} _{H_C^*}$. Conversely, if $(V,j) \in \mathbf{A} _{H_C^*}$, then $(V,j \circ g) \in \mathbf{A} _R$, and it is easy to see that this is functorial, and provides an inverse to F. $\square$

Example 5.7

Let G be a p-group, then we will see in Theorem 6.3 that $\mathbf{A} _{H_G^*}$ is equivalent to the category $\mathbf{A} _G$ whose objects are the elementary abelian p-subgroups of G. Moreover, the center of $H_G^*$ is just the group-theoretic center of G. It follows that G has p-central defect 0 if and only if the maximal central elementary abelian p-subgroup is maximal among all elementary abelian p-subgroups of G. Such groups are known as p-central groups. For example, $G = Q_8$ (the quaternion group of order 8) is 2-central, while $D_8$ (the dihedral group of order 8) is not 2-central; in our terminology, $H_{Q_8}^*$ has 2-central defect 0, and $H_{D_8}^*$ has 2-central defect 1. In terms of the previous lemma, the elementary abelian subgroup lattices of $Q_8$ and $D_8$ are given respectively (up to conjugacy) by

In both cases, the center is isomorphic to $C_2$, however $\mathbf{A} _{H_{Q_8}^*} \simeq \mathbf{A} _{H_{C_2}^*}$ while $\mathbf{A} _{H_{D_8}^*} \not \simeq \mathbf{A} _{H_{C_2}^*}$.

Example 5.8

Let $S^3 \langle 3 \rangle$ denote the 3-connected cover of $S^3$, then $\mathbf{A} _{H^*(S^3\langle 3 \rangle )}$ has a single non-trivial object $(\mathbb {Z}/p,f)$ which is also central, see [29, Example 3.7] for the map f. Thus, this has p-central defect 0.

For algebras of p-central defect 0, we have an immediate estimate for $d_0(R)$.

Proposition 5.9

Suppose that $R \ne 0$ has p-central defect 0 and that Hypothesis 4.20 holds, then ${{\,\mathrm{depth}\,}}(R) = c(R)$ and

$$\begin{aligned} d_0(R) \le e(R) + {{\,\mathrm{Reg}\,}}(R). \end{aligned}$$

Proof

By Remark 5.3 we have ${{\,\mathrm{depth}\,}}(R) = c(R)$, and then the estimate for $d_0(R)$ is an immediate consequence of the fact that $R \cong {{\,\mathrm{CEss}\,}}(R)$, and Theorem 4.24. $\square$

We note the following behavior of the p-central defect under tensor products. We once again thank the referee for the proof that the Krull dimension is additive.

Lemma 5.10

Let $R_1$ and $R_2$ be connected Noetherian unstable algebras, then the p-central defect of $R_1 \otimes R_2$ is equal to the sum of the p-central defects of $R_1$ and $R_2$.

Proof

Using Lemma 3.20 we reduce to the claim that $p(R_1 \otimes R_2) = p(R_1) + p(R_2)$. This follows directly from work of Powell [50, Theorem 3 and Theorem 4], along with Proposition 2.7(2). As noted by the referee, we can also prove this directly. Firstly, if $(E_1,f_1) \in \mathbf{A} _{R_1}$ and $(E_2,f_2) \in \mathbf{A} _{R_2}$, then $(E_1 \otimes E_2,f_1 \otimes f_2) \in \mathbf{A} _{R_1 \otimes R_2}$. It follows that $p(R_1 \otimes R_2) \ge p(R_1) + p(R_2)$.

For the converse, suppose we are given $f :R_1 \rightarrow H_V^* \in \mathbf{V} _{R_1}$ and $g :R_2 \rightarrow H_V^* \in \mathbf{V} _{R_2}$, so that $\widetilde{f} :R_1 \rightarrow H^*_{V/\ker (f)} \in \mathbf{A} _R$ and $\widetilde{g} :R_2 \rightarrow H^*_{V/\ker (g)} \in \mathbf{A} _R$. There is a commutative diagram of the form

The composite $f \coprod g :R_1 \oplus R_2 \rightarrow H_V^*$ gives an element of $\mathbf{V} _{R_1 \oplus R_2}$, and the commutative diagram shows that $\ker (f \coprod g) = \ker (f) \cap \ker (g)$. In particular, the rank of $V/(\ker (f) \cap \ker (g))$ is at most the sum of the ranks of $V/\ker (f)$ and $V/\ker (g)$, so that $p(R_1 \otimes R_2) \le p(R_1) \oplus p(R_2)$. Together, we see that $p(R_1 \otimes R_2) = p(R_1) + p(R_2)$, as claimed. $\square$

We can therefore construct unstable algebras of arbitrarily high p-central defect. For example, $H^*_{D_8^{\times n}}$ has 2-central defect of exactly n.

The unstable algebra $H^*(S^3 \langle 3 \rangle )$ considered above is the cohomology of a H-space. More generally, if X is a connected Noetherian H-space, we recall from Example 3.17 that the mod 2 cohomology satisfies

$$\begin{aligned} H^*(X) \cong \mathbb {F}_2[x_1,\ldots ,x_r] \otimes \frac{\mathbb {F}_2[y_1,\ldots ,y_s]}{(y_1^{2^{a_1}},\ldots ,y_s^{2^{a_s}})}. \end{aligned}$$

(5.11)

while

$$\begin{aligned} H^*(X;\mathbb {F}_p) \cong \frac{\mathbb {F}_p[y_1,\ldots ,y_s]}{(y_1^2,\ldots ,y_s^2)} \otimes \mathbb {F}_p[\beta y_1,\ldots , \beta y_k,x_{k+1},\ldots ,x_n] \otimes \frac{\mathbb {F}_p[z_1,\ldots ,z_t]}{(z_1^{p^{a_1}},\ldots ,z_t^{p^{a_t}})}, \end{aligned}$$

(5.12)

when p is odd.

Both these rings are Gorenstein because they are Cohen–Macaulay, and the quotient by $(x_1,\ldots ,x_r)$ for $p = 2$ (or $(\beta y_1,\ldots ,x_n)$ for p odd) is a Poincaré duality algebra of formal dimension $\sum _{i=1}^s (|y_i|^{2^{a_s-1}})$ for $p = 2$ (or $\sum _{i=1}^s |y_i| + \sum _{i=1}^t |z_i|^{p^{a_t-1}})$ for p odd), see Proposition I.1.4 and the remark on the same page of [47].

Definition 5.13

Let X be a connected H-space with Noetherian mod 2 cohomology given as in (5.11), then the Poincaré dimension of $H^*(X)$ is $\sum _{i=1}^s (|y_i|^{2^{a_s-1}})$.

Proposition 5.14

Let X be a connected Noetherian H-space with cohomology as in (5.11).

If $p = 2$, then the following hold:

• (1) (Broto–Crespo) There exists a central elementary abelian 2-subgroup E of rank r and a central morphism $f :H^*(X) \rightarrow H_{E}^*$. Moreover, there is a basis $u_1,\ldots ,u_r$ of $H^1_E$ such that $f(x_i) = u_i^{2^{\beta _i}}$ for $\beta _i \ge 0$ and $i = 1,\ldots ,r$.

• (2) $H^*(X)$ has 2-central defect 0.

If p is odd, then the following hold:

• (1) (Crespo) There exists a central elementary abelian p-subgroup E of rank n and a central morphism $f :H^*(X) \rightarrow H_{E}^*$. Moreover, there is a basis $u_1,\ldots ,u_n$ of $H^1_E$ such that

  $$\begin{aligned} f(y_j) = {\left\{ \begin{array}{ll} u_j &{} 1 \le j \le r \quad r \le k \\ 0 &{} i > k \end{array}\right. } \end{aligned}$$

  and

  $$\begin{aligned} f(x_i) = (\beta u_i)^{p^{a_i}}. \end{aligned}$$

• (2) $H^*(X)$ has p-central defect 0.

Proof

Let $p = 2$, then the existence of the map f and the description of the image is [1, Theorem 2.2] (where the map f is denoted $\mu _X$). That f is central has already been discussed in Example 3.17. Finally, $H^*(X)$ has p-central defect 0 because $H^*(X)$ has dimension r.

For p odd, the same argument works using [18, Theorem 2.6 and Corollary 2.7] (where the map f is denoted $\ell$). $\square$

Theorem 5.15

Suppose X is a connected H-space with Noetherian mod p cohomology. If X satisfies Hypothesis 4.20 and has Poincaré dimension d, then $d_0(H^*(X)) \le d$.

Proof

We first consider the case $p = 2$. Because $H^*(X)$ is Gorenstein, its local cohomology is concentrated in a single degree, namely in degree $c(H^*(X))$. From the definitions, this implies that ${{\,\mathrm{Reg}\,}}(H^*(X)) = d + \sum _{i=1}^r(1 - |x_i|)$. Because $H^*(X)$ has 2-central defect 0, we can then use Corollary 5.9 to see that

$$\begin{aligned} d_0(H^*(X)) \le e(H^*(X)) + d + \sum _{i=1}^r(1 - |x_i|). \end{aligned}$$

From the description of the image in the previous proposition, we have ${{\,\mathrm{Im}\,}}(f) \cong \mathbb {F}_p[u_1^{2^{\beta _1}},\ldots ,u_r^{2^{\beta _{r}}}]$, and so

$$\begin{aligned} e(H^*(X)) = \sum _{i=i}^r(2^{\beta _i}-1) = \sum _{i=1}^r (|x_i| - 1). \end{aligned}$$

Thus,

$$\begin{aligned} d_0(H^*(X)) \le \sum _{i=1}^r (|x_i| - 1) + d + \sum _{i=1}^r(1 - |x_i|) = d, \end{aligned}$$

as claimed.

The argument for p odd is very similar. First we note that because Hypothesis 4.20 holds, we must have that $k = 0$ in (5.12). We have ${{\,\mathrm{Reg}\,}}(H^*(X)) = d + \sum _{i=1}^n(1-|x_i|)$, and by the assumption we can apply Corollary 5.9 to see that

$$\begin{aligned} d_0(H^*(X)) \le e(H^*(X)) + d + \sum _{i=1}^n(1 - |x_i|). \end{aligned}$$

The Duflot algebra is then of the form ${{\,\mathrm{Im}\,}}(f) \cong \mathbb {F}_p[(\beta u_{1})^{p^{a_{1}}},\ldots , (\beta u_{n})^{p^{a_{n}}}]$, and

$$\begin{aligned} e(H^*(X)) = \sum _{i=1}^n (2p^{a_i}-1) = \sum _{i=1}^n (|x_i|-1). \end{aligned}$$

Thus, as above,

$$\begin{aligned} d_0(H^*(X)) \le \sum _{i=1}^n (|x_i| - 1) + d + \sum _{i=1}^n(1 - |x_n|) = d, \end{aligned}$$

as claimed. $\square$

Remark 5.16

If p is odd, then we note that Proposition 5.14 shows that $H^*(X)$ does not always satisfy the assumptions of Hypothesis 4.20.

5.2 The topological nilpotence degree of an unstable algebra

In this section we prove our main result (Theorem 5.1), which gives an estimate for $d_0(R)$. We begin with the following.

Proposition 5.17

For any connected Noetherian unstable algebra R with center (C, g) we have

$$\begin{aligned} d_0(R) \le \max _{(C,g) \subseteq (E,f) \in \mathbf{A} _R}\{d_0({{\,\mathrm{CEss}\,}}(T_E(R;f))) \}. \end{aligned}$$

Proof

Suppose that R has p-central defect d. The proof will be by induction on d. If $d = 0$, then the statement of the proposition is clear (in fact, in this case the inequality is even an equality). Inductively, we assume that the proposition holds for all connected Noetherian unstable algebras of p-central defect $0 \le k < d$.

Choose a pair (E, f) with $(C,g) \subsetneq (E,f)$, and let $(C_E,\tilde{g}_E)$ denote the center of $T_E(R;f)$. By Proposition 3.3 there exists $h :T_E(R;f) \rightarrow H_E^*$ such that (E, h) is central in $\mathbf{A} _{T_E(R;f)}$ and the following diagram commutes:

By centrality, we have $(E,h) \subseteq (C_E,\tilde{g}_E)$, and hence (by composing with $\rho _{R,(E,f)}$) we have $(C,g) \subsetneq (E,f) \subseteq (C_E,g_E)$, where $g_E = \rho _{R,(E,f)} \circ \tilde{g}_E$. By Lemma 5.5 the p-central defect of $T_E(R;f)$ is less than that of R, and in particular, the inductive hypothesis applies to show that

$$\begin{aligned} d_0(T_E(R;f)) \le \max \{ d_0({{\,\mathrm{CEss}\,}}(T_V(T_E(R;f);\tilde{j}))) \mid (C_E,\tilde{g}_E) \subseteq (V,\tilde{j}) \in \mathbf{A} _{T_E(R;f)} \}. \end{aligned}$$

(5.18)

Let $j = \rho _{R,(E,f)} \circ \tilde{j}$, then the assumptions of Lemma 3.27 are satisfied (since $(E,h) \subseteq (C_E,\widetilde{g}_E) \subseteq (V,\widetilde{j})$), and show that

$$\begin{aligned} T_V(T_E(R;f);\tilde{j}) \cong T_V(R;j), \end{aligned}$$

where $(R,j) \in \mathbf{A} _R$. By (5.18) we then have

$$\begin{aligned} d_0(T_E(R;f)) \le \max \{ d_0({{\,\mathrm{CEss}\,}}(T_V(R;j))) \mid (C_E,g_E) \subseteq (V,j) \in \mathbf{A} _{R} \}. \end{aligned}$$

From the definition of the central essential ideal and Proposition 2.22, we have

$$\begin{aligned} d_0(R) \le \max \{d_0({{\,\mathrm{CEss}\,}}(R)),d_0(T_E(R;f)) \mid (C,g) \subsetneq (E,f) \}. \end{aligned}$$

Combining the previous two equations and observing that $(C,g) \subsetneq (C_E,g_E)$ gives the desired result. $\square$

We now prove Theorem 5.1. For this we need to assume that $T_E(R;f)$ satisfies the assumptions of Hypothesis 4.20 for all $(C,g) \subseteq (E,f)$. We note that this is automatic if $p = 2$, or if R is concentrated in even degrees, as then so is $T_E(R;f)$ by Lemma 2.17.

Proof of Theorem 5.1

Combine Theorems 4.24 and 4.25 and Proposition 5.17. $\square$

6 Computations of the topological nilpotence degree

We finish with examples from group theory, and homotopical group theory, giving results analogous to Kuhn’s in the case of compact Lie groups.

6.1 Group theory

We now focus on unstable algebras of the form $R = H_G^*$ where G is a group. In this case, Rector’s category will take a particularly nice form. We will need the following definition.

Definition 6.1

The Quillen category associated to a group G at the prime p is the category $\mathbf{A} _G$ with objects elementary abelian p-subgroups $E \le G$ and with morphisms $E \rightarrow V$ those monomorphisms induced by conjugation in G.

While most of the groups we study should be familiar to the reader, we first explain the class of groups considered by Broto and Kitchloo [6].

Definition 6.2

(Broto–Kitchloo) Let $\mathcal {X}$ be a class of compactly generated Hausdorff topological groups, and let $\mathcal {K}_1(\mathcal {X})$ be the new class of groups, such that a compactly generated Hausdorff topological group G belongs to $\mathcal {K}_1(\mathcal {X})$ if and only if there exists a finite G-CW complex X with the following two properties:

• (1) The isotropy subgroups of X belong to the class $\mathcal {X}$.

• (2) For every finite p-subgroup $\pi < G$, the fixed point space $X^{\pi }$ is p-acyclic.

If $\mathcal {X}$ is the class of compact Lie groups, then Kac–Moody groups are an example of a group in $\mathcal {K}_1(\mathcal {X})$, see [6, Section 5].

With this we get the following, which is a compendium of results of Quillen [52, 53], Rector [54], Lannes [38, 39] Henn [31] and Broto–Kitchloo [6], see [29, Theorem 4.1 and Theorem 4.8] for the precise details.

Theorem 6.3

Assume we are in one of the following cases:

• (1) G is a compact Lie group.

• (2) G is a discrete group for which there exists a mod p acyclic G-CW complex with finitely many G-cells and finite isotropy groups.

• (3) G is a profinite group such that the continuous mod p cohomology $H_G^*$ is Noetherian.

• (4) G is a group of finite virtual cohomological dimension such that $H_G^*$ is finite generated as an $\mathbb {F}_p$-algebra.

• (5) G is in $\mathcal {K}_1\mathcal {X}$ where $\mathcal {X}$ is the class of compact Lie groups (for example, a Kac–Moody group).

Then the following hold:

• (1) The mod p cohomology $H_G^*$ is a Noetherian unstable algebra, and there is an equivalence of categories $\mathbf{A} _G \simeq \mathbf{A} _{H_G^*}$ given by associating to $E \le G$ the pair $(E,{{\,\mathrm{res}\,}}_{G,E}^*)$ where ${{\,\mathrm{res}\,}}_{G,E}^*$ is the restriction homomorphism $H_G^* \rightarrow H_E^*$.

• (2) There are isomorphisms

  $$\begin{aligned} T_E(H_G^*;{{\,\mathrm{res}\,}}_{G,E}^*) \cong H_{C_G(E)}^*. \end{aligned}$$

Definition 6.4

(Mislin [45]) An elementary abelian subgroup $E < G$ is said to be cohomologically p-central if $C_G(E) \rightarrow G$ is a mod p cohomology equivalence, i.e., $H^*_G \rightarrow H_{C_G(E)}^*$ is an isomorphism.

Under the equivalence of categories $\mathbf{A} _G \simeq \mathbf{A} _{H_G^*}$, these are precisely the central elements as considered throughout this paper (compare Example 2.18 for the case of compact Lie groups). We use the terminology cohomological p-central so as to not conflict with the usual group theoretic notion of central elementary abelian p-subgroup. The two are related in the following way, where we let $C_p(G)$ denote the maximal cohomologically p-central subgroup of G (which is only unique up to conjugacy, see Theorem 3.13), and Z(G)[p] the maximal central elementary abelian p-subgroup in the usual sense.

Lemma 6.5

(Mislin) If $E < G$ is a central elementary abelian p-subgroup, then $C_G(E)$ is cohomologically p-central. Moreover, there is an injective homomorphism $\phi :Z(G)[p] \hookrightarrow C_p(G)$.

Proof

The first claim is clear because in this case $C_G(E) \cong G$. The injective homomorphism $\phi$ is constructed exactly as by Mislin [45]. We recall his argument now. Let $x \in Z(G)[p]$ be represented by a map $\tilde{\phi } (x) :\mathbb {Z}/p \rightarrow G$, and write f for the induced map $f :H^*_G \rightarrow H_{\mathbb {Z}/p}^*$. The pair $(\mathbb {Z}/p,f)$ is central, because $H_{G}^* \rightarrow T_{\mathbb {Z}/p}(H_{G}^*;f)$ corresponds to the map induced by $C_G(\langle x \rangle ) \rightarrow G$. We then set $\phi (x) = f$. This is clearly injective, because if $\phi (x) = \phi (y)$, then x and y are conjugate in G, and hence equal, as they are central. $\square$

Remark 6.6

If G is a finite p-group, then the main result of [45] implies that $Z(G)[p] \cong C_p(G)$, however in general $\phi$ is not surjective. A counterexample is given by the group $\Sigma _3$ at $p = 2$, as in Example 3.15. This means that the definition of ${{\,\mathrm{CEss}\,}}(H_{G}^*)$ does not necessarily agree with Kuhn’s definition of ${{\,\mathrm{CEss}\,}}(G)$. For example, we have ${{\,\mathrm{CEss}\,}}(H_{\Sigma _3}^*) \cong H^*_{\Sigma _3}$ (i.e., ${{\,\mathrm{CEss}\,}}(\Sigma _3)$ has p-central defect 0), while ${{\,\mathrm{CEss}\,}}(\Sigma _3)$ is trivial, as it is the kernel of the restriction map $H^*_{\Sigma _3} \rightarrow H^*_{C_2}$. Of course, in any case one gets the same result, namely that $d_0(H_{\Sigma _3}^*) = 0$.

Theorem 6.7

Let G be one of the groups considered in Theorem 6.3, then for any prime p we have

$$\begin{aligned} d_0(H_G^*) \le \underset{\begin{array}{c} C_p(G) \le E \in \mathbf{A} _G \\ {{\,\mathrm{depth}\,}}(H_{C_{{G}}(E)}^*) = c(C_{{G}}(E)) \end{array}}{\max }\{e(H_{C_{{G}}(E)}^*) + {{\,\mathrm{Reg}\,}}(H_{C_{{G}}(E)}^*)\} \end{aligned}$$

where $c(C_G(E))$ is the rank of the maximal central cohomologically p-central subgroup of G.

Moreover, if G is a compact Lie group, then ${{\,\mathrm{Reg}\,}}(H^*_{C_G(E)}) \le -\dim (C_G(E))$, with equality if $\pi _0(C_G(E))$ is a finite p-group.

Proof

This will be a consequence of Theorems 5.1 and 6.3, but we first explain why we are able to prove this without assuming anything about the Duflot algebra, using an observation of Nick Kuhn.² The point is that for a group we can always assume that the Duflot algebra is polynomial (this has already been observed by Kuhn in the case of compact Lie groups, see [37, Page 160]). Indeed, since the action of G on $\mathbb {F}_p$ is trivial $H^1_G \cong {{\,\mathrm{Hom}\,}}_{\mathbb {Z}}(G,\mathbb {Z}/p)$ (these homomorphisms need be continuous in the case G is a profinite group). In particular, elements in the image of ${{\,\mathrm{res}\,}}_{G,C_p(G)}^* :H_G^1 \rightarrow H_{C_p(G)}^1$ are exactly homomorphisms from $C_p(G) \rightarrow \mathbb {Z}/p$ that factor through G. Recall that the image of $H_G^* \rightarrow H_{C_p(G)}$ is the form

$$\begin{aligned} \mathbb {F}_p[y_1^{p^{j_1}},\ldots ,y_b^{p^{j_b}},y_{b+1},\ldots ,y_c] \otimes \Lambda (x_{b+1},\ldots ,x_c) \end{aligned}$$

Using the observation above it is not hard to see that $c-b$ is the rank of the largest subgroup of C splitting off G as a direct summand (compare the discussion on page 158 of [37]). Write $G = L \times E$ where $E = (\mathbb {Z}/p)^d$, then one sees that $d_0(H_{L \times E}^*) \cong d_0(H_L^*)$ and similar for $e_{{{\,\mathrm{prim}\,}}}$ and $e_{{{\,\mathrm{indec}\,}}}$. Thus, we can assume reduce to the case of the group L, which necessarily has polynomial Duflot algebra. Thus, in this case Theorem 5.1 is valid for all primes p.

Finally, the regularity statement is due to Symonds. [58]. $\square$

Remark 6.8

It is not true that there is always an equality ${{\,\mathrm{Reg}\,}}(H^*_{G}) = -\dim (G)$ for a compact Lie group. For example, if $G = O(2)$ and p is odd, then ${{\,\mathrm{Reg}\,}}(H^*_{O(2)}) = -3$ (apply [58, Lemma 1.4(2)], noting that $H^*_{O(2)} \cong \mathbb {F}_p[x_4]$), while $-\dim (O(2)) = -1$.

Remark 6.9

Of course, one can restate this theorem as

$$\begin{aligned} d_0(H_G^*) \le \max _{E < G \in \mathbf{A} _G} \{e(H_{C_{{G}}(E)}^*) + {{\,\mathrm{Reg}\,}}(H_{C_{{G}}(E)}^*)\} \end{aligned}$$

to obtain a result that is analogous to that obtained by Kuhn in the case of compact Lie groups.

Example 6.10

Consider the profinite group ${{\,\mathrm{GL}\,}}_2(\mathbb {Z}_3)$. This admits a splitting ${{\,\mathrm{GL}\,}}_2(\mathbb {Z}_3) \cong \mathbb {Z}_3 \times {{\,\mathrm{GL}\,}}^1_2(\mathbb {Z}_3)$ where ${{\,\mathrm{GL}\,}}^1_2(\mathbb {Z}/3)$ is the subgroup of ${{\,\mathrm{GL}\,}}_2(\mathbb {Z}/3)$ which is the preimage of $\mathbb {Z}/2 \subset \mathbb {Z}_3^{\times }$ under the determinant map. Moreover, $H^*_{{{\,\mathrm{GL}\,}}^1_2(\mathbb {Z}_3)} \cong (H^*_{{{\,\mathrm{SL}\,}}_2(\mathbb {Z}_3)})^{\mathbb {Z}/2}$. Both of these facts can be found in the proof of Proposition 5.5 of [31]. By Proposition 2.22 we obtain

$$\begin{aligned} d_0(H_{{{\,\mathrm{GL}\,}}_2(\mathbb {Z}_3)}^*) = d_0(H_{\mathbb {Z}_3}^*) + d_0(H_{{{\,\mathrm{GL}\,}}^1_2(\mathbb {Z}_3)}^*) \quad \text { and } \quad d_0(H_{{{\,\mathrm{GL}\,}}^1_2(\mathbb {Z}_3)}^*) \le d_0(H_{{{\,\mathrm{SL}\,}}_2(\mathbb {Z}_3)}^*) \end{aligned}$$

Because $H_{\mathbb {Z}_3}^* \cong \Lambda _{\mathbb {F}_3}(e)$ with $|e| = 1$ we can apply Proposition 2.22 again to obtain $d_0(H_{\mathbb {Z}_3}^*) = 1$.

In order to compute $d_0(H^*_{{{\,\mathrm{SL}\,}}_2(\mathbb {Z}_3)}$), we observe that this has a single elementary abelian subgroup $\mathbb {Z}/3$ whose centralizer in ${{\,\mathrm{SL}\,}}_2(\mathbb {Z}_3)$ is isomorphic to $\mathbb {Z}/2 \times \mathbb {Z}/3 \times \mathbb {Z}_3$, so that $H^*_{C_{\mathbb {Z}/3}({{\,\mathrm{SL}\,}}_2(\mathbb {Z}_3))} \cong \mathbb {F}_3[y] \otimes \Lambda _{\mathbb {F}_3}(x,e)$, with $|y| = 2$ and $|x| = |e| = 1$, see the discussion after Proposition 5.5 (as well as Theorem 5.2) of [31]. It follows that $H^*_{{{\,\mathrm{SL}\,}}_2(\mathbb {Z}_3)}$ has trivial 3-cohomological center, and hence that ${{\,\mathrm{CEss}\,}}(H^*_{{{\,\mathrm{SL}\,}}_2(\mathbb {Z}_3)})$ is the kernel of the restriction map

By [31, Proposition 5.6] we deduce that ${{\,\mathrm{CEss}\,}}(H^*_{{{\,\mathrm{SL}\,}}_2(\mathbb {Z}_3)})$ is trivial. Since we work at $p = 3$, we have $H^*_{C_{\mathbb {Z}/3}({{\,\mathrm{SL}\,}}_2(\mathbb {Z}_3))} \cong H^*_{\mathbb {Z}/3 \times \mathbb {Z}_3}$. This has depth 1, and $c(\mathbb {Z}/3 \times \mathbb {Z}_3) = 1$. Moreover, it is of 3-central defect 0, so that ${{\,\mathrm{CEss}\,}}(H^*_{\mathbb {Z}/3 \times \mathbb {Z}_3}) \cong H^*_{\mathbb {Z}/3 \times \mathbb {Z}_3}$. We deduce that

$$\begin{aligned} d_0(H^*_{{{\,\mathrm{SL}\,}}_2(\mathbb {Z}_3)} ) = d_0(H^*_{\mathbb {Z}/3 \times \mathbb {Z}_3})) = d_0(H^*_{\mathbb {Z}/3}) + d_0(H^*_{\mathbb {Z}_3}) = 0 + 1 = 1. \end{aligned}$$

Putting these observations together, we conclude that

$$\begin{aligned} 1 \le d_0(H^*_{{{\,\mathrm{GL}\,}}_2(\mathbb {Z}_3)}) \le 2. \end{aligned}$$

Example 6.11

Consider the 2nd Morava stabilizer group $S_2$ at the prime 3. This admits a decomposition $S_2 \cong S_2^1 \times \mathbb {Z}_3$ and so

$$\begin{aligned} d_0(H_{S_2}^*) = d_0(H_{S_2^1}^*) + d_0(H_{\mathbb {Z}_3}^*) = d_0(H_{S_2^1}^*) + 1. \end{aligned}$$

The group $S_2^1$ has two conjugacy classes of elementary abelian 3-subgroups $E_i$ for $i = 1,2$ with $C_{S_2^1}(E_i) \cong \mathbb {Z}/3 \times \mathbb {Z}_3$ in both cases. We note that both $S_2^1$ and $C_{S_2^1}(E_i)$ are 3-adic Lie groups. We also observe that $H_{S_2^1}^*$ has trivial 3-cohomological center, and hence ${{\,\mathrm{CEss}\,}}(H_{S_2^1}^*)$ is the kernel of the product of restriction maps

By [31, Proposition 4.3] we deduce that ${{\,\mathrm{CEss}\,}}(H_{S_2^1}^*)$ is trivial. One then deduces from Proposition 2.22 that $d_0(H^*_{S_2^1}) \le d_0(H^*_{C_{S_2^1}(E_1)})$ (of course, one can use either $E_1$ or $E_2$ here). However, the T-functor computations show that $H^*_{C_{S_2^1}(E_1)}$ is a summand of $T_{E_1}(H^*_{S_2^1})$ and so $d_0(H^*_{S_2^1}) \ge d_0(H^*_{C_{S_2^1}(E_1)})$. Thus, $d_0(H^*_{S_2^1}) = d_0(H^*_{C_{S_2^1}(E_1)}) = d_0(H_{\mathbb {Z}/3 \times \mathbb {Z}_3}^*) = 1$. We deduce that $d_0(H_{S_2}^*) = 2$.

6.2 Homotopical groups

We now move onto the case of homotopical groups, namely the p-local finite and compact groups of Broto, Levi, and Oliver [8, 10]. Once we have set up the right language, the results take essentially the same form as for ordinary groups. The canonical references for both p-local finite and compact groups are the aforementioned papers of Broto, Levi, and Oliver, however the reader may also find the survey article [9] valuable.

To begin, we recall the definition of the fusion system $\mathcal {F}_p(G)$ associated to a finite group G. This is a category whose objects are the p-subgroups of G, and where

$$\begin{aligned} {{\,\mathrm{Hom}\,}}_{\mathcal {F}_p(G)} = {{\,\mathrm{Hom}\,}}_G(P,Q) {:}{=} \{ \alpha \in {{\,\mathrm{Hom}\,}}(P,Q) \mid \alpha = c_x, \text { for some } x \in G \}. \end{aligned}$$

i.e., $\alpha$ is a homomorphism induced by conjugation in G. To this one can associate another category, the centric linking system $\mathcal {L}_p^c(G)$. Then, by [7, Proposition 1.1] there is a homotopy equivalence $|\mathcal {L}_p^c(G)|^{\wedge }_p \simeq BG^{\wedge }_p$.

The idea of p-local finite groups is to begin with a finite p-group S, and try and mimic the constructions above. Thus, a fusion system $\mathcal {F}$ associated to S is a category whose objects are subgroups of S, and whose morphism sets ${{\,\mathrm{Hom}\,}}_{\mathcal {F}}(P,Q)$ satisfy the following conditions:

• (1) ${{\,\mathrm{Hom}\,}}_S(P,Q) \subseteq {{\,\mathrm{Hom}\,}}_{\mathcal {F}}(P,Q) \subseteq {{\,\mathrm{Inj}\,}}(P,Q) \text { for all } P,Q \le S$.

• (2) Every morphism in $\mathcal {F}$ factors as an isomorphism in $\mathcal {F}$ followed by an inclusion.

This is not quite enough; Broto, Levi, and Oliver additionally require that the fusion system is saturated, see [8, Definition 1.2]. A centric linking system $\mathcal {L}$ associated to $\mathcal {F}$ is another category whose objects are a certain subset of S. The centric linking system contains the additional data to associate a classifying space to the fusion system $\mathcal {F}$.

A p-local finite group is a triple $\mathcal {G} = (S,\mathcal {F},\mathcal {L})$ where S is a finite p-group, $\mathcal {F}$ is a saturated fusion system over S, and $\mathcal {L}$ is a centric linking system associated to $\mathcal {F}$. The classifying space of $\mathcal {G}$ is defined as $B\mathcal {G} = |\mathcal {L}|^{\wedge }_p$, the p-completed nerve of the category $\mathcal {L}$. We write $H_{\mathcal {G}}^* {:}{=} H^*(B\mathcal {G})$ for the mod p cohomology of $\mathcal {G}$.

If instead of a finite p-group we begin with a discrete p-toral group S - that is a group that contains a normal subgroup $T \cong (\mathbb {Z}/p^{\infty })^{r}$, and such that T has finite index in S - then we can define saturated fusion systems $\mathcal {F}$ over S, and centric linking systems over $\mathcal {F}$, see [10]. A p-local compact group is a triple $\mathcal {G} = (S,\mathcal {F},\mathcal {L})$ where S is a discrete p-toral group, $\mathcal {F}$ is a saturated fusion system over S, and $\mathcal {L}$ is a centric linking system associated to $\mathcal {F}$. In fact, it was later shown that every saturated fusion system over a discrete p-toral group has an associated centric linking system which is unique up to isomorphism [17, 40]. Thus, we often define our p-local compact groups as simply a pair $\mathcal {G} = (S,\mathcal {F})$.

Example 6.12

Here we list some examples of p-local compact groups.

• (1) If G is a compact Lie group, with p-toral subgroup S, then there exists a p-local compact group $\mathcal {G} = (S,\mathcal {F}_S(G))$ along with an equivalence of classifying spaces $BG^{\wedge }_p \simeq B\mathcal {G}$ [10, Theorem 9.10]. $\square$

• (2) Suppose that X is a p compact group, that is a triple (X, BX, e) where X is a space with $H^*(X;\mathbb {F}_p)$ finite, BX is a pointed p-complete space, and $e :X \rightarrow \Omega (BX)$ is an equivalence [24]. There is a notion of a Sylow subgroup $f :S \rightarrow X$, and moreover, there exists a p-local compact group $\mathcal {G} = (S,\mathcal {F}_{S,f}(X))$ with $B\mathcal {G} \simeq BX$ [10, Theorem 10.7]. More generally, the p-completion of any finite loop space gives rise to a p-local compact group [11].

Remark 6.13

Because, up to p-completion, every compact Lie group can be modeled by a p-local compact group, this section recovers the result for compact Lie groups in the previous section. This follows because the classifying space of a compact Lie group is always p-good (see [5, Proposition VII.5.1]) and so $H_{G}^* \cong H^*(BG^\wedge _p)$.

One has an immediate upper bound for $d_0(H_{{{\,\mathrm{\mathcal {G}}\,}}}^*)$ coming from the group S in the case of p-local finite groups.

Proposition 6.14

Let $\mathcal {G} = (S,{{\,\mathrm{\mathcal {F}}\,}})$ be a p-local finite group, then $d_0(H_{{{\,\mathrm{\mathcal {G}}\,}}}^*) \le d_0(H_S^*)$.

Proof

By [8, Proposition 5.5] $H_{{{\,\mathrm{\mathcal {G}}\,}}}^*$ is a direct summand of $H_S^*$ as an unstable algebra, and so Proposition 2.22 furnishes the result. $\square$

Even for finite groups, it is known that this inclusion is strict in general. For example, Henn–Lannes–Schwartz [34, Section II.4.7] give the example $G = GL_2(\mathbb {F}_3)$ and $S = SD_{16}$, then $d_0(H_G^*) = 0$, but $d_0(H_S^*) = 2$.

We now identify Rector’s category $\mathbf{A} _{H_{\mathcal {G}}^*}$ and present the relevant T-functor calculations. We let $\mathcal {F}^e$ be the full subcategory of F whose objects are elementary abelian p-subgroups $E \le S$ which are fully-centralized in $\mathcal {F}$ in the sense of [10, Definition 2.2]. This assumption ensures that the centralizer p-compact group $C_{\mathcal {G}}(E) = (C_S(E),C_{\mathcal {F}}(E))$ exists [26, Section 1.2], where $C_{\mathcal {F}}(E)$ is the fusion system over $C_S(E)$ with objects $Q \le C_S(E)$ and morphisms

$$\begin{aligned} {{\,\mathrm{Hom}\,}}_{C_{\mathcal {F}}(E)}(Q,Q')= \{ \psi \in {{\,\mathrm{Hom}\,}}_{\mathcal {F}}(Q,Q') \mid \exists \phi \in {{\,\mathrm{Hom}\,}}_{\mathcal {F}}(QE,Q'E),\phi |_Q = \psi , \phi |_E = \text {id}_E\}. \end{aligned}$$

Moreover, we note that any elementary abelian p-subgroup $E \le S$ is isomorphic in $\mathcal {F}$ to one that is fully $\mathcal {F}$-centralized.

For the following, we note that there is a canonical map $\theta :BS \rightarrow B\mathcal {G}$. Then, for any $E \le S$, there is a map $j_E :H_{\mathcal {G}}^* \rightarrow H_E^*$ given as the composite $H_{\mathcal {G}}^* \xrightarrow {\theta ^*} H_S^* \rightarrow H_E^*$.

Proposition 6.15

Let $\mathcal {G} = (S,\mathcal {F})$ be a p-local compact group, then $H_{\mathcal {G}}^*$ is a finitely-generated $\mathbb {F}_p$-algebra, and there is an equivalence of categories

$$\begin{aligned} \mathbf{A} _{H_{\mathcal {G}}^*} \simeq \mathcal {F}^e \end{aligned}$$

given by associating to a fully centralized subgroup $E \le S$ the pair $(E,j_E)$.

Proof

The finite generation is [2, Corollary 4.26], while the identification of $\mathbf{A} _{H_{\mathcal {G}^*}}$ is [29, Proposition 4.18]. $\square$

Let $E < S$ be an elementary abelian p-subgroup, then the map $C_S(E) \times E \rightarrow S$ induces $H_S^* \rightarrow H_E^* \otimes H_{C_S(E)}^*$. The adjoint induces a map $\phi _E :T_E(H_S^*;{{\,\mathrm{res}\,}}_{S,E}^*) \rightarrow H_{C_S(E)}^*$. The following is shown by Gonzalez [26, Lemma 5.1].

Lemma 6.16

For any $E \in \mathcal {F}^e$ there is an isomorphism

$$\begin{aligned} T_E(H_{\mathcal {G}}^*;j_E) \xrightarrow {\cong } H_{C_{\mathcal {G}}(E)}^* \end{aligned}$$

which is the restriction of the homomorphism $\phi _E$.

For $E \in \mathcal {F}^e$ a special case of [26, Theorem 5.4] identifies $BC_{\mathcal {G}}(E)$ with ${{\,\mathrm{Map}\,}}(BE,B\mathcal {G})_{B\iota }$ where $\iota :E \rightarrow S$, and so $H_{C_{\mathcal {G}}(E)}^* \cong H^*({{\,\mathrm{Map}\,}}(BE,B\mathcal {G})_{B\iota })$. Under this, the map $\rho _{H_{\mathcal {G}}^*,(E,j_E)} :H^*_{\mathcal {G}} \rightarrow T_E(H_{\mathcal {G}}^*;j_E)$ can be identified with the map induced by the evaluation map ${{\,\mathrm{Map}\,}}(BE,B\mathcal {G})_{B\iota } \rightarrow B\mathcal {G}$.

Definition 6.17

Let $\mathcal {G} = (S,\mathcal {F})$ be a p-local compact group, then $E \in \mathcal {F}^e$ is called central if ${{\,\mathrm{Map}\,}}(BE,B\mathcal {G})_{B\iota } \rightarrow B\mathcal {G}$ is a homotopy equivalence.

This does not conflict with the notion of centrality used previously in this paper, by the following lemma.

Lemma 6.18

$E \in \mathcal {F}^e$ is central if and only if $\rho = \rho _{H_{\mathcal {G}}^*,(E,j_E)} :H_{\mathcal {G}}^* \rightarrow T_E(H_{\mathcal {G}}^*;j_E) \cong H^*_{C_{\mathcal {G}}(E)}$ is an equivalence. In other words, $E \in \mathcal {F}^e$ is central if and only if $(E,j_E) \in \mathbf{A} _{H_{\mathcal {G}}^*}$ is central.

Proof

If $E \in \mathcal {F}^e$ is central then this is clear from the discussion before the definition of centrality. For the converse, suppose that $\rho$ is an equivalence. Because the classifying space of a p-local compact group is p-good (combine [10, Proposition 4.4] and [5, Proposition I.5.2]), the map ${{\,\mathrm{Map}\,}}(BE,B\mathcal {G})_{B\iota } \rightarrow B\mathcal {G}$ is a homotopy equivalence. $\square$

Remark 6.19

By [10, Theorem 7.4] if $E \in \mathcal {F}^e$ is central, then the p-local compact groups $\mathcal {G}$ and $C_{\mathcal {G}}(E)$ are isomorphic in the sense discussed on [10, pp. 374-375]. In particular, there are isomorphisms of groups and categories $\alpha :S \rightarrow C_S(E)$ and $\alpha _{\mathcal {F}} :\mathcal {F} \rightarrow C_{\mathcal {F}}(E)$ which are compatible in a certain sense.

Note that we have a natural definition of p-centrality for a p-local compact group. For the following, we let $C(\mathcal {G})$ denote the maximal central elementary abelian p-subgroup $E \in \mathcal {F}^e$, which exists by Theorem 3.13 and the previous lemma.

Definition 6.20

Let $\mathcal {G} = (S,\mathcal {F})$ be a p-local compact group, then $\mathcal {G}$ is p-central if the p-rank of $\mathcal {F}^e$ (i.e., the rank of a maximal elementary abelian p-group in $\mathcal {F}^e$) is equal to the rank of $C(\mathcal {G})$.

Lemma 6.21

$\mathcal {G}$ is p-central if and only if $H_{\mathcal {G}}^*$ has p-central defect 0.

Proof

This follows immediately from the definition and Lemma 6.18. $\square$

Theorem 6.22

Let $\mathcal {G} = (S,\mathcal {F})$ be a p-local compact group and assume that $H_{C_{\mathcal {G}(E)}}^*$ satisifies Hypothesis 4.20 for all $E \in \mathcal {F}^e$, then

$$\begin{aligned} d_0(H_{\mathcal {G}}^*) \le \underset{\begin{array}{c} C(\mathcal {G}) \le E \in \mathcal {F}^e \\ {{\,\mathrm{depth}\,}}(H_{C_{\mathcal {G}}(E)}^*) = c(C_{\mathcal {G}}(E)) \end{array}}{\max }\{e(H_{C_{\mathcal {G}}(E)}^*) + {{\,\mathrm{Reg}\,}}(H_{C_{\mathcal {G}}(E)}^*)\} \end{aligned}$$

If S is a finite p-group (i.e., $\mathcal {G}$ is a p-local finite group), then ${{\,\mathrm{Reg}\,}}(H_{C_{\mathcal {G}}(E)}^*) = 0$.

Proof

Combine Theorem 5.1 with Proposition 6.15 and Lemma 6.16. The computation of the regularity is due to Symonds [58, Proposition 6.1] and Kessar–Linckelmann [35, Theorem 0.4]. $\square$

Remark 6.23

Currently, there is only a single example of an exotic family of 2-local finite groups, namely the Solomon 2-local compact groups ${{\,\mathrm{Sol}\,}}(q)$ for q an odd prime power, where S is a Sylow 2-subgroup of ${{\,\mathrm{Spin}\,}}_7(q)$ [41]. Grbić [27, Proposition 2] has shown that $H^*_{{{\,\mathrm{Sol}\,}}(q)}$ has $H^*_{DI(4)}$ as a split summand in the category of unstable algebras, where DI(4) is the exotic 2-compact group of Dwyer and Wilkerson [23]. By Proposition 2.22 we have $d_0(H^*_{{{\,\mathrm{Sol}\,}}(q)}) \le d_0(H^*_{DI(4)})$. Because $H^*_{DI(4)}$ realizes the mod 4 Dickson invariants, there is an inclusion $H^*_{DI(4)} \rightarrow H_{(\mathbb {Z}/2)^4}^*$ of unstable algebras, so that $d_0(H^*_{DI(4)}) = 0$.

$$\begin{aligned} d_0(H^*_{{{\,\mathrm{Sol}\,}}(q)}) = 0. \end{aligned}$$

Unfortunately, the relevant calculations for the centralizer 2-local finite groups are not known, so we cannot compare this to the estimate from Theorem 6.22.

At odd primes, the p-local finite groups with $S = p_+^{1+2}$, the extraspecial groups of order $p^3$ and exponent p, have been calculated by Ruiz and Viruel [55]. In particular, at $p = 7$, they construct three new, exotic, examples of p-local finite groups. By Proposition 6.14 we have $d_0(H_{\mathcal {G}}^*) \le d_0(H_{S}^*)$ for any of these three groups. By [59, Theorem 13.21] we can deduce that $d_0(H_{\mathcal {G}}^*) \le 4$.

Appendices

Appendix A: Borel equivariant cohomology

We recall from Sect. 2.3 that the work of Henn–Lannes–Schwartz shows that if R is a Noetherian unstable algebra, and $M \in R_{fg}-\mathcal {U}$, then $d_0(M)$ is finite, and that

$$\begin{aligned} \phi _M :M \rightarrow \prod _{(E,f) \in \mathbf{A} _R} H_E^* \otimes T_E(M;f)^{\le n} \end{aligned}$$

is injective for $n \ge d_0(M)$. In this work, we have focused on the case where $M = R$. In this appendix, we specialize to the case where $R = H_G^*$ for a compact Lie group G, and $M = H_G^*(X)$ for X a manifold. As in Example 2.5$M \in R_{fg}-\mathcal {U}$ by Quillen [52, 53]. In this case, using [38] (see also [32, Theorem 2.6]) the previous equation takes the form

$$\begin{aligned} H_G^*(X) \rightarrow \prod _{E \le G} H_E^* \otimes H^{\le n}_{C_G(E)}(X^E), \end{aligned}$$

(A.1)

see [34, Theorem 5.5].

It is worth explain how the maps in this theorem arise (following the discussion on [34, p. 48]). The canonical homomorphism $E \times C_G(E) \rightarrow C_G(E)$ induces a map $BE \times (EC_G(E) \times _{C_G(E)} X^E) \rightarrow EC_G(E) \times _{C_G(E)} X^E$. We then define $c_E$ as the composite of the previous map with the map $EC_G(E) \times _{C_G(E)} X^E \rightarrow EG \times _{G} X$. The induced maps

$$\begin{aligned} c_E^* :H_G^*(X) \rightarrow H_E^* \otimes H^*_{C_{G}(E)}(X^E) \end{aligned}$$

induce the homomorphism in (A.1) as E runs over the elementary abelian p-subgroups of G.

We will show that slight adaptations of our techniques hold in this case. The observation we use here is that we have a good notion of centrality in this case. Indeed, suppose that E, V are central subgroups of G acting trivially on X. Then the subgroup $E \circ V$ generated by E and V is still central, and also acts trivially on X. Thus, there is a maximal central subgroup of G that acts trivially on X. Throughout this section, we let $C=C(G,X)$ denote this maximal central subgroup, and let e(G, X) denote the top degree of a generator of the finitely generated $H_G^*$-module $H_C^*$.

We observe (see [3]) that $H_G^*(X)$ is a $H_C^*$-comodule and that the image of the restriction map $H_G^*(X) \rightarrow H_C^*$ is a sub-Hopf algebra of $H_C^*$. Applying the Borel structure theorem, we can identify the image of this exactly as in Corollary 3.23.

The central essential ideal is defined in the obvious way, namely as the kernel

One deduces, as in Theorem 4.3 that the Krull dimension of ${{\,\mathrm{CEss}\,}}(G,X)$ is at most the rank of C. The regularity of $H_G^*(X)$ is also known in this case; it is a theorem of Symonds [58, Theorem 0.1] that ${{\,\mathrm{Reg}\,}}(H_G^*(X)) \le \dim (X) - \dim (G)$.

The same argument as in the body of the paper then gives the following result.

Theorem A.2

Let G be a compact Lie group, X a manifold, and suppose that the Duflot algebra for $H_{C_G(E)}^*(X^E)$ is polynomial for all $C(G;X) \le E$, then

$$\begin{aligned} d_0(H_G^*(X)) \le \max _{C(G,X) \le E < G}\{e(C_G(E),X^E) + \dim (X^E) - \dim (C_G(E)) \} \end{aligned}$$

Appendix B: Depth and dimension

In this appendix we briefly recall the notions of depth and dimension of graded-commutative connected Noetherian k-algebras for k a field. Given such a k-algebra we write $R^j$ for the degree j part of R. Hence, R connected means that $R^0 \cong \mathbb {F}_p$ and $R^i = 0$ for $i<0$. We let $\mathfrak m = R^{> 0}$ denote the maximal homogeneous ideal of R. With these assumptions, the commutative algebra of R is much like that of a local ring. We will follow the convention that, unless noted otherwise, everything is taken in the graded sense and ideals and elements of R-modules are always taken to be homogeneous.

Definition B.1

The Krull dimension of R, denoted $\dim (R)$ is the supremum of lengths of strictly increasing chains of prime ideals. For an R-module M, the dimension of M, $\dim _R(M)$ is defined as the dimension of $R/{{\,\mathrm{Ann}\,}}_R(M)$, where ${{\,\mathrm{Ann}\,}}_R(M) = \bigcap _{m \in M}{{\,\mathrm{Ann}\,}}_R(m)$ and

$$\begin{aligned} {{\,\mathrm{Ann}\,}}_R(m) = \{r \in R \mid rm= 0\}. \end{aligned}$$

Definition B.2

Let M be an R-module, then an M-regular sequence is a sequence $y_1,\ldots ,y_m$ in $\mathfrak m$ such that $y_i$ is a non-zero divisor on $M/(y_i,\ldots ,y_{i-1})$ for $i = 1,\ldots ,m$. If M is finitely generated over R then the depth of M, denoted ${{\,\mathrm{depth}\,}}_R(M)$ is the supremum of the length of all M -regular sequences in $\mathfrak m$.

We have the following useful characterization of M-regular sequences, see [19, Proposition 12.2.1].

Lemma B.3

Let M be a finitely-generated R-module. A sequence $y_1,\ldots ,y_m \in \mathfrak m$ of homogeneous elements of $\mathfrak m$ is an M-regular sequence if and only if $y_1,\ldots ,y_m$ are algebraically independent in R and M is a free module over the polynomial subring $k[y_1,\ldots ,y_m] \subseteq R$.

We recall that the $\mathfrak m$-torsion in M is

$$\begin{aligned} H_{\mathfrak m}^0(M) = \{ x \in M \mid \text { there exists } n \in \mathbb {N} \text { with } m^{\mathfrak n}x = 0\}. \end{aligned}$$

This functor is left exact, and we let $H_{\mathfrak m}^i(M)$ denote the higher derived functors, which are the local cohomology modules of M. Depth and dimension are related to local cohomology in the following way, see [12, Corollary 6.2.8].

Proposition B.4

Suppose that R is Noetherian and connected, and let M be a finitely generated R-module.

• (1) The depth of M is the smallest i for which $H_{\mathfrak m}^i(M) \ne 0$.

• (2) The dimension of M is the largest i for which $H_{\mathfrak m}^i(M) \ne 0$.

The characterization of depth in terms of local cohomology, and the independence theorem for local cohomology (see [12, Theorem 14.1.7]) give the following.

Lemma B.5

Let R and $R'$ be connected Noetherian unstable algebras, and $f :R \rightarrow R'$ a finite homomorphism. Let M be a finitely-generated $R'$-module, then

$$\begin{aligned} {{\,\mathrm{depth}\,}}_R(M) = {{\,\mathrm{depth}\,}}_{R'}(M) \end{aligned}$$

where M is an R-module by restriction of scalars. In particular,

$$\begin{aligned} {{\,\mathrm{depth}\,}}_R(R') = {{\,\mathrm{depth}\,}}(R'). \end{aligned}$$

Finally, we will need the following version of a group theoretic theorem of Carlson [19], which is proved by the author in [29, Theorem 3.5].

Theorem B.6

Let R be a connected Noetherian unstable algebra, and suppose $(E,f) \in \mathbf{A} _R$ is central. If $x_1,\ldots ,x_n$ is a sequence of homogeneous elements in R such that the restrictions of $x_1,\ldots ,x_n$ form a regular sequence in $H_E^*$, then $x_1,\ldots ,x_n$ is a regular sequence in R.

An easy consequence is the following, see [29, Corollary 3.6], which was originally proved in the case $R = H_G^*$ for G a finite group by Duflot [20].

Corollary B.7

Let R be a Noetherian unstable algebra with center (C, g), then

$$\begin{aligned} {{\,\mathrm{depth}\,}}(R) \ge {{\,\mathrm{rank}\,}}(C). \end{aligned}$$

We will say that R has minimal depth if ${{\,\mathrm{depth}\,}}(R) = {{\,\mathrm{rank}\,}}(C)$.