Abstract
This paper establishes a new combinatorial framework for the study of coarse median spaces, bridging the worlds of asymptotic geometry, algebra and combinatorics. We introduce a simple and entirely algebraic notion of coarse median algebra which simultaneously generalises the concepts of bounded geometry coarse median spaces and classical discrete median algebras. We study the coarse median universe from the perspective of intervals, with a particular focus on cardinality as a proxy for distance. In particular we prove that the metric on a quasi-geodesic coarse median space of bounded geometry can be constructed up to quasi-isometry using only the coarse median operator. Finally we develop a concept of rank for coarse median algebras in terms of the geometry of intervals and show that the notion of finite rank coarse median algebra provides a natural higher dimensional analogue of Gromov’s concept of \(\delta \)-hyperbolicity.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Gromov’s notion of a CAT(0) cube complex has played a significant role in major results in topology, geometry and group theory. Its power stems from the beautiful interplay between the non-positively curved geometry of the space and the median algebra structure supported on the vertices as outlined by Roller [15]. Coarse median spaces as introduced by Bowditch [6] provide a geometric coarsening of CAT(0) cube complexes which additionally includes \(\delta \)-hyperbolic spaces, mapping class groups and hierarchically hyperbolic groups [3, 4].
The interaction between the geometry and combinatorics of a CAT(0) cube complex is mediated by the fact that the edge metric can be computed entirely in terms of the median. In contrast, for a coarse median space the metric is an essential part of the data, as evidenced by the fact that almost any ternary algebra can be made into a coarse median space by equipping it with a bounded metric. This prompts the question to what extent there could be a combinatorial characterisation of coarse medians mirroring the notion of a median algebra. We will provide the missing combinatorial framework by defining coarse median algebras.
1.1 Bowditch’s definition of coarse median space
Definition 1.1
(Bowditch [6]) A coarse median space is a triple  , where (X, d) is a metric space and
, where (X, d) is a metric space and  is a ternary operator on X satisfying the following:
is a ternary operator on X satisfying the following:
-
(M1)
For all \(a,b\in X, \);
-
(M2)
For all \(a,b,c\in X, \);
-
(B1)
There are constants k, h(0) such that for all \(a,b,c,a',b',c'\in X\) we have

-
(B2)
There is a function \(h:{\mathbb {N}}\rightarrow {\mathbb {R}}^{+}\) with the following property. Suppose that \(A\subseteq X\) with \(1\leqslant |A| \leqslant p < \infty \), then there is a finite median algebra
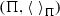 and maps \(\pi \,{:}\,A\rightarrow \Pi \) and \(\lambda \,{:}\,\Pi \rightarrow X\) such that for all \(x,y,z\in \Pi \) we have $$\begin{aligned} d\left( \lambda (\langle x,y,z\rangle _\Pi ), \langle {\lambda (x)}, {\lambda (y)}, {\lambda (z)}\rangle \right) \leqslant h(p), \end{aligned}$$
and maps \(\pi \,{:}\,A\rightarrow \Pi \) and \(\lambda \,{:}\,\Pi \rightarrow X\) such that for all \(x,y,z\in \Pi \) we have $$\begin{aligned} d\left( \lambda (\langle x,y,z\rangle _\Pi ), \langle {\lambda (x)}, {\lambda (y)}, {\lambda (z)}\rangle \right) \leqslant h(p), \end{aligned}$$and for all \(a \in A\) we have
$$\begin{aligned} d(a, \lambda \pi (a))\leqslant h(p). \end{aligned}$$
The metric plays the crucial role of measuring and controlling the extent to which the ternary operator (referred to as the coarse median) approximates a classical median operator. Our observation is that the additional metric data can be replaced by the structure of the intervals in the space which are intrinsic to the median operator: the cardinality of intervals serves as a proxy for distance.Footnote 1
1.2 Coarse median algebras
We now define the new notion of coarse median algebra as the algebraic parallel of coarse median spaces.
Recall that a ternary algebra is a set X equipped with a function  where
where  denotes the value at (x, y, z).
denotes the value at (x, y, z).
Definition 1.2
Let  be a ternary algebra. For any \(a,b\in X\), the interval [a, b] is the set
be a ternary algebra. For any \(a,b\in X\), the interval [a, b] is the set  . We say that
. We say that  has finite intervals if for every \(a,b\in X\) the interval [a, b] is a finite set.
has finite intervals if for every \(a,b\in X\) the interval [a, b] is a finite set.
A discrete median algebra, which is familiar to geometric group theorists as the vertex set of a CAT(0) cube complex, is simply a median algebra with finite intervals (see for example, [15]).
Definition 1.3
A coarse median algebra is a ternary algebra  with finite intervals such that:
with finite intervals such that:
-
(M1)
For all \(a,b\in X, \);
-
(M2)
For all \(a,b,c\in X, \);
-
(M3)’
There exists a constant \(K\geqslant 0\) such that for all \(a,b,c,d,e\in X\) the cardinality of the interval
 is at most K (Fig. 1).
is at most K (Fig. 1).
Putting \(K=1\) in the definition reduces (M3)\(^{\prime }\) to the classical 5-point condition  defining a median algebra, so Definition 1.3 generalises the notion of discrete median algebra.
defining a median algebra, so Definition 1.3 generalises the notion of discrete median algebra.
1.3 The induced metric
At first sight the data defining a coarse median algebra appears to carry a lot less information than Bowditch’s coarse median spaces. However as we will see in Sect. 5, the finite intervals condition will allow us to define a metric  on the ternary algebra purely in terms of the operator
on the ternary algebra purely in terms of the operator  . Moreover any bounded geometryFootnote 2 coarse median space is a coarse median algebra. Indeed generalising the notion of bounded valency for a graph (see Definition 6.1), we have the following equivalence.
. Moreover any bounded geometryFootnote 2 coarse median space is a coarse median algebra. Indeed generalising the notion of bounded valency for a graph (see Definition 6.1), we have the following equivalence.
Theorem 1.4
Let  be a bounded valency ternary algebra. The following are equivalent:
be a bounded valency ternary algebra. The following are equivalent:
-
(1)
 is a coarse median algebra;
is a coarse median algebra; -
(2)
 is a coarse median space;
is a coarse median space; -
(3)
There exists a metric d such that
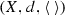 is a bounded geometry coarse median space.
is a bounded geometry coarse median space.
As an application of these ideas we show that for any bounded geometry quasi-geodesic coarse median space, the metric is uniquely determined by the coarse median operator up to quasi-isometry.
Theorem 1.5
For a bounded geometry quasi-geodesic coarse median space  , the metric d is unique up to quasi-isometry.
, the metric d is unique up to quasi-isometry.
Indeed within this equivalence class of metrics there is a canonical representative  defined purely in terms of the coarse median operator
defined purely in terms of the coarse median operator  (see Theorem 5.6).
(see Theorem 5.6).
This theorem fails without the quasi-geodesic condition as shown by Example 5.7, but the failure in this example is suggestive. It is interesting to speculate to what extent the non-uniqueness could be described.
1.4 Rank
As well as providing a relatively simple characterisation of a coarse median operator, our combinatorial approach introduces a new perspective on the notion of rank in the coarse median world. We provide three new ways to characterise rank each of which is a higher rank analogue of one of the classical characterisations of Gromov’s \(\delta \)-hyperbolicity:
Hyperbolic spaces | Coarse median spaces/algebras of rank n |
|---|---|
Approximating finite subsets by trees | Approximating finite subsets by CAT(0) cube complexes of dimension n [6] |
Gromov’s inner product (“thin squares”) condition | Thin \((n+1)\)-cubes condition: Theorem 4.1 (3) and Lemma 6.9 |
Slim triangle condition | \((n+1)\)-Multi-median condition: Theorem 4.1 (2) |
Pencils of quasi-geodesics grow linearly | Interval growth is \(o(n+1)\): Theorem 4.15 |
The thin \((n+1)\)-cubes condition reduces, in the case of \(n=1\), to the existence of a non-decreasing function \(\varphi \) such that for all a, b, c and p we have

For geodesic coarse median spaces, this is a characterisation of hyperbolicity (see Sect. 4.1).
The above inequality has the virtue that it is quasi-isometry invariant: the disadvantage of Gromov’s 4-point condition, when applied to non-geodesic spaces, is that it is not. The class of quasi-geodesic coarse median spaces satisfying our variant of the 4-point condition is closed under quasi-isometry, so we propose the class of rank 1 coarse median algebras as a more robust generalisation of hyperbolicity beyond the (quasi)-geodesic world.
1.5 Outline of the paper
The paper is organised as follows. In Sect. 2, we recall background definitions including coarse median spaces, their ranks and Špakula and Wright’s notion of iterated coarse median operators from [14, 17].
In Sect. 3, by analogy with Sholander’s results for median algebras and interval structures [16], we give a characterisation of coarse median spaces entirely in terms of their intervals.
In Sect. 4, we introduce and study characterisations of rank in the context of coarse interval structures and show that the correspondences from Sect. 3 preserve rank for coarse median spaces.
In Sect. 5, we study the intrinsic metric on a ternary algebra and show that it is unique up to quasi-isometry for any quasi-geodesic coarse median space of bounded geometry. Motivated by this in Sect. 6, we study the geometry of coarse median algebras. We establish that these simultaneously generalise the notions of:
-
(1)
Classical discrete median algebras.
-
(2)
Geodesic hyperbolic spaces of bounded geometry.
-
(3)
Bounded geometry coarse median spaces.
The correspondences established in this paper can also be couched as correspondences between (or equivalences of) suitable categories. In the “Appendix” we examine the notion of morphisms and the definitions of the functors required by that approach.
2 Preliminaries
We follow the conventions established in [14].
2.1 Metrics and geodesics
Definition 2.1
Let (X, d) be a metric space.
-
(1)
A subset \(A \subseteq X\) is bounded, if its diameter \(\mathrm {diam}\,(A):=\sup \{d(x,y):x,y\in A\}\) is finite; A is a net in X if there exists some constant \(C>0\) such that for any \(x\in X\), there exists some \(a\in A\) such that \(d(a,x) \leqslant C\).
-
(2)
The metric space (X, d) is said to be uniformly discrete if there exists a constant \(C>0\) such that for any \(x \ne y \in X, d(x,y)>C\).
-
(3)
The metric space (X, d) is said to have bounded geometry if, for any \(r>0\), there exists some constant \(n \in {\mathbb {N}}\) such that \(\sharp ~B(x,r) \leqslant n\) for any \(x\in X\).
-
(4)
Points \(x,y\in X\) are said to be s-close (with respect to the metric d) if \(d(x,y)\leqslant s\). If x is s-close to y, we write \(x\thicksim _s y\). Maps \(f,g:X\rightarrow Y\) are said to be s-close, written \(f\thicksim _s g\), if \(f(x)\thicksim _s g(x)\) for all \(x\in X\).
Definition 2.2
Let \((X,d), (Y,d')\) be metric spaces and \(L,C>0\) be constants.
-
(1)
An (L, C)-large scale Lipschitz map from (X, d) to \((Y,d')\) is a map \(f\,{:}\,X\rightarrow Y\) such that for any \(x,x'\in X, d'(f(x),f(x'))\leqslant Ld(x,x')+C\).
-
(2)
An (L, C)-quasi-isometric embedding from (X, d) to \((Y,d')\) is a map \(f\,{:}\,X\rightarrow Y\) such that for any \(x,x'\in X, L^{-1} d(x,x')-C\leqslant d'(f(x),f(x'))\leqslant Ld(x,x')+C\).
-
(3)
An (L, C)-quasi-isometry from (X, d) to \((Y, d')\) is an (L, C)-large scale Lipschitz map \(f:X\rightarrow Y\) such that there exists another (L, C)-large scale Lipschitz map \(g: Y \rightarrow X\) with \(f\circ g\thicksim _C \mathrm {Id}_Y\) and \(g\circ f\thicksim _C \mathrm {Id}_X\).
-
(4)
(X, d) is said to be (L, C)-quasi-geodesic if for any two points \(x,y\in X\) there exists an (L, C)-quasi-isometric embedding of the interval [0, d(x, y)] into X taking the endpoints to x, y respectively. If we do not care about the constant C we say that (X, d) is L-quasi-geodesic. If (X, d) is (1, 0)-quasi-geodesic then we say that X is geodesic.
We will take the liberty of omitting the parameters L, C where their values are not germane to the discussion.
Definition 2.3
Let \((X,d), (Y,d')\) be metric spaces, \(\rho \,{:}\,{\mathbb {R}}^{+}\rightarrow {\mathbb {R}}^{+}\) a proper function and \(C>0\) a constant.
-
(1)
A \(\rho \)-bornologous map from (X, d) to \((Y,d')\) is a function \(f:X\rightarrow Y\) such that for all \(x,x'\in X, d'(f(x), f(x')) \leqslant \rho (d(x,x'))\).
-
(2)
f is proper if given any bounded subset \(B \subseteq Y, f^{-1}(B)\) is bounded.
-
(3)
A \(\rho \)-coarse map from (X, d) to \((Y,d')\) is a proper \(\rho \)-bornologous map.
-
(4)
A \((\rho ,C)\)-coarse equivalence from (X, d) to \((Y, d')\) is a \(\rho \)-coarse map \(f:X\rightarrow Y\) such that there exists another \(\rho \)-coarse map \(g: Y \rightarrow X\) with \(f\circ g\thicksim _C \mathrm {Id}_Y\) and \(g\circ f\thicksim _C \mathrm {Id}_X\). In this case, g is called a \((\rho ,C)\)-coarse inverse of f.
When the parameters \(\rho ,C\) are not germane to the discussion we omit them.
2.2 Median algebras
As discussed in [1] there are a number of equivalent formulations of the axioms for median algebras. We will use the following formulation from [5]:
Definition 2.4
Let X be a set and  a ternary operation on X. Then
a ternary operation on X. Then  is a median operator and the pair
is a median operator and the pair  is a median algebra if the following are satisfied:
is a median algebra if the following are satisfied:
-
(M1)
Localisation:
 for all \(a,b\in X\).
for all \(a,b\in X\). -
(M2)
Symmetry:
 for all \(a_1,a_2,a_3\in X\) and permutation \(\sigma \) of \(\{1,2,3\}\);
for all \(a_1,a_2,a_3\in X\) and permutation \(\sigma \) of \(\{1,2,3\}\); -
(M3)
The 5-point condition:
 for all \(a,b,c,d,e\in X\).
for all \(a,b,c,d,e\in X\).
Axiom (M3) is equivalent to the 4-point condition given in [12], see also [2]:

This can be viewed as an associativity axiom: For each \(b\in X\) the binary operator

is associative. Note that this binary operator is also commutative by (M2).
Example 2.5
An important example is furnished by the median n -cube, denoted by \(I^n\), which is the n-dimensional vector space over \({\mathbb {Z}}_2\) with the median operator  given by majority vote on each coordinate. More generally as remarked in the introduction, a discrete median algebra is one in which the intervals
given by majority vote on each coordinate. More generally as remarked in the introduction, a discrete median algebra is one in which the intervals  are finite. These algebras are precisely the ones that arise as the vertex sets of CAT(0) cube complexes.
are finite. These algebras are precisely the ones that arise as the vertex sets of CAT(0) cube complexes.
2.3 Coarse median spaces
In [14] we showed how to replace Bowditch’s original definition of a coarse median space (Definition 1.1), involving n-point approximations for all n, in terms of a 4-point condition mirroring the classical 4-point condition for median algebras. This may also be viewed as an analogue of Gromov’s 4-point condition for hyperbolicity.
Proposition 2.6
[14, Theorem 3.1] A triple  is a coarse median space if the pair (X, d) is a metric space and
is a coarse median space if the pair (X, d) is a metric space and  is a ternary operator satisfying axioms (M1), (M2) together with the following:
is a ternary operator satisfying axioms (M1), (M2) together with the following:
- (C1):
-
Affine control: There exists an affine function \(\rho :[0,+\infty )\rightarrow [0,+\infty )\) such that for all \(a,a',b,c\in X\), we have

- (C2):
-
Coarse 4-point condition: There exists a constant \({\kappa _4}>0\) such that for any \(a,b,c,d\in X\), we have

In the same way that axiom (M3) for a median algebra is equivalent to the 4-point condition (1), Bowditch’s condition (B2) for a coarse median space ensures that there exists a constant \({\kappa _5}>0\) such that for any five points \(a,b,c,d,e\in X\) we have

By Proposition 2.6, the constant \({\kappa _5}\) depends only on the parameters \(\rho \) and \({\kappa _4}\). However it is convenient to carry it with us in calculations. With this in mind we make the following definition.
Definition 2.7
We define the notion of parameters for a coarse median space  to be any 3-tuple \((\rho , {\kappa _4}, {\kappa _5})\) of constants satisfying the axioms in Definition 2.8 together with estimate (2). Writing the control function \(\rho \) in the form of \(\rho (t)=Kt+H_0\) for some positive constants K and \(H_0\), we also refer to the 4-tuple \((K,H_0,{\kappa _4}, {\kappa _5})\) as parameters of
to be any 3-tuple \((\rho , {\kappa _4}, {\kappa _5})\) of constants satisfying the axioms in Definition 2.8 together with estimate (2). Writing the control function \(\rho \) in the form of \(\rho (t)=Kt+H_0\) for some positive constants K and \(H_0\), we also refer to the 4-tuple \((K,H_0,{\kappa _4}, {\kappa _5})\) as parameters of  .
.
As remarked by Bowditch [6] (in the discussion following Lemma 8.1 there), one can relax axioms (M1) and (M2) without loss to the following:
- (C0):
-
Coarse localisation and coarse symmetry: There is a constant \({\kappa _0}>0\) such that for all points \(a_1,a_2,a_3\) in \(X, \) and
 for any permutation \(\sigma \) of \(\{1,2,3\}\).
for any permutation \(\sigma \) of \(\{1,2,3\}\).
Any such ternary operator can be replaced by an operator satisfying the localisation and symmetry conditions (M1) and (M2) of Definition 2.4 at the cost of moving the values  only a uniformly bounded distance. These axioms are more robust under coarse constructions so we make the following definition:
only a uniformly bounded distance. These axioms are more robust under coarse constructions so we make the following definition:
Definition 2.8
A coarse median structure on a metric space (X, d) is a triple  satisfying axioms (C0), (C1) and (C2). Parameters for the structure are given by the function \(\rho \) from (C1) together with the constants \({\kappa _0}, {\kappa _4}, {\kappa _5}\).
satisfying axioms (C0), (C1) and (C2). Parameters for the structure are given by the function \(\rho \) from (C1) together with the constants \({\kappa _0}, {\kappa _4}, {\kappa _5}\).
Remark 2.9
The discussion above can be summarised as the assertion that any coarse median structure  can be replaced by a coarse median space
can be replaced by a coarse median space  such that the maps
such that the maps  and
and  are uniformly close. Abusing terminology, we say that the space is uniformly close to the structure.
are uniformly close. Abusing terminology, we say that the space is uniformly close to the structure.
2.4 Rank for a coarse median space
As in the case of median algebras, there is a notion of rank for a coarse median space. In terms of Bowditch’s original definition of coarse medians, the rank is simply the least upper bound on the ranks of the required approximating median algebras given by condition (B2).
Using the formulation of coarse median given in Definition 2.8 (which only indirectly implies the existence of approximations for all finite subsets by median algebras), a characterisation of ranks in terms of suitable embeddings of cubes is more useful.
Definition 2.10
For a ternary algebra  and a coarse median space
and a coarse median space  , a map \(f:X \rightarrow Y\) is said to be a C -quasi-morphism for some \(C>0\), if for \(a,b,c\in X\) we have
, a map \(f:X \rightarrow Y\) is said to be a C -quasi-morphism for some \(C>0\), if for \(a,b,c\in X\) we have  .
.
Proposition 2.11
[14, Theorem 4.11] Let  be a coarse median space and \(n\in {\mathbb {N}}\). Then the following conditions are equivalent.
be a coarse median space and \(n\in {\mathbb {N}}\). Then the following conditions are equivalent.
-
(1)
\(\mathrm {rank}\,X \leqslant n\);
-
(2)
For any \(\lambda >0\) there exists a constant \(C=C(\lambda )\) such that for any \(a,b\in X\) and \(e_1,\ldots ,e_{n+1}\in [a,b]\) with \(\langle e_i,a,e_j\rangle \thicksim _\lambda a\) for all \(i\ne j\), one of the points \(e_i\) is C-close to a;
-
(3)
For any \(L>0\) there exists a constant \(C=C(L)\) such that for any L-quasi-morphism \(\sigma \) from the median cube \(I^{n+1}\) to X, the image \(\sigma ({\bar{e}}_i)\) of one of the cube vertices \({\bar{e}}_i\) adjacent to the origin \({{\bar{{\mathbf {0}}}}}\) is C-close to the image \(\sigma ({{\bar{{\mathbf {0}}}}})\).
We note that while part (3) of this theorem is slightly different from that stated in [14, Theorem 4.11], the given proof establishes this version too.
We also need the following notion of coarse median isomorphisms when we characterise rank via interval growths in Sect. 4.
Definition 2.12
Let \((X,d_X), (Y,d_Y)\) be metric spaces and \(, \) be coarse medians on them, respectively. A map \(f\,{:}\,X \rightarrow Y\) is called a \((\rho ,C)\)-coarse median isomorphism for some proper function \(\rho \,{:}\,{\mathbb {R}}^+ \rightarrow {\mathbb {R}}^+\) and constant \(C>0\), if f is a \((\rho ,C)\)-coarse equivalence as well as a C-quasi-morphism.
There is a categorical explanation of this terminology given in Appendix A.1. We will show in Remark A.5 that for a \((\rho _+,C)\)-coarse median isomorphism f, any \((\rho _+,C)\)-coarse inverse g is a \(C'\)-quasi-morphism with the constant \(C'\) depending only on \(\rho _+,C\) and parameters of X, Y. In this case, we will also refer to g as an inverse of f.
2.5 Iterated coarse medians
We recall the following definition from [17]:
Definition 2.13
Let  be a coarse median space and \(b\in X\). For \(x_1\in X\), define:
be a coarse median space and \(b\in X\). For \(x_1\in X\), define:

For \(k \geqslant 1\) and \(x_1,\ldots ,x_{k+1} \in X\), define the coarse iterated median

Note that this definition “agrees” with the original coarse median operator  in the sense that for any a, b, c in X, we have
in the sense that for any a, b, c in X, we have  .
.
It was established in [17, Section 5] that in a median algebra, the iterated median  is characterised by the fact that the interval [m, b] is the intersection of the intervals \([x_i,b]\) for \(i=1,\ldots , k+1\).
is characterised by the fact that the interval [m, b] is the intersection of the intervals \([x_i,b]\) for \(i=1,\ldots , k+1\).
Fixing a point b and (as in Sect. 2.2) writing the coarse median  as \(x_1\mathop *_b x_2\), the iterated median
as \(x_1\mathop *_b x_2\), the iterated median  can be written as \(( (x_1\mathop *_b x_2)\mathop *_bx_3)\mathop *_b\cdots \mathop *_bx_k\). In this notation the four point condition is, precisely the statement that \((x_1\mathop *_b x_2)\mathop *_bx_3\) is uniformly close to the product \(x_1\mathop *_b( x_2\mathop *_bx_3)\). This along with the commutativity of the operation \(\mathop *_b\) allows the rearrangement of iterated medians. See Lemma 2.15 below.
can be written as \(( (x_1\mathop *_b x_2)\mathop *_bx_3)\mathop *_b\cdots \mathop *_bx_k\). In this notation the four point condition is, precisely the statement that \((x_1\mathop *_b x_2)\mathop *_bx_3\) is uniformly close to the product \(x_1\mathop *_b( x_2\mathop *_bx_3)\). This along with the commutativity of the operation \(\mathop *_b\) allows the rearrangement of iterated medians. See Lemma 2.15 below.
In [14, Lemmas 2.16–2.19] we established the following estimates:
Lemma 2.14
Let  be a coarse median space with parameters \((\rho , {\kappa _4}, {\kappa _5})\). Then there exist non-decreasing functions \(\rho _n, H_n:{\mathbb {R}}^{+}\rightarrow {\mathbb {R}}^{+}\) and constants \(C_n, D_n\) depending only on \(\rho , {\kappa _4}, {\kappa _5}\) such that for any \(a, a_0,a_1,\ldots ,a_n\) and \(b, b_0,b_1,\ldots ,b_n \in X\) we have:
be a coarse median space with parameters \((\rho , {\kappa _4}, {\kappa _5})\). Then there exist non-decreasing functions \(\rho _n, H_n:{\mathbb {R}}^{+}\rightarrow {\mathbb {R}}^{+}\) and constants \(C_n, D_n\) depending only on \(\rho , {\kappa _4}, {\kappa _5}\) such that for any \(a, a_0,a_1,\ldots ,a_n\) and \(b, b_0,b_1,\ldots ,b_n \in X\) we have:
-
(1)
 .
. -
(2)
Let
 be a median algebra and \(\sigma :\Pi \rightarrow X\) an L-quasi-morphism. For any \(x_1,\ldots ,x_n,b\in \Pi \), we have $$\begin{aligned} \sigma (\langle x_1,\ldots ,x_n;b\rangle _\Pi )\thicksim _{H_n(L)}\langle \sigma (x_1),\ldots ,\sigma (x_n);\sigma (b)\rangle . \end{aligned}$$
be a median algebra and \(\sigma :\Pi \rightarrow X\) an L-quasi-morphism. For any \(x_1,\ldots ,x_n,b\in \Pi \), we have $$\begin{aligned} \sigma (\langle x_1,\ldots ,x_n;b\rangle _\Pi )\thicksim _{H_n(L)}\langle \sigma (x_1),\ldots ,\sigma (x_n);\sigma (b)\rangle . \end{aligned}$$ -
(3)
 .
. -
(4)
 .
.
Here we provide additional estimates that will give us the control we need later to analyse the structure of coarse cubes in Sect. 4.3.
Lemma 2.15
Let  be a coarse median space with parameters \((\rho , {\kappa _4}, {\kappa _5})\). Then for any \(n\in {\mathbb {N}}\), there exists a constant \(G_n\) depending only on \(\rho , {\kappa _4}, {\kappa _5}\) such that for any \(a_1,\ldots ,a_n,b\in X\) and any permutation \(\sigma \in S_n\), we have
be a coarse median space with parameters \((\rho , {\kappa _4}, {\kappa _5})\). Then for any \(n\in {\mathbb {N}}\), there exists a constant \(G_n\) depending only on \(\rho , {\kappa _4}, {\kappa _5}\) such that for any \(a_1,\ldots ,a_n,b\in X\) and any permutation \(\sigma \in S_n\), we have

Proof
We proceed by induction on n. When \(n=1\) or 2, we may take \(G_1=G_2=0\) by definition and axiom (M2).
Now assume that the result holds for \(1,2,\ldots ,n-1\) and we consider the case of n. As usual it is sufficient to prove the lemma when \(\sigma \) is a transposition of the form (1j). If \(j<n\) then by definition, we have

Inductively \(\langle a_1,\ldots ,a_j;b\rangle \thicksim _{G_j} \langle a_j,a_2,\ldots ,a_{j-1},a_1;b\rangle \) and the result follows by Lemma 2.14 (1). It remains to check the case \(\sigma =(1n)\). By the inductive step, we have

Hence for the transposition (1n), we have

This completes the proof. \(\square \)
Lemma 2.16
Let  be a coarse median space with parameters \((\rho , {\kappa _4}, {\kappa _5})\). Then for any n, there exists a constant \(E_n\) depending only on \(\rho , {\kappa _4}, {\kappa _5}\) such that for any \(1\leqslant k\leqslant n\) and \(a_1,\ldots ,a_n,b \in X\), we have
be a coarse median space with parameters \((\rho , {\kappa _4}, {\kappa _5})\). Then for any n, there exists a constant \(E_n\) depending only on \(\rho , {\kappa _4}, {\kappa _5}\) such that for any \(1\leqslant k\leqslant n\) and \(a_1,\ldots ,a_n,b \in X\), we have

Proof
Fix an n. By Axiom (B2), there exists a constant \(h_{n+1}>0\) such that for any \(a_1,\ldots ,a_n,b \in X\) there exist a finite median algebra  , points \({\bar{a}}_1, \ldots , {\bar{a}}_n, {\bar{b}} \in \Pi \) and an \(h_{n+1}\)-quasi-morphism \(\lambda \,{:}\,\Pi \rightarrow X\) satisfying \(\lambda ({\bar{a}}_i) \thicksim _{h_{n+1}} a_i\) for \(i=1,\ldots , n\) and \(\lambda ({\bar{b}}) \thicksim _{h_{n+1}} b\). From parts (1) and (2) of Lemma 2.14 with the control functions \(H_n\) and \(\rho _n\) therein, we have
, points \({\bar{a}}_1, \ldots , {\bar{a}}_n, {\bar{b}} \in \Pi \) and an \(h_{n+1}\)-quasi-morphism \(\lambda \,{:}\,\Pi \rightarrow X\) satisfying \(\lambda ({\bar{a}}_i) \thicksim _{h_{n+1}} a_i\) for \(i=1,\ldots , n\) and \(\lambda ({\bar{b}}) \thicksim _{h_{n+1}} b\). From parts (1) and (2) of Lemma 2.14 with the control functions \(H_n\) and \(\rho _n\) therein, we have

Similarly for any \(1\leqslant k\leqslant n\), we have

and putting \(K = \rho _n(nh_{n+1}+ \rho _n((n+1)h_{n+1})+ H_n(h_{n+1}))\), we get

It follows directly from [17, Lemma 5.3] that in the actual median algebra  , the iterated median \(\langle {\bar{a}}_1,\ldots ,{\bar{a}}_n;{\bar{b}}\rangle _\Pi \) is nothing but the projection of \({\bar{b}}\) onto the convex hull of \({\bar{a}}_1,\ldots ,{\bar{a}}_n\). Hence we have
, the iterated median \(\langle {\bar{a}}_1,\ldots ,{\bar{a}}_n;{\bar{b}}\rangle _\Pi \) is nothing but the projection of \({\bar{b}}\) onto the convex hull of \({\bar{a}}_1,\ldots ,{\bar{a}}_n\). Hence we have
Combining the above together and taking \(E_n:=\rho _n(nh_{n+1}+\rho _n((n+1)h_{n+1}) + H_n(h_{n+1})) + \rho _n((n+1)h_{n+1}) + 2H_n(h_{n+1})\), Equality (3) holds. \(\square \)
3 Coarse interval structures
Sholander studied the relation between intervals and median operators, and we will generalise this approach to the coarse context.
Classically Sholander defined the interval between two points a and b in a median algebra  to be the set
to be the set  . This (in the context of median algebras) agrees with our definition of interval (Definition 1.2) since for any
. This (in the context of median algebras) agrees with our definition of interval (Definition 1.2) since for any  , we have
, we have

Of course the two definitions of interval do not necessarily coincide in the coarse context.
Theorem 3.1
[16] For every median algebra  , the binary operation \([\cdot ,\cdot ]: X\times X\rightarrow {\mathcal {P}}(X)\) defined by \((a,b)\mapsto [a,b]\) has the following properties:
, the binary operation \([\cdot ,\cdot ]: X\times X\rightarrow {\mathcal {P}}(X)\) defined by \((a,b)\mapsto [a,b]\) has the following properties:
-
\([a,a] =\{a\}\).
-
if \(c\in [a,b]\) then \([a,c]\subseteq [b,a]\).
-
\([a,b]\cap [b,c]\cap [c,a]\) has cardinality 1.
Conversely, every operation \(X^2 \rightarrow {\mathcal {P}}(X)\) with the preceding properties induces a ternary operator  whereby
whereby  is the unique point in \([a,b]\cap [b,c]\cap [c,a]\) such that
is the unique point in \([a,b]\cap [b,c]\cap [c,a]\) such that  is a median algebra.
is a median algebra.
As remarked by the referee, it requires a little work to extract the proof of the converse statement from Sholander, however we are fortunate that this is explained in some detail in [8, Section 2]. Here we will provide a coarse analogue of Sholander’s theorem. We start by considering the properties of intervals in a coarse median space.
Proposition 3.2
Let  be a coarse median space with parameters \(\rho ,{\kappa _4}\) and \({\kappa _5}\). Then the map \([\cdot ,\cdot ]\,{:}\, X^2 \rightarrow {\mathcal {P}}(X)\) defined by
be a coarse median space with parameters \(\rho ,{\kappa _4}\) and \({\kappa _5}\). Then the map \([\cdot ,\cdot ]\,{:}\, X^2 \rightarrow {\mathcal {P}}(X)\) defined by  satisfies:
satisfies:
-
(I1).
For all \(a,b\in X, [a,a]=\{a\}, [a,b]=[b,a]\).
-
(I2).
There exists a non-decreasing function \(\phi \,{:}\,{\mathbb {R}}^{+}\rightarrow {\mathbb {R}}^{+}\) such that for any \(a,b\in X\) and \(c\in {\mathcal {N}}_R([a,b])\), we have \([a,c] \subseteq {\mathcal {N}}_{\phi (R)}([a,b])\);
-
(I3).
There exists a non-decreasing function \(\psi \,{:}\,{\mathbb {R}}^{+}\rightarrow {\mathbb {R}}^{+}\) such that for any \(a,b,c\in X\), we have \([a,b] \cap [b,c] \cap [c,a] \ne \emptyset \) and
$$\begin{aligned} \mathrm {diam}\,( {\mathcal {N}}_R([a,b]) \cap {\mathcal {N}}_R([b,c]) \cap {\mathcal {N}}_R([c,a]) ) \leqslant \psi (R). \end{aligned}$$
Proof
Property (I1) follows directly from axioms (M1) and (M2) for a coarse median space. Now we consider (I2). Since \(c\in {\mathcal {N}}_R([a,b])\), there exists \(x\in X\) such that  . Then it follows from axioms (C1), (C2) and (M2) that for any \(y\in X\) we have
. Then it follows from axioms (C1), (C2) and (M2) that for any \(y\in X\) we have

which implies \(\langle a,c,y\rangle \in {\mathcal {N}}_{\rho (R)+{\kappa _4}}([a,b])\). So we can take \(\phi (R)=\rho (R)+{\kappa _4}\), and (I2) holds. For (I3), we know that  so the intersection is non-empty. Furthermore given a point \(z\in {\mathcal {N}}_R([a,b]) \cap {\mathcal {N}}_R([b,c]) \cap {\mathcal {N}}_R([c,a])\) there exists \(w\in X\) such that
so the intersection is non-empty. Furthermore given a point \(z\in {\mathcal {N}}_R([a,b]) \cap {\mathcal {N}}_R([b,c]) \cap {\mathcal {N}}_R([c,a])\) there exists \(w\in X\) such that  . So by (C1) and (C2), we have
. So by (C1) and (C2), we have

Similarly for b, c and for c, a. Hence we obtain that

where \(\kappa ':=\rho (R)+R+{\kappa _4}=\phi (R)+R\). Combining with (C1) and (2), we obtain

The above estimate implies that the diameter of \({\mathcal {N}}_R([a,b]) \cap {\mathcal {N}}_R([b,c]) \cap {\mathcal {N}}_R([c,a])\) is bounded by
\(\square \)
With this in mind, we define the concept of a coarse interval space as follows.
Definition 3.3
Let (X, d) be a metric space and \([\cdot ,\cdot ]: X^2 \rightarrow {\mathcal {P}}(X)\) be a map satisfying (I1)\(\sim \)(I3) in Proposition 3.2. Then \({\mathcal {I}}=(X,d,[\cdot ,\cdot ])\) is called a coarse interval space. The functions \(\phi ,\psi \) in the conditions are called parameters for \({\mathcal {I}}\). As with the notion of a coarse median space, the parameters are not uniquely defined and are not part of the data. It is only their existence that is required.
Note that conditions (I1) and (I3) together imply that any interval [a, b] must contain a, since the intersection \([a,a]\cap [a,b]\cap [b,a]\) is simultaneously non-empty and contained in \([a,a]:=\{a\}\). Since \([a,b]=[b,a]\) by (I1) as well, it must also contain b.
Given a coarse median space  , the triple \((X,d,[\cdot , \cdot ])\) given by
, the triple \((X,d,[\cdot , \cdot ])\) given by  is said to be the coarse interval space induced by
is said to be the coarse interval space induced by  .
.
On the other hand, suppose we are given a coarse interval space \((X,d,[\cdot ,\cdot ])\). Axiom (I3) implies that for any \(a,b,c\in X\) we can always choose a point in \([a,b] \cap [b,c] \cap [c,a]\), denoted by  , which is invariant under any permutation of \(\{a,b,c\}\) (i.e., the choice satisfies axiom (M2)), while (I1) and (I3) together ensure that we can only choose a for the triple a, a, b ensuring that it also satisfies (M1). Making such a choice for all a, b, c gives us a ternary operator
, which is invariant under any permutation of \(\{a,b,c\}\) (i.e., the choice satisfies axiom (M2)), while (I1) and (I3) together ensure that we can only choose a for the triple a, a, b ensuring that it also satisfies (M1). Making such a choice for all a, b, c gives us a ternary operator  on X which we will refer to as the induced (ternary) operator. By axiom (I3),
on X which we will refer to as the induced (ternary) operator. By axiom (I3),  is uniquely determined up to bounded error.
is uniquely determined up to bounded error.
Our proof that the induced ternary operator is a coarse median operator on X is inspired by Sholander’s argument in [16], though more care needs to be taken with the estimates introduced by the coarse conditions. For clarity we divide the proof into several lemmas.
Lemma 3.4
Let \((X,d,[\cdot ,\cdot ])\) be a coarse interval space and  be the induced operator. Given parameters \(\phi ,\psi \) for the space, then for any \(a,a',b,c\in X\), we have
be the induced operator. Given parameters \(\phi ,\psi \) for the space, then for any \(a,a',b,c\in X\), we have

In particular, axiom (C1) holds for  with \(\rho =\psi \circ \phi \).
with \(\rho =\psi \circ \phi \).
Proof
Set \(R=d(a,a')\), then \(a' \in {\mathcal {N}}_R([a,b])\) and \(a' \in {\mathcal {N}}_R([c,a])\). By (I1) and (I2), we have
Hence

Combined with (I3), we obtain that  . \(\square \)
. \(\square \)
Convention Following this lemma, given parameters \(\phi , \psi \) we will fix the function \(\rho :=3\psi \circ \phi \) so that 
We now turn our attention to axiom (C2). Fix a coarse interval space \((X,d,[\cdot ,\cdot ])\) with parameters \(\phi ,\psi \) and the induced operator  . We begin with the following elementary lemma, which can be deduced directly from the definition.
. We begin with the following elementary lemma, which can be deduced directly from the definition.
Lemma 3.5
If  , then \(c\in {\mathcal {N}}_R([a,b])\); conversely, if \(c\in {\mathcal {N}}_R([a,b])\) then
, then \(c\in {\mathcal {N}}_R([a,b])\); conversely, if \(c\in {\mathcal {N}}_R([a,b])\) then  for any \(a,b,c\in X\).
for any \(a,b,c\in X\).
The following estimates are a little less obvious.
Lemma 3.6
Let \(b\in {\mathcal {N}}_{R_1}([a,c])\) and \(c\in {\mathcal {N}}_{R_2}([a,d])\). Then \(c\in {\mathcal {N}}_{h(R_1,R_2)}([b,d])\) where \(h(R_1,R_2)=\psi (R_2)+\psi (\phi (R_1+\phi (R_2)))\).
Proof
Since \(b\in {\mathcal {N}}_{R_1}([a,c])\), axioms (I1) and (I2) imply that \([b,c] \subseteq {\mathcal {N}}_{\phi (R_1)}([a,c])\). Since \(c\in {\mathcal {N}}_{R_2}([a,d])\), again by (I2) we have \([a,c] \subseteq {\mathcal {N}}_{\phi (R_2)}([a,d])\). Hence \(b \in {\mathcal {N}}_{R_1}([a,c]) \subseteq {\mathcal {N}}_{R_1+\phi (R_2)}([a,d])\), and consequently \([b,d] \subseteq {\mathcal {N}}_{\phi (R_1+\phi (R_2))}([a,d])\) by axioms (I1) and (I2). Combining them together with axiom (I3), we have

which implies  (we use Lemma 3.5 in the second estimate since \(c\in {\mathcal {N}}_{R_2}([a,d])\)). So the conclusion holds. \(\square \)
(we use Lemma 3.5 in the second estimate since \(c\in {\mathcal {N}}_{R_2}([a,d])\)). So the conclusion holds. \(\square \)
Corollary 3.7
Suppose the Hausdorff distance \(d_H([a,b],[a,c]) \leqslant R\), then \(d(b,c)\leqslant h(R,R)\).
Proof
By assumption, \(b\in {\mathcal {N}}_{R}([a,c])\) and \(c\in {\mathcal {N}}_{R}([a,b])\). Now putting \(d:=b\) and applying Lemma 3.6, we have \(c\in {\mathcal {N}}_{h(R,R)}([b,b])\). Since \([b,b]=\{b\}\) by axiom (I1), we have \(d(b,c)\leqslant h(R,R)\). \(\square \)
Lemma 3.8
For any \(a,b,c,d\in X\), we have  , where \(\kappa ''=\psi (\phi (0)+\psi \phi ^2(0))\). Here we use the notation \(\phi ^2(0):=\phi \circ \phi (0)\).
, where \(\kappa ''=\psi (\phi (0)+\psi \phi ^2(0))\). Here we use the notation \(\phi ^2(0):=\phi \circ \phi (0)\).
Proof
Setting  , we consider
, we consider  . Taking
. Taking  , we have \([a,y] \subseteq {\mathcal {N}}_{\phi (0)}([a,c])\) by (I2), which implies \(m \in {\mathcal {N}}_{\phi (0)}([a,c])\). Again by (I2),
, we have \([a,y] \subseteq {\mathcal {N}}_{\phi (0)}([a,c])\) by (I2), which implies \(m \in {\mathcal {N}}_{\phi (0)}([a,c])\). Again by (I2),  , so \(m\in [y,d] \subseteq {\mathcal {N}}_{\phi ^2(0)}([c,d])\). Combining them together, we have
, so \(m\in [y,d] \subseteq {\mathcal {N}}_{\phi ^2(0)}([c,d])\). Combining them together, we have
which implies  by (I3). Hence
by (I3). Hence  . Finally, by Lemma 3.5, we have
. Finally, by Lemma 3.5, we have  . \(\square \)
. \(\square \)
From now on, let us fix the constant \(\kappa ''=\psi (\phi (0)+\psi \phi ^2(0))\).
Lemma 3.9
For any \(R_1,R_2>0\), there exists a constant \(\lambda (R_1,R_2)>0\) such that for any \(b\in {\mathcal {N}}_{R_1}([a,c]) \cap {\mathcal {N}}_{R_2}([a,d])\) and \(x\in [c,d]\) we have \(b\in {\mathcal {N}}_{\lambda (R_1,R_2)}([a,x])\). In particular, taking  we have:
we have:

Proof
Since \(b\in {\mathcal {N}}_{R_1}([a,c])\), it follows from Lemmas 3.4 and 3.8 that

This implies  . Together with \(b\in {\mathcal {N}}_{R_2}([a,d])\) and Lemma 3.6, we have
. Together with \(b\in {\mathcal {N}}_{R_2}([a,d])\) and Lemma 3.6, we have  . On the other hand, since \(x\in [c,d]\), it follows from Lemmas 3.4, 3.5 and 3.8 that
. On the other hand, since \(x\in [c,d]\), it follows from Lemmas 3.4, 3.5 and 3.8 that

This implies  , hence
, hence  . Combining them together, we have
. Combining them together, we have
Now taking
the lemma holds. \(\square \)
Finally we are in the position to prove the following theorem.
Theorem 3.10
Let \((X,d,[\cdot ,\cdot ])\) be a coarse interval space with the induced operator  , then
, then  is a coarse median space.
is a coarse median space.
Proof
It only remains to verify (C2). In other words, we need to find a constant \(\kappa \) such that for any \(a,b,c,d\in X\), we have

By axiom (I2) and Lemma 3.9, we have:

Similarly we have

The above two estimates imply:

Finally it follows from Corollary 3.7 that

for \(\kappa =h(\lambda (\phi ^2(0),\lambda (\phi ^2(0),\phi (0))),\lambda (\phi ^2(0),\lambda (\phi ^2(0),\phi (0))))\). \(\square \)
Analogous to relaxing axioms (M1) and (M2) for a coarse median operator to axiom (C0), we consider the following notion of a coarse interval structure.
Definition 3.11
A coarse interval structure on a metric space (X, d) is a triple \({\mathcal {I}}=(X,d,[\cdot ,\cdot ])\), where \([\cdot ,\cdot ]\) is a map from \(X^2\) to \({\mathcal {P}}(X)\) such that there exists a constant \({\kappa _0}>0\) for which the following conditions hold:
-
(I1)’.
For all \(a,b\in X, d_H([a,a], \{a\}) \leqslant {\kappa _0}\) and \(d_H([a,b],[b,a])\leqslant {\kappa _0}\);
-
(I2).
There exists a non-decreasing function \(\phi : {\mathbb {R}}^{+}\rightarrow {\mathbb {R}}^{+}\) such that for any \(a,b\in X\) and \(c\in {\mathcal {N}}_R([a,b])\), we have \([a,c] \subseteq {\mathcal {N}}_{\phi (R)}([a,b])\);
-
(I3)’.
There exists a non-decreasing function \(\psi : [{\kappa _0},+\infty ) \rightarrow {\mathbb {R}}^{+}\) such that for any \(a,b,c\in X\) and \(R \geqslant {\kappa _0}\), we have \({\mathcal {N}}_{\kappa _0}([a,b]) \cap {\mathcal {N}}_{\kappa _0}([b,c]) \cap {\mathcal {N}}_{\kappa _0}([c,a]) \ne \emptyset \) and \(\mathrm {diam}\,( {\mathcal {N}}_R([a,b]) \cap {\mathcal {N}}_R([b,c]) \cap {\mathcal {N}}_R([c,a]) ) \leqslant \psi (R)\).
The constant \({\kappa _0}\) and functions \(\phi ,\psi \) in the conditions are called parameters for \({\mathcal {I}}\).
Remark 3.12
By (I1)\(^{\prime }\), for any point a the interval [a, a] lies in \(B(a,{\kappa _0})\). By (I3)\(^{\prime }\), the intersection \({\mathcal {N}}_{\kappa _0}([a,a]) \cap {\mathcal {N}}_{\kappa _0}([a,b])\) must be non-empty for all b. As \({\mathcal {N}}_{\kappa _0}([a,a])\) lies in \(B(a,2{\kappa _0})\), it follows that a must lie in \({\mathcal {N}}_{3{\kappa _0}}([a,b])\). Similarly \(b\in {\mathcal {N}}_{3{\kappa _0}}([a,b])\).
Recall that every coarse median is uniformly close to some coarse median satisfying axioms (M1) and (M2). Similarly we will show that a coarse interval structure is always “close” to another satisfying (I1)–(I3) in the following sense.
Definition 3.13
Let \((X,d, [\cdot , \cdot ])\) and \((X,d, [\cdot , \cdot ]')\) be coarse interval structures. We say they are uniformly close if there exists a constant \(C>0\) such that \(d_H([x,y],[x,y]')\leqslant C\) for any \(x,y\in X\).
Lemma 3.14
Let \((X,d,[\cdot ,\cdot ])\) be a coarse interval structure. Then there exists a map \([\cdot , \cdot ]'\) which is uniformly close to \([\cdot , \cdot ]\) and such that \((X,d,[\cdot , \cdot ]')\) is a coarse interval space.
Proof
We define ‘fattened’ intervals:
for \(a\ne b\), and define \([a,a]':=\{a\}\). It is easy to see from (I1)\(^{\prime }\) that \([a,a]'=\{a\}\) is \(\kappa _0\)-close to [a, a] and that \({\mathcal {N}}_{\kappa _0}([a,b])\cup {\mathcal {N}}_{\kappa _0}([b,a])\) is \(2\kappa _0\)-close to [a, b]. By Remark 3.12, the points a, b are \(3\kappa _0\)-close to [a, b], hence \([a,b]'\) is \(3\kappa _0\)-close to [a, b].
By construction, \([\cdot ,\cdot ]'\) satisfies (I1) and clearly it still satisfies (I2). The fattening of the intervals together with (I3)\(^{\prime }\) ensures that \([a,b]'\cap [b,c]'\cap [c,a]'\) is non-empty for a, b, c distinct. Now taking repeated points, \([a,b]'\cap [b,b]'\cap [b,a]'=\{b\}\) by construction. Hence \([a,b]'\cap [b,c]'\cap [c,a]'\) is non-empty in all cases. The above analysis shows that the R-neighbourhood of the interval \([a,b]'\) is contained in the \((R+3\kappa _0)\)-neighbourhood of the interval [a, b], so the intersection \( {\mathcal {N}}_R([a,b]') \cap {\mathcal {N}}_R([b,c]') \cap {\mathcal {N}}_R([c,a]')\) is contained in the intersection \( {\mathcal {N}}_{R+3\kappa _0}([a,b]) \cap {\mathcal {N}}_{R+3\kappa _0}([b,c]) \cap {\mathcal {N}}_{R+3\kappa _0}([c,a])\). It therefore has diameter bounded by \(\psi (R+3\kappa _0)\) by (I3)\(^{\prime }\). This establishes (I3). \(\square \)
Adapting the arguments we made above, we have the following correspondence between coarse median structures and coarse interval structures.
Theorem 3.15
-
(1)
Given a coarse median structure
 , the map \((a,b)\mapsto [a,b]\) provided by Definition 1.2 gives an induced coarse interval structure \((X,d,[\cdot ,\cdot ])\).
, the map \((a,b)\mapsto [a,b]\) provided by Definition 1.2 gives an induced coarse interval structure \((X,d,[\cdot ,\cdot ])\). -
(2)
Let \((X,d,[\cdot ,\cdot ])\) be a coarse interval structure with parameters \({\kappa _0},\phi ,\psi \). For any \(a,b,c\in X\), choose a point in \({\mathcal {N}}_{\kappa _0}([a,b]) \cap {\mathcal {N}}_{\kappa _0}([b,c]) \cap {\mathcal {N}}_{\kappa _0}([c,a])\), denoted by
 . Making such a choice gives an induced coarse median structure
. Making such a choice gives an induced coarse median structure  .
. -
(3)
Furthermore the above two procedures are inverse to each other up to uniform bounds:
-
For a coarse median structure
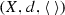 with induced coarse interval structure \((X,d,[\cdot ,\cdot ])\), any induced coarse median structure
with induced coarse interval structure \((X,d,[\cdot ,\cdot ])\), any induced coarse median structure  is uniformly close to
is uniformly close to  ;
; -
For a coarse interval structure \((X,d, [\cdot , \cdot ])\) with any induced coarse median structure
 , the induced coarse interval structure is uniformly close to \((X,d, [\cdot , \cdot ])\).
, the induced coarse interval structure is uniformly close to \((X,d, [\cdot , \cdot ])\).
-
Proof
-
(1).
By Remark 2.9,
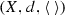 is uniformly close to a coarse median space
is uniformly close to a coarse median space  . Now Proposition 3.2 shows that the map \(X^2 \rightarrow {\mathcal {P}}(X)\) given by
. Now Proposition 3.2 shows that the map \(X^2 \rightarrow {\mathcal {P}}(X)\) given by  gives a coarse interval space \((X,d,[\cdot ,\cdot ]')\). Since
gives a coarse interval space \((X,d,[\cdot ,\cdot ]')\). Since  and
and  are uniformly close, \([\cdot , \cdot ]\) and \([\cdot ,\cdot ]'\) are uniformly close as well. Hence \((X,d,[\cdot ,\cdot ])\) is a coarse interval structure.
are uniformly close, \([\cdot , \cdot ]\) and \([\cdot ,\cdot ]'\) are uniformly close as well. Hence \((X,d,[\cdot ,\cdot ])\) is a coarse interval structure. -
(2).
From Lemma 3.14, \((X,d,[\cdot ,\cdot ])\) is uniformly close to some coarse interval space \((X,d,[\cdot ,\cdot ]')\). We now apply Theorem 3.10 to construct an induced coarse median space
 . Since \([\cdot ,\cdot ]\) and \([\cdot ,\cdot ]'\) are uniformly close,
. Since \([\cdot ,\cdot ]\) and \([\cdot ,\cdot ]'\) are uniformly close,  and
and  are uniformly close as well. Hence
are uniformly close as well. Hence  is a coarse median structure.
is a coarse median structure. -
(3).
First we start with the coarse median structure
 with parameters \(\rho , {\kappa _0}, {\kappa _4},{\kappa _5}\) and induced coarse interval structure \((X,d,[\cdot ,\cdot ])\) with some parameters \({\kappa _0}',\phi ,\psi \). Let
with parameters \(\rho , {\kappa _0}, {\kappa _4},{\kappa _5}\) and induced coarse interval structure \((X,d,[\cdot ,\cdot ])\) with some parameters \({\kappa _0}',\phi ,\psi \). Let  be any induced coarse median structure of \((X,d,[\cdot ,\cdot ])\). By definition for any \(x,y,z\in X, \) is some point chosen from the intersection \({\mathcal {N}}_{{\kappa _0}'}([x,y])\cap {\mathcal {N}}_{{\kappa _0}'}([y,z])\cap {\mathcal {N}}_{{\kappa _0}'}([z,x])\), a fortiori it is in the intersection \({\mathcal {N}}_{{\kappa _0}''}([x,y])\cap {\mathcal {N}}_{{\kappa _0}''}([y,z])\cap {\mathcal {N}}_{{\kappa _0}''}([z,x])\) where \({\kappa _0}''=\max \{{\kappa _0},{\kappa _0}'\}\). The latter contains
be any induced coarse median structure of \((X,d,[\cdot ,\cdot ])\). By definition for any \(x,y,z\in X, \) is some point chosen from the intersection \({\mathcal {N}}_{{\kappa _0}'}([x,y])\cap {\mathcal {N}}_{{\kappa _0}'}([y,z])\cap {\mathcal {N}}_{{\kappa _0}'}([z,x])\), a fortiori it is in the intersection \({\mathcal {N}}_{{\kappa _0}''}([x,y])\cap {\mathcal {N}}_{{\kappa _0}''}([y,z])\cap {\mathcal {N}}_{{\kappa _0}''}([z,x])\) where \({\kappa _0}''=\max \{{\kappa _0},{\kappa _0}'\}\). The latter contains  and is uniformly bounded with diameter at most \(\psi ({\kappa _0}'')\). Hence
and is uniformly bounded with diameter at most \(\psi ({\kappa _0}'')\). Hence  and
and  are uniformly close.
are uniformly close.
Conversely given a coarse interval structure \((X,d,[\cdot ,\cdot ])\) with parameters \({\kappa _0},\phi ,\psi \) and any induced coarse median structure  , we consider the induced coarse interval structure \((X,d,[\cdot ,\cdot ]')\) of
, we consider the induced coarse interval structure \((X,d,[\cdot ,\cdot ]')\) of  . By definition for any \(x,y,z\in X, \) is some point chosen from \({\mathcal {N}}_{{\kappa _0}}([x,z])\cap {\mathcal {N}}_{{\kappa _0}}([z,y])\cap {\mathcal {N}}_{{\kappa _0}}([y,x])\). Hence
. By definition for any \(x,y,z\in X, \) is some point chosen from \({\mathcal {N}}_{{\kappa _0}}([x,z])\cap {\mathcal {N}}_{{\kappa _0}}([z,y])\cap {\mathcal {N}}_{{\kappa _0}}([y,x])\). Hence  , which implies \([x,y]' \subseteq {\mathcal {N}}_{2{\kappa _0}}([x,y])\). On the other hand for any \(z\in [x,y]\), Remark 3.12 implies \(z\in {\mathcal {N}}_{{\kappa _0}}([y,x])\cap {\mathcal {N}}_{3{\kappa _0}}([z,y]) \cap {\mathcal {N}}_{3{\kappa _0}}([x,z])\). It follows that both z and
, which implies \([x,y]' \subseteq {\mathcal {N}}_{2{\kappa _0}}([x,y])\). On the other hand for any \(z\in [x,y]\), Remark 3.12 implies \(z\in {\mathcal {N}}_{{\kappa _0}}([y,x])\cap {\mathcal {N}}_{3{\kappa _0}}([z,y]) \cap {\mathcal {N}}_{3{\kappa _0}}([x,z])\). It follows that both z and  lie in \({\mathcal {N}}_{{\kappa _0}}([y,x])\cap {\mathcal {N}}_{3{\kappa _0}}([z,y]) \cap {\mathcal {N}}_{3{\kappa _0}}([x,z])\). So by axiom (I3)\(^{\prime }\), we have
lie in \({\mathcal {N}}_{{\kappa _0}}([y,x])\cap {\mathcal {N}}_{3{\kappa _0}}([z,y]) \cap {\mathcal {N}}_{3{\kappa _0}}([x,z])\). So by axiom (I3)\(^{\prime }\), we have  for \(K=\psi (3{\kappa _0})\). Hence \([x,y]\subseteq {\mathcal {N}}_K([x,y]')\), which implies \(d_H([x,y],[x,y]') \leqslant \max \{2{\kappa _0},K\}\) for any \(x,y\in X\). Therefore \([\cdot , \cdot ]\) and \([\cdot , \cdot ]'\) are uniformly close. \(\square \)
for \(K=\psi (3{\kappa _0})\). Hence \([x,y]\subseteq {\mathcal {N}}_K([x,y]')\), which implies \(d_H([x,y],[x,y]') \leqslant \max \{2{\kappa _0},K\}\) for any \(x,y\in X\). Therefore \([\cdot , \cdot ]\) and \([\cdot , \cdot ]'\) are uniformly close. \(\square \)
4 Rank, generalised hyperbolicity and interval growth
4.1 Generalised hyperbolicity for higher rank coarse median spaces
Here we will provide the following characterisations of rank for a coarse median space.
Theorem 4.1
Let  be a coarse median space and \(n \in \mathbb N\setminus \{0\}\), then the following are equivalent:
be a coarse median space and \(n \in \mathbb N\setminus \{0\}\), then the following are equivalent:
-
(1)
\(\mathrm {rank}\,X \leqslant n\);
-
(2)
Multi-median condition: There exists a non-decreasing function \(\psi \) such that for any \(\lambda >0\) and any \(x_1,\ldots ,x_{n+1},q \in X\), we have
$$\begin{aligned} \bigcap _{i \ne j} {\mathcal {N}}_\lambda ([x_i,x_j]) \subseteq \bigcup _{i=1}^{n+1} {\mathcal {N}}_{\psi (\lambda )}([x_i,q]); \end{aligned}$$ -
(3)
Thin \((n\!+\!1)\)-cubes condition: There exists a non-decreasing function \(\varphi \), such that
$$\begin{aligned} \min \{d(p,\langle x_i,p,q\rangle ):i=1,\ldots ,n+1\} \leqslant \varphi (\max \{d(p,\langle x_i,x_j,p\rangle ): i\ne j\}) \end{aligned}$$for any \(x_1,\ldots ,x_{n+1}\) and \(p,q \in X\).
As Bowditch showed in [6], a geodesic coarse median space has rank 1 if and only if it is hyperbolic, and it is instructive to consider conditions (2) and (3) above in that context. Here condition (2) reduces to a version of the generalised slim triangles condition abstracted from classical hyperbolic geometry, while condition (3) reduces to the Gromov inequality (see Eq. 5 below) motivated by the geometry of trees. From this perspective, Theorem 4.1 provides higher rank analogues of these two characterisations.
To be more precise, recall that in [14, Theorem 4.4] we established the following result in the special case where b is required to range over those points in the interval [a, c]. To deduce the more general result stated here, one only needs to consider the effect of replacing the general point b by the coarse median  and then use the fact that the intervals
and then use the fact that the intervals  and
and  both lie in a uniformly bounded neighbourhood of the interval [a, c]:
both lie in a uniformly bounded neighbourhood of the interval [a, c]:
Theorem 4.2
[14] For a coarse median space  , the following are equivalent:
, the following are equivalent:
-
(1)
\(\mathrm {rank}\,X \leqslant 1\);
-
(2)
There exists a constant \(\delta >0\) such that for any \(a,b,c \in X\), we have
$$\begin{aligned}{}[a,c] \subseteq {\mathcal {N}}_\delta ([a,b]) \cup {\mathcal {N}}_\delta ([b,c]). \end{aligned}$$
We also showed in [14, Theorem 4.2] that the intervals in a rank 1 geodesic coarse median space are uniformly close to geodesics, so Theorem 4.2 is a version of the slim triangles condition for hyperbolicity. Clearly Theorem 4.1 generalises this, providing a higher rank analogue of the slim triangles condition which holds even in the non-geodesic context.
Remark 4.3
The closeness of geodesics and intervals is a unique (and not a priori obvious) feature of the rank 1 case. Combining this fact with Proposition 3.2, we deduce that any geodesic metric space admits at most one coarse median of rank one up to uniform bound. As Zeidler showed in [18, Example 2.2.8], this is not true for higher rank cases (indeed, even in rank 2). The classical median on the Euclidean plane (corresponding to the Cartesian coordinates) is given by taking the interval from the origin to the point (x, y) to be the rectilinear area with diagonal between these points and extending this by the translation action to an interval structure on the plane, equipped with its usual metric. Rotating the frame by an angle of \(\pi /4\) one obtains a new interval structure but of course the metric does not change. To see that the new median is not equivalent to the standard one, one observes that while the points (n, 0), (0, 0), (0, n) have standard median (0, 0) their median in the new structure is \((\frac{n}{\sqrt{2}}, \frac{n}{\sqrt{2}})\) which diverges to infinity.
Turning now to Gromov’s inner product, we recall the definition. Fixing a base point p in a metric space (X, d), and for \(a,b\in X\), we set
Theorem 4.4
[10] A geodesic metric space (X, d) is Gromov hyperbolic if and only if there exists some constant \(\delta >0\) such that the following inequality holds for any \(a,b,c,p \in X\):
Note that the Gromov product is determined by the properties \((z|y)_x+(z|x)_y=d(x,y)\) and symmetry: \((z|y)_x=(y|z)_x\) for all x, y, z.
If \(i_y\) is the intermediate point on a geodesic from x to z such that \(d(x,i_y)=(y|z)_x\) and \(d(z,i_y)=d(x,z)-d(x,i_y)=(y|x)_z\), then we have
Since this is symmetric in x, z for such points, we obtain \((y|x)_{i_y}=(y|z)_{i_y}\).
Lemma 4.5
A geodesic space X is hyperbolic if and only if there exists \(\delta >0\) such that for all \(x,y,z\in X\) and p on a geodesic from x to z, we have
Proof
The condition is a special case of Gromov’s 4-point condition, so is implied by hyperbolicity.
Now we consider the converse. For any \(x,y,z\in X\), let \(i_x,i_y,i_z\) be intermediate points on geodesics from y to z, x to z and x to y respectively such that \(d(x,i_y)=d(x,i_z)=(y|z)_x\), etc.
As noted above \((y|x)_{i_y}=(y|z)_{i_y}\), so by hypothesis both of these are at most \(\delta \). Thus we have
meaning intuitively that \(i_x\) is ‘almost’ on a geodesic from x to y.
On the other hand, \(d(x,i_z)+d(i_z,y)=d(x,y)\) and \(d(i_z,y)=(x|z)_y=d(i_x,y)\). So we have \(d(x,i_x)\leqslant d(x,i_z)+2\delta \). We will show a fellow travelling result that bounds \(d(i_x,i_z)\).
Since \(i_z\) is on the geodesic from x to y, our hypothesis implies one of \((i_x|x)_{i_z},(i_x|y)_{i_z}\) is at most \(\delta \). In other words, for some \(u\in \{x,y\}\) we have
When \(u=y\) we have \(d(i_x,u)=d(u,i_z)\), while \(u=x\) implies \(d(i_x,u)\leqslant d(u,i_z)+2\delta \). Hence in either case, we have \(d(i_x,i_y)\leqslant 4\delta \).
Interchanging the roles of x, y, z we see that \(\{i_x,i_y,i_z\}\) has diameter at most \(4\delta \), which implies hyperbolicity by [9, III.H.1.17(3)]. \(\square \)
We note that neither the Gromov 4-point condition nor our special case of this is quasi-isometry invariant, however we can give a quasi-isometrically invariant form in terms of medians as follows. To allow for this coarsening we consider the following condition: there exists a non-decreasing function \(\varphi \) such that for any \(x,y,z;p\in X\), we have
This is a priori weaker than the Gromov 4-point condition, but stronger than the hypothesis in Lemma 4.5 (taking \(\delta =\varphi (0)\)), so in the geodesic case inequality (5) characterises hyperbolicity.
Now for a rank 1 geodesic coarse median space  , there exists a constant \(C>0\) such that for any \(a,b,p \in X, (a|b)_p \thicksim _C d(p,\langle a,b,p\rangle )\). This follows directly from the fact that intervals and geodesics are uniformly close to each other [14, Theorem 4.2]. Hence in this situation, the coarse inequality (5) above can be rewritten to give the following characterisation of hyperbolicity:
, there exists a constant \(C>0\) such that for any \(a,b,p \in X, (a|b)_p \thicksim _C d(p,\langle a,b,p\rangle )\). This follows directly from the fact that intervals and geodesics are uniformly close to each other [14, Theorem 4.2]. Hence in this situation, the coarse inequality (5) above can be rewritten to give the following characterisation of hyperbolicity:

This inequality has the virtue that it is quasi-isometry invariant. Hence the class of quasi-geodesic coarse median spaces satisfying this variant of the 4-point condition is closed under quasi-isometry, providing a natural generalisation of geodesic hyperbolic spaces.
Equation (6) is the rank 1 case of Theorem 4.1 (3), so this theorem provides a higher rank generalisation of the Gromov inner product characterisation of hyperbolicity. We now turn to the proof of the theorem.
Proof of Theorem 4.1
Assume \((\rho ,{\kappa _4}{, {\kappa _5}})\) are parameters of  .
.
\((3) \Rightarrow (2)\): For any \(p \in \bigcap _{i \ne j} {\mathcal {N}}_\lambda ([x_i,x_j])\) and \(i \ne j\), there exists \(p' \in [x_i,x_j]\) such that \(p\thicksim _\lambda p'\). So we have
Hence from condition (3), there exists some \(i=1,\ldots ,n+1\) such that

Taking \(\psi (\lambda )=\varphi (\rho (\lambda )+\lambda +{\kappa _4})\), we have \(p \in {\mathcal {N}}_{\psi (\lambda )}([x_i,q])\) as required.
\((2) \Rightarrow (3)\): For any p, q and \(x_1,\ldots ,x_{n+1} \in X\), take \(\xi =\max \{d(p,\langle x_i,x_j,p\rangle ): i\ne j\}\). Then \(p\thicksim _{\xi }\langle x_i,x_j,p\rangle \in [x_i,x_j]\). By condition 2), there exists some \(i=1,\ldots ,n+1\) such that \(p \in {\mathcal {N}}_{\psi (\xi )}([x_i,q])\), i.e., there exists some \(p' \in [x_i,q]\) such that \(p \thicksim _{\psi (\xi )}p'\). Hence

Taking \(\varphi (\xi )=\rho (\psi (\xi ))+\psi (\xi )+{\kappa _4}\), we are done.
\((1)\Rightarrow (3)\): Since the rank is at most n, Theorem 2.11 implies that for any \(\lambda >0\) there exists a constant \(C=C(\lambda )\) such that for any \(a,b\in X\) and \(e_1,\ldots ,e_{n+1}\in [a,b]\) with \(\langle e_i,a,e_j\rangle \thicksim _\lambda a\) (\(i\ne j\)), one of the points \(e_i\)’s is C-close to a. Set \(\xi =\max \{d(p,\langle x_i,x_j,p\rangle ): i\ne j\}\), then by the coarse 4-point axiom (C2) we have:
for any \(i \ne j\). Therefore we have

Taking \(\varphi (\xi )=C(\rho (\xi )+{\kappa _5})\), we are done.
\( (3) \Rightarrow (1)\): Assume \(e_1,\ldots ,e_{n+1} \in [a,b]\) with \(\langle e_i,a,e_j\rangle \thicksim _\lambda a\). Condition 3) implies that

Since \(e_i\in [a,b]\), we have  . Hence
. Hence
Taking \(C(\lambda )=\varphi (\lambda )+{\kappa _4}, \) has rank at most n by Theorem 2.11. \(\square \)
This suggests a natural notion of rank for coarse interval spaces as follows.
Definition 4.6
Let \((X,d,[\cdot ,\cdot ])\) be a coarse interval structure. We say that the rank of \((X,d,[\cdot ,\cdot ])\) is at most n if there exists a non-decreasing function \(\psi \) such that
for any \(\lambda >0\) and \(x_1,\ldots ,x_{n+1},q \in X\).
Note that in the higher rank case (\(n\geqslant 2\)), the intersection on the left must be uniformly bounded by axiom (I3) and can be thought of as a generalised centroid of the points \(x_1, \ldots , x_{n+1}\). So the axiom asserts that the generalised centroid must be close to at least one of those coarse intervals.
With this definition and combining Theorem 3.15, we obtain the following:
Corollary 4.7
For a metric space, any coarse median of rank n induces a coarse interval structure of rank n and vice versa.
4.2 Cubes in coarse median spaces
In this subsection we will provide a structure theorem which describes a coarse cube in a coarse median space as a product of coarse intervals. It will play a key role in our characterisation of finite rank coarse median spaces in terms of the growth of coarse intervals.
Recall that median cubes are the fundamental building blocks for median algebras. Equipping the median n-cube  with the \(\ell ^1\)-metric \(d_{\ell ^1}\) makes it a coarse median space
with the \(\ell ^1\)-metric \(d_{\ell ^1}\) makes it a coarse median space  .
.
Definition 4.8
An L-coarse cube of rank n in a coarse median structure  is an L-quasi-morphism c from
is an L-quasi-morphism c from  to
to  . An edge in an L-coarse cube c is a set of points \(\{c({{\bar{a}}}), c({{\bar{b}}})\}\) in the image such that \({{\bar{a}}}, \bar{b}\) are adjacent vertices in the median cube. Two edges in an L-coarse cube c are said to be parallel if there exist parallel edges in the median cube which map to them under c.
. An edge in an L-coarse cube c is a set of points \(\{c({{\bar{a}}}), c({{\bar{b}}})\}\) in the image such that \({{\bar{a}}}, \bar{b}\) are adjacent vertices in the median cube. Two edges in an L-coarse cube c are said to be parallel if there exist parallel edges in the median cube which map to them under c.
We will denote the origin of the median n-cube by \({\bar{{\mathbf {0}}}}\), the vertex diagonally opposite to \({\bar{{\mathbf {0}}}}\) by \({\bar{{\mathbf {1}}}}\) and the vertices adjacent to \({\bar{{\mathbf {0}}}}\) by \({\bar{e}}_1,\ldots ,{\bar{e}}_n\). Given an L-coarse cube c, where there is no risk of confusion we will denote the images of the vertices \({\bar{{\mathbf {0}}}},{\bar{{\mathbf {1}}}},{\bar{e}}_1,\ldots ,{\bar{e}}_n\) under the map c by \({\mathbf {0}}, {\mathbf {1}}, e_1, \ldots , e_n\) respectively. The convention that elements of the median cube are barred while their images are not corresponds to the view that the median cube is an approximation (in the sense of Bowditch, see Definition 1.1) to the finite set of vertices \({\mathbf {0}}, {\mathbf {1}}, e_1, \ldots , e_n\).
Note that in Definition 4.8 we do not impose any control on the distances between the points of the image, since we wish to allow cubes of arbitrarily large diameter. By analogy with Zeidler’s result in [18], we have the following lemma, which controls the relationship between lengths of parallel edges in a coarse cube.
Lemma 4.9
Given an edge e of length d in an L-coarse cube c, all edges parallel to e in c have length bounded by \(\rho (d)+2L\), where \(\rho \) is a control function parameter for the coarse median.
The proof is similar to that of [18, Lemma 2.4.5] and is therefore omitted. Given that there is control between the lengths of parallel edges but no control on the lengths of “perpendicular” edges, it may be helpful to think of a coarse cube as a coarse cuboid.
Definition 4.10
Given an interval [a, b] in a coarse median structure  , we may define a new ternary operator on [a, b] by \(\langle x,y,z \rangle _{a,b}:= \langle a,\langle x,y,z\rangle ,b\rangle \). By [14, Lemma 2.22], the triple
, we may define a new ternary operator on [a, b] by \(\langle x,y,z \rangle _{a,b}:= \langle a,\langle x,y,z\rangle ,b\rangle \). By [14, Lemma 2.22], the triple  is a coarse median structure and
is a coarse median structure and  , where C is independent of a, b.
, where C is independent of a, b.
Given an L-coarse cube \(f\,{:}\,I^n\rightarrow X\), define the following coarse median spaces:

where \(d_{\ell ^1}\) denotes the \(\ell ^1\)-product of the induced metrics on the intervals \([{\mathbf {0}}, e_i]\) and  is defined by
is defined by  . Also define maps as follows:
. Also define maps as follows:

Theorem 4.11
Let  be a coarse median space and \(f\,{:}\,I^n\rightarrow X\) be an L-coarse cube of rank n in X. Then the map \(\Phi :{\mathcal {A}} \rightarrow {\mathcal {B}}\) defined above provides a \((\rho _+,C)\)-coarse median isomorphism with inverse \(\Psi \), where \(\rho _+(t)=Kt+H_0\) and \(K,H_0,C\) depend only on n, L and parameters of
be a coarse median space and \(f\,{:}\,I^n\rightarrow X\) be an L-coarse cube of rank n in X. Then the map \(\Phi :{\mathcal {A}} \rightarrow {\mathcal {B}}\) defined above provides a \((\rho _+,C)\)-coarse median isomorphism with inverse \(\Psi \), where \(\rho _+(t)=Kt+H_0\) and \(K,H_0,C\) depend only on n, L and parameters of  .
.
Proof
Assume \(\rho ,{\kappa _4},{\kappa _5}\) are parameters of  . First we show that \(\Phi ,\Psi \) are bornologous. By axiom (C1), for any \(x,y \in [{\mathbf {0}},{\mathbf {1}}]\) we have:
. First we show that \(\Phi ,\Psi \) are bornologous. By axiom (C1), for any \(x,y \in [{\mathbf {0}},{\mathbf {1}}]\) we have:

which implies \(\Phi \) is \((n\rho )\)-bornologous. On the other hand, for any \(\vec {x}=(x_1, \ldots , x_n)\) and \(\vec {y}=(y_1, \ldots , y_n) \in [{\mathbf {0}},e_1]\times \cdots \times [{\mathbf {0}}, e_n]\), axiom (C1) implies:

Here the last inequality follows from the control over iterated coarse medians provided by Lemma 2.14(1). This implies \(\Psi \) is \((\rho \circ \rho _n)\)-bornologous. Since \(\rho \) and \(\rho _n\) are both affine so is the function \(\rho _+:= n\rho +\rho \circ \rho _n\).
Next we show that \(\Phi \) is a quasi-morphism. For \(x,y,z \in [{\mathbf {0}},{\mathbf {1}}], \) and  . So by axiom (C1) and the estimate (2), we have
. So by axiom (C1) and the estimate (2), we have
Applying the same argument again, denoting the projection from \([{\mathbf {0}},e_1]\times \cdots \times [{\mathbf {0}}, e_n]\) onto the i-th coordinate by \(pr_i\), we have:
Hence \(\Phi \) is a \(C'\)-quasi-morphism for \(C'=n[\rho (\rho (2{\kappa _4})+{\kappa _5})+\rho ({\kappa _4})+\rho ({\kappa _5})+{\kappa _4}+2{\kappa _5}]\).
Note that in the canonical cube \(I^n\), the iterated median \(\langle {\bar{e}}_1, \ldots , {\bar{e}}_n;{\bar{{\mathbf {1}}}}\rangle _n={\bar{{\mathbf {1}}}}\). It follows that by Lemma 2.14(2), there exists a constant \(H_n(L)\) such that

Now by Lemma 2.14(3), there is a constant \(C_n\) such that for any \(x \in [{\mathbf {0}},{\mathbf {1}}]\) we have

Hence \( \Psi \circ \Phi \) is \(C''\)-close to the identity on \(\mathcal A\) for \(C'':=\rho ^2(H_n(L))+\rho (C_n)+2{\kappa _4}\).
Since f is an L-coarse median morphism, we have  and \(\langle {\mathbf {0}},e_i, e_j\rangle \thicksim _L {\mathbf {0}}\) for \(i\ne j\). For any \(\vec {x}=(x_1, \ldots , x_n) \in [{\mathbf {0}},e_1]\times \cdots \times [{\mathbf {0}}, e_n]\), we have:
and \(\langle {\mathbf {0}},e_i, e_j\rangle \thicksim _L {\mathbf {0}}\) for \(i\ne j\). For any \(\vec {x}=(x_1, \ldots , x_n) \in [{\mathbf {0}},e_1]\times \cdots \times [{\mathbf {0}}, e_n]\), we have:

where the final estimate follows from Lemma 2.14(3). Since \(x_i\in [{\mathbf {0}},e_i]\), we have  ; while for \(j\not =i\), we have
; while for \(j\not =i\), we have
Hence applying Lemma 2.14(1) we obtain that

where if \(i = 1\) then trivially \(m=n-1\) and otherwise \(m=n-i+1\). Here \(C''':=\rho _n((n-1)(\rho ({\kappa _4})+{\kappa _4}+\rho (L))+{\kappa _4})\). Since all of these iterated medians lie in \([{\mathbf {0}},{\mathbf {1}}]\), the cost of removing the last zero is \({\kappa _4}\). Hence at worst (removing \((n-2)\) zeros) we have:

Combining them together we obtain that \(\Phi \circ \Psi \) is \([n(3\rho (L)+(n+1){\kappa _4}+C_n+C''')]\)-close to the identity on \({\mathcal {B}}\).
To sum up, taking
we have proved that both \(\Phi \) and \(\Psi \) are \(\rho _+\)-bornologous, \(\Phi \) is a C-quasi-morphism and \(\Phi \circ \Psi \thicksim _C id_{{\mathcal {B}}}, \Psi \circ \Phi \thicksim _C id_{{\mathcal {A}}}\). Hence by definition, \(\Phi \) is a \((\rho _+,C)\)-coarse median isomorphism with inverse \(\Psi \). \(\square \)
The above theorem suggests that we may regard the space \({\mathcal {A}}\) as a coarse cube (or, at least, cuboid) in our coarse median space. We now consider a natural family of subspaces, regarded as subcubes of \({\mathcal {A}}\). Given points \(x_i \in [{\mathbf {0}},e_i]\) and taking \(x:=\Psi ((x_1,\ldots ,x_n))\) in \([{\mathbf {0}},{\mathbf {1}}]\), we consider the following coarse median spaces:

where \(d_{\ell ^1}\) denotes the \(\ell ^1\)-product of the induced metrics on the intervals \([{\mathbf {0}}, x_i]\) and  is defined by
is defined by  . Also define maps as follows:
. Also define maps as follows:

Corollary 4.12
Let  be a coarse median space and \(f:I^n\rightarrow X\) be an L-coarse cube of rank n in X. Then the map \(\Phi ':\mathcal A' \rightarrow {\mathcal {B}}'\) defined above provides a \((\rho '_+,C')\)-coarse median isomorphism with inverse \(\Psi '\), where \(\rho '_+(t)=K't+H'_0\) and \(K',H'_0,C'\) depend only on n, L and parameters of
be a coarse median space and \(f:I^n\rightarrow X\) be an L-coarse cube of rank n in X. Then the map \(\Phi ':\mathcal A' \rightarrow {\mathcal {B}}'\) defined above provides a \((\rho '_+,C')\)-coarse median isomorphism with inverse \(\Psi '\), where \(\rho '_+(t)=K't+H'_0\) and \(K',H'_0,C'\) depend only on n, L and parameters of  .
.
Proof
It follows from the same arguments in the first part of the proof of Theorem 4.11 that \(\Phi ',\Psi '\) are \(\rho _+\)-bornologous and \(\Phi '\) is a C-coarse median morphism for the same constants \(\rho _+,C\) as in Theorem 4.11. It suffices to prove that \(\Psi ' \circ \Phi '\) and \(\Phi ' \circ \Psi '\) are close to the corresponding identities.
\(\bullet \) Recall that for \(\Phi \) and \(\Psi \), the map \(\Phi \circ \Psi \) is C-close to the identity. So we have

which implies that  for each i. As shown in the proof of Theorem 4.11, we have
for each i. As shown in the proof of Theorem 4.11, we have  . Combining them together with parts (1), (2) and (4) of Lemma 2.14, we obtain that
. Combining them together with parts (1), (2) and (4) of Lemma 2.14, we obtain that

i.e.,  for \(\alpha _n(L):=\rho (H_n(L))+\rho _n(nC+{\kappa _4})+D_n+{\kappa _4}\). Now for any \(y \in [{\mathbf {0}},x]\), we have:
for \(\alpha _n(L):=\rho (H_n(L))+\rho _n(nC+{\kappa _4})+D_n+{\kappa _4}\). Now for any \(y \in [{\mathbf {0}},x]\), we have:

Hence \( \Psi ' \circ \Phi '\) is \(C''\)-close to \(\mathrm {Id}_{\mathcal A'}\) for \(C'':=\rho ^2(\alpha _n(L))+\rho (C_n)+2{\kappa _4}\).
\(\bullet \) For the other direction,  implies:
implies:

Hence for any \(\vec {y}=(y_1, \ldots , y_n) \in [{\mathbf {0}},x_1]\times \cdots \times [{\mathbf {0}}, x_n]\), we have

where the final estimate follows from Lemma 2.14(3).
On the other hand, since \(\langle e_i,{\mathbf {0}},e_j\rangle \thicksim _L {\mathbf {0}}\) for \(i\ne j\), we have
This implies that
In other words, \(\langle x_i,{\mathbf {0}},x_j\rangle \thicksim _{\beta _n(L)}{\mathbf {0}}\) for \(\beta _n(L):=\rho (\rho (L)+\rho ({\kappa _4})+{\kappa _4})+\rho ({\kappa _4})+{\kappa _4}\). Notice that  , so for \(j\not = i\) we have
, so for \(j\not = i\) we have
Now using the same arguments as in the proof of Theorem 4.11, we obtain that for the constant
we have

Therefore \(\Phi ' \circ \Psi '\) is \(D'\)-close to \(\mathrm {Id}_{{\mathcal {B}}'}\) for
Finally setting \(\rho _+'=\rho _+\) and \(C'=\max \{C,C'',nD'\}\), we finish the proof. \(\square \)
4.3 Rank and coarse interval growth
In this subsection, we will give a characterisation of rank in terms of interval growth as a converse to a result of Bowditch from [7].
First we notice that the cardinality of intervals can always be bounded in terms of the distance between its endpoints in the context of bounded geometry coarse median spaces.
Lemma 4.13
Let  be a coarse median space with parameters \((\rho , {\kappa _4}, {\kappa _5})\). If \(a,b\in X\) with \(d(a,b) \leqslant r\), then \([a,b] \subseteq B(a,\rho (r))\). If in addition (X, d) has bounded geometry, then there exists a constant C(r) such that \(\sharp [a,b] \leqslant C(r)\).
be a coarse median space with parameters \((\rho , {\kappa _4}, {\kappa _5})\). If \(a,b\in X\) with \(d(a,b) \leqslant r\), then \([a,b] \subseteq B(a,\rho (r))\). If in addition (X, d) has bounded geometry, then there exists a constant C(r) such that \(\sharp [a,b] \leqslant C(r)\).
Proof
For any \(c\in [a,b]\), there exists some \(x\in X\) such that  . Now by axiom (C1), we have
. Now by axiom (C1), we have

which implies \(c\in B(a,\rho (r))\). The second statement follows directly by the definition of bounded geometry. \(\square \)
For the remainder of this section, we will specialise to the context of uniformly discrete quasi-geodesic coarse median spaces with bounded geometry. Recall that for a metric space (X, d) and \(C>0\), the Rips complex is the simplicial complex, in which \(\sigma =[x_0,x_1,\ldots ,x_n]\) is an n-simplex for \(x_0,x_1,\ldots ,x_n \in X\) if and only if \(d(x_i,x_j) \leqslant C\).
Bowditch proved in [7] that for a uniformly discrete coarse median space of bounded geometry and finite rank, there is a polynomial bound on growth within intervals. Now given an interval [a, b] in such a space X with parameters \((K,H_0,{\kappa _4},{\kappa _5})\), any point \(x\in [a,b]\) can be written in the form  . Hence
. Hence

which implies that \(\mathrm {diam}\,([a,b]) \leqslant 2Kd(a,b)+2H_0\). Taking the subset \(Q=[a,b]\subseteq [a,b]_{\kappa _4}\) (where \([a,b]_{\kappa _4}\) is Bowditch’s definition of coarse interval), we obtain the following as a corollary to Bowditch’s result [7, Proposition 9.8].
Proposition 4.14
Let  be a uniformly discrete quasi-geodesic coarse median space with bounded geometry and rank at most n. Then there is a function \(p: {\mathbb {N}} \rightarrow {\mathbb {N}}\) with \(p(r)=o(r^{n+\epsilon })\) for all \(\epsilon >0\), such that \(\sharp [a,b] \leqslant p(d(a,b))\) for any \(a,b\in X\).
be a uniformly discrete quasi-geodesic coarse median space with bounded geometry and rank at most n. Then there is a function \(p: {\mathbb {N}} \rightarrow {\mathbb {N}}\) with \(p(r)=o(r^{n+\epsilon })\) for all \(\epsilon >0\), such that \(\sharp [a,b] \leqslant p(d(a,b))\) for any \(a,b\in X\).
Proof
Bowditch proved this result in the context that X is a connected bounded valency graph with edge-path metric. We replace our metric d with the edge-path metric provided by the Rips complex. Since the metric space (X, d) is quasi-geodesic and has bounded geometry, taking the Rips parameter sufficiently large ensures that this metric provides X with the structure of a connected bounded valency graph as required. Furthermore this new metric \(d'\) is quasi-isometric to d, again using the fact that the space is quasi-geodesic. Applying Bowditch’s result, \(\sharp [a,b]\) is \(o(r^{n+\epsilon })\) where \(r=d'(a,b)\). Since d is \(O(d')\) the result follows. \(\square \)
We now provide a converse to Bowditch’s theorem, showing that this growth condition indeed characterises the rank.
Theorem 4.15
Let  be a uniformly discrete, quasi-geodesic coarse median space with bounded geometry and n be a natural number. The following are equivalent:
be a uniformly discrete, quasi-geodesic coarse median space with bounded geometry and n be a natural number. The following are equivalent:
-
(1)
 has rank at most n.
has rank at most n. -
(2)
there is a function \(p: {\mathbb {R}}^{+}\rightarrow {\mathbb {R}}^{+}\) with \(p(r)=o(r^{n+\epsilon })\) for all \(\epsilon >0\), such that \(\sharp ~ [a,b] \leqslant p(d(a,b))\) for any \(a,b\in X\).
-
(3)
there is a function \(p: {\mathbb {R}}^{+}\rightarrow {\mathbb {R}}^{+}\) with \(p(r)/r^{n+1}{\mathop {\longrightarrow }\limits ^{r\rightarrow \infty }}0\), such that \(\sharp ~ [a,b] \leqslant p(d(a,b))\) for any \(a,b\in X\).
Proof of Theorem 4.15
\((1)\Rightarrow (2)\) is given by Proposition 4.14, while \((2)\Rightarrow (3)\) a fortiori. For \((3) \Rightarrow (1)\), suppose X is \((\alpha ,\beta )\hbox {-}quasi\hbox {-}geodesic,\) \((K,H_0, {\kappa _4}, {\kappa _5})\) are parameters of X and \(\mathrm {rank}\,X>n\) (note that we do not assume X has finite rank). By Theorem 2.11, there exists a constant \(L_0>0\), such that for any \(C>0\), there exists an \(L_0\)-coarse cube \(\sigma : I^{n+1} \rightarrow X\) with \(d(\sigma ({\bar{e}}_i),\sigma ({\bar{{\mathbf {0}}}}))>C\) for all i. After setting \({\mathbf {0}}:=\sigma ({\bar{{\mathbf {0}}}}), {\mathbf {1}}:=\sigma ({\bar{{\mathbf {1}}}})\) and \(e_i:=\sigma ({\bar{e}}_i)\) for each i, we have \(d(e_i,{\mathbf {0}})>C\).
Now choose a discrete \((\alpha , \beta )\)-quasi-geodesic \({\mathbf {0}}=p_0, \ldots p_k=e_i\) and construct \(q_j=\langle {\mathbf {0}},p_j,e_i\rangle \) to get a sequence of points in \([{\mathbf {0}}, e_i]\) with \(d(q_j, q_{j-1})\leqslant G\) where \(G=K(\alpha +\beta )+H_0\) is independent of C. Since \(d({\mathbf {0}}, q_0)=0\) and \(d({\mathbf {0}}, q_k)>C\), we may choose the first j such that \(d({\mathbf {0}}, q_j)\geqslant C\) and for this j we also have \(d({\mathbf {0}}, q_j)<C+G\). Setting \(x_i:=q_j\in [{\mathbf {0}}, e_i]\), we have \(C\leqslant d({\mathbf {0}}, x_i)<C+G\).
Choose a discrete \((\alpha ,\beta )\)-quasi-geodesic \(z_0,z_1,\ldots ,z_k\in X\) connecting \({\mathbf {0}}\) and \(x_1\). Projecting \(z_i\) into \([{\mathbf {0}},x_1]\), we obtain a sequence \({\mathbf {0}}=y_0,y_1,\ldots ,y_k=x_1\) with \(d(y_i,y_{i-1}) \leqslant {G}\), where  . We will inductively “de-loop” this sequence to define a subsequence \(y_{j_0},\ldots ,y_{j_l}\) such that the points in it are distinct, but still satisfy \(d(y_{j_p},y_{j_{p-1}}) \leqslant {G}\). Let \(j_0\) be the maximal index such that \(y_{j_0}=y_0\). Then for \(l>0\), set \(j_p\) to be the maximal index such that \(y_{j_p}=y_{j_{p-1}+1}\) to obtain the required sequence. This process allows us to assume that we have picked the sequence \({\mathbf {0}}=y_0,y_1,\ldots ,y_l=x_1\) to be distinct while ensuring that \(d(y_i,y_{i-1}) \leqslant {G}\) for each i. Now we have:
. We will inductively “de-loop” this sequence to define a subsequence \(y_{j_0},\ldots ,y_{j_l}\) such that the points in it are distinct, but still satisfy \(d(y_{j_p},y_{j_{p-1}}) \leqslant {G}\). Let \(j_0\) be the maximal index such that \(y_{j_0}=y_0\). Then for \(l>0\), set \(j_p\) to be the maximal index such that \(y_{j_p}=y_{j_{p-1}+1}\) to obtain the required sequence. This process allows us to assume that we have picked the sequence \({\mathbf {0}}=y_0,y_1,\ldots ,y_l=x_1\) to be distinct while ensuring that \(d(y_i,y_{i-1}) \leqslant {G}\) for each i. Now we have:
which implies \(\sharp [{\mathbf {0}},x_1] \geqslant l\geqslant {CG^{-1}}\). Similar estimate holds for each \([{\mathbf {0}},x_i]\). Hence we obtain that for the constant \(\gamma :={G}^{-(n+1)}\),
Now set  . By Corollary 4.12, there exists:
. By Corollary 4.12, there exists:
-
a constant \(\lambda _0:=\max \{K', H'_0, C'\}\), depending only on \(n,L_0\) and parameters of the space;
-
a \((\lambda _0t+\lambda _0,\lambda _0)\)-coarse median isomorphism
$$\begin{aligned} \Psi ':[{\mathbf {0}},x_1]\times \cdots \times [{\mathbf {0}},x_{n+1}] \rightarrow [{\mathbf {0}},x]. \end{aligned}$$
In particular for any \(\vec {z},\vec {y} \in [{\mathbf {0}},x_1]\times \cdots \times [{\mathbf {0}},x_{n+1}]\) we have:
Since X has bounded geometry, there exists a constant N depending only on \(\lambda _0\) such that \(\sharp \Psi '^{-1}(\{y\}) \leqslant N\) for any \(y\in [{\mathbf {0}},x]\). In other words, \(\Psi '\) may collapse at most N points to a single point. Hence \(\sharp \Psi '(A) \geqslant \frac{1}{N}\sharp A\) for any \(A\subseteq [{\mathbf {0}},x_1]\times \cdots \times [{\mathbf {0}},x_{n+1}]\). In particular, we have
Now we would like to estimate the distance \(d({\mathbf {0}},x)\) and show that it is approximately linear in C. First notice that \(\Psi '(\vec {0})={\mathbf {0}}\) and by definition we have

where the estimate in the third line follows from Lemma 2.16 and the constant \(E_n\) depends only on \(n,\lambda _0\) and \({\kappa _4}\). Combining with (7), we have:
After rearranging, we get
Combining with (8), we obtain:
On the other hand, (7) implies that
So \(d({\mathbf {0}},x) \rightarrow \infty \) as \(C \rightarrow \infty \).
Therefore for any \(C>0\) we have constructed an interval \([{\mathbf {0}},x]\) such that the distance \(d({\mathbf {0}},x)\) goes to infinity as \(C \rightarrow \infty \), and the cardinality \(\sharp [{\mathbf {0}},x]\) is bounded below by a polynomial of degree \(n+1\) in \(d({\mathbf {0}},x)\) with positive leading coefficient \(\frac{\gamma }{N(\lambda _0(n+1))^{n+1}}\). This contradicts the existence of the function p. \(\square \)
Theorem 4.15 allows us to characterise the rank of a coarse interval space purely in terms of the growth of intervals:
Corollary 4.16
A uniformly discrete, bounded geometry, quasi-geodesic coarse interval space \((X, d,[\cdot ,\cdot ])\) has rank at most n if and only if there is a function \(p\,{:}\,{\mathbb {R}}^{+}\rightarrow {\mathbb {R}}^{+}\) with \(\lim \nolimits _{r\rightarrow \infty }p(r)/r^{n+1}=0\), such that \(\sharp [a,b] \leqslant p(d(a,b))\) for any \(a,b\in X\).
5 Intervals and metrics for ternary algebras
Bowditch observed that perturbing the metric for a coarse median space up to quasi-isometry respects the coarse median axioms. It is not, however, a priori obvious the extent to which the metric is determined by the coarse median operator. We will now show that for a quasi-geodesic coarse median space  of bounded geometry the metric is determined uniquely up to quasi-isometry by
of bounded geometry the metric is determined uniquely up to quasi-isometry by  . This motivates our definition of coarse median algebra, as given in the introduction.
. This motivates our definition of coarse median algebra, as given in the introduction.
To establish the uniqueness of the metric, we will construct a canonical metric defined purely in terms of the intervals associated to the coarse median operator. The construction may be of independent interest since it can be defined for any ternary operator satisfying some weakening of axioms (M1) and (M2), and therefore in the context of a more general notion of interval structure. (The following reversal axiom can in fact be weakened to the existence of bijections between the corresponding intervals [a, b] and [b, a].)
5.1 Abstract ternary algebras and induced metrics
Consider a ternary algebra  satisfying the following axioms:
satisfying the following axioms:
- (T1):
-
Majority vote:
 for all \(a,x\in X\);
for all \(a,x\in X\); - (T2):
-
Reversal:
 for all \(a,x,b\in X\).
for all \(a,x,b\in X\).
Classically it is natural to think of the ternary operator  as furnishing a notion of betweenness, whereby c lies between a, b if and only if
as furnishing a notion of betweenness, whereby c lies between a, b if and only if  . This definition is not well adapted to the coarse world, where statements are typically true up to controlled distortion. Regarding the operation
. This definition is not well adapted to the coarse world, where statements are typically true up to controlled distortion. Regarding the operation  instead as providing a projection onto the interval
instead as providing a projection onto the interval  is better suited to this environment.
is better suited to this environment.
Axiom (T1) ensures that the interval [a, a] is the singleton \(\{a\}\) while axiom (T2) ensures that \([a,b]=[b,a]\). These axioms together are a slight weakening of axioms (M1) and (M2) for a (coarse) median algebra.
Example 5.1
Let \(\Gamma \) be a connected graph and for any \(a,b,x\in V(\Gamma )\) choose a vertex, denoted  , which lies on an edge geodesic from a to b and minimises distance to x among all such choices. Clearly we can do so to satisfy axiom (T2), while axiom (T1) is immediate. With this definition of the ternary operator, the interval [a, b] is exactly the set of vertices on edge geodesics from a to b.
, which lies on an edge geodesic from a to b and minimises distance to x among all such choices. Clearly we can do so to satisfy axiom (T2), while axiom (T1) is immediate. With this definition of the ternary operator, the interval [a, b] is exactly the set of vertices on edge geodesics from a to b.
We will use cardinalities of intervals to measure distances. In order to ensure that these distances are finite, we need to impose a condition that points can be joined by chains of finite intervals.
Definition 5.2
A ternary algebra  is said to satisfy the finite interval chain condition, if for any \(a,b\in X\) there exists a sequence \(a=x_0, x_1, \ldots , x_n:=b\) in X such that the cardinality of each interval \([x_i, x_{i+1}]\) is finite for \(i=0,1,\ldots , n-1\).
is said to satisfy the finite interval chain condition, if for any \(a,b\in X\) there exists a sequence \(a=x_0, x_1, \ldots , x_n:=b\) in X such that the cardinality of each interval \([x_i, x_{i+1}]\) is finite for \(i=0,1,\ldots , n-1\).
Definition 5.3
Given a ternary algebra  satisfying the finite interval chain condition, we define the induced function
satisfying the finite interval chain condition, we define the induced function  on \(X\times X\) as follows: for any \(a,b \in X\),
on \(X\times X\) as follows: for any \(a,b \in X\),

It is routine to check that  satisfies the triangle inequality. The imposition of axioms (T1) and (T2) ensure that the function
satisfies the triangle inequality. The imposition of axioms (T1) and (T2) ensure that the function  also satisfies the obvious symmetry, reflexivity and positivity conditions so that
also satisfies the obvious symmetry, reflexivity and positivity conditions so that  is a metric in this case. When (T1) and (T2) are satisfied we will refer to
is a metric in this case. When (T1) and (T2) are satisfied we will refer to  as the induced metric.
as the induced metric.
Example 5.4
Let  be a discrete median algebra and let Z be its geometric realisation as a CAT(0) cube complex. Then the induced metric
be a discrete median algebra and let Z be its geometric realisation as a CAT(0) cube complex. Then the induced metric  is the edge-path metric on the vertices of Z.
is the edge-path metric on the vertices of Z.
Example 5.5
Let \(\Gamma \) be a connected graph and  the projection operator defined in Example 5.1. Then the induced metric
the projection operator defined in Example 5.1. Then the induced metric  is the edge-path metric on the vertices of \(\Gamma \).
is the edge-path metric on the vertices of \(\Gamma \).
5.2 Uniqueness of coarse median metrics
It is easy to show that one can change the metric of a coarse median space arbitrarily within its quasi-isometry class. It is a remarkable fact, as we will now show, that the quasi-isometry class of the metric is determined uniquely by the coarse median operator. Indeed the induced metric is the unique coarse median metric up to quasi-isometry:
Theorem 5.6
For a bounded geometry quasi-geodesic coarse median space  , the metric d is quasi-isometric to the induced metric
, the metric d is quasi-isometric to the induced metric  .
.
As an immediate corollary we have the following:
Theorem 1.5. For a bounded geometry quasi-geodesic coarse median space  , the metric d is unique up to quasi-isometry.
, the metric d is unique up to quasi-isometry.
Proof of Theorem 5.6
Let  be an (L, C)-quasi-geodesic coarse median space with bounded geometry and parameters \((K, H_0, {}{\kappa _4},{\kappa _5})\).
be an (L, C)-quasi-geodesic coarse median space with bounded geometry and parameters \((K, H_0, {}{\kappa _4},{\kappa _5})\).
First we will show that d can be controlled by  . Given \(a,b\in X\), let \(a=a_0,\ldots ,a_n=b\) be a sequence of points such that
. Given \(a,b\in X\), let \(a=a_0,\ldots ,a_n=b\) be a sequence of points such that

Fix i and choose an (L, C)-quasi-geodesic \(\gamma _i\) with respect to the metric d connecting \(a_{i-1}\) and \(a_i\). If \(n_i=\lfloor d(a_{i-1},a_i) \rfloor \), the integer part of \(d(a_{i-1},a_i)\), and
then \(d(x_{i-1},x_i) \leqslant L+C\). Letting \(y_j=\langle a_{i-1},a_i,x_j\rangle \in [a_{i-1},a_i]\), axiom (C1) ensures that \(d(y_{j-1},y_j) \leqslant K(L+C)+H_0\). We set \(C':=K(L+C)+H_0\).
As in the proof of Theorem 4.15 we can “de-loop” the sequence \(y_0,y_1,\ldots ,y_{n_i+1}\) to a subsequence \(y_{j_0},\ldots ,y_{j_l}\) in \([a_{i-1},a_i]\) with the property that the points in it are distinct, but still satisfy \(d(y_{j_k},y_{j_{k-1}}) \leqslant C'\). Hence we have
The same estimate holds for other i as well. Therefore we obtain that

Second we will show that  can be controlled by d. For any \(a,b\in X\) choose an (L, C)-quasi-geodesic \(\gamma \) with respect to the metric d connecting them, and take \(a_i=\gamma (i)\) for \(i=0,1,\ldots ,n-1=\lfloor d(a,b) \rfloor \) and \(a_n=\gamma (d(a,b))\), which implies \(d(a_{i-1},a_i) \leqslant L+C\). By Lemma 4.13 there exists a constant \(C''\) (depending on \(L+C\)) such that the intervals \([a_{i-1},a_i]\) all have cardinality at most \(C''\). Hence we have
can be controlled by d. For any \(a,b\in X\) choose an (L, C)-quasi-geodesic \(\gamma \) with respect to the metric d connecting them, and take \(a_i=\gamma (i)\) for \(i=0,1,\ldots ,n-1=\lfloor d(a,b) \rfloor \) and \(a_n=\gamma (d(a,b))\), which implies \(d(a_{i-1},a_i) \leqslant L+C\). By Lemma 4.13 there exists a constant \(C''\) (depending on \(L+C\)) such that the intervals \([a_{i-1},a_i]\) all have cardinality at most \(C''\). Hence we have

In conclusion we have shown that for any \(a,b\in X\),

This completes the proof. \(\square \)
Without the assumption that (X, d) is quasi-geodesic, Theorem 1.5 fails. Indeed (X, d) can have bounded geometry and  have balls of infinite cardinality as the following example shows:
have balls of infinite cardinality as the following example shows:
Example 5.7
Let \(F_\infty \) be the free group on countably many generators \(\{g_i\}\). The Cayley graph of \(F_\infty \) is a tree and therefore the group admits a median  . Note that the induced metric
. Note that the induced metric  is the edge-path metric on the Cayley graph. With this metric \(F_\infty \) is a coarse median space which does not have bounded geometry since each of the intervals \([e, g_i]\) has cardinality 2. However, for d a proper left invariant metric on \(F_\infty \) (e.g., setting \(d(g_i,e)=i\)), the space
is the edge-path metric on the Cayley graph. With this metric \(F_\infty \) is a coarse median space which does not have bounded geometry since each of the intervals \([e, g_i]\) has cardinality 2. However, for d a proper left invariant metric on \(F_\infty \) (e.g., setting \(d(g_i,e)=i\)), the space  is again a coarse median space. With this metric the space has bounded geometry. Hence
is again a coarse median space. With this metric the space has bounded geometry. Hence  admits two coarse median metrics which are not quasi-isometric.
admits two coarse median metrics which are not quasi-isometric.
Remark 5.8
If we just focus on uniformly discrete metrics, then it is clear that “quasi-isometry” can be replaced by “bi-Lipschitz equivalence” in Theorem 1.5.
6 Coarse median algebras
We have seen that intervals play a key role in determining the structure and geometry of a coarse median space. In particular, as shown in Theorem 1.5, for a quasi-geodesic coarse median space of bounded geometry the metric is determined by the interval structure and is therefore redundant in the description. This leads us to the following purely algebraic notion of coarse median algebra.
Definition 1.3. A coarse median algebra is a ternary algebra  with finite intervals such that:
with finite intervals such that:
-
(M1)
For all \(a,b\in X, \);
-
(M2)
For all \(a,b,c\in X, \);
-
(M3)’
There exists a constant \(K\geqslant 0\) such that for all \(a,b,c,d,e\in X\) the cardinality of the interval
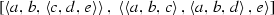 is at most K.
is at most K.
As remarked in the introduction if we take \(K=1\) then this reduces to the classical definition of a discrete median algebra.
6.1 Bounded geometry for a ternary algebra
Definition 6.1
A ternary algebra  is said to have bounded valency if there is a function \(\phi :{\mathbb {R}}^+\rightarrow {\mathbb {R}}^+\) such that for all \(x\in X\), we have
is said to have bounded valency if there is a function \(\phi :{\mathbb {R}}^+\rightarrow {\mathbb {R}}^+\) such that for all \(x\in X\), we have
The terminology is motivated by the example of a median graph, where bounded valency in our sense agrees with its classical meaning.
Lemma 6.2
Let  be a ternary algebra satisfying (T1) and (T2) together with the finite interval chain condition. Then it has bounded valency if and only if the induced metric
be a ternary algebra satisfying (T1) and (T2) together with the finite interval chain condition. Then it has bounded valency if and only if the induced metric  has bounded geometry.
has bounded geometry.
Proof
Fix \(x\in X\) and \(R>1\). Since  , we have
, we have
Hence bounded geometry of  implies bounded valency. On the other hand, suppose X has bounded valency with parameter \(\phi \). For any \(y\in B_R(x)\) there is an interval chain \(x=x_0, \ldots , x_n=y\) with \(n\leqslant R\) and such that each interval \([x_i, x_{i+1}]\) has at most \(R+1\) points. It follows that given \(x_i\) the number of possible choices for \(x_{i+1}\) is at most \(\phi (R+1)\), so \(B_R(x)\) has cardinality at most \(\phi (R+1)^R\). \(\square \)
implies bounded valency. On the other hand, suppose X has bounded valency with parameter \(\phi \). For any \(y\in B_R(x)\) there is an interval chain \(x=x_0, \ldots , x_n=y\) with \(n\leqslant R\) and such that each interval \([x_i, x_{i+1}]\) has at most \(R+1\) points. It follows that given \(x_i\) the number of possible choices for \(x_{i+1}\) is at most \(\phi (R+1)\), so \(B_R(x)\) has cardinality at most \(\phi (R+1)^R\). \(\square \)
Theorem 1.4. Let  be a bounded valency ternary algebra. The following are equivalent:
be a bounded valency ternary algebra. The following are equivalent:
-
(1)
 is a coarse median algebra;
is a coarse median algebra; -
(2)
 is a coarse median space;
is a coarse median space; -
(3)
There exists a metric d such that
 is a bounded geometry coarse median space.
is a bounded geometry coarse median space.
Proof
\((1)\Rightarrow (2)\): Suppose  is a bounded valency coarse median algebra. We impose the induced metric
is a bounded valency coarse median algebra. We impose the induced metric  , which has bounded geometry by Lemma 6.2. Axiom (M3)\(^{\prime }\) gives us an upper bound on the distance between the two iterated medians,
, which has bounded geometry by Lemma 6.2. Axiom (M3)\(^{\prime }\) gives us an upper bound on the distance between the two iterated medians,  and
and  , which specialises to the 4-point axiom (C2) by setting \(y=b\). It only remains to establish axiom (C1).
, which specialises to the 4-point axiom (C2) by setting \(y=b\). It only remains to establish axiom (C1).
To do so, we choose a finite interval chain \(a=x_0, \ldots , x_n=a'\) which realises the distance  . For each i, let
. For each i, let  and consider the interval chain
and consider the interval chain  which gives an upper bound for
which gives an upper bound for  . For each point
. For each point

in the interval \([y_i, y_{i+1}]\), the interval from \(\langle z, y_i, y_{i+1}\rangle \) to  has cardinality at most K by axiom (M3)\(^{\prime }\). Clearly the set
has cardinality at most K by axiom (M3)\(^{\prime }\). Clearly the set  has cardinality bounded by the cardinality of \([x_i, x_{i+1}]\). So by bounded valency, the interval \([y_i, y_{i+1}]\) has cardinality bounded by \(\phi (K) \cdot \sharp [x_i,x_{i+1}]\). It follows that
has cardinality bounded by the cardinality of \([x_i, x_{i+1}]\). So by bounded valency, the interval \([y_i, y_{i+1}]\) has cardinality bounded by \(\phi (K) \cdot \sharp [x_i,x_{i+1}]\). It follows that

Therefore  is a coarse median space.
is a coarse median space.
\((2)\Rightarrow (3)\): This is trivial.
\((3)\Rightarrow (1)\): Suppose there exists a bounded geometry metric d on X such that  is a coarse median space. As remarked after Definition 2.6, the five point condition in Eq. (2) holds up to some constant \({\kappa _5}'\). Hence Lemma 4.13 implies that (M3)\(^{\prime }\) holds for the constant \({\kappa _5}=C({\kappa _5}')\) where C is the function provided therein. Therefore
is a coarse median space. As remarked after Definition 2.6, the five point condition in Eq. (2) holds up to some constant \({\kappa _5}'\). Hence Lemma 4.13 implies that (M3)\(^{\prime }\) holds for the constant \({\kappa _5}=C({\kappa _5}')\) where C is the function provided therein. Therefore  is a coarse median algebra. \(\square \)
is a coarse median algebra. \(\square \)
Remark 6.3
While it is tempting to conflate the ideas of bounded geometry and bounded valency in this context, some care should be taken in the general world of coarse median spaces. In this context the metric is only loosely associated with the median structure as illustrated by Example 5.7: the free group \(F_\infty \), equipped with a proper left invariant metric and its natural median, is a coarse median space which has bounded geometry but not bounded valency. Of course this example is not quasi-geodesic and as we saw in Theorem 1.5 we have much better control in the quasi-geodesic world.
6.2 Quasi-geodesic ternary algebras
Definition 6.4
A ternary algebra  satisfying (T1) and (T2) is said to be quasi-geodesic if there exist constants \(L,C>0\) such that for any \(a,b\in X\), there exist \(a=y_0,\ldots ,y_n=b\) with \(\sharp [y_j,y_{j+1}] \leqslant C+1\) and \(n \leqslant L\sharp [a,b]\).
satisfying (T1) and (T2) is said to be quasi-geodesic if there exist constants \(L,C>0\) such that for any \(a,b\in X\), there exist \(a=y_0,\ldots ,y_n=b\) with \(\sharp [y_j,y_{j+1}] \leqslant C+1\) and \(n \leqslant L\sharp [a,b]\).
Note that the finite interval chain condition is subsumed in this definition so does not need to be imposed separately.
This definition has a natural interpretation in the terms of the following analogue of the classical Rips Complex.
Definition 6.5
For  a ternary algebra, let
a ternary algebra, let  denote the simplicial complex in which \(\sigma =[x_0,x_1,\ldots ,x_n]\) is an n-simplex for \(x_0,x_1,\ldots ,x_n \in X\) if and only if \(\sharp [x_i,x_j] \leqslant C+1\).
denote the simplicial complex in which \(\sigma =[x_0,x_1,\ldots ,x_n]\) is an n-simplex for \(x_0,x_1,\ldots ,x_n \in X\) if and only if \(\sharp [x_i,x_j] \leqslant C+1\).
Recall for comparison that if (X, d) is a metric space then for \(C>0\) the Rips complex is the simplicial complex, in which \(\sigma =[x_0,x_1,\ldots ,x_n]\) is an n-simplex for \(x_0,x_1,\ldots ,x_n \in X\) if and only if \(d(x_i,x_j) \leqslant C\).
When the complex  is connected, its vertex set X inherits the edge-path metric which is of course a geodesic metric, denoted \(d_{P_C}\).
is connected, its vertex set X inherits the edge-path metric which is of course a geodesic metric, denoted \(d_{P_C}\).
Proposition 6.6
Let  be a ternary algebra satisfying conditions (T1) and (T2) together with the finite interval chain condition. Let
be a ternary algebra satisfying conditions (T1) and (T2) together with the finite interval chain condition. Let  denote the induced metric . Then the following are equivalent:
denote the induced metric . Then the following are equivalent:
-
(1)
The metric
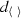 is quasi-geodesic.
is quasi-geodesic. -
(2)
The ternary algebra
 is quasi-geodesic.
is quasi-geodesic. -
(3)
There exists \(C>0\) such that the complex
 is connected and
is connected and  is bi-Lipschitz to the edge-path metric \(d_{P_C}\) on the complex.
is bi-Lipschitz to the edge-path metric \(d_{P_C}\) on the complex.
Proof
\((1) \Rightarrow (2)\): Assume  is \((L',C')\)-quasi-geodesic and \(a\ne b\in X\). Let \(\gamma : [0,m] \rightarrow X\) be an \((L',C')\)-quasi-isometric embedding with \(\gamma (0)=a\) and \(\gamma (m)=b\). Without loss of generality we may take m to be an integer. Let \(x_i=\gamma (i)\) and note that
is \((L',C')\)-quasi-geodesic and \(a\ne b\in X\). Let \(\gamma : [0,m] \rightarrow X\) be an \((L',C')\)-quasi-isometric embedding with \(\gamma (0)=a\) and \(\gamma (m)=b\). Without loss of generality we may take m to be an integer. Let \(x_i=\gamma (i)\) and note that  . On the other hand
. On the other hand  so
so  , where \(L''=L'+L'C'\).
, where \(L''=L'+L'C'\).
Now fix i and take a chain \(y_i^0,\dots y_i^{n_i}\) realising the distance from \(x_i\) to \(x_{i+1}\), i.e.,

Since  it follows that each set \([y_i^j,y_i^{j+1}]\) has cardinality at most \(C+1\).
it follows that each set \([y_i^j,y_i^{j+1}]\) has cardinality at most \(C+1\).
Furthermore, without loss of generality, we may assume that \(y_i^j\ne y_i^{j+1}\) for each j, which implies  . Concatenating these chains gives the required chain from a to b. Putting \(L=CL''\), the number of terms is:
. Concatenating these chains gives the required chain from a to b. Putting \(L=CL''\), the number of terms is:

\((2) \Rightarrow (3)\): Assuming  is (L, C)-quasi-geodesic, the Rips complex
is (L, C)-quasi-geodesic, the Rips complex  is connected. If \(d_{P_C}(a,b)=n\) then there exist \(x_0=a,x_1,\ldots ,x_n=b\) with each interval \([x_{i-1},x_i]\) having cardinality at most \(C+1\), and hence
is connected. If \(d_{P_C}(a,b)=n\) then there exist \(x_0=a,x_1,\ldots ,x_n=b\) with each interval \([x_{i-1},x_i]\) having cardinality at most \(C+1\), and hence

Now we fix \(a,b\in X\) and choose mutually different points \(a=z_0, z_1, \ldots , z_{k-1}, z_k=b\) in X such that

For each \(i=0,1,\ldots ,k-1\), applying condition (2) to \(z_i, z_{i+1}\) produces a number \(k_i \in {\mathbb {N}}\) and points \(z_i=w_i^0,w_i^1,\ldots ,w_i^{k_i-1}, w_i^{k_i}=z_{i+1}\) in X with \(\sharp [w_i^j,w_i^{j+1}] \leqslant C+1\) and \(k_i \leqslant L\sharp [z_i, z_{i+1}]\). Since \(\sharp [z_i, z_{i+1}] \geqslant 2\), we have \(\sharp [z_i, z_{i+1}] \leqslant 2(\sharp [z_i, z_{i+1}]-1)\). Hence

Concatenating these chains provides a chain \(a=w_0,w_1,\ldots ,w_p=b\) with \(\sharp [w_i,w_{i+1}] \leqslant C+1\) and  , which gives an upper bound
, which gives an upper bound

\((3)\Rightarrow (1)\): As \(d_{P_C}\) is geodesic it follows that  is quasi-geodesic. \(\square \)
is quasi-geodesic. \(\square \)
Combining Theorem 1.4 with Proposition 6.6 and Theorem 1.5, we obtain:
Theorem 6.7
A ternary algebra is a bounded valency quasi-geodesic coarse median algebra if and only if it admits a bounded geometry, quasi-geodesic coarse median metric. Such a metric, when it exists, is unique up to quasi-isometry.
Proof
For a bounded valency quasi-geodesic coarse median algebra  , Theorem 1.4 implies that the triple
, Theorem 1.4 implies that the triple  is a coarse median space of bounded geometry, where
is a coarse median space of bounded geometry, where  is the induced metric. Now Proposition 6.6 implies that
is the induced metric. Now Proposition 6.6 implies that  is quasi-geodesic.
is quasi-geodesic.
Conversely, for a bounded geometry quasi-geodesic coarse median metric  , Theorem 1.5 implies that d is quasi-isometric to the induced metric
, Theorem 1.5 implies that d is quasi-isometric to the induced metric  . Hence Lemma 6.2 implies that
. Hence Lemma 6.2 implies that  has bounded valency and Proposition 6.6 implies that
has bounded valency and Proposition 6.6 implies that  is quasi-geodesic. \(\square \)
is quasi-geodesic. \(\square \)
6.3 The rank of a coarse median algebra
Motivated by Theorem 4.1, we make the following definition.
Definition 6.8
A coarse median algebra  is said to have rank at most n if there is a non-decreasing function \(\varphi : {\mathbb {R}}^{+}\rightarrow {\mathbb {R}}^{+}\) such that for any \(x_1,\ldots ,x_{n+1}\) and \(p,q \in X\), we have
is said to have rank at most n if there is a non-decreasing function \(\varphi : {\mathbb {R}}^{+}\rightarrow {\mathbb {R}}^{+}\) such that for any \(x_1,\ldots ,x_{n+1}\) and \(p,q \in X\), we have

Lemma 6.9
The rank of a bounded valency coarse median algebra  agrees with the rank of the corresponding coarse median space
agrees with the rank of the corresponding coarse median space  provided by Theorem 1.4.
provided by Theorem 1.4.
Proof
Lemma 4.13 provides a non-decreasing function \(C:{\mathbb {R}}^{+}\rightarrow {\mathbb {R}}^{+}\) such that

If the coarse median algebra  has rank at most n, then by definition there exists a non-decreasing \(\varphi :{\mathbb {R}}^{+}\rightarrow {\mathbb {R}}^{+}\) such that for any \(x_1,\ldots ,x_{n+1}\) and \(p,q \in X\),
has rank at most n, then by definition there exists a non-decreasing \(\varphi :{\mathbb {R}}^{+}\rightarrow {\mathbb {R}}^{+}\) such that for any \(x_1,\ldots ,x_{n+1}\) and \(p,q \in X\),

So by Theorem 4.1 the coarse median space  has rank at most n.
has rank at most n.
Conversely if the coarse median space  has rank at most n, then by Theorem 4.1 there exists a non-decreasing \(\varphi :{\mathbb {R}}^{+}\rightarrow {\mathbb {R}}^{+}\) such that for any \(x_1,\ldots ,x_{n+1}\) and \(p,q \in X\),
has rank at most n, then by Theorem 4.1 there exists a non-decreasing \(\varphi :{\mathbb {R}}^{+}\rightarrow {\mathbb {R}}^{+}\) such that for any \(x_1,\ldots ,x_{n+1}\) and \(p,q \in X\),

So the coarse median algebra  also has rank at most n. \(\square \)
also has rank at most n. \(\square \)
It is interesting to consider this in the context of spaces of rank 1 where we obtain a correspondence between quasi-geodesic, bounded valency coarse median algebras of rank 1 and bounded geometry geodesic hyperbolic spaces up to quasi-isometry. One direction is provided by [6, Lemma 3.1] and Theorem 1.4. For the converse we have:
Theorem 6.10
Let  be a bounded valency, quasi-geodesic coarse median algebra of rank 1. Then there exists a metric d such that (X, d) is a geodesic hyperbolic metric space and its natural coarse median is uniformly close to
be a bounded valency, quasi-geodesic coarse median algebra of rank 1. Then there exists a metric d such that (X, d) is a geodesic hyperbolic metric space and its natural coarse median is uniformly close to  .
.
Proof
By Proposition 6.6 there exists \(C>0\) such that the complex  is connected and
is connected and  is bi-Lipschitz to the edge-path metric \(d_{P_C}\) on the complex. We take \(d=d_{P_C}\). Since this is geodesic [14, Theorem 4.2] shows that (quasi)-geodesics in
is bi-Lipschitz to the edge-path metric \(d_{P_C}\) on the complex. We take \(d=d_{P_C}\). Since this is geodesic [14, Theorem 4.2] shows that (quasi)-geodesics in  are close to intervals, and hence by Theorem 4.2 the slim triangle condition holds.
are close to intervals, and hence by Theorem 4.2 the slim triangle condition holds.
The natural coarse median of three points a, b, c in this hyperbolic space is chosen from the intersection of \(\delta \)-neighbourhoods of the geodesics \(\vec {ab},\vec {bc},\vec {ca}\) and is therefore in the intersection of K-neighbourhoods of the intervals [a, b], [b, c], [c, a] for some fixed K. This is a (uniformly) bounded set containing the original median, hence the new and original medians are uniformly close. \(\square \)
Notes
This is perhaps counterintuitive: firstly because interval cardinality is far from being a metric, and secondly because even in a geodesic coarse median space the geodesic between two points can lie well outside the corresponding interval (see [14, Theorem 5.1]).
Throughout the paper, we only consider the notion of bounded geometry in the setting of discrete metric spaces. See Definition 2.1(3).
References
Bandelt, H.-J., Hedlíková, J.: Median algebras. Discrete Math. 45(1), 1–30 (1983)
Bandelt, H.-J., Chepoi, V.: Metric graph theory and geometry: a survey. Contemp. Math. 453, 49–86 (2008)
Behrstock, J., Hagen, M., Sisto, A., et al.: Hierarchically hyperbolic spaces. I: Curve complexes for cubical groups. Geom. Topol. 21(3), 1731–1804 (2017)
Behrstock, J., Hagen, M.F., Sisto, A.: Hierarchically hyperbolic spaces II: combination theorems and the distance formula. arXiv preprint arXiv:1509.00632 (2015)
Birkhoff, G., Kiss, S.A.: A ternary operation in distributive lattices. Bull. Am. Math. Soc. 53(8), 749–752 (1947)
Bowditch, B.H.: Coarse median spaces and groups. Pac. J. Math. 261(1), 53–93 (2013)
Bowditch, B.H.: Embedding median algebras in products of trees. Geom. Dedic. 170(1), 157–176 (2014)
Bowditch, B.H.: Some properties of median metric spaces. Groups Geom. Dyn. 10(1), 279–318 (2016)
Bridson, M.R., Häfliger, A.: Metric spaces of non-positive curvature, volume 319 of Grundlehren der Mathematischen Wissenschaften [Fundamental Principles of Mathematical Sciences]. Springer, Berlin (1999)
Gromov, M.: Hyperbolic groups. In: Essays in Group Theory, pp. 75–263. Springer, Berlin (1987)
Jacobson, N.: Basic Algebra I. Courier Corporation, Chelmsford (2012)
Kolibiar, M., Marcisová, T.: On a question of J. Hashimoto. Mat. časopis 24(2), 179–185 (1974)
Lane, S.M.: Categories for the Working Mathematician, vol. 5. Springer, Berlin (2013)
Niblo, G.A., Wright, N., Zhang, J.: A four point characterisation for coarse median spaces. Groups Geom. Dyn. 13(3), 939–980 (2019)
Roller, M.: POC sets, median algebras and group actions. an extended study of Dunwoody’s construction and Sageev’s theorem. Southampton Preprint Archive (1998)
Sholander, M.: Medians and betweenness. Proc. Am. Math. Soc. 5(5), 801–807 (1954)
Špakula, J., Wright, N.: Coarse medians and property A. Algebr. Geom. Topol. 17(4), 2481–2498 (2017)
Zeidler, R.: Coarse median structures on groups. Master’s thesis, University of Vienna, Vienna, Austria (2013)
Acknowledgements
We would like to thank the anonymous referee for many useful suggestions to make the paper more readable.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
J. Zhang was supported for this research by a Fellowship from the Sino-British Trust, International Exchanges 2017 Cost Share (China) Grant EC/NSFC/170341, NSFC11871342 and NSFC11811530291.
Appendix A: A categorical viewpoint
Appendix A: A categorical viewpoint
To amplify and clarify the claim that coarse median spaces, coarse interval spaces and coarse median algebras are in some sense the same we will define suitable categories and show that they are equivalent.
1.1 The coarse median (space) category
Definition A.1
Let  and
and  be coarse median structures (see Definition 2.8). A map \(f: X \rightarrow Y\) is a \((\rho _+,C)\)-coarse median map if it is a C-quasi-morphism as well as a \(\rho _+\)-coarse map. As usual, we omit mentioning parameters unless we are keeping track of the values.
be coarse median structures (see Definition 2.8). A map \(f: X \rightarrow Y\) is a \((\rho _+,C)\)-coarse median map if it is a C-quasi-morphism as well as a \(\rho _+\)-coarse map. As usual, we omit mentioning parameters unless we are keeping track of the values.
Remark A.2
Note that without the assumption of coarseness for the map in this definition, it is not the case that coarse median maps compose to give coarse median maps. The issue is that while the coarse median of the three points fg(a), fg(b), fg(c) is necessarily close to the image under f of the coarse median of g(a), g(b), g(c), without requiring f to be coarse we cannot control the distance between this image and the image under fg of the coarse median  .
.
Given a set X and a metric space \((Y,d_Y)\) and functions \(f,g: X\rightarrow Y\) we will write \(f \sim g\) if f is s-close to g for some \(s\geqslant 0\). This is an equivalence relation and the equivalence class of f is denoted by [f]. Applying this to coarse median maps  on X recovers the notion of uniform closeness discussed in Section 2.
on X recovers the notion of uniform closeness discussed in Section 2.
Definition A.3
The coarse median category, denoted \(\mathcal {CM}\), is defined as follows:
-
The objects are coarse median structures
 ;
; -
Given two objects
 and
and  the morphism set is $$\begin{aligned} \mathrm {Mor}_{\mathcal {CM}}({\mathcal {X}},{\mathcal {Y}}):=\{ \text{ coarse } \text{ median } \text{ maps } \text{ from } X \text{ to } Y~\}/\sim ; \end{aligned}$$
the morphism set is $$\begin{aligned} \mathrm {Mor}_{\mathcal {CM}}({\mathcal {X}},{\mathcal {Y}}):=\{ \text{ coarse } \text{ median } \text{ maps } \text{ from } X \text{ to } Y~\}/\sim ; \end{aligned}$$ -
Compositions are induced by compositions of maps.
The coarse median space category, denoted \(\mathcal {CMS}\), is the full subcategory whose objects are coarse median spaces, i.e., those whose coarse median additionally satisfies axioms (M1) and (M2).
The objects of \(\mathcal {CM}\) are those satisfying Bowditch’s original definition [6, Section 8]. We now characterise categorical isomorphisms in a more practical way.
Lemma A.4
Let \({\mathcal {X}}, {\mathcal {Y}}\) be objects in \(\mathcal {CM}\) and \([f]\in \mathrm {Mor}_\mathcal {CM}({\mathcal {X}}, {\mathcal {Y}})\). Then [f] is an isomorphism in the category \(\mathcal {CM}\) if and only if f is a coarse equivalence.
Proof
Let  and
and  . Suppose [f] is an isomorphism in the category \(\mathcal {CM}\), i.e., there exists another coarse median map \(g: Y \rightarrow X\) such that \([f][g]=[\mathrm {Id}_Y]\) and \([g][f]=[\mathrm {Id}_X]\). Hence clearly, f is a coarse equivalence.
. Suppose [f] is an isomorphism in the category \(\mathcal {CM}\), i.e., there exists another coarse median map \(g: Y \rightarrow X\) such that \([f][g]=[\mathrm {Id}_Y]\) and \([g][f]=[\mathrm {Id}_X]\). Hence clearly, f is a coarse equivalence.
On the other hand, suppose \(f: X \rightarrow Y\) is a \((\rho _+,C)\)-coarse median map as well as a \((\rho _+,C)\)-coarse equivalence. In other words, there exists a \(\rho _+\)-coarse map \(g: Y\rightarrow X\) such that fg and gf are C-close to the identities. It suffices to show that g is a coarse median map. For any \(x,y,z\in Y, fg \thicksim _C \mathrm {Id}_Y\) implies that there exist \(a,b,c\in X\) such that \(f(a)\thicksim _C x, f(b)\thicksim _C y\) and \(f(c)\thicksim _C z\). Since g is \(\rho _+\)-bornologous, we have \(gf(a) \thicksim _{\rho _+(C)}g(x), gf(b) \thicksim _{\rho _+(C)}g(y)\) and \(gf(c) \thicksim _{\rho _+(C)}g(z)\). Let \(\rho _X,\rho _Y\) be the uniform bornology parameters of \({\mathcal {X}},{\mathcal {Y}}\) provided by (C1). Then we have

We also have

Combining these, we have

for \(C'=\rho _X(3\rho _+(C))+\rho _X(3C)+\rho _+(\rho _Y(3C))+\rho _+(C)+C\). \(\square \)
Remark A.5
Recall from Definition 2.12 that a \((\rho _+,C)\)-coarse median isomorphism f is a \((\rho _+,C)\)-coarse median map and a \((\rho _+,C)\)-coarse equivalence. Hence the previous lemma states that such an f is a \((\rho _+,C)\)-coarse median isomorphism if and only if it represents a categorical isomorphism. Any \((\rho _+,C)\)-coarse inverse g for f is a \((\rho _+,C')\)-coarse median isomorphism with the constant \(C'\) depending only on \(\rho _+,C\) and parameters of X, Y. And in this case, [g] is a categorical inverse of [f].
We now discuss the relationship between the categories of coarse median spaces \(\mathcal {CMS}\) and coarse median structures \(\mathcal {CM}\).
Proposition A.6
The inclusion functor \(\iota _{\mathcal {M}}:\mathcal {CMS}\hookrightarrow \mathcal {CM}\) gives an equivalence of categories.
Proof
As \(\mathcal {CMS}\) is a full subcategory of \(\mathcal {CM}\), it suffices to show that each object in \(\mathcal {CM}\) is isomorphic to an object of \(\mathcal {CMS}\) (see for example [13, Theorem 1, Section IV.4] or [11, Proposition 1.3, Chapter 1]). For  an object in \(\mathcal {CM}\), as remarked before Definition 2.8,
an object in \(\mathcal {CM}\), as remarked before Definition 2.8,  is uniformly close to another coarse median
is uniformly close to another coarse median  satisfying (M1) and (M2). The identity map \(\mathrm {Id}_X\) is then a coarse median map from
satisfying (M1) and (M2). The identity map \(\mathrm {Id}_X\) is then a coarse median map from  to
to  which provides the required isomorphism in \(\mathcal {CM}\). \(\square \)
which provides the required isomorphism in \(\mathcal {CM}\). \(\square \)
1.2 The coarse interval (space) category
We will define the coarse interval category and the coarse interval space category in this subsection. As we did in the coarse median case, let us start with morphisms.
Definition A.7
Let \((X,d_X, [\cdot , \cdot ]_X)\) and \((Y,d_Y,[\cdot , \cdot ]_Y)\) be coarse interval structures (see Definition 3.11). A map \(f: X \rightarrow Y\) is said to be a \((\rho _+,C)\)-coarse interval map if f is a \(\rho _+\)-coarse map and for any \(a,b\in X, f([a,b]) \subseteq {\mathcal {N}}_C([f(a),f(b)])\). As usual, we omit parameters unless they are required.
Given coarse interval maps f, g from X to Y, we introduce the notation \(f \sim g\) if f is s-close to g for some s. This is an equivalence relation and we denote the equivalence class of f by [f].
Definition A.8
The coarse interval category, denoted \(\mathcal {CI}\), is defined as follows:
-
The objects are coarse interval structures \((X,d_X,[\cdot ,\cdot ]_X)\);
-
Given two objects: \({\mathcal {X}}=(X,d_X,[\cdot ,\cdot ]_X)\) and \({\mathcal {Y}}=(Y,d_Y,[\cdot ,\cdot ]_Y)\), the morphism set is
$$\begin{aligned} \mathrm {Mor}_{\mathcal {CI}}({\mathcal {X}},\mathcal Y):=\{ \text{ coarse } \text{ interval } \text{ maps } \text{ from } X \text{ to } Y~\}/\sim ; \end{aligned}$$ -
Compositions are induced by compositions of maps.
The coarse interval space category, denoted \(\mathcal {CIS}\), is the full subcategory whose objects are coarse interval spaces, i.e., those satisfying the stronger axioms (I1)–(I3).
As in Lemma A.4, we can characterise categorical isomorphisms in a more practical way. Let us start with the following observation.
Lemma A.9
Let \((X,d_X,[\cdot ,\cdot ]_X),(Y,d_Y,[\cdot ,\cdot ]_Y)\) be coarse interval structures and \(f:X \rightarrow Y\) be a coarse interval map as well as a coarse equivalence. Then there exists some constant \(D>0\) such that for any \(a,b\in X\),
Proof
Suppose f is a \((\rho _+,C)\)-coarse interval map with \(C\geqslant 3{\kappa _0}\) where \({\kappa _0}\) is the parameter of \([\cdot ,\cdot ]_Y\) given in axioms (I1)\(^{\prime }\) and (I3)\(^{\prime }\) and \(g:Y\rightarrow X\) is a \(\rho _+\)-bornologous map such that \(f\circ g\thicksim _C \mathrm {Id}_{Y}\) and \(g\circ f \thicksim _C \mathrm {Id}_{X}\). For \(z\in [f(a),f(b)]\) and for \(c=g(z)\), we have \(f(c)\thicksim _C z\). Hence by Remark 3.12 as \(C\geqslant 3{\kappa _0}\), we have
On the other hand, since f is a \((\rho _+,C)\)-coarse interval map, we have
This has diameter at most \(C'\) for some constant \(C'\) by axiom (I3)\(^{\prime }\). Hence there exists \(c'\in [a,b]\) such that \(f(c)\thicksim _{C'}f(c')\) which implies that \(z\thicksim _C f(c)\thicksim _{C'}f(c')\), i.e., \(z\in {\mathcal {N}}_{C+C'}(f([a,b]))\). Taking \(D=C+C'\) we have \(d_H(f([a,b]),[f(a),f(b)])\leqslant D\) as required. \(\square \)
Now we give a characterisation of categorical isomorphism in \(\mathcal {CI}\) and \(\mathcal {CIS}\).
Lemma A.10
Let \((X,d_X,[\cdot ,\cdot ]_X)\) and \((Y,d_Y,[\cdot ,\cdot ]_Y)\) be two coarse interval structures and \(f\,{:}\,X \rightarrow Y\) be a coarse interval map. Then [f] is an isomorphism in \(\mathcal {CI}\) if and only if f is a coarse equivalence. The same holds in \(\mathcal {CIS}\) by restricting to this full subcategory.
Proof
Suppose [f] is an isomorphism in \(\mathcal {CI}\), i.e., there exists another coarse interval map \(g: Y \rightarrow X\) such that \([f][g]=[\mathrm {Id}_Y]\) and \([g][f]=[\mathrm {Id}_X]\). Hence clearly, f is a coarse equivalence.
On the other hand, suppose f is a \((\rho _+,C)\)-interval morphism and \(g\,{:}\,Y\rightarrow X\) is \(\rho _+\)-coarse such that \(fg\thicksim _C \mathrm {Id}_{Y}\) and \(gf \thicksim _C \mathrm {Id}_{X}\). It suffices to show that there exists some constant \(C'>0\) such that for any \(z,w\in Y, g([z,w]) \subseteq {\mathcal {N}}_{C'}(g(z),g(w))\). Since \(fg\thicksim _C \mathrm {Id}_{Y}\), we have \(z \thicksim _C f(z')\) and \(w \thicksim _C f(w')\) for \(z'=g(z)\) and \(w'=g(w)\). By axioms (I1)\(^{\prime }\) and (I2), there exists some constant \(K>0\) such that \([z,w] \subseteq {\mathcal {N}}_K([f(z'),f(w')]\). Hence
By Lemma A.9, there exists a constant \(D>0\) such that \([f(z'),f(w')]\subseteq {\mathcal {N}}_D(f[z',w'])\), which implies that
where \(C'=\rho _+(K)+\rho _+(D)+C\) depends only on \(\rho _+,C\) and parameters of \([\cdot ,\cdot ]_X\) and \([\cdot ,\cdot ]_Y\). \(\square \)
Proposition A.11
The inclusion functor \(\iota _{{\mathcal {I}}}:\mathcal {CIS}\hookrightarrow \mathcal {CI}\) gives an equivalence of categories.
Proof
This follows from Lemma 3.14. The argument is similar to the proof of Proposition A.6, hence omitted. \(\square \)
1.3 Equivalence of the coarse median and coarse interval categories
Now we construct functors connecting categories \(\mathcal {CM}\) and \(\mathcal {CI}\) (also \(\mathcal {CM}{\mathcal {S}}\) and \(\mathcal {CI}{\mathcal {S}}\)), and show that these functors give equivalences of categories. Theorem 3.15 (1) offers a functor from \(\mathcal {CM}\) to \(\mathcal {CI}\) as follows:
Lemma A.12
Let  and
and  be objects in the category \(\mathcal {CM}\) and \(f:X\rightarrow Y\) be a \((\rho _+,C)\)-coarse median map. Suppose \((X,d_X,[\cdot ,\cdot ]_X)\) and \((Y,d_Y,[\cdot ,\cdot ]_Y)\) are the induced coarse interval structures. Then f is a \((\rho _+,C)\)-coarse interval map from \((X, d_X, [\cdot ,\cdot ]_X)\) to \((Y, d_Y, [\cdot ,\cdot ]_Y)\).
be objects in the category \(\mathcal {CM}\) and \(f:X\rightarrow Y\) be a \((\rho _+,C)\)-coarse median map. Suppose \((X,d_X,[\cdot ,\cdot ]_X)\) and \((Y,d_Y,[\cdot ,\cdot ]_Y)\) are the induced coarse interval structures. Then f is a \((\rho _+,C)\)-coarse interval map from \((X, d_X, [\cdot ,\cdot ]_X)\) to \((Y, d_Y, [\cdot ,\cdot ]_Y)\).
Proof
For any \(x,y,z\in X\) we have  . Hence for
. Hence for  we have
we have  . So \(f([x,y]) \subseteq {\mathcal {N}}_C([f(x),f(y)])\) which completes the proof. \(\square \)
. So \(f([x,y]) \subseteq {\mathcal {N}}_C([f(x),f(y)])\) which completes the proof. \(\square \)
Definition A.13
We define a functor \(F\,{:}\,\mathcal {CM}\rightarrow \mathcal {CI}\) by setting  to be the induced coarse interval structure \((X,d_X,[\cdot ,\cdot ]_X)\) and defining \(F[f]=[f]\) on morphisms. This is well defined by Lemma A.12 and also restricts to give a functor \(F_{{\mathcal {S}}}\,{:}\,\mathcal {CMS}\rightarrow \mathcal {CIS}\) by Proposition 3.2.
to be the induced coarse interval structure \((X,d_X,[\cdot ,\cdot ]_X)\) and defining \(F[f]=[f]\) on morphisms. This is well defined by Lemma A.12 and also restricts to give a functor \(F_{{\mathcal {S}}}\,{:}\,\mathcal {CMS}\rightarrow \mathcal {CIS}\) by Proposition 3.2.
Now we consider the opposite direction. Theorem 3.15 (2) provides a functor from \(\mathcal {CI}\) to \(\mathcal {CM}\) as follows:
Lemma A.14
Let \((X,d_X,[\cdot ,\cdot ]_X)\) and \((Y,d_Y,[\cdot ,\cdot ]_Y)\) be objects in the category \(\mathcal {CI}\) and let \(f\,{:}\,X\rightarrow Y\) be a \((\rho _+,C)\)-coarse interval map. Suppose  and
and  are any induced coarse median structures. Then f is a \((\rho _+, \psi (\rho _+({\kappa _0})+C))\)-coarse median map from
are any induced coarse median structures. Then f is a \((\rho _+, \psi (\rho _+({\kappa _0})+C))\)-coarse median map from  to
to  , where \({\kappa _0}\) is the parameter in axiom (I1)\(^{\prime }\) for \((X,d_X,[\cdot ,\cdot ]_X)\) and \(\psi \) is the parameter in axiom (I3)\(^{\prime }\) for \((Y,d_Y,[\cdot ,\cdot ]_Y)\).
, where \({\kappa _0}\) is the parameter in axiom (I1)\(^{\prime }\) for \((X,d_X,[\cdot ,\cdot ]_X)\) and \(\psi \) is the parameter in axiom (I3)\(^{\prime }\) for \((Y,d_Y,[\cdot ,\cdot ]_Y)\).
Proof
By definition \(f([x,y]) \subseteq {\mathcal {N}}_C([f(x),f(y)])\) for any \(x,y\in X\). Now we have:

for \(C'=\rho _+({\kappa _0})+C\) and any \(a,b,c \in X\). Hence we have

which implies that f is a \((\rho _+, \psi (\rho _+({\kappa _0})+C))\)-coarse median map. \(\square \)
Definition A.15
We define a functor \(G\,{:}\,\mathcal {CI}\rightarrow \mathcal {CM}\) by setting  , where
, where  is some (chosen) induced coarse median on X. The choice here is well defined up to equivalence of coarse medians and we define \(G[f]=[f]\) on morphisms. This definition makes sense by Theorem 3.15 and Lemma A.14 and restricts to give a functor \(G_{{\mathcal {S}}}: \mathcal {CIS}\rightarrow \mathcal {CMS}\) by Theorem 3.10.
is some (chosen) induced coarse median on X. The choice here is well defined up to equivalence of coarse medians and we define \(G[f]=[f]\) on morphisms. This definition makes sense by Theorem 3.15 and Lemma A.14 and restricts to give a functor \(G_{{\mathcal {S}}}: \mathcal {CIS}\rightarrow \mathcal {CMS}\) by Theorem 3.10.
Theorem A.16
The functors F and G from Definitions A.13, A.15 provide an equivalence of categories between coarse median structures \(\mathcal {CM}\) and coarse interval structures \(\mathcal {CI}\). This equivalence restricts to give an equivalence of categories between coarse median spaces \(\mathcal {CMS}\) and coarse interval spaces \(\mathcal {CIS}\).
Proof
We are required to show that \(G\circ F\) is naturally isomorphic to \(\mathrm {Id}_{\mathcal {CM}}\) and that \(F\circ G\) is naturally isomorphic to \(\mathrm {Id}_{\mathcal {CI}}\).
(1). First consider \(G\circ F\). Given a metric space \((X,d_X)\) with a coarse median  , by definition
, by definition  is the induced coarse interval structure \((X,d_X,[\cdot ,\cdot ]_X)\). Now apply G to the triple \((X,d_X,[\cdot ,\cdot ]_X)\) and denote the chosen induced operator by
is the induced coarse interval structure \((X,d_X,[\cdot ,\cdot ]_X)\). Now apply G to the triple \((X,d_X,[\cdot ,\cdot ]_X)\) and denote the chosen induced operator by  . It follows directly from Theorem 3.15(3) that
. It follows directly from Theorem 3.15(3) that  and
and  are uniformly close. Hence the identity
are uniformly close. Hence the identity  gives an isomorphism in the category \(\mathcal {CM}\). Furthermore, for any coarse median structure
gives an isomorphism in the category \(\mathcal {CM}\). Furthermore, for any coarse median structure  and coarse median map \(f\,{:}\,X \rightarrow Y\), the following diagram commutes since G, F do not change the morphisms:
and coarse median map \(f\,{:}\,X \rightarrow Y\), the following diagram commutes since G, F do not change the morphisms:

Hence the natural transformation  gives a natural isomorphism from \(\mathrm {Id}_{CM}\) to \(G\circ F\). This restricts to give a natural isomorphism from \(\mathrm {Id}_\mathcal {CMS}\) to \(G_{{\mathcal {S}}}\circ F_{\mathcal {S}}\).
gives a natural isomorphism from \(\mathrm {Id}_{CM}\) to \(G\circ F\). This restricts to give a natural isomorphism from \(\mathrm {Id}_\mathcal {CMS}\) to \(G_{{\mathcal {S}}}\circ F_{\mathcal {S}}\).
(2). Next consider \(F\circ G\). Given a coarse interval structure \((X,d_X,[\cdot ,\cdot ]_X)\), we have  where
where  is the chosen induced coarse median operator on X. Apply F to the coarse median structure
is the chosen induced coarse median operator on X. Apply F to the coarse median structure  and denote the induced interval structure by \((X, d_X, [\cdot ,\cdot ]_X')\). It follows directly from Theorem 3.15(3) that \([\cdot ,\cdot ]_X\) and \([\cdot ,\cdot ]'_X\) are uniformly close. Therefore, the identity \(\mathrm {Id}_X: (X,d_X,[\cdot ,\cdot ]_X) \rightarrow (X,d_X,[\cdot ,\cdot ]'_X)\) gives an isomorphism in the category \(\mathcal {CI}\). Furthermore, for any other coarse interval structure \((Y,d_Y,[\cdot ,\cdot ]_Y)\) and coarse interval map \(f\,{:}\,X \rightarrow Y\), the following diagram again clearly commutes:
and denote the induced interval structure by \((X, d_X, [\cdot ,\cdot ]_X')\). It follows directly from Theorem 3.15(3) that \([\cdot ,\cdot ]_X\) and \([\cdot ,\cdot ]'_X\) are uniformly close. Therefore, the identity \(\mathrm {Id}_X: (X,d_X,[\cdot ,\cdot ]_X) \rightarrow (X,d_X,[\cdot ,\cdot ]'_X)\) gives an isomorphism in the category \(\mathcal {CI}\). Furthermore, for any other coarse interval structure \((Y,d_Y,[\cdot ,\cdot ]_Y)\) and coarse interval map \(f\,{:}\,X \rightarrow Y\), the following diagram again clearly commutes:

Hence the natural transformation \((X,d_X,[\cdot ,\cdot ]_X) \mapsto {[}\mathrm {Id}_X]\) gives a natural isomorphism from \(\mathrm {Id}_\mathcal {CI}\) to \(F\circ G\). As usual this restricts to give a natural isomorphism from \(\mathrm {Id}_\mathcal {CIS}\) to \(F_{{\mathcal {S}}}\circ G_{\mathcal {S}}\). \(\square \)
Combining Propositions A.6, A.11, Theorem A.16 and Corollary 4.7, we obtain the following.
Theorem A.17
Consider the following diagram:

We have:
-
\(F \circ \iota _{{\mathcal {M}}} = \iota _{{\mathcal {I}}} \circ F_{{\mathcal {S}}}\);
-
\(\iota _{{\mathcal {M}}} \circ G_{{\mathcal {S}}} = G \circ \iota _{{\mathcal {I}}}\);
-
\(\iota _{{\mathcal {M}}}\) gives an equivalence of categories between \(\mathcal {CMS}\) and \(\mathcal {CM}\);
-
\(\iota _{{\mathcal {I}}}\) gives an equivalence of categories between \(\mathcal {CIS}\) and \(\mathcal {CI}\);
-
(F, G) gives an equivalence of categories between \(\mathcal {CM}\) and \(\mathcal {CI}\);
-
\((F_{{\mathcal {S}}},G_{{\mathcal {S}}})\) gives an equivalence of categories between \(\mathcal {CMS}\) and \(\mathcal {CIS}\).
Furthermore all of these functors preserve rank in the sense of coarse median structures and coarse interval structures.
Remark A.18
We finally note that one can restrict the allowed metric spaces to quasi-geodesic spaces. In this case the above equivalences of categories restrict to equivalences between the full subcategories of quasi-geodesic coarse median spaces and quasi-geodesic coarse interval spaces.
1.4 Comparing the categories of coarse median algebras and coarse median spaces
In the spirit of Sect. A.1, we now consider the category of bounded valency coarse median algebras. By analogy with the notion of coarse median map, we define a coarse median algebra homomorphism from  to
to  to be a function \(f\,{:}\,X\rightarrow Y\) such that
to be a function \(f\,{:}\,X\rightarrow Y\) such that
-
(1)
there exist a constant C such that that for all \(a,b,c\in X\),

-
(2)
there exists a non-decreasing function \(\rho :{\mathbb {R}}^{+}\rightarrow {\mathbb {R}}^{+}\) such that for all \(a,b\in X\),
$$\begin{aligned} \sharp [f(a), f(b)]\leqslant \rho (\sharp [a,b]); \end{aligned}$$ -
(3)
f is finite-to-1.
Where we need to keep track of \(C, \rho \) we will refer to f as a \((C,\rho )\)-coarse median algebra homomorphism.
Note that the requirement of “finite-to-1” is analogous to properness in the definition of coarse map. When C can be taken to be 1 then  and f is a homomorphism of ternary algebras. In particular if X and Y are median algebras and \(C=1\) then f is a homomorphism of median algebras and the second and third conditions require that f is also a coarse map in the geometric sense. From the algebraic point of view one would not expect the latter conditions to be required, however without them the composition of coarse median algebra homomorphisms would not in general yield another coarse median algebra homomorphism (cf. Remark A.2).
and f is a homomorphism of ternary algebras. In particular if X and Y are median algebras and \(C=1\) then f is a homomorphism of median algebras and the second and third conditions require that f is also a coarse map in the geometric sense. From the algebraic point of view one would not expect the latter conditions to be required, however without them the composition of coarse median algebra homomorphisms would not in general yield another coarse median algebra homomorphism (cf. Remark A.2).
Lemma A.19
Let  and
and  be coarse median algebra homomorphisms between bounded valency coarse median algebras
be coarse median algebra homomorphisms between bounded valency coarse median algebras  and
and  . Then the composition
. Then the composition  is a coarse median algebra homomorphism as well.
is a coarse median algebra homomorphism as well.
Proof
Let f be a \((C_f, \rho _f)\)-coarse median algebra homomorphism and g a \((C_g, \rho _g)\)-coarse median algebra homomorphism. Since  has bounded valency, Lemma 6.2 and Theorem 1.4 imply that the induced metric
has bounded valency, Lemma 6.2 and Theorem 1.4 imply that the induced metric  has bounded geometry and
has bounded geometry and  is a coarse median space. From Lemma 4.13 there exists a non-decreasing function \(\phi _Z\,{:}\,{\mathbb {R}}^{+}\rightarrow {\mathbb {R}}^{+}\) such that for any \(u,v\in Z\) we have
is a coarse median space. From Lemma 4.13 there exists a non-decreasing function \(\phi _Z\,{:}\,{\mathbb {R}}^{+}\rightarrow {\mathbb {R}}^{+}\) such that for any \(u,v\in Z\) we have

Now for any \(a,b,c\in X\) we have:

and

Hence

Thus condition (1) holds for gf. As for condition (2), we have
Finally, since f, g are finite-to-1, their composition gf is finite-to-1 as well so gf is a coarse median algebra homomorphism. \(\square \)
Two coarse median algebra homomorphisms f, g are said to be equivalent, denoted by \(f \sim g\), if there is a constant D such that for all \(x\in X, \sharp [ f(x), g(x)]_Y\leqslant D\). Now Lemma A.19 allows us to make the following definition:
Definition A.20
The bounded valency coarse median algebra category, denoted by \(\mathcal {BCMA}\), is defined as follows:
-
The objects are coarse median algebras
 of bounded valency;
of bounded valency; -
Given two objects:
 and
and  , the morphism set is $$\begin{aligned} \{ \text{ coarse } \text{ median } \text{ algebra } \text{ homomorphisms } \text{ from } X \text{ to } Y~\}/\sim ; \end{aligned}$$
, the morphism set is $$\begin{aligned} \{ \text{ coarse } \text{ median } \text{ algebra } \text{ homomorphisms } \text{ from } X \text{ to } Y~\}/\sim ; \end{aligned}$$ -
Compositions are induced by compositions of homomorphisms.
Let \(\mathcal {BCMS}\) denote the full subcategory of \(\mathcal {CMS}\) whose objects are bounded geometry coarse median spaces. We will construct a functor \(H\,{:}\,\mathcal {BCMA} \rightarrow \mathcal {BCMS}\) given by equipping each coarse median algebra  with its induced metric.
with its induced metric.
Lemma A.21
Defining \(H([f]) = [f]\) makes this a functor.
Proof
We first show that for bounded valency coarse median algebras \(, \) and a \((C_f, \rho _f)\)-coarse median algebra homomorphism \(f\,{:}\,X \rightarrow Y, f\) is also a coarse median map between  and
and  .
.
Clearly for any \(a,b,c\in X\), the distance between \(\langle f(a),f(b),f(c) \rangle _Y\) and  is bounded by the cardinality of the associated interval, which is uniformly bounded by \(C_f\). Hence f is a \(C_f\)-quasi-morphism. As in the proof of Lemma A.19,
is bounded by the cardinality of the associated interval, which is uniformly bounded by \(C_f\). Hence f is a \(C_f\)-quasi-morphism. As in the proof of Lemma A.19,  having bounded valency implies that there exists a non-decreasing function \(\phi _X:{\mathbb {R}}^{+}\rightarrow {\mathbb {R}}^{+}\) such that for any \(u,v\in X\), we have
having bounded valency implies that there exists a non-decreasing function \(\phi _X:{\mathbb {R}}^{+}\rightarrow {\mathbb {R}}^{+}\) such that for any \(u,v\in X\), we have

This implies

Hence f is \(\rho _f\circ \phi _X\)-bornologous. Bounded geometry and the fact that f is finite-to-1 imply that f is proper. Therefore, f is a coarse median map.
Now suppose that \(g\,{:}\,X\rightarrow Y\) is a coarse median algebra homomorphism which is equivalent to f. Now consider  . By assumption the latter is bounded hence f is close to g. \(\square \)
. By assumption the latter is bounded hence f is close to g. \(\square \)
While the forgetful map which converts a bounded valency, bounded geometry coarse median space to the underlying coarse median algebra is a left inverse to H, this is not in general functorial.
Example A.22
Consider the tree T obtained from \({\mathbb {Z}}\) by adding a spike of length |n| to each integer n. All edges are taken to have length 1. As a tree this is naturally a discrete median space and can be viewed as a coarse median space with its natural path metric. Now take the subspace X consisting of the original points of \({\mathbb {Z}}\), together with the leaves of the tree, and equip this with the subspace metric (see Fig. 2). This is a median subalgebra and the inclusion is a morphism of coarse median spaces. However it is not a morphism of coarse median algebras, since taking a to be the leaf on the spike based at the integer b the interval \([a,b]_X\) has cardinality 2, while its image in T has cardinality \(|b|+1\) contravening the second condition. Once again this illustrates that it is possible to endow a coarse median algebra with a metric which does not fully respect the algebraic structure. However restricting to the quasi-geodesic world, or more generally, imposing the induced metric prevents these problems and makes the forgetful map functorial.
Just as CAT(0) cube complexes can be studied combinatorially as median algebras, we can apply Theorem 6.7 to obtain the following theorem showing that coarse median spaces can be studied as coarse median algebras.
Theorem A.23
The forgetful functor, together with the “induced metric” functor provide an equivalence of categories from bounded geometry quasi-geodesic coarse median spaces to bounded valency quasi-geodesic coarse median algebras, and this equivalence preserves rank.
Proof
First let us show that the forgetful map is indeed a functor in this case. Let  and
and  be two bounded geometry quasi-geodesic coarse median spaces, and \(f:X \rightarrow Y\) be a coarse median map. Theorem 6.7 implies that
be two bounded geometry quasi-geodesic coarse median spaces, and \(f:X \rightarrow Y\) be a coarse median map. Theorem 6.7 implies that  and
and  are bounded valency quasi-geodesic coarse median algebras and for some \(L',C'>0\) the induced metrics
are bounded valency quasi-geodesic coarse median algebras and for some \(L',C'>0\) the induced metrics  are \((L',C')\)-quasi-isometric to \(d_X, d_Y\), respectively.
are \((L',C')\)-quasi-isometric to \(d_X, d_Y\), respectively.
Since f is a quasi-morphism there exists \(C>0\) such that for any \(a,b,c \in X\)

Since \((Y,d_Y)\) has bounded valency, Lemma 4.13 provides a non-decreasing function \(\phi _Y:{\mathbb {R}}^{+}\rightarrow {\mathbb {R}}^{+}\) such that for any \(u,v\in Y\), we have \(\sharp [u,v]_Y\leqslant \phi _Y(d_Y(u,v))\). Thus we obtain:

On the other hand, assume that f is \(\rho _f\)-coarse, then we have:

Note that we use the fact that \(d_X\) and  are \((L',C')\)-quasi-isometric in the third inequality, which fails in Example A.22, and this is the only place we need the condition of quasi-geodesity. Finally properness and bounded geometry imply that f is finite-to-1. In conclusion, we have shown that f is a coarse median algebra homomorphism which implies that the forgetful map is indeed a functor.
are \((L',C')\)-quasi-isometric in the third inequality, which fails in Example A.22, and this is the only place we need the condition of quasi-geodesity. Finally properness and bounded geometry imply that f is finite-to-1. In conclusion, we have shown that f is a coarse median algebra homomorphism which implies that the forgetful map is indeed a functor.
The rest of the statement follows directly from Theorem 6.7 and Lemma 6.9. \(\square \)
Finally we note that while the definition of a coarse median space requires affine control (in axiom (C1)) the morphisms in the category \(\mathcal {CMS}\) are only required to be coarse, not large-scale Lipschitz. As mentioned in [14], this suggests a generalisation of the notion of coarse median to allow bornologous control: replace the affine control axiom (C1) with the requirement that the map  is bornologous uniformly in b, c. Many of the results of this paper should carry over to this context.
is bornologous uniformly in b, c. Many of the results of this paper should carry over to this context.
However this does not greatly extend the class of examples for the following reasons. Firstly in the quasi-geodesic case this is not a generalisation as bornologous control implies affine control. More generally suppose that  is a triple satisfying the generalised bornologous version of (C1) along with (M1), (M2) and (C2). If this has bounded geometry then the proof of Theorem 1.4 (3) \(\implies \) (1) remains valid to show that
is a triple satisfying the generalised bornologous version of (C1) along with (M1), (M2) and (C2). If this has bounded geometry then the proof of Theorem 1.4 (3) \(\implies \) (1) remains valid to show that  is a coarse median algebra. If moreover we have bounded valency then by Theorem 1.4,
is a coarse median algebra. If moreover we have bounded valency then by Theorem 1.4,  is a coarse median space in the usual (affine) sense. Thus, in the context of bounded geometry bounded valency spaces, the metric can always be adjusted to ensure affine control.
is a coarse median space in the usual (affine) sense. Thus, in the context of bounded geometry bounded valency spaces, the metric can always be adjusted to ensure affine control.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Niblo, G.A., Wright, N. & Zhang, J. Coarse median algebras: the intrinsic geometry of coarse median spaces and their intervals. Sel. Math. New Ser. 27, 20 (2021). https://doi.org/10.1007/s00029-021-00623-8
Accepted:
Published:
DOI: https://doi.org/10.1007/s00029-021-00623-8




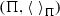 and maps
and maps  is at most K (Fig.
is at most K (Fig. 
 is a coarse median algebra;
is a coarse median algebra; is a coarse median space;
is a coarse median space;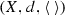 is a bounded geometry coarse median space.
is a bounded geometry coarse median space. for all
for all  for all
for all  for all
for all 

 for any permutation
for any permutation  .
. be a median algebra and
be a median algebra and  .
. .
. , the map
, the map  . Making such a choice gives an induced coarse median structure
. Making such a choice gives an induced coarse median structure  .
.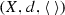 with induced coarse interval structure
with induced coarse interval structure  is uniformly close to
is uniformly close to  ;
; , the induced coarse interval structure is uniformly close to
, the induced coarse interval structure is uniformly close to 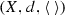 is uniformly close to a coarse median space
is uniformly close to a coarse median space  . Now Proposition
. Now Proposition  gives a coarse interval space
gives a coarse interval space  and
and  are uniformly close,
are uniformly close,  . Since
. Since  and
and  are uniformly close as well. Hence
are uniformly close as well. Hence  is a coarse median structure.
is a coarse median structure. with parameters
with parameters  be any induced coarse median structure of
be any induced coarse median structure of  and is uniformly bounded with diameter at most
and is uniformly bounded with diameter at most  and
and  are uniformly close.
are uniformly close. has rank at most n.
has rank at most n. for all
for all  for all
for all 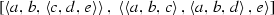 is at most K.
is at most K. is a coarse median algebra;
is a coarse median algebra; is a coarse median space;
is a coarse median space; is a bounded geometry coarse median space.
is a bounded geometry coarse median space.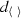 is quasi-geodesic.
is quasi-geodesic. is quasi-geodesic.
is quasi-geodesic. is connected and
is connected and  is bi-Lipschitz to the edge-path metric
is bi-Lipschitz to the edge-path metric  ;
; and
and  the morphism set is
the morphism set is 
 of bounded valency;
of bounded valency; and
and  , the morphism set is
, the morphism set is 