Determinant map for the prestack of Tate objects

Abstract

We construct a map from the prestack of Tate objects over a commutative ring k to the stack of ${\mathbb {G}}_{\mathrm{m}}$-gerbes. The result is obtained by combining the determinant map from the stack of perfect complexes as proposed by Schürg–Toën–Vezzosi with a relative $S_{\bullet }$-construction for Tate objects as studied by Braunling–Groechenig–Wolfson. Along the way we prove a result about the K-theory of vector bundles over a connective ${\mathbb {E}}_{\infty }$-ring spectrum which is possibly of independent interest.

Proofs for Sect. 1

In this section we prove some of the main results about K-theory that we summarized in Sect. 1. Our goal is to present some of the arguments in a slicker form than what can be found in the literature, though all of those results were already in [4, 15, 25].

1.1 Realization fibrations

In this section we introduce a preliminary technical tool, developed by Rezk [29], which allows for a simple proof of the Additivity theorem in the next section.

Definition A.1

Let I be a small category and $f:X \rightarrow Y$ a morphism in $\text{ Fun }(I^{\mathrm{op}},\text{ Spc})$. We say that f is a realization fibration if for every pullback

the diagram obtained by taking the colimit over I

is a pullback diagram in $\text{ Spc }$.

Remark A.2

Notice that any map f which induces an equivalence upon passing to colimits is a realization fibration diagram, and that the class of such is stable under pullbacks.

In [29], the following definition is introduced as part of the local-to-global principle to check that a map is a realization fibration.

Definition A.3

Let J be a small category, $F,G:J \rightarrow {\mathscr {C}}$ be functors and $p:F \rightarrow G$ a natural transformation, one says that p is J-equifibered if for every morphism $f:j_2 \rightarrow j_1$ in J the diagram

is a pullback square.

Rezk then proves the following useful criterion.⁴⁵

Proposition A.4

([29, Theorem 2.6]) Let J be a small category, $F,G: J \rightarrow {\mathscr {P}}(I)$⁴⁶ functors and $p:F \rightarrow G$ a natural transformation, suppose that p is a J-equifibered map, and that for each $j \in J$ the map $p(j):F(j) \rightarrow G(j)$ is a realization fibration. Then

$$\begin{aligned} {{\,\mathrm{colim}\,}}_J F(j) \rightarrow {{\,\mathrm{colim}\,}}_J G(j) \end{aligned}$$

is a realization fibration.

In the particular case when $I = \Delta$ Rezk proves the following result, which can be seen as a way to bypass the $\pi _*$-Kan condition.

Lemma A.5

([29, Proposition 5.4]) For $f: X \rightarrow Y$ a map of simplicial spaces, if for all $[m] \in \Delta ^{\mathrm{op}}$ the map

$$\begin{aligned} Y([m]) \rightarrow Y([0]) \end{aligned}$$

induces an isomorphism on $\pi _0$, then f is a realization fibration.

An important consequence of Lemma A.5 is the following

Lemma A.6

For any $[m] \in \Delta ^{\mathrm{op}}$ and any Waldhausen category ${\mathscr {C}}$ the maps

• (i)
  $$\begin{aligned} q^{(m)}: S_{\bullet +m+1}{\mathscr {C}}\rightarrow S_{m}{\mathscr {C}}\end{aligned}$$
• (ii)
  $$\begin{aligned} p^{(m)}: S_{\bullet +m+1}{\mathscr {C}}\rightarrow S_{\bullet }{\mathscr {C}}, \end{aligned}$$

where $q^{(m)}$ is the projection onto the last $(m-1)$ elements and $p^{(m)}$ is given by the projection onto the first elements of the simplicial set, induce equivalences upon geometric realization.⁴⁷

Proof

We prove (i); the argument for (ii) is completely analogous. Since ${\mathscr {C}}$ is pointed, $|S_{m}{\mathscr {C}}|$ is contractible. Hence, it is enough to check that the map $p^{(m)}$ is a realization fibration. By Lemma A.5 it is enough to check that it induces an equivalence on $\pi _0$, and that again follows from the fact that $S_{m+1}{\mathscr {C}}$ is pointed. $\square$

1.2 Additivity theorem

Our exposition is heavily influenced by the paper [27]. First we introduce some notation and prove a couple of preliminary results. For $X \in \text{ Fun }(N\Delta ^{\mathrm{op}},{\mathscr {C}})$ a simplicial object in a category ${\mathscr {C}}$, we denote by $X^R$ and $X^L$ the bisimplicial objects obtained as

$$\begin{aligned} X^L_{n,m} = X_n \;\;\; \text{ and }\;\;\; X^R_{n,m} = X_m. \end{aligned}$$

Suppose that $F: {\mathscr {C}}\rightarrow {\mathscr {D}}$ is a functor between Waldhausen categories. Then we have an induced functor ${\mathscr {S}}_{\bullet }F: {\mathscr {S}}_{\bullet }{\mathscr {C}}\rightarrow {\mathscr {S}}_{\bullet }{\mathscr {D}}$ of simplicial objects in $\text{ Wald}_{\infty }$. We consider the bisimplicial object ${\mathscr {S}}_{\bullet _{2}}\left. F\right| _{{\mathscr {D}}}$ whose value on ([n], [m]) is defined as the following pullback

where $p^{(m)}_{n}$ is the projection onto the first $n+1$ elements of ${\mathscr {S}}_{n+m+1}{\mathscr {D}}$.⁴⁸ As before we will denote by unscripted S the corresponding objects obtained by passing to the underlying $\infty$-groupoid.

By construction we have maps of bisimplicial objects

$$\begin{aligned} \pi ^{F}_{\bullet _2}: S_{\bullet _{2}}\left. F\right| _{{\mathscr {D}}} \rightarrow S^{\mathrm{L}}_{\bullet _2}{\mathscr {C}}\end{aligned}$$

and

$$\begin{aligned} \rho ^{F}_{\bullet _2}: S_{\bullet _{2}}\left. F\right| _{{\mathscr {D}}} \rightarrow S^{\mathrm{R}}_{\bullet _2}{\mathscr {D}}, \end{aligned}$$

where $\rho ^F_{n,m}$ is the composite of the projection onto $S_{n+m+1}{\mathscr {D}}$ with $d^{n+1}_0: S_{n+m+1}{\mathscr {D}}\rightarrow S_{m}{\mathscr {D}}$.

Proposition A.7

The following are equivalent

• (a) the map $S_{\bullet }F$ induces an equivalence upon geometric realization;

• (b) the map $\rho ^{F}_{\bullet _2}$ induces an equivalence upon geometric realization.

Proof

Consider the diagram

We claim that (1) $S_{\bullet _2}\text{ id}_{{\mathscr {D}}}$, (2) $\rho ^{\text{ id}_{{\mathscr {D}}}}_{\bullet _2}$, (3) $\pi ^{\text{ id}_{{\mathscr {D}}}}_{\bullet _2}$ and (4) $\pi ^{F}_{\bullet _2}$ induce equivalences upon geometric realization.

The claim for (1) is clear, i.e. isomorphisms are realization fibrations.

For (2), notice that for each $[m] \in \Delta ^{\mathrm{op}}$, $\rho ^{\text{ id}_{{\mathscr {D}}}}_{\bullet ,m}$ is the composite

$$\begin{aligned} \left. S_{\bullet ,m}F\right| _{{\mathscr {D}}} \rightarrow S_{\bullet +m+1}{\mathscr {D}}\overset{q^{(m)}}{\rightarrow } S_m{\mathscr {D}}, \end{aligned}$$

where the first map is induced by the pullback of $\text{ id}_{{\mathscr {D}},\bullet }$ in the defining square of $\left. {\mathscr {S}}_{\bullet ,m}F\right| _{{\mathscr {D}}}$. Thus, the first map of the composition induces an equivalence upon geometric realization, by Lemma A.6(i), the second map also induces an equivalence upon geometric realization.

For (3) and (4), notice that for any functor $F:{\mathscr {C}}\rightarrow {\mathscr {D}}$ and $[m] \in \Delta ^{\mathrm{op}}$ one has

$$\begin{aligned} \text{ Fib }(\pi ^F_{\bullet ,m}) \simeq \text{ Fib }(p^{(m)}_{\bullet }), \end{aligned}$$

where $p^{(m)}_{n}: {\mathscr {S}}_{n+m+1}{\mathscr {D}}\rightarrow {\mathscr {S}}_{n}{\mathscr {D}}$. So the result follows again from Lemma A.6(ii). $\square$

Here is essentially a reformulation of Proposition A.7 in the language of Sect. A.1.

Proposition A.8

If the map of bi-simplicial objects $\rho ^F_{\bullet _2}$ is a realization fibration, then so is $S_{\bullet }F$.

Proof

Let ${\mathscr {E}}_{\bullet }$ be a simplicial space and consider the pullback diagram

This induces two pullback diagrams of bi-simplicial space by considering the functors $(-)^{L}$ and $(-)^R$ applied to everything in sight. Now consider the ${\tilde{{\mathscr {E}}}}_{\bullet _2}$ and $\tilde{{\mathscr {E}}'}_{\bullet _2}$ defined as the following pullbacks

Thus, we obtain the following diagram living over the diagram (37)

where the maps are the pullback of the corresponding maps in diagram (37).

By considering the new six-term diagram

$$\begin{aligned} \text{ Fib }\left( (xm{38}) \rightarrow (37)\right) \end{aligned}$$

and passing to its geometric realization we see that if $\pi ^F_{\bullet _2}$, $S_{\bullet _2}\text{ id}_{{\mathscr {D}}}$, $\rho ^{\text{ id}_{{\mathscr {D}}}}_{\bullet _2}$, $\pi ^{\text{ id}_{{\mathscr {D}}}}_{\bullet _2}$ and $\rho ^F_{\bullet _2}$ are realization fibrations, then so is $S_{\bullet _2}F$. However, by Proposition A.7 the maps $S_{\bullet _2}\text{ id}_{{\mathscr {D}}}$, $\rho ^{\text{ id}_{{\mathscr {D}}}}_{\bullet _2}$, $\pi ^{\text{ id}_{{\mathscr {D}}}}_{\bullet _2}$ and $\pi ^F_{\bullet _2}$ induce equivalences upon geometric realization. This finishes the proof. $\square$

The final piece to prove the Additivity Theorem is the following.

Proposition A.9

For any functor $F: {\mathscr {C}}\rightarrow {\mathscr {D}}$ between Waldhausen categories, the induced map of bi-simplicial spaces

$$\begin{aligned} \rho ^F_{\bullet _2}: S_{\bullet _2}\left. F\right| _{{\mathscr {D}}} \rightarrow S^R_{\bullet _2}{\mathscr {D}}\end{aligned}$$

is a realization fibration.

Proof

Notice that the geometric realization of any bi-simplicial set ${\mathscr {E}}_{\bullet _2}$ is equivalent to

$$\begin{aligned} \mathop {{{\,\mathrm{colim}\,}}}\limits _{[m] \in \Delta ^{\mathrm{op}}}\left| {\mathscr {E}}_{\bullet ,m}\right| , \end{aligned}$$

where $\left| {\mathscr {E}}_{\bullet ,m}\right|$ is the geometric realization of $[n] \mapsto {\mathscr {E}}_{n,m}$. Thus, we are in the situation to apply [29, Theorem 2.6]. We check its two conditions:

• (1) for all $[m] \rightarrow [m']$ in $\Delta$ the diagram

  

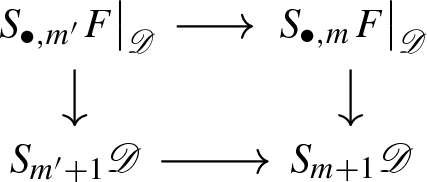
  is a pullback diagram. This follows immediately from the definition of $\left. S_{\bullet _2}F\right| _{{\mathscr {D}}}$, see diagram (36).

• (2) for all $[m] \in \Delta ^{\mathrm{op}}$ the map

  $$\begin{aligned} \rho ^F_{\bullet ,m}: \left. S_{\bullet ,m}\right| _{{\mathscr {D}}} \rightarrow S_{m+1}{\mathscr {D}}\end{aligned}$$

  is a realization fibration, where the right-hand side is the constant simplicial space $S_{m+1}{\mathscr {D}}$. This follows from Lemma A.5.

$\square$

Recall the set up of the Additivity Theorem, for ${\mathscr {C}}$ a Waldhausen category we considered the functor

$$\begin{aligned} F: \text{ Fun }([1],{\mathscr {C}}) \rightarrow {\mathscr {C}}\times {\mathscr {C}}\end{aligned}$$

given by evaluation on the source and taking the fiber of the morphism.

Proposition A.10

For any Waldhausen category ${\mathscr {C}}$ the functor F induces an equivalence of K-theory spectra.

Proof

From the construction of K-theory (see Sect. 1.1.1) it is enough to prove that the induced map

$$\begin{aligned} S_{\bullet }\text{ Fun }([1],{\mathscr {C}}) \rightarrow S_{\bullet }{\mathscr {C}}\times S_{\bullet }{\mathscr {C}}\end{aligned}$$

(39)

induces an equivalence upon passing to geometric realization. Equivalently, if one considers the fiber of (39) over the first factor of the right-hand side one has a fiber sequence

$$\begin{aligned} S_{\bullet }{\mathscr {C}}\rightarrow S_{\bullet }\text{ Fun }([1],{\mathscr {C}}) \rightarrow S_{\bullet }{\mathscr {C}}, \end{aligned}$$

(40)

where the first factor was identified with the $S_{\bullet }$-construction of the category whose objects are $X \in {\mathscr {C}}$ with a map from $*\in {\mathscr {C}}$, which is equivalent to ${\mathscr {C}}$. So it is enough to check that (40) induces a fiber sequence upon geometric realization, i.e. that the map

$$\begin{aligned} S_{\bullet }\text{ Fun }([1],{\mathscr {C}}) \rightarrow S_{\bullet }{\mathscr {C}}\end{aligned}$$

is a realization fibration.

This follows from Proposition A.8 and Proposition A.9 applied to the functor $\text{ ev }: \text{ Fun }(\Delta ^1,{\mathscr {C}}) \rightarrow {\mathscr {C}}$. $\square$

1.3 Cell decomposition theorem

In this section we give the proof of Theorem 1.32. We follow closely the strategy of Waldhausen (cf. Section 1.7 in [39]). For alternate accounts the reader is refered to [15] and [25, Lectures 19 and 20].

Let ${\mathscr {C}}$ be a Waldhausen category that admits finite colimits equipped with a bounded and non-degenerate weight structure $({\mathscr {C}}_{w \le 0},{\mathscr {C}}_{w,\ge 0})$. We introduce the category of cell decomposition.

For each $n \ge 0$ let ${\mathscr {E}}_n({\mathscr {C}})$ be defined as the following pullback

where ${\mathscr {C}}^n_w = {\mathscr {C}}_{w\le n}\cap {\mathscr {C}}_{w \ge n}$, and ${\mathscr {F}}_n{\mathscr {C}}$ is the category of objects $X \in {\mathscr {C}}$ with an n step filtration, i.e.

$$\begin{aligned} {\mathscr {F}}_n{\mathscr {C}}= \{X_0 \hookrightarrow X_1 \hookrightarrow \cdots \hookrightarrow X_n \; | \; \forall i, \; X_i \in {\mathscr {C}}\} \end{aligned}$$

and the map q is given by

$$\begin{aligned} q(X_0 \hookrightarrow X_1 \hookrightarrow \cdots \hookrightarrow X_n) = (X_0,X_1/X_0,\ldots ,X_n/X_{n-1}). \end{aligned}$$

Notice that for any n the category ${\mathscr {C}}_{w \le n}$ is a Waldhausen category, where the cofibrations are those maps that are cofibrations in ${\mathscr {C}}$ and whose cofiber belongs to ${\mathscr {C}}_{w \le n}$. Similarly for ${\mathscr {C}}_{w \ge n}$ and ${\mathscr {C}}^n_w$. The categories ${\mathscr {F}}_n{\mathscr {C}}$ are also Waldhausen categories (see [4, Definition 5.6]). Thus, the category ${\mathscr {E}}_n({\mathscr {C}})$ is a Waldhausen category, since the category $\text{ Wald}_{\infty }$ admits finite limits (see [4, Proposition 4.4]).

We now endow the category ${\mathscr {E}}_n({\mathscr {C}})$ with a labeling, where we say that a morphism $f: X \rightarrow Y$ belongs to $w{\mathscr {E}}_{n}({\mathscr {C}})$ if $f_n:X_n \rightarrow Y_n$ is an equivalence.

The strategy of the proof is to apply the Fibration Theorem (Theorem 1.28) to $({\hat{{\mathscr {C}}}}_n,w{\hat{{\mathscr {C}}}}_n)$ and take the colimit on n. We first prove some lemmas that identify the categories that will show up.

Lemma A.11

For $n\ge 1$, the natural map

$$\begin{aligned} {\mathscr {E}}_n({\mathscr {C}})^w \overset{\simeq }{\rightarrow } {\mathscr {C}}^{\heartsuit }_{w} \end{aligned}$$

given by inclusion into ${\mathscr {E}}_n({\mathscr {C}})$ and projection into the first factor is an equivalence of Waldhausen categories.

Proof

We proceed by induction on n. The base case is clear since it consists of objects $X_0 \hookrightarrow 0$, where $X_0 \in {\mathscr {C}}^{\heartsuit }_{w}$ and the projection just sends $X_0$ to itself in ${\mathscr {C}}^{\heartsuit }_{w}$.

Suppose that the result holds for $n-1$ and consider the fiber sequence

$$\begin{aligned} X_{n-1} \hookrightarrow X_{n} \rightarrow X_{n}/X_{n-1}, \end{aligned}$$

where $X_n \simeq 0$. By definition of ${\mathscr {E}}_n({\mathscr {C}})$ we have that $X_n/X_{n-1} \in {\mathscr {C}}^{n}_w$, hence one has

$$\begin{aligned} \tau _{w\le (n-1)}(X_n) \simeq X_{n-1} \end{aligned}$$

since $X_{n-1}\in {\mathscr {C}}_{w\le (n-1)}$, this gives that $X_{n-1}\simeq 0$. $\square$

Lemma A.12

For $n\ge 1$, one has an equivalence of Waldhausen categories

$$\begin{aligned} \alpha _n: {\mathscr {E}}_n({\mathscr {C}})^w\times {\mathscr {C}}^{1}_w \times \cdots \times {\mathscr {C}}^n_w \overset{\simeq }{\rightarrow } {\mathscr {E}}_n({\mathscr {C}}). \end{aligned}$$

Proof

Again we proceed by induction. For $n=1$ one has the functor

$$\begin{aligned} \alpha _1((X_0 \hookrightarrow 0),Y) = (X_0 \hookrightarrow X_0\oplus Y) \end{aligned}$$

which clearly gives an equivalence.

For general n we consider the functor $\beta : {\mathscr {E}}_{n-1}({\mathscr {C}})\times {\mathscr {C}}^n_{w} \rightarrow {\mathscr {E}}_n({\mathscr {C}})$ given by

$$\begin{aligned} \beta ((X_0 \hookrightarrow \cdots X_{n-1}),X_{n}) = (X_0,\ldots , X_{n-1},X_{n-1}\oplus X_n). \end{aligned}$$

This also gives an equivalence so the result for n follows from the result for $n-1$. $\square$

Lemma A.13

One has an equivalence of Waldhausen categories

$$\begin{aligned} \mathop {{{\,\mathrm{colim}\,}}}\limits _{n \ge 1} {\mathscr {E}}_n({\mathscr {C}}) \overset{\simeq }{\rightarrow } {\mathscr {C}}. \end{aligned}$$

Proof

We first note that an object $X \in {{\,\mathrm{colim}\,}}_{n \ge 1}{\mathscr {E}}_n({\mathscr {C}})$ is a filtered object, such that

$$\begin{aligned} X_n \simeq X_{n+1} \end{aligned}$$

for some $n>> 0$. Thus, the map from the colimit is just sending an object to its stable part. To check that this is an equivalence we use the bounded condition of the weight structure on ${\mathscr {C}}$. Thus, the map $X \mapsto (\tau _{w \le 0}X \hookrightarrow \tau _{w \le 1}X \hookrightarrow \ldots \hookrightarrow \tau _{w \le n}X \simeq \tau _{w \le n+1}X \hookrightarrow \ldots )$ is an inverse to the previous maps. $\square$

Lemma A.14

For every n the labeled $\infty$-Waldhausen category $({\mathscr {E}}_n({\mathscr {C}}),w{\mathscr {E}}_n({\mathscr {C}}))$ has enough cofibrations.

Proof

By Definition 1.26 we need to produce an endofunctor F of $\text{ Fun }(\Delta ^1,{\mathscr {E}}_n({\mathscr {C}}))$ and a natural transformation $\eta : \text{ id }\rightarrow F$, satisfying the three properties of the definition.

Given an object $(X \overset{f}{\rightarrow } Y) \in \text{ Fun }(\Delta ^1,{\mathscr {E}}_n({\mathscr {C}})$ represented by a diagram

we inductively define $F(X \overset{f}{\rightarrow } Y)$ as follows

$$\begin{aligned} F(X_n) = X_n \; \text{ and } \; F(Y_n) = Y_n, \end{aligned}$$

and for $i < n$, we let

$$\begin{aligned} F(X_i) = Y_i\times _{Y_{i+1}}F(X_{i+1}). \end{aligned}$$

The natural transformation $\eta : \text{ id }\Rightarrow F$ is the natural map from $X_i$ to the pullback $Y_{i}\times _{Y_n}X_n \simeq F(X_i)$. Notice that the maps $F(X_i) \hookrightarrow F(X_{i+1})$ are cofibrations because those are isomorphic to the maps $Y_i \hookrightarrow Y_{i+1}$.

We now check the conditions of Definition 1.26.

Condition (i): Recall that f is labeled if $f_{n}$ is an equivalence, thus we need to argue that if $f_n$ is an equivalence then (42) is a cofibration in ${\mathscr {F}}_n({\mathscr {C}})$. Barwick describes the cofibrations in ${\mathscr {F}}_n({\mathscr {C}})$ as diagrams (42) where any square is a cofibration as a morphism in ${\mathscr {F}}_1({\mathscr {C}})$. Then Lemma 5.8. from [4] characterizes a map in ${\mathscr {F}}_1({\mathscr {C}})$ as a cofibration if $g_0$ is a cofibration in the diagram

and for any U extending the above diagram to

the map h is a cofibration.

In our example we obtain the diagram

where the map $f'_n$ is an equivalence, since it is the pushout of an equivalence, and $f_n$ is an equivalence by assumption. Thus, h is an equivalence, in particular it is also a cofibration.

Condition (ii): We need to show that $\eta _f$ is an equivalence for any f a labeled cofibration. We recall that Barwick defined the cofibrations on ${\mathscr {F}}_1({\mathscr {C}})$ as the smallest class generated by

We notice that by construction of F we only need to check that

$$\begin{aligned} X_{i} \overset{\simeq }{\rightarrow } F(X_i) = Y_i\times _{Y_{i+1}}F(X_{i+1}) \end{aligned}$$

for $0 \le i \le n-1$. Since $F(X_i) \simeq Y_i$ it is enough to check that

$$\begin{aligned} f_i: X_i \rightarrow Y_i \end{aligned}$$

is an equivalence for all $0\le i\le n-1$ when $f_n$ is an equivalence and a cofibration.

By applying the description of cofibrations we see that either $f_n$ is the pushout of $f_{n-1}$ by b), or that $f_{n-1}$ is an isomorphism. In either case we obtain by induction that $f_i$ is an isomorphism for all $0 \le i \le n$.

Condition (iii): We need to check that if f is labeled, then $\eta _f$ is objectwise labeled, i.e. $X_n \rightarrow F(X_n)$ is an equivalence, which follows from the definiton of F. $\square$

Theorem A.15

Let ${\mathscr {C}}$ be a Waldhausen category that admits finite colimits equipped with a bounded and non-degenerate weight structure $({\mathscr {C}}_{w \le 0},{\mathscr {C}}_{w,\ge 0})$. Then the canonical inclusion map

$$\begin{aligned} {\text {K}}({\mathscr {C}}^{\heartsuit }_{w}) \rightarrow {\text {K}}({\mathscr {C}}) \end{aligned}$$

is an equivalence of K-theory spectra.

Proof

Consider $({\mathscr {E}}_n({\mathscr {C}}),w{\mathscr {E}}_n({\mathscr {C}})$, which is a labeled Waldhausen category with enough fibrations by Lemma A.14, so we can apply Theorem 1.28 to obtain the following fiber sequence

By Lemma A.11 and Lemma A.12 we can rewrite the upper row of the above diagram to get

Thus, by the Additivity Theorem (see Theorem 1.20), we identify

$$\begin{aligned} \jmath _!{\text {K}}({\mathscr {B}}({\mathscr {E}}_n({\mathscr {C}}),w{\mathscr {E}}_n({\mathscr {C}}))) \simeq {\text {K}}({\mathscr {C}}^1_w\times \cdots \times {\mathscr {C}}^n_w). \end{aligned}$$

(44)

Finally, by taking the colimit on n of the diagram (43) and using that filtered colimits commute with fiber sequences we obtain

The term on the lower right corner vanishes by an Eilenberg swindle argument and Lemma A.13 gives the desired result.

This finishes the proof of the theorem. $\square$

Remark A.16

Consider the following modification of diagram (41)

where t is given by

$$\begin{aligned} t(X_0 \hookrightarrow X_1 \hookrightarrow \cdots \hookrightarrow X_n) = (\tau _{w\le 0}X_1,\tau _{w\le 1}X_2,\ldots ,\tau _{w\le (n-1)}X_n, X_n). \end{aligned}$$

We can proceed exactly as we did in this section to obtain the result that the canonical map

$$\begin{aligned} {\text {K}}({\mathscr {C}}_{w\le 0}) \overset{\simeq }{\rightarrow } {\text {K}}({\mathscr {C}}) \end{aligned}$$

is an equivalence of spectra, for ${\mathscr {C}}$ satisfying the same conditions as in Theorem A.15.

1.4 Additive K-theory

In this section we prove Theorem 1.19.

Recall that we have ${\mathscr {C}}$, a Waldhausen category which admits finite direct sums. We constructed a map in Remark 1.18 which induces a map between the underlying $\infty$-groupoids:

$$\begin{aligned} G_n: {\text {B}}_n{\mathscr {C}}\rightarrow S_n{\mathscr {C}}\end{aligned}$$

(45)

given by $G_n(X_1,\ldots ,X_n) = (X_1 \hookrightarrow X_1\oplus X_2 \hookrightarrow \cdots \hookrightarrow \oplus ^n_{i=1}X_i)$.

Remark A.17

For a pointed category ${\mathscr {C}}$, if its homotopy category ${\mathscr {h}}{\mathscr {C}}$ is additive, then for every $X,Y \in {\mathscr {C}}$ the canonical map

$$\begin{aligned} X \sqcup Y \rightarrow X\times Y \end{aligned}$$

admits a splitting.

The following lemma is key prove the comparison result.

Lemma A.18

Suppose that ${\mathscr {C}}$ is a Waldhausen category with split cofibrations and finite direct sums such that ${\text {h}}{\mathscr {C}}$ is additive. For every $n\ge 2$, consider the action of ${\text {B}}_{n-1}{\mathscr {C}}$ on $S_{n}{\mathscr {C}}$ given as

$$\begin{aligned} a_n: {\text {B}}_{n-1}{\mathscr {C}}\times S_n{\mathscr {C}}&\rightarrow S_n{\mathscr {C}}\\ ((Y_1,\ldots ,Y_{n-1},(X_1\rightarrow \cdots \rightarrow X_n))&\mapsto (X_1 \rightarrow X_1\oplus Y_1 \rightarrow X_1\oplus Y_1 \oplus Y_2 \rightarrow \cdots \\&\rightarrow X_n\oplus \oplus ^{n-1}_{i=1}Y_i) \end{aligned}$$

Then

$$\begin{aligned} S_{n}{\mathscr {C}}\otimes _{{\text {B}}_{n-1}{\mathscr {C}}}*\rightarrow {\mathscr {C}}^{\simeq }, \end{aligned}$$

i.e. the one-sided bar construction, is an equivalence in the category of spaces.

Proof

It is enough to consider the fiber of the above map over a fixed object $Z \in {\mathscr {C}}^{\simeq }$. Let $S_{n}{\mathscr {C}}_{Z/}$ be the subcategory of $S_n{\mathscr {C}}$ spanned by objects of the form

$$\begin{aligned} (Z \rightarrow X_{2} \rightarrow \cdots \rightarrow X_n). \end{aligned}$$

This subcategory has coproducts given by taking the coproduct relative to Z, thus its underlying $\infty$-groupoid $S_n{\mathscr {C}}_{Z/}$ is an ${\mathbb {E}}_{\infty }$-monoid in spaces. The action $a_n$ on $S_n{\mathscr {C}}$ restricts to the sub-$\infty$-groupoid $S_n{\mathscr {C}}_{Z/}$ and we claim that

$$\begin{aligned} S_n{\mathscr {C}}_{Z/}\otimes _{{\text {B}}_{n-1}{\mathscr {C}}}*\simeq *. \end{aligned}$$

(46)

We have a map

$$\begin{aligned} g_{n-1}: {\text {B}}_{n-1}{\mathscr {C}}\rightarrow S_n{\mathscr {C}}_{Z/} \end{aligned}$$

given by $g_{n-1}((Y_i)_I) = a_{n}((Y_i)_I,(Z \rightarrow Z \rightarrow \cdots \rightarrow Z))$ and Eq. (46) is equivalent to

$$\begin{aligned} \text{ Cofib }(g_{n-1}) \simeq *. \end{aligned}$$

(47)

We notice that $g_{n-1}$ is surjective on $\pi _0$, thus $\text{ Cofib }(g_{n-1})$ is automatically grouplike, hence it is contractible if and only if its group completion is contractible.

Now we consider the map

$$\begin{aligned} S_n{\mathscr {C}}_{Z/}&\overset{q_{n-1}}{\rightarrow } {\text {B}}_{n-1}{\mathscr {C}}\\ (Z \rightarrow X_2 \rightarrow X_3 \rightarrow \cdots \rightarrow X_n)&\mapsto (X_2/Z,X_3/X_2,\cdots ,X_n/X_{n-1}). \end{aligned}$$

From the definition it is clear that $q_{n-1}\circ g_{n-1}$ is the identity on ${\text {B}}_{n-1}{\mathscr {C}}$. We check that the opposite composition naturally satisfies

$$\begin{aligned} (g_{n-1}\circ q_{n-1}) \sqcup \text{ id}_{S_n{\mathscr {C}}_{Z/}} \simeq \text{ id}_{S_n{\mathscr {C}}_{Z/}} \sqcup \text{ id}_{S_n{\mathscr {C}}_{Z/}}, \end{aligned}$$

(48)

which will prove that $(g_{n-1}\circ q_{n-1})$ is homotopic to the identity upon group completion.

Indeed, the left-hand side of (48) applied to $(Z\rightarrow X_2 \rightarrow \cdots \rightarrow X_{n})$ gives

$$\begin{aligned} Z \rightarrow X_2/Z \oplus Z \oplus Z_2/Z \rightarrow X_3/X_2\oplus X_2/Z \oplus X \oplus X_3/X_2 \oplus X_2/Z \rightarrow \cdots \end{aligned}$$

whereas the right-hand side of (48) applied to $(Z\rightarrow X_2 \rightarrow \cdots \rightarrow X_{n})$ gives

$$\begin{aligned} Z \rightarrow X_2\sqcup _{Z}X_2 \rightarrow X_3\sqcup _{Z}X_3 \rightarrow \cdots . \end{aligned}$$

However, Remark A.17 implies that the fold map

$$\begin{aligned} X_2\sqcup _{Z}X_2 \rightarrow X_2 \end{aligned}$$

has a canonical splitting by the inclusion of $X_2$, i.e.

$$\begin{aligned} X_2\sqcup _{Z}X_2 \simeq X_2 \oplus (X_2/Z). \end{aligned}$$

This finishes the proof of the lemma. $\square$

Proposition A.19

Let ${\mathscr {C}}$ be a Waldhausen category with split cofibrations and finite direct sums. Moreover assume that ${\mathscr {h}}{\mathscr {C}}$ is an additive category,⁴⁹ then the maps (45) induce an equivalence

$$\begin{aligned} {\text {K}}_{\mathrm{add}}({\mathscr {C}}) \rightarrow {\text {K}}({\mathscr {C}}). \end{aligned}$$

Proof

Note that due to the Dold-Kan equivalence, we can think of the spectra ${\text {K}}_{\mathrm{add}}({\mathscr {C}})$ and ${\text {K}}({\mathscr {C}})$ as grouplike ${\mathbb {E}}_{\infty }$-monoids. That is, one has an adjuction

between ${\mathbb {E}}_{\infty }$-monoids and spectra.

Thus, applying the unit of (49) to $\Sigma {\text {K}}_{\mathrm{add}}({\mathscr {C}})$ we obtain

$$\begin{aligned} \Sigma {\text {K}}_{\mathrm{add}}({\mathscr {C}}) = \left| {\text {B}}_{\bullet }{\mathscr {C}}\right| \overset{\simeq }{\rightarrow } \Omega ^{\infty }\left| {\text {B}}_{\bullet }{\mathscr {C}}\right| ^{\mathrm{gp}} \simeq \Omega ^{\infty }\left| {\text {B}}_{\bullet }{\mathscr {C}}^{\mathrm{gp}}\right| , \end{aligned}$$

where in the last term we apply the group completion level-wise and the equivalence follows from the fact that group completion commutes with colimits.

Similarly, one has

$$\begin{aligned} \Sigma {\text {K}}({\mathscr {C}}) = \left| S_{\bullet }{\mathscr {C}}\right| \overset{\simeq }{\rightarrow } \Omega ^{\infty }\left| S_{\bullet }{\mathscr {C}}\right| ^{\mathrm{gp}} \simeq \Omega ^{\infty }\left| S_{\bullet }{\mathscr {C}}^{\mathrm{gp}}\right| , \end{aligned}$$

where as above we apply group completion level-wise and the last equivalence follows for the same reason.

Hence its is enough to show that the maps (45) induce equivalences after group completion.

For each $n\ge 2$ we consider the diagram

where $\imath '_1(X_1,\ldots ,X_{n-1}) = (0,X_1,\ldots ,X_{n-1})$, $\pi _1$ is the projection onto the first factor and $\text{ ev}_1(X_1 \rightarrow \cdots \rightarrow X_n) = X_1$.

We want to prove that the maps $f_{n}$ are equivalences after group completion. It is enough to prove that the right squares are pullback squares after group completion. Since the category ${\mathbb {E}}_{\infty }\text{-Mon }$ is stable, this is the same as proving that the right square is a pushout square after group completion. We notice that the left square is a pushout diagram, so we are reduced to proving that the outer square is a pushout diagram after group completion. This follows from Lemma A.18. $\square$