Reflexive polytopes arising from bipartite graphs with $\gamma$-positivity associated to interior polynomials

Abstract

In this paper, we introduce polytopes ${\mathscr {B}}_G$ arising from root systems $B_n$ and finite graphs G, and study their combinatorial and algebraic properties. In particular, it is shown that ${\mathscr {B}}_G$ is reflexive if and only if G is bipartite. Moreover, in the case, ${\mathscr {B}}_G$ has a regular unimodular triangulation. This implies that the $h^*$-polynomial of ${\mathscr {B}}_G$ is palindromic and unimodal when G is bipartite. Furthermore, we discuss stronger properties, namely the $\gamma$-positivity and the real-rootedness of the $h^*$-polynomials. In fact, if G is bipartite, then the $h^*$-polynomial of ${\mathscr {B}}_G$ is $\gamma$-positive and its $\gamma$-polynomial is given by an interior polynomial (a version of the Tutte polynomial for a hypergraph). The $h^*$-polynomial is real-rooted if and only if the corresponding interior polynomial is real-rooted. From a counterexample to Neggers–Stanley conjecture, we construct a bipartite graph G whose $h^*$-polynomial is not real-rooted but $\gamma$-positive, and coincides with the h-polynomial of a flag triangulation of a sphere.

1 Introduction

A lattice polytope ${\mathscr {P}}\subset {\mathbb R}^d$ is a convex polytope all of whose vertices have integer coordinates. Ardila et al. [1] constructed a unimodular triangulation of the convex hull of the roots of the classical root lattices of type $A_n$, $B_n$, $C_n$ and $D_n$, and gave an alternative proof for the known growth series of these root lattices by using the triangulation.

In [23], lattice polytopes arising from the root system of type $A_n$ and finite graphs were introduced. Let G be a finite simple undirected graph on the vertex set $[d]=\{1, \ldots , d\}$ with the edge set E(G). We denote ${\mathscr {A}}_G \subset {\mathbb R}^d$ the convex hull of the set

$$\begin{aligned} A(G) =\{\mathbf{0}\} \cup \{\pm (\mathbf{e}_i - \mathbf{e}_j) : \{i,j\} \in E(G)\}, \end{aligned}$$

where ${\mathbf{e}}_i$ is the i-th unit coordinate vector in ${\mathbb R}^d$ and $\mathbf{0}$ is the origin of ${\mathbb R}^d$. Then ${\mathscr {A}}_G$ is centrally symmetric, i.e., for any facet ${\mathscr {F}}$ of ${\mathscr {A}}_G$, $-{\mathscr {F}}$ is also a facet of ${\mathscr {A}}_G$, and $\mathbf{0}$ is the unique (relative) interior lattice point of ${\mathscr {A}}_G$. Note that, if G is a complete graph, then ${\mathscr {A}}_G$ coincides with the convex hull of the roots of the root lattices of type $A_n$ studied in [1]. This polytope ${\mathscr {A}}_G$ is called the symmetric edge polytope of G and several combinatorial properties of ${\mathscr {A}}_G$ are well-studied [22, 23, 30].

In this paper, we introduce lattice polytopes arising from the root system of type $B_n$ and finite graphs, and study their algebraic and combinatorial properties. Let ${\mathscr {B}}_G \subset {\mathbb R}^d$ denote the convex hull of the set

$$\begin{aligned} B(G) =\{\mathbf{0} , \pm \mathbf{e}_1, \ldots , \pm \mathbf{e}_d\} \cup \{\pm \mathbf{e}_i \pm \mathbf{e}_j : \{i,j\} \in E(G)\}. \end{aligned}$$

Then $\dim {\mathscr {B}}_G =d$, ${\mathscr {B}}_G$ is centrally symmetric and $\mathbf{0}$ is the unique interior lattice point of ${\mathscr {B}}_G$. Note that, if G is a complete graph, then ${\mathscr {B}}_G$ coincides with the convex hull of the roots of the root lattices of type $B_n$ studied in [1]. Several classes of lattice polytopes arising from graphs have been studied from viewpoints of combinatorics, graph theory, geometric and commutative algebra. In particular, edge polytopes give interesting examples in commutative algebra ( [18, 33,34,35, 43]). Note that edge polytopes of bipartite graphs are called root polytopes and play important roles in the study of generalized permutohedra [41] and interior polynomials [25].

There is a strong relation between ${\mathscr {B}}_G$ and edge polytopes. In fact, one of the key properties of ${\mathscr {B}}_G$ is that ${\mathscr {B}}_G$ is divided into $2^d$ edge polytopes of certain non-simple graphs $\widetilde{G}$ (Proposition 1.1). This fact helps us to find and show interesting properties of ${\mathscr {B}}_G$. In Sect. 1, by using this fact, we will classify graphs G such that ${\mathscr {B}}_G$ has a unimodular covering (Theorem 1.3). We remark that ${\mathscr {A}}_G$ always has a unimodular covering.

On the other hand, the fact that ${\mathscr {B}}_G$ has a unique interior lattice point $\mathbf{0}$ leads us to consider when ${\mathscr {B}}_G$ is reflexive. A lattice polytope ${\mathscr {P}}\subset {\mathbb R}^d$ of dimension d is called reflexive if the origin of ${\mathbb R}^d$ is a unique lattice point belonging to the interior of ${\mathscr {P}}$ and its dual polytope

$$\begin{aligned} {\mathscr {P}}^\vee :=\{{\mathbf{y}}\in {\mathbb R}^d : \langle {\mathbf{x}},{\mathbf{y}}\rangle \le 1 \ \text {for all}\ {\mathbf{x}}\in {\mathscr {P}}\} \end{aligned}$$

is also a lattice polytope, where $\langle {\mathbf{x}},{\mathbf{y}}\rangle$ is the usual inner product of ${\mathbb R}^d$. It is known that reflexive polytopes correspond to Gorenstein toric Fano varieties, and they are related to mirror symmetry (see, e.g., [2, 9]). In each dimension there exist only finitely many reflexive polytopes up to unimodular equivalence [28] and all of them are known up to dimension 4 [27]. Here two lattice polytopes ${\mathscr {P}}\subset {\mathbb R}^d$ and ${\mathscr {P}}' \subset {\mathbb R}^{d'}$ are said to be unimodularly equivalent if there exists an affine map from the affine span $\mathrm{aff} ({\mathscr {P}})$ of ${\mathscr {P}}$ to the affine span $\mathrm{aff} ({\mathscr {P}}')$ of ${\mathscr {P}}'$ that maps ${\mathbb Z}^d \cap \mathrm{aff}({\mathscr {P}})$ bijectively onto ${\mathbb Z}^{d'} \cap \mathrm{aff} ({\mathscr {P}}')$ and that maps ${\mathscr {P}}$ to ${\mathscr {P}}'$. Every lattice polytope is unimodularly equivalent to a full-dimensional one. In Sect. 2, we will classify graphs G such that ${\mathscr {B}}_G$ is a reflexive polytope. In fact, we will show the following.

Theorem 0.1

Let G be a finite graph. Then the following conditions are equivalent:

• (i) ${\mathscr {B}}_G$ is reflexive and has a regular unimodular triangulation;

• (ii) ${\mathscr {B}}_G$ is reflexive;

• (iii) G is a bipartite graph.

We remark that not all unimodular equivalence classes of reflexive polytopes are represented by a polytope of the form ${\mathscr {B}}_G$. Indeed, ${\mathscr {B}}_G$ is always centrally symmetric but not all reflexive polytopes are centrally symmetric. On the other hand, ${\mathscr {A}}_G$ is always (unimodularly equivalent to) a centrally symmetric reflexive polytope. However, the class of reflexive polytopes ${\mathscr {A}}_G$ is different from that of ${\mathscr {B}}_G$. For example, if G is a complete bipartite graph, then ${\mathscr {B}}_G$ is not unimodularly equivalent to ${\mathscr {A}}_{G'}$ for any graph $G'$.

Next, by characterizing when the toric ideal of ${\mathscr {B}}_G$ has a Gröbner basis consisting of squarefree quadratic binomials for a bipartite graph G, we can classify graphs G such that ${\mathscr {B}}_G$ is a reflexive polytope with a flag regular unimodular triangulation. In fact,

Theorem 0.2

Let G be a bipartite graph. Then the following conditions are equivalent:

• (i) The reflexive polytope ${\mathscr {B}}_G$ has a flag regular unimodular triangulation;

• (ii) Any cycle of G of length $\ge 6$ has a chord (“chordal bipartite graph”).

Now, we turn to the discussion of the $h^*$-polynomial $h^*({\mathscr {B}}_G, x)$ of ${\mathscr {B}}_G$. Thanks to the key property (Proposition 1.1), we can compute the $h^*$-polynomial of ${\mathscr {B}}_G$ in terms of that of edge polytopes of some graphs. On the other hand, since it is known that the $h^*$-polynomial of a reflexive polytope with a regular unimodular triangulation is palindromic and unimodal [7], Theorem 0.1 implies that the $h^*$-polynomial of ${\mathscr {B}}_G$ is palindromic and unimodal if G is bipartite. In Sect. 3, we will show a stronger result, namely for any bipartite graph G, the $h^*$-polynomial $h^*({\mathscr {B}}_G, x)$ is $\gamma$-positive. The theory of interior polynomials (a version of the Tutte polynomials for hypergraphs) introduced by Kálmán [24] and the theory of generalized permutohedra [31, 41] play important roles.

Theorem 0.3

Let G be a bipartite graph on [d]. Then $h^*$-polynomial of the reflexive polytope ${\mathscr {B}}_G$ is

$$\begin{aligned} h^*({\mathscr {B}}_G, x) = (x+1)^d I_{\widehat{G}} \left( \frac{4x}{(x+1)^2} \right) , \end{aligned}$$

where $\widehat{G}$ is a connected bipartite graph defined in (1) later and $I_{\widehat{G}}(x)$ is the interior polynomial of $\widehat{G}$. In particular, $h^*({\mathscr {B}}_G, x)$ is $\gamma$-positive. Moreover, $h^*({\mathscr {B}}_G,x)$ is real-rooted if and only if $I_{\widehat{G}}(x)$ is real-rooted.

In addition, we discuss the following relations between interior polynomials and other important polynomials in combinatorics:

• If G is bipartite, then the interior polynomial of $\widehat{G}$ is described in terms of k-matchings of G (Proposition 3.4);

• If G is a forest, then the interior polynomial of $\widehat{G}$ coincides with the matching generating polynomial of G (Proposition 3.5);

• If G is a bipartite permutation graph associated with a poset P, then the interior polynomial of $\widehat{G}$ coincides with the P-Eulerian polynomial of P (Proposition 3.6).

By using these results and a poset appearing in [47] as a counterexample to Neggers–Stanley conjecture, we will construct an example of a centrally symmetric reflexive polytope such that the $h^*$-polynomial is $\gamma$-positive and not real-rooted (Example 3.7). This $h^*$-polynomial coincides with the h-polynomial of a flag triangulation of a sphere (Proposition 3.8). Hence this example is a counterexample to “Real Root Conjecture” that has been already disproved by Gal [11]. Finally, inspired by a simple description for the $h^*$-polynomials of symmetric edge polytopes of complete bipartite graphs [23], we will compute the $h^*$-polynomial of ${\mathscr {B}}_G$ when G is a complete bipartite graph (Example 3.9).

2 A key property of ${\mathscr {B}}_G$ and unimodular coverings

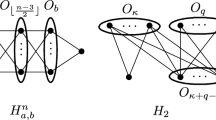
In this section, we see a relation between ${\mathscr {B}}_G$ and edge polytopes. First, we recall what edge polytopes are. Let G be a graph on [d] (only here we do not assume that G has no loops) with the edge (including loop) set E(G). Then the edge polytope $P_G$ of G is the convex hull of $\{\mathbf{e}_i + \mathbf{e}_j : \{i,j\} \in E(G)\}$. Note that $P_G$ is a (0, 1)-polytope if and only if G has no loops. Given a graph G on [d], let $\widetilde{G}$ be a graph on $[d+1]$ whose edge set is

$$\begin{aligned} E(G) \cup \{ \{1, d+1\}, \{2, d+1\}, \ldots , \{d+1,d+1\} \}. \end{aligned}$$

Here, $\{d+1,d+1\}$ is a loop (a cycle of length 1) at $d+1$. See Fig. 1. If G is a

Fig. 1

Example of $\widetilde{G}$

bipartite graph with a bipartition $V_1 \cup V_2 =[d]$, let $\widehat{G}$ be a connected bipartite graph on $[d+2]$ whose edge set is

$$\begin{aligned} E(\widehat{G}) = E(G) \cup \{ \{i, d+1\} : i \in V_1\} \cup \{ \{j, d+2\} : j \in V_2 \cup \{d+1\}\}. \end{aligned}$$

(1)

See Fig. 2.

Fig. 2

Example of $\widehat{G}$

Now, we show the key proposition of this paper. Given $\varepsilon = (\varepsilon _1,\ldots , \varepsilon _d) \in \{-1,1\}^d$, let ${\mathscr {O}}_\varepsilon$ denote the closed orthant $\{ (x_1,\ldots , x_d) \in {\mathbb R}^d : x_i \varepsilon _i \ge 0 \text{ for } \text{ all } i \in [d]\}$. For a lattice polytope ${\mathscr {P}}$, let ${\text {Vol}}({\mathscr {P}})$ denote the normalized volume of ${\mathscr {P}}$.

Proposition 1.1

Work with the same notation as above. Then we have the following:

• (a) Each ${\mathscr {B}}_G \cap {\mathscr {O}}_\varepsilon$ is the convex hull of the set $B(G) \cap {\mathscr {O}}_\varepsilon$ and unimodularly equivalent to the edge polytope $P_{\widetilde{G}}$ of $\widetilde{G}$. Moreover, if G is bipartite, then ${\mathscr {B}}_G \cap {\mathscr {O}}_\varepsilon$ is unimodularly equivalent to the edge polytope $P_{\widehat{G}}$ of $\widehat{G}$. In particular, one has ${\text {Vol}}({\mathscr {B}}_G)=2^d{\text {Vol}}(P_{\widetilde{G}})$.

• (b) The edge polytope of G is a face of ${\mathscr {B}}_G$.

Proof

(a) Let ${\mathscr {P}}$ be the convex hull of the set $B(G) \cap {\mathscr {O}}_\varepsilon$. The inclusion ${\mathscr {B}}_G \cap {\mathscr {O}}_\varepsilon \supset {\mathscr {P}}$ is trivial. Let ${\mathbf{x}}= (x_1,\ldots ,x_d) \in {\mathscr {B}}_G \cap {\mathscr {O}}_\varepsilon$. Then ${\mathbf{x}}= \sum _{i=1}^s \lambda _i {\mathbf{a}}_i$, where $\lambda _i >0$, $\sum _{i=1}^s \lambda _i = 1$, and each ${\mathbf{a}}_i$ belongs to B(G). Suppose that the k-th component of ${\mathbf{a}}_i$ is positive and the k-th component of ${\mathbf{a}}_j$ is negative. Then ${\mathbf{a}}_i$ and ${\mathbf{a}}_j$ satisfy

$$\begin{aligned} {\mathbf{a}}_i + {\mathbf{a}}_j = ({\mathbf{a}}_i - {\mathbf{e}}_k )+ ({\mathbf{a}}_j + {\mathbf{e}}_k), \end{aligned}$$

where ${\mathbf{a}}_i - {\mathbf{e}}_k, {\mathbf{a}}_j + {\mathbf{e}}_k \in B(G)$. By using the above relations for ${\mathbf{a}}_i + {\mathbf{a}}_j$ finitely many times, we may assume that the k-th component of each vector ${\mathbf{a}}_i$ is nonnegative (resp. nonpositive) if $x_k \ge 0$ (resp. $x_k \le 0$). Then each ${\mathbf{a}}_i$ belongs to $B(G) \cap {\mathscr {O}}_\varepsilon$ and hence ${\mathbf{x}}\in {\mathscr {P}}$.

Next, we show that each ${\mathscr {B}}_G \cap {\mathscr {O}}_{\varepsilon }$ is unimodularly equivalent to the edge polytope $P_{\widetilde{G}}$. Set ${\mathscr {Q}}={\mathscr {B}}_G \cap {\mathscr {O}}_{(1,\ldots ,1)}$. It is easy to see that each ${\mathscr {B}}_G \cap {\mathscr {O}}_{\varepsilon }$ is unimodularly equivalent to ${\mathscr {Q}}$ for all $\varepsilon$. Moreover, one has

$$\begin{aligned} B(G) \cap {\mathscr {O}}_{(1,\ldots ,1)} = \{\mathbf{0}, \mathbf{e}_1, \ldots , \mathbf{e}_d\} \cup \{\mathbf{e}_i + \mathbf{e}_j : \{i,j\} \in E(G)\}. \end{aligned}$$

Hence $P_{\widetilde{G}}$ is unimodularly equivalent to ${\mathscr {Q}}\times \{2\}$. In particular, ${\mathscr {B}}_G$ consists of $2^d$ copies of the edge polytope $P_{\widetilde{G}}$. This implies ${\text {Vol}}({\mathscr {B}}_G)=2^d{\text {Vol}}(P_{\widetilde{G}})$. Similarly, if G is bipartite, it follows that $P_{\widehat{G}}$ is unimodularly equivalent to ${\mathscr {Q}}\times \{1\}^2$.

(b) The edge polytope $P_G$ of G is the face of ${\mathscr {B}}_G$ with the supporting hyperplane ${\mathscr {H}}= \{ (x_1,\ldots , x_d) \in {\mathbb R}^d : x_1 + \cdots + x_d= 2 \}.$ $\square$

Let ${\mathscr {P}}\subset {\mathbb R}^d$ be a lattice polytope. A (lattice) covering of ${\mathscr {P}}$ is a finite collection $\Delta$ of lattice simplices such that the union of the simplices in $\Delta$ is ${\mathscr {P}}$, i.e., ${\mathscr {P}}=\bigcup _{\delta \in \Delta } \delta$. A (lattice) triangulation of ${\mathscr {P}}$ is a covering $\Delta$ of ${\mathscr {P}}$ such that

• (i) every face of a member of $\Delta$ is in $\Delta$, and

• (ii) any two elements of $\Delta$ intersect in a common (possibly empty) face.

Note that their interiors may overlap in coverings but not in triangulations. A unimodular simplex is a lattice simplex whose normalized volume equals 1. We now focus on the following properties.

• (VA) We say that ${\mathscr {P}}$ is very ample if for all sufficiently large $k \in {\mathbb Z}_{\ge 1}$ and for all ${\mathbf{x}}\in k {\mathscr {P}}\cap {\mathbb Z}^d$, there exist ${\mathbf{x}}_1,\ldots ,{\mathbf{x}}_k \in {\mathscr {P}}\cap {\mathbb Z}^d$ with ${\mathbf{x}}={\mathbf{x}}_1+\cdots +{\mathbf{x}}_k$.

• (IDP) We say that ${\mathscr {P}}$ possesses the integer decomposition property (or is IDP for short) if for all $k \in {\mathbb Z}_{\ge 1}$ and for all ${\mathbf{x}}\in k {\mathscr {P}}\cap {\mathbb Z}^d$, there exist ${\mathbf{x}}_1,\ldots ,{\mathbf{x}}_k \in {\mathscr {P}}\cap {\mathbb Z}^d$ with ${\mathbf{x}}={\mathbf{x}}_1+\cdots +{\mathbf{x}}_k$.

• (UC) We say that ${\mathscr {P}}$ has a unimodular covering if ${\mathscr {P}}$ admits a lattice covering consisting of unimodular simplices.

• (UT) We say that ${\mathscr {P}}$ has a unimodular triangulation if ${\mathscr {P}}$ admits a lattice triangulation consisting of unimodular simplices.

These properties satisfy the implications

$$\begin{aligned} \mathrm{(UT)} \Rightarrow \mathrm{(UC)} \Rightarrow \mathrm{(IDP)} \Rightarrow \mathrm{(VA)}, \end{aligned}$$

see, e.g., [13, Section 4.2]. On the other hand, it is known that the opposite implications are false. However, for edge polytopes, the first three properties are equivalent ( [8, 33, 43]). We say that a graph G satisfies the odd cycle condition if, for any two odd cycles $C_1$ and $C_2$ that belong to the same connected component of G and have no common vertices, there exists an edge $\{i,j\}$ of G such that i is a vertex of $C_1$ and j is a vertex of $C_2$.

Proposition 1.2

[8, 33, 43] Let G be a finite (not necessarily simple) graph. Suppose that there exists an edge $\{i,j\}$ of G whenever G has loops at i and j with $i \ne j$. Then the following conditions are equivalent:

• (i) $P_G$ has a unimodular covering;

• (ii) $P_G$ is IDP;

• (iii) $P_G$ is very ample;

• (iv) G satisfies the odd cycle condition.

We now show that the same assertion holds for ${\mathscr {B}}_G$. Namely, we prove the following.

Theorem 1.3

Let G be a finite simple graph. Then the following conditions are equivalent:

• (i) ${\mathscr {B}}_G$ has a unimodular covering;

• (ii) ${\mathscr {B}}_G$ is IDP;

• (iii) ${\mathscr {B}}_G$ is very ample;

• (iv) G satisfies the odd cycle condition.

Before proving Theorem 1.3, we recall a well-known result.

Lemma 1.4

Every face of a very ample polytope is very ample.

Proof

Let ${\mathscr {P}}\subset {\mathbb R}^d$ be a lattice polytope of dimension d. Assume that there exists a facet ${\mathscr {F}}$ of ${\mathscr {P}}$ such that ${\mathscr {F}}$ is not very ample. Then we should show that ${\mathscr {P}}$ is not very ample. Let ${\mathscr {H}}\subset {\mathbb R}^d$ be the hyperplane in ${\mathbb R}^d$ defined as ${\mathscr {H}}=\{ {\mathbf{x}}\in {\mathbb R}^d \mid \langle {\mathbf{x}}, {\mathbf{a}}\rangle =b \}$, with some lattice point ${\mathbf{a}}\in {\mathbb Z}^d$ and some integer b such that ${\mathscr {F}}={\mathscr {H}}\cap {\mathscr {P}}$ and ${\mathscr {P}}\subset {\mathscr {H}}^{(+)}$, where ${\mathscr {H}}^{(+)}=\{ {\mathbf{x}}\in {\mathbb R}^d \mid \langle {\mathbf{x}}, {\mathbf{a}}\rangle \le b \}$. Since ${\mathscr {F}}$ is not very ample, there exist a positive integer k and a lattice point ${\mathbf{x}}\in k {\mathscr {F}}\cap {\mathbb Z}^d$ such that there are no lattice points ${\mathbf{x}}_1, \ldots , {\mathbf{x}}_k$ in ${\mathscr {F}}$ with ${\mathbf{x}}={\mathbf{x}}_1+\cdots +{\mathbf{x}}_k$. Suppose that there are lattice points ${\mathbf{y}}_1, \ldots , {\mathbf{y}}_k$ in ${\mathscr {P}}$ with ${\mathbf{x}}={\mathbf{y}}_1+\cdots +{\mathbf{y}}_k$. Then for each ${\mathbf{y}}_i$, one has $\langle {\mathbf{y}}_i, {\mathbf{a}}\rangle \le b$. Since $\langle {\mathbf{x}}, {\mathbf{a}}\rangle = kb$, it follows that for each i, $\langle {\mathbf{y}}_i, {\mathbf{a}}\rangle =b$, hence, ${\mathbf{y}}_i \in {\mathscr {F}}$. This is a contradiction. Therefore, ${\mathscr {P}}$ is not very ample. $\square$

Remark 1.5

Similarly, we can prove that every face of an IDP polytope is IDP. Moreover, it is clear that if a lattice polytope has a unimodular triangulation (resp. a unimodular covering), then so does any face.

Now, we prove Theorem 1.3.

Proof of Theorem 1.3

First, implications (i) $\Rightarrow$ (ii) $\Rightarrow$ (iii) hold in general.

(iii) $\Rightarrow$ (iv): Suppose that G does not satisfy the odd cycle condition. By Proposition 1.2, the edge polytope $P_G$ of G is not very ample. Since $P_G$ is a face of ${\mathscr {B}}_G$ by Proposition 1.1 (b) and Lemma 1.4, ${\mathscr {B}}_G$ is not very ample.

(iv) $\Rightarrow$ (i): Suppose that G satisfies the odd cycle condition. Then so does $\widetilde{G}$. Hence Proposition 1.2 guarantees that $P_{\widetilde{G}}$ has a unimodular covering. By Proposition 1.1 (a), ${\mathscr {B}}_G$ has a unimodular covering. $\square$

Example 1.6

Let G be a graph in Fig. 3. Since G satisfies the odd cycle condition,

Fig. 3

A graph in [34]

${\mathscr {B}}_G$ has a unimodular covering. However, since the edge polytope $P_G$ has no regular unimodular triangulations [34], so does ${\mathscr {B}}_G$ by Proposition 1.1 (b). We do not know whether ${\mathscr {B}}_G$ has a (nonregular) unimodular triangulation or not.

3 Reflexive polytopes and flag triangulations of ${\mathscr {B}}_G$

In the present section, we classify graphs G such that

• ${\mathscr {B}}_G$ is a reflexive polytope.

• ${\mathscr {B}}_G$ is a reflexive polytope with a flag regular unimodular triangulation.

In other words, we prove Theorems 0.1 and 0.2. First, we see some examples that ${\mathscr {B}}_G$ is reflexive.

Examples 2.1

(a) If G is an empty graph, then ${\mathscr {B}}_G$ is a cross polytope.

(b) Let G be a complete graph with 2 vertices. Then ${\mathscr {B}}_G \cap {\mathbb Z}^2$ is the column vectors of the matrix

$$\begin{aligned} \begin{pmatrix} 0 &{}\quad 1 &{}\quad 0 &{}\quad 1 &{}\quad 1 &{}\quad -1 &{} \quad 0 &{}\quad -1 &{}\quad -1\\ 0 &{}\quad 0 &{} \quad 1 &{}\quad 1 &{}\quad -1 &{}\quad 0 &{}\quad -1 &{}\quad -1 &{}\quad 1 \end{pmatrix}, \end{aligned}$$

and ${\mathscr {B}}_G$ is a reflexive polytope having a regular unimodular triangulation. See Fig. 4. Since the matrix

$$\begin{aligned} \begin{pmatrix} 1 &{}\quad 0 &{}\quad 1 &{} \quad 1 \\ 0 &{} \quad 1 &{}\quad 1 &{}\quad -1 \end{pmatrix} \end{aligned}$$

is not unimodular, we cannot apply [36, Lemma 2.11] to show this fact.

Fig. 4

Regular unimodular triangulation of ${\mathscr {B}}_G$ in Examples 2.1 (b)

In order to show that a lattice polytope is reflexive, we can use an algebraic technique on Gröbner bases. We recall basic materials and notation on toric ideals. Let $K[\mathbf{t}^{\pm 1}, s] = K[t_{1}^{\pm 1}, \ldots , t_{d}^{\pm 1}, s]$ be the Laurent polynomial ring in $d+1$ variables over a field K. If ${\mathbf{a}}= (a_{1}, \ldots , a_{d}) \in {\mathbb Z}^{d}$, then $\mathbf{t}^{{\mathbf{a}}}s$ is the Laurent monomial $t_{1}^{a_{1}} \cdots t_{d}^{a_{d}}s \in K[\mathbf{t}^{\pm 1}, s]$. Let ${\mathscr {P}}\subset {\mathbb R}^{d}$ be a lattice polytope and ${\mathscr {P}}\cap {\mathbb Z}^d=\{{\mathbf{a}}_1,\ldots ,{\mathbf{a}}_n\}$. Then, the toric ring of ${\mathscr {P}}$ is the subring $K[{\mathscr {P}}]$ of $K[\mathbf{t}^{\pm 1}, s]$ generated by $\{{\mathbf{t}}^{{\mathbf{a}}_1}s ,\ldots ,{\mathbf{t}}^{{\mathbf{a}}_n}s \}$ over K. We regard $K[{\mathscr {P}}]$ as a graded ring by setting each $\text {deg } t_i =0$ and $\text {deg } s=1$. Note that, if two lattice polytopes are unimodularly equivalent, then their toric rings are isomorphic as graded rings. Let $K[{\mathbf{x}}]=K[x_1,\ldots , x_n]$ denote the polynomial ring in n variables over K. The toric ideal $I_{{\mathscr {P}}}$ of ${\mathscr {P}}$ is the kernel of the surjective homomorphism $\pi : K[{\mathbf{x}}] \rightarrow K[{\mathscr {P}}]$ defined by $\pi (x_i)={\mathbf{t}}^{{\mathbf{a}}_i}s$ for $1 \le i \le n$. It is known that $I_{{\mathscr {P}}}$ is generated by homogeneous binomials. See, e.g., [13, Chapter 3] and [48, Chapter 4]. Let < be a monomial order on $K[\mathbf{x}]$ and $\mathrm{in}_{<}(I_{{\mathscr {P}}})$ the initial ideal of $I_{{\mathscr {P}}}$ with respect to <. The initial ideal $\mathrm{in}_{<}(I_{{\mathscr {P}}})$ is called squarefree (resp. quadratic) if $\mathrm{in}_{<}(I_{{\mathscr {P}}})$ is generated by squarefree (resp. quadratic) monomials. We recall a relation between initial ideal $\mathrm{in}_{<}(I_{{\mathscr {P}}})$ and a triangulation of ${\mathscr {P}}$. Set

$$\begin{aligned} \Delta ({\mathscr {P}},<)= \left\{ \mathrm{conv} (S) : S \subset {\mathscr {P}}\cap {\mathbb Z}^d, \prod _{{\mathbf{a}}_i \in S} x_i \notin \sqrt{ \mathrm{in}_{<}(I_{{\mathscr {P}}})} \right\} . \end{aligned}$$

Then we have

Proposition 2.2

[48, Theorem 8.3] Let ${\mathscr {P}}\subset {\mathbb R}^d$ be a lattice polytope and < a monomial order on $K[\mathbf{x}]$. Then $\Delta ({\mathscr {P}}, <)$ is a regular triangulation of ${\mathscr {P}}$.

Here we say that a lattice triangulation $\Delta$ of a lattice polytope ${\mathscr {P}}\subset {\mathbb R}^d$ is regular if it arises as the projection of the lower hull of a lifting of the lattice points of ${\mathscr {P}}$ into ${\mathbb R}^{d+1}$. A simplicial complex is called flag if all minimal non-faces contain only two elements. We say that a lattice triangulation is flag if it is flag as a simplicial complex. Then we have

Proposition 2.3

[48, Corollary 8.9] Let ${\mathscr {P}}\subset {\mathbb R}^d$ be a lattice polytope and < a monomial order on $K[\mathbf{x}]$. Suppose that any lattice point in ${\mathbb Z}^{d+1}$ is a linear integer combination of the lattice points in ${\mathscr {P}}\times \{1\}$. Then $\Delta ({\mathscr {P}}, <)$ is unimodular (resp. flag unimodular) if and only if $\mathrm{in}_{<}(I_{{\mathscr {P}}})$ is squarefree (resp. squarefree quadratic).

By definition, a lattice polytope ${\mathscr {P}}\subset {\mathbb R}^d$ is reflexive if and only if the lattice distance between the origin $\mathbf{0}$ and all affine hyperplanes generated by facets of ${\mathscr {P}}$ equals 1. Hence if $\mathbf{0}$ is contained in the interior of ${\mathscr {P}}$, and ${\mathscr {P}}$ has a unimodular triangulation such that $\mathbf{0}$ is a vertex of any maximal simplex of the triangulation, then ${\mathscr {P}}$ is reflexive. Now, we introduce an algebraic technique to show that a lattice polytope is reflexive.

Lemma 2.4

[16, Lemma 1.1] Let ${\mathscr {P}}\subset {\mathbb R}^d$ be a lattice polytope of dimension d such that the origin of ${\mathbb R}^d$ is contained in its interior and ${\mathscr {P}}\cap {\mathbb Z}^d=\{{\mathbf{a}}_1,\ldots ,{\mathbf{a}}_n \}$. Suppose that ${\mathbb Z}^d = \{\sum _{i=1}^n z_i {\mathbf{a}}_i : z_i \in {\mathbb Z}\}$ and there exists an ordering of the variables $x_{i_1}< \cdots < x_{i_n}$ for which ${\mathbf{a}}_{i_1}= \mathbf {0}$ such that the initial ideal $\text {in}_{<}(I_{{\mathscr {P}}})$ of $I_{{\mathscr {P}}}$ with respect to the reverse lexicographic order < on $K[{\mathbf{x}}]$ induced by the ordering is squarefree. Then ${\mathscr {P}}$ is reflexive and has a regular unimodular triangulation.

Proof

The assertion follows since $\mathbf{0}$ is contained in the interior of ${\mathscr {P}}$ and since the triangulation $\Delta ({\mathscr {P}}, <)$ is unimodular and $\mathbf{0}$ is a vertex of any maximal simplex of the triangulation. $\square$

By using this technique, several families of reflexive polytopes with regular unimodular triangulations are constructed in [15,16,17, 19,20,21, 37]. In order to apply Lemma 2.4 to show Theorem 0.1, we see a relation between the toric ideal of ${\mathscr {B}}_{G}$ and that of $P_{\widetilde{G}}$. Let G be a simple graph on [d] with edge set E(G) and let $R_G$ denote the polynomial ring in $2d+1+4 |E(G)|$ variables

$$\begin{aligned} z, \ \ x_{i+}, x_{i-} \ \ (1 \le i \le d), \ \ y_{ij++}, y_{ij--}, y_{ij+-}, y_{ij-+} \ \ (\{i,j\} \in E(G)) \end{aligned}$$

over a field K. Then the toric ideal $I_{{\mathscr {B}}_G}$ of ${\mathscr {B}}_G$ is the kernel of a ring homomorphism $\pi : R_G \rightarrow K[t_1^\pm ,\ldots ,t_d^\pm , s]$ defined by $\pi (z) = s$, $\pi (x_{i+}) = t_i s$, $\pi (x_{i-}) = t_i^{-1} s$, $\pi (y_{ij++}) = t_i t_j s$, $\pi (y_{ij--}) = t_i^{-1} t_j^{-1} s$, $\pi (y_{ij+-}) = t_i t_j^{-1} s$, and $\pi (y_{ij-+}) = t_i^{-1} t_j s$. Let $S_G$ denote the subring of $R_G$ generated by the $d+1+ |E(G)|$ variables

$$\begin{aligned} z, \ \ x_{i+} \ \ (1 \le i \le d), \ \ y_{ij++} \ \ (\{i,j\} \in E(G)). \end{aligned}$$

Then the toric ideal $I_{P_{\widetilde{G}}}$ of $P_{\widetilde{G}}$ is the kernel of $\pi |_{S_G}$. For each $\varepsilon = (\varepsilon _1,\ldots , \varepsilon _d) \in \{-1,1\}^d$, we define a ring homomorphism $\varphi _\varepsilon : S_G \rightarrow R_G$ by $\varphi _\varepsilon (x_{i+}) =x_{i \alpha }$ and $\varphi _\varepsilon (y_{ij++}) =y_{ij \alpha \beta }$ where $\alpha$ is the sign of $\varepsilon _i$ and $\beta$ is the sign of $\varepsilon _j$. In particular, $\varphi _{(1,\ldots ,1)}: S_G \rightarrow R_G$ is an inclusion map.

Lemma 2.5

Let ${\mathscr {G}}$ be a Gröbner basis of $I_{P_{\widetilde{G}}}$ with respect to a reverse lexicographic order $<_S$ on $S_G$ such that $z< \{x_{i+}\} < \{y_{ij++}\}$. Let $<_R$ be a reverse lexicographic order such that $z< \{x_{i+}, x_{i-}\} < \{y_{ij++}, y_{ij--}, y_{ij+-}, y_{ij-+}\}$ and that (i) $\varphi _\varepsilon (x_{i+})<_R \varphi _\varepsilon (x_{j+}) \text{ if } x_{i+} <_S x_{j+}$ and (ii) $\varphi _\varepsilon (y_{ij++})<_R \varphi _\varepsilon (y_{k\ell ++}) \text{ if } y_{ij++} <_S y_{k\ell ++}$ for all $\varepsilon \in \{-1,1\}^d$. Then

$$\begin{aligned} {\mathscr {G}}'= & {} \left( \bigcup _{\varepsilon \in \{-1,1\}^d} \varphi _\varepsilon ({\mathscr {G}}) \right) \cup \{ \underline{ x_{i \alpha } y_{i j \beta \gamma } } - x_{j \gamma } z : \{i,j\} \in E(G), \alpha \ne \beta \}\\&\cup \{ \underline{ y_{i j \alpha \gamma } y_{i k \beta \delta } } - x_{j \gamma } x_{k \delta } : \{i,j\} ,\{i,k\}\in E(G), \alpha \ne \beta \} \\&\cup \{ \underline{ x_{i+} x_{i-}} - z^2 : 1 \le i \le d \} \end{aligned}$$

is a Gröbner basis of $I_{{\mathscr {B}}_G}$ with respect to $<_R$, where the underlined monomial is the initial monomial of each binomial. (Here we identify $y_{ij \alpha \beta }$ with $y_{ji \beta \alpha }$.) In particular, if $\mathrm{in}_{<_S}( I_{P_{\widetilde{G}}})$ is squarefree (resp. quadratic), then so is $\mathrm{in}_{<_R} (I_{{\mathscr {B}}_G})$.

Proof

It is easy to see that ${\mathscr {G}}'$ is a subset of $I_{{\mathscr {B}}_G}$. Assume that ${\mathscr {G}}'$ is not a Gröbner basis of $I_{{\mathscr {B}}_G}$ with respect to $<_R$. Let $\mathrm{in}({\mathscr {G}}') = \langle \mathrm{in}_{<_R} (g) : g \in {\mathscr {G}}' \rangle$. By [13, Theorem 3.11], there exists a non-zero irreducible homogeneous binomial $f = u-v \in I_{{\mathscr {B}}_G}$ such that neither u nor v belongs to $\mathrm{in}({\mathscr {G}}')$. Since both u and v are divided by none of $x_{i+} x_{i-},$ $x_{i \alpha } y_{i j \beta \gamma }$, $y_{i j \alpha \gamma } y_{i k \beta \delta }$ ($\alpha \ne \beta$), they are of the form

$$\begin{aligned} u= \prod _{i \in I} ({x_{i \alpha _i}})^{u_i} \prod _{\{j,k\} \in E_1} (y_{j k \alpha _j \alpha _k})^{u_{jk}}, \ \ \ v= \prod _{i \in I'} (x_{i \alpha _i'})^{v_i} \prod _{\{j,k\} \in E_2} (y_{j k \alpha _j' \alpha _k'})^{v_{jk}}, \end{aligned}$$

where $I, I' \subset [d]$, $E_1, E_2 \subset E(G)$ and $0 < u_i, u_{jk}, v_i, v_{jk} \in {\mathbb Z}$. Since f belongs to $I_{{\mathscr {B}}_G}$, the exponent of $t_\ell$ in $\pi (u)$ and $\pi (v)$ are the same. Hence, one of $x_{\ell \alpha _\ell }$ and $y_{\ell m \alpha _\ell \alpha _m}$ appears in u if and only if one of $x_{\ell \alpha _\ell '}$ and $y_{\ell n \alpha _\ell ' \alpha _n'}$ appears in v with $\alpha _\ell = \alpha _\ell '$. Let $\varepsilon$ be a vector in $\{-1,1\}^d$ such that the sign of the i-th component of $\varepsilon$ is $\alpha _i$ if one of $x_{i \alpha _i}$ and $y_{i j \alpha _i \alpha _j}$ appears in u. Then f belongs to the ideal $\varphi _\varepsilon (I_{P_{\widetilde{G}}})$. Let $f' \in I_{P_{\widetilde{G}}}$ be a binomial such that $\varphi _\varepsilon (f') = f$. Since ${\mathscr {G}}$ is a Gröbner basis of $I_{P_{\widetilde{G}}}$, there exists a binomial $g \in {\mathscr {G}}$ whose initial monomial $\mathrm{in}_{<_R} (g)$ divides the one of the monomials in $f'$. By the definition of $<_R$, we have $\mathrm{in}_{<_R} (\varphi _\varepsilon (g) ) =\varphi _\varepsilon (\mathrm{in}_{<_R} (g) )$. Hence $\mathrm{in}_{<_R} (\varphi _\varepsilon (g) )$ divides one of the monomials in $f = \varphi _\varepsilon (f')$. This is a contradiction. $\square$

Using this Gröbner basis with respect to a reverse lexicographic order, we verify which ${\mathscr {B}}_G$ is a reflexive polytope. Namely, we prove Theorem 0.1.

Proof of Theorem 0.1

The implication (i) $\Rightarrow$ (ii) is trivial.

(ii) $\Rightarrow$ (iii): Suppose that G is not bipartite. Let $G_1, \ldots , G_s$ be the connected components of G and let $d_i$ be the number of vertices of $G_i$. In particular, we have $d = \sum _{i=1}^s d_i$. Since G is not bipartite, we may assume that $G_1$ is not bipartite. Let ${\mathbf{w}}= \sum _{i=1}^s {\mathbf{w}}_i$, where ${\mathbf{w}}_i = \sum _{k=1}^\ell {\mathbf{e}}_{p_k} \in {\mathbb R}^d$ if $G_i$ is a non-bipartite graph on the vertex set $\{p_1, \ldots , p_\ell \}$, and ${\mathbf{w}}_i = \sum _{k=1}^\ell 2 {\mathbf{e}}_{p_k} \in {\mathbb R}^d$ if $G_i$ is a bipartite graph whose vertices are divided into two independent sets $\{p_1, \ldots , p_\ell \}$ and $\{q_1, \ldots , q_m\}$. It then follows that ${\mathscr {H}}= \{ {\mathbf {x}}\in {\mathbb R}^d : \langle {\mathbf {w}}, {\mathbf {x}}\rangle = 2 \}$ is a supporting hyperplane of ${\mathscr {B}}_G$ and the corresponding face ${\mathscr {F}}_{\mathbf{w}}= {\mathscr {B}}_G \cap {\mathscr {H}}$ is the convex hull of $H=\bigcup _{i=1}^s H_i$, where $H_i= \{\mathbf{e}_u + \mathbf{e}_v : \{u,v\} \in E(G_i)\}$ if $G_i$ is not bipartite, and $H_i= \{\mathbf{e}_u + \mathbf{e}_v : \{u,v\} \in E(G_i)\} \cup \{{\mathbf{e}}_{p_1}, \ldots , {\mathbf{e}}_{p_\ell }\} \cup \{\mathbf{e}_{p_k} - \mathbf{e}_v : \{p_k,v\} \in E(G_i)\}$ if $G_i$ is a bipartite graph with ${\mathbf{w}}_i = \sum _{k=1}^\ell 2 {\mathbf{e}}_{p_k} \in {\mathbb R}^d$. We will show that ${\mathscr {F}}_{\mathbf{w}}$ is a facet of ${\mathscr {B}}_G$. The convex hull of $\{\mathbf{e}_u + \mathbf{e}_v : \{u,v\} \in E(G_i)\}$ is the edge polytope $P_{G_i}$ of $G_i$ and it is known [33, Proposition 1.3] that

$$\begin{aligned} \dim P_{G_i} = \left\{ \begin{array}{cc} d_i-1 &{} \text{ if } G_i \text{ is } \text{ not } \text{ bipartite, }\\ d_i-2 &{} \text{ otherwise. } \end{array} \right. \end{aligned}$$

If $G_i$ is not bipartite, then the dimension of $\mathrm{conv}(H_i) = P_{G_i}$ is $d_i-1$. If $G_i$ is bipartite, then $d_i -2 = \dim P_{G_i} < \dim \mathrm{conv}(H_i)$ since $P_{G_i} \subset \mathrm{conv}(H_i)$ and a hyperplane ${\mathscr {H}}= \{ (x_1,\ldots , x_d) \in {\mathbb R}^d : x_1 + \cdots + x_d= 2 \}$ satisfies ${\mathbf{e}}_{p_1} \notin {\mathscr {H}}\supset P_{G_i}$. Hence the dimension of the face ${\mathscr {F}}_{\mathbf{w}}$ is at least $s -1 + \sum _{i=1}^s (d_i-1) = d-1$, i.e., ${\mathscr {F}}_{\mathbf{w}}$ is a facet of ${\mathscr {B}}_G$. Since $G_1$ is not bipartite, we have $\frac{1}{2} \cdot {\mathbf{w}}\notin {\mathbb Z}^d$. Thus ${\mathscr {B}}_G$ is not reflexive.

(iii) $\Rightarrow$ (i): Suppose that G is bipartite. Let $<_S$ and $<_R$ be any reverse lexicographic orders satisfying the condition in Lemma 2.5. It is known [13, Theorem 5.24] that any triangulation of the edge polytope of a bipartite graph is unimodular. By [48, Corollary 8.9], the initial ideal of the toric ideal of $P_{\widehat{G}}$ with respect to $<_S$ is squarefree. Thanks to Lemmas 2.4 and 2.5, we have the desired conclusion. $\square$

We now give a theorem on quadratic Gröbner bases of $I_{{\mathscr {B}}_G}$ when G is bipartite. This theorem implies that Theorem 0.2. The same result is known for edge polytopes ( [35]).

Theorem 2.6

Let G be a bipartite graph. Then the following conditions are equivalent:

• (i) The toric ideal $I_{{\mathscr {B}}_G}$ of ${\mathscr {B}}_G$ has a squarefree quadratic initial ideal

  (i.e., ${\mathscr {B}}_G$ has a flag regular unimodular triangulation);

• (ii) The toric ring $K[{\mathscr {B}}_G]$ of ${\mathscr {B}}_G$ is a Koszul algebra;

• (iii) The toric ideal $I_{{\mathscr {B}}_G}$ of ${\mathscr {B}}_G$ is generated by quadratic binomials;

• (iv) Any cycle of G of length $\ge 6$ has a chord (“chordal bipartite graph”).

Proof

Implications (i) $\Rightarrow$ (ii) $\Rightarrow$ (iii) hold in general.

(iii) $\Rightarrow$ (iv): Suppose that G has a cycle of length $\ge 6$ without chords. By the theorem in [35], the toric ideal of $P_G$ is not generated by quadratic binomials. Since the edge polytope $P_G$ is a face of ${\mathscr {B}}_G$, the toric ring $K[P_G]$ is a combinatorial pure subring [32] of $K[{\mathscr {B}}_G]$. Hence $I_{{\mathscr {B}}_G}$ is not generated by quadratic binomials.

(iv) $\Rightarrow$ (i): Suppose that any cycle of G of length $\ge 6$ has a chord. By Lemma 2.5, it is enough to show that the initial ideal of $I_{P_{\widehat{G}}}$ is squarefree and quadratic with respect to a reverse lexicographic order $<_S$ such that $z< \{x_{i+}\} < \{y_{k \ell ++}\}$. Let $A = (a_{ij})$ be the incidence matrix of G whose rows are indexed by $V_1$ and whose columns are indexed by $V_2$. Then the incidence matrix of $\widehat{G}$ is

$$\begin{aligned} A' = \left( \begin{array}{cccc} &{} &{} &{} 1\\ &{} A &{} &{} \vdots \\ &{} &{} &{} 1\\ 1 &{} \cdots &{} 1 &{} 1 \end{array} \right) \end{aligned}$$

By the same argument as in the proof of the theorem in [35], we may assume that $A'$ contains no submatrices $\left( \begin{array}{cc} 1 &{} 1\\ 1 &{} 0 \end{array} \right)$ if we permute the rows and columns of A in $A'$. Each quadratic binomial in $I_{P_{\widehat{G}}}$ corresponds to a submatrix $\left( \begin{array}{cc} 1 &{} 1\\ 1 &{} 1 \end{array} \right)$ of $A'$. The proof of the theorem in [35] guarantees that the initial ideal is squarefree and quadratic if the initial monomial of each quadratic binomial corresponds to $\left( \begin{array}{cc} &{} 1\\ 1 &{} \end{array} \right)$. It is easy to see that there exists a such reverse lexicographic order which satisfies $z< \{x_{i+}\} < \{y_{k \ell ++}\}$. $\square$

4 $\gamma$-positivity and real-rootedness of the $h^*$-polynomial of ${\mathscr {B}}_{G}$

In this section, we study the $h^*$-polynomial of ${\mathscr {B}}_G$ for a graph G. First, we recall what $h^*$-polynomials are. Let ${\mathscr {P}}\subset {\mathbb R}^d$ be a lattice polytope of dimension d. Given a positive integer n, we define

$$\begin{aligned} L_{{\mathscr {P}}}(n)=|n {\mathscr {P}}\cap {\mathbb Z}^d|. \end{aligned}$$

The study on $L_{{\mathscr {P}}}(n)$ originated in Ehrhart [10] who proved that $L_{{\mathscr {P}}}(n)$ is a polynomial in n of degree d with the constant term 1. We say that $L_{{\mathscr {P}}}(n)$ is the Ehrhart polynomial of ${\mathscr {P}}$. The generating function of the lattice point enumerator, i.e., the formal power series

$$\begin{aligned} \text {Ehr}_{\mathscr {P}}(x)=1+\sum \limits _{k=1}^{\infty }L_{{\mathscr {P}}}(k)x^k \end{aligned}$$

is called the Ehrhart series of ${\mathscr {P}}$. It is well known that it can be expressed as a rational function of the form

$$\begin{aligned} \text {Ehr}_{\mathscr {P}}(x)=\frac{h^*({\mathscr {P}},x)}{(1-x)^{d+1}}. \end{aligned}$$

The polynomial $h^*({\mathscr {P}},x)$ is a polynomial in x of degree at most d with nonnegative integer coefficients ( [44]) and it is called the $h^*$-polynomial (or the $\delta$-polynomial) of ${\mathscr {P}}$. Moreover, one has ${\text {Vol}}({\mathscr {P}})=h^*({\mathscr {P}},1)$. Refer the reader to [3] for the detailed information about Ehrhart polynomials and $h^*$-polynomials.

Thanks to Proposition 1.1 (a), we give a formula for $h^*$-polynomial of ${\mathscr {B}}_G$ in terms of that of edge polytopes of some graphs. By the following formula, we can calculate the $h^*$-polynomial of ${\mathscr {B}}_G$ if we can calculate each $h^*(P_{\widetilde{H}}, x)$.

Proposition 3.1

Let G be a graph on [d]. Then the $h^*$-polynomial of ${\mathscr {B}}_G$ satisfies

$$\begin{aligned} h^*({\mathscr {B}}_G, x)= & {} \sum _{j=0}^d \ \ 2^j (x-1)^{d-j} \sum _{H \in S_j(G)} h^*(P_{\widetilde{H}}, x), \end{aligned}$$

(2)

where $S_j(G)$ denote the set of all induced subgraph of G with j vertices.

Proof

By Proposition 1.1 (a), ${\mathscr {B}}_G$ is divided into $2^d$ lattice polytopes of the form ${\mathscr {B}}_G \cap {\mathscr {O}}_\varepsilon$. Each ${\mathscr {B}}_G \cap {\mathscr {O}}_\varepsilon$ is unimodularly equivalent to $P_{\widetilde{G}}$. In addition, the intersection of ${\mathscr {B}}_G \cap {\mathscr {O}}_\varepsilon$ and ${\mathscr {B}}_G \cap {\mathscr {O}}_{\varepsilon '}$ is of dimension $d-1$ if and only if $\varepsilon - \varepsilon ' \in \{\pm 2 {\mathbf{e}}_1, \ldots , \pm 2 {\mathbf{e}}_d\}$. If $\varepsilon - \varepsilon ' = 2 {\mathbf{e}}_k$, then $({\mathscr {B}}_G \cap {\mathscr {O}}_\varepsilon ) \cap ({\mathscr {B}}_G \cap {\mathscr {O}}_{\varepsilon '}) = {\mathscr {B}}_G \cap {\mathscr {O}}_\varepsilon \cap {\mathscr {O}}_{\varepsilon '} \simeq {\mathscr {B}}_{G'} \cap {\mathscr {O}}_{\varepsilon ''},$ where $G'$ is the induced subgraph of G obtained by deleting the vertex k, and $\varepsilon ''$ is obtained by deleting the k-th component of $\varepsilon$. Hence the Ehrhart polynomial $L_{{\mathscr {B}}_G}(n)$ satisfies the following:

$$\begin{aligned} L_{{\mathscr {B}}_G}(n) = \sum _{j=0}^d \ \ 2^j (-1)^{d-j} \sum _{H \in S_j(G)} L_{P_{\widetilde{H}}}(n). \end{aligned}$$

Thus the Ehrhart series satisfies

$$\begin{aligned} \frac{h^*({\mathscr {B}}_G, x)}{(1-x)^{d+1}}= & {} \sum _{j=0}^d \ \ 2^j (-1)^{d-j} \sum _{H \in S_j(G)} \frac{h^*(P_{\widetilde{H}}, x)}{(1-x)^{j+1}}, \end{aligned}$$

as desired. $\square$

Let $f= \sum _{i=0}^{d}a_i x^i$ be a polynomial with real coefficients and $a_d \ne 0$. We now focus on the following properties.

• (RR) We say that f is real-rooted if all its roots are real.

• (LC) We say that f is log-concave if $a_i^2 \ge a_{i-1}a_{i+1}$ for all i.

• (UN) We say that f is unimodal if $a_0 \le a_1 \le \cdots \le a_k \ge \cdots \ge a_d$ for some k.

If all its coefficients are positive, then these properties satisfy the implications

$$\begin{aligned} \mathrm{(RR)} \Rightarrow \mathrm{(LC)} \Rightarrow \mathrm{(UN)}. \end{aligned}$$

On the other hand, the polynomial f is said to be palindromic if $f(x)=x^df(x^{-1})$. It is $\gamma$-positive if there are $\gamma _0,\gamma _1,\ldots ,\gamma _{\lfloor d/2\rfloor } \ge 0$ such that $f(x)=\sum _{i \ge 0} \gamma _i \ x^i (1+x)^{d-2i}$. The polynomial $\sum _{i \ge 0}\gamma _i \ x^i$ is called $\gamma$-polynomial of f. We can see that a $\gamma$-positive polynomial is real-rooted if and only if its $\gamma$-polynomial had only real roots ([40, Observation 4.2]).

By the following proposition, we are interested in connected bipartite graphs.

Proposition 3.2

Let G be a bipartite graph and $G_1,\ldots , G_s$ the connected components of G. Then the $h^*$-polynomial of ${\mathscr {B}}_{G}$ is palindromic, unimodal and

$$\begin{aligned} h^*({\mathscr {B}}_G,x)=h^*({\mathscr {B}}_{G_1},x) \cdots h^*({\mathscr {B}}_{G_s},x). \end{aligned}$$

Proof

It is known [14] that the $h^*$-polynomial of a lattice polytope P with the interior lattice point $\mathbf{0}$ is palindromic if and only if P is reflexive. Moreover, if a reflexive polytope P has a unimodular triangulation, then the $h^*$-polynomial of P is unimodal (see [7]). It is easy to see that, ${\mathscr {B}}_G$ is the free sum of ${\mathscr {B}}_{G_1}, \ldots , {\mathscr {B}}_{G_s}$. Thus we have a desired conclusion by Theorem 0.1 and [6, Theorem 1]. $\square$

In the rest of the present paper, we discuss the $\gamma$-positivity and the real-rootedness of the $h^*$-polynomial of ${\mathscr {B}}_G$ when G is a bipartite graph. The edge polytope $P_G$ of a bipartite graph G is called the root polytope of G, and it is shown [25] that the $h^*$-polynomial of $P_G$ coincides with the interior polynomial $I_G(x)$ of a hypergraph induced by G. First, we discuss interior polynomials introduced by Kálmán [24] and developed in many papers.

A hypergraph is a pair ${\mathscr {H}}= (V, E)$, where $E=\{e_1,\ldots ,e_n\}$ is a finite multiset of non-empty subsets of $V=\{v_1,\ldots ,v_m\}$. Elements of V are called vertices and the elements of E are the hyperedges. Then we can associate ${\mathscr {H}}$ to a bipartite graph $\mathrm{Bip} {\mathscr {H}}$ with a bipartition $V \cup E$ such that $\{v_i, e_j\}$ is an edge of $\mathrm{Bip} {\mathscr {H}}$ if $v_i \in e_j$. Assume that $\mathrm{Bip} {\mathscr {H}}$ is connected. A hypertree in ${\mathscr {H}}$ is a function $\mathbf{f}: E \rightarrow {\mathbb Z}_{\ge 0}$ such that there exists a spanning tree $\Gamma$ of $\mathrm{Bip} {\mathscr {H}}$ whose vertices have degree $\mathbf{f} (e) +1$ at each $e \in E$. Then we say that $\Gamma$ induce $\mathbf{f}$. Let $\mathrm{HT}({\mathscr {H}})$ denote the set of all hypertrees in ${\mathscr {H}}$. A hyperedge $e_j \in E$ is said to be internally active with respect to the hypertree $\mathbf{f}$ if it is not possible to decrease $\mathbf{f}(e_j)$ by 1 and increase $\mathbf{f}(e_{j'})$ ($j' < j$) by 1 so that another hypertree results. We call a hyperedge internally inactive with respect to a hypertree if it is not internally active and denote the number of such hyperedges of $\mathbf{f}$ by $\overline{\iota } (\mathbf{f})$. Then the interior polynomial of ${\mathscr {H}}$ is the generating function $I_{\mathscr {H}}(x) = \sum _{\mathbf{f} \in \mathrm{HT} ({\mathscr {H}})} x^{ \overline{\iota } (\mathbf{f}) }$. It is known [24, Proposition 6.1] that $\deg I_{\mathscr {H}}(x) \le \min \{|V|,|E|\} - 1$. If $G = \mathrm{Bip} {\mathscr {H}}$, then we set $I_G (x) = I_{\mathscr {H}}(x)$. In [25] Kálmán and Postnikov proved the following.

Proposition 3.3

[25, Theorems 1.1 and 3.10] Let G be a connected bipartite graph. Then we have

$$\begin{aligned} I_G(x) = h^*(P_G , x). \end{aligned}$$

Interior polynomials of disconnected bipartite graphs are defined by Kato [26] and the same assertion of Proposition 3.3 holds for all bipartite graphs. Note that if G is a bipartite graph, then the bipartite graph $\widehat{G}$ arising from G is connected. Hence we can use this formula to study the Eq. (2) in Proposition 3.1.

A k-matching of G is a set of k pairwise non-adjacent edges of G. Let

$$\begin{aligned} M(G, k)= \left\{ \{v_{i_1},\ldots , v_{i_k}, e_{j_1},\ldots ,e_{j_k}\} : \begin{array}{c} \text{ there } \text{ exists } \text{ a } k\text{-matching } \text{ of } G\\ \text{ whose } \text{ vertex } \text{ set } \text{ is } \{v_{i_1},\ldots , v_{i_k}, e_{j_1},\ldots ,e_{j_k}\} \end{array} \right\} . \end{aligned}$$

For $k=0$, we set $M(G,0) = \{\emptyset \}$. Using the theory of generalized permutohedra [31, 41], we have the following important fact on interior polynomials:

Proposition 3.4

Let G be a bipartite graph. Then we have

$$\begin{aligned} I_{\widehat{G}} (x) = \sum _{k \ge 0} | M(G, k)| \ x^k. \end{aligned}$$

(3)

Proof

Let $V \cup E$ denote a bipartition of G, where $V = \{v_2,\ldots , v_m\}$ and $E=\{e_2,\ldots ,e_n\}$ with $d = m+n-2$. Then $\widehat{G}$ is a connected bipartite graph with a bipartition $V' \cup E'$ with $V' = \{v_1\} \cup V$ and $E' = \{e_1\} \cup E$. Recall that $\{v_i, e_j\}$ is an edge of $\widehat{G}$ if and only if either $(i-1)(j-1) = 0$ or $\{v_i, e_j\}$ is an edge of G. Let $\mathrm{HT}(\widehat{G})$ be the set of all hypertrees in the hypergraph associated with $\widehat{G}$. Given a hypertree ${\mathbf{f}} \in \mathrm{HT}(\widehat{G})$, let $\Gamma$ be a spanning tree that induces $\mathbf{f}$. From [24, Lemma 3.3], we may assume that $\{v_1, e_j\}$ is an edge of $\Gamma$ for all $1 \le j \le n$. Note that the degree of each $v_i$ $(2 \le i \le m)$ is 1.

By definition, $e_1$ is always internally active. We show that, $e_j$ ($j \ge 2$) is internally active if and only if $\mathbf{f} (e_j) =0$. By definition, if $\mathbf{f} (e_j) =0$, then $e_j$ is internally active. Suppose $\mathbf{f} (e_j) > 0$. Then there exists $i \ge 2$ such that $\{v_i, e_j\}$ is an edge of $\Gamma$. Let $\mathbf{f}' \in \mathrm{HT}(\widehat{G})$ be a hypertree induced by a spanning tree obtained by replacing $\{v_i, e_j\}$ with $\{v_i, e_1\}$ in $\Gamma$. Then we have $\mathbf{f}' (e_j) = \mathbf{f} (e_j) -1$, $\mathbf{f}' (e_1) = \mathbf{f} (e_1) +1$ and $\mathbf{f}' (e_k) = \mathbf{f} (e_k)$ for all $1 < k \ne j$. Hence $e_j$ is not internally active. Thus $\overline{\iota } (\mathbf{f})$ is the number of $e_j$ ($j \ge 2$) such that there exists an edge $\{v_i, e_j\}$ of $\Gamma$ for some $i \ge 2$.

In order to prove the equation (3), it is enough to show that, for fixed hyperedges $e_{j_1},\ldots ,e_{j_k}$ with $2 \le j_1< \cdots < j_k \le n$, the cardinality of

$$\begin{aligned} {\mathscr {S}}_{j_1,\ldots ,j_k}= \{\mathbf{f} \in \mathrm{HT}(\widehat{G}) : e_{j_1},\ldots ,e_{j_k} \text{ are } \text{ not } \text{ internally } \text{ active } \text{ and } \overline{\iota } (\mathbf{f}) = k \} \end{aligned}$$

is equal to the cardinality of

$$\begin{aligned} {\mathscr {M}}_{j_1,\ldots ,j_k}= \left\{ \{v_{i_1},\ldots , v_{i_k}\} : \begin{array}{c} \text{ there } \text{ exists } \text{ a } k\text{-matching } \text{ of } G\\ \text{ whose } \text{ vertex } \text{ set } \text{ is } \{v_{i_1},\ldots , v_{i_k}, e_{j_1},\ldots ,e_{j_k}\} \end{array} \right\} . \end{aligned}$$

Let $G_{j_1,\ldots ,j_k}$ be the induced subgraph of G on the vertex set $V \cup \{ e_{j_1},\ldots ,e_{j_k}\}$. If $e_{j_\ell }$ is an isolated vertex in $G_{j_1,\ldots ,j_k}$, then both ${\mathscr {S}}_{j_1,\ldots ,j_k}$ and ${\mathscr {M}}_{j_1,\ldots ,j_k}$ are empty sets. If $v_i$ is an isolated vertex in $G_{j_1,\ldots ,j_k}$, then there is no relations between $v_i$ and two sets, and hence we can ignore $v_i$. Thus we may assume that $G_{j_1,\ldots ,j_k}$ has no isolated vertices.

It is known that ${\mathscr {M}}_{j_1,\ldots ,j_k}$ is the set of bases of a transversal matroid associated with $G_{j_1,\ldots ,j_k}$. See, e.g., [39, Section 1.6]. For $i=2,\ldots , m$, let

$$\begin{aligned}I_i = \{0\} \cup \{\ell : \{v_i, e_{j_\ell }\} \text{ is } \text{ an } \text{ edge } \text{ of } G_{j_1,\ldots ,j_k} \} \subset \{0,1,\ldots ,k\} .\end{aligned}$$

Oh [31] defines a lattice polytope $P_{{\mathscr {M}}_{j_1,\ldots ,j_k}}$ to be the generalized permutohedron [41] of the induced subgraph of $\widehat{G}$ on the vertex set $V \cup \{e_1, e_{j_1},\ldots ,e_{j_k}\}$, i.e., $P_{{\mathscr {M}}_{j_1,\ldots ,j_k}}$ is the Minkowski sum $\Delta _{I_2} + \cdots + \Delta _{I_m},$ where $\Delta _{I} = \mathrm{conv}(\{{\mathbf{e}}_j : j \in I\}) \subset {\mathbb R}^{k+1}$ and ${\mathbf{e}}_0,{\mathbf{e}}_1,\ldots ,{\mathbf{e}}_k$ are unit coordinate vectors in ${\mathbb R}^{k+1}$. By [31, Lemma 22 and Proposition 26], the cardinality of ${\mathscr {M}}_{j_1,\ldots ,j_k}$ is equal to the number of the lattice point $(x_0,x_1,\ldots ,x_k) \in P_{{\mathscr {M}}_{j_1,\ldots ,j_k}} \cap {\mathbb Z}^{k+1}$ with $x_1, x_2 ,\ldots , x_k \ge 1$. In addition, by [41, Proposition 14.12], any lattice point $(x_0,x_1,\ldots ,x_k) \in P_{{\mathscr {M}}_{j_1,\ldots ,j_k}} \cap {\mathbb Z}^{k+1}$ is of the form ${\mathbf{e}}_{i_2} + \cdots + {\mathbf{e}}_{i_m}$, where $i_\ell \in I_\ell$ for $2 \le \ell \le m$. By a natural correspondence $(x_0,x_1,\ldots ,x_k) \in P_{{\mathscr {M}}_{j_1,\ldots ,j_k}} \cap {\mathbb Z}^{k+1}$ with $x_1, x_2 ,\ldots , x_k \ge 1$ and $(\mathbf{f}(e_1),\mathbf{f}(e_{j_1}), \ldots , \mathbf{f}(e_{j_k}))$ with $\mathbf{f} \in {\mathscr {S}}_{j_1,\ldots ,j_k}$, it follows that the number of the lattice point $(x_0,x_1,\ldots ,x_k) \in P_{{\mathscr {M}}_{j_1,\ldots ,j_k}} \cap {\mathbb Z}^{k+1}$ with $x_1, x_2 ,\ldots , x_k \ge 1$ is equal to the cardinality of ${\mathscr {S}}_{j_1,\ldots ,j_k}$, as desired. $\square$

Now, we show that the $h^*$-polynomial of ${\mathscr {B}}_G$ is $\gamma$-positive if G is a bipartite graph. In fact, we prove Theorem 0.3.

Proof of Theorem 0.3

By Propositions 3.1 and 3.4, the $h^*$-polynomial of ${\mathscr {B}}_{G}$ is

$$\begin{aligned} h^*({\mathscr {B}}_G, x)= & {} \sum _{j=0}^d \ \ 2^j (x-1)^{d-j} \sum _{H \in S_j(G)} I_{\widehat{H}} (x)\\= & {} \sum _{j=0}^d 2^j (x-1)^{d-j} \sum _{H \in S_j(G)} \sum _{k \ge 0} |M(H, k)| \ x^k. \end{aligned}$$

Note that, for each $\{v_{i_1}, \ldots , v_{i_k},e_{j_1},\ldots ,e_{j_k}\} \in M(G, k)$ there exist $\left( {\begin{array}{c}d-2k\\ j -2k\end{array}}\right)$ induced subgraphs $H \in S_j(G)$ such that $\{v_{i_1}, \ldots , v_{i_k},e_{j_1},\ldots ,e_{j_k}\} \in M(H, k)$ for $j = 2k, 2k+1, \ldots , d$. Thus we have

$$\begin{aligned} h^*({\mathscr {B}}_G, x)= & {} \sum _{k \ge 0} \sum _{j=2k}^d 2^j (x-1)^{d-j} | M(G, k)| \left( {\begin{array}{c}d-2k\\ j-2k\end{array}}\right) x^k\\= & {} \sum _{k \ge 0} |M(G, k)| \ 2^{2 k} x^k (2+(x-1))^{d-2 k}\\= & {} (x+1)^d \sum _{k \ge 0} | M(G, k) | \ \left( \frac{4x}{(x+1)^2}\right) ^k\\= & {} (x+1)^d I_{\widehat{G}} \left( \frac{4x}{(x+1)^2} \right) , \end{aligned}$$

as desired. $\square$

By Proposition 3.4, it follows that, if G is a forest, then $I_{\widehat{G}} (x)$ coincides with the matching generating polynomial of G.

Proposition 3.5

Let G be a forest. Then we have

$$\begin{aligned} I_{\widehat{G}} (x) = \sum _{k \ge 0} m_k(G) \ x^k, \end{aligned}$$

where $m_k(G)$ is the number of k-matchings in G. In particular, $I_{\widehat{G}} (x)$ is real-rooted.

Proof

Let $M_1$ and $M_2$ be k-matchings of G. Suppose that $M_1$ and $M_2$ have the same vertex set $\{v_{i_1}, \ldots , v_{i_k},e_{j_1},\ldots ,e_{j_k}\}$. If $M=(M_1 \cup M_2) \setminus (M_1 \cap M_2)$ is not empty, then M corresponds to a subgraph of G such that the degree of each vertex is 2. Hence M has at least one cycle. This contradicts that G is a forest. Hence we have $M_1 = M_2$. Thus $m_k(G)$ is the cardinality of M(G, k) . In general, it is known that $\sum _{k \ge 0} m_k(G) \ x^k$ is real-rooted for any graph G. See, e.g., [12, 29]. $\square$

Next we will show that, if a bipartite graph G is a “permutation graph” associated with a poset P, then the interior polynomial $I_{\widehat{G}} (x)$ coincides with the P-Eulerian polynomial W(P)(x). A permutation graph is a graph on [d] with edge set

$$\begin{aligned} \{ \{i,j\} : L_i \text{ and } L_j \text{ intersect } \text{ each } \text{ other } \}, \end{aligned}$$

where there are d points $1,2,\ldots ,d$ on two parallel lines ${\mathscr {L}}_1$ and ${\mathscr {L}}_2$ in the plane, and the straight lines $L_i$ connect i on ${\mathscr {L}}_1$ and i on ${\mathscr {L}}_2$. If G is a bipartite graph with a bipartition $V_1 \cup V_2$, the following conditions are equivalent:

• (i) G is a permutation graph;

• (ii) The complement of G is a comparability graph of a poset;

• (iii) There exist orderings $<_1$ on $V_1$ and $<_2$ on $V_2$ such that

  $$\begin{aligned} i, i' \in V_1, i<_1 i', \ \ j, j' \in V_2, j <_2 j', \ \ \{i,j\}, \{i', j'\} \in E(G)\\ \Longrightarrow \{i,j'\}, \{i', j\} \in E(G); \end{aligned}$$

• (iv) For any three vertices, there exists a pair of them such that there exists no path containing the two vertices that avoids the neighborhood of the remaining vertex.

See [5, p. 93] for details. On the other hand, let P be a naturally labeled poset on [d]. Then the order polynomial $\Omega (P,m)$ of P is defined for $0 < m \in {\mathbb Z}$ to be the number of order-preserving maps $\sigma : P \rightarrow [m]$. It is known that

$$\begin{aligned} \sum _{m \ge 0} \Omega (P,m+1) x^m = \frac{ \sum _{\pi \in {\mathscr {L}} (P)} x^{d(\pi )}}{ (1-x)^{d+1} }, \end{aligned}$$

where ${\mathscr {L}} (P)$ is the set of linear extensions of P and $d(\pi )$ is the number of descents of $\pi$. The P-Eulerian polynomial W(P)(x) is defined by

$$\begin{aligned} W(P)(x) = \sum _{\pi \in {\mathscr {L}} (P)} x^{d(\pi )} .\end{aligned}$$

See, e.g., [46] for details. We now see a relation between the interior polynomial of a bipartite permutation graph and the P-Eulerian polynomial of a finite poset.

Proposition 3.6

Let G be a bipartite permutation graph and let P be a poset whose comparability graph is the complement of G. Then we have

$$\begin{aligned}I_{\widehat{G}} (x) = W(P)(x). \end{aligned}$$

Proof

In this case, ${\mathscr {B}}_G \cap {\mathscr {O}}_{(1,\ldots ,1)}$ is the chain polytope ${\mathscr {C}}_{P}$ of P. It is known that the $h^*$-polynomial of ${\mathscr {C}}_{P}$ is the P-Eulerian polynomial W(P)(x). See [45, 46] for details. Thus we have $I_{\widehat{G}} (x) = h^*(P_{\widehat{G}}, x)= W(P)(x),$ as desired. $\square$

It was conjectured by Neggers–Stanley that W(P)(x) is real-rooted. However this is false in general. The first counterexample was constructed in [4] (not naturally labeled posets). Counterexamples of naturally labeled posets were given in [47]. Counterexamples in these two papers are narrow posets, i.e., elements of posets are partitioned into two chains. It is easy to see that P is narrow poset if and only if the comparability graph of P is the complement of a bipartite graph. Since Stembridge found many counterexamples which are naturally labeled narrow posets, there are many bipartite permutation graphs G such that $h^*({\mathscr {B}}_G ,x)$ are not real-rooted. We give one of them as follows.

Example 3.7

Let P be a naturally labeled poset in Fig. 5 given in [47]. Then

Fig. 5

A counterexample to Neggers–Stanley conjecture [47]

$$\begin{aligned} W(P)(x)= 3 x^8+86 x^7+658 x^6+1946 x^5+2534 x^4+1420 x^3+336 x^2+32 x+1 \end{aligned}$$

has a conjugate pair of zeros near $-1.85884 \pm 0.149768 i$ as explained in [47]. Let G be the complement of the comparability graph of P. Then G is a bipartite graph with 17 vertices and 32 edges. The $h^*$-polynomial of ${\mathscr {B}}_G$ is

$$\begin{aligned} h^*({\mathscr {B}}_G ,x)= & {} (x+1)^{17} W(P)\left( \frac{4x}{(x+1)^2}\right) \\= & {} x^{17}+145 x^{16}+7432 x^{15}+174888 x^{14}+2128332 x^{13}\\&\quad +\,14547884 x^{12}+59233240 x^{11}\\&\quad +\,148792184 x^{10}+234916470 x^9+234916470 x^8+148792184 x^7\\&\quad +59233240 x^6 +\,14547884 x^5+2128332 x^4+174888 x^3\\&\quad +7432 x^2+145 x+1 \end{aligned}$$

and has conjugate pairs of zeros near $-3.88091 \pm 0.18448 i$ and $-0.257091\pm 0.0122209 i$. (We used Mathematica to compute approximate values.) On the other hand, $h^*({\mathscr {B}}_G ,x)$ is log-concave.

By the following proposition, it turns out that this example is a counterexample to “Real Root Conjecture” that has been already disproved by Gal [11].

Proposition 3.8

Let G be a bipartite permutation graph. Then $h^*({\mathscr {B}}_G, x)$ coincides with the h-polynomial of a flag complex that is a triangulation of a sphere.

Proof

It is known [5, p.94] that any bipartite permutation graph satisfies the condition (iv) in Theorem 2.6. Hence there exists a squarefree quadratic initial ideal with respect to a reverse lexicographic order such that the smallest variable corresponds to the origin. This means that there exists a flag regular unimodular triangulation $\Delta$ such that the origin is a vertex of any maximal simplex in $\Delta$. Then $h^*({\mathscr {B}}_G, x)$ coincides with the h-polynomial of a flag triangulation of the boundary of a convex polytope ${\mathscr {B}}_G$ arising from $\Delta$. $\square$

In [23], for a (p, q)-complete bipartite graph $K_{p,q}$, a simple description for the $h^*$-polynomial of ${\mathscr {A}}_{K_{p,q}}$ was given. In fact, one has

$$\begin{aligned} h^*({\mathscr {A}}_{K_{p+1,q+1}}, x) = \sum _{i = 0}^{\min \{p,q\}} \left( {\begin{array}{c}2i\\ i\end{array}}\right) \left( {\begin{array}{c}p\\ i\end{array}}\right) \left( {\begin{array}{c}q\\ i\end{array}}\right) x^i (x+1)^{p+q+1 - 2 i}. \end{aligned}$$

(4)

Moreover, it was shown that $h^*({\mathscr {A}}_{K_{p+1,q+1}}, x)$ is $\gamma$-positive and real-rooted. Similarly, we can obtain a simple description for the $h^*$-polynomial of ${\mathscr {B}}_{K_{p,q}}$ and show that $h^*({\mathscr {B}}_{K_{p,q}}, x)$ is $\gamma$-positive and real-rooted.

Example 3.9

Let $K_{p,q}$ be a (p, q)-complete bipartite graph. Then the comparability graph of a poset P consisting of two disjoint chains $1< 2< \cdots < p$ and $p+1< p+2< \cdots < p+q$ is the complement of $K_{p,q}$. It is easy to see that

$$\begin{aligned} W(P)(x) = \sum _{i = 0}^{\min \{p,q\}} \left( {\begin{array}{c}p\\ i\end{array}}\right) \left( {\begin{array}{c}q\\ i\end{array}}\right) x^i. \end{aligned}$$

Hence we have

$$\begin{aligned} h^*({\mathscr {B}}_{K_{p,q}}, x) = (x+1)^{p+q} W(P) \left( \frac{4x}{(x+1)^2} \right) = \sum _{i = 0}^{\min \{p,q\}} 4^i \left( {\begin{array}{c}p\\ i\end{array}}\right) \left( {\begin{array}{c}q\\ i\end{array}}\right) x^i (x+1)^{p+q - 2 i}. \end{aligned}$$

(5)

Simion [42] proved that W(P)(x) is real-rooted if P is a naturally labeled and disjoint union of chains. Thus the $h^*$-polynomial $h^*({\mathscr {B}}_{K_{p,q}}, x)$ is real-rooted.

Remark 3.10

In a very recent work [38], it is shown that the $h^*$-polynomials of symmetric edge polytopes of certain graphs can be computed by that of ${\mathscr {B}}_G$. For example, the Eq. (4) can be obtained from the Eq. (5) ([38, Example 5.10]).

In [23], for the proof of the real-rootedness of $h^*({\mathscr {A}}_{K_{p,q}},x)$, interlacing polynomials techniques were used. Let f and g be real-rooted polynomials with roots $a_1\ge a_2 \ge \cdots$, respectively, $b_1 \ge b_2 \ge \cdots$. Then g is said to interlace f if

$$\begin{aligned} a_1 \ge b_1 \ge a_2 \ge b_2 \ge \cdots . \end{aligned}$$

In this case, we write $f \preceq g$. In [23], it is shown that

$$\begin{aligned} h^*({\mathscr {A}}_{K_{p,q}},x) \preceq h^*({\mathscr {A}}_{K_{p,q+1}},x). \end{aligned}$$

By a similar way of [23], we can prove the following.

Proposition 3.11

For all $p, q \ge 1$, one has

$$\begin{aligned} h^*({\mathscr {B}}_{K_{p,q}},x) \preceq h^*({\mathscr {B}}_{K_{p,q+1}},x). \end{aligned}$$

Proof

Set $\gamma ({\mathscr {B}}_{K_{p,q}},x)=\sum _{i \ge 0} 4^i \left( {\begin{array}{c}p\\ i\end{array}}\right) \left( {\begin{array}{c}q\\ i\end{array}}\right) x^i$. Since $\{\left( {\begin{array}{c}p\\ i\end{array}}\right) \}_{i \ge 0}$ is a multiplier sequence (see [23]) and since $(4x+1)^{q} \preceq (4x+1)^{q+1}$, one has $\gamma ({\mathscr {B}}_{K_{p,q}},x) \preceq \gamma ({\mathscr {B}}_{K_{p,q+1}},x).$ By [23, Lemma 4.10], we obtain $h^*({\mathscr {B}}_{K_{p,q}},x) \preceq h^*({\mathscr {B}}_{K_{p,q+1}},x).$ $\square$