Skip to main content
Springer Nature Link
Log in

Existence and Stability of Pseudo Almost Periodic Solutions for a Delayed Multispecies Logarithmic Population Model with Feedback Control

  • Published:
Qualitative Theory of Dynamical Systems Aims and scope Submit manuscript

Abstract

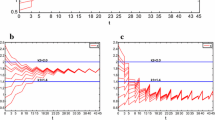
This paper studies a delayed multispecies Logarithmic population model with feedback control. By using Krasnoselskii’s fixed point theorem and constructing Lyapunov functions, we obtain some sufficient conditions which guarantee the existence and the exponential stability of the pseudo almost periodic solutions. Meanwhile, a numerical example is also given to illustrate the feasibility of the obtained results.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1

Similar content being viewed by others

Data Availibility Statement

All data generated or analysed during this study are included in this published article.

References

  1. Alvarez, E.: Composition and convolution theorems for \(\mu \)-Stepanov pseudo almost periodic functions and applications to fractional integro-differential equations. Electron. J. Differ. Equ. 2018, 1–15 (2018)

    MathSciNet  Google Scholar 

  2. Alzabut, J.O., Stamov, G.T., Sermutlu, E.: On almost periodic solutions for an impulsive delay Logarithmic population model. Math. Comput. Model. 51, 625–631 (2010)

    Article  MathSciNet  MATH  Google Scholar 

  3. Alzabut, J.O., Stamov, G.T., Sermutlu, E.: Positive almost periodic solutions for a delay Logarithmic population model. Math. Comput. Model. 53, 161–167 (2011)

    Article  MathSciNet  MATH  Google Scholar 

  4. Antonets, M.A., Shereshevskii, I.A.: Weyl quantization on compact Abelian groups and the quantum mechanics of almost periodic systems. Theoret. Math. Phys. 48, 597–604 (1981)

    Article  MathSciNet  MATH  Google Scholar 

  5. Aouiti, C., Dridi, F., Kong, F.: Pseudo almost automorphic solutions of hematopoiesis model with mixed delays. Comput. Appl. Math. 39, 87 (2020)

    Article  MathSciNet  MATH  Google Scholar 

  6. Barchielli, A., Belavkin, V.P.: Measurements continuous in time and a posteriori states in quantum mechanics. J. Phys. A 24, 1495–1514 (1991)

    Article  MathSciNet  Google Scholar 

  7. Burton, T.A.: A fixed-point theorem of Krasnoselskii. Appl. Math. Lett. 11, 85–88 (1998)

    Article  MathSciNet  MATH  Google Scholar 

  8. Chen, F.: Periodic solutions and almost periodic solutions for a delay multispecies Logarithmic population model. Appl. Math. Comput. 171, 760–770 (2005)

    MathSciNet  MATH  Google Scholar 

  9. Chen, X., Chen, F.: Almost-periodic solutions of a delay population equation with feedback control. Nonlinear Anal. Real World Appl. 7, 559–571 (2006)

    Article  MathSciNet  MATH  Google Scholar 

  10. Chen, F., Chen, X., Cao, J., Chen, A.: Positive periodic solutions of a class of non-autonomous single species population model with delays and feedback control. Acta Math. Sin. (Engl. Ser.) 21, 1319–1336 (2005)

    Article  MathSciNet  MATH  Google Scholar 

  11. Chen, C., Li, P., Jia, Z.: Cascade control of automatic generation control time-delay system considering saturation. Autom. Electr. Power Syst. 41, 66–71 (2017)

    Google Scholar 

  12. Chen, S., Wang, T., Zhang, J.: Positive periodic solution for non-autonomous competition Lotka–Volterra patch system with time delay. Nonlinear Anal. Real World Appl. 5, 409–419 (2004)

    Article  MathSciNet  MATH  Google Scholar 

  13. Chen, F., Xie, X., Shi, J.: Existence, uniqueness and stability of positive periodic solution for a nonlinear prey-competition model with delays. J. Comput. Appl. Math. 194, 368–387 (2006)

    Article  MathSciNet  MATH  Google Scholar 

  14. Chen, S., Zhang, J., Young, T.: Existence of positive periodic solution for nonautonomous predator-prey system with diffusion and time delay. J. Comput. Appl. Math. 159, 375–386 (2003)

    Article  MathSciNet  MATH  Google Scholar 

  15. Coppel, W.A.: Dichotomies in Stability Theory. Springer, New York (1978)

    Book  MATH  Google Scholar 

  16. Diagana, T.: Almost Automorphic Type and Almost Periodic Type Functions in Abstract Spaces. Springer, New York (2013)

    Book  MATH  Google Scholar 

  17. Ding, X., Wang, Y.: Positive periodic solution for a Gause-type ratio-dependent predator-prey system with diffusion and time delay. Int. J. Biomath. 1, 339–354 (2008)

    Article  MathSciNet  MATH  Google Scholar 

  18. Eberlein, W.F.: Abstract ergodic theorems and weak almost periodic functions. Trans. Am. Math. Soc. 67, 217–240 (1949)

    Article  MathSciNet  MATH  Google Scholar 

  19. Ezzinbi, K., Zabsonre, I.: Pseudo almost periodic solutions of infinite class for some functional differential equations. Appl. Anal. 92, 1627–1642 (2013)

    Article  MathSciNet  MATH  Google Scholar 

  20. Farassat, F.: Discontinuities in aerodynamics and aeroacoustics: the concept and applications of generalized derivatives. J. Sound Vib. 55, 165–193 (1977)

    Article  MATH  Google Scholar 

  21. Faria, T., Muroya, Y.: Global attractivity and extinction for Lotka–Volterra systems with infinite delay and feedback controls. Proc. R. Soc. Edinb. Sect. A 145, 301–330 (2015)

    Article  MathSciNet  MATH  Google Scholar 

  22. Kong, F., Nieto, J.J.: Almost periodic dynamical behaviors of the hematopoiesis model with mixed discontinuous harvesting terms. Discrete Contin. Dyn. Syst. Ser. B 24, 5803–5830 (2019)

    MathSciNet  MATH  Google Scholar 

  23. Gopalsamy, K.: Stability and Oscillations in Delay Differential Equations of Population Dynamics. Kluwer Academic Publishers, Dordrecht (1992)

    Book  MATH  Google Scholar 

  24. Haartsen, M.W., Pride, S.R.: Electroseismic waves from point sources in layered media. J. Geophys. Res. 102, 24745–24769 (1997)

    Article  Google Scholar 

  25. Kirlinger, G.: Permanence in Lotka–Volterra equations: linked prey-predator systems. Math. Biosci. 82, 165–191 (1986)

    Article  MathSciNet  MATH  Google Scholar 

  26. Liu, Z.J.: Positive periodic solutions for delay multispecies Logarithmic population model. Chin. J. Eng. Math. 4, 11–16 (2002)

    Article  MathSciNet  MATH  Google Scholar 

  27. Liu, G., Yan, J.: Positive periodic solutions for a neutral differential system with feedback control. Comput. Math. Appl. 52, 401–410 (2006)

    Article  MathSciNet  MATH  Google Scholar 

  28. Lu, S.P., Ge, W.G.: Existence of positive periodic solutions for neutral Logarithmic population model with multiple delays. J. Comput. Appl. Math. 166, 371–383 (2004)

    Article  MathSciNet  MATH  Google Scholar 

  29. Luo, Z., Luo, L.: Existence and stability of positive periodic solutions for a neutral multispecies Logarithmic population model with feedback control and impulse. Abstr. Appl. Anal. 2013, 741043 (2013)

    Article  MathSciNet  MATH  Google Scholar 

  30. Pinto, M., Vidal, C.: Pseudo-almost-periodic solutions for delayed differential equations with integrable dichotomies and bi-almost-periodic Green functions. Math. Methods Appl. Sci. 40, 6998–7012 (2017)

    Article  MathSciNet  MATH  Google Scholar 

  31. Qu, Z., Dawson, D.M.: Continuous state feedback control guaranteeing exponential stability for uncertain dynamical systems. In: 1991 Proceedings of the 30th IEEE Conference on Decision and Control, pp. 2636–2638. IEEE (2002)

  32. Stallmann, C.F., Engelbrecht, A.P.: Gramophone noise detection and reconstruction using time delay artificial neural networks. IEEE Trans. Syst. Man Cybern. Syst. 47, 893–905 (2017)

    Article  Google Scholar 

  33. Toka, D.: Almost Automorphic Type and Almost Periodic Type Functions in Abstract Spaces. Springer, New York (2013)

    MATH  Google Scholar 

  34. Wang, C., Shi, J.: Periodic solution for a delay multispecies Logarithmic population model with feedback control. Appl. Math. Comput. 193, 257–265 (2007)

    MathSciNet  MATH  Google Scholar 

  35. Wang, Q., Wang, Y., Dai, B.: Existence and uniqueness of positive periodic solutions for a neutral Logarithmic population model. Appl. Math. Comput. 213, 137–147 (2009)

    MathSciNet  MATH  Google Scholar 

  36. Wang, R., Zhang, X.: Positive periodic solution for a neutral Logarithmic population model with feedback control. Appl. Math. Comput. 217, 7692–7702 (2011)

    MathSciNet  MATH  Google Scholar 

  37. Wang, Q., Zhang, H., Wang, Y.: Existence and stability of positive almost periodic solutions and periodic solutions for a Logarithmic population model. Nonlinear Anal. 72, 4384–4389 (2010)

    Article  MathSciNet  MATH  Google Scholar 

  38. Xia, Y.: Almost periodic solution of a population model: via spectral radius of matrix. Bull. Malays. Math. Sci. Soc. 37, 249–259 (2014)

    MathSciNet  MATH  Google Scholar 

  39. Yan, Z., Jia, X.: Pseudo almost periodicity and its applications to impulsive nonautonomous partial functional stochastic evolution equations. Int. J. Nonlinear Sci. Numer. Simul. 19, 511–529 (2018)

    Article  MathSciNet  MATH  Google Scholar 

  40. Yan, J., Zhao, A., Nieto, J.J.: Existence and global attractivity of positive periodic solution of periodic single-species impulsive Lotka–Volterra systems. Math. Comput. Model. 40, 509–518 (2004)

    Article  MathSciNet  MATH  Google Scholar 

  41. Zhang, C.: Almost Periodic Type Functions and Ergodicity. Kluwer Academic Publishers, London (1992)

    Google Scholar 

  42. Zhang, C.: Pseudo-almost-periodic solutions of some differential equations. J. Math. Anal. Appl. 181, 62–76 (1994)

    Article  MathSciNet  MATH  Google Scholar 

  43. Zhang, C.: Pseudo almost periodic solutions of some differential equations II. J. Math. Anal. Appl. 192, 543–561 (1995)

    Article  MathSciNet  MATH  Google Scholar 

  44. Zhang, Y., Wei, Y.: Variable structure control for a singular biological economic model with time delay and stage structure. Adv. Differ. Equ. 2017, 381 (2017)

    Article  MathSciNet  MATH  Google Scholar 

  45. Zhao, K.: Existence of positive periodic solutions for the impulsive Lotka–Volterra cooperative population model with time-delay and harvesting control on time scales. Adv. Differ. Equ. 2018, 228 (2018)

    Article  MathSciNet  MATH  Google Scholar 

  46. Zhao, W.: New results of existence and stability of periodic solution for a delay multispecies Logarithmic population model. Nonlinear Anal. Real World Appl. 10, 544–553 (2009)

    Article  MathSciNet  MATH  Google Scholar 

  47. Zhao, Y., Wang, L., Zhao, H.: Existence and exponential stability of almost periodic solutions for a neutral multi-species Logarithmic population model. Appl. Math. Comput. 218, 5346–5356 (2012)

    MathSciNet  MATH  Google Scholar 

Download references

Funding

This research is supported by the National Natural Science Foundation of China (Nos. 11771197 and 11971317), the Natural Science Foundation of Fujian Province of China (No. 2019J01064), and the Scientific Research Funds of Huaqiao University.

Author information

Authors and Affiliations

  1. School of Mathematical Sciences, Huaqiao University, Quanzhou, 362021, China

    Yi Wu & Shengfu Deng

  2. Department of Mathematics, Zhejiang Normal University, Jinhua, 321004, China

    Yonghui Xia

Authors
  1. Yi Wu
    View author publications

    You can also search for this author inPubMed Google Scholar

  2. Yonghui Xia
    View author publications

    You can also search for this author inPubMed Google Scholar

  3. Shengfu Deng
    View author publications

    You can also search for this author inPubMed Google Scholar

Corresponding author

Correspondence to Shengfu Deng.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Wu, Y., Xia, Y. & Deng, S. Existence and Stability of Pseudo Almost Periodic Solutions for a Delayed Multispecies Logarithmic Population Model with Feedback Control. Qual. Theory Dyn. Syst. 20, 6 (2021). https://doi.org/10.1007/s12346-020-00445-7

Download citation

  • Received:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s12346-020-00445-7

Keywords