1 Introduction

Mathematical models describing the dynamics of infectious diseases have continue to serve as reliable guides for the formulation of public health policies that results in minimizing the incidence or even the eradication of such diseases. From tuberculosis to HIV, syphilis to malaria, hepatitis to SARS, and Ebola to several zoonotic diseases, several researchers have proposed and tested epidemic models to better understand the underlying mechanisms that drives the epidemic e.g. see the fine review in [7]. Generally, a classic condition for the eradication of a disease (wherein the disease-free equilibrium (DFE) can be shown to be asymptotically stable) is for the basic (effective) reproduction number to be less than unity; the unique endemic equilibrium will be asymptotically stable as far as the basic (effective) reproduction number is greater than unity and, by implication, the DFE will lose its stability. However, several researchers have demonstrated that it is possible for the DFE to co-exists with two endemic equilibria even when the reproduction number is less than unity, leading to the phenomenon of backward bifurcation [5, 13, 14]. With the existence of this phenomenon, relying on the reproduction number for disease control and eradication is now only necessary but no longer sufficient as the DFE of the model can no longer be guaranteed globally stable when the reproduction number is less than unity.

Several works have examined the causes of backward bifurcation in epidemic models [5, 6, 8, 11, 12, 14, 21, 23,24,25,26]. The work in [24] describes the existence of backward bifurcation in an epidemic model with saturated treatment function. However this work will examine the twin effect of using saturated functions to represent the treatment of non-isolated infected individuals and isolation of infected persons on the generation of a backward bifurcation in the system, when the reproduction number is less than unity.

The nonlinear, saturating function, sometimes called Holling type II function, was first used by Capasso and Serio [4] for studying the population dynamics of cholera [17]. Since then, several mathematical models have been formulated with saturated functions representing the incidence of a disease or control measures like treatment [4, 16,17,18, 22, 24]. The reason for this is due to the fact that a saturated incidence rate carries the idea of an inhibiting effect due to changes in behavioural patterns from the susceptible group when there is an increase in their number in response to the severity of the disease or a crowding effect of infected individuals [17, 24] (and other references therein), hence the number of effective contacts between susceptible and infected individuals may saturate at high infective levels [17].

The saturated isolation and treatment functions are used to describe the effect of delays in isolating and treatment of infectious individuals, especially in cases of sudden outbreak of a highly infectious disease and the population lacks sufficient medical personnel to handle the situation, far distances to be covered by infected individuals in order to receive treatment, availability of isolation centers but no sufficient materials therein such as beds, utensils e.t.c. For example, see [24] for the general treatment case. Isolation is very crucial in the control of infectious diseases especially in settings where the outbreak of the disease is sudden [13, 18, 20]; hence studying the effect of delay in isolation in a population that has treatment in place is important.

The purpose of this work is to demonstrate the effect of the degree of delays in the isolation and treatment (non-isolated) of infected individuals on the occurrence of a backward bifurcation in the system, either when the delays occur singly or jointly. Treatment is carried out for out-patients and for those isolated. However, if there are delays in the treatment of out-patients (non-isolated) and isolation of some infected individuals, then it is possible to have the backward bifurcation phenomenon in the system.

2 Mathematical Model

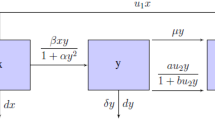
We will consider a population, at time t, denoted by N(t), that is divided into the following mutually-exclusive compartments: Susceptible individuals (S(t)), Infected (and infectious) individuals (I(t)), isolated (quarantined) individuals (Q(t)) and recovered individuals (R(t)), so that

$$\begin{aligned} N(t) = S(t) + I(t) + Q(t) + R(t). \end{aligned}$$

The model to be considered in this work is based on the typical susceptible-infected-quarantined-recovered (SIQR) model, where recovered individuals acquire permanent immunity; diseases such as measles, small pox and rubella are generally assumed to confer permanent immunity [7, 17].

Let \(\Lambda \) represent the recruitment rate of newborns and immigrants (assumed susceptible) into the population, \(\beta \) be the disease transmission rate, and \(\mu \) be the natural death rate (natural removal by death occurs in all epidemiological compartments at this rate). Susceptible individuals acquire infection at the rate \(\lambda _a(t)\), where

$$\begin{aligned} \lambda _a(t) = \frac{\beta I}{1+\xi I} \end{aligned}$$
(1)

is the saturated force of infection, with \(\xi \ge 0\). Thus, the rate of change of the susceptible population is given by

$$\begin{aligned} \frac{dS}{dt} = \Lambda - \lambda _a S - \mu S. \end{aligned}$$
(2)

The population of infected individuals is generated by the disease infections of susceptible individuals (at the rate \(\lambda _a(t)\)) but reduced due to natural recovery (at the rate \(\gamma \)), disease-induced death (at the rate \(\delta \)), natural death, treatment of non-isolated infected persons (at the rate \(\lambda _t(t)\)) and isolation of infected individuals (at the rate \(\lambda _s(t)\)), where

$$\begin{aligned} \lambda _t(t)= \frac{p}{1+\omega I}\quad \text {and} \quad \lambda _s(t)= \frac{q}{1+\psi I} \end{aligned}$$
(3)

are the saturated treatment and isolation functions, respectively, with p and q being positive while \(\omega \) and \(\psi \) are nonnegative parameters. As was discussed for models involving saturated treatment functions in [8, 24], the parameter \(\omega \) in the treatment function measures the extent of the effect of delaying the treatment of non-isolated infected persons, with p being the treatment rate of such individuals. Also, the parameter \(\psi \) in the isolation function measures the extent of the effect of delaying isolating infected individuals from the population of infected persons, with q being the isolation rate. Of course, setting \(\omega = 0\) and \(\psi = 0\) makes the system have linear treatment and isolation terms. Hence, the rate of change of infected individuals is given by

$$\begin{aligned} \frac{dI}{dt} = \lambda _a S - \lambda _t I - \lambda _s I - (\mu +\delta +\gamma )I. \end{aligned}$$
(4)

The population of isolated (infected) individuals is generated by the number of infected individuals that are isolated (at the saturated rate \(\lambda _s\)). This population is decreased by natural death and treatment (at the rate \(\phi \)), so that the rate of change for this group is given by

$$\begin{aligned} \frac{dQ}{dt} = \lambda _s I - (\mu + \phi )Q. \end{aligned}$$
(5)

Finally, the population of recovered individuals is generated by natural recovery of infected individuals (at the rate \(\gamma \)), treatment of isolated individuals (at the rate \(\phi \)) and treatment of non-isolated infected individuals (at the saturating rate \(\lambda _t\)). It is decreased by natural death, so that

$$\begin{aligned} \frac{dR}{dt} = \gamma I + \phi Q + \lambda _t I - \mu R. \end{aligned}$$
(6)

Thus, the model is given by the following system of nonlinear ordinary differential equations:

$$\begin{aligned} \begin{aligned} \frac{dS}{dt}&= \Lambda - \lambda _a S - \mu S,\\ \frac{dI}{dt}&= \lambda _a S - \lambda _t I - \lambda _s I - (\mu +\delta +\gamma )I,\\ \frac{dQ}{dt}&= \lambda _s I - (\mu + \phi )Q,\\ \frac{dR}{dt}&= \gamma I + \phi Q + \lambda _t I - \mu R. \end{aligned} \end{aligned}$$
(7)

2.1 Basic Properties

Since the model (7) monitors human populations, it is expected that all its associated parameters are nonnegative. Further, the following nonnegativity result holds

Theorem 2.1

Let the initial data for the model (7) be \(S(0) > 0\), \(I(0) > 0\), \(Q(0) > 0\), and \(R(0) > 0\). Then, the solutions

$$\begin{aligned} (S(t), I(t), Q(t), R(t)) \end{aligned}$$

of the model (7), with positive initial data, will remain positive for all time \(t > 0\).

Proof

Let \(t_1 = sup\{t>0: S(t)>0, I(t)>0, Q(t)>0, R(t)>0\} > 0\). It follows from (7) that

$$\begin{aligned} \frac{dS}{dt}=\Lambda - \lambda _a S - \mu S, \end{aligned}$$

which can be written as

$$\begin{aligned} \frac{d}{dt}\bigg \{S(t){ exp}\bigg [\mu t + \int _{0}^{t}\lambda _a(\tau )d\tau \bigg ]\bigg \} = \Lambda \bigg \{{ exp}\bigg [ \mu t + \int _{0}^{t}\lambda _a(\tau )d\tau \bigg ]\bigg \}. \end{aligned}$$

Thus,

$$\begin{aligned} S(t_1){ exp}\bigg [\mu t_1 + \int _{0}^{t_1}\lambda _a(\tau )d\tau \bigg ] - S(0) = \int _0^{t_1}\Lambda \bigg \{{ exp}\bigg [ \mu y + \int _{0}^{y}\lambda _a(\tau )d\tau \bigg ]\bigg \}dy. \end{aligned}$$

so that,

$$\begin{aligned} \begin{aligned} S(t_1)&= S(0){ exp}\bigg [- \mu t_1 - \int _{0}^{t_1}\lambda _a(\tau )d\tau \bigg ] \\&\quad +\, { exp}\bigg [-\mu t_1 - \int _{0}^{t_1}\lambda _a(\tau )d\tau \bigg ]\\&\quad \times \,\int _0^{t_1}\Lambda \bigg \{{ exp}\bigg [\mu y + \int _{0}^{y}\lambda _a(\tau )d\tau \bigg ]\bigg \}dy > 0. \end{aligned} \end{aligned}$$

Similarly, it can be shown that \(I(t)>0, Q(t)>0\), and \(R(t)>0\) for all time \(t>0\). Hence all solutions of the model (7) remain positive for all non-negative initial conditions, as required. \(\square \)

We now claim the following

Theorem 2.2

The closed set

$$\begin{aligned} \mathcal {D} = \left\{ (S, I, Q, R)\in \mathbb {R}_{+}^{4}; N\le \frac{\Lambda }{\mu }\right\} \end{aligned}$$

is positively-invariant and attracts all positive solutions of the model (7).

Proof

Adding the equations of the model (7) gives

$$\begin{aligned} \frac{dN}{dt} = \Lambda -\mu N - \delta I. \end{aligned}$$
(8)

Since the right hand side of the above equality is bounded by \(\Lambda - \mu N\), a standard comparison theorem [10] can be used to show that

$$\begin{aligned} N(t) \le N(0)e^{-\mu t} + \frac{\Lambda }{\mu }\left( 1-e^{-\mu t}\right) . \end{aligned}$$
(9)

In particular, if \(N(0) \le \frac{\Lambda }{\mu }\), then \(N(t) \le \frac{\Lambda }{\mu }\). Thus, \( \mathcal {D} \) is a positively invariant set. Furthermore, if \(N(0) \ge \frac{\Lambda }{\mu }\), then either the solution enters \(\mathcal {D} \) in finite time or N(t) approaches to \(\frac{\Lambda }{\mu }\) as \(t \rightarrow \infty \). Hence no solution path leave through any boundary of \(\mathcal {D} \) and the region \(\mathcal {D} \) attracts all solutions in \(\mathbb {R}_{+}^{7}\). \(\square \)

3 Analysis of Model

Since the first two equations in (7) are independent of the variables Q and R (and in fact, the results from the first two differential equations serves as the inputs for the equations for Q and R), it is sufficient to consider and analyse the following reduced model:

$$\begin{aligned} \begin{aligned} \frac{dS}{dt}&= \Lambda - \frac{\beta S I}{1+\xi I} - \mu S,\\ \frac{dI}{dt}&= \frac{\beta S I}{1+\xi I} - \frac{pI}{1+\omega I} - \frac{qI}{1+\psi I} - (\mu +\delta +\gamma )I. \end{aligned} \end{aligned}$$
(10)

3.1 Local Stability of Disease-Free Equilibrium

The model (10) has a disease-free equilibrium (DFE), given by \(\mathcal {E}_0 = (S^*,I^*) = (\frac{\Lambda }{\mu },0)\). To determine the local stability of the DFE, we will linearize the system (10) around the DFE. The Jacobian of the system (10), evaluated at the DFE, is given by

$$\begin{aligned} J|_{\mathcal {E}_0}= \begin{pmatrix} -\mu &{} -\beta \frac{\Lambda }{\mu }\\ 0&{}\quad \beta \frac{\Lambda }{\mu }-(\mu +\delta +\gamma +p+q) \end{pmatrix}, \end{aligned}$$

which has eigenvalues \(\lambda _1 = -\mu < 0\) and \(\lambda _2 = (\mu +\delta +\gamma +p+q)(\mathcal {R}_T - 1)\), where

$$\begin{aligned} \mathcal {R}_T = \frac{\beta \Lambda }{\mu (\mu +\delta +\gamma +p+q)} \end{aligned}$$
(11)

is the effective reproduction number of the model (10). Clearly, the eigenvalue, \(\lambda _2\), is negative if and only if \(\mathcal {R}_T < 1\). Hence, the DFE is locally-asymptotically stable when \(\mathcal {R}_T < 1\) and unstable when \(\mathcal {R}_T > 1\).

Lemma 3.1

The DFE (\(\mathcal {E}_0\)) of the model (10) is locally-asymptotically stable (LAS) if \(\mathcal {R}_T < 1\) and unstable if \(\mathcal {R}_T > 1\).

The threshold quantity, \({\mathcal {R}_T}\), is the effective reproduction number of the disease [7, 19]. It represents the average number of secondary infections generated by a typical infected individual in a completely susceptible population where there are already control measures such as treatment [7, 19]. The epidemiological implication of Lemma 3.1 is that when \(\mathcal {R}_T\) is less than unity, the disease can be eliminated from the population if the initial sizes of the sub-population of the model are in the basin of attraction of the DFE (\(\mathcal {E}_0\)). Hence, a small influx of infected individuals into the community will not generate large disease outbreaks, and the disease dies out in time.

3.2 Existence and Stability of Endemic Equilibria

The endemic equilibria, given by \(\mathcal {E}_1 = (S^{**}, I^{**})\), are obtained from setting the right hand side of (10) to zero and solving for the state variables, S and I. This gives

$$\begin{aligned} S^{**} = \frac{\Lambda \left( 1+\xi I^{**}\right) }{\mu \left( 1+\xi I^{**}\right) +\beta I^{**}} \end{aligned}$$
(12)

and the following polynomial for \(I^{**}\):

$$\begin{aligned} A_1 {I^{**}}^3 + A_2 {I^{**}}^2 + A_3 I^{**} + A_4 = 0, \end{aligned}$$
(13)

where

$$\begin{aligned} \begin{aligned} A_1&= \omega \psi (\mu +\delta +\gamma )(\mu \xi +\beta ),\\ A_2&= \mu \omega \psi (\mu +\delta +\gamma )+[(\mu +\delta +\gamma +q)\omega +(\mu +\delta +\gamma +p)\psi ](\mu \xi +\beta )\\&\quad -\beta \Lambda \omega \psi ,\\ A_3&= \mu (\omega +\psi )(\mu +\delta +\gamma )+(\mu +\delta +\gamma +p+q)(\mu \xi +\beta )+\mu (p\psi +q\omega )\\&\quad -\beta \Lambda (\omega +\psi ),\\ A_4&= \mu (\mu +\delta +\gamma +p+q)(1-\mathcal {R}_T). \end{aligned} \end{aligned}$$
(14)

We will now study the polynomial in (13) to gain insight into the effects of \(\omega \) and \(\psi \) on the existence of the endemic equilibria.

3.2.1 Case 1: \(\omega = \psi = 0\)

The polynomial (13) reduces to a linear equation in \(I^{**}\), with a unique solution

$$\begin{aligned} I^{**} = - \frac{A_4}{A_3}, \end{aligned}$$

which is positive if and only if \(\mathcal {R}_T > 1\). Hence we now establish that if \(\omega = \psi = 0\), then a unique endemic equilibrium exist if \(\mathcal {R}_T > 1\) and there cannot be such an endemic equilibrium if \(\mathcal {R}_T < 1\). In other words, if there is no delay in the treatment of out-patients as well as no delay in isolation of some infected individuals (before such persons are treated under isolation), then it is not possible to have an endemic steady state solution when the effective reproduction number is less than unity, hereby ruling out the possibility of a backward bifurcation in this case.

We will now show that, for this case where \(\psi =0\) and \(\omega =0\), the disease-free equilibrium is globally-asymptotically stable in \(\mathcal {D}\) when \(\mathcal {R}_T < 1\). We claim the following

Theorem 3.1

The disease-free equilibrium (DFE) of the model (10), with \(\psi =\omega =0\), is globally-asymptotically stable in \(\mathcal {D}\) when \(\mathcal {R}_T < 1\).

Proof

Consider the model (10) with \(\psi = \omega = 0\). Further, consider the following nonlinear Lyapunov function

$$\begin{aligned} \mathcal {V} = S-S^*-S^*\text {ln}\frac{S}{S^*}+I \end{aligned}$$

with Lyapunov derivative (where a dot represents differentiation with respect to t)

$$\begin{aligned} \dot{\mathcal {V}} = \dot{S}-S^*\frac{\dot{S}}{S}+\dot{I}. \end{aligned}$$
(15)

Substituting the right hand side of (10), with \(\psi = \omega = 0\), into (15), after several algebraic manipulations, leads to

$$\begin{aligned} \dot{\mathcal {V}} = \mu S^*\bigg (2-\frac{S}{S^*}-\frac{S^*}{S}\bigg )-\frac{(\mu +\delta +\gamma +p+q)I}{1+\xi I}\bigg [\xi I + (1-\mathcal {R}_T)\bigg ]. \end{aligned}$$

Since the arithmetic mean exceeds the geometric mean, it follows that

$$\begin{aligned} 2-\frac{S}{S^*}-\frac{S^*}{S} \le 0. \end{aligned}$$

Also it is easy to see that when \(\mathcal {R}_T \le 1\) (condition for the existence of the DFE), then

$$\begin{aligned} \xi I + (1-\mathcal {R}_T) > 0. \end{aligned}$$

Hence it follows that \(\dot{\mathcal {V}} \le 0\) when \(\mathcal {R}_T \le 1\). Therefore \(\mathcal {V}\) is a Lyapunov function in \(\mathcal {D}\) and it follows from the LaSalle’s invariance principle [9], that every solution to the equations in (10) (with \(\psi =\omega =0\)) with initial conditions in \(\mathcal {D}\) converges to \(\mathcal {E}_0\) as \(t\rightarrow \infty \). i.e. \(I(t)\rightarrow 0\) as \(t\rightarrow \infty \). Substituting \(I=0\) into the first equation of (10) gives \(S(t)\rightarrow \frac{\Lambda }{\mu }\) as \(t\rightarrow \infty \).

Thus \((S,I)\rightarrow (\frac{\Lambda }{\mu },0)\) as \(t\rightarrow \infty \) for \(\mathcal {R}_T\le 1\), so that the DFE, \(\mathcal {E}_0\), is GAS in \(\mathcal {D}\) if \(\mathcal {R}_T\le 1\) for the case \(\psi = \omega = 0\). \(\square \)

The epidemiological implication of this theorem is that if there are no delays in the treatment of non-isolated infected persons and in the isolation of some infected individuals, then the disease can be eradicated from the community if \(\mathcal {R}_T < 1\).

3.2.2 Case 2: \(\psi = 0\) and \(\omega > 0\)

Consider the situation where there is delay in treating outpatients but no delay in isolation of infected individuals in the population i.e. \(\psi = 0\) and \(\omega > 0\). In this case, the polynomial (13) reduces to

$$\begin{aligned} \hat{A_2} {I^{**}}^2 + \hat{A_3} I^{**} + A_4 = 0, \end{aligned}$$
(16)

where

$$\begin{aligned} \begin{aligned} \hat{A_2}&= \omega (\mu +\delta +\gamma +q)(\mu \xi +\beta ) > 0,\\ \hat{A_3}&= \mu \omega (\mu +\delta +\gamma +q)+(\mu +\delta +\gamma +p+q)(\mu \xi +\beta )-\beta \Lambda \omega ,\\ A_4&= \mu (\mu +\delta +\gamma +p+q)(1-\mathcal {R}_T). \end{aligned} \end{aligned}$$
(17)

Note that \(A_4 < 0\) if and only if \(\mathcal {R}_T > 1\), \(A_4 = 0\) if and only if \(\mathcal {R}_T = 1\) and \(A_4 > 0\) if and only if \(\mathcal {R}_T < 1\).

Since \(\omega > 0\), then the quadratic (16) has a unique positive root, hence a unique endemic equilibrium will exist, if \(\mathcal {R}_T > 1\) (\(A_4 < 0\)); this regardless of the sign of \(\hat{A_3}\). If \(\mathcal {R}_T = 1\), then \(A_4 = 0\) and a unique positive solution exists for the quadratic (16) if and only if \(\hat{A_3} < 0\) since \(I^{**} = -\frac{\hat{A_3}}{\hat{A_2}}\). Hence a unique solution exists for \(\mathcal {R}_T = 1\) only if \(\hat{A_3} < 0\).

Since the existence of the endemic equilibria [which are determined by the positive roots of (16)] depends on whether \(\mathcal {R}_T\) is greater than, equal to or less than unity, it is imperative to state that there will be two positive roots for the quadratic (16) when \(\mathcal {R}_T < 1\) (i.e. \(A_4 > 0\)), leading to the conclusion that the system will have two endemic equilibria when the reproduction number \(\mathcal {R}_T < 1\). We then claim the following.

Theorem 3.2

The system (10), with \(\psi = 0\) and \(\omega > 0\), exhibits backward bifurcation at \(\mathcal {R}_T = 1\) if and only if \(\hat{A_3} < 0\).

It is important to obtain a threshold condition on \(\omega \) for the backward bifurcation to occur. Since the bifurcation occur at \(\mathcal {R}_T = 1\), then we have that \(A_4 = 0\) which leads to

$$\begin{aligned} \beta \Lambda = \mu (\mu +\delta +\gamma +p+q). \end{aligned}$$
(18)

Substituting the expression for \(\beta \Lambda \) in (18) into the inequality \(\hat{A_3} < 0\) gives

$$\begin{aligned} (\mu +\delta +\gamma +p+q)(\mu \xi +\beta ) < \mu \omega p \end{aligned}$$

which rearranges to

$$\begin{aligned} \omega > \frac{(\mu +\delta +\gamma +p+q)(\mu \xi +\beta )}{\mu p} = \frac{\beta \Lambda (\mu \xi +\beta )}{\mu ^2 p} \equiv \omega _0 \end{aligned}$$
(19)

Hence a backward bifurcation occurs at \(\mathcal {R}_T = 1\) if and only if \(\omega > \omega _0\) when \(\psi =0\). This shows that the delay in treatment of non-isolated infected individuals (outpatients) during the course of an epidemic (in the absence of any delay in isolating some of the infected individuals) can cause a backward bifurcation to occur in the system. If the delay in treatment of non-isolated infected individuals, characterized by the value of \(\omega \), is higher than a threshold, given in (19) as \(\omega _0\), then the backward bifurcation phenomenon will occur for the system (10) at \(\mathcal {R}_T = 1\).

It is also important to calculate the length of the backward bifurcation range, from a critical value of \(\mathcal {R}_T\), which we will depict as \(\mathcal {R}_T^{c1}\), to \(\mathcal {R}_T = 1\). We know that the quadratic (16) will have two positive roots (corresponding to two endemic equilibria) if \(A_4 > 0\) and \(\hat{A_3} < 0\) with \( \hat{A_3}^2 > 4\hat{A_2}A_4\). Hence \(\mathcal {R}_T^{c1}\) can be calculated as a function of \(\Lambda \) by substituting the expressions for \(\hat{A_2}, \hat{A_3}\) and \(A_4\) into \( \hat{A_3}^2 = 4\hat{A_2}A_4\) to obtain a quadratic equation in \(\Lambda \). Solving the resultant quadratic equation in \(\Lambda \) then gives the following roots:

$$\begin{aligned} \begin{aligned} \Lambda&= \frac{\mu \omega (\mu +\delta +\gamma +q)+(\mu +\delta +\gamma +p+q)(\mu \xi +\beta )-2(\mu +\delta +\gamma +q)(\mu \xi +\beta )}{\omega \beta }\\&\quad \pm \,2\frac{\sqrt{p(\mu +\delta +\gamma +q)(\mu \xi +\beta )(\omega \mu -\mu \xi -\beta )}}{\omega \beta }. \end{aligned} \end{aligned}$$

We know that for the backward bifurcation to occur, it is required that \(A_4 < 0\) and \(\mathcal {R}_T < 1\). Using both conditions, we have that

$$\begin{aligned} \frac{\mu \omega (\mu +\delta +\gamma +q)+(\mu +\delta +\gamma +p+q)(\mu \xi +\beta )}{\omega \beta }<\Lambda < \frac{\mu (\mu +\delta +\gamma +p+q)}{\beta }. \end{aligned}$$
(20)

Using the condition in (20), we can now obtain the critical value for \(\Lambda \) for the backward bifurcation to occur i.e.

$$\begin{aligned} \begin{aligned} \Lambda ^{c1}&= \frac{\mu \omega (\mu +\delta +\gamma +q)+(\mu +\delta +\gamma +p+q)(\mu \xi +\beta )-2(\mu +\delta +\gamma +q)(\mu \xi +\beta )}{\omega \beta }\\&\quad + \,2\frac{\sqrt{p(\mu +\delta +\gamma +q)(\mu \xi +\beta )(\omega \mu -\mu \xi -\beta )}}{\omega \beta }. \end{aligned} \end{aligned}$$

It is easy to show that

$$\begin{aligned} 2\sqrt{p(\mu +\delta +\gamma +q)(\mu \xi +\beta )(\omega \mu -\mu \xi -\beta )} - 2(\mu +\delta +\gamma +q)(\mu \xi +\beta ) > 0 \end{aligned}$$

if

$$\begin{aligned} \omega > \frac{(\mu +\delta +\gamma +p+q)(\mu \xi +\beta )}{\mu p}, \end{aligned}$$

the condition on \(\omega \) required for the backward bifurcation to occur at \(\mathcal {R}_T = 1\).

Hence, the critical value of \(\mathcal {R}_T\) that defines the backward bifurcation range is given by

$$\begin{aligned} \mathcal {R}_T^{c1} = \frac{\beta \Lambda ^{c1}}{\mu (\mu +\delta +\gamma +p+q)}. \end{aligned}$$

To determine the local behaviour of the system around the endemic equilibrium, for the case \(\psi =0\) and \(\omega >0\), we linearize the model (10) around the endemic equilibrium, which exists when \(\mathcal {R}_T > 1\). The Jacobian of (10) evaluated at the endemic equilibrium is given by

$$\begin{aligned} J|_{\mathcal {E}_1}= \begin{pmatrix} -\mu -\frac{\beta I^{**}}{1+\xi I^{**}}&{} -\frac{\mu +\delta +\gamma }{1+\xi I^{**}}-\frac{p}{\left( 1+\xi I^{**}\right) \left( 1+\omega I^{**}\right) }-\frac{q}{1+\xi I^{**}}\\ \frac{\beta I^{**}}{1+\xi I^{**}}&{}\frac{\mu +\delta +\gamma }{1+\xi I^{**}}+\frac{p}{\left( 1+\xi I^{**}\right) \left( 1+\omega I^{**}\right) }+\frac{q}{1+\xi I^{**}}-(\mu +\delta +\gamma +q)-\frac{p}{\left( 1+\xi I^{**}\right) ^2}, \end{pmatrix}, \end{aligned}$$

using the fact that, at steady state, from (10),

$$\begin{aligned} \frac{\beta S^{**}}{\left( 1+\xi I^{**}\right) ^2} = \frac{\mu +\delta +\gamma }{1+\xi I^{**}}+\frac{p}{\left( 1+\xi I^{**}\right) \left( 1+\omega I^{**}\right) }+\frac{q}{1+\xi I^{**}}. \end{aligned}$$

The determinant of \(J|_{\mathcal {E}_1}\) is given by

$$\begin{aligned} \begin{aligned} \text {det}(J|_{\mathcal {E}_1})&= \frac{I^{**}}{\left( 1+\xi I^{**}\right) \left( 1+\omega I^{**}\right) ^2}\bigg [(\mu +\delta +\gamma )\left( 1+\omega I^{**}\right) ^2(\xi \mu +\beta )\\&\quad +\,q\left( 1+\omega I^{**}\right) ^2(\xi \mu +\beta )+p(\xi \mu +\beta )-p\omega \mu \bigg ]. \end{aligned} \end{aligned}$$

Clearly \(\text {det}(J|_{\mathcal {E}_1})\) is positive if and only if

$$\begin{aligned} (\mu +\delta +\gamma +q)(\xi \mu +\beta )\left( 1+\omega I^{**}\right) ^2+p(\xi \mu +\beta )>p\omega \mu . \end{aligned}$$

It is easy to see that

$$\begin{aligned}&(\mu +\delta +\gamma +q)(\xi \mu +\beta )\left( 1+\omega I^{**}\right) ^2\\&\qquad +\,p(\xi \mu +\beta ) > (\mu +\delta +\gamma +p+q)(\xi \mu +\beta ), \end{aligned}$$

since \(I^{**} > 0\).

Hence we can conclude that \(\text {det}(J|_{\mathcal {E}_1}) > 0\) if \((\mu +\delta +\gamma +p+q)(\xi \mu +\beta ) > p\omega \mu \), which implies that

$$\begin{aligned} \omega < \frac{(\mu +\delta +\gamma +p+q)(\mu \xi +\beta )}{\mu p} \equiv \omega _0 \end{aligned}$$

The trace of \((J|_{\mathcal {E}_1})\), written as \(\text {tr}(J|_{\mathcal {E}_1})\), is given by

$$\begin{aligned} \begin{aligned} \text {tr}(J|_{\mathcal {E}_1})&= \frac{1}{\left( 1+\xi I^{**}\right) \left( 1+\omega I^{**}\right) ^2}\bigg [-\mu \left( 1+\omega I^{**}\right) ^2\left( 1+\xi I^{**}\right) - \beta I^{**}\left( 1+\omega I^{**}\right) ^2\\&\quad - \,(\mu +\delta +\gamma )\xi I^{**}\left( 1+\omega I^{**}\right) ^2 -q\xi I^{**}\left( 1+\omega I^{**}\right) ^2+p\omega I^{**} - p\xi I^{**}\bigg ]. \end{aligned} \end{aligned}$$

The trace, \(\text {tr}(J|_{\mathcal {E}_1})\), is negative if and only if

$$\begin{aligned}&\mu \left( 1+\omega I^{**}\right) ^2\left( 1+\xi I^{**}\right) +\beta I^{**}\left( 1+\omega I^{**}\right) ^2\\&\quad +\,(\mu +\delta +\gamma +q)\xi I^{**}\left( 1+\omega I^{**}\right) ^2 +p\xi I^{**} > p\omega I^{**}. \end{aligned}$$

Again, it is easy to see that

$$\begin{aligned} \begin{aligned}&\mu \left( 1+\omega I^{**}\right) ^2\left( 1+\xi I^{**}\right) +\beta I^{**}\left( 1+\omega I^{**}\right) ^2 +(\mu +\delta +\gamma +q)\xi I^{**}\left( 1+\omega I^{**}\right) ^2\\&\quad +p\xi I^{**} > \mu \xi I^{**} + \beta I^{**}+ (\mu +\delta +\gamma +p+q)\xi I^{**}, \end{aligned} \end{aligned}$$

so that we assume that

$$\begin{aligned} \mu \xi I^{**} + \beta I^{**}+ (\mu +\delta +\gamma +p+q)\xi I^{**} > p\omega I^{**}. \end{aligned}$$

Hence, we have that

$$\begin{aligned} \omega < \frac{\mu \xi + \beta + (\mu +\delta +\gamma +p+q)\xi }{p}\equiv \omega _1 \end{aligned}$$

With the condition that the det\((J|_{\mathcal {E}_1}) > 0\) and tr\((J|_{\mathcal {E}_1}) < 0\), we have guaranteed that all eigenvalues of the Jacobian, \((J|_{\mathcal {E}_1})\), will be negative and claim the following

Theorem 3.3

The unique endemic equilibrium of the model (10), with \(\psi =0\) and \(\omega > 0\), is locally-asymptotically stable if \(\omega < \text {min}(\omega _0,\omega _1)\), when \(\mathcal {R}_T > 1\).

Using the Dulac criteria [15], in order to exclude limit cycles, we can show that the endemic equilibrium is globally-asymptotically stable in \(\mathcal {D}\) when \(\mathcal {R}_T > 1\). Let

$$\begin{aligned} \begin{aligned} P(S,I)&= \Lambda - \frac{\beta S I}{1+\xi I} - \mu S, \quad \text {and}\\ Q(S,I)&= \frac{\beta S I}{1+\xi I} - \frac{pI}{1+\omega I} - qI - (\mu +\delta +\gamma )I. \end{aligned} \end{aligned}$$

Let the Dulac function, D, be given by

$$\begin{aligned} D = \frac{1+\xi I}{I}. \end{aligned}$$

We now have that

$$\begin{aligned} \frac{\partial PD}{\partial S} + \frac{\partial QD}{\partial I} = -\frac{\mu (1+\xi I)}{I}-\beta -\xi (\mu +\delta +\gamma +q)-\frac{p(\xi -\omega )}{(1+\omega I)^2}, \end{aligned}$$

which is negative when

$$\begin{aligned} \begin{aligned}&\mu (1+\omega I)^2(1+\xi I)+\beta I(1+\omega I)^2 +(\mu +\delta +\gamma +q)\xi I(1+\omega I)^2\\&\quad +p\xi I - p\omega I > 0. \end{aligned} \end{aligned}$$

As discussed above, this inequality holds if

$$\begin{aligned} \omega < \frac{\mu \xi + \beta + (\mu +\delta +\gamma +p+q)\xi }{p}\equiv \omega _1. \end{aligned}$$

We now claim the following

Theorem 3.4

The system (10), with \(\psi =0\) and \(\omega >0\), has no limit cycle in \(\mathcal {D}\) when \(\omega < \omega _1\).

Hence we can conclude the global stability of the endemic equilibrium when \(\mathcal {R}_T > 1\).

Theorem 3.5

The unique endemic equilibrium of the model (10), with \(\psi =0\) and \(\omega >0\), is globally-asymptotically stable in \(\mathcal {D}\) if \(\omega < \text {min}\{\omega _0,\omega _1\}\), when \(\mathcal {R}_T > 1\).

3.2.3 Case 3: \(\psi > 0\) and \(\omega = 0\)

In this case, we have a situation where there are no delays in the treatment of non-isolated infected individuals but there are delays in isolating some of the infectious individuals. This can be due to shortages in isolation centers, long distances to be covered by infected persons to isolation units, or in the event of a natural disaster, it could be difficult to set up new isolation centers and most infected persons would have to be treated as non-isolated individuals (more or less like out-patients).

With \(\psi > 0\) and \(\omega = 0\), the polynomial (13) reduces to

$$\begin{aligned} \tilde{A_2} {I^{**}}^2 + \tilde{A_3} I^{**} + A_4 = 0, \end{aligned}$$
(21)

where

$$\begin{aligned} \begin{aligned} \tilde{A_2}&= \psi (\mu +\delta +\gamma +p)(\mu \xi +\beta ) > 0,\\ \tilde{A_3}&= \mu \psi (\mu +\delta +\gamma +p)+(\mu +\delta +\gamma +p+q)(\mu \xi +\beta )-\beta \Lambda \psi ,\\ A_4&= \mu (\mu +\delta +\gamma +p+q)(1-\mathcal {R}_T). \end{aligned} \end{aligned}$$
(22)

Following the approaches in Sect. 3.2.2, we can demonstrate that the parameter \(\psi \) is the cause of a backward bifurcation in the system when \(\mathcal {R}_T < 1\) and \(\omega = 0\). This occurs since it is possible to have two positive roots (implying two endemic equilibria) from the quadratic Eq. (21). We can claim the following.

Theorem 3.6

The system (10), with \(\psi > 0\) and \(\omega = 0\), exhibits backward bifurcation at \(\mathcal {R}_T = 1\) if and only if \(\tilde{A_3} < 0\).

We can also show that a critical value of \(\psi \) required for the existence of a backward bifurcation is for

$$\begin{aligned} \psi > \frac{(\mu +\delta +\gamma +p+q)(\mu \xi +\beta )}{\mu q}=\frac{\beta \Lambda (\mu \xi +\beta )}{\mu ^2 q}\equiv \psi _0. \end{aligned}$$
(23)

Hence a backward bifurcation will occur at \(\mathcal {R}_T = 1\) if and only if \(\psi > \psi _0\). Therefore, if there is no delay in the treatment of non-isolated infected persons but there is a delay in the isolation of some infected individuals and this delay in isolation is stronger than some value (\(\psi _0\)), then the backward bifurcation will occur in the system.

As was also done for the previous case, we can show that the critical value of the reproduction number which determines the length of the backward bifurcation range, \(\mathcal {R}_T^{c2}\), is given by

$$\begin{aligned} \mathcal {R}_T^{c2} = \frac{\beta \Lambda ^{c2}}{\mu (\mu +\delta +\gamma +p+q)}, \end{aligned}$$

where

$$\begin{aligned} \begin{aligned} \Lambda ^{c2}&= \frac{\mu \psi (\mu +\delta +\gamma +p)+(\mu +\delta +\gamma +p+q)(\mu \xi +\beta )-2(\mu +\delta +\gamma +p)(\mu \xi +\beta )}{\psi \beta }\\&\quad + 2\frac{\sqrt{q(\mu +\delta +\gamma +p)(\mu \xi +\beta )(\psi \mu -\mu \xi -\beta )}}{\psi \beta }. \end{aligned} \end{aligned}$$

Using the approaches in Sect. 3.2.2, the following results can also be established.

Theorem 3.7

The model (10), with \(\psi > 0\) and \(\omega = 0\), has a locally-asymptotically stable endemic equilibrium, when \(\mathcal {R}_T > 1\) if \(\psi < \text {min}\{\psi _0,\psi _1\}\), where

$$\begin{aligned} \psi _1 = \frac{\mu \xi +\beta +(\mu +\delta +\gamma +p+q)\xi }{q}. \end{aligned}$$

Theorem 3.8

The model (10), with \(\psi > 0\) and \(\omega = 0\), has no limit cycles in \(\mathcal {D}\) when \(\psi < \psi _1\).

Theorem 3.9

The unique endemic equilibrium of the model (10), with \(\psi >0\) and \(\omega =0\), is globally-asymptotically stable in \(\mathcal {D}\) if \(\psi < \text {min}\{\psi _0,\psi _1\}\), when \(\mathcal {R}_T > 1\).

3.2.4 Case 4: \(\psi > 0\) and \(\omega > 0\)

Now, let us consider the worse case scenario where there are delays in treatment of non-isolated infected persons and isolation of infected individuals. We recall that the endemic equilibria for the model (10) will satisfy the following polynomial

$$\begin{aligned} A_1 {I^{**}}^3 + A_2 {I^{**}}^2 + A_3 I^{**} + A_4 = 0, \end{aligned}$$
(24)

where some of the coefficients are now re-written as

$$\begin{aligned} \begin{aligned} A_1&= \omega \psi (\mu +\delta +\gamma )(\mu \xi +\beta ) > 0,\\ A_2&= \mu \omega \psi (\mu +\delta +\gamma )(1-\mathcal {R}_0)+[(\mu +\delta +\gamma +q)\omega \\&\quad +(\mu +\delta +\gamma +p)\psi ](\mu \xi +\beta ),\\ A_3&= \mu \omega (\mu +\delta +\gamma +q)(1-\mathcal {R}_\psi )+\mu \psi (\mu +\delta +\gamma +p)(1-\mathcal {R}_\omega )\\&\quad +(\mu +\delta +\gamma +p+q)(\mu \xi +\beta ),\\ A_4&= \mu (\mu +\delta +\gamma +p+q)(1-\mathcal {R}_T), \end{aligned} \end{aligned}$$
(25)

with

$$\begin{aligned} \mathcal {R}_0= & {} \frac{\beta \Lambda }{\mu (\mu +\delta +\gamma )},\quad \mathcal {R}_\psi = \frac{\beta \Lambda }{\mu (\mu +\delta +\gamma +q)},\quad \text {and}\\ \mathcal {R}_\omega= & {} \frac{\beta \Lambda }{\mu (\mu +\delta +\gamma +p)}. \end{aligned}$$

In the expressions above, \(\mathcal {R}_0\) is the basic reproduction number of the model (10) in the absence of any control strategy like treatment and isolation, \(\mathcal {R}_\psi \) is the effective reproduction number in the presence of isolation while \(\mathcal {R}_\omega \) is the effective reproduction number of the model (10) in the presence of treatment of non-isolated infected individuals.

It is easy to see that

  1. (i)

    \(\mathcal {R}_0> \mathcal {R}_\psi> \mathcal {R}_\omega > \mathcal {R}_T\) if \(q < p\);

  2. (ii)

    \(\mathcal {R}_0> \mathcal {R}_\omega> \mathcal {R}_\psi > \mathcal {R}_T\) if \(q > p\);

  3. (iii)

    \(\mathcal {R}_0> \mathcal {R}_\psi = \mathcal {R}_\omega > \mathcal {R}_T\) if \(q = p\);

It is important to find out the possibility of having more than one endemic equilibrium, which is characterized by the existence of more than one positive root for the polynomial (13), when \(\mathcal {R}_T < 1\), indicating the presence of a backward bifurcation whereby the DFE will co-exist with two endemic equilibria. Looking at the coefficients of (13), we observe that the number of positive roots of the polynomial (13), when \(\mathcal {R}_T < 1\), is largely determined by the signs of \(A_2\) and \(A_3\), since \(A_1 > 0\) and \(A_4 > 0\) when \(\mathcal {R}_T < 1\). Of course, the signs of \(A_2\) and \(A_3\) are significantly affected by the values of \(\mathcal {R}_0\), \(\mathcal {R}_\psi \) and \(\mathcal {R}_\omega \). We claim the following.

Theorem 3.10

The model (10) will undergo a backward bifurcation at \(\mathcal {R}_T = 1\) if \(A_2 >(<)\) 0 and \(A_3 < 0\) or \(A_2 < 0\) and \(A_3 > 0\). However, if \(A_2 > 0\) and \(A_3 > 0\), then the model will not under a backward bifurcation at \(\mathcal {R}_T = 1\). The model (10) has a unique endemic equilibrium when \(\mathcal {R}_T > 1\).

Basically, using the descartes rule of signs, we can conclude that the polynomial (13) will not have two positive roots (implying the non-existence of two endemic equilibria) when \(\mathcal {R}_T < 1\) if \(A_2 > 0\) and \(A_3 > 0\) otherwise there are two positive roots for (13) when \(\mathcal {R}_T < 1\).

The following relationships between the reproduction numbers gives conditions for the existence of the backward bifurcation in the system when \(\mathcal {R}_T < 1\):

  1. (i)

    \(\mathcal {R}_0 > 1, \mathcal {R}_\psi< 1, \mathcal {R}_\omega < 1\);

  2. (ii)

    \(\mathcal {R}_0> 1, \mathcal {R}_\psi > 1, \mathcal {R}_\omega < 1\);

  3. (iii)

    \(\mathcal {R}_0> 1, \mathcal {R}_\psi> 1, \mathcal {R}_\omega > 1\);

  4. (iv)

    \(\mathcal {R}_0> 1, \mathcal {R}_\psi < 1, \mathcal {R}_\omega > 1\);

  5. (v)

    \(\mathcal {R}_0 > 1, \mathcal {R}_\psi = 1, \mathcal {R}_\omega = 1\);

  6. (vi)

    \(\mathcal {R}_0 > 1, \mathcal {R}_\psi = 1, \mathcal {R}_\omega < 1\);

  7. (vii)

    \(\mathcal {R}_0 > 1, \mathcal {R}_\psi < 1, \mathcal {R}_\omega = 1\).

However, for the following situations, we cannot have a backward bifurcation at \(\mathcal {R}_T = 1\):

  1. (i)

    \(\mathcal {R}_0< 1, \mathcal {R}_\psi< 1, \mathcal {R}_\omega < 1\);

  2. (ii)

    \(\mathcal {R}_0 = 1, \mathcal {R}_\psi< 1, \mathcal {R}_\omega < 1\).

Using \(A_2 > 0\) and \(A_3 > 0\), we can obtain threshold conditions on \(\omega \) and \(\psi \) for the system not to undergo a backward bifurcation. Hence if such threshold conditions are not satisfied, then the system (10) will undergo a backward bifurcation at \(\mathcal {R}_T = 1\).

Making \(\mathcal {R}_T = 1\) means that \(A_4 = 0\), which implies that

$$\begin{aligned} \beta \Lambda = \mu (\mu +\delta +\gamma +p+q). \end{aligned}$$

Substituting this expression for \(\beta \Lambda \) into \(A_2 > 0\) and \(A_3 > 0\) gives

$$\begin{aligned} {[}\omega (\mu +\delta +\gamma +q)+\psi (\mu +\delta +\gamma +p)](\mu \xi +\beta )-\mu \psi \omega (p+q) < 0 \end{aligned}$$
(26)

and

$$\begin{aligned} \mu p\omega + \mu q\psi - (\mu +\delta +\gamma +p)(\mu \xi +\beta ) < 0, \end{aligned}$$
(27)

respectively. Hence, for the system (10) not to undergo a backward bifurcation at \(\mathcal {R}_T = 1\), the inequalities in (26) and (27) must be simultaneously satisfied for \(\psi > 0\) and \(\omega > 0\).

If we fix \(\psi \), then (26) can be used in obtaining a threshold condition on \(\omega \) thus:

$$\begin{aligned} \omega < \frac{\psi (\mu +\delta +\gamma +p)(\mu \xi +\beta )}{\mu \psi (p+q)-(\mu +\delta +\gamma +q)(\mu \xi +\beta )}\equiv \omega _3 \end{aligned}$$
(28)

Similarly, (27) leads to

$$\begin{aligned} \omega < \frac{(\mu +\delta +\gamma +p+q)(\mu \xi +\beta )-\mu q\psi }{\mu p}\equiv \omega _4. \end{aligned}$$
(29)

Now the expression in (28) is positive only if

$$\begin{aligned} \psi < \frac{(\mu +\delta +\gamma +q)(\mu \xi +\beta )}{\mu (p+q)}\equiv \psi _2, \end{aligned}$$

while the expression in (29) is positive as far as \(\psi < \psi _0\). We claim the following.

Theorem 3.11

Fixing \(\psi \), the model (10) will not undergo a backward bifurcation at \(\mathcal {R}_T = 1\) if \(\omega < \text {min}\{\omega _3,\omega _4\}\), for \(\psi < \text {min}\{\psi _0,\psi _2\}\).

Also, if we fix \(\omega \) and using the expressions in (26) and (27), we see that the system will not undergo a backward bifurcation at \(\mathcal {R}_T = 1\) if

$$\begin{aligned} \psi < \frac{\omega (\mu +\delta +\gamma +q)(\mu \xi +\beta )}{\mu \omega (p+q)-(\mu +\delta +\gamma +p)(\mu \xi +\beta )}\equiv \psi _3 \end{aligned}$$
(30)

and

$$\begin{aligned} \psi < \frac{(\mu +\delta +\gamma +p+q)(\mu \xi +\beta )-\mu p\omega }{\mu q}\equiv \psi _4, \end{aligned}$$
(31)

respectively. The expressions in (30) and (31) are positive if

$$\begin{aligned} \omega < \frac{(\mu +\delta +\gamma +p)(\mu \xi +\beta )}{\mu (p+q)}\equiv \omega _2, \end{aligned}$$

and \(\omega < \omega _0\), respectively. Hence we claim the following.

Theorem 3.12

Fixing \(\omega \), the model (10) will not undergo a backward bifurcation at \(\mathcal {R}_T = 1\) if \(\psi < \text {min}\{\psi _3,\psi _4\}\), for \(\omega < \text {min}\{\omega _0,\omega _2\}\).

Outside the backward bifurcation range, we can show that the DFE is globally asymptotically stable when \(\mathcal {R}_T < 1\) when \(\omega > 0\) and \(\psi > 0\). Consider the following nonlinear Lyapunov function

$$\begin{aligned} \mathcal {Z} = S-S^*-S^*\text {ln}\frac{S}{S^*}+I \end{aligned}$$

with Lyapunov derivative (where a dot represents differentiation with respect to t )

$$\begin{aligned} \dot{\mathcal {Z}} = \dot{S}-S^*\frac{\dot{S}}{S}+\dot{I}. \end{aligned}$$
(32)

Substituting the right hand side of (10) into (32), after several algebraic manipulations, leads to

$$\begin{aligned} \dot{\mathcal {Z}} = \mu S^*\bigg (2-\frac{S}{S^*}-\frac{S^*}{S}\bigg )-\frac{I}{(1+\xi I)(1+\omega I)(1+\psi I)}h(I), \end{aligned}$$

where \(h(I) = aI^3 + bI^2 + cI + d\) and

$$\begin{aligned} \begin{aligned} a&= \omega \psi \xi (\mu +\delta +\gamma ) > 0,\\ b&= \omega (\mu +\delta +\gamma )(\xi +\psi )+p\xi \psi +q\omega \xi +\xi \psi (\mu +\delta +\gamma )-\beta \psi \omega S^*,\\ c&= (\omega +\psi +\xi )(\mu +\delta +\gamma )+p(\xi +\psi )+q(\xi +\omega )-\beta (\omega +\psi )S^*,\\ d&= (\mu +\delta +\gamma +p+q)-\beta S^*. \end{aligned} \end{aligned}$$
(33)

Since the arithmetic mean exceeds the geometric mean, the follows that

$$\begin{aligned} 2-\frac{S}{S^*}-\frac{S^*}{S} \le 0. \end{aligned}$$

Hence we need to show the positivity of h(I) in order to conclude that \(\dot{\mathcal {Z}} \le 0\).

Now, \(d \ge 0\) implies that \(1-\mathcal {R}_T \ge 0\) leading to \(\mathcal {R}_T \le 1\). Also, \(c\ge 0\) implies that \(\mathcal {R}^b \ge \mathcal {R}_T\) while \(b\ge 0\) implies that \(\mathcal {R}^a \ge \mathcal {R}_T\), where

$$\begin{aligned} \mathcal {R}^a = \frac{(\mu +\delta +\gamma )}{\mu +\delta +\gamma +p+q}+\frac{\xi }{\psi }\frac{(\mu +\delta +\gamma +q)}{\mu +\delta +\gamma +p+q}+ \frac{\xi }{\omega }\frac{(\mu +\delta +\gamma +p)}{\mu +\delta +\gamma +p+q}, \end{aligned}$$

and

$$\begin{aligned} \mathcal {R}^b = \frac{\omega }{\omega +\psi }\frac{(\mu +\delta +\gamma +q)}{\mu +\delta +\gamma +p+q}+\frac{\xi }{\psi +\omega }+ \frac{\psi }{\psi +\omega }\frac{(\mu +\delta +\gamma +p)}{\mu +\delta +\gamma +p+q}. \end{aligned}$$

So \(h(I) > 0\) with \(I \ge 0\) if \(\mathcal {R}_T \le \text {min}\{1,\mathcal {R}^a,\mathcal {R}^b\}\).

Thus \(\dot{\mathcal {Z}} \le 0\) when \(\mathcal {R}_T \le \text {min}\{1,\mathcal {R}^a,\mathcal {R}^b\}\). Therefore \(\mathcal {Z}\) is a Lyapunov function in \(\mathcal {D}\) and it follows from the LaSalle’s invariance principle [9], that every solution to the equations in (10) with initial conditions in \(\mathcal {D}\) converges to \(\mathcal {E}_0\) as \(t\rightarrow \infty \). i.e. \(I(t)\rightarrow 0\) as \(t\rightarrow \infty \). Substituting \(I=0\) into the first equation of (10) gives \(S(t)\rightarrow \frac{\Lambda }{\mu }\) as \(t\rightarrow \infty \).

Thus \((S,I)\rightarrow (\frac{\Lambda }{\mu },0)\) as \(t\rightarrow \infty \) for \(\mathcal {R}_T \le \text {min}\{1,\mathcal {R}^a,\mathcal {R}^b\}\), so that the DFE, \(\mathcal {E}_0\), is GAS in \(\mathcal {D}\) if \(\mathcal {R}_T \le \text {min}\{1,\mathcal {R}^a,\mathcal {R}^b\}\). We state the following.

Theorem 3.13

The model (10) has a globally-asymptotically stable disease-free equilibrium when \(\mathcal {R}_T \le \text {min}\{1,\mathcal {R}^a,\mathcal {R}^b\}\).

It is easy to show that the thresholds \(\mathcal {R}^a\) and \(\mathcal {R}^b\) can be used in demonstrating that the DFE will co-exist with two endemic equilibria (indicating a backward bifurcation) when they are less than unity. That is why the effective reproduction number, \(\mathcal {R}_T\), must be strictly less than the minimum of \(1,\mathcal {R}^a\), and \(\mathcal {R}^b\) to move out of the backward bifurcation range and guarantee the global stability of the DFE.

Using the Dulac criteria, we can exclude the existence of limits cycles in \(\mathcal {D}\) when \(\mathcal {R}_T > 1\), in order to prove the global-asymptotic stability of the unique endemic equilibria. Let

$$\begin{aligned} \begin{aligned} P(S,I)&= \Lambda - \frac{\beta S I}{1+\xi I} - \mu S, \quad \text {and}\\ Q(S,I)&= \frac{\beta S I}{1+\xi I} - \frac{pI}{1+\omega I} - \frac{qI}{1+\psi I} - (\mu +\delta +\gamma )I. \end{aligned} \end{aligned}$$

Let the Dulac function, D, be given by

$$\begin{aligned} D = \frac{1+\xi I}{I}. \end{aligned}$$

We now have that

$$\begin{aligned} \frac{\partial PD}{\partial S} + \frac{\partial QD}{\partial I} = -\frac{\mu (1+\xi I)}{I}-\beta -\xi (\mu +\delta +\gamma )-\frac{p(\xi -\omega )}{(1+\omega I)^2}-\frac{q(\xi -\psi )}{(1+\psi I)^2}, \end{aligned}$$

which is negative when

$$\begin{aligned} \begin{aligned}&\mu (1+\psi I)^2(1+\omega I)^2(1+\xi I)+\beta I(1+\omega I)^2(1+\psi I)^2\\&\quad +(\mu +\delta +\gamma )\xi I(1+\omega I)^2(1+\psi I)^2\\&\quad +pI(\xi -\omega )(1+\psi I)^2 + qI(\xi -\psi )(1+\omega I)^2 > 0. \end{aligned} \end{aligned}$$
(34)

Using the approach in Sect. 3.2.2, we can show that a condition required for the local stability of the unique endemic equilibrium, when \(\mathcal {R}_T > 1\) is for the trace of the Jacobian of the model (10), evaluated at the endemic equilibrium, to be negative; the trace eventually reduces to the inequality in (34). We can now state the following.

Theorem 3.14

The model (10) has no limit cycles in \(\mathcal {D}\) as far as the inequality in (34) are satisfied, for \(\omega > 0\) and \(\psi > 0\).

Hence, we claim the following.

Theorem 3.15

The unique endemic equilibrium of the model (10) is globally-asymptotically stable in \(\mathcal {D}\) when \(\mathcal {R}_T > 1\).

In “Appendix A” section, we provide another proof of the global asymptotic stability of the unique endemic equilibrium of the model (10) when \(\mathcal {R}_T > 1\), using an appropriately formulated nonlinear Lyapunov function.

3.3 Investigating Backward Bifurcation Using the Center Manifold Theory

It would be interesting to investigate the occurrence of the backward bifurcation phenomenon in model (10) when \(\mathcal {R}_T < 1\), using the center manifold theory. Now, if \(\mathcal {R}_T = 1\) i.e. \(\frac{\beta \Lambda }{\mu } = \mu +\delta +\gamma +p+q\), we see that one of the eigenvalues of the Jacobian of system (10), evaluated at the disease-free equilibrium with \(\mathcal {R}_T = 1\), is zero while the other eigenvalue is \(-\mu \). Hence we cannot apply the Hartman–Grobman’s theory to investigate the behaviour of the DFE when \(\mathcal {R}_T = 1\), and therefore resort to using the center manifold theory.

To begin, we first transform the disease-free equilibrium (\(\mathcal {E}_0\)) of the system (10) into the origin. Let \(\hat{S} = S - \frac{\Lambda }{\mu }\) and \(\hat{I} = I\); then, we have that the model (10) becomes

$$\begin{aligned} \begin{aligned} \frac{d\hat{S}}{dt}&= - \frac{\beta \left( \hat{S} + \frac{\Lambda }{\mu }\right) \hat{I}}{1+\xi \hat{I}} - \mu \hat{S},\\ \frac{d\hat{I}}{dt}&= \frac{\beta \left( \hat{S} + \frac{\Lambda }{\mu }\right) \hat{I}}{1+\xi \hat{I}} - \frac{p\hat{I}}{1+\omega \hat{I}} - \frac{q\hat{I}}{1+\psi \hat{I}} - (\mu +\delta +\gamma )\hat{I}. \end{aligned} \end{aligned}$$
(35)

Since we have that \(\hat{I} = I\), we will ignore the hat sign and simply use I instead.

The new system (35) has an equilibrium \(\hat{\mathcal {E}_0} = (0,0)\). Using the transformation

$$\begin{aligned} \begin{pmatrix} \hat{S}\\ I \end{pmatrix} = \begin{pmatrix} 1&{}\quad -\frac{\beta \Lambda }{\mu ^2}\\ 0&{}\quad 1\end{pmatrix} \begin{pmatrix} u\\ v \end{pmatrix}, \end{aligned}$$

we can rewrite the system (35) as

$$\begin{aligned} \begin{aligned} \frac{dv}{dt}&= f(v,u),\\ \frac{du}{dt}&= -\mu u + g(v,u), \end{aligned} \end{aligned}$$
(36)

where

$$\begin{aligned} f(v,u) = \frac{\beta \left( \mu ^2 u - \beta \Lambda v + \Lambda \mu \right) v}{\mu ^2 (1+\xi v)} - \frac{pv}{1+\omega v} - \frac{qv}{1+\psi v} -(\mu + \delta + \gamma )v, \end{aligned}$$

and

$$\begin{aligned} \begin{aligned} g(v,u)&= - \frac{\beta \left( \mu ^2 u - \beta \Lambda v + \Lambda \mu \right) v}{\mu ^2 (1+\xi v)} + \frac{\beta \Lambda v}{\mu }\\&\quad + \frac{\beta \Lambda }{\mu ^2}\left\{ \frac{\beta \left( \mu ^2 u - \beta \Lambda v + \Lambda \mu \right) v}{\mu ^2 (1+\xi v)}- \frac{pv}{1+\omega v} - \frac{qv}{1+\psi v} -(\mu + \delta + \gamma )v\right\} . \end{aligned} \end{aligned}$$

Based on the center manifold theorem [1, 15], the system (36) has a center manifold of the form \(u = h(v)\), where \(h(v) = a_0 v^2 + a_1 v^3 + O(v^4)\), and the flow in the center manifold (and therefore in the system (10)) is given by

$$\begin{aligned} v' = f(v,h(v)). \end{aligned}$$

Expanding the system (36) in Taylor series at \((u,v) = (0,0)\), noting the above, the center manifold \(W^c(0)\) of the system (36) can be approximately represented, to the second order, by

$$\begin{aligned} W^c(0) = \left\{ (u,v)|u = \frac{\beta \Lambda (-\beta ^2\Lambda + \beta \mu (\mu -\Lambda \xi )+\mu ^2(\mu \xi +q\psi +p\omega ))}{\mu ^5}v^2 + O\left( v^3\right) \right\} ,\nonumber \\ \end{aligned}$$
(37)

with the flow equation approximated by

$$\begin{aligned} v' = \left( q\psi + p\omega - \frac{\beta ^2 \Lambda }{\mu ^2} - \frac{\beta \Lambda \xi }{\mu }\right) v^2 + O\left( v^3\right) . \end{aligned}$$
(38)

Therefore, the dynamics of the solutions near \(\hat{\mathcal {E}_0} = (0,0)\) is given by the quadratic term, when this term is not equal to zero. Clearly, this term is zero if and only if

$$\begin{aligned} q\psi + p\omega = \frac{\beta ^2 \Lambda }{\mu ^2} + \frac{\beta \Lambda \xi }{\mu }. \end{aligned}$$

Hence, based on [15], the system (10) will undergo a backward bifurcation at \(\mathcal {R}_T = 1\) if

$$\begin{aligned} q\psi + p\omega > \frac{\beta ^2 \Lambda }{\mu ^2} + \frac{\beta \Lambda \xi }{\mu } = \frac{\beta \Lambda (\beta + \mu \xi )}{\mu ^2}. \end{aligned}$$
(39)

Consider the case where \(\omega = \psi = 0\). Here, we observe that the inequality in (39) reduces to \(- \frac{\beta \Lambda (\beta + \mu \xi )}{\mu ^2} < 0\); hence the system will not undergo a backward bifurcation at \(\mathcal {R}_T = 1\), just as we concluded in Sect. 3.2.1.

For the case \(\omega > 0, \psi = 0\), the inequality in (39) becomes

$$\begin{aligned} \omega > \frac{\beta \Lambda (\mu \xi +\beta )}{\mu ^2 p}, \end{aligned}$$

the condition on \(\omega \) required for the backward bifurcation to occur at \(\mathcal {R}_T = 1\), just as we claimed in Sect. 3.2.2. Also, for the case \(\omega = 0, \psi > 0\), the inequality in (39) becomes

$$\begin{aligned} \psi > \frac{\beta \Lambda (\mu \xi +\beta )}{\mu ^2 q} \end{aligned}$$

the condition on \(\omega \) required for the backward bifurcation to occur at \(\mathcal {R}_T = 1\), as concluded in Sect. 3.2.3. When \(\omega> 0, \psi > 0\), the conditions on \(\omega \) and \(\psi \) required for the existence of the backward bifurcation [given in (39)] is the same as that obtained earlier when one of either parameters (\(\omega \) and \(\psi \)) are fixed (see Sect. 3.2.4).

4 Numerical Simulations

The model (10) is now simulated using the parameter estimates stated in the captions of the figures to demonstrate some of the qualitative properties of the model discussed in the previous section.

Fig. 1
figure 1

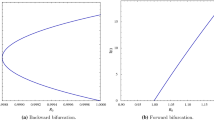
Backward bifurcation diagram for the model (10), showing the prevalence as a function of the effective reproduction number \((\mathcal {R}_T)\). Parameter values used are: \(\Lambda =12\), \(\beta =0.01\), \(\mu =0.1\), \(d=0.01\), \(\gamma =0.1\), \(p=2\), \(\omega = 10\), \(\xi =0.1\), \(q=1\), \(\psi =1\)

Full size image
Fig. 2
figure 2

Phase diagram showing the co-existing stable DFE (\(E_0\)), endemic equilibrium (\(E_1\)) with the unstable endemic equilibrium \(E_2\), when \(\mathcal {R}_T < 1\). Here, the parameter values used are: \(\Lambda =12\), \(\beta =0.01\), \(\mu =0.1\), \(d=0.01\), \(\gamma =0.1\), \(p=2\), \(\omega = 10\), \(\xi =0.1\), \(q=0\), \(\psi =0\)

Full size image
Fig. 3
figure 3

Phase diagram showing the co-existing stable DFE (\(E_0\)), endemic equilibrium (\(E_1\)) with the unstable endemic equilibrium \(E_2\), when \(\mathcal {R}_T < 1\). The parameter values used are: \(\Lambda =19\), \(\beta =0.01\), \(\mu =0.1\), \(d=0.01\), \(\gamma =0.1\), \(p=2\), \(\omega = 10\), \(\xi =0.1\), \(q=1\), \(\psi =2\)

Full size image
Fig. 4
figure 4

Phase diagram showing the co-existing stable DFE (\(E_0\)), endemic equilibrium (\(E_1\)) with the unstable endemic equilibrium \(E_2\) when \(\mathcal {R}_T < 1\). Here, \(\Lambda =12\), \(\beta =0.01\), \(\mu =0.1\), \(d=0.01\), \(\gamma =0.1\), \(p=2\), \(\omega = 10\), \(\xi =0.1\), \(q=1\), \(\psi =1\)

Full size image
Fig. 5
figure 5

Phase diagram showing the global stability of the DFE, where \(\Lambda =12\), \(\beta =0.01\), \(\mu =0.1\), \(d=0.01\), \(\gamma =0.1\), \(p=2\), \(\omega = 10\), \(\xi =0.1\), \(q=1\), \(\psi =0\)

Full size image
Fig. 6
figure 6

Phase diagram showing the global stability of the DFE. Here, \(\Lambda =12\), \(\beta =0.01\), \(\mu =0.1\), \(d=0.01\), \(\gamma =0.1\), \(p=2\), \(\omega = 1\), \(\xi =0.1\), \(q=1\), \(\psi =1\)

Full size image
Fig. 7
figure 7

Phase diagram showing the global stability of the unique endemic equilibrium when \(\mathcal {R}_T > 1\). Here, \(\Lambda =40\), \(\beta =0.01\), \(\mu =0.1\), \(d=0.01\), \(\gamma =0.1\), \(p=2\), \(\omega = 10\), \(\xi =0.1\), \(q=1\), \(\psi =10\) and \(\mathcal {R}_T = 1.2461\)

Full size image

Figure 1 shows the occurrence of a backward bifurcation in the system when \(\mathcal {R}_T < 1\); clearly, we see the backward bifurcation range which shows the region of co-existence of the DFE and two endemic equilibria. In Figs. 2, 3 and 4, we have phase plots showing the occurrence of two endemic equilibria [stable (\(E_1\)) and instable (\(E_2\))] with the DFE (\(E_0\)) when \(\mathcal {R}_T < 1\). In Fig. 2, the co-existence occurred in the absence of isolation. The level of endemicity is well illustrated in Figs. 3 and 4, whereby we have a higher stable endemic level (with \(\psi = 2\)) in the former compared to the lower stable endemic level (with \(\psi = 1\)) in the latter figure; this shows the effect of increasing the delay in isolation of infected persons on the existence of multiple equilibria when \(\mathcal {R}_T < 1\).

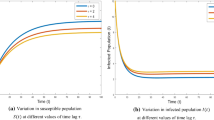
Figures 5 and 6 depicts phase plots showing the global asymptotic stability of the DFE when \(\mathcal {R}_T < 1\), in the absence of a backward bifurcation. With little delay values for both the treatment of non-isolated infected individuals and isolation of some infected individuals, it was still possible to achieve the GAS of the DFE since these parameters, \(\omega \) and \(\psi \), did not violate the appropriate threshold conditions imposed on them in order to avoid having a backward bifurcation in the system. Note that in Fig. 5, there is no delay in isolation while in Fig. 6, there are slight delays in both treatment of non-isolated infected persons and isolation of infected individuals. Figure 7 shows a phase plot with a globally-asymptotically stable endemic equilibrium when \(\mathcal {R}_T > 1\), in the presence of strong delays in treatment of non-isolated infected individuals and isolation of infected persons.

5 Discussion

In this work, we studied a SIQR model with saturated incidence, treatment (of non-isolated infected individuals) and isolation functions. We showed that the disease-free equilibrium is locally stable whenever the effective reproduction number is less than unity. However, we demonstrated that the system is capable of undergoing the phenomenon of backward bifurcation whereby the stable DFE will co-exist with a stable endemic equilibrium and an unstable endemic equilibrium, when the effective reproduction number is less than unity. We showed that this phenomenon is caused by the delays in the treatment of non-isolated infected individuals and the isolation of some of the infected individuals. This work show that if certain threshold conditions are violated by the parameters that characterized these delays, then the system will undergo a backward bifurcation when the effective reproduction number is less than unity.

It was shown that the delay in treatment of non-isolated infected persons and strict isolation of infected individuals can cause the backward bifurcation phenomenon either singly or jointly; in other words, even if there is no delay in the isolation of infected persons, a delay in the treatment of non-isolated persons e.g. infected individuals treated as outpatients, can still cause a backward bifurcation in the system and then the effective reproduction number becomes only a necessary condition for disease control but no longer sufficient for disease eradication. Ditto for the case where there is delay in the treatment of non-isolated infected persons but no delay in isolation of some infected persons. Of course, it was demonstrated that if there is a delay in both cases of isolation and outpatient treatments, then the system will definitely undergo a backward bifurcation if the delay parameters violates certain threshold conditions.

The overall results suggests the importance of not delaying the treatment and isolation of infected individuals. In the event of natural disasters, it may be very challenging to handle a disease epidemic, especially the setting up of isolation centers, in the case of a very infectious disease; for example, considering the recent Ebola (EVD) epidemic in parts of West Africa, it was clearly seen that immediate isolation (even of suspected cases) and quick treatment of confirmed cases was key for disease control [2, 3]. Therefore efforts must be geared towards not only investing more on beds in health centers [24], but also on increasing isolation centers for catering for severe disease emergencies and preparing for the treatment of other infected individuals who may not be isolated but could still treated, thereby reducing the infectious period of any infected individual remaining in the population.