Skip to main content
SpringerLink
Log in

Bifurcations of Traveling Wave Solutions for a Modified Novikov’s Cubic Equation

  • Published:
Qualitative Theory of Dynamical Systems Aims and scope Submit manuscript

Abstract

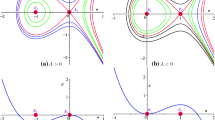
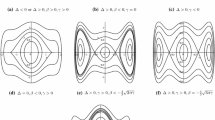
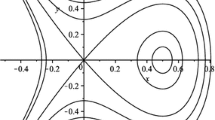
Exact traveling solutions for a modified Novikov’s cubic equation is considered based on the bifurcation method of dynamical systems in this paper. The two-dimensional system of modified Novikov’s cubic equation exists singular curve \(\phi ^2+a^2y^2=R\) when \(R>0\) and then it is proved that the corresponding traveling wave system of the modified Novikov’s cubic equation exists smooth solitary wave solutions and breaking wave solutions.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8

Similar content being viewed by others

References

  1. Camassa, R., Holm, D.D.: An integrable shallow water equation with peaked solitons. Phys. Rev. Lett. 71, 1661–1664 (1993)

    Article  MathSciNet  MATH  Google Scholar 

  2. Camassa, R., Holm, D.D., Hyman, J.M.: A new integrable shallow water equation. Adv. Appl. Mech. 31, 1–33 (1994)

    Article  MATH  Google Scholar 

  3. Qiao, Z.J.: The Camassa–Holm hierarchy, N-dimensional integrable systems, and algebro-geometric solution on a symplectic submanifold. Commun. Math. Phys. 239, 309–341 (2003)

    Article  MathSciNet  MATH  Google Scholar 

  4. Fisher, M., Schiff, J.: The Camassa Holm equation: conserved quantities and the initial value problem. Phys. Lett. A 259, 371–376 (1999)

    Article  MathSciNet  MATH  Google Scholar 

  5. Fokas, A.S.: On a class of physically important integrable equations. Phys. D 87, 145–150 (1995)

    Article  MathSciNet  MATH  Google Scholar 

  6. Degasperis, A., Procesi, M.: Asymptotic integrability. In: Gaeta, G. (ed.) Symmetry and Perturbation Theory. World Scientific Publishing, Singapore (1999)

    Google Scholar 

  7. Degasperis, A., Holm, D.D., Hone, A.N.W.: A new integrable equation with peakon solutions. Theor. Math. Phys. 133, 1463–1474 (2002)

    Article  MathSciNet  Google Scholar 

  8. Dullin, H.R., Gottwald, G.A., Holm, D.D.: Camassa–Holm, Korteweg-de Vries-5 and other asymptotically equivalent shallow water wave equations. Fluid Dyn. Res. 33, 73–95 (2003)

    Article  MATH  Google Scholar 

  9. Novikov, V.S.: Generalizations of the Camassa–Holm equation. J. Phys. A Math. Theor. 42, 342002 (2009)

    Article  MathSciNet  MATH  Google Scholar 

  10. Li, J.B.: Exact cuspon and compactons of the Novikov equation. Int. J. Bifurcat. Chaos 24, 1450037 (2014)

    Article  MathSciNet  MATH  Google Scholar 

  11. Zhang, L.N., Tang, R.R.: Bifurcation of peakons and cuspons of the integrable Novikov equation. Proc. Rom. Acad. 16, 168175 (2015)

    MathSciNet  Google Scholar 

  12. Li, J.B., Qiao, Z.J.: Bifurcations and exact traveling wave solutions for a generalized Camassa–Holm equation. Int. J. Bifurcat. Chaos 3, 1350057 (2013)

    Article  MathSciNet  MATH  Google Scholar 

  13. Ma, W.X., Lee, J.H.: A transformed rational function method and exact solutions to the (3+1) dimensional Jimbo–Miwa equation. Chaos Solitons Fract. 42, 1356–1363 (2009)

    Article  MathSciNet  MATH  Google Scholar 

  14. Batwa, S., Ma, W.X.: Lump solutions to a (2+1)-dimensional fifth-order KdV-like equation. Adv. Math. Phys. 5, 1–6 (2018)

    Article  MathSciNet  MATH  Google Scholar 

  15. Yang, J.Y., Ma, W.X., Qin, Z.Y.: Lump and lump-soliton solutions to the (2+1)-dimensional Ito equation. Anal. Math. Phys. 8, 427–436 (2018)

    Article  MathSciNet  MATH  Google Scholar 

  16. Chen, S.T., Ma, W.X.: Lump solutions to a generalized Bogoyavlensky–Konopelchenko equation. Front. Math. China 13, 525–534 (2018)

    Article  MathSciNet  MATH  Google Scholar 

  17. Li, J.B., Dai, H.H.: On the Study of Singular Nonlinear Travelling Wave Equations: Dynamical Approach. Science Press, Beijing (2007)

    Google Scholar 

  18. Guckenheimer, J., Holmes, P.: Nonlinear Oscillations, Dynamical System, and Bifurcation of Vector Fields. Springer, New York (1983)

    Book  MATH  Google Scholar 

Download references

Acknowledgements

The author is grateful to Professor Zhijun Qiao for his enthusiastic guidance and help during her visit to University of Texas-Rio Grande Valley, USA. It is also a pleasure to thank the Professor Shengqiang Tang, Guilin University of Electronic Technology, for several enlightening advice and illuminating discussions. This work were supported by National Natural Science Foundation of China (Nos. 41461110, 11461001) and Guangxi College Enhancing Youths Capacity Project (KY2016LX315), Guangxi University of Finance and Economics project (2017QN09).

Author information

Authors and Affiliations

  1. Deparment of Applied Mathematics, Guangxi University of Finance and Economics, Nanning, 530003, Guangxi, People’s Republic of China

    Minzhi Wei

Authors
  1. Minzhi Wei
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Minzhi Wei.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Wei, M. Bifurcations of Traveling Wave Solutions for a Modified Novikov’s Cubic Equation. Qual. Theory Dyn. Syst. 18, 667–686 (2019). https://doi.org/10.1007/s12346-018-0306-z

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s12346-018-0306-z

Keywords

Search

Navigation