Skip to main content
SpringerLink
Log in

Exact Multiplicity and Stability of Periodic Solutions for Duffing Equation with Bifurcation Method

  • Published:
Qualitative Theory of Dynamical Systems Aims and scope Submit manuscript

Abstract

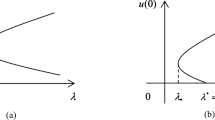
Under some \(L^p\)-norms(\(p\in [1,\infty ]\)) assumptions for the derivative of the restoring force, the exact multiplicity and the stability of \(2\pi \)-periodic solutions for Duffing equation are considered. The nontrivial \(2\pi \)-periodic solutions of it are positive or negative, and the bifurcation curve of it is a unique reversed S-shaped curve. The class of the restoring force is extended, comparing with the class of \(L^{\infty }\)-norm condition. The proof is based on the global bifurcation theorem, topological degree and the estimates for periodic eigenvalues of Hill’s equation by \(L^p\)-norms(\(p\in [1,\infty ]\)).

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Alonso, J.M., Ortega, R.: Boundedness and global asymptotic stability of forced oscillator. Nonlinear Anal. 25, 297–309 (1995)

    Article  MathSciNet  MATH  Google Scholar 

  2. Čepička, A., Drábek, P., Jenšiková, J.: On the stability of periodic solutions of the damped pendulum equation. J. Math. Anal. Appl. 209, 712–723 (1997)

    Article  MathSciNet  MATH  Google Scholar 

  3. Chen, H., Li, Y., Hou, X.: Exact multiplicity for periodic solutions of Duffing type. Nonlinear Anal. 55, 115–124 (2003)

    Article  MathSciNet  MATH  Google Scholar 

  4. Chen, H., Li, Y.: Rate of decay of stable periodic solutions of Duffing equations. J. Differ. Equ. 236, 493–503 (2007)

    Article  MathSciNet  MATH  Google Scholar 

  5. Chen, H., Li, Y.: Existence, uniqueness and stability of periodic solutions of an equation of Duffing type. Discrete Contin. Dyn. Syst. 18, 793–807 (2007)

    Article  MathSciNet  MATH  Google Scholar 

  6. Chen, H., Li, Y.: Bifurcation and stability of periodic solutions of Duffing equations. Nonlinearity 21, 2485–2503 (2008)

    Article  MathSciNet  MATH  Google Scholar 

  7. Chu, J., Zhang, M.: Rotation numbers and Lyapunov stability of elliptic periodic solutions. Discrete Contin. Dyn. Syst. 21, 1071–1094 (2008)

    Article  MathSciNet  MATH  Google Scholar 

  8. Coddington, E.A., Levinson, N.: Theory of Ordinary Differential Equations. McGraw-Hill Inc., New York (1987)

    MATH  Google Scholar 

  9. Deimling, K.: Nonlinear Functional Analysis. Springer, Berlin (1980)

    MATH  Google Scholar 

  10. Fabry, C., Mawhin, J., Nkashama, M.N.: A multiplicity result for periodic solutions of forced nonlinear second order differential equations. Bull. Lond. Math. Soc. 18, 173–180 (1986)

    Article  MathSciNet  MATH  Google Scholar 

  11. Feng, H., Zhang, M.: Optimal estimates on rotation number of almost periodic systems. Z. Angew. Math. Phys. 57, 183–204 (2006)

    Article  MathSciNet  MATH  Google Scholar 

  12. Katriel, G.: Uniqueness of periodic solutions for asymptotically linear Duffing equations with strong forcing. Topol. Methods Nonlinear Anal. 12, 263–274 (1998)

    Article  MathSciNet  MATH  Google Scholar 

  13. Kielhöfer, H.: Bifurcation Theory: An Introduction with Applications to PDE’s. Springer, New York (2003)

    Google Scholar 

  14. Korman, P., Ouyang, T.: Exact multiplicity results for two classes of periodic equations. J. Math. Anal. Appl. 194, 763–779 (1995)

    Article  MathSciNet  MATH  Google Scholar 

  15. Korman, P., Ouyang, T.: Multiplicity results for two classes of boundary-value problems. SIAM J. Math. Anal. 26, 180–189 (1995)

    Article  MathSciNet  MATH  Google Scholar 

  16. Korman, P., Li, Y., Ouyang, T.: An exact multiplicity result for a class of semilinear equations. Commun. Partial Differ. Equ. 22, 661–684 (1997)

    Article  MathSciNet  MATH  Google Scholar 

  17. Lazer, A.C., McKenna, P.J.: On the existence of stable periodic solutions of differential equations of Duffing type. Proc. Am. Math. Soc. 110, 274–293 (1990)

    Article  MathSciNet  MATH  Google Scholar 

  18. Lazer, A.C., McKenna, P.J.: Large-amplitude periodic oscillations in suspension bridges: some new connections with nonlinear analysis. SIAM Rev. 32, 537–578 (1990)

    Article  MathSciNet  MATH  Google Scholar 

  19. Liang, S.: The rate of decay of stable periodic solutions for Duffing equation with \(L^p\)-conditions. NoDEA Nonlinear Differ. Equ. Appl. 23, 15 (2016)

    Article  MATH  Google Scholar 

  20. Liang, S.: Exact multiplicity and stability of periodic solutions for a Duffing equation. Mediterr. J. Math. 10, 189–199 (2013)

    Article  MathSciNet  MATH  Google Scholar 

  21. Liu, W., Li, Y.: Existence of \(2\pi \)-periodic solutions for the non-dissipative Duffing equation under asymptotic behaviors of potential function. Z. Angew. Math. Phys. 57, 1–11 (2006)

    Article  MathSciNet  MATH  Google Scholar 

  22. Llibre, J., Roberto, L.A.: On the periodic solutions of a class of Duffing differential equations. Discrete Contin. Dyn. Syst. 33, 277–282 (2013)

    MathSciNet  MATH  Google Scholar 

  23. Loud, W.S.: Periodic solutions of \(x^{\prime \prime }+cx^{\prime }+g(x)=\epsilon f(t)\). Mem. Am. Math. Soc. 31, 58 (1959)

    MathSciNet  MATH  Google Scholar 

  24. Mawhin, J.: Global results for the forced pendulum equation. In: Cañada, A., Drábek, P., Fonda, A. (eds.) Handbook of Differential Equation: Ordinary Differential Equation, vol. 1, pp. 533–589. Elsevier BV, Amsterdam (2008)

    Chapter  Google Scholar 

  25. Njoku, F.I., Omari, P.: Stability properties of periodic solutions of a Duffing equation in the presence of lower and upper solutions. Appl. Math. Comp. 135, 471–490 (2003)

    Article  MathSciNet  MATH  Google Scholar 

  26. Ortega, R.: Prevalence of non-degenerate periodic solutions in the forced pendulum equation. Adv. Nonlinear Stud. 13, 219–229 (2013)

    Article  MathSciNet  MATH  Google Scholar 

  27. Ortega, R.: Some applications of the topological degree to stability theory. In: Granas, A., Frigon, M. (eds.) Topological Methods in Differential Equations and Inclusions, pp. 377–409. Kluwer, Dordrecht (1995)

    Chapter  Google Scholar 

  28. Ortega, R.: The first interval of stability of a periodic equation of Duffing type. Proc. Am. Math. Soc. 115, 1061–1067 (1992)

    Article  MathSciNet  MATH  Google Scholar 

  29. Ortega, R.: Stability and index of periodic solutions of an equation of Duffing type. Boll. UMI B 3, 533–546 (1989)

    MathSciNet  MATH  Google Scholar 

  30. Ouyang, T., Shi, J.: Exact multiplicity of positive solutions for a class of semilinear problem II. J. Differ. Equ. 158, 94–151 (1999)

    Article  MathSciNet  MATH  Google Scholar 

  31. Talenti, G.: Best constant in Sobolov inequality. Ann. Mat. Pura Appl. 110, 353–372 (1976)

    Article  MathSciNet  MATH  Google Scholar 

  32. Tarantello, G.: On the number of solutions for the forced pendulum equation. J. Differ. Equ. 80, 79–93 (1989)

    Article  MathSciNet  MATH  Google Scholar 

  33. Torres, P.J.: Existence and stability of periodic solution of a Duffing equation by using a new maximum principle. Mediterr. J. Math. 1, 479–486 (2004)

    Article  MathSciNet  MATH  Google Scholar 

  34. Torres, P.J.: Existence of one-signed periodic solutions of some second-order differential equations via a Krasnoselskii fixed point theorem. J. Differ. Equ. 190, 643–662 (2003)

    Article  MathSciNet  MATH  Google Scholar 

  35. Torres, P.J., Zhang, M.: A monotone iterative scheme for a second order nonlinear equation based a generalized anti-maximum principle. Math. Nachr. 251, 101–107 (2003)

    Article  MathSciNet  MATH  Google Scholar 

  36. Van Horssen, W.T., Pischanskyy, O.V.: On the stability properties of a damped oscillator with a periodically time-varying mass. J. Sound Vib. 330, 3257–3269 (2011)

    Article  Google Scholar 

  37. Wang, H., Li, Y.: Existence and uniqueness of periodic solutions for Duffing equations across many points of resonance. J. Differ. Equ. 108, 152–169 (1994)

    Article  MathSciNet  MATH  Google Scholar 

  38. Wang, S., Yeh, T.: A theorem on reversed S-shaped bifurcation curves for a class of boundary value problems and its application. Nonlinear Anal. 71, 126–140 (2009)

    Article  MathSciNet  MATH  Google Scholar 

  39. Zhang, M.: Optimal conditions for maximum and antimaximum principles of the periodic solution problem. Bound. Value Probl. 2010, 1–26 (2010)

    Article  MathSciNet  Google Scholar 

  40. Zhang, M.: Certain classes of potentials for \(P\)-Laplacian to be non-degenerate. Math. Nachr. 278, 1823–1836 (2005)

    Article  MathSciNet  MATH  Google Scholar 

  41. Zhang, M.: The rotation number approach to eigenvalue of the one-dimensional \(p\)-Laplacian with periodic potentials. J. Lond. Math. Soc. 2(64), 125–143 (2001)

    Article  MathSciNet  MATH  Google Scholar 

  42. Zhang, M., Li, W.: A Lyapunov-type stability criterion using \(L^{\alpha }\) norms. Proc. Am. Math. Soc. 130, 3325–3333 (2002)

    Article  MathSciNet  MATH  Google Scholar 

  43. Zeidler, E.: Applied Functional Analysis: Main Principles and Their Applications, Applied Mathematical Sciences 109, vol. 2. Springer, Berlin (1991)

    Google Scholar 

  44. Zitan, A., Ortega, R.: Existence of asymptotically stable periodic solutions of a forced equation of Liénard type. Nonlinear Anal. 22, 993–1003 (1994)

    Article  MathSciNet  MATH  Google Scholar 

Download references

Acknowledgements

The author would like to express sincere thank to the anonymous referee whose valuable comments greatly improve the manuscript.

Author information

Authors and Affiliations

  1. School of Mathematics, Jilin University, Changchun, 130012, People’s Republic of China

    Shuqing Liang

Authors
  1. Shuqing Liang
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Shuqing Liang.

Additional information

Supported by National Natural Science Foundation of China Grant No. 11501240.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Liang, S. Exact Multiplicity and Stability of Periodic Solutions for Duffing Equation with Bifurcation Method. Qual. Theory Dyn. Syst. 18, 477–493 (2019). https://doi.org/10.1007/s12346-018-0296-x

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s12346-018-0296-x

Keywords

Mathematics Subject Classification

Search

Navigation