Reducible M-curves for Le-networks in the totally-nonnegative Grassmannian and KP-II multiline solitons

Abstract

We associate real and regular algebraic–geometric data to each multi-line soliton solution of Kadomtsev–Petviashvili II (KP) equation. These solutions are known to be parametrized by points of the totally non-negative part of real Grassmannians $Gr^{\mathrm{TNN}}(k,n)$. In [3] we were able to construct real algebraic–geometric data for soliton data in the main cell $Gr^{\mathrm{TP}} (k,n)$ only. Here we do not just extend that construction to all points in $Gr^{\mathrm{TNN}}(k,n)$, but we also considerably simplify it, since both the reducible rational $\texttt {M}$-curve $\Gamma$ and the real regular KP divisor on $\Gamma$ are directly related to the parametrization of positroid cells in $Gr^{\mathrm{TNN}}(k,n)$ via the Le-networks introduced in [63]. In particular, the direct relation of our construction to the Le-networks guarantees that the genus of the underlying smooth $\texttt {M}$-curve is minimal and it coincides with the dimension of the positroid cell in $Gr^{\mathrm{TNN}}(k,n)$ to which the soliton data belong to. Finally, we apply our construction to soliton data in $Gr^{\mathrm{TP}}(2,4)$ and we compare it with that in [3].

Appendix A The totally nonnegative Grassmannian

In this appendix we recall some useful definitions and theorems from [63] to make the paper self-contained. For more details on the topological properties of $Gr^{\mathrm{TNN}}(k,n)$ and on generalizations of total positivity to reductive groups we refer to [53, 54, 57, 64, 65]. In particular we use Postnikov rules to represent each Le-tableau D by a unique bipartite trivalent oriented network ${{\mathcal {N}}}$ in the disk. In Sect. 4.1 we use the Le-graph ${{\mathcal {G}}}$ of ${{\mathcal {N}}}$ to construct a curve $\Gamma ({{\mathcal {G}}})$, which is a rational degeneration of a smooth ${\texttt {M}}$-curve of genus equal to the dimension d of the corresponding positroid cell.

Definition A.1

(The totally non-negative part of Gr(k, n) [63]) The totally non-negative Grassmannian $Gr^{\mathrm{TNN}}(k,n)$ is the subset of the Grassmannian Gr(k, n) with all Plücker coordinates non-negative, i.e. it may be defined as the following quotient: $Gr^{\mathrm{TNN}}(k,n)= GL^+_k \backslash \text{ Mat }^{\mathrm{TNN}}_{kn}$. Here $GL^+_k$ is the group of $k\times k$ matrices with positive determinant, and $\text{ Mat }^{\mathrm{TNN}}_{kn}$ is the set of real $k\times n$ matrices A of rank k such that all maximal minors are non-negative, i.e. $\Delta _I (A) \ge 0$, for all k-element subsets $I\subset [n]$.

The totally positive Grassmannian $Gr^{\mathrm{TP}} (k,n)\subset Gr^{\mathrm{TNN}}(k,n)$ is the subset of Gr(k, n) whose elements may be represented by $k\times n$ matrices with all strictly positive maximal minors $\Delta _I(A)$.

It is well-known that Gr(k, n) is decomposed into a disjoint union of Schubert cells $\Omega _{\lambda }$ indexed by partitions $\lambda \subset (n-k)^k$ whose Young diagrams fit inside the $k\times (n-k)$ rectangle (we use the so-called English notation in our text). A refinement of this decomposition was proposed in [33, 34]. Intersecting the matroid strata with $Gr^{\mathrm{TNN}}(k,n)$ one obtains the totally non-negative Grassmann cells [63] with the following property: each cell is birationally equivalent to an open octant of appropriate dimension, and this birational map is also a topological homeomorphism.

Let us recall these constructions. The Schubert cells are indexed by partitions, or, equivalently by pivot sets. To each partition $\lambda =(\lambda _1,\ldots ,\lambda _k)$, $n-k\ge \lambda _1\ge \lambda _2\ldots \ge \lambda _k\ge 0$, $\lambda _j\in {\mathbb {Z}}$ there is associated a pivot set $I(\lambda ) =\{ 1\le i_1< \cdots < i_k \le n\}$ defined by the following relations:

$$\begin{aligned} i_j = n-k+j-\lambda _j, \ \ j\in [k]. \end{aligned}$$

(A.1)

Each Schubert cell is the union of all Grassmannian points sharing the same set of pivot columns. Therefore, any point in $\Omega _{\lambda }$ with pivot set I can be represented by a matrix in canonical reduced row echelon form, i.e. a matrix A such that $A^i_{i_l}=1$ for $l\in [k]$ and all the entries to the left of these 1’s are zero. The Young diagram representing the Schubert cell $\Omega _{\lambda }$ is a collection of boxes arranged in k rows, aligned on the left such that the j-th row contains $\lambda _j$ boxes, $j\in [k]$.

Fig. 17

The Young diagram associated to the partition (5, 3, 1, 0), $k=4$, $n=10$

Remark A.1

In this paper we use the ship battle rule to enumerate the boxes of the Young diagram of a given partition $\lambda$. Let $I=I(\lambda )$ be the pivot set of the k vertical steps in the path along the SE boundary of the Young diagram proceeding from the NE vertex to the SW vertex of the $k\times (n-k)$ bound box, and let ${{\bar{I}}} = [n]\backslash I$ be the non-pivot set. Then the box $B_{ij}$ corresponds to the pivot element $i\in I$ and the non-pivot element $j\in {{\bar{I}}}$ (see Fig. 17 for an example).

Each stratum in the refined decomposition of Gr(k, n) into matroid strata [33] is composed by the points of the Grassmannian which share the same set of nonzero Plücker coordinates. Each Plücker coordinate is indexed by a base, i.e. a k-element subset in [n], and, for a given stratum, the set of these bases forms a matroid ${{\mathcal {M}}}$, i.e. for all $I, J\in {{\mathcal {M}}}$ for each $i\in I$ there exists $j\in J$ such that $I\backslash \{i\}\cup \{j\}\in {{\mathcal {M}}}$. Then the stratum ${{\mathcal {S}}}_{{\mathcal {M}}}\subset Gr(k,n)$ is defined as

$$\begin{aligned} {{\mathcal {S}}}_{{\mathcal {M}}} = \{ [A] {\in } Gr(k,n){:} \Delta _I (A) \not = 0 \; \iff I{\in } {{\mathcal {M}}}\}. \end{aligned}$$

A matroid ${{\mathcal {M}}}$ is called realizable if ${{\mathcal {S}}}_{{\mathcal {M}}}\ne \emptyset$. The pivot set I is the lexicographically minimal base of the matroid ${{\mathcal {M}}}$. In [63], Postnikov studies the analogous stratification for $Gr^{\mathrm{TNN}}(k,n)$.

Definition A.2

(Positroid cell [63]) The totally nonnegative Grassmann (positroid) cell ${{\mathcal {S}}}_{{\mathcal {M}}}^{\mathrm{TNN}}$ is the intersection of the matroid stratum ${{\mathcal {S}}}_{{\mathcal {M}}}$ with the totally nonnegative Grassmannian $Gr^{\mathrm{TNN}}(k,n)$:

The matroid ${\mathcal {M}}$ is totally nonnegative if the matroid stratum ${{\mathcal {S}}}_{{\mathcal {M}}}^{\mathrm{TNN}}\not = \emptyset$.

Example A.1

$Gr^{\mathrm{TP}} (k,n)$ is the top dimensional cell and corresponds to the complete matroid ${{\mathcal {M}}} = \left( {\begin{array}{c}[n]\\ k\end{array}}\right)$.

Fig. 18

The Le-rule $a,c\not =0$ imply $b\not =0$

A useful tool to classify positroid cells are Le-diagrams and Le-graphs [63].

Definition A.3

(Le-diagram and Le-tableau [63]) For a partition $\lambda$, a Le-diagram D of shape $\lambda$ is a filling of the boxes of its Young diagram with 0’s and 1’s such that, for any three boxes indexed (i, k), (l, k), (l, j), where $i<l$ and $k<j$, filled correspondingly with a, b, c, if $a,c\not =0$, then $b\not =0$ (see Fig. 18). For such a diagram denote by d the number of boxes of D filled with 1s.

The Le-tableau T is obtained from a Le-diagram D of shape $\lambda$, by replacing all 1s in D by positive numbers $w_{ij}$ (weights).

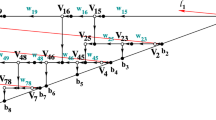
The construction of the Le-graph ${{\mathcal {G}}}$ associated to a given Le-diagram is as follows [63]. The boundary of the Young diagram of $\lambda$ gives the lattice path of length n from the upper right corner to the lower left corner of the rectangle $k \times (n-k)$. A vertex is placed in the middle of each step in the lattice path and is marked $b_1,\dots ,b_n$ proceeding NE to SW. The vertices $b_i$, $i\in I\equiv I(\lambda )$ corresponding to vertical steps are the sources of the network and the remaining vertices $b_j$, $j\in {{\bar{I}}}$, corresponding to horizontal steps are the sinks. Then the upper right corner is connected to the lower left corner by another path to obtain a simple close curve containing the Young diagram. For each box of the Le-diagram (i, j) filled by 1 an internal vertex $V_{ij}$ is placed in the middle of the box; from such vertex one draws a vertical line downwards to the boundary sink $b_j$ and a horizontal line to the right till it reaches the boundary source $b_i$. By the Le-property any intersection of such lines is also a vertex. All edges are oriented either to the left or downwards.

To obtain a Le-network ${{\mathcal {N}}}$ from a Le-tableaux of shape $\lambda$ one constructs the Le-graph from the corresponding Le-diagram, assigns the weight $w_{ij}>0$ from the box $B_{ij}$ to the horizontal edge e which enters $V_{ij}$ and assigns unit weights $w_e=1$ to all vertical edges [63]. The correspondence between the Le-tableau and the Le-network is illustrated in Fig. 19.

The map $T\mapsto {{\mathcal {N}}}$ gives the isomorphism ${\mathbb R}^{d}_{>0} \simeq {\mathbb R}^{E(G)}_{>0}$ between the set of Le-tableaux T with fixed Le-diagram D and the set of Le-networks (modulo gauge transformations) with fixed graph ${\mathcal {G}}$ corresponding to the diagram D as above.

Fig. 19

The Le-diagram and the Le-network of Example A.2. The horizontal edges are oriented from right to left while the vertical ones from top to bottom

Given a Le-tableau T with pivot set I it is possible to reconstruct both the matroid and the representing matrix in reduced row echelon form using the Lindström lemma.

Proposition A.1

[63] Let ${{\mathcal {N}}}$ be the Le-network associated to the Le-diagram D and let I be the pivot set. For any k-elements subset $J\subset [n]$, let $K=I\backslash J$ and $L=J\backslash I$. Then the maximal minor $\Delta _J(A)$ of the matrix $A=A({{\mathcal {N}}})$ is given by the following subtraction-free polynomial expression in the edge weights $w_e$:

$$\begin{aligned} \Delta _J (A) = \sum \limits _P \prod \limits _{i=1}^r w(P_i), \end{aligned}$$

where the sum is over all non-crossing collections $P=(P_1,\dots ,P_r)$ of paths joining the boundary vertices $b_i$, $i\in K$ with boundary vertices $b_j$, $j\in L$.

Let $i_r\in I$, where $r\in [k]$ and $j\in [n]$. Then the element $A^r_j$ of the matrix A in reduced row echelon form (RREF) associated to the Le-network ${{\mathcal {N}}}$ is

$$\begin{aligned} A^{r}_j = \left\{ \begin{array}{ll} 0 &{}\quad \quad j<i_r,\\ 1 &{}\quad \quad j=i_r,\\ (-1)^{\sigma _{i_r j}} \sum \limits _{P : i_r \mapsto j} \left( \prod \limits _{e\in P} w_e \right) &{}\quad \quad j>i_r, \end{array} \right. \end{aligned}$$

(A.2)

where the sum is over all paths P from the boundary source $b_{i_r}$ to the boundary sink $b_j$, $j\in {{\bar{I}}}$, and $\sigma _{i_r j}$ is the number of pivot elements $i_s\in I$ such that $i_r<i_s <j$.

Example A.2

Let us consider the Le-diagram D and Le-network represented in Fig. 19. Then $I= (1,2,4,7)$ and the matrix in reduced row echelon form is

$$\begin{aligned} A = \left( \begin{array}{c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c} 1 &{} 0 &{} 0 &{} 0 &{} w_{15} &{} w_{15}(w_{16}+w_{46}) &{} 0 &{} -w_{15}w_{48}(w_{16}+w_{46}) &{} -w_{15}w_{48}w_{49} (w_{16}+w_{46})-w_{15}w_{16}w_{19} \\ 0 &{} 1 &{} w_{23} &{} 0 &{} -w_{23}w_{25} &{}-w_{23}w_{25}w_{46} &{} 0 &{} w_{23}w_{25}w_{46}w_{48} &{} w_{23}w_{25}w_{46}w_{48}w_{49}\\ 0 &{} 0 &{} 0 &{} 1 &{} w_{45} &{} w_{45}w_{46} &{} 0 &{} -w_{45}w_{46}w_{48} &{} -w_{45}w_{46}w_{48}w_{49}\\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 1 &{} w_{78} &{} 0 \end{array}\right) . \end{aligned}$$

The same example is used in [47] to illustrate the combinatorial properties of the KP-soliton tropical asymptotics in the limit $t\rightarrow -\infty$.

Remark A.2

(Reducible positroid cells) A totally non-negative cell ${{\mathcal {S}}}_{{\mathcal {M}}}^{\mathrm{TNN}}\subset Gr^{\mathrm{TNN}}(k,n)$ is reducible if its Le-diagram contains either columns or rows filled by 0s [63]. The Le-diagram has the j-th column filled by zeros if and only if no base in ${\mathcal {M}}$ contains the element j. Similarly, the Le-diagram has the r-th row filled by zeros if and only if all bases in ${\mathcal {M}}$ contain $i_r$, the r-th element in the lexicographically minimal base $I\in {\mathcal {M}}$.

In the first case, there is no path in the Le-network with destination j, and the RREF matrix A has the j-th column filled by zeroes. One can then shift by one all indexes bigger than j in ${\mathcal {M}}$, call ${\mathcal {M}}^{\prime }$ the resulting matroid of k element subsets in $[n-1]$, correspondingly eliminate the j-th column from the Le-diagram and the j-th column from the matrix A, and represent the same point in the totally non-negative cell ${{\mathcal {S}}}^{\mathrm{TNN}}_{{\mathcal {M}}^{\prime }}\subset Gr^{\mathrm{TNN}} (k,n-1)$.

In the second case, there is no path in the Le-network starting from the boundary source $b_{i_r}$, and the r-th row of A contains just the pivot element. One can then eliminate $i_r$ from all the bases in ${\mathcal {M}}$ and shift by one all the indexes greater than $i_r$, call ${\mathcal {M}}^{\prime }$ the resulting matroid of $k-1$ elements in $[n-1]$, correspondingly eliminate the r-th row of the Le-diagram, eliminate the r-th row and the $i_r$-th columns from the matrix A and change the sign of all elements of $A^i_j$ with $i<r$ and $j>i_r$, and represent the same point in the totally non-negative cell ${{\mathcal {S}}}^{\mathrm{TNN}}_{{\mathcal {M}}^{\prime }}\subset Gr^{\mathrm{TNN}} (k-1,n-1)$.

Fig. 20

All internal vertices of the Le-network are transformed to trivalent vertices, preserving the boundary measurement map

In Sect. 4.1 we associate a unique universal curve to each positroid cell, by modeling the construction of a rational degeneration of an $\texttt {M}$-curve on the Le-graph: vertices of the graph correspond to copies of ${\mathbb {CP}}^1$, whereas the edges govern the positions of the double points. To provide a construction of the curve without parameters, we require that each copy of ${\mathbb {CP}}^1$ associated to an internal vertex has three marked points. Moreover, the recursive construction of the wave function and the characterization of its divisor is technically simpler if modeled on a bipartite graph where black and white vertices alternate. For the above reasons we follow Postnikov’s rules to transform the Le-network ${{\mathcal {N}}}$ into a planar bipartite perfect network with internal vertices of degree at most three, and we continue to denote it with ${{\mathcal {N}}}$, since this transformation is well-defined. We remark that, after such transformation, ${{\mathcal {N}}}$ is perfect since each boundary vertex has degree one and each internal vertex in ${\mathcal {G}}$ is either the initial vertex of exactly one edge or the final vertex of exactly one edge. For the Le-graph the only relevant transformation concerns the degree four internal vertices which become couples of trivalent vertices of opposite colour [63] (see Fig. 20). Moreover, following Postnikov [63], we assign black color to each internal vertex with exactly one outgoing edge and white color to each trivalent internal vertex with exactly one incoming edge. We also assign black color to all boundary vertices. Finally we move all boundary vertices to the same line (see Fig. 21). Therefore we get to the following definition.

Fig. 21

Transformation of graph at the boundary source $b_i$

Definition A.4

(The trivalent bipartite Le-network used to construct the curve $\Gamma ({{\mathcal {G}}})$) The acyclically oriented network associated to the Le-tableau T is transformed into a perfect trivalent bipartite network ${{\mathcal {N}}}$ in the disk with the following rules:

• (1) If the box $B_{ij}$ of T is filled with 1, the vertex $V_{ij}$ is transformed into a couple of one black vertex $V^{\prime }_{ij}$ and one white vertex $V_{ij}$ (see Fig. 20 [left]); following [63] the horizontal edge joining the black vertex $V_{ij}^{\prime }$ to the white vertex $V_{ij}$ has unit weight, while all other weights are unchanged (see Fig. 20 [right]);

• (2) All boundary vertices have black colour and degree one. Any isolated boundary source $b_i$ is joined by a vertical edge to a white vertex $V_i$. If the boundary source $b_i$ is not isolated, we add a white vertex $V_i$ to the edge of weight w starting at $b_i$, we assign unit weight to the edge joining $b_i$ to $V_i$ and weight w to the other edge at $V_i$ (see Fig. 21 middle);

• (3) All internal vertices corresponding to a given row r in T, included $V_{i_r}$, lie on a common horizontal line;

• (4) The contour of the disk is continuously deformed in such a way that all of the boundary sources and boundary sinks lay on the same horizontal segment and the edge at each boundary vertex is vertical; in this process the positions of all internal vertices are left invariant (see Fig. 21 right).

In Fig. 22 we show the bipartite Le-network for Example A.2.

Fig. 22

The bipartite Le-network for Example A.2 (see Fig. 19). The weights refer to the perfect orientation associated to the pivot base [1, 2, 4, 7] of the matroid: the vertical edges starting at the boundary sources $b_1,b_2,b_4$ and $b_7$ are oriented upwards, all other vertical edges are oriented downwards, while all horizontal edges are oriented from right to left

Remark A.3

Let ${{\mathcal {G}}}$ be the bipartite Le-graph associated to the Le-diagram D. Then in ${{\mathcal {G}}}$

• (1) Each black vertex has at most one vertical edge;

• (2) Each white vertex has exactly one vertical edge;

• (3) The total number of white vertices is $d+k$;

• (4) If D is irreducible, then the total number of trivalent white vertices is $d-k$, while the total number of trivalent black vertices is $d-n+k$.

For any $r\in [k]$, we denote $N_{r}$ the number of boxes filled with 1 in the r-th row of the Le-diagram D. By construction we have

$$\begin{aligned} d \equiv \sum \limits _{i_r\in I} N_{r}, \quad \quad \text{ with } N_{r} \equiv \# \, \{ \text{ boxes } B_{i_r j} \text{ filled } \text{ by } \text{1, } \text{ for } j \in {{\bar{I}}} \} \end{aligned}$$

(A.3)

We also introduce an index to simplify the counting of boxes filled by ones. For any fixed $r\in [k]$, let $1\le j_1< j_2 \dots < j_{N_r}\le n$ be the non-pivot indexes of the boxes $B_{i_r j_s}$, $s\in {{\hat{N}}}_r$, filled by one in the r-th row. Then for any $r\in [k]$, we define the index

$$\begin{aligned} \chi ^{i_r}_{l} = \left\{ \begin{array}{ll} 1 &{}\quad \text{ if } \text{ there } \text{ exists } s\in [N_r] \text{ such } \text{ that } l=j_s, \\ 0 &{}\quad \text{ if } B_{i_r l} \text{ is } \text{ filled } \text{ by } \text{0 } \text{ or } l<i_r. \\ \end{array}\right. \end{aligned}$$

(A.4)