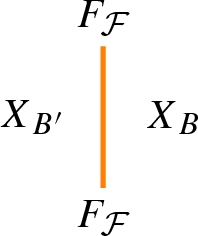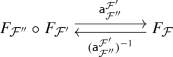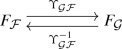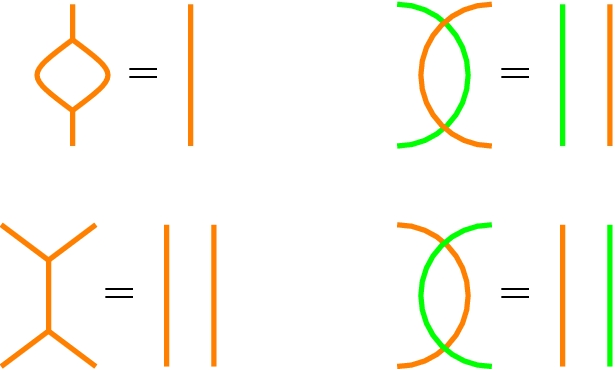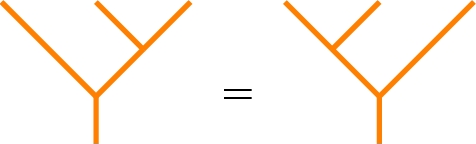Skip to main content
SpringerLink
Log in

Coxeter categories and quantum groups

  • Published:
Selecta Mathematica Aims and scope Submit manuscript

Abstract

We define the notion of braided Coxeter category, which is informally a monoidal category carrying compatible, commuting actions of a generalised braid group \(B_W\) and Artin’s braid groups \(B_n\) on the tensor powers of its objects. The data which defines the action of \(B_W\) bears a formal similarity to the associativity constraints in a monoidal category, but is related to the coherence of a family of fiber functors. We show that the quantum Weyl group operators of a quantised Kac–Moody algebra \(U_{\hbar }{{\mathfrak {g}}}\), together with the universal R-matrices of its Levi subalgebras, give rise to a braided Coxeter category structure on integrable, category \({\mathcal {O}}\)-modules for \(U_{\hbar }{{\mathfrak {g}}}\). By relying on the 2-categorical extension of Etingof–Kazhdan quantisation obtained in Appel and Toledano Laredo (Selecta Math NS 24:3529–3617, 2018), we then prove that this structure can be transferred to integrable, category \({\mathcal {O}}\)-representations of \({\mathfrak {g}}\). These results are used in Appel and Toledano Laredo (arXiv:1512.03041, p 48, 2015) to give a monodromic description of the quantum Weyl group operators of \(U_{\hbar }{{\mathfrak {g}}}\), which extends the one obtained by the second author for a semisimple Lie algebra.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

Notes

  1. The notation \(V^{\otimes n}_{b}\) indicates that n copies of V have been tensored together according to b. For example, if \(b=(x_1x_2)x_3\), \(V_b^{\otimes 3}=((V\otimes V)\otimes V)\).

  2. We use the term diagram to denote an undirected graph, with mo mutiple edges or loops.

  3. If \(D={\textsf {A} }_{n-1}\), \(B=D\) and \(B'\) corresponds to the pair of parentheses \(x_1\ldots x_{i-1}\cdot (x_i\ldots x_j)\cdot x_{j+1} \ldots x_n\), a maximal nested set on B relative to \(B'\) consists of a complete bracketing of the monomial \(x_1\ldots x_{i-1}\cdot x_{ij} \cdot x_{j+1}\ldots x_n\).

  4. A labelling on D is the additional data of integers \(m_{ij}\in \{2,\dots ,\infty \}\) for any two \(i\ne j \in {\mathbf {I}}\) such that \(m_{ij}=m_{ji}\) and \(m_{ij}=2\) if \(i\perp j\).

  5. In a braided monoidal category with braiding \(\beta \), the opposite braiding is \(\beta ^{\scriptscriptstyle {\text {op}}} _{X,Y}:=\beta _{Y,X}^{-1}\).

  6. Equivalently, we require that the composition \(H_{{\mathfrak {b}}_{B'}}^{-1}\circ {{\,\mathrm{Res}\,}}_{{\mathcal {Q}}({\mathfrak {b}}_{B'}),{\mathcal {Q}}({\mathfrak {b}}_B)}\circ H_{{\mathfrak {b}}_B}\) be isomorphic, as a non-monoidal functor, to \({{\,\mathrm{Res}\,}}_{{\mathfrak {b}}_{B'},{\mathfrak {b}}_B}\).

  7. The symbol \(\infty \) refers to the fact that we allow infinite-dimensional weight spaces. This is required by the fact that the restriction corresponding to \(\overline{{\mathfrak {g}}}_{B'}\subset \overline{{\mathfrak {g}}}_B\) or \(U_{\hbar }{\overline{{\mathfrak {g}}}_{B'}}\subset U_{\hbar }{\overline{{\mathfrak {g}}}_B}\) does not preserve the finite-dimensionality of weight spaces if \(B'\subsetneq B\).

  8. Note that if \({\mathcal {K}}_1 \subseteq {\mathcal {K}}_2\in {{\mathsf {Ns}} }(B,B')\) then \({{\mathsf {Mns}} }_{{\mathcal {K}}_1}(B,B')\supseteq {{\mathsf {Mns}} }_{{\mathcal {K}}_2}(B,B')\), and there is a forgetful map \({{\,\mathrm{Hom}\,}}({\mathcal {C}},{\mathcal {C}}')[{\mathcal {K}}_1]\rightarrow {{\,\mathrm{Hom}\,}}({\mathcal {C}},{\mathcal {C}}')[{\mathcal {K}}_2]\).

  9. Note that the composition \(F'\circ F\) forgets some of the data of F, namely the 1-morphisms \(F_{{{\mathcal {F}}}}\) and 2-morphisms \(\Upsilon _{{{\mathcal {F}}}{{\mathcal {G}}}}\) corresponding to \({{\mathcal {F}}},{{\mathcal {G}}}\in {{\mathsf {Mns}} }_{{\mathcal {K}}}(B,B'')\setminus {{\mathsf {Mns}} }_{{\mathcal {K}}\cup {\mathcal {K}}'}(B,B'')\).

  10. Note that \({{{\mathsf {s}} }}_{D}\) is technically a pseudo 2-functor, since it preserves the composition only up to a coherent 2-isomorphism. Namely, for any \(B''\subseteq B'\subseteq B\), set \({\mathcal {K}}={{\mathsf {conn}} } (B)\cup {{\mathsf {conn}} } (B')\), \({\mathcal {K}}'={{\mathsf {conn}} } (B')\cup {{\mathsf {conn}} } (B'')\) and \({\mathcal {K}}''={{\mathsf {conn}} } (B)\cup {{\mathsf {conn}} } (B'')\). Then, the 2-isomorphism \({\mathcal {K}}'\cup {\mathcal {K}}\rightarrow {\mathcal {K}}''\) in \(\mathfrak {Ns}(D)\) gives an identification\( {{{\mathsf {s}} }}_D(B'\rightarrow B'')\circ {{{\mathsf {s}} }}_D(B\rightarrow B')\rightarrow {{{\mathsf {s}} }}_D(B\rightarrow B'')\).

  11. The terminology adopted here differs from the one in [37], where the adjective lax is not used in particular. In the present paper, we reserve the term diagrammatic algebra for a lax diagrammatic algebra such that \(m_B\circ i_{BB'}\otimes i_{BB''}:A_{B'}\otimes A_{B''}\rightarrow A_ B\) is an isomorphism for any \(B=B'\sqcup B''\), which implies in particular that \(A_\emptyset ={{{\mathsf {k}} }}\) (see Remark 5.14).

  12. In [37], a morphism of lax diagrammatic algebras is referred to as a strict morphism.

  13. Note that the commutativity of \(A_{B'}, A_{B''}\) in \(A_{B}\), for any \(B',B''\subseteq B\) with \(B'\perp B''\), has no relevance in the above construction of pre-Coxeter structure on \({{\,\mathrm{Rep}\,}}(A)\). On the other hand, this feature is particularly convenient in the construction of examples arising from the quantisation of Lie bialgebras (cf. Sect. 10, in particular Lemma 10.9).

  14. Here, \({\mathfrak {h}}_B\) is the Cartan subalgebra of \({\mathfrak {g}}_B\subseteq {\mathfrak {g}}_D\), \({\mathfrak {h}}_{B/B'}\subseteq {\mathfrak {h}}_{B}\) is the orthogonal complement of \({\mathfrak {h}}_{B'}\), and \(({\mathfrak {h}}_{B/B'})_{{\text {reg}}}\) is the complement in \({\mathfrak {h}}_{B/B'}\) to the root hyperplanes in \({\mathfrak {h}}_B\) not containing \({\mathfrak {h}}_{B/B'}\).

  15. In a braided monoidal category with braiding \(\beta \), the opposite braiding is \(\beta ^{\scriptscriptstyle {\text {op}}}_{X,Y}:=\beta _{Y,X}^{-1}\).

  16. Note that the Lie algebra grading on \({\mathfrak {b}}_+\) inherited from \({\mathfrak {g}}\) differs from that induced by the identification \({\mathfrak {b}}_+\cong {\mathfrak {b}}_-^\star \) by a shift since the inner product yields an isomorphism \(({\mathfrak {b}}_{-,n})^*\cong {\mathfrak {b}}_{+,-n+d}\). Note also that the isotropy of \({\mathfrak {b}}_\pm \) implies that \({\mathfrak {b}}_{-,n}=0\) if \(n\leqslant d-1\) and \({\mathfrak {b}}_{+,n}=0\) if \(n\geqslant d+1\).

  17. In the sequel, we shall abusively refer to such a \({\mathfrak {b}}\) as an \({\mathbb {N}}\)-graded Lie bialgebra.

  18. Note that such an i is necessarily an embedding.

  19. The requirements on \(p_{B'B}\) are formulated so as to mirror those in 5.9. Note, however, that 1) \(p_{BB}={{\,\mathrm{id}\,}}_{{\mathfrak {b}}_B}\) follows from \(p_{BB}\circ i_{BB}={{\,\mathrm{id}\,}}_{b_B}\) and \(i_{BB}={{\,\mathrm{id}\,}}_{{\mathfrak {b}}_B}\) and 2) the fact that \(p_{B'B}\oplus p_{B''B}\) is the inverse of \(i_{BB'}+i_{BB''}\) implies that it is a Lie (bi)algebra morphism. Note also that since \(p_{CB}\circ i_{BC}={{\,\mathrm{id}\,}}_{b_C}\) for \(C=B',B''\), the requirement that \(p_{B'B}\oplus p_{B''B}=(i_{BB'}+i_{BB''})^{-1}\) is equivalent to \(p_{B'B}\circ i_{BB''} =0\) for any \(B'\perp B''\).

  20. Note that \({\mathcal {P}}(D)\) is the opposite category to the category \({\mathfrak {P}}(D)\) introduced in 3.5.

  21. The notion of admissible Drinfeld–Yetter module is due to P. Etingof (private communication), and is studied in detail in [3, 2.20–2.22].

  22. In a monoidal category \(({\mathcal {C}},\otimes )\), \(V^{\otimes n}_{b_n}\) denotes the n-fold tensor product of \(V\in {\mathcal {C}}\) bracketed according to \(b_n\). For example \(V^{\otimes 3}_{(\bullet \bullet )\bullet }=(V\otimes V)\otimes V\).

  23. Note that the requirement (7.1) determines J uniquely. In fact, given any functor \({{\mathcal {G}}}:{{{{\mathsf {P}} }}}\rightarrow {\mathcal {N}}\) such that \({{\mathcal {G}}}([n])={{\mathcal {G}}}([1])^{\otimes n}_{b_n}\), (7.1) defines a family of isomorphisms \(J_{m,n}:{{\mathcal {G}}}([m])\otimes {{\mathcal {G}}}([n])\rightarrow {{\mathcal {G}}}([m+n])\), which is easily seen to be compatible with the commutativity and associativity constraints in \({{{{\mathsf {P}} }}}\) and \({\mathcal {N}}\). Such a J, however, need not be natural with respect to morphisms in \({{{{\mathsf {P}} }}}\), that is satisfy \({{\mathcal {G}}}(f\otimes g)=J_{m_2,n_2}\cdot G(f)\otimes G(g)\cdot J_{m_1,n_1}^{-1}\) for any \(f\in {{{{\mathsf {P}} }}}([m_1],[m_2])\) and \(g\in {{{{\mathsf {P}} }}}([n_1],[n_2])\). For example, if \({\mathcal {N}}\) is strict, then \(J={{\,\mathrm{id}\,}}\), and J is natural if and only if \({{\mathcal {G}}}\) is multiplicative with respect to tensor products of morphisms.

  24. If p, q are idempotents, \((p+q)^2=p+q\) is equivalent to \(pq=-qp\). This implies \(pq=pq^2=-qpq=q^2p=qp\), and therefore \(pq=0\).

  25. Here B is identified with the unique element in \({{\mathsf {Mns}} }(B,B)\).

  26. There is a natural action of \({\mathfrak {S}}_n\) on \({\mathfrak {U}}_{B}^{n}\) given by permutations of \(\underline{{{{\mathsf {V}} }}}_{1}\otimes \cdots \otimes \underline{{{{\mathsf {V}} }}}_{n}\) (cf. [4, Sec. 7.2]), which is a propic version of the action of \({\mathfrak {S}}_n\) on \(U{\mathfrak {g}}_{{\mathfrak {b}}}^{\otimes n}\).

  27. Note that \(\textsf {DY} _{{\mathfrak {c}}}^{\hbar }\) can also be identified with the category of Drinfeld–Yetter modules over the Lie bialgebra \({{\mathfrak {c}}}_{\hbar }=({{\mathfrak {c}}}{\llbracket \hbar \rrbracket },\hbar [\cdot ,\cdot ],\delta )\) whose action is divisible by \(\hbar \). The corresponding realisation functors for \({\mathfrak {b}}_{B,\hbar }\) yield the same homomorphism \(\widehat{\rho }_{{\mathfrak {b}}}^{n}:\widehat{{\mathfrak {U}}}_{}^{n}\rightarrow \widehat{{\mathcal {U}}}_{{\mathfrak {b}}}^{n}\).

  28. Note that the realisation functors corresponding to the tuples \(({\mathfrak {b}}^\hbar _{B};V_1, \ldots ,V_n)\) and \(({\mathfrak {b}}_B;V_1,\ldots ,V_n)\), where \(V_1,\ldots ,V_n\in \textsf {DY} _{{\mathfrak {b}}^\hbar _B}^{\scriptscriptstyle {\text {adm}}}\cong \textsf {DY} _{{\mathfrak {b}}_B}^{\hbar }\) do not lead to the same homomorphism \({\mathfrak {U}}_{}^{n}\rightarrow \widehat{{\mathcal {U}}}_{{\mathfrak {b}}}^{n}\) because \({\mathfrak {b}}^\hbar _{B}\) is not isomorphic to \({\mathfrak {b}}_B\llbracket \hbar \rrbracket \) as Lie bialgebras.

  29. In [4] we only consider \({{{\mathsf {a}} }}_{}^{}\)-strict braided pre-Coxeter structures and for simplicity refer to them as braided pre-Coxeter structures. Note also that such a structure is essentially a quasi-Coxeter quasitriangular quasi-Hopf algebra structure on the diagrammatic algebra \(\widehat{{\mathfrak {U}}}_{}^{\bullet }\), as defined in [37].

  30. Note that \(\underline{{\mathsf {LBA}} }\) (resp. \(\widehat{{\mathfrak {U}}}_{{{\mathsf {LBA}} }}^{\bullet }\)) coincides with the \(\textsf {PROP} \) (resp. universal algebra) \(\underline{{\mathsf {LBA}} }_D\) (resp. \(\widehat{{\mathfrak {U}}}_{D}^{\bullet }\)) for a diagram D consisting of a single vertex.

  31. The order of the factors is irrelevant, since the images of \(\widehat{{\mathfrak {U}}}_{{\mathop {\circ }\limits ^{1}}}^{n}\) and \(\widehat{{\mathfrak {U}}}_{{\mathop {\circ }\limits ^{2}}}^{n}\) commute in \(\widehat{{\mathfrak {U}}}_{{\mathop {\circ }\limits ^{1}}\;{\mathop {\circ }\limits ^{2}}}^{n}=\widehat{{\mathfrak {U}}}_{{{{\mathsf {o}} }}}^{n}\) by Proposition 8.5.

  32. To alleviate the notation, tensor structures are suppressed from the diagram (10.3).

  33. In [24], V is additionally required to be of dimension \(2 |{\mathbf {I}}|-{{\,\mathrm{rank}\,}}({\textsf {A} })\).

  34. If \({{\mathsf {A}} }\) is a symmetrisable generalised Cartan matrix (i.e., \(a_{ii}=2\), \(a_{ij}\in {\mathbb {Z}}_{\leqslant 0}\), \(i\ne j\), and \(a_{ij}=0\) implies \(a_{ji}=0\)), the ideal \(\widetilde{I}\) is generated by the Serre relations \({{\mathsf {ad}} }(e_i)^{1-a_{ij}}(e_j)=0={{\mathsf {ad}} }(f_i)^{1-a_{ij}} (f_j)\) for any \(i\ne j\) [20]. Note that our terminology differs slightly from the one given in [24] where \({\mathfrak {g}}({\textsf {A} })\) is called a Kac–Moody algebra only if \({\textsf {A} }\) is a generalised Cartan matrix.

  35. The (co)action of \(\overline{{\mathfrak {h}}}\) is defined by restricting that of \(\overline{{\mathfrak {b}}}_-\) as in 5.12, since the inclusion \(i_0:\overline{{\mathfrak {h}}}\rightarrow \overline{{\mathfrak {b}}}_-\) is a split embedding with left inverse \(p_0\): \(\rho _V=\pi _V\circ i_0\otimes {{\,\mathrm{id}\,}}_V\), \(\rho ^*_V=p_ 0\otimes {{\,\mathrm{id}\,}}_V\circ \pi ^*_V\).

  36. Note that in order to have an action of the quantum Weyl group operators \(S_i^\hbar \), which do not commute with the action of \({\mathfrak {h}}\), the diagrammatic categories \(({\mathbb {O}}_{{\mathfrak {g}}}^{\Phi ,{\scriptscriptstyle {\text {int}}}})_\emptyset \) and \(({\mathbb {O}}_{U_{\hbar }{\mathfrak {g}}}^{{\scriptscriptstyle {\text {int}}}})_\emptyset \) have to be taken to be \({{\,\mathrm{Vect}\,}}_{{{{{\mathsf {k}} }}}{\llbracket \hbar \rrbracket }}\), rather than category \({\mathcal {O}}\) for \({\mathfrak {l}}_\emptyset ={\mathfrak {h}}\). Note also that the example in Proposition 12.3 shows that the minimal realisation of Kac–Moody algebras does not lead to a diagrammatic structure, even if the orthogonality requirement is omitted. It is therefore not possible in general to formulate an analogue of Theorem 13.9 involving minimal realisations, rather than Levi subalgebras.

  37. The crossings

    figure r

    represent the identity on \(H_B\).

References

  1. Appel, A.: Monodromy theorems in the affine setting. Thesis (Ph.D.). Northeastern University. ProQuest LLC, Ann Arbor, MI (2013)

  2. Appel, A., Toledano Laredo, V.: Quasi-Coxeter categories and a relative Etingof–Kazhdan quantisation functor, arXiv:1212.6720, p. 63 (2012)

  3. Appel, A., Toledano Laredo, V.: A 2-categorical extension of Etingof–Kazhdan quantisation. Selecta Math. (N.S.) 24, 3529–3617 (2018)

    Article  MathSciNet  Google Scholar 

  4. Appel, A., Toledano Laredo, V.: Uniqueness of Coxeter structures on Kac–Moody algebras. Adv. Math. 347, 1–104 (2019)

    Article  MathSciNet  Google Scholar 

  5. Appel, A., Toledano Laredo, V.: Monodromy of the Casimir connection of a symmetrisable Kac–Moody algebra. arXiv:1512.03041, p. 48 (2015)

  6. Bénabou, J.: Introduction to Bicategories. Reports of the Midwest Category Seminar. Springer, Berlin (1967)

    Book  Google Scholar 

  7. Bezrukavnikov, R., Etingof, P.: Parabolic induction and restriction functors for rational Cherednik algebras. Selecta Math. (N.S.) 14, 397–425 (2009)

    Article  MathSciNet  Google Scholar 

  8. Chari, V., Pressley, A.: A Guide to Quantum Groups. Cambridge University Press, Cambridge (1994)

    MATH  Google Scholar 

  9. De Concini, C., Procesi, C.: Hyperplane arrangements and holonomy equations. Selecta Math. (N.S.) 1, 495–535 (1995)

    Article  MathSciNet  Google Scholar 

  10. Deligne, P.: Une définition de catégorie tréssée (1989) (unpublished note)

  11. Drinfeld, V.G.: Quantum groups. Proceedings of the International Congress of Mathematicians, Berkeley, CA (1986), pp. 798–820, Amer Math Soc (1987)

  12. Enriquez, B., Etingof, P.: On the invertibility of quantization functors. J. Algebra 289, 321–345 (2005)

    Article  MathSciNet  Google Scholar 

  13. Enriquez, B., Geer, N.: Compatibility of quantization functors of Lie bialgebras with duality and doubling operations. Selecta Math. (N.S.) 15, 1–59 (2009)

    Article  MathSciNet  Google Scholar 

  14. Ehresmann, C.: Catégories et Structures. Dunod, Paris (1965)

    MATH  Google Scholar 

  15. Etingof, P., Kazhdan, D.: Quantization of Lie bialgebras, I. Selecta Math. (N.S.) 2, 1–41 (1996)

    Article  MathSciNet  Google Scholar 

  16. Etingof, P., Kazhdan, D.: Quantization of Lie bialgebras, II. Selecta Math. (N.S.) 4, 213–231 (1998)

    Article  MathSciNet  Google Scholar 

  17. Etingof, P., Kazhdan, D.: Quantization of Lie bialgebras. VI. Quantization of generalized Kac–Moody algebras. Transform. Groups 13, 527–539 (2008)

    Article  MathSciNet  Google Scholar 

  18. Feigin, B., Zelevinsky, A.: Representations of contragradient Lie algebras and the Kac–Macdonald identities. Representations of Lie groups and Lie algebras, Budapest (1971), pp. 25–77. Akad. Kiado, Budapest (1985)

  19. Finkelberg, M., Schechtman, V.: Microlocal approach to Lusztig’s symmetries. arXiv:1401.5885, p. 20 (2014)

  20. Gabber, O., Kac, V.G.: On defining relations of certain infinite-dimensional Lie algebras. Bull. Am. Math. Soc. (N.S.) 5, 185–189 (1981)

    Article  MathSciNet  Google Scholar 

  21. Gavarini, F.: The quantum duality principle. Ann. Inst. Fourier (Grenoble) 52, 809–834 (2002)

    Article  MathSciNet  Google Scholar 

  22. Jimbo, M.: A \(q\)-analog of \(U(\mathfrak{gl}(N +1))\), Hecke algebra, and the Yang–Baxter equation. Lett. Math. Phys. 11, 247–252 (1986)

    Article  MathSciNet  Google Scholar 

  23. Joyal, A., Street, R.: The geometry of tensor calculus. I. Adv. Math. 88(1), 55–112 (1991)

    Article  MathSciNet  Google Scholar 

  24. Kac, V.G.: Infinite-Dimensional Lie Algebras, 3rd edn. Cambridge University Press, Cambridge (1991)

    Google Scholar 

  25. Lack, S.: A 2–categories companion. Towards Higher Categories, pp. 105–191, IMA, vol. 152. Math. Appl. Springer (2010)

  26. Lauda, A.D.: A categorification of quantum \({\rm sl}(2)\). Adv. Math. 225(6), 3327–3424 (2010)

    Article  MathSciNet  Google Scholar 

  27. Lawvere, F.W.: Functorial semantics of algebraic theories. Proc. Nat. Acad. Sci. USA 50, 869–872 (1963)

    Article  MathSciNet  Google Scholar 

  28. Lusztig, G.: Introduction to Quantum Groups. Birkhäuser, Boston (1993)

    MATH  Google Scholar 

  29. MacLane, S.: Categorical algebra. Bull. Am. Math. Soc. 71, 40–106 (1965)

    Article  MathSciNet  Google Scholar 

  30. Majid, S.: Foundations of Quantum Group Theory. Cambridge University Press, Cambridge (1995)

    Book  Google Scholar 

  31. Radford, D.: The structure of Hopf algebras with a projection. J. Algebra 92, 322–347 (1985)

    Article  MathSciNet  Google Scholar 

  32. Shan, P.: Crystals of Fock spaces and cyclotomic rational double affine Hecke algebras. Ann. Sci. Éc. Norm. Supér. (4) 44, 147–182 (2011)

    Article  MathSciNet  Google Scholar 

  33. Snyder, N., Tingley, P.: The half-twist for \(U_{q}\mathfrak{g}\) representations. Algebra Number Theory 3, 809–834 (2009)

    Article  MathSciNet  Google Scholar 

  34. Tits, J.: Normalisateurs de tores I. Groupes de Coxeter étendus. J. Algebra 4, 96–116 (1966)

    Article  MathSciNet  Google Scholar 

  35. Toledano Laredo, V.: A Kohno-Drinfeld theorem for quantum Weyl groups. Duke Math. J. 112, 421–451 (2002)

    Article  MathSciNet  Google Scholar 

  36. Toledano Laredo, V.: Cohomological construction of relative twists. Adv. Math. 210, 375–403 (2007)

    Article  MathSciNet  Google Scholar 

  37. Toledano Laredo, V.: Quasi-Coxeter algebras, Dynkin diagram cohomology and quantum Weyl groups. Math. Res. Pap. IMRP, Art. ID rpn009 (2008)

  38. Toledano Laredo, V.: Quasi-Coxeter quasitriangular quasibialgebras and the Casimir connection. arXiv:1601.04076, p. 55 (2016)

  39. Yetter, D.N.: Quantum groups and representations of monoidal categories. Math. Proc. Camb. Philos. Soc. 108, 261–290 (1990)

    Article  MathSciNet  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. School of Mathematics, University of Edinburgh, James Clerk Maxwell Building, Peter Guthrie Tait Road, Edinburgh, EH9 3FD, UK

    Andrea Appel

  2. Department of Mathematics, Northeastern University, 360 Huntington Avenue, Boston, MA, 02115, USA

    Valerio Toledano Laredo

Authors
  1. Andrea Appel
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Valerio Toledano Laredo
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Valerio Toledano Laredo.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Andrea Appel was supported in part through the ERC Grant 637618 and the NSF Grant DMS-1255334, Valerio Toledano Laredo through the NSF Grants DMS-1505305 and DMS-1802412.

Appendix A. Graphical calculus for Coxeter objects

Appendix A. Graphical calculus for Coxeter objects

We describe below the axioms of Coxeter objects in a 2-category \({\mathfrak {X}}\) in terms of graphical calculus.

1.1 Graphical notation

In the following, we use the graphical notation of string diagrams to describe relations between 2-morphisms in a 2-category \({\mathfrak {X}}\) (e.g., [23, 26]). We represent objects, 1-morphisms, and 2-morphisms with two dimensional, one dimensional and zero dimensional cells, respectively. Let \(X,Y\in {\mathfrak {X}}\), \(F,G\in {\mathfrak {X}}^{(1)}(X,Y)\) and \(\alpha \in {\mathfrak {X}}^{(2)}(F,G)\). Then, we represent \(\alpha \) as

figure a

where the diagram on the right-hand side is read from bottom to top, and from right to left. Similarly, a 2-morphism \(\alpha :F\circ G\rightarrow H\) will be represented as follows:

figure b

and more generally we represent \(\alpha : F_n\circ \dots \circ F_1\Rightarrow G_m\circ \dots \circ G_1\) as

figure c

When no confusion is possible, we omit the labels and identify the 1-morphisms with the color of the string, and the 2-morphism with the underlying diagram.

1.2 Coxeter objects (cf. 3.10)

A Coxeter object in a 2-category \({\mathfrak {X}}\) is the datum of

  • for any \(B\subseteq D\), an object \(X_{B}\)

  • for any \({{\mathcal {F}}}\in {{\mathsf {Mns}} }(B,B')\), a 1-morphism \(F_{{{\mathcal {F}}}}: X_{B}\rightarrow X_{B'}\) which we represent as the identity 2-morphisms \({{\,\mathrm{id}\,}}_{F_{{{\mathcal {F}}}}}\)

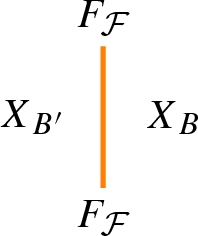
    figure d

  • for any \({{\mathcal {F}}}'\in {{\mathsf {Mns}} }(B,B'), {{\mathcal {F}}}''\in {{\mathsf {Mns}} }(B',B'')\) and \({{\mathcal {F}}}={{\mathcal {F}}}'\cup {{\mathcal {F}}}''\), a 2-morphism

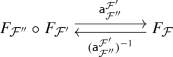
    represented as

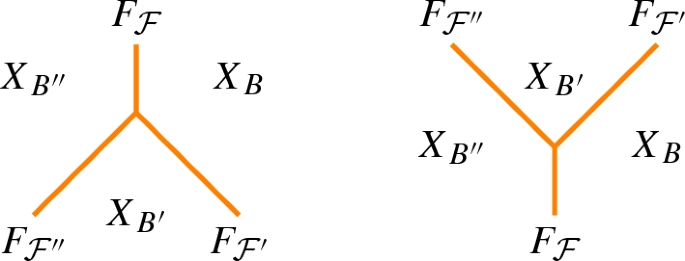
    figure e

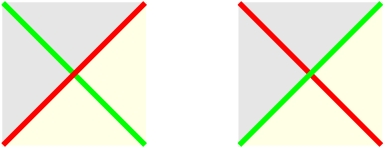
  • for any \({{\mathcal {F}}},{{\mathcal {G}}}\in {{\mathsf {Mns}} }(B,B')\) a pair of 2-morphisms

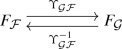
    represented as fake crossings

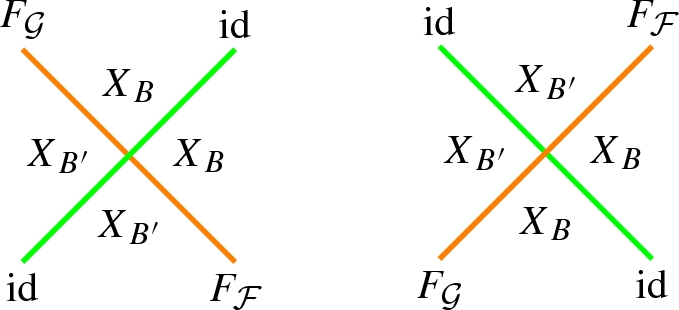
    figure f

  • for any \(i\in D\), an invertible 1-morphism \(S_i:F_{\{\emptyset ,i\}}\rightarrow F_{\{\emptyset ,i\}}\)

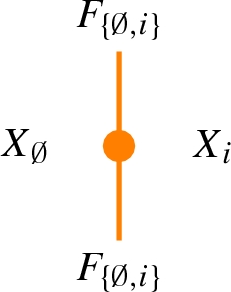
    figure g

satisfying the following relations. To alleviate the notation, the labels of objects and 1-morphisms are omitted unless necessary.

  • Invertibility

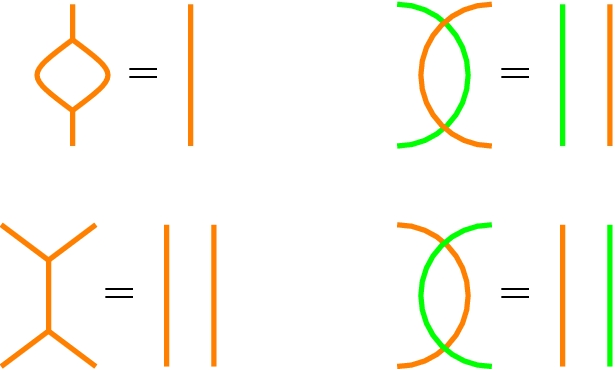
    figure h

  • Associativity

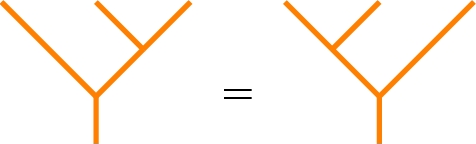
    figure i

  • Vertical and horizontal factorisation

    figure j

  • Braid relations For any \(i,j\in B\subseteq D\), \({{\mathcal {F}}},{{\mathcal {G}}},{{\mathcal {H}}}\in {{\mathsf {Mns}} }(B)\) such that \(i\ne j\), \(m_{ij}<\infty \), \(\{i\}\in {{\mathcal {H}}}\), \(\{j\}\in {{\mathcal {G}}}\),

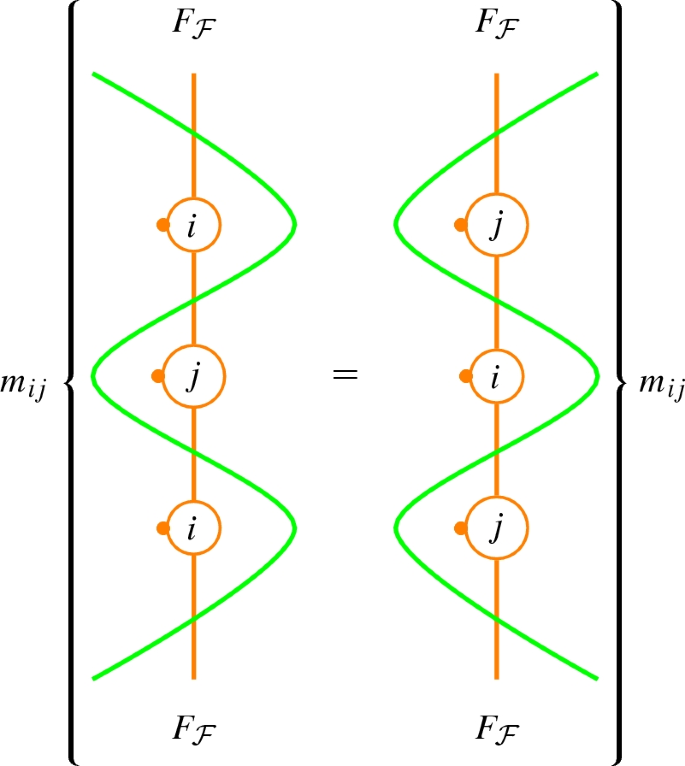
    figure k

1.3 1-morphisms

Let \(X,X'\) be Coxeter objects in \({\mathfrak {X}}\). We distinguish between them by assigning a different color to their 2–cells (specifically, yellow for X, gray for \(X'\)). We represent their defining data as

figure l
figure m

Then a 1-morphisms of Coxeter objects \(H:X\Rightarrow X'\) is the datum of

  • for any \(B\subseteq D\), a 1-morphism \(H_{B}:X_{B}\rightarrow X'_{B}\)

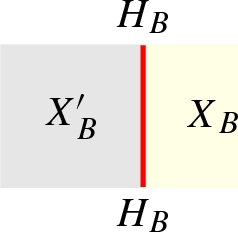
    figure n

  • for any \({{\mathcal {F}}}\in {{\mathsf {Mns}} }(B,B')\) a pair of 2-morphisms

    represented as

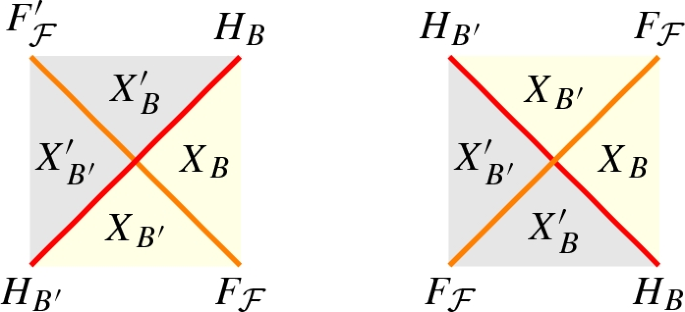
    figure o

satisfying the following relations

  • Invertibility

    figure p

  • Vertical factorization

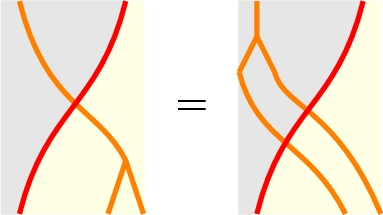
    figure q

  • Preserving associators Footnote 37

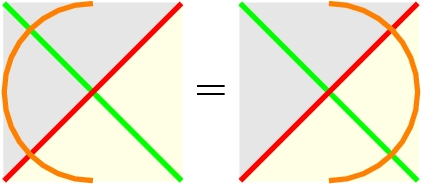
    figure s

  • Preserving local monodromies.

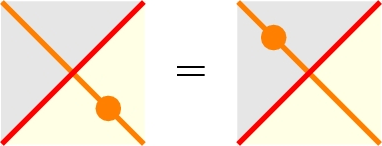
    figure t

1.4 2-morphisms

Let \(H,H':X\rightarrow X'\) be two 1-morphisms,

figure u
figure v

A 2-morphism \(u:H\Rightarrow H'\) is the datum, for any \(B\subseteq D\), of an invertible 2-morphism \(u_{B}:H_{B}\Rightarrow H'_{B}\)

figure w

satisfying

figure x

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Appel, A., Toledano Laredo, V. Coxeter categories and quantum groups. Sel. Math. New Ser. 25, 44 (2019). https://doi.org/10.1007/s00029-019-0490-y

Download citation

  • Published:

  • DOI: https://doi.org/10.1007/s00029-019-0490-y

Keywords

Mathematics Subject Classification

Search

Navigation