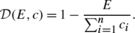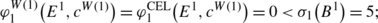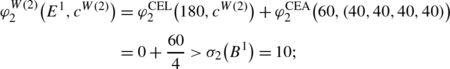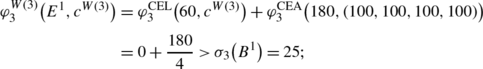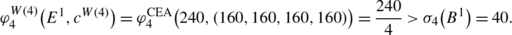Abstract
As it is known, there is no rule satisfying additivity in the complete domain of bankruptcy problems. This paper proposes a notion of partial additivity in this context, to be called μ-additivity. We find out that this property, together with two quite compelling axioms, equal treatment of equals and continuity, identify the minimal overlap rule, introduced by O’Neill (Math. Soc. Sci. 2:345–371, 1982).
Similar content being viewed by others
Notes
The reader can find an overview of the main bankruptcy rules in Thomson (2003).
Section 3 discusses the rationale of such a fact from both economic and mathematical viewpoints.
Jiménez-Gómez and Marco-Gil (2008) summarize the analysis of the concept of guarantee in the bankruptcy literature and propose a new method to establish lower bounds on awards.
A permutation is a bijection applying \(\mathcal{N}\) to itself. In this paper, and abusing notation, π(c) will denote the claim vector obtained by applying permutation π to its components, i.e. the ith component of π(c) is c j whenever j=π(i). Similar reasoning considerations apply for π[φ(E,c)].
We are implicitly assuming that the set of creditors, \(\mathcal{N}\), is the same for both firms and that there are no intra-group debts, i.e. F is not G’s creditor or debtor.
The notion of bankruptcy degree is introduced by Alcalde et al. (2012) as follows. Given a bankruptcy problem (E,c) with c≠0, we can define its bankruptcy degree as the expression
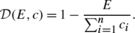
Throughout this proof, and for notational convenience, we will consider \(c_{0} = c_{0}^{E} = 0\).
References
Alcalde J, Marco MC, Silva JA (2008) The minimal overlap rule revisited. Soc Choice Welf 31:109–128
Alcalde J, Marco-Gil MC, Silva JA (2012) Tax burden degree as a tool to design tax systems. QM&ET working paper no 12-11
Aumann RJ, Maschler M (1985) Game theoretic analysis of a bankruptcy problem from the Talmud. J Econ Theory 36:195–213
Bergantiños G, Méndez-Naya L (2001) Additivity in bankruptcy problems and in allocation problems. Span Econ Rev 3:223–229
Billingsley RS, Johnson DJ, Marquette RP (1988) Bankruptcy avoidance as a merger incentive. Manag Finance 14:25–33
Chun Y, Thomson W (2005) Convergence under replication of rules to adjudicate conflicting claims. Games Econ Behav 50:129–142
Curiel IJ, Maschler M, Tijs SH (1987) Bankruptcy games. Z Oper-Res 31:A143–A159
Jiménez-Gómez JM, Marco-Gil MC (2008) A new approach for bounding awards in bankruptcy problems. IVIE WP AD 2008-07
Moreno-Ternero JD, Villar A (2004) The Talmud rule and the securement of agents’ awards. Math Soc Sci 47:245–257
Moretti S, Patrone F (2008) Transversality of the Shapley value. Top 16:1–41
Moulin H (2002) Axiomatic cost and surplus-sharing. In: Arrow K, Sen A, Suzumura K (eds) The handbook of social choice and welfare, vol 1. Elsevier, Amsterdam, pp 289–357
O’Neill B (1982) A problem of rights arbitration from the Talmud. Math Soc Sci 2:345–371
Peters H (1986) Simultaneity of issues and additivity in bargaining. Econometrica 54:153–169
Shapley LS (1953) A value for n-person games. In: Kuhn H, Tucker A (eds) Contributions to the theory of games, vol. II. Annals of mathematics studies, vol 28. Princeton University Press, Princeton, pp 307–317
Shrieves RE, Stevens DL (1979) Bankruptcy avoidance as a motive for merger. J Financ Quant Anal 14:501–515
Thomson W (2003) Axiomatic and game-theoretic analysis of bankruptcy and taxation problems: a survey. Math Soc Sci 45:249–297
Weitzel U, McCarthy KJ (2011) Theory and evidence on mergers and acquisitions by small and medium enterprises. Int J Entrepreneurship Innov Manag 14:248–275
Young HP (1988) Distributive justice in taxation problems. J Econ Theory 38:78–100
Acknowledgements
We are grateful to Hervé Moulin, William Thomson, the anonymous referees and the Editor-in-Chief, Justo Puerto, for their helpful comments. This work is partially supported by the Instituto Valenciano de Investigaciones Económicas and the Spanish Ministerio de Educación y Ciencia, project SEJ2007-62656 (Alcalde) and the Consellería de la Generalitat Valenciana, project PROMETEO/2009/068 (Silva-Reus).
Author information
Authors and Affiliations
Corresponding author
Appendices
Appendix A: General remark
We note how to check if a creditor \(i\in \mathcal{N}\) is privileged (Definition 6) when facing a problem B=(E,c). This reasoning will be used in Examples 2 and 3 as well as in Appendix B.
Let us introduce the constrained equal awards rule, which will be useful in the sequel. This rule is the function \(\varphi^{\mathrm{CEA}} \colon \mathcal{B}\rightarrow \mathbb{R}_{+}^{n}\) that associates, to each problem \((E, c ) \in \mathcal{B}\) and each creditor \(i \in \mathcal{N}\), the amount

where α is such that \(\sum_{i\in \mathcal{N}}\min \{c_{i}, \alpha \} = E\).
We define, for each creditor \(i\in \mathcal{N}\), the bankruptcy solution \(\varphi^{W (i )}: \mathcal{B} \rightarrow \mathbb{R}_{+}^{n}\) that associates, to each \((E, c ) \in \mathcal{B}\) and each creditor \(j \in \mathcal{N}\), the amount

where

This rule will be useful to determine the worst situation that agent i might face when distributing the estate. In what follows, we describe which situation will be understood as the worst one for agent i. Let us remember that we assume that creditors’ claims are increasingly ordered.
First, let us note that for each \((E, c ) \in \mathcal{B}\), and each \(i \in \mathcal{N}\),

This follows from the way in which φ W(i) is described. Now, for each problem \((E, c ) \in \mathcal{B}\) and creditor i, let us denote

Finally, let us associate, to each \((E, c ) \in \mathcal{B}\) and \(i \in \mathcal{N}\), vector c W(i) such that for each \(j \in \mathcal{N}\),

This implies that

From the previous facts we have that, for each \((E, c ) \in \mathcal{B}\) and \(i \in \mathcal{N}\), φ W(i)(E,c W(i)) will provide the smallest part of the estate for agent i among all the minimally fair rules and all the configurations of claims in C′(i). We call the pair (φ W(i),c W(i)) the worst situation for agent i, since it corresponds to the least favorable situation for such a creditor with regard to both the rest of agents’ claims demanding less than she does and the rule that prevails. Therefore, we can establish:
Remark 1
To prove that creditor i is privileged it will be enough to check that some of the conditions, (a) or (b), in Definition 6 is satisfied in the worst situation for such a creditor.
To illustrate the notion of privileged creditor we present, taking into account Remark 1, the partition of the set of creditors according to such a qualification for two different problems. In the first one, all the claims are lower than the estate, whereas in the second problem, there is some creditor who claims more than the debtor’s assets.
Example 2
Let B 1=(E 1,c 1)=(240,(20,40,100,160)). By definition, the security levels vector is

and the claims vectors c W(i) are

Therefore,
-
(1)
creditor 1 is non-privileged since
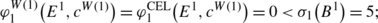
-
(2)
creditor 2 is privileged since
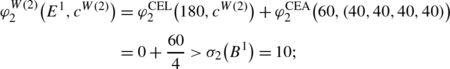
-
(3)
creditor 3 is also privileged since
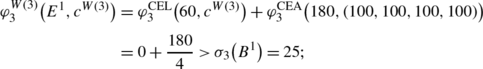
-
(4)
finally, creditor 4 is privileged since
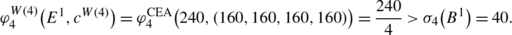
Example 3
Let B 2=(E 2,c 2)=(140,(60,60,120,180)). By definition, the security levels vector is

and the claims vectors c W(i) are

Therefore, we have that
-
(1)
creditors 1 and 2 are non-privileged since for i=1,2,
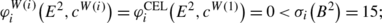
-
(2)
creditor 3 is also non-privileged since
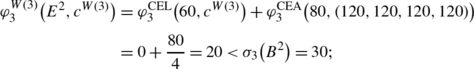
-
(3)
finally, creditor 4 is privileged since

Appendix B: Proof of Proposition 1
Firstly we show that Definition 6 implies conditions (a) and (b) of Proposition 1.
By Remark 1 we have that it is sufficient to check that the consequence holds for φ W(i)(E,c W(i)).
Let (E,c) be a problem, and \(i \in \mathcal{N}\) be a creditor. If i is privileged in (E,c) then E>∑ j>i (c j −c i ); otherwise, \(\varphi^{W (i )}_{i} (E, c^{W (i )} ) = 0\) and neither (a) nor (b) in Definition 6 would be met. Thus, for each privileged agent i,

Let \(i \in \mathcal{N}\) be a privileged creditor in \((E, c ) \in \mathcal{B}\). We have one of the two following cases.
Case 1
\(\varphi^{W (i )}_{i} (E, c^{W (i )} ) > \sigma_{i} (E, c )\).
By Eq. (4), we have that

which implies that

Let us define

and let \(S \subset \mathcal{N}\) be the subset of creditors, whose cardinality is denoted by s, such that k∈S if and only if k≠i and c k ≥c i , and let \(\beta = \frac{1}{s}\min \{c_{i}, \alpha \}\). Now we define \(\tau \in \mathbb{R}_{+}^{n}\) such that

Thus

is a problem in \(\mathcal{B}\) and for all \(j \in \mathcal{N}\), j≠i, \(\min \{c_{i}^{\prime}, E^{\prime} \} > \min \{c_{j}^{\prime}, E^{\prime} \}\).
Case 2
\(\varphi_{i}^{W (i )} (E, c^{W (i )} ) = \sigma_{i} (E, c )\), and σ i (E,c)>σ j (E,c) for all \(j \in \mathcal{N}\), j≠i.
By Definition 5, the previous inequality is equivalent to \(c_{i}^{E} > c_{j}^{E}\) for all \(j \in \mathcal{N}\), j≠i. Therefore, for \(\tau \in \mathbb{R}_{+}^{n}\) such that τ i =0 for all \(i \in \mathcal{N}\), conditions (a) and (b) of Proposition 1 are satisfied.
Secondly we show that conditions (a) and (b) of Proposition 1 imply Definition 6.
Let us suppose that there is \(\tau \in \mathbb{R}_{+}^{n}\) such that
-
(a)
\(B^{\prime} = (E^{\prime}, c^{\prime} ) = (E - \sum_{h = 1}^{n}\tau_{h}, c - \tau ) \in \mathcal{B}\), and
-
(b)
\(\min \{c_{i}^{\prime}, E^{\prime} \} > \min \{c_{j}^{\prime}, E^{\prime} \}\) for all \(j \in \mathcal{N}\), j≠i.
This implies that for all \(j \in \mathcal{N}\), j≠i, either \(E^{\prime} \geq c_{i}^{\prime} > c_{j}^{\prime}\) or \(c_{i}^{\prime} > E^{\prime} > c_{j}^{\prime}\). Therefore, there is τ such that in the residual problem, (E′,c′), \(c_{i}^{\prime}>c_{j}^{\prime}\) for all \(j \in \mathcal{N}\). Let us look for the minimum partial reimbursement of debts, τ ∗, for which

Let us consider the following two cases.
Case 1
c i =c n >c n−1.
Then τ ∗=0 and, by Remark 1, φ W(i)=φ CEA. If E>c i ,

and condition (a) in Definition 6 is satisfied. Otherwise, i.e. if c i >E>c n−1,

which implies condition (b) in Definition 6.
Case 2
There is \(j \in \mathcal{N}\), j≠i such that c j ≥c i .
Then it is possible to partially reimburse debts in such a way that: (i) no creditor has a new claim greater than creditor i does, and (ii) what is left of estate is greater than c i . Otherwise conditions (a) and (b) of Proposition 1 would not be fulfilled. Therefore, the previous statement is equivalent to

where \(\tau^{\ast} \in \mathbb{R}_{+}^{n}\) is such that \(\tau_{h}^{\ast} = \max \{c_{h} - c_{i}, 0 \}\) for all \(h \in \mathcal{N}\).
From the previous inequality,

Now, taking into account Remark 1,

which implies condition (a) in Definition 6.
Appendix C: Proof of Proposition 2
Let φ be a rule satisfying μ-additivity and continuity. Let (E,c) be a problem where \(0 < E <c_{n} = \max_{i \in \mathcal{N}} \{c_{i} \}\); and let \(S\subset \mathcal{N}\) be the subset of agents claiming zero. Let us consider the following two cases.
Case 1
E≤c n−1.
By μ-additivity,

for all r∈ℕ such that

By continuity,

Case 2
E>c n−1.
By μ-additivity,

for all r∈ℕ such that

Therefore, by continuity,

Appendix D: Proof of Theorem 1
Firstly, it is straightforward to verify that the minimal overlap rule satisfies equal treatment of equals, continuity and μ-additivity.
Now, let φ be a rule satisfying these axioms. Given a problem \((E, c ) \in \mathcal{B}\), let us consider the following two cases.
Case 1
E≤c n .
By Proposition 2,

Let us denote \(P^{1} = c_{1}^{E}\); \(P^{i} = c_{i}^{E} - c_{i - 1}^{E}\) for 1<i≤n and \(c^{P^{h}} = ( (0 )_{j < h}, (P^{h} )_{j \geq h} )\), for each \(h \in \mathcal{N}\).
Now, let us consider the following two subcases.
Subcase (a)
\(c^{E}_{n} = c^{E}_{n - 1}\).
μ-additivity implies that

By equal treatment of equals and Proposition 2,

i.e.

with c 0=0.Footnote 8 Thus, for each agent h,

Since, for any j>h we have that \(c_{h}^{P^{j}}=0\),

Subcase (b)
\(c^{E}_{n} \neq c^{E}_{n-1}\).
Let q(j) denote the cardinality of the set {i≤j:P i≠0}. μ-Additivity implies that

where r∈ℕ is such that

Now, by continuity,

By using the reasoning of the Subcase (a) above, we obtain that for each agent h,

Case 2
E>c n .
In such a case, there is a unique t, 0≤t<c n , such that

Let k be the unique agent such that c k −t>0, and c k−1−t≤0. Note that this implies that each agent j, with j≥k, is privileged in (E,c). Then, for each r∈ℕ such that

by μ-additivity,

by continuity,

Observe that the problem \(( t, ( \min \{ c_{i},t \} )_{i\in \mathcal{N}} ) \) was analyzed in Case 1 above. Therefore, for each agent h,
Moreover, note that for agent h,
Since by construction,
we conclude that for each agent h,
Finally, by combining Eqs. (5), (6), and (7), we have that, for each agent h,
Rights and permissions
About this article
Cite this article
Alcalde, J., del Carmen Marco-Gil, M. & Silva-Reus, J.A. The minimal overlap rule: restrictions on mergers for creditors’ consensus. TOP 22, 363–383 (2014). https://doi.org/10.1007/s11750-012-0262-8
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11750-012-0262-8