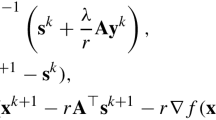Abstract
We consider the semi-infinite optimization problem:
where f,g are polynomials and X⊂ℝn as well as Y x ⊂ℝp, x∈X, are compact basic semi-algebraic sets. To approximate f ∗ we proceed in two steps. First, we use the “joint+marginal” approach of Lasserre (SIAM J. Optim. 20:1995–2022, 2010) to approximate from above the function x↦Φ(x)=sup {g(x,y):y∈Y x } by a polynomial Φ d ≥Φ, of degree at most 2d, with the strong property that Φ d converges to Φ for the L 1-norm, as d→∞ (and in particular, almost uniformly for some subsequence (d ℓ ), ℓ∈ℕ). Therefore, to approximate f ∗ one may wish to solve the polynomial optimization problem \(f^{0}_{d}=\min_{\mathbf{x}\in\mathbf{X}} \{f(\mathbf{x}): \varPhi _{d}(\mathbf{x})\leq0\}\) via a (by now standard) hierarchy of semidefinite relaxations, and for increasing values of d. In practice d is fixed, small, and one relaxes the constraint Φ d ≤0 to Φ d (x)≤ε with ε>0, allowing us to change ε dynamically. As d increases, the limit of the optimal value \(f^{\epsilon}_{d}\) is bounded above by f ∗+ε.
Similar content being viewed by others
References
Ash RB (1972) Real analysis and probability. Academic Press, Boston
Bhattacharjee B, Green WH Jr, Barton PI (2005) Interval methods for semi-infinite programs. Comput Optim Appl 30:63–93
Calafiore GC, Dabbene F (2007) A probabilistic analytic center cutting plane method for feasibility of uncertain LMIs. Automatica 43:2022–2033
Henrion D, Lasserre JB, Lofberg J (2009) GloptiPoly 3: moments, optimization and semidefinite programming. Optim Methods Softw 24:761–779
Lasserre JB (2001) Global optimization with polynomials and the problem of moments. SIAM J Optim 11:796–817
Lasserre JB (2006) Convergent SDP-relaxations in polynomial optimization with sparsity. SIAM J Optim 17:822–843
Lasserre JB (2009) Moments, positive polynomials and their applications. Imperial College Press, London
Lasserre JB (2010) A “joint+marginal” approach to parametric polynomial optimization. SIAM J Optim 20:1995–2022
Mitsos A, Lemonidis P, Cha Kun Lee, Barton PI (2008) Relaxation-based bounds for semi-infinite programs. SIAM J Optim 19:77–113
Parpas P, Rustem B (2009) An algorithm for the global optimization of a class of continuous minimax problems. J Optim Theory Appl 141:461–473
Waki H, Kim S, Kojima M, Maramatsu M (2006) Sums of squares and semidefinite programming relaxations for polynomial optimization problems with structured sparsity. SIAM J Optim 17:218–242
Author information
Authors and Affiliations
Corresponding author
Additional information
This work was performed during a visit in November 2010 at CRM (Centre de Recerca Matematica), a Mathematics center from UAB (Universidad Autonoma de Barcelona), and the author wishes to gratefully acknowledge financial support from CRM.
Rights and permissions
About this article
Cite this article
Lasserre, J.B. An algorithm for semi-infinite polynomial optimization. TOP 20, 119–129 (2012). https://doi.org/10.1007/s11750-011-0172-1
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11750-011-0172-1