On cal situar-se per mirar un quadre?

Als nostres museus no sempre és fàcil trobar el punt que ens permetrà admirar un quadre des de la perspectiva adequada, la que l’artista va definir. Les relacions entre art, geometria i percepció, que descriu l’anomenat teorema de l’observador, ajuden a resoldre el problema. És important, doncs, considerar la complexitat de la visió humana si volem gaudir al màxim de la realitat i de l’art que la representa.

Si seguim la proclama de Marcel Duchamp «és qui mira qui fa el quadre» el problema de la percepció de l’art esdevé un acte individual i subjectiu. I campi qui pugui. El que aquí ens agradaria compartir amb el lector és una pregunta ben allunyada del subjectivisme: hi ha un lloc privilegiat des d’on mirar un quadre?

Què passa si el quadre està alt o volem veure una escultura col·locada dalt d’un pedestal alt? Aquest és el problema clàssic dit de Johann Müller  i té com a solució determinar el punt on la nostra vista veu l’objecte d’art amb el millor angle visual possible. En la fotografia, escultura de Richard Serra al Museu Guggenheim de Bilbao. Foto: Miguel Lorenzo

La pregunta deixa de tenir sentit en un quadre de Miró, en una representació egípcia, en una trama de Mondrián i en la majoria de l’art abstracte. Però en totes aquelles obres en què era intenció del pintor «la representació fidel de la realitat» (existent o imaginada) la nostra qüestió és pertinent. Si mirem de molt lluny o de massa prop certament no gaudirem d’una visió òptima. Des d’on li agradaria a Piero della Francesca o a Velázquez que miréssim les seves obres? Per intentar contestar això ens veiem obligats a adoptar un discurs interdisciplinari que ens fa veure la complexitat de la percepció humana amb tot el que això implica per a la creació artística.

Complexitat de la visió

La sensació de «veure» és el resultat d’un complicat procés perceptiu. Els raigs de llum arriben a l’ull, incideixen en la còrnia, són desviats cap a l’iris, s’encaminen cap el cristal·lí, es projecten en la retina on es recullen imatges invertides; l’ull va permetent enfocar objectes situats a distàncies diverses i l’energia lluminosa reconvertida en senyals és transmesa pel nervi òptic al cervell, darrer culpable de la «visió» final.

«No hi ha “una visió” d’una realitat sinó moltes visions combinades»

Tampoc hem d’oblidar ací l’important paper que en la visió representen les capacitats musculars per a moure el cap i anar encadenant visions diferents i memoritzant imatges anteriors. No hi ha «una visió» d’una realitat, sinó moltes visions combinades (el nostre camp visual varia verticalment en uns 120º i, horitzontalment, en uns 200º, amb deformacions del 100% a 45º).

Si la perspectiva conceptual o la naïf havia iniciat els temes de la representació de la realitat en temps immemorials, la geometria clàssica dels grecs (tan ben sintetitzada en els Elements d’Euclides) no es preocupà del tema artístic del dibuix. Va ser de la mà dels pintors que va néixer la geometria de la representació i sols molts anys després aquesta geometria es va veure integrada en la matemàtica, ja sigui en la formalització teòrica de la geometria projectiva o en el vessant gràfic de la geometria descriptiva de Gaspar Monge.

Brunelleschi, Alberti, Leonardo, Piero della Francesca són noms referencials a l’hora d’establir les bases per a una teoria i una praxis de la perspectiva com a fonament de la pintura, malgrat que les seves idees sobre òptica i percepció eren més que limitades i que tot es va fer pensant en un observador «cíclop» que mira l’art amb un sol ull, no amb dos.

En la figura 1 (Alsina i Franco, 1982) podem apreciar les perspectives de tres esferes idèntiques i equidistants del punt de vista V, essent π el pla vertical de representació, d’acord amb els principis de la perspectiva clàssica. Mesurant les àrees d’aquestes el·lipses hom pot calcular paràmetres de mesura de la deformació (per exemple (1+ExExE)­–1, on E és l’excentricitat). Anàlogament, s’estudien deformacions en la representació d’altres objectes a d’altres sistemes axonomètrics.

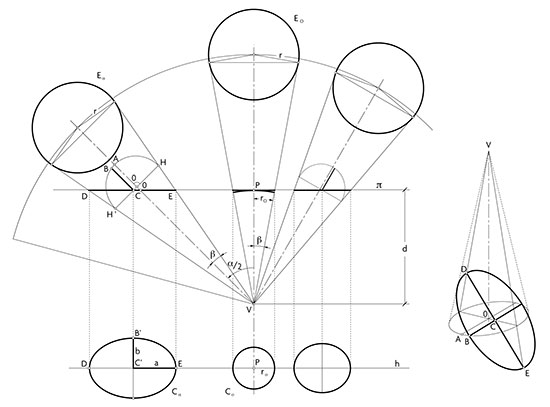
Figura 1.

No ha estat fins a èpoques molt properes que E. Panofsky, G. Haack o E. H. Gombrich han fet possible una revisió rigurosa dels ideals renaixentistes de lligar realitat i representació. Per això els hi va caldre enriquir l’anàlisi de la pintura amb aportacions de la filosofia o la psicologia.

Teorema de l’observador

A partir dels principis rigorosos de la perspectiva li­neal introduïts i descrits per Brunelleschi, l’obra pictòrica com a representació de la realitat ha d’oferir a l’ull de l’observador la mateixa visió que l’artista ha volgut materialitzar en el curs d’elaboració de la seva obra. Així, qualsevol família de rectes paral·leles a la realitat, es representarà en el quadre incidents en un punt de fuga o punt de l’infinit. Aquest punt de fuga serà necessàriament el punt del dibuix d’intersecció del segment teòric que «passant per l’ull de l’artista» és paral·lel a la família de rectes paral·leles considerades. En conseqüència, la visió ideal del quadre la tindrem si aconseguim col·locar el nostre ull en aquest punt de l’espai davant del quadre on se situà el de l’artista (punt de l’observador). Però és possible ara redescobrir quin era aquest punt? Seguint les idees de C. Zeeman veurem que això és possible. Observem en la figura 2 un cub representat amb tres punts de fuga A, B i C corresponents a les tres famílies de rectes paral·leles que determinen les arestes del cub.

«Només amb matemàtiques no es podria fer art però sense elles tampoc»

Si acostem molt el dibuix a un ull i assagem diferents punts de mira no veurem pas la figura com un cub. On caldrà col·locar l’ull per veure realment una forma cúbica? Per definició, per cada punt de fuga del quadre passen totes les rectes que en la realitat tridimensional formen una família de paral·leles d’una mateixa direcció. Si volem «veure» que AP i PB formen un angle recte (com cal en un cub) aleshores l’ull haurà d’estar en un punt de superfície de l’esfera davant del quadre i de diàmetre AB (ja que tot segment a l’espai pot ser vist amb un angle de 90º des de la superfície esfèrica de diàmetre del segment donat). Però també en el cub voldrem veure AP i PC perpendiculars i el mateix amb BP i PC. Així, doncs, convé col·locar l’ull en la intersecció de tres superfícies semiesfèriques davant del quadre i que tenen per diàmetres AB, BC, i AC respectivament. Però les primeres dues mitges superfícies esfèriques davant del quadre es tallaran en una semicircumferència, i aquesta tallarà la tercera superfície semiesfèrica en un punt. Vet aquí el que resulta curiós: el teorema de l’observador assenyala que «hi ha un únic punt davant d’un quadre fet amb un dibuix perspectiu i que té tres punts principals de fuga des d’on es pot veure el quadre perfectament».

Noteu que amb tres llapis perpendiculars entre ells també podríem orientar la nostra visió ideal. També hom pot calcular mesurant les distàncies pertinents on es troba el punt de l’observador. De fet, molts museus podrien fer el gest d’indicar aquests punts de visió òptima i no condemnar-nos a fer una recerca personal insòlita davant de les obres.

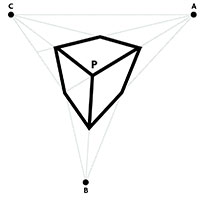
Figura 2.

Angles de visió

El teorema de l’observador ens resol el problema si realment tenim el quadre davant dels nostres ulls a la mateixa altura que el va tenir el seu creador quan el pintava. Què passa si el quadre està alt o volem veure una escultura col·locada dalt d’un pedestal alt? Aquest és el problema clàssic dit de Johann Müller (Regiomontanus) i té com a solució determinar el punt on la nostra vista veu l’objecte d’art amb el millor angle visual possible (el més gran): l’ull ha d’estar en un punt de l’arc capaç corresponent a l’objecte a contemplar, arc que a la vegada sigui tangent a la línia horitzontal corresponent al nostre ull quan es desplaça.

També en la mirada dirigida a l’escenari d’un teatre o a la pantalla d’un cinema s’hi amaguen problemes d’angle de visió. Són les anomenades corbes i superfícies isòptiques que garanteixen la visió. Ja el disseny circular del teatre grec és un exemple històric de com es resolia aquest problema. Un cop més podem refermar allò que només amb matemàtiques no es podria fer art, però sense tampoc.